Reduction of Coupling Interface Degrees of Freedom in Mixed-Interface Component Mode Synthesis
Abstract
:1. Introduction
2. A Brief Review of the Traditional MCMS
3. Normal Mode Correction for the Master Substructure
3.1. Static Condensation of the Slave Substructure
3.2. Partition of the Master Substructure
3.3. Mode Synthesis in the Revised MCMS Method [40]
4. Reduction of the Coupling Interface DOFs
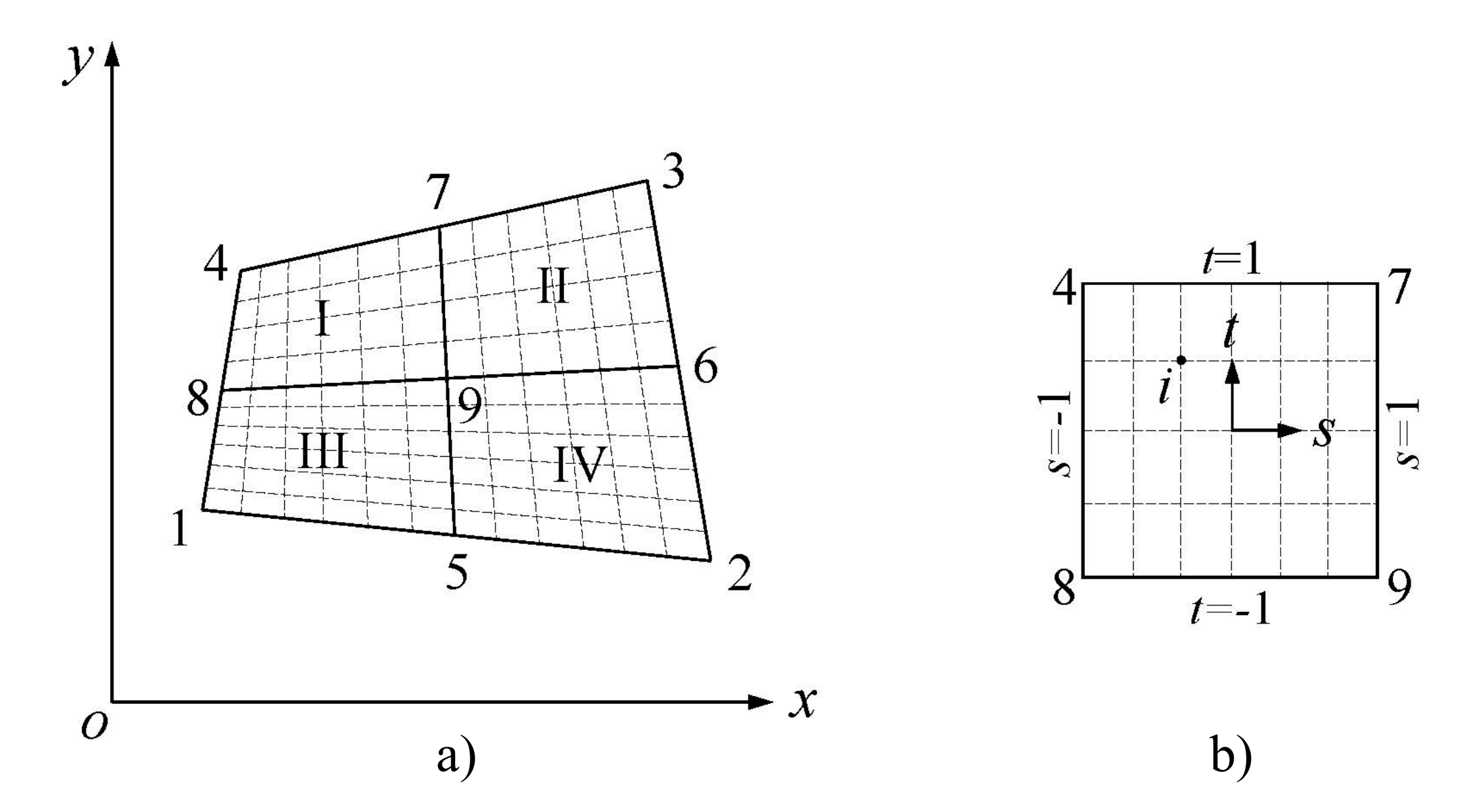
4.1. Formulation
4.2. Mode Synthesis with Reduced Coupling Interface DOFs
5. Numerical Examples
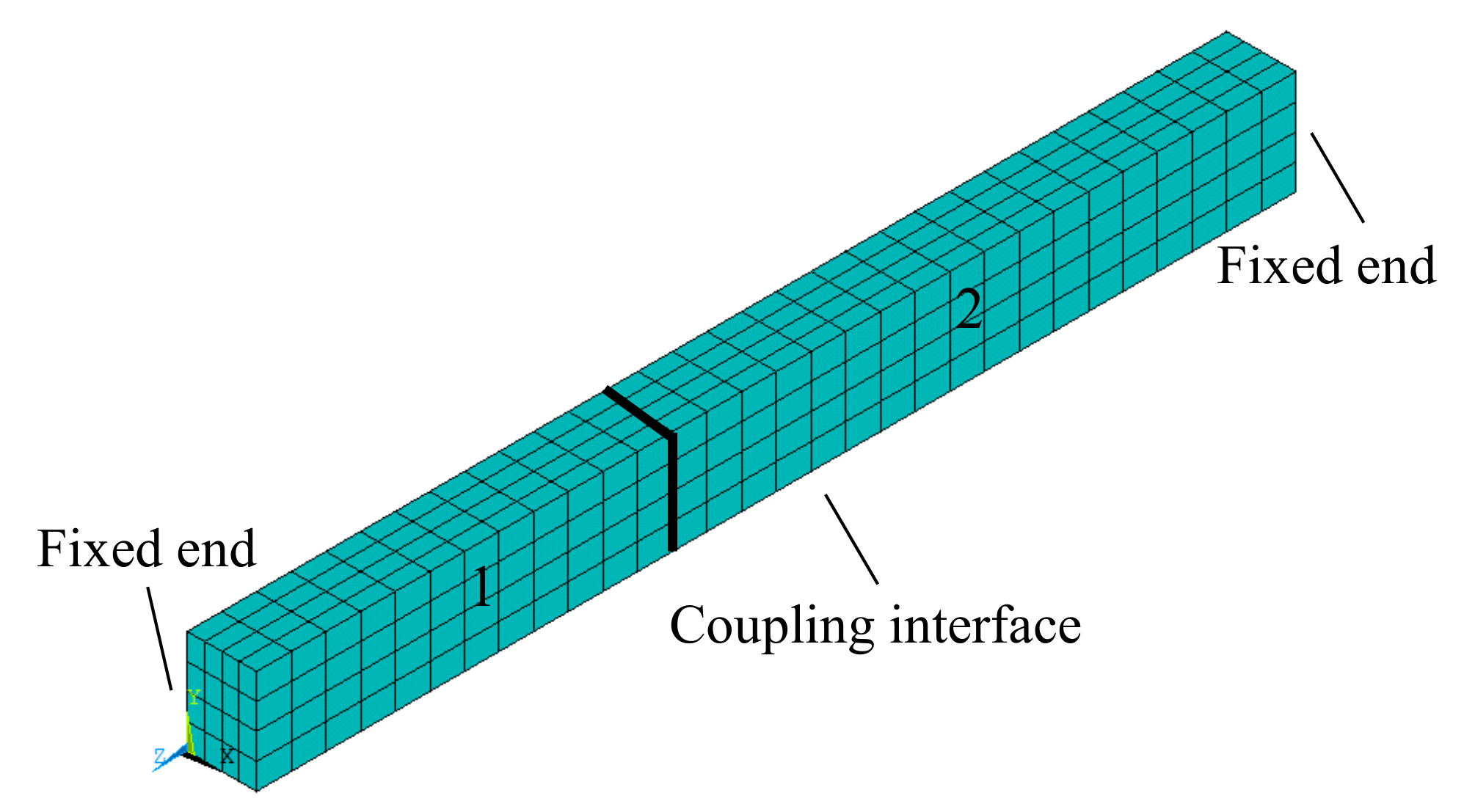
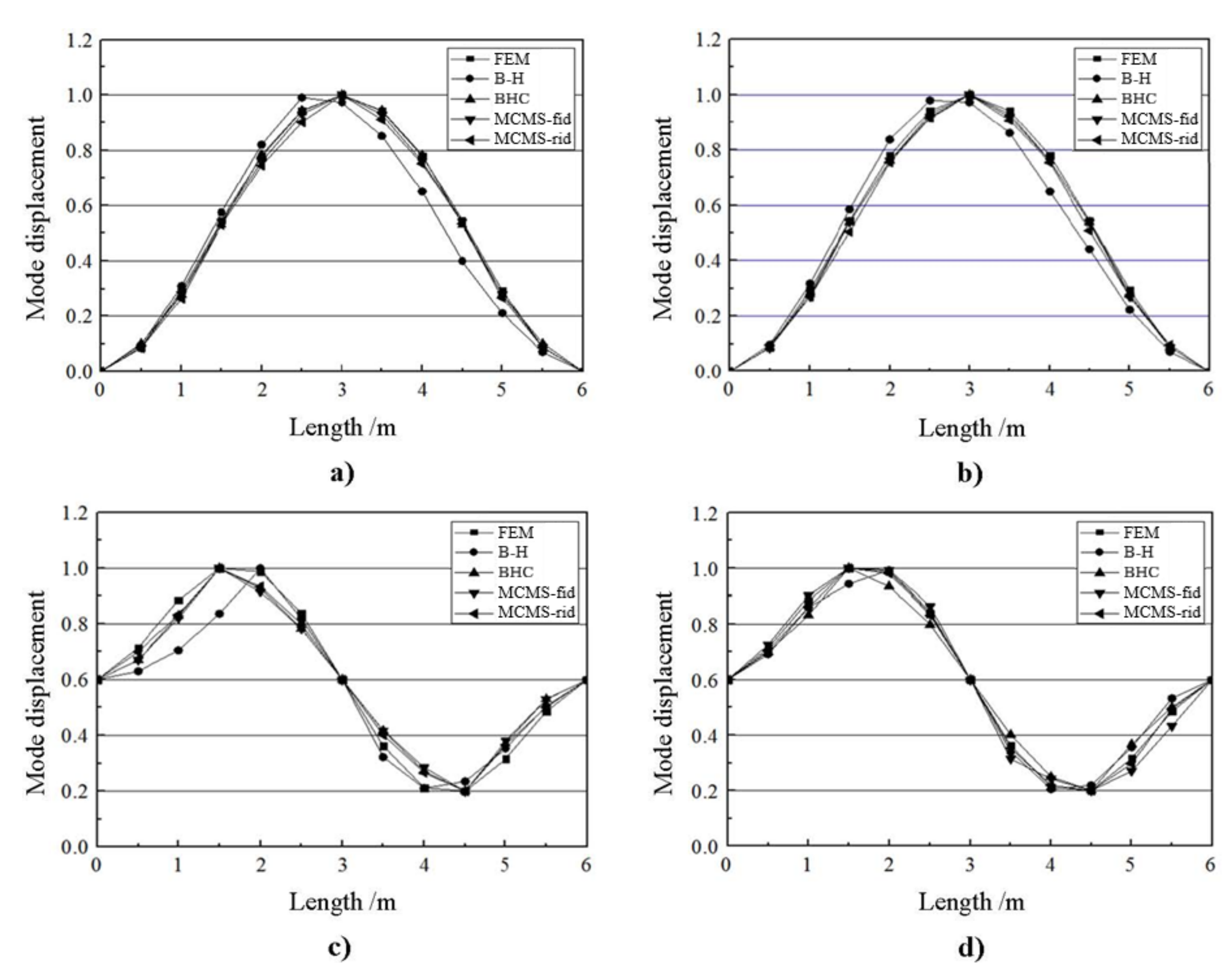
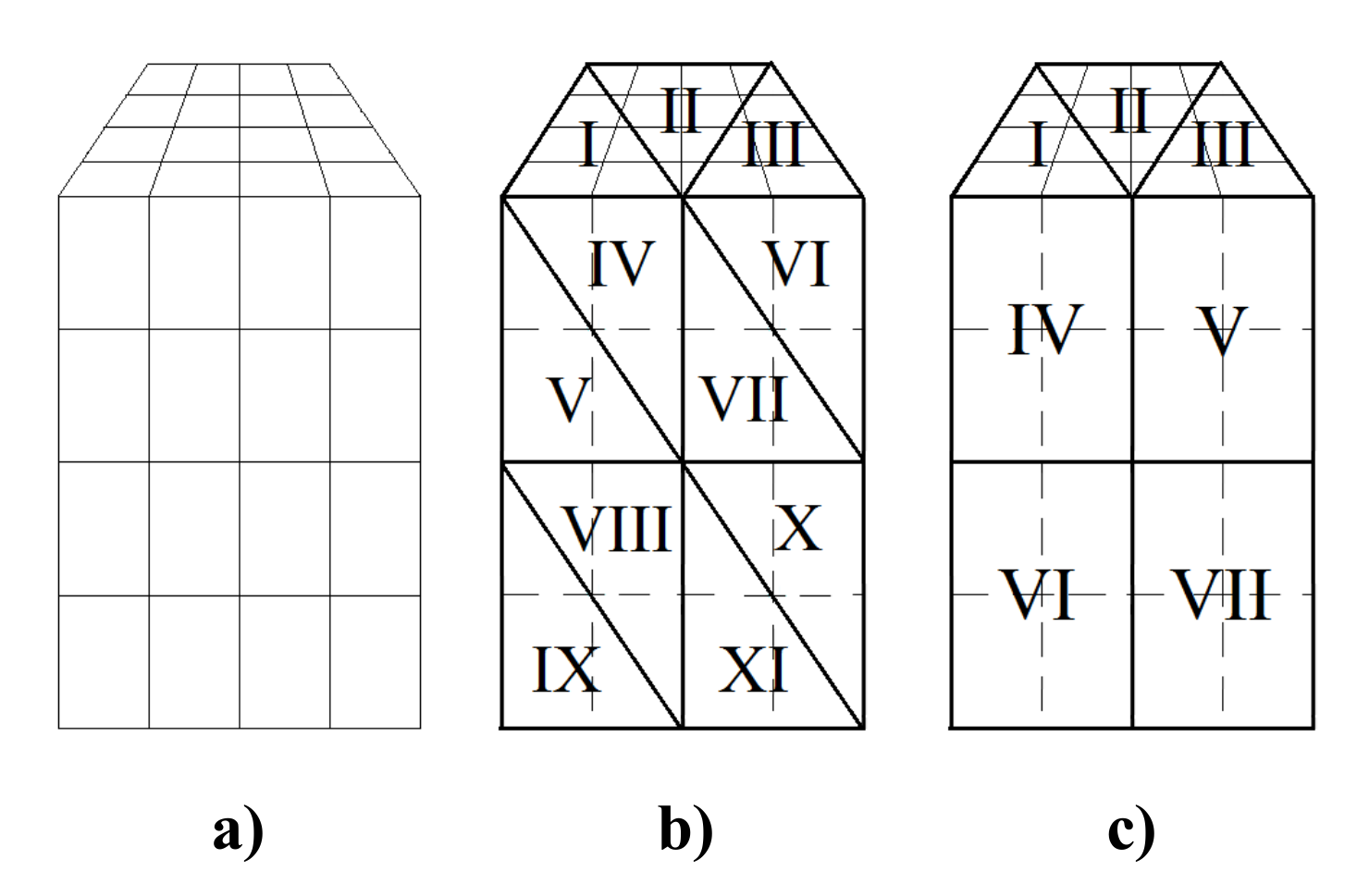
5.1. Example 1
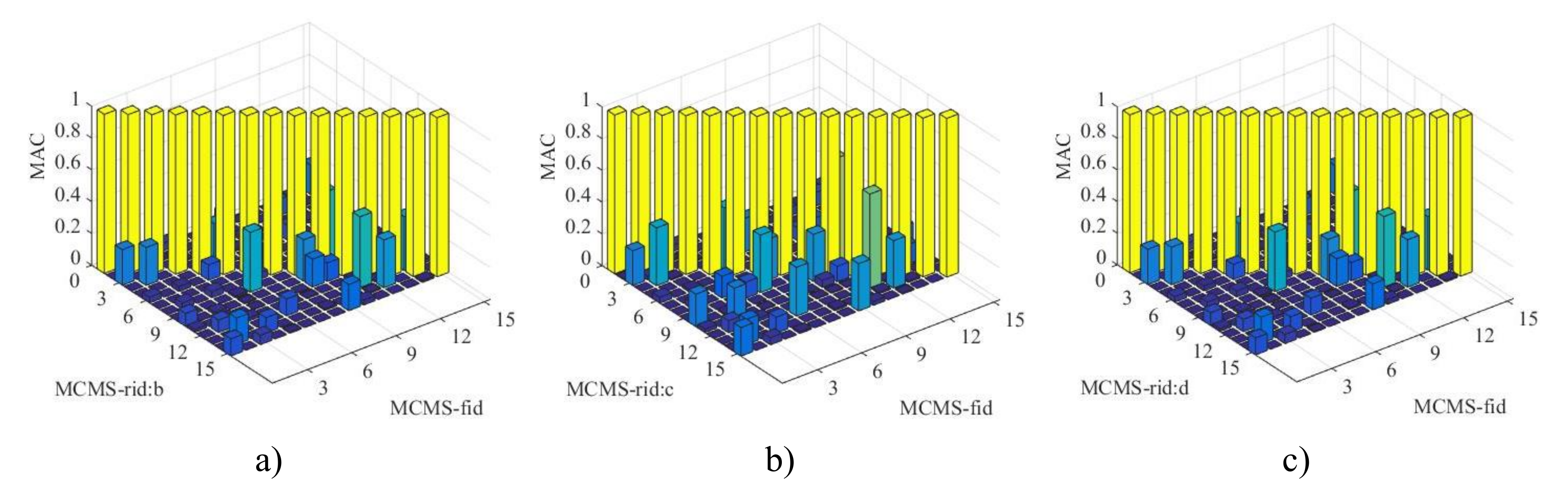
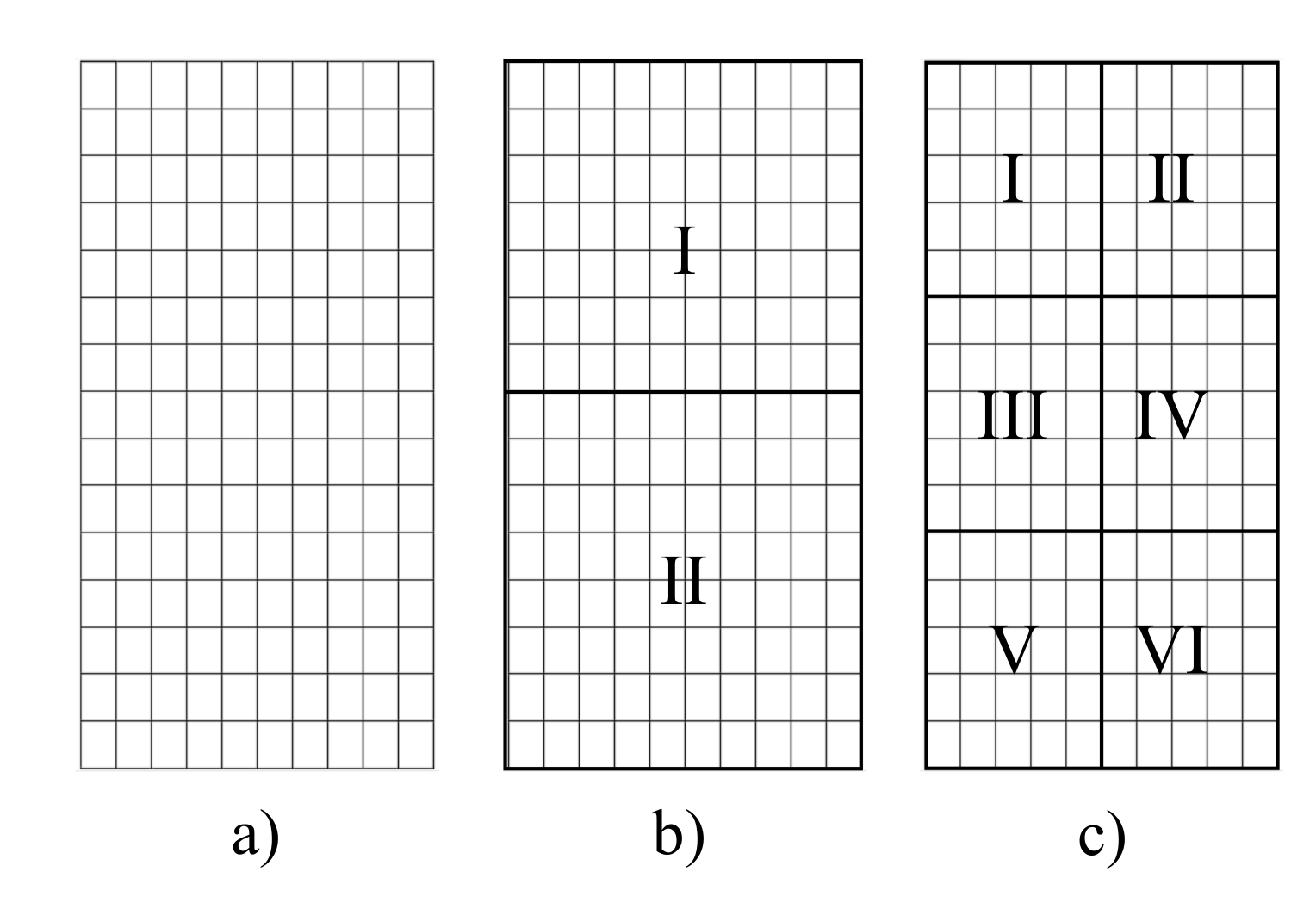
5.2. Example 2
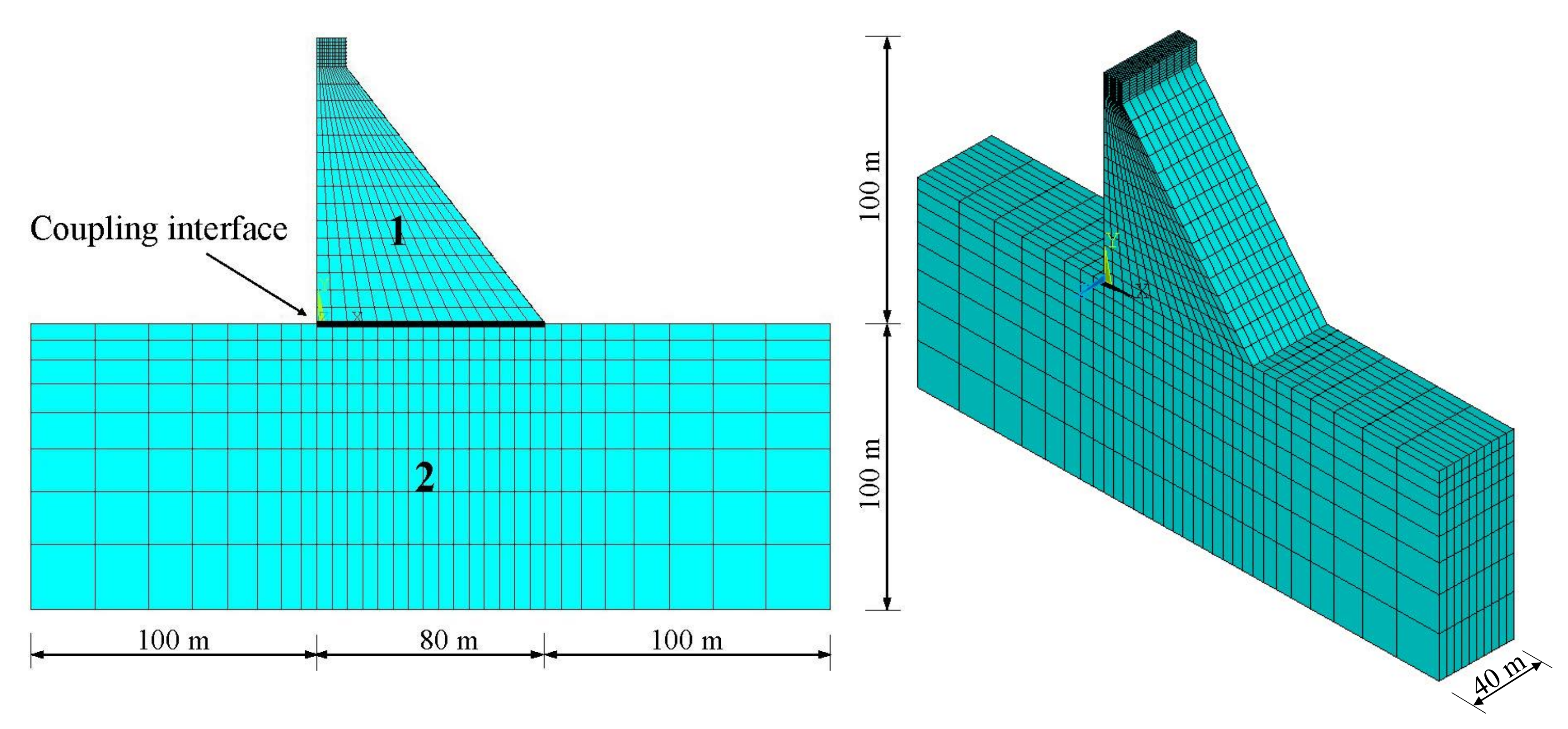
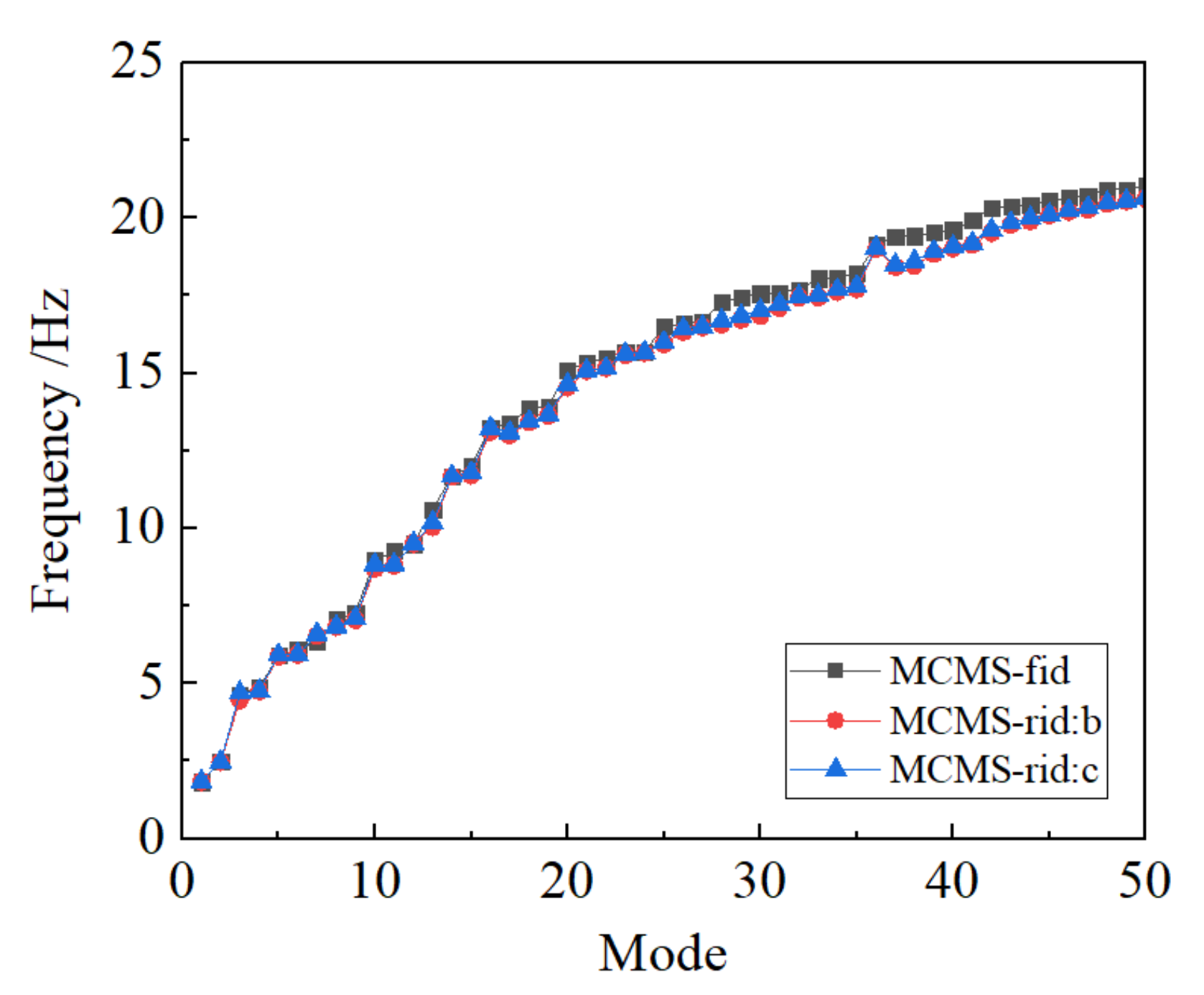
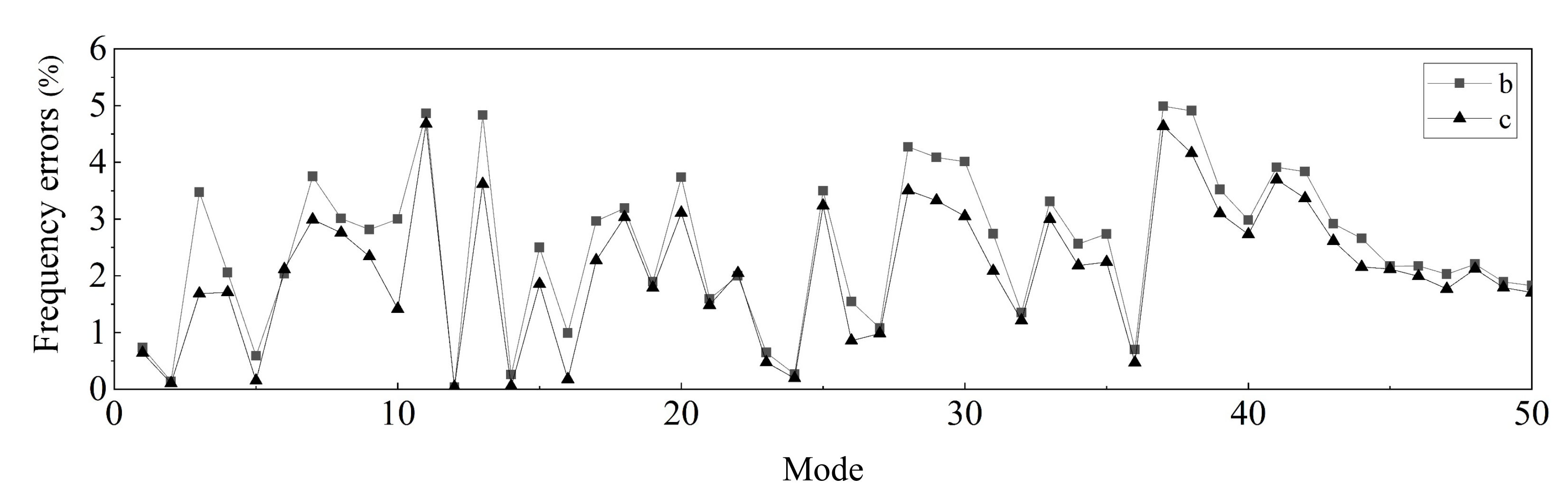
5.3. Example 3
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rixen, D.J. A dual Craig-Bampton method for dynamic substructuring. J. Comput. Appl. Math. 2004, 168, 383–391. [Google Scholar] [CrossRef]
- Cunedioglua, Y.; Mugana, A.; Akay, H. Frequency domain analysis of model order reduction techniques. Finite Elem. Anal. Des. 2006, 42, 367–403. [Google Scholar] [CrossRef]
- Klerk, D.D.; Rixen, D.J.; Voormeeren, S.N. General framework for dynamic substructuring: History, review, and classification of techniques. AAIA J. 2008, 46, 1169–1181. [Google Scholar] [CrossRef]
- David, A.; Charbel, F.; Carlberg, K.; Farhat, C. A method for interpolating on manifolds structural dynamics reduced-order models. Int. J. Numer. Methods Eng. 2009, 80, 1241–1258. [Google Scholar]
- David, A.; Charbel, F.; Carlberg, K.; Farhat, C. An online method for interpolating linear parametric reduced-order models. SIAM J. Sci. Comput. 2011, 33, 2169–2198. [Google Scholar]
- David, A.; Charbel, F.; Bernard, H. Special issue on model reduction. Int. J. Numer. Methods Eng. 2015, 102, 931–932. [Google Scholar]
- Kim, J.G.; Park, Y.J.; Lee, G.H.; Kim, D.N. A general model reduction with primal assembly in structural dynamics. Comput. Methods Appl. Mech. Eng. 2017, 324, 1–28. [Google Scholar] [CrossRef]
- Kim, S.M.; Kim, J.G.; Park, K.; Chae, S.W. A component mode selection method based on a consistent perturbation expansion of interface displacement. Comput. Methods Appl. Mech. Eng. 2018, 330, 578–597. [Google Scholar] [CrossRef]
- Hurty, W.C. Vibration of structure systems by component mode synthesis. J. Eng. Mech. Div. 1960, 86, 51–69. [Google Scholar]
- Hurty, W.C. Dynamic analysis of structural systems using component modes. AAIA J. 1965, 3, 678–685. [Google Scholar] [CrossRef]
- Bampoton, M.C.C.; Craig, R.R. Coupling of substructures for dynamic analysis. AAIA J. 1968, 6, 1313–1319. [Google Scholar]
- Hou, S.N. Review of modal synthesis techniques and new approach. Shock Vib. Bull. 1969, 40, 25–399. [Google Scholar]
- Benfield, W.A.; Hruda, R.F. Vibration analysis of structures by component mode substitution. AAIA J. 1971, 9, 1225–1261. [Google Scholar] [CrossRef]
- Gruber, F.M.; Rixen, D.J. Evaluation of Substructure Reduction Techniques with Fixed and Free Interfaces. Stroj Vestn J. Mech. E 2016, 62, 452–462. [Google Scholar] [CrossRef]
- Barbone, P.E.; Givoli, D.; Patlashenko, I. Optimal modal reduction of vibrating substructures. Int. J. Numer. Methods Eng. 2003, 57, 341–369. [Google Scholar] [CrossRef]
- Givoli, D.; Barbone, P.E.; Patlashenko, I. Which are the important modes of a subsystem? Int. J. Numer. Methods Eng. 2004, 59, 1657–1678. [Google Scholar] [CrossRef]
- Bai, Z.; Liao, B.S. Towards an optimal substructuring method for model reduction. Int. Workshop Appl. Parallel Comput. 2004, 3732, 276–285. [Google Scholar]
- Tayeb, S.; Givoli, D. Optimal modal reduction of dynamic subsystems: Extensions and improvements. Int. J. Numer. Methods Eng. 2011, 85, 1–30. [Google Scholar] [CrossRef]
- Park, K.C.; Kim, J.G.; Lee, P.S. A mode selection criterion based on flexibility approach in component mode synthesis. In Proceedings of the 53th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; pp. 1883–2012. [Google Scholar]
- Kim, J.G.; Lee, P.S.; Park, K.C. A mode selection algorithm for the flexibility based component mode synthesis. In Proceedings of the 5th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete Island, Greece, 25–27 May 2015; pp. 3162–3171. [Google Scholar]
- Kim, S.M.; Kim, J.G.; Chae, S.W.; Park, K.C. Evaluating mode selection methods for component mode synthesis. AIAA J. 2016, 54, 2856–2863. [Google Scholar] [CrossRef]
- Roettgen, D.; Seeger, B.; Tai, W.C.; Baek, S.; Dossogne, T.; Allen, M.; Kuether, R.; Brake, M.R.W.; Mayes, R. A Comparison of Reduced Order Modeling Techniques Used in Dynamic Substructuring. Conf. Proc. Soc. Exp. Mech. Ser. 2016, 4, 511–528. [Google Scholar]
- Rubin, S. Improved component-mode representation for structural dynamic analysis. AIAA J. 1975, 13, 995–1006. [Google Scholar] [CrossRef]
- Majed, A.; Henkel, E.E. Improved method of mixed-boundary component-mode representation for structural dynamic analysis. J. Spacecr. Rocket. 2005, 42, 825–831. [Google Scholar] [CrossRef]
- Petrov, E. A high-accuracy model reduction for analysis of nonlinear vibrations in structures with contact interfaces. J. Eng. Gas. Turbines Power 2011, 133, 102503. [Google Scholar] [CrossRef]
- Kim, J.G.; Boo, S.H.; Lee, P.S. An enhanced AMLS method and its performance. Comput. Methods Appl. Mech. Eng. 2015, 287, 90–111. [Google Scholar] [CrossRef]
- Gruber, F.E.; Gille, M.; Rixen, D.J. A strategy to stabilize the transient analysis and increase the approximation accuracy of dual Craig-Bampton reduced systems. Finite Elem. Anal. Des. 2019, 160, 32–45. [Google Scholar] [CrossRef]
- Lou, M.L. Introduction of the component mode synthesis. In Substructue Methods for Dynamic Analysis of Structures; Tongji University Press: Shanghai, China, 1997; pp. 71–103. [Google Scholar]
- Becker, J.; Gau, L. CMS Methods for Efficient Damping Prediction for Structures with Friction. In Proceedings of the IMAC-XXVI, Orlando, FL, USA, 9–12 February 2009; pp. 3–13. [Google Scholar]
- Gaul, L.; Becker, J. Damping prediction of structures with bolted joints. Shock Vib. 2010, 17, 359–371. [Google Scholar] [CrossRef]
- Lee, J. Maenghyo ChobAn interpolation-based parametric reduced order model combined with component mode synthesis. Comput. Methods Appl. Mech. Eng. 2018, 319, 258–286. [Google Scholar] [CrossRef]
- Park, K.C.; Park, Y.H. Partitioned component mode synthesis via a flexibility approach. AIAA J. 2004, 42, 1236–1245. [Google Scholar] [CrossRef]
- Markovic, D.; Park, K.C.; Ibrahimbegovic, A. Reduction of substructure interface degrees of freedom in flexibility-based component mode synthesis. Int. J. Numer. Methods Eng. 2007, 70, 163–180. [Google Scholar] [CrossRef]
- Gruber, F.M.; Burchner, T.L.; Rixen, D.J. Dual Craig-Bampton Method with Reduction of Interface Coordinates. Conf. Proc. Soc. Exp. Mech. Ser. 2017, 4, 143–163. [Google Scholar]
- Battiatoa, G.; Firronea, C.M.; Berrutia, T.M.; Epureanu, B.I. Reduction and coupling of substructures via Gram–Schmidt Interface modes. Comput. Methods Appl. Mech. Eng. 2018, 336, 187–212. [Google Scholar] [CrossRef]
- Jeong, G.; Song, Y.; Youn, S.; Park, K.C. A new approach for nonmatching interface construction by the method of localized Lagrange multipliers. Comput. Methods Appl. Mech. Eng. 2020, 361, 112728. [Google Scholar] [CrossRef]
- Lou, M.L.; Yin, L. Degrees of freedom reduction technique for interface of constrained substructure based on node displacement interpolation. Eng. Mech. 2012, 29, 25–29, 36. [Google Scholar]
- Lou, M.L.; Tang, Y.; Yin, L. Degrees of freedom reduction technique for free interface substructure based on nodal force interpolation. J. Tongji Univ. (Nat. Sci.) 2015, 43, 662–667. [Google Scholar]
- Guyan, R.J. Reduction of stiffness and mass matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]
- Yin, X.; Dong, M.; Huang, H. The revised mode method for mix-interface mode synthesis method. Comput. Struct. Mech. Appl. 1997, 4, 89–94. [Google Scholar]
- Lou, M.L. Mix-interface component mode synthesis. In Substructue Methods for Dynamic Analysis of Structures; Tongji University Press: Shanghai, China, 1997; pp. 107–165. [Google Scholar]
- Bathe, K.J. Finite Element Procedures; Prentice Hall: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Lou, M.L.; Zhao, Y.L. Substructure method for dynamic analysis of dam-rock foundation interaction. J. Vib. Eng. 1994, 7, 161–166. [Google Scholar]



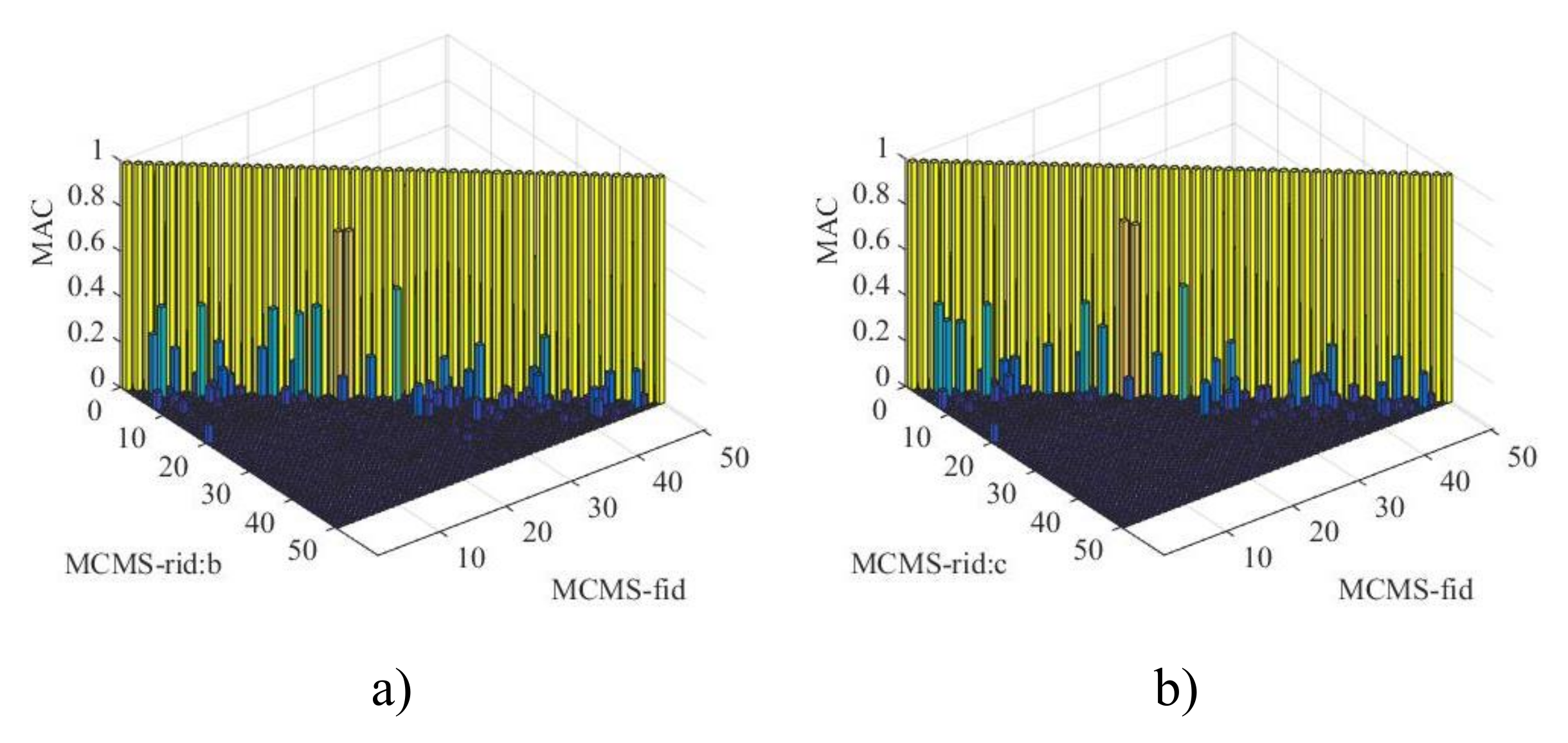
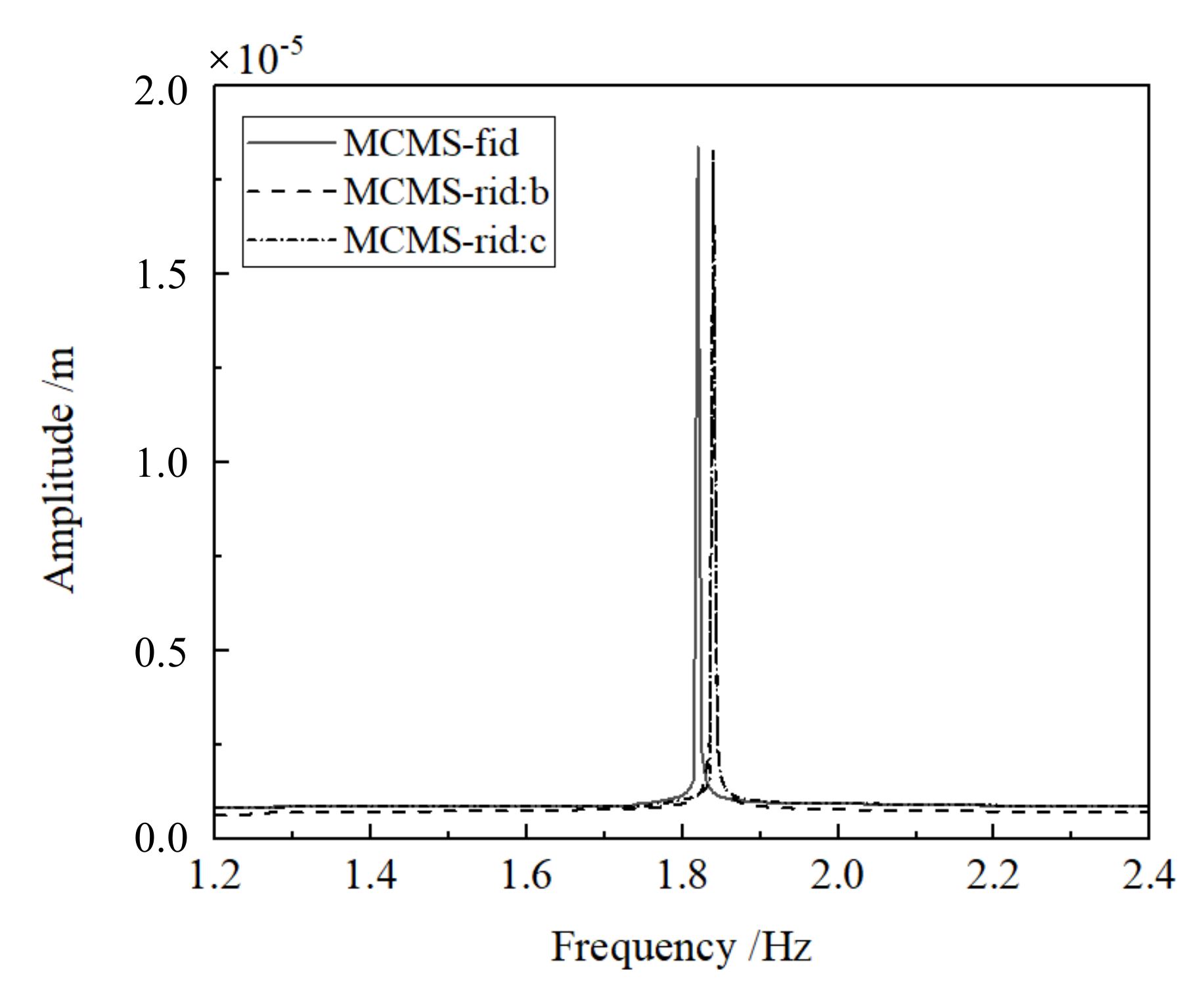
| Method | Mode | DOFs | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| FEM | 39.10 | 56.62 | 104.63 | 146.16 | 157.97 | 197.94 | 266.41 | 290.81 | 2175 |
| B-H | 41.35 | 59.54 | 89.13 | 126.89 | 162.43 | 231.80 | 306.17 | 309.75 | 15 |
| (5.74) | (5.16) | (14.81) | (13.18) | (2.82) | (17.11) | (14.92) | (6.51) | ||
| BHC | 39.51 | 56.44 | 85.77 | 121.06 | 159.43 | 224.84 | 293.84 | 299.62 | 1500 |
| (1.04) | (0.31) | (18.03) | (17.17) | (0.92) | (13.59) | (10.09) | (3.03) | ||
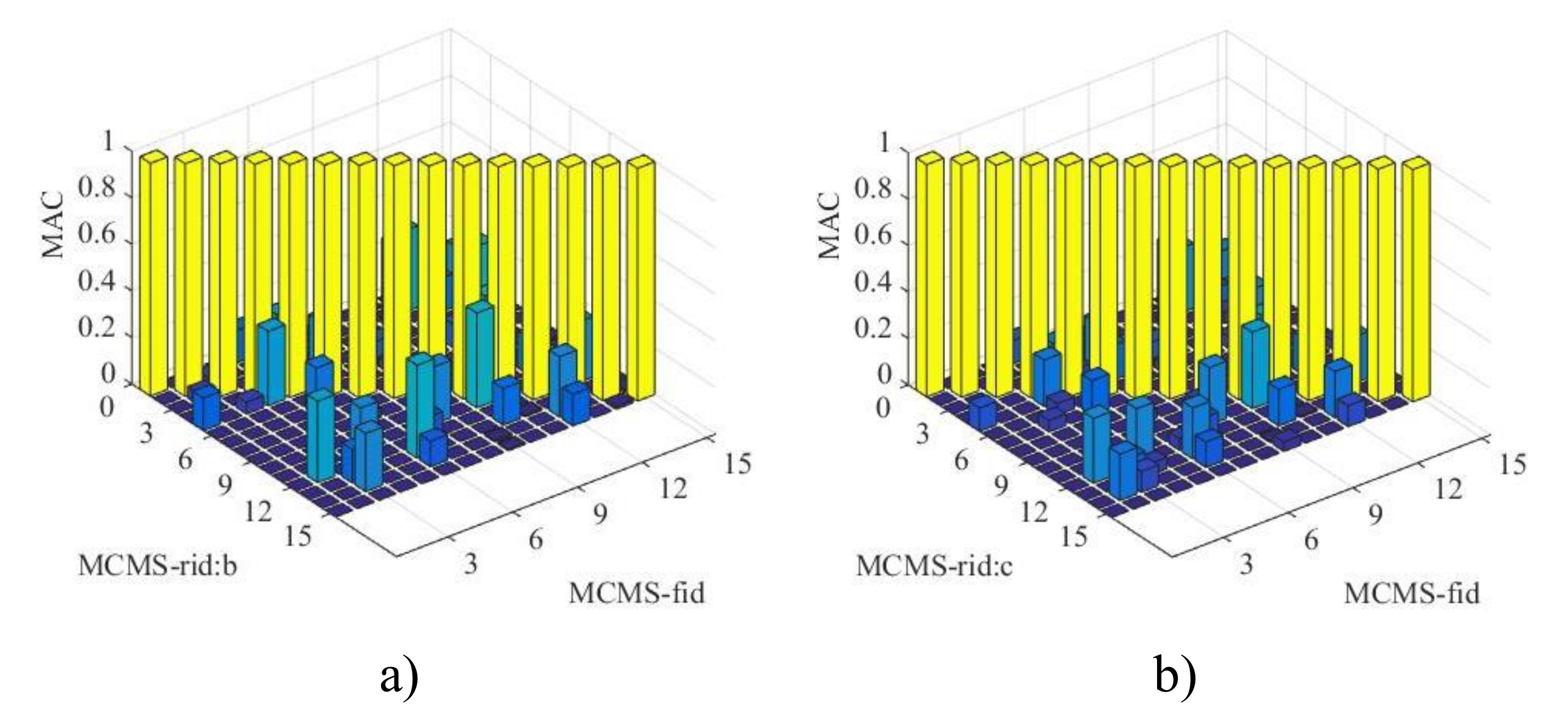
| MCMS-fid | 39.47 | 56.36 | 95.67 | 134.88 | 159.02 | 214.40 | 284.67 | 298.65 | 165 |
| (0.94) | (0.46) | (8.56) | (7.72) | (0.66) | (8.32) | (6.85) | (2.70) | ||
| MCMS-rid | 39.89 | 56.28 | 95.05 | 133.63 | 159.97 | 217.61 | 279.00 | 299.90 | 69 |
| (2.02) | (0.60) | (9.16) | (8.57) | (1.26) | (9.94) | (4.72) | (3.13) | ||
| Scheme | Mode | DOFs | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| a | 39.47 | 56.36 | 95.67 | 134.88 | 159.02 | 214.40 | 284.67 | 298.65 | 165 |
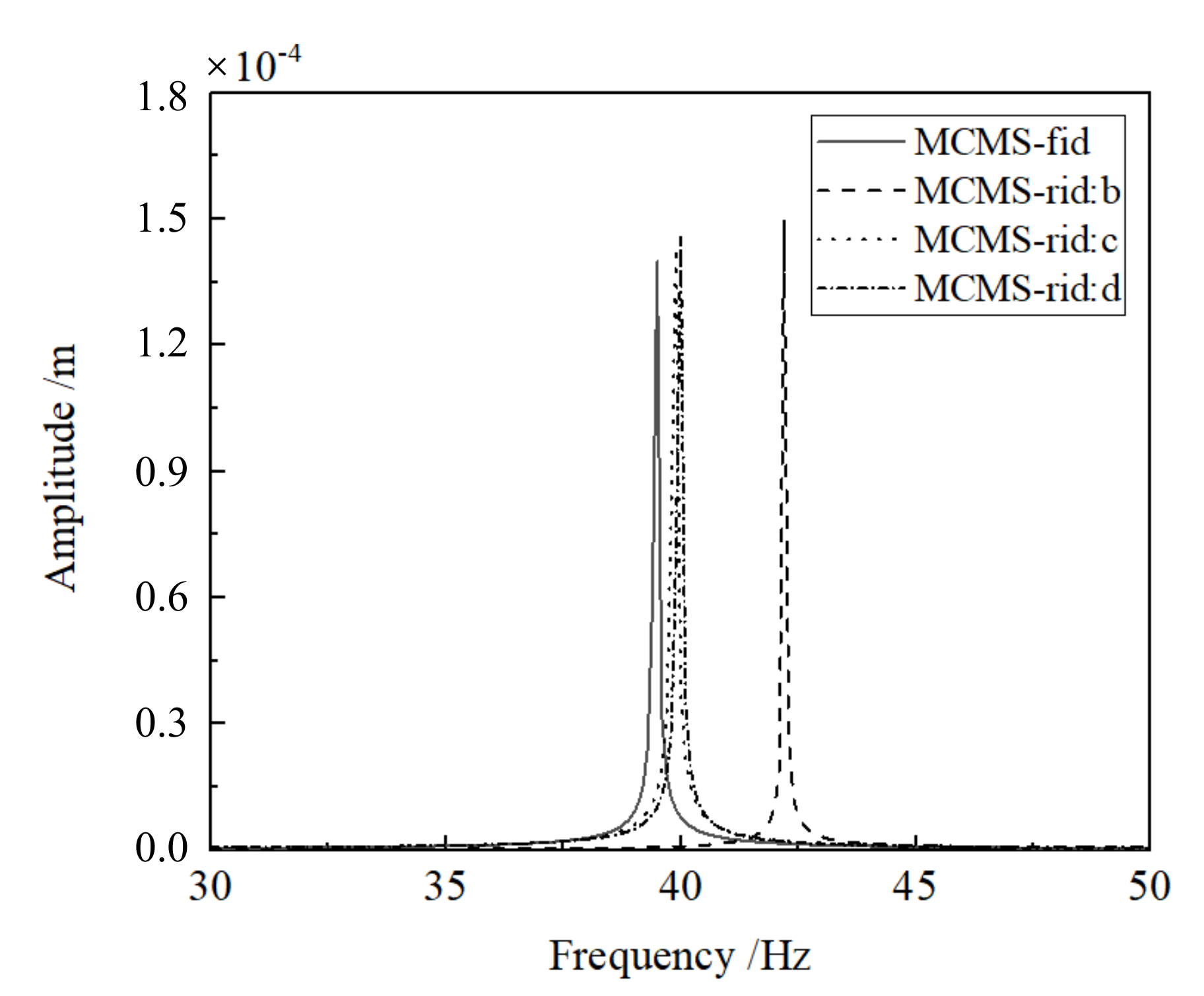
| b | 39.89 | 56.28 | 95.05 | 133.63 | 159.97 | 217.61 | 279.00 | 299.90 | 69 |
| (1.06) | (0.14) | (0.65) | (0.93) | (0.60) | (1.50) | (1.99) | (0.42) | ||
| c | 42.23 | 58.22 | 88.79 | 132.56 | 165.71 | 226.48 | 293.96 | 307.52 | 39 |
| (6.99) | (3.30) | (7.19) | (1.72) | (4.21) | (5.63) | (3.26) | (2.97) | ||
| d | 40.04 | 56.05 | 96.35 | 134.23 | 160.22 | 218.18 | 281.08 | 297.34 | 80 |
| (1.44) | (0.55) | (0.71) | (0.48) | (0.75) | (1.76) | (1.26) | (0.44) | ||
| Scheme | Mode | DOFs | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
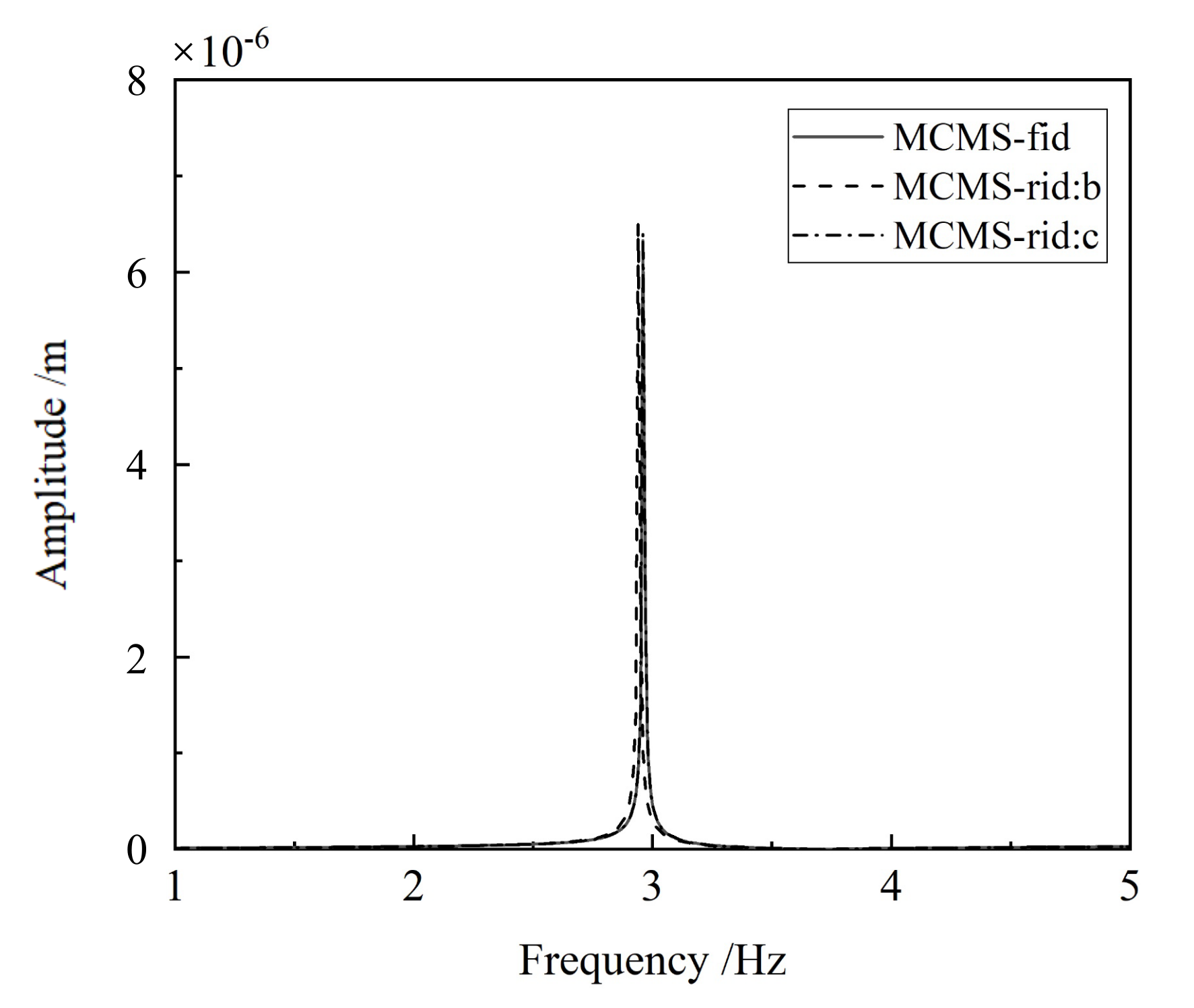
| a | 2.96 | 3.73 | 5.13 | 5.25 | 9.19 | 9.42 | 10.28 | 10.75 | 210 |
| b | 2.94 | 3.77 | 5.33 | 5.27 | 9.66 | 9.68 | 10.76 | 11.16 | 126 |
| (0.59) | (1.12) | (3.90) | (0.45) | (5.11) | (2.76) | (4.68) | (3.83) | ||
| c | 2.96 | 3.56 | 5.35 | 5.26 | 9.44 | 9.59 | 10.67 | 11.01 | 126 |
| (0.08) | (0.14) | (4.32) | (0.14) | (2.77) | (1.83) | (3.80) | (2.46) | ||
| Density (kg/m) | Elastic Modulus (GPa) | Passion Ratio | |
|---|---|---|---|
| Dam | 2450 | 20 | 0.25 |
| Foundation | 2700 | 12 | 0.17 |
| FE Model | # Node | # Element | # DOF |
|---|---|---|---|
| Dam | 4224 | 3810 | 12,672 |
| Foundation | 3168 | 2728 | 7792 |
| Interface | 176 | 150 | 528 |
| CPU | CPU | CPU | CPU | |||
|---|---|---|---|---|---|---|
| 780.46 | 59.46 | 30.91 | 32.37 | 0.0762 | 0.0396 | 0.0414 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Qin, H. Reduction of Coupling Interface Degrees of Freedom in Mixed-Interface Component Mode Synthesis. Appl. Sci. 2020, 10, 2759. https://doi.org/10.3390/app10082759
Tang Y, Qin H. Reduction of Coupling Interface Degrees of Freedom in Mixed-Interface Component Mode Synthesis. Applied Sciences. 2020; 10(8):2759. https://doi.org/10.3390/app10082759
Chicago/Turabian StyleTang, Yu, and Hui Qin. 2020. "Reduction of Coupling Interface Degrees of Freedom in Mixed-Interface Component Mode Synthesis" Applied Sciences 10, no. 8: 2759. https://doi.org/10.3390/app10082759
APA StyleTang, Y., & Qin, H. (2020). Reduction of Coupling Interface Degrees of Freedom in Mixed-Interface Component Mode Synthesis. Applied Sciences, 10(8), 2759. https://doi.org/10.3390/app10082759






