1. Introduction
The finite element method (FEM) is one of the most effective way of solving structural dynamic problems. With a rapid increasing of computation capability, the demand for large scale FE models with huge number of degrees-of-freedom (DOFs) has raised even more quickly, which makes structural dynamic calculations much time-consuming. Hence, it is crucial to reduce computational cost, especially when physical structures are large and complex. A variety of model reduction methods have been developed during the last decades, and the focus in model reduction is mainly on reducing computational cost without too much accuracy being lost [
1,
2,
3,
4,
5,
6,
7,
8]. One of the most well known model reduction methods is component modes synthesis (CMS).
CMS was firstly proposed by Hurty, and it is an efficient method for analysing the dynamics of large, complex structures which are often described by separate interconnected components/substructures [
9]. Hurty used three displacement modes (i.e., rigid-body, constraint and normal modes) to form a complete set of modes for each substructure, and he constructed a transformation relating component coordinates to system coordinates [
10]. Craig and Bampoton improved the approach by Hurty, and they employed two forms of generalized coordinates: one is interface generalized coordinates that is related to constraint modes, the other is normal modes that is related to the free vibration modes of the substructures [
11]. As completely restrained interfaces are imposed on each component at the connections, this approach can be classified as constrained-interface CMS (CCMS). Hou provided a new modal synthesis technique, in which the interface conditions used for determining component vibration modes were free-free and both compatibility and equilibrium at boundaries were satisfied for modal coupling [
12]. This approach can be classified as free-interface CMS (FCMS). Benfield and Hruda developed a comprehensive method of component modal substitution that is applicable to redundant complex structures [
13]. Using this method, the natural modes of vibration for each component are determined with both free-free and constrained interface conditions (known as MCMS). In general, CMS methods have relied on a bottom-up approach, which can be described by the following steps. First, partition the original structure into several substructures with same or different interface conditions; second, carry out the eigenvalue problem in each substructure, and generalized mass, stiffness, damping matrices are determined; third, transform the component physical coordinates to the modal coordinates by reduced normal modes; forth, assemble all the components based on the displacement-compatibility or/and force-equilibrium at the connections; fifth, carry out the reduced global eigenvalue problem. As the number of the retained component modes is substantially smaller than the global physical DOFs, the computational size of modal synthesis is greatly reduced [
14].
In any type of the CMS methods, the most important and difficult task is choosing an appropriate reduced component modes involving modal reduction and mode synthesis, and this continues to be an area of research [
15,
16,
17,
18,
19,
20,
21,
22]. Lots of work have been done to make improvements on modal reduction of internal DOFs [
23,
24,
25,
26,
27], but no order reduction is performed on the boundary. Though the internal DOFs dominate the FE models of substructures, they are greatly reduced by the process of coordinate transformations based on traditional CMS theory, as only a small number of low-frequency modes are truncated. However, if the number of substructures is increasing, or if the coupling interface is large and the FE mesh is fine, the coupling interface DOFs will rule the following works, and retaining a full dimension of the coupling interface DOFs will definitely lower the computational efficiency of mode synthesis. Thus, it is necessary to establish an approach to reduce the number of interface DOFs without too much accuracy diminished, and this will result in incomplete boundary conditions [
28]. To date, different interface reduction methods have been proposed by various researchers, and most of them can be classified by two categories. One is to replace full size of constrain modes by a subset of interface modes via performing a second modal analysis related to the interface DOFs [
29,
30,
31]; the other is to introduce additional variables such as Lagrange multipliers that represent the interface generalized vectors [
32,
33,
34,
35,
36]. However, in general, the validity of these methods are heavily rely on a good selection of special interface modes, and they may be time-consuming by performing supplementary modal analysis for the interface modes.
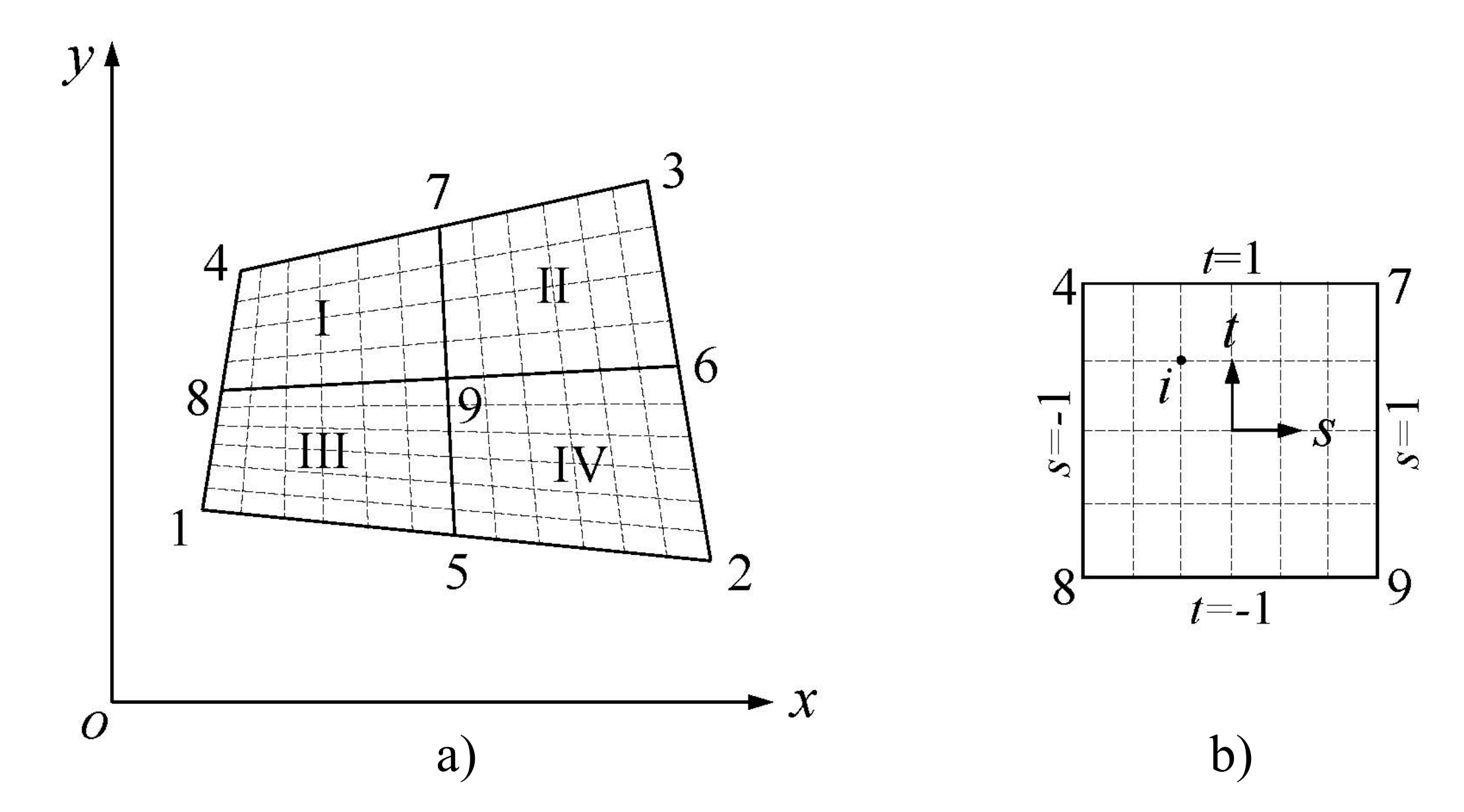
In this work, a new coupling interface degrees of freedom reduction technique for the MCMS method (referred to as the MCMS-rid method) is established properly. In MCMS-rid, a set of interpolation functions via the linear interpolation (LI) [
37,
38] suitable for both nodal displacements and nodal forces are built, and then the corresponding coordinate transformation matrices for constrained interfaces and free interfaces are derived respectively. Different from the methods aforementioned, the interpolation functions representing the reduced interface DOFs are established based on the initial interface DOFs of substructures, in which no additional variables or supplementary modal analysis are needed. Therefore, the corresponding coordinate transformation can be carried out within each substructure before assembling or even in individual processors of a parallel computer. The other advantage of this method is that the number of the retained interface DOFs are distributed between the separate substructures in an optimal sense.
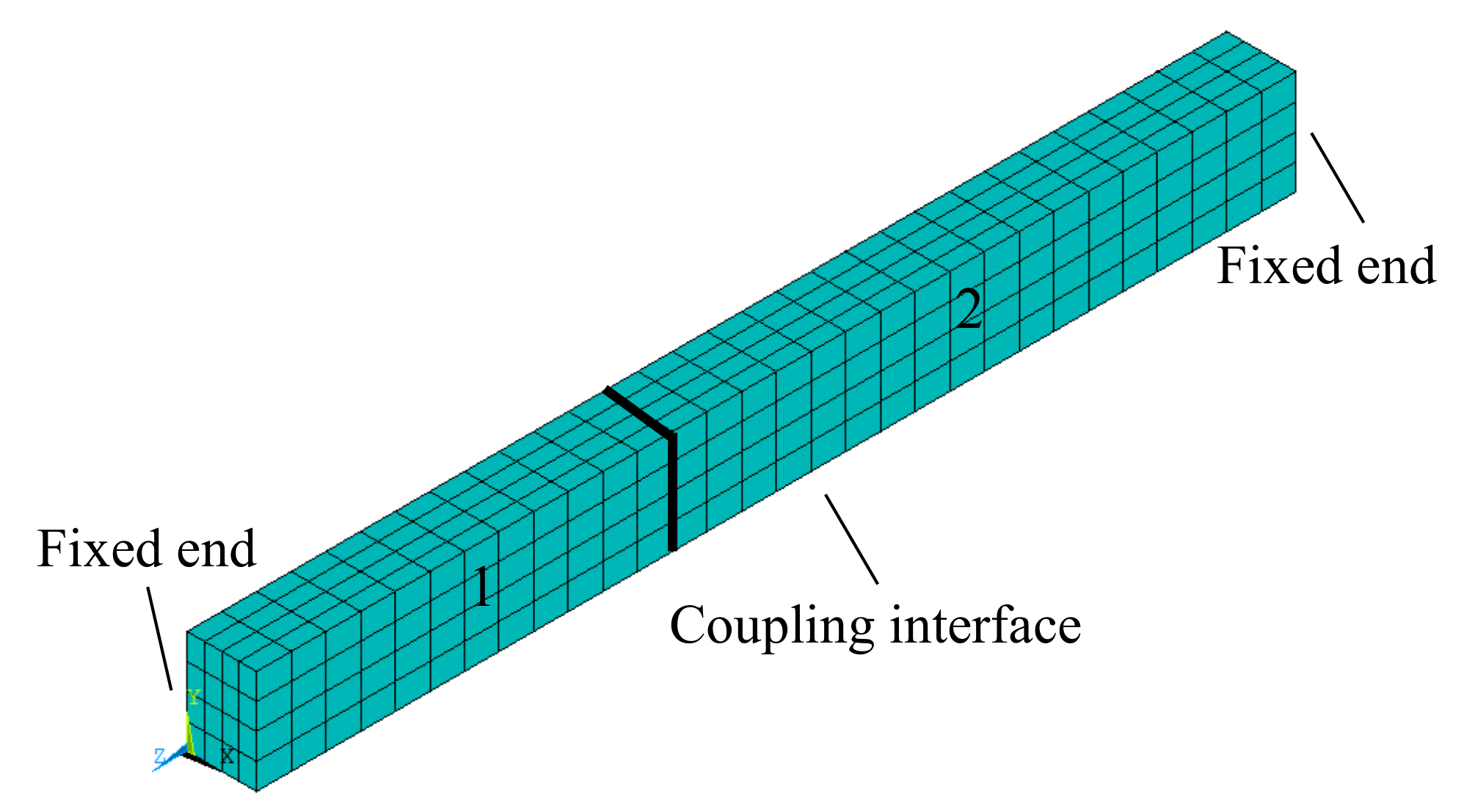
It should be noted that we seek a consistently reduced model for MCMS, whose size depends exclusively on the physics of the problem rather than the FE models. Thus, the presented work is aimed to propose a coupling interface DOFs reduction procedure which has to satisfy the following two conditions: (i) the numerical precision with respect to the full interface dimension model should be kept in an acceptable level, and (ii) the interface modes selection shall be based on a robust criterion. The efficiency of the approach is demonstrated by eigenvalue analyses of three typical numerical examples, including a rectangular beam with two ends fixed, a non-rectangular beam with the button fixed and a simplified dam-foundation system. The optimal number and distribution of the interpolation nodes are discussed on structural dynamic analysis as well.
2. A Brief Review of the Traditional MCMS
This section provides a brief review of the traditional MCMS proposed by Benfield and Hruda (also called the B-H method for short) [
13]. In a global domain, the linear equation of motion (EOM) of a N-DOFs structure is written as
where
,
and
are the mass matrix, the damping matrix and the stiffness matrix of the global structure, respectively;
,
and
are the acceleration vector, the velocity vector and the displacement vector, respectively;
is the external force vector.
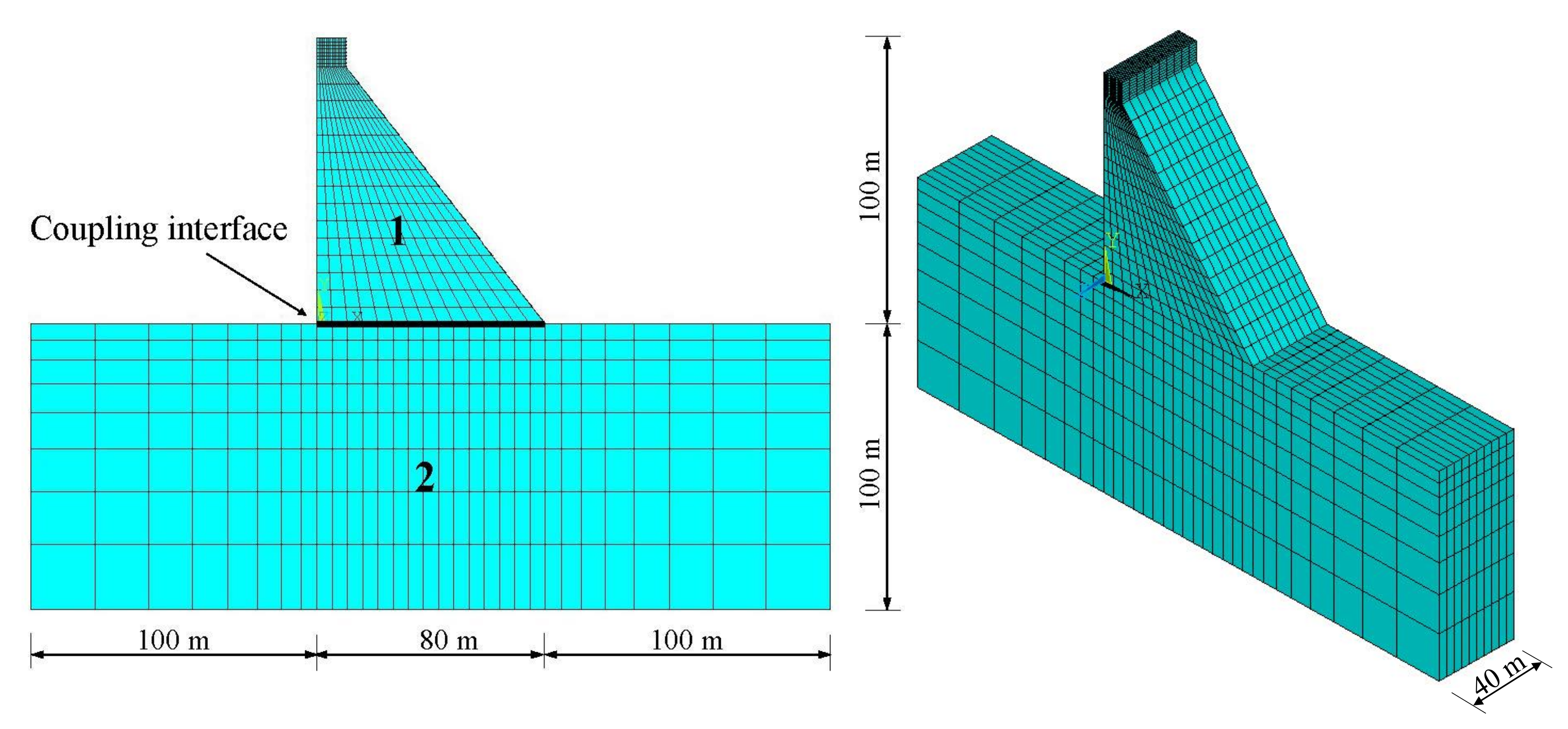
In the B-H method, the original system is divided into two groups: master substructures and slave substructures. All the substructures are non-overlapping so that each node belongs to exactly one substructure except for the nodes on the coupling interface. In
Figure 1, only one master substructure and one slave substructure are shown as demonstration. Different interconnection conditions are imposed on each part, where the interconnection of the master substructure is constrained while that of the slave substructure is free. Then, Equation (
1) can be rewritten in block matrices as
in which, subscripts
c and
f indicate the master substructure with constrained interconnections and the slave substructure with free interconnections, respectively; superscripts
I and
B indicate the internal DOFs and the interface DOFs. The linear equations of motion of each structure are,
where,
is the reaction force vector relative to the coupling DOFs of the substructure.
The first coordinate transformations that transforming the physical coordinates
to generalized coordinates
are done in each substructure according to the different interconnection conditions. That is,
where
and
are the truncated normal mode involving in mode synthesis;
is the constrained mode;
is the first coordinate transformation matrix. The corresponding generalized stiffness and mass matrix can be written as
and
In the B-H method, only the displacement-compatibility is involved in mode synthesis. That is,
Substituting Equation (
9) into Equation (
6), the second coordinate transformation for the slave substructure and the corresponding generalized stiffness and mass matrix can be expressed as
Assembling all the generalized stiffness and mass matrices of the master and slave substructures, the global reduced stiffness and mass matrices are
The uncoupled eigenvalue problem is shown in Equation (
13), and the order number of the eigenvalue problem equals to
.
6. Conclusions
The CMS method is one of the well-developed modal order reduction technique that describes the whole structure with several independent components/substructures. Modal analysis are carried out in each component and then mode synthesis are done based on the displacement-coordination or/and force-equilibrium at the interfaces of substructures. As the internal DOFs are greatly reduced by the first coordinate transformation, the number of the coupling interface DOFs involved in mode synthesis will rule the following computational efficiency and accuracy. In this paper, we focus on reducing the coupling interface DOFs to solve the problems of docking difficulties and incomplete boundary conditions. The following conclusions may be drawn:
(a) Displacement and force interpolation functions of the coupling interface DOFs using nodal displacement interpolation formulations based on FEM are set up for the MCMS method. The corresponding interpolation transformation is done before mode synthesis, and only a small number of IBNs are kept so that the proposed method is very computationally efficient for solving eigenvalue problems.
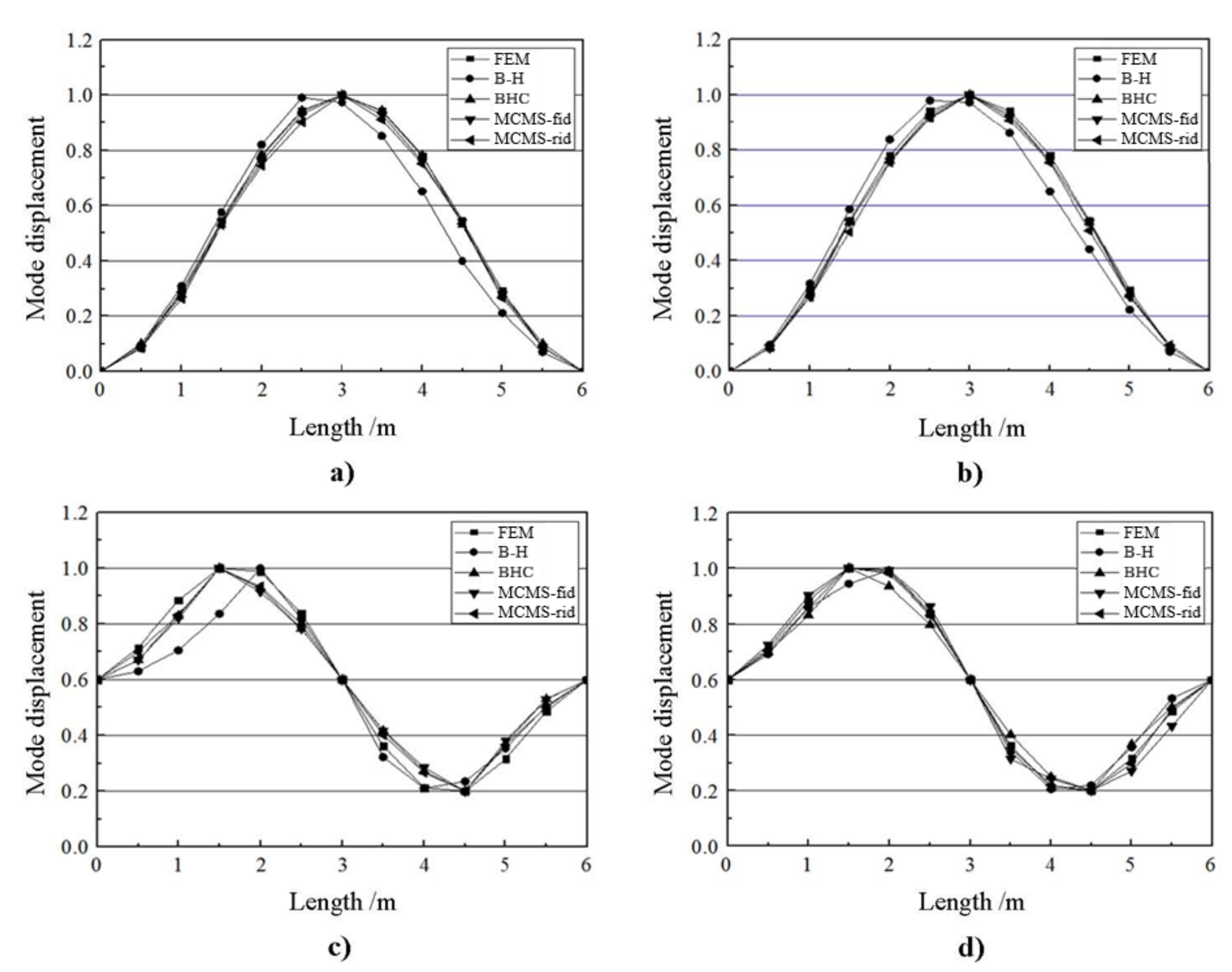
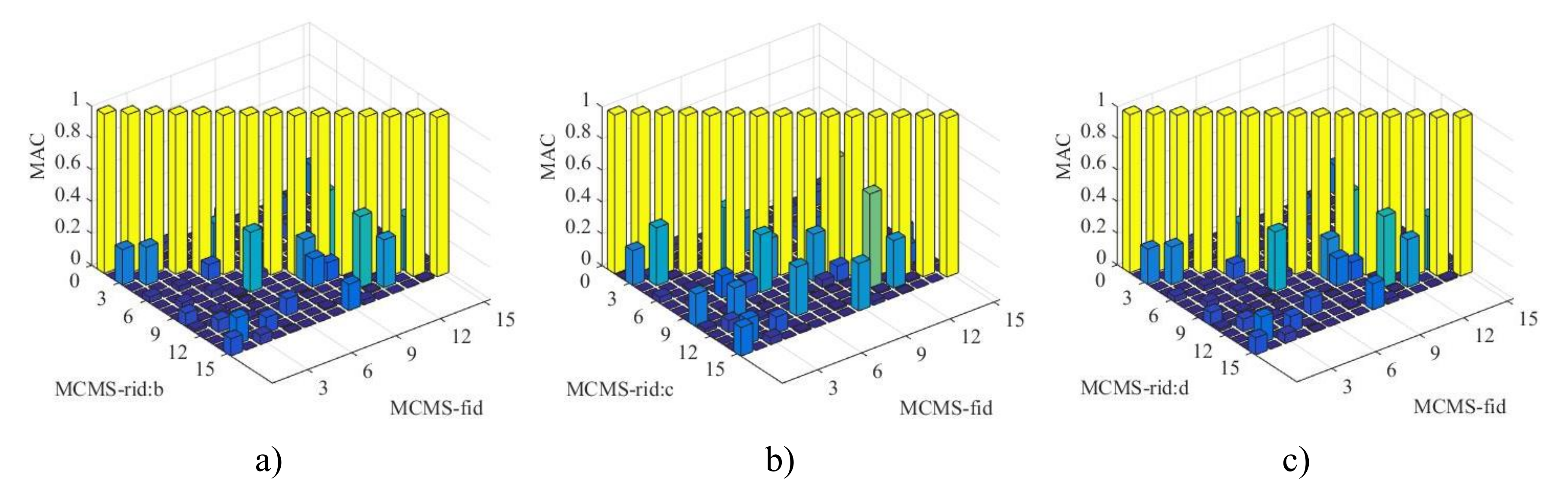
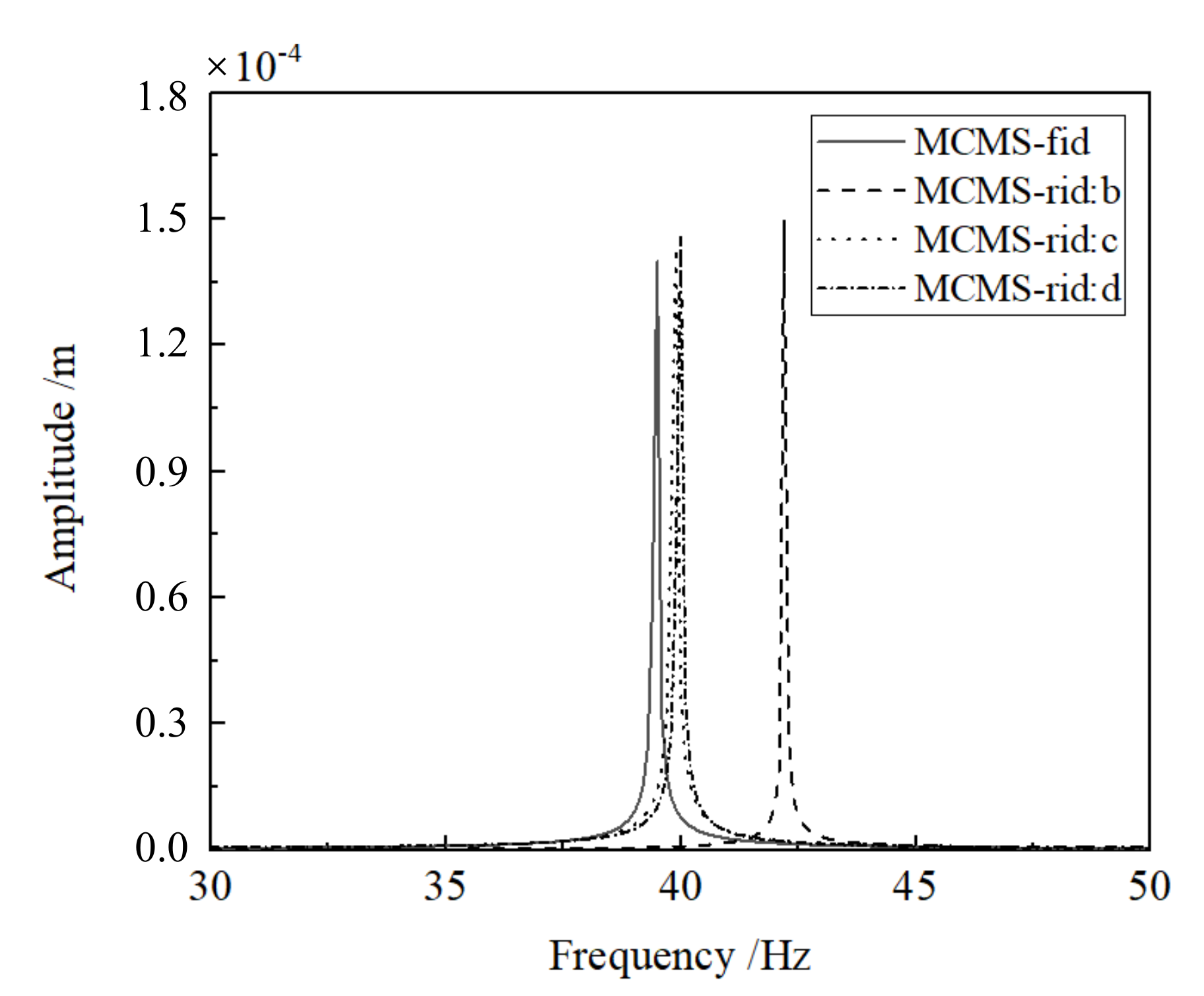
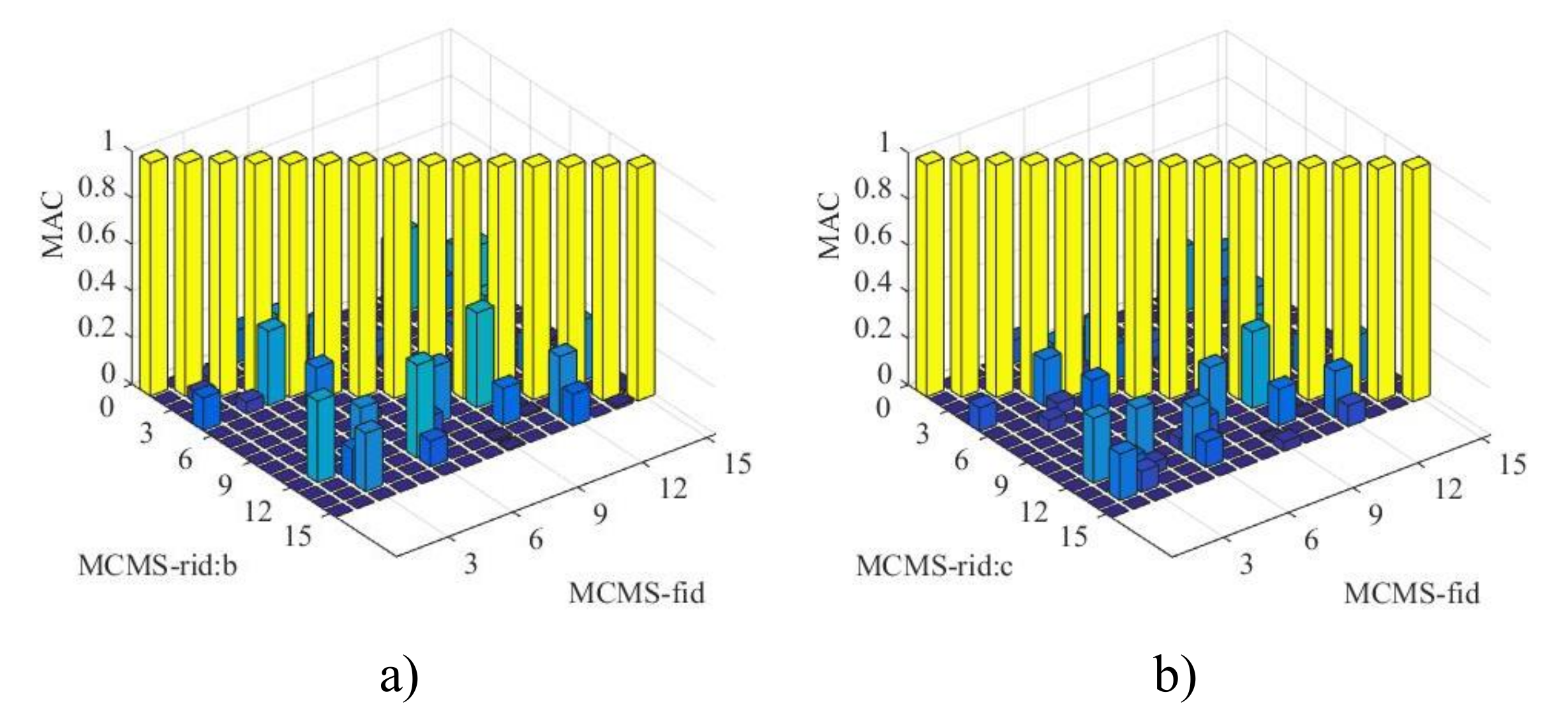
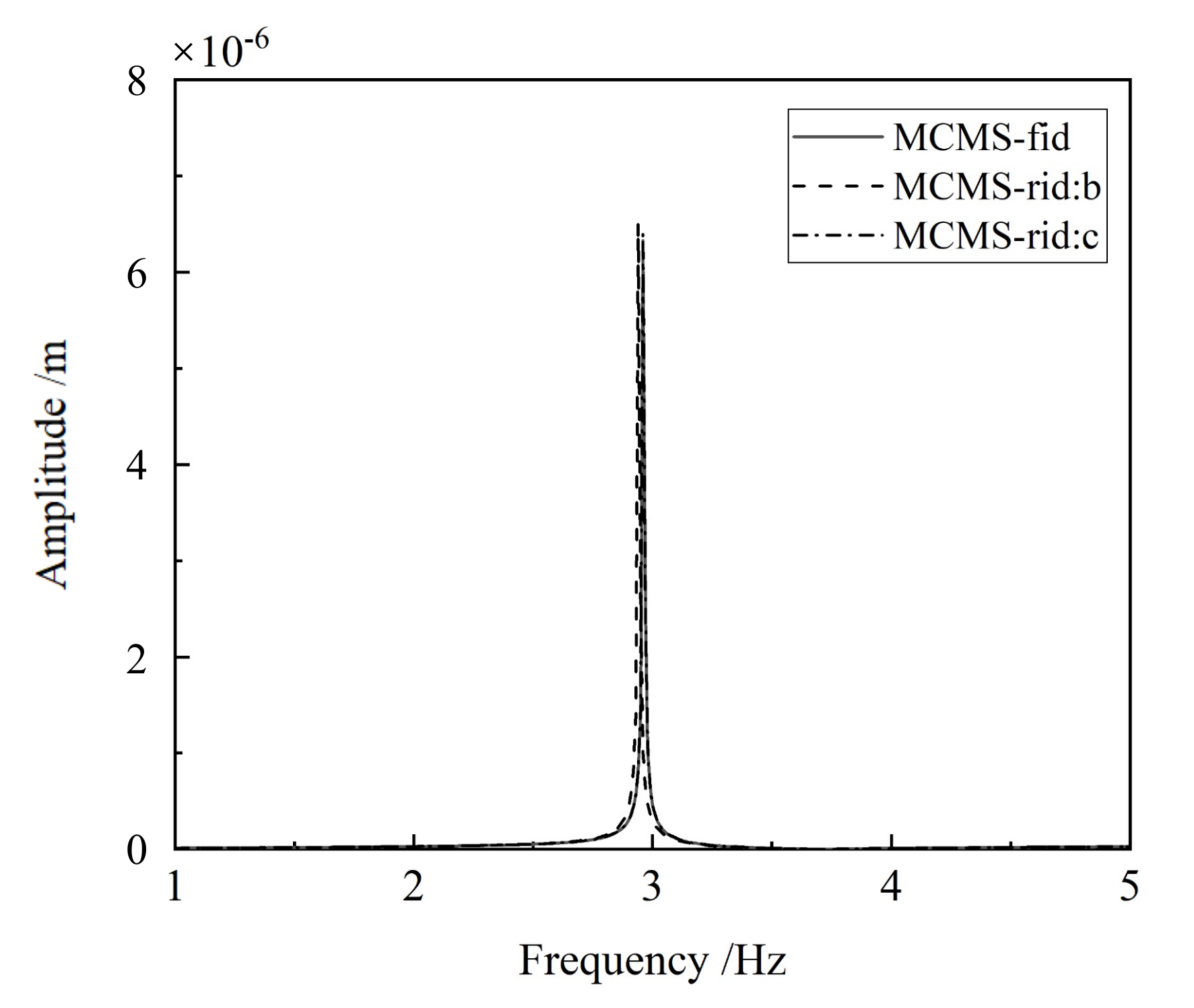
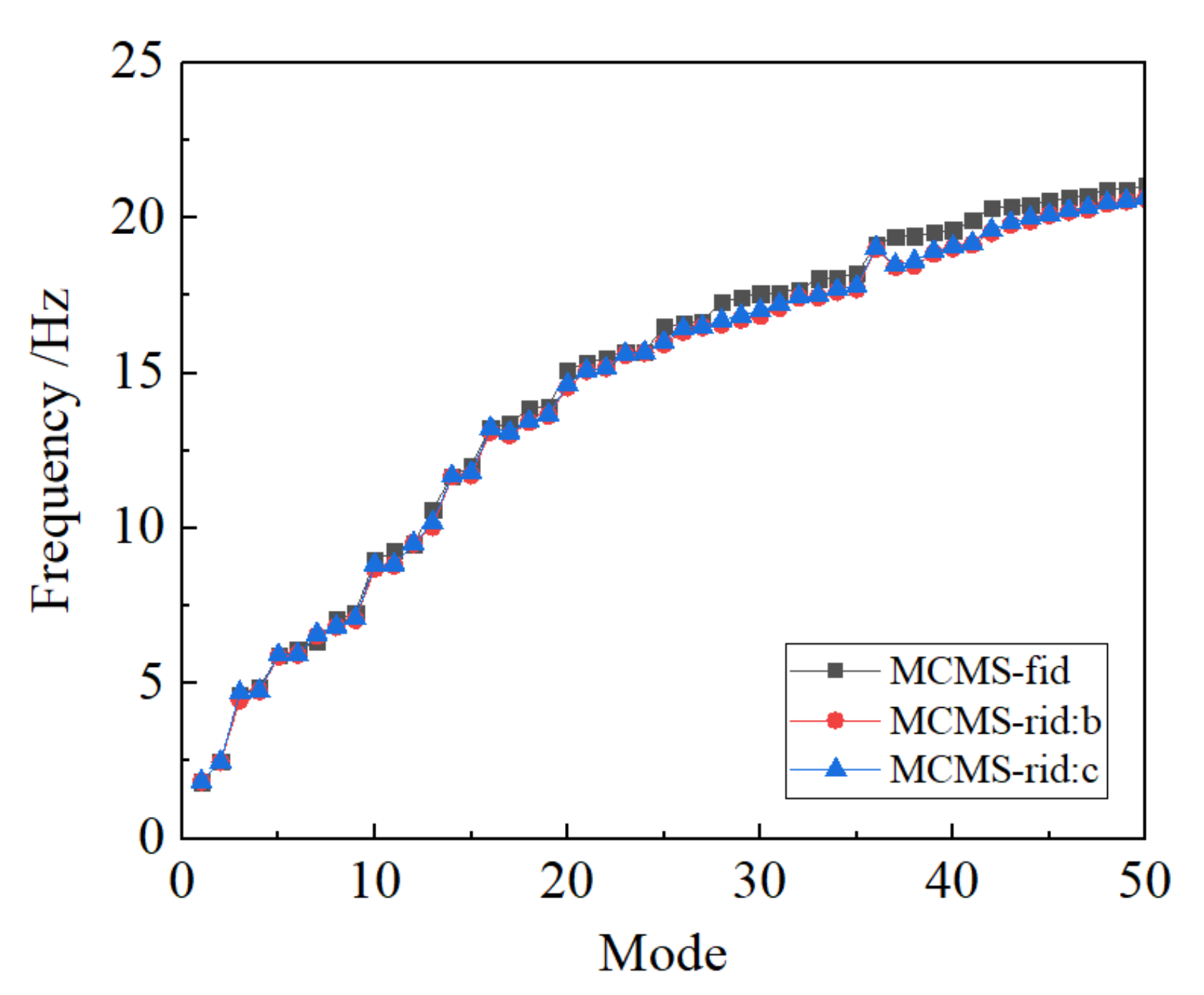
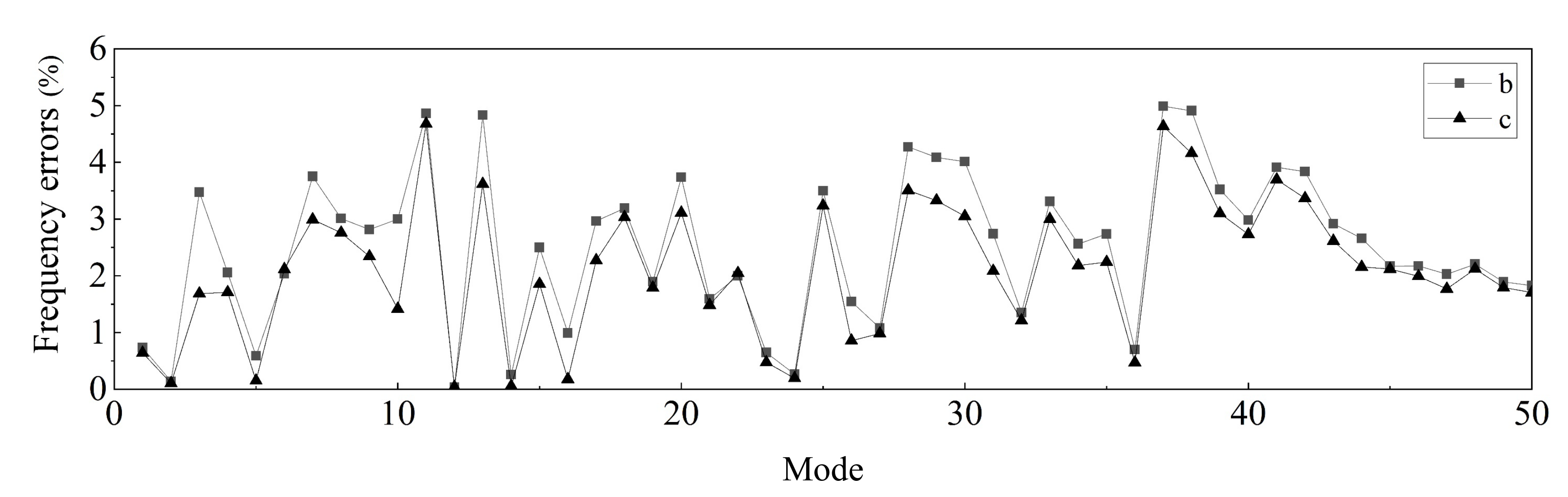
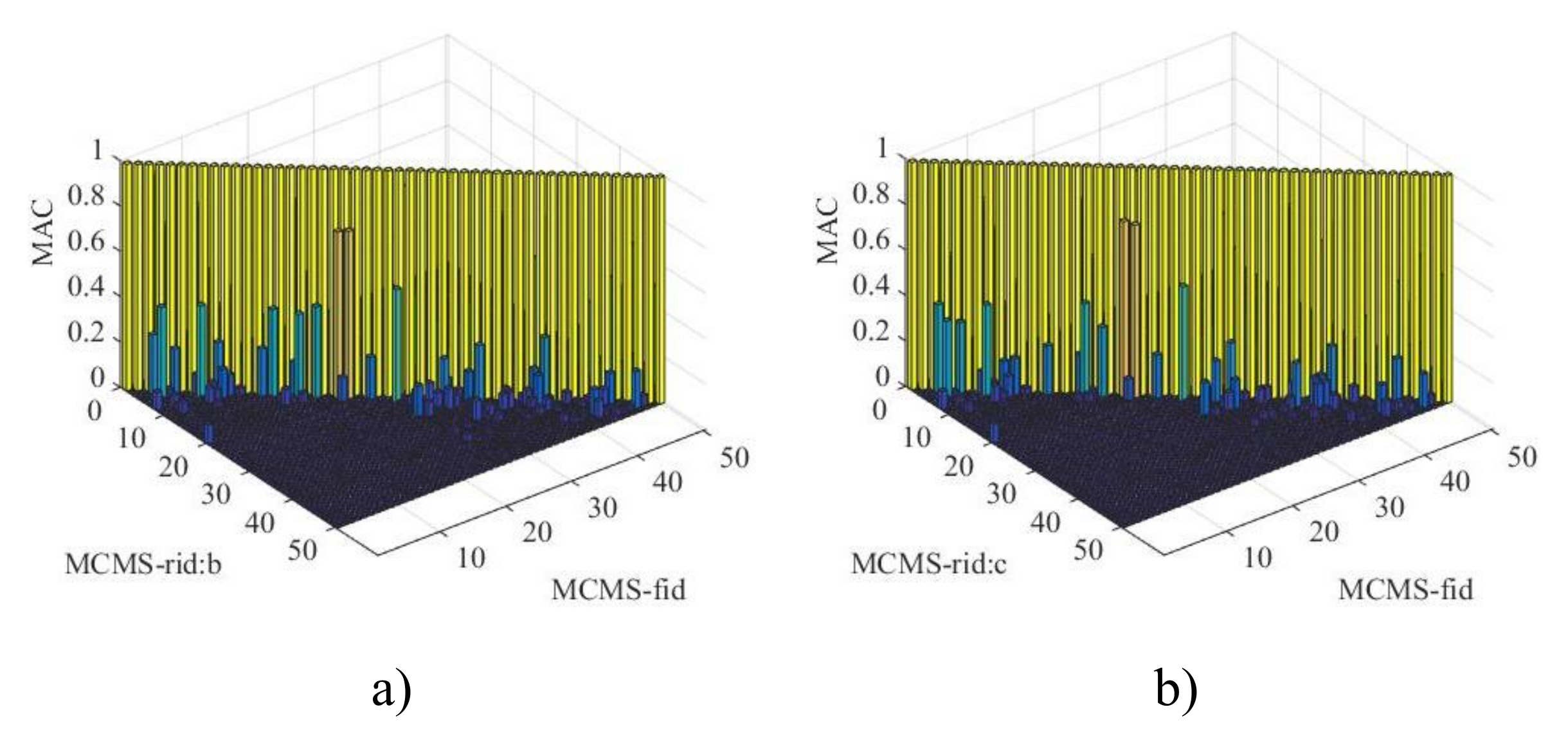
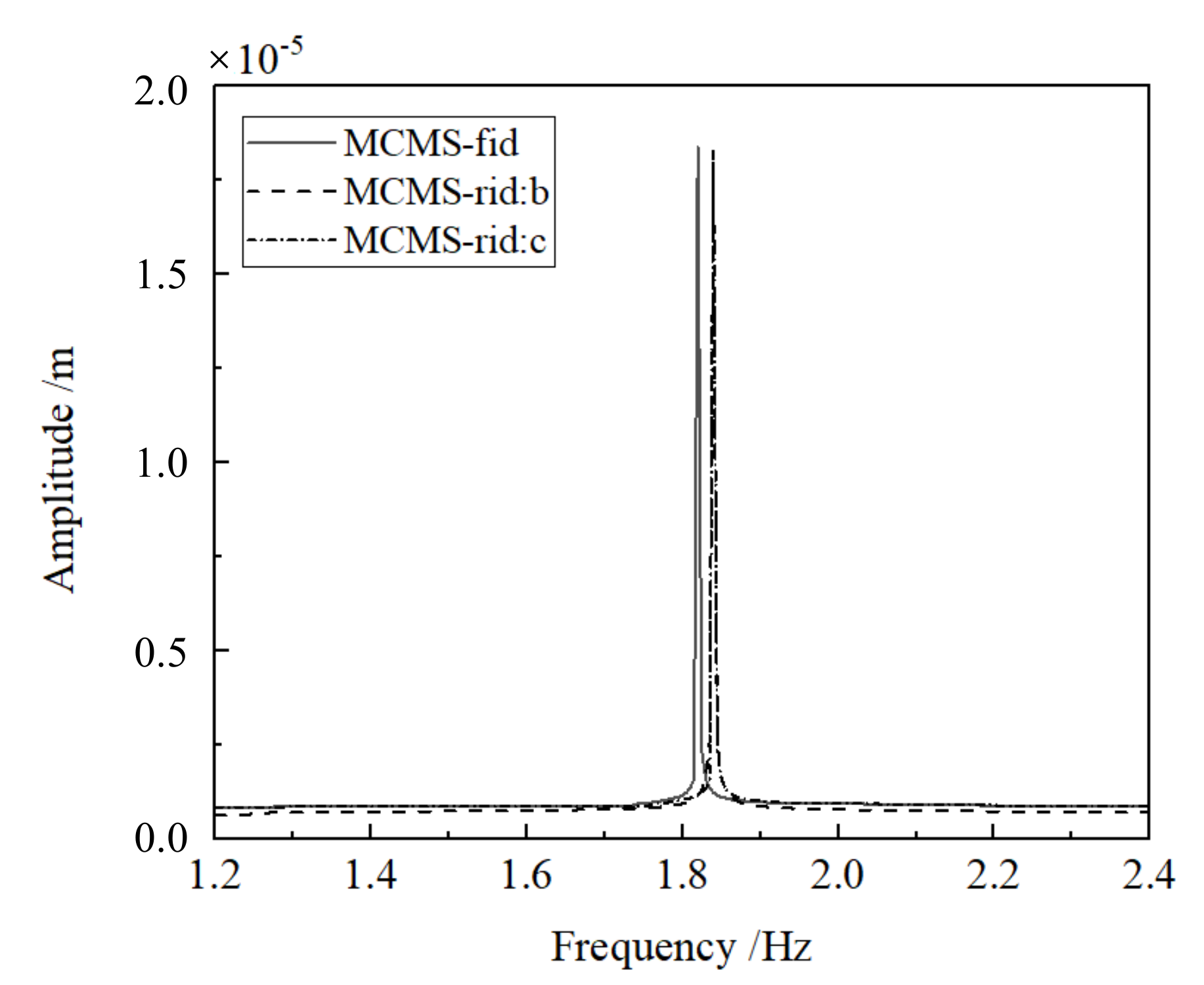
(b) The numerical performance of the MCMS-rid method is demonstrated by three different examples, where different structural properties and FE model size are discussed properly. The results indicate that favourable accuracy with a least number of the retained DOFs involved in modal synthesis can be obtained when compared with other MCMS methods.
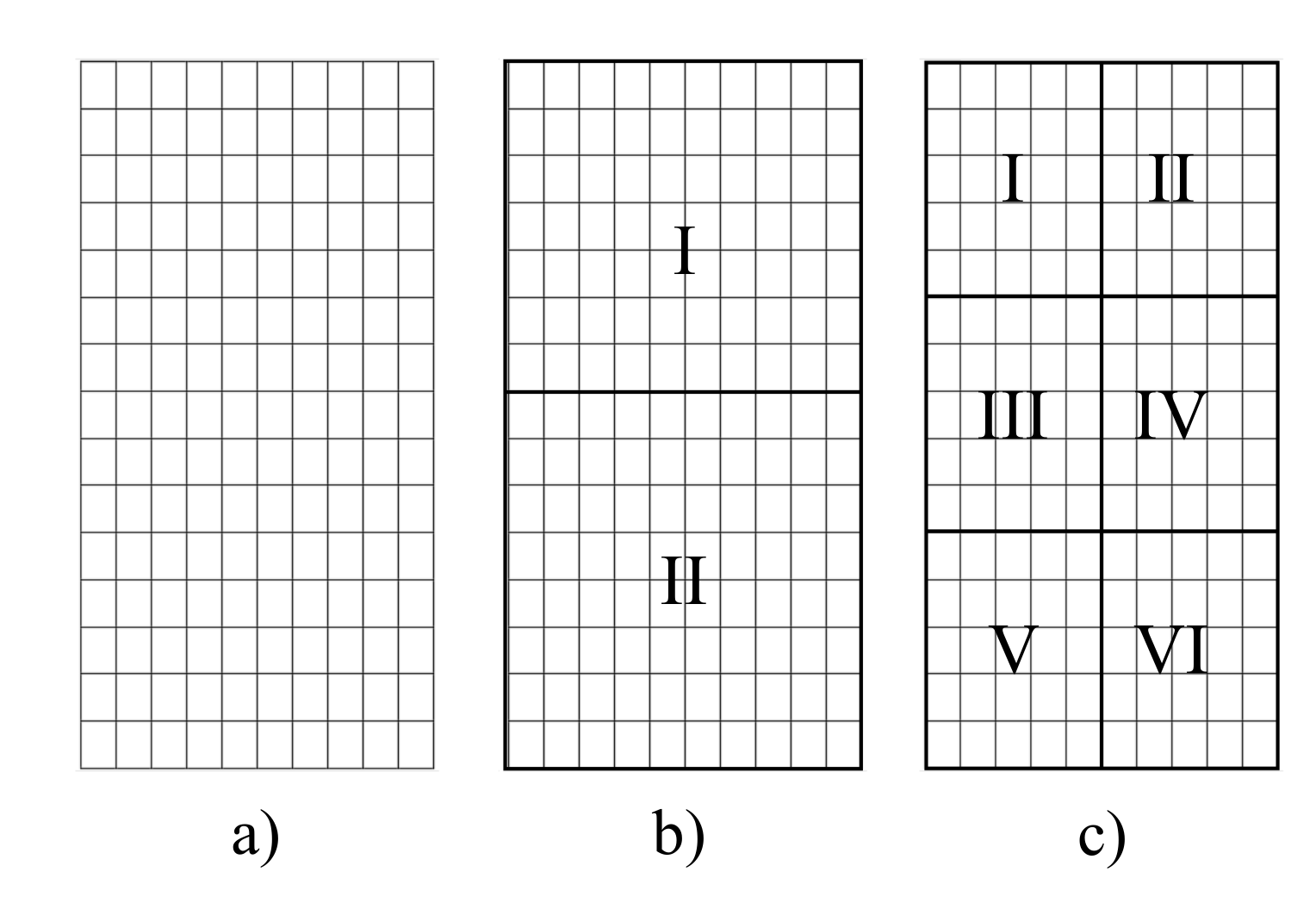
(c) The number and distribution of IBNs chosen for mode synthesis have significant influence on the numerical precision. It is noticed that the more the IBNs involved, the higher the calculation accuracy will be obtained. And when the IBNs uniformly distribute on the coupling interface, the accuracy is the best.
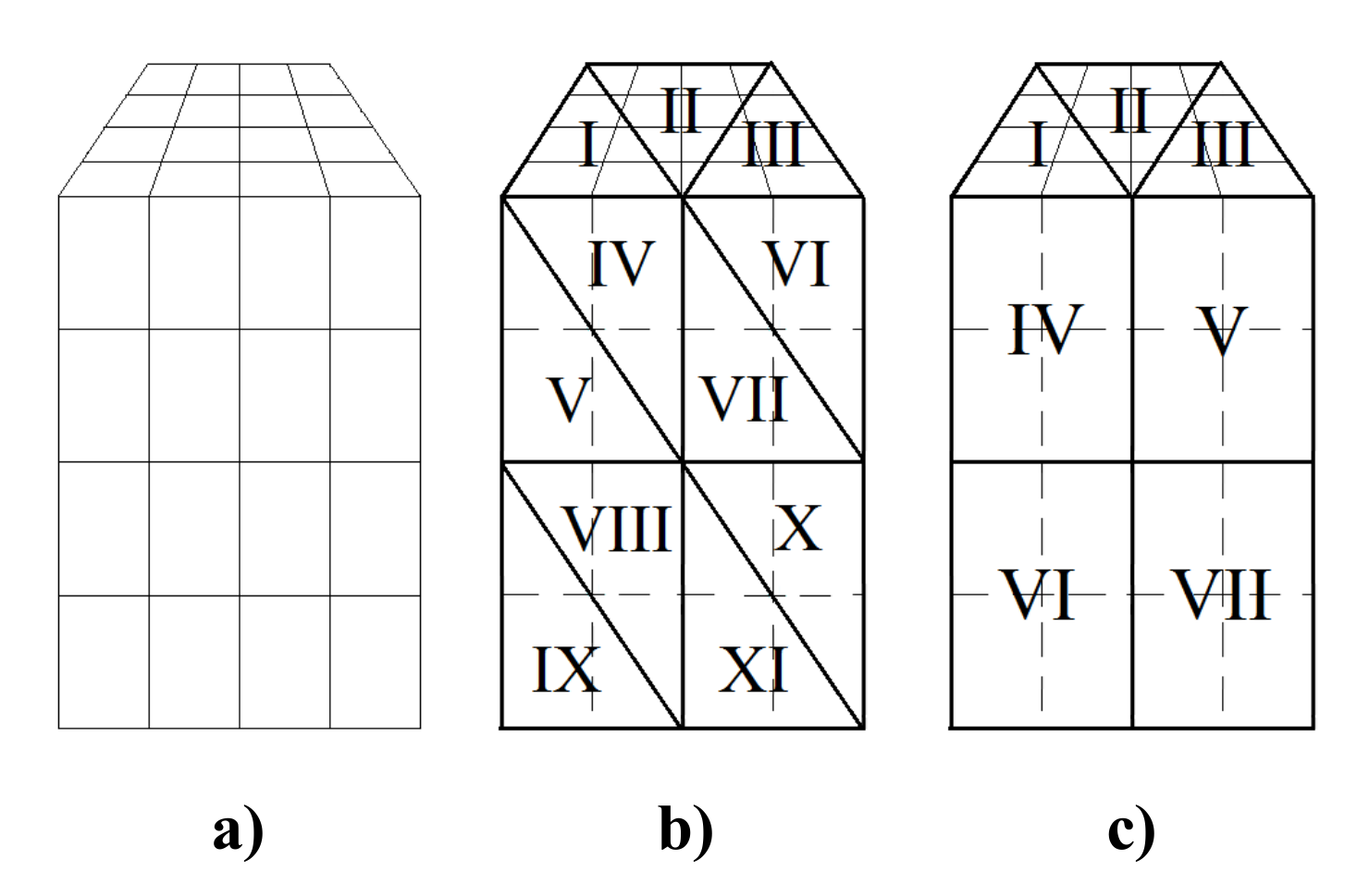
(d) The shape of sub-regions also greatly effects the computational accuracy. Dividing the interface with quadrangular interpolation sub-regions may receive a better accuracy than that with triangle ones. However, the triangle interpolation sub-regions show advantages when the coupling interface is irregular.