Health Monitoring of Civil Infrastructures by Subspace System Identification Method: An Overview
Abstract
:1. Introduction
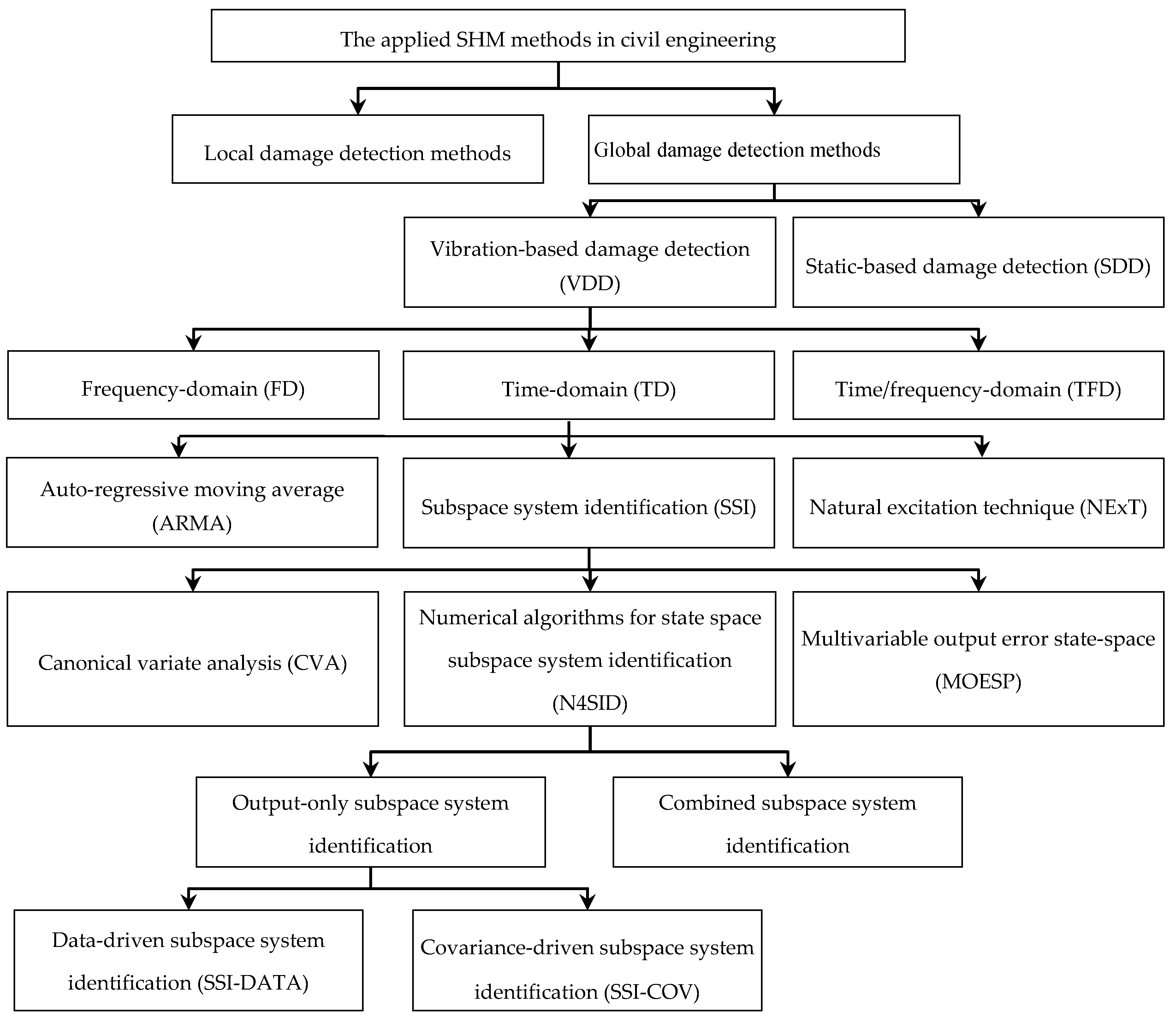
2. Structural Health Monitoring (SHM)
3. Vibration-Based Damage Detection (VDD)
3.1. Frequency-Domain (FD) Methods
- peak picking (PP) methods;
- complex mode indication function (CMIF) methods; and,
- least squares complex frequency-domain (LSCF) methods.
3.2. Time-Domain (TD) Methods
- NExT methods;
- ARMA methods; and,
- SSI methods.
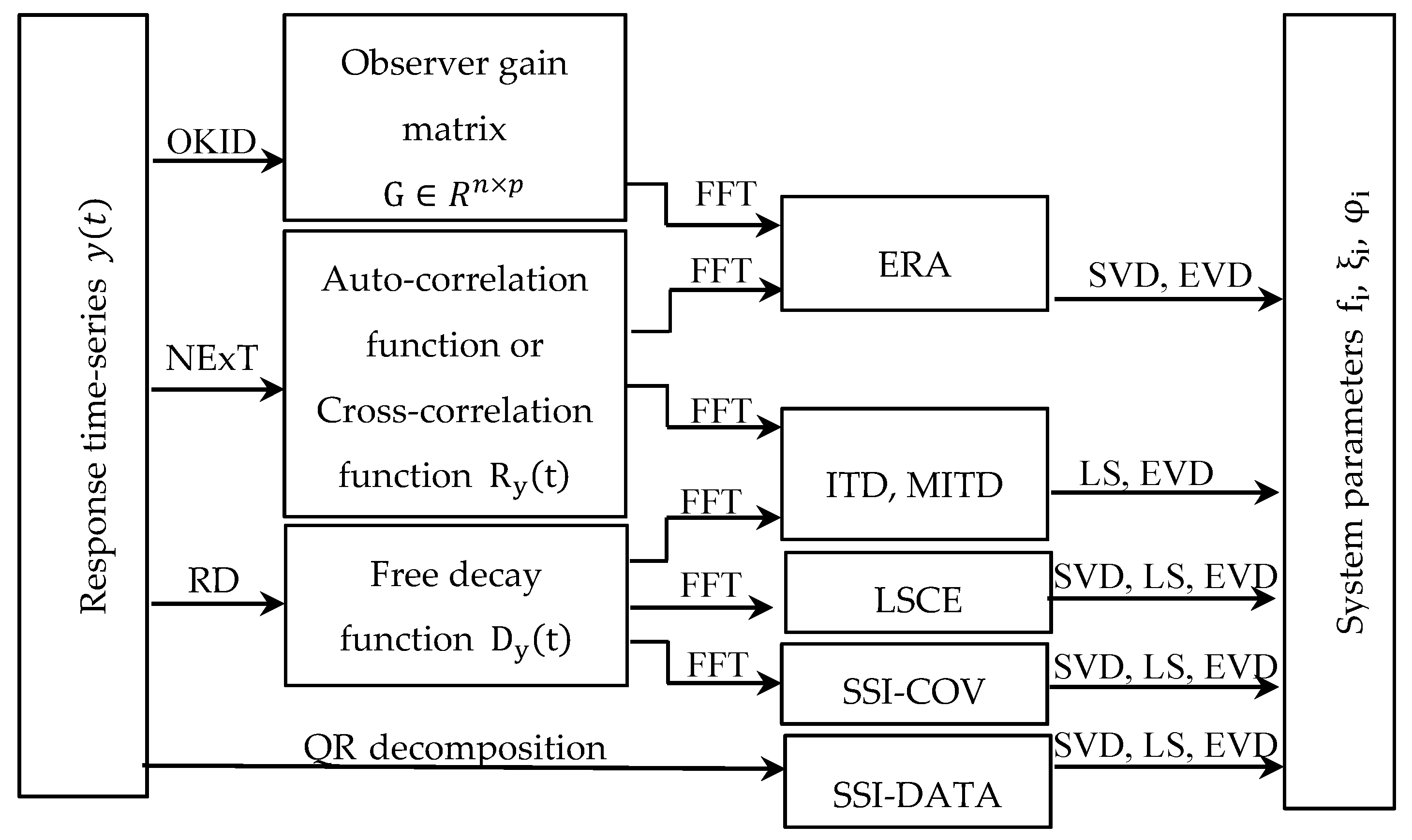
3.2.1. Natural Excitation Technique (NExT) Methods
3.2.2. Auto-Regressive Moving Average (ARMA) Methods
3.2.3. Subspace System Identification (SSI) Methods
- CVA methods;
- MOESP methods; and,
- N4SID methods.
Data-Driven Stochastic Subspace Identification Method (SSI-DATA)
Covariance-Driven Stochastic Subspace Identification (SSI-COV) Method
4. Comparison between SSI and Other System Identification Algorithms
5. Challenges of SSI in Practical Application
6. Application of Subspace Identification in Civil Engineering Structures
- beams and two dimensional (2D) frames;
- three dimensional (3D) frames and building structures; and,
- bridges and other structures.
7. Application of Subspace Identification in Civil Engineering Structures
8. Future Research Directions
9. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| AR | Auto regressive |
| ARMA | Auto-regressive moving average |
| ARMAX | Auto-Regressive Moving Average with eXogenous variable |
| ARX | Auto-Regressiv with eXogenous input |
| BFD | Basic frequency-domain |
| CE | Complex exponential |
| CMIF | Complex mode indication function |
| CVA | Canonical variate analysis |
| EFDD | Enhanced frequency domain decomposition |
| eFRF | Enhanced frequency response function |
| ERA | Eigensystem realization algorithm |
| ERA/DC. | ERA using data correlations |
| ERA-OKID-OO | Output-only ERA-OKID |
| ET | Eddy current test |
| EVD | Eigen-vector decomposition |
| FD | Frequency-domain |
| FE | Finite element |
| FFT | Fast Fourier transforms |
| FRF | Frequency response functions |
| IPCE | Improved polyreference complex exponential |
| ITD | Ibrahim time-domain |
| LS | Least-squares |
| LSCE | Least-squares complex exponential |
| MA | Moving average |
| MIMO | Multiple-input multiple-output |
| MOESP | Multivariable output error state-space |
| MRITD | Multiple references Ibrahim time-domain |
| N4SID | Numerical algorithms for state-space subspace system identification |
| NDE | Non-destructive evaluation |
| NExT | Natural excitation technique |
| O3KID | Output-only observer/Kalman filter identification |
| OKID | Observer/Kalman filter identification |
| PAUT | Phased array ultrasonic test |
| pLSCF | Poly-reference least squares complex frequency-domain |
| PolyMAX | Polyreference least-squares complex frequency-domain method |
| PP | Peak picking |
| PRCE | Polyreference complex exponential |
| RD | Random decrement |
| RDS | Random decrement signatures |
| RT | Radiographic test |
| SDD | Static-based damage detection |
| SHM | Structural health monitoring |
| SIMO | Single-input multiple-output |
| SISO | Single-input single-output |
| SSI | Subspace system identification |
| SSI-COV | Covariance-driven subspace system identification |
| SSI-DATA | Data-driven subspace system identification |
| SVD | Singular value decomposition |
| TARMA | Time-dependent auto-regressive moving average |
| TD | Time-domain |
| TFD | Time/frequency domain |
| UT | Ultrasonic test |
| VDD | Vibration-based damage detection |
References
- Zhao, H.; Ding, Y.; Nagarajaiah, S.; Li, A. Longitudinal Displacement Behavior and Girder End Reliability of a Jointless Steel-Truss Arch Railway Bridge during Operation. Appl. Sci. 2019, 9, 2222. [Google Scholar] [CrossRef] [Green Version]
- Artese, S.; Nico, G. TLS and GB-RAR Measurements of Vibration Frequencies and Oscillation Amplitudes of Tall Structures: An Application to Wind Towers. Appl. Sci. 2020, 10, 2237. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Guo, J.; Wen, X.; Ma, J.; Yang, F.; Wang, C.; Zhang, D. Monitoring and Analysis of Dynamic Characteristics of Super High-rise Buildings using GB-RAR: A Case Study of the WGC under Construction, China. Appl. Sci. 2020, 10, 808. [Google Scholar] [CrossRef] [Green Version]
- Zinno, R.; Artese, S.; Clausi, G.; Magarò, F.; Meduri, S.; Miceli, A.; Venneri, A. Structural Health Monitoring (SHM). Internet Things Smart Urban Ecosyst; Springer: Cham, Switzerland, 2019; pp. 225–249. [Google Scholar]
- Li, H.-N.; Ren, L.; Jia, Z.-G.; Yi, T.-H.; Li, D.-S. State-of-the-art in structural health monitoring of large and complex civil infrastructures. J. Civ. Struct. Heal. Monit. 2016, 6, 3–16. [Google Scholar] [CrossRef]
- Kurka, P.R.G.; Cambraia, H.N. Application of a multivariable input–output subspace identification technique in structural analysis. J. Sound Vib. 2008, 312, 461–475. [Google Scholar] [CrossRef]
- Rytter, A. Vibration Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Aalborg Univ Denmark, Aalborg, Denmark, 1993. [Google Scholar]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef] [Green Version]
- Qiao, L.; Esmaeily, A. An Overview of Signal-Based Damage Detection Methods. Appl. Mech. Mater. 2011, 94–96, 834–851. [Google Scholar] [CrossRef]
- Artese, S.; Zinno, R. TLS for Dynamic Measurement of the Elastic Line of Bridges. Appl. Sci. 2020, 10, 1182. [Google Scholar] [CrossRef] [Green Version]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Heal. Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Ozer, E.; Feng, Q.M. Structural Reliability Estimation with Participatory Sensing and Mobile Cyber-Physical Structural Health Monitoring Systems. Appl. Sci. 2019, 9, 2840. [Google Scholar] [CrossRef] [Green Version]
- Ljung, L. System Identification; Wiley Online Library: Hoboken, NJ, USA, 1999. [Google Scholar]
- Wu, B.; Wu, G.; Yang, C.; He, Y. Damage identification method for continuous girder bridges based on spatially-distributed long-gauge strain sensing under moving loads. Mech. Syst. Signal Process. 2018, 104, 415–435. [Google Scholar] [CrossRef]
- Chen, C.-C.; Wu, W.-H.; Liu, C.-Y.; Lai, G. Damage detection of a cable-stayed bridge based on the variation of stay cable forces eliminating environmental temperature effects. Smart Struct. Syst. 2016, 17, 859–880. [Google Scholar] [CrossRef] [Green Version]
- Yu, Z.; Xia, H.; Goicolea, J.M.; Xia, C. Bridge damage identification from moving load induced deflection based on wavelet transform and Lipschitz exponent. Int. J. Struct. Stab. Dyn. 2016, 16, 1550003. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.; Ni, Y.-Q.; Jin, H.; Inaudi, D.; Laory, I. A temperature-driven MPCA method for structural anomaly detection. Eng. Struct. 2019, 190, 447–458. [Google Scholar] [CrossRef]
- Cardini, A.J.; Dewolf, J.T. Implementation of a long-term bridge weigh-in-motion system for a steel girder bridge in the interstate highway system. J. Bridge Eng. 2009, 14, 418–423. [Google Scholar] [CrossRef] [Green Version]
- Cantero, D.; Karoumi, R.; González, A. The Virtual Axle concept for detection of localised damage using Bridge Weigh-in-Motion data. Eng. Struct. 2015, 89, 26–36. [Google Scholar] [CrossRef]
- Gonzalez, I.; Karoumi, R. BWIM aided damage detection in bridges using machine learning. J. Civ. Struct. Heal. Monit. 2015, 5, 715–725. [Google Scholar] [CrossRef]
- Kalyankar, R.; Uddin, N. Axle detection on prestressed concrete bridge using bridge weigh-in-motion system. J. Civ. Struct. Heal. Monit. 2017, 7, 191–205. [Google Scholar] [CrossRef]
- Xu, X.; Ren, Y.; Huang, Q.; Fan, Z.Y.; Tong, Z.J.; Chang, W.J.; Liu, B. Anomaly detection for large span bridges during operational phase using structural health monitoring data. Smart Mater. Struct. 2020, 29, 45029. [Google Scholar] [CrossRef]
- Kroll, A.; Schulte, H. Benchmark problems for nonlinear system identification and control using soft computing methods: Need and overview. Appl. Soft Comput. 2014, 25, 496–513. [Google Scholar] [CrossRef]
- Staszewski, W.J. Identification of non-linear systems using multi-scale ridges and skeletons of the wavelet transform. J. Sound Vib. 1998, 214, 639–658. [Google Scholar] [CrossRef]
- Qiao, L. Structural Damage Detection Using Signal-Based Pattern Recognition. Ph.D. Thesis, Kansas State University, Manhattan, KS, USA, 2009. [Google Scholar]
- Karbhari, V.M.; Guan, H. Sikorsky, C. Operational Modal Analysis for Vibration-based Structural Health Monitoring of Civil Structures. In Structural Health Monitoring of Civil Infrastructure Systems; Woodhead Publishing: Sawston/Cambridge, UK, 2009; pp. 213–259. [Google Scholar]
- Runtemund, K.; Cottone, G.; Müller, G. Treatment of arbitrarily autocorrelated load functions in the scope of parameter identification. Comput. Struct. 2013, 126, 29–40. [Google Scholar] [CrossRef] [Green Version]
- Pavlov, G.K. Design of Health Monitoring System to Detect Tower Oscilations. Master’s Thesis, Technical University of Denmark, Lyngby, Denmark, 2008. [Google Scholar]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Koloor, S.S.R.; Petru, M. Application of the Subspace-based Methods in Health Monitoring of the Civil Structures: A Systematic Review and Meta-analysis. Appl. Sci. 2020. (under review). [Google Scholar]
- Sohn, H.; Farrar, C.R.; Hemez, F.M.; Shunk, D.D.; Stinemates, D.W.; Nadler, B.R.; Czarnecki, J.J. A Review of Structural Health Monitoring Literature: 1996–2001; Los Alamos National Laboratory: Los Alamos, NM, USA, 2003.
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Koloor, S.S.R.; Petru, M. A Comparative Study of the Data-driven Stochastic Subspace Methods for Health Monitoring of Structures: A Bridge Case Study. Appl. Sci. 2020. (under review). [Google Scholar]
- Senthilnathan, K.; Hiremath, C.P.; Naik, N.K.; Guha, A.; Tewari, A. Microstructural damage dependent stiffness prediction of unidirectional CFRP composite under cyclic loading. Compos. Part A Appl. Sci. Manuf. 2017, 100, 118–127. [Google Scholar] [CrossRef]
- Yu, Y.; Zou, Y.; Al Hosani, M.; Tian, G. Conductivity Invariance Phenomenon of Eddy Current NDT: Investigation, Verification, and Application. IEEE Trans. Magn. 2017, 53, 1–7. [Google Scholar] [CrossRef]
- Alwash, M.; Breysse, D.; Sbartaï, Z.M.; Szilágyi, K.; Borosnyói, A. Factors affecting the reliability of assessing the concrete strength by rebound hammer and cores. Constr. Build. Mater. 2017, 140, 354–363. [Google Scholar] [CrossRef]
- Epp, T.; Cha, Y.-J. Wavelet Transform-Based Damage Detection in Reinforced Concrete Using an Air-Coupled Impact-Echo Method. In Structural Health Monitoring & Damage Detection; Springer: Cham, Switzerland, 2017; Volume 7, pp. 23–25. [Google Scholar]
- Davis, A.G.; Ansari, F.; Gaynor, R.D.; Lozen, K.M.; Rowe, T.J.; Caratin, H.; Heidbrink, F.D.; Malhotra, V.M.; Simons, B.P.; Carino, N.J.; et al. Nondestructive Test Methods for Evaluation of Concrete in Structures; American Concrete Institute, ACI: Farmington Hills, MI, USA, 1998. [Google Scholar]
- Kaiser, H.; Karbhari, V.M. Non-destructive testing techniques for FRP rehabilitated concrete. I: A critical review. Int. J. Mater. Prod. Technol. 2004, 21, 349–384. [Google Scholar] [CrossRef]
- Ettouney, M.M.; Alampalli, S. Infrastructure Health in Civil Engineering: Theory and Components; CRC Press: Boca Raton, FL, USA, 2016; Volume 1. [Google Scholar]
- Terlaje, A.; Gould, P.; Dyke, S. An Algorithm and Methodology for Static Response Based Damage Detection in Structural Systems. IEEE Trans. Signal Process. 1994, 8, 2146–2157. [Google Scholar]
- Eun, H.C.; Park, S.Y.; Lee, M.S. Static-Based Damage Detection Using Measured Strain and Deflection Data. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; Volume 256, pp. 1097–1100. [Google Scholar]
- Gul, M.; Catbas, F.N. Structural health monitoring and damage assessment using a novel time series analysis methodology with sensor clustering. J. Sound Vib. 2011, 330, 1196–1210. [Google Scholar] [CrossRef]
- Song, G.; Wang, C.; Wang, B. Structural Health Monitoring (SHM) of Civil Structures. Appl. Sci. 2017, 7, 789. [Google Scholar] [CrossRef]
- Reynders, E. System identification methods for (operational) modal analysis: Review and comparison. Arch. Comput. Methods Eng. 2012, 19, 51–124. [Google Scholar] [CrossRef]
- Ingle, V.; Proakis, J. Digital Signal Processing Using MATLAB; Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Bendat, J.S.; Piersol, A.G. Engineering Applications of Correlation and Spectral Analysis; Wiley-Interscience: New York, NY, USA, 1980. [Google Scholar]
- Brincker, R.; Zhang, L.; Andersen, P. Modal identification of output-only systems using frequency domain decomposition. Smart Mater. Struct. 2001, 10, 441. [Google Scholar] [CrossRef] [Green Version]
- Pioldi, F.; Rizzi, E. A refined Frequency Domain Decomposition tool for structural modal monitoring in earthquake engineering. Earthq. Eng. Eng. Vib. 2017, 16, 627–648. [Google Scholar] [CrossRef]
- Khalilinia, H.; Zhang, L.; Venkatasubramanian, V. Fast frequency-domain decomposition for ambient oscillation monitoring. IEEE Trans. Power Deliv. 2015, 30, 1631–1633. [Google Scholar] [CrossRef]
- Allemang, R.J.; Brown, D.L. A complete review of the complex mode indicator function (CMIF) with applications. In Proceedings of the ISMA International Conference on Noise and Vibration Engineering, Katholieke Universiteit Leuven, Leuven, Belgium, 18–20 September 2006; Volume 38, pp. 36–44. [Google Scholar]
- Guillaume, P.; Verboven, P.; Vanlanduit, S. Frequency-domain maximum likelihood identification of modal parameters with confidence intervals. In Proceedings of the International Seminar on Modal Analysis, Katholieke Universiteit Leuven, Leuven, Belgium, 16 September 1998; Volume 1, pp. 359–366. [Google Scholar]
- Peeters, B.; Van der Auweraer, H.; Guillaume, P.; Leuridan, J. The PolyMAX frequency-domain method: A new standard for modal parameter estimation? Shock Vib. 2004, 11, 395–409. [Google Scholar] [CrossRef]
- El-Kafafy, M.; Guillaume, P.; Peeters, B.; Marra, F.; Coppotelli, G. Advanced frequency-domain modal analysis for dealing with measurement noise and parameter uncertainty. In Topics in Modal Analysis I; Springer: New York, NY, USA, 2012; Volume 5, pp. 179–199. [Google Scholar]
- Kim, J.; Lynch, J.P. Comparison study of output-only subspace and frequency-domain methods for system identification of base excited civil engineering structures. In Civil Engineering Topics; Springer: New York, NY, USA, 2011; Volume 4, pp. 305–312. [Google Scholar]
- Liu, C.W.; Wu, J.Z.; Zhang, Y.G. Review and prospect on modal parameter identification of spatial lattice structure based on ambient excitation. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2011; Volume 94, pp. 1271–1277. [Google Scholar]
- Magalhães, F.; Caetano, E.; Cunha, Á. Challenges in the application of stochastic modal identification methods to a cable-stayed bridge. J. Bridge Eng. 2007, 12, 746–754. [Google Scholar] [CrossRef] [Green Version]
- Redif, S.; Weiss, S.; McWhirter, J.G. Relevance of polynomial matrix decompositions to broadband blind signal separation. Signal Process. 2017, 134, 76–86. [Google Scholar] [CrossRef] [Green Version]
- Cunha, A.; Caetano, E.; Magalhaes, F.; Moutinho, C. Recent perspectives in dynamic testing and monitoring of bridges. Struct. Control Heal. Monit. 2013, 20, 853–877. [Google Scholar] [CrossRef]
- James, G.H.; Carne, T.G.; Lauffer, J.P. The Natural Excitation Technique (NExT) for Modal Parameter Extraction from Operating Wind Turbines; Sandia National Labs: Albuquerque, NM, USA, 1993.
- Brown, D.L.; Allemang, R.J.; Zimmerman, R.; Mergeay, M. Parameter estimation techniques for modal analysis. SAE Technical paper. SAE Trans. 1979, 13, 176–186. [Google Scholar]
- Vold, H.; Kundrat, J.; Rocklin, G.T.; Russell, R. A Multi-Input Modal Estimation Algorithm for Mini-Computers; SAE Technical Paper; SAE: Warrendale, PA, USA, 1982. [Google Scholar]
- Juang, J.-N.; Pappa, R.S. An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. Control. Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]
- Juang, J.-N.; Cooper, J.E.; Wright, J.R. An eigensystem realization algorithm using data correlations (ERA/DC) for modal parameter identification. Control Adv. Technol. 1988, 4, 5–14. [Google Scholar]
- Zhang, L.; Yao, Y.; Lu, M. An improved time domain polyreference method for modal identification. Mech. Syst. Signal Process. 1987, 1, 399–413. [Google Scholar] [CrossRef]
- Zhang, L. An overview of major developments and issues in modal identification. In Proceedings of the 22nd International Modal Analysis Conference (IMAC), Detroit, MI, USA, 12 August 2004; pp. 1–8. [Google Scholar]
- Fukuzono, K. Investigation of Multiple-Reference Ibrahim Time Domain Modal Parameter Estimation Technique. Ph. D. Thesis, University of Cincinnati, Cincinnati, OH, USA, 1986. [Google Scholar]
- Juang, J.-N. Applied System Identification; Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Chang, M.; Pakzad, S.N. Observer Kalman Filter Identification for Output-Only Systems Using Interactive Structural Modal Identification Toolsuite. J. Bridge Eng. 2013, 19, 4014002. [Google Scholar] [CrossRef] [Green Version]
- Vicario, F.; Phan, M.Q.; Betti, R.; Longman, R.W. Output-only observer/Kalman filter identification (O3KID). Struct. Control Heal. Monit. 2014, 22, 847–872. [Google Scholar] [CrossRef]
- Cole, Jr. On-line Failure Detection and Damping Measurement of Aerospace Structures by Random Decrement Signatures; NASA: Washington, DC, USA, 1973; Volume 37.
- Brincker, R.; Rodrigues, J.; Brincker, R. Application of the random decrement technique in operational modal analysis. In Proceedings of the 1st International Operational Modal Analysis Conference (IOMAC), Aalborg Universitet, Aalborg, Denmark, 26–27 April 2005. [Google Scholar]
- Ljung, L. System Identification: Theory for the User, PTR Prentice Hall Information and System Sciences Series; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Sohn, H.; Czarnecki, J.A.; Farrar, C.R. Structural health monitoring using statistical process control. J. Struct. Eng. 2000, 126, 1356–1363. [Google Scholar] [CrossRef]
- Sohn, H.; Farrar, C.R. Damage diagnosis using time series analysis of vibration signals. Smart Mater. Struct. 2011, 10, 446–451. [Google Scholar] [CrossRef] [Green Version]
- Bodeux, J.B.; Golinval, J.C. Application of ARMAV models to the identification and damage detection of mechanical and civil engineering structures. Smart Mater. Struct. 2001, 10, 479–489. [Google Scholar] [CrossRef]
- Fasel, T.R.; Gregg, S.W.; Johnson, T.J.; Farrar, C.R.; Sohn, H. Experimental modal analysis and damage detection in a simulated three story building. In Proceedings of the 20th International Modal Analysis Conference, Los Angeles, CA, USA, 4–7 February 2002; pp. 122–135. [Google Scholar]
- Huang, C.S. Structural identification from ambient vibration measurement using the multivariate AR model. J. Sound Vib. 2001, 241, 337–359. [Google Scholar] [CrossRef] [Green Version]
- Hung, C.F.; Ko, W.J. Identification of modal parameters from measured output data using vector backward autoregressive model. J. Sound Vib. 2002, 256, 249–270. [Google Scholar] [CrossRef]
- Bodeux, J.B.; Golinval, J.C. Modal identification and damage detection using the data-driven stochastic subspace and ARMAV methods. Mech. Syst. Signal Process. 2003, 17, 83–89. [Google Scholar] [CrossRef]
- Bertha, M.; Golinval, J.-C. Identification of non-stationary dynamical systems using multivariate ARMA models. Mech. Syst. Signal Process. 2017, 88, 166–179. [Google Scholar] [CrossRef]
- Nair, K.K.; Kiremidjian, A.S.; Law, K.H. Time series-based damage detection and localization algorithm with application to the ASCE benchmark structure. J. Sound Vib. 2006, 291, 349–368. [Google Scholar] [CrossRef]
- Carden, E.P.; Brownjohn, J.M.W. ARMA modelled time-series classification for structural health monitoring of civil infrastructure. Mech. Syst. Signal Process. 2008, 22, 295–314. [Google Scholar] [CrossRef] [Green Version]
- Nair, K.K.; Kiremidjian, A.S. Time series based structural damage detection algorithm using Gaussian mixtures modeling. J. Dyn. Syst. Meas. Control 2007, 129, 285. [Google Scholar] [CrossRef]
- Omenzetter, P.; Brownjohn, J. Application of time series analysis for bridge monitoring. Smart Mater. Struct. 2006, 15, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Spiridonakos, M.D.; Poulimenos, A.G.; Fassois, S.D. Output-only identification and dynamic analysis of time-varying mechanical structures under random excitation: A comparative assessment of parametric methods. J. Sound Vib. 2010, 329, 768–785. [Google Scholar] [CrossRef]
- Gil, P.; Santos, F.; Palma, L.; Cardoso, A. Recursive subspace system identification for parametric fault detection in nonlinear systems. Appl. Soft Comput. 2015, 37, 444–455. [Google Scholar] [CrossRef]
- Brincker, R.; Andersen, P. Understanding stochastic subspace identification. In Proceedings of the 24th IMAC, St. Louis, MO, USA, 30 January–2 February 2006; p. 126. [Google Scholar]
- Gomez, H.C. System Identification of Highway Bridges using Long-Term Vibration Monitoring Data. Ph.D. Thesis, University of California, Irvine, CA, USA, 2012. [Google Scholar]
- Larimore, W.E. Canonical variate analysis in identification, filtering, and adaptive control. In Proceedings of the 29th IEEE Conference on Decision and Control, Honolulu, HI, USA, 5–7 December 1990; pp. 596–604. [Google Scholar]
- Akaike, H. Markovian representation of stochastic processes by canonical variables. SIAM J. Control 1975, 13, 162–173. [Google Scholar] [CrossRef]
- Verhaegen, M. Identification of the deterministic part of MIMO state space models given in innovations form from input-output data. Automatica 1994, 30, 61–74. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B.L. Subspace Identification for Linear Systems: Theory-Implementation-Applications; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Shokravi, H.; Bakhary, N.H. Comparative analysis of different weight matrices in subspace system identification for structural health monitoring. IOP Conf. Ser. Mater. Sci. Eng. 2017, 271, 12092. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B.; Dehandschutter, W.; Swevers, J. A subspace algorithm for the identification of discrete time frequency domain power spectra. Automatica 1997, 33, 2147–2157. [Google Scholar] [CrossRef]
- Basseville, M.; Abdelghani, M.; Benveniste, A. Subspace-based fault detection algorithms for vibration monitoring. Automatica 2000, 36, 101–109. [Google Scholar] [CrossRef]
- Yan, A.-M.M.; De Boe, P.; Golinval, J.-C.C. Structural damage diagnosis by Kalman model based on stochastic subspace identification. Struct. Heal. Monit. 2004, 3, 103–119. [Google Scholar] [CrossRef]
- Yan, A.-M.; Golinval, J.-C. Null subspace-based damage detection of structures using vibration measurements. Mech. Syst. Signal Process. 2006, 20, 611–626. [Google Scholar] [CrossRef] [Green Version]
- Reynders, E.; De Roeck, G. Reference-based combined deterministic–stochastic subspace identification for experimental and operational modal analysis. Mech. Syst. Signal Process. 2008, 22, 617–637. [Google Scholar] [CrossRef]
- Urgessa, G.S. Vibration properties of beams using frequency-domain system identification methods. J. Vib. Control 2010, 17, 1287–1294. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Golinval, J.-C. Fault detection based on kernel principal component analysis. Eng. Struct. 2010, 32, 3683–3691. [Google Scholar] [CrossRef]
- Goursat, M.; Döhler, M.; Mevel, L.; Andersen, P. Crystal clear SSI for operational modal analysis of aerospace vehicles. In Structural Dynamics; Springer: New York, NY, USA, 2011; Volume 3, pp. 1421–1430. [Google Scholar]
- Loh, C.H.; Weng, J.H.; Liu, Y.C.; Lin, P.Y.; Huang, S.K. Structural damage diagnosis based on on-line recursive stochastic subspace identification. Smart Mater. Struct. 2011, 20, 34–55. [Google Scholar] [CrossRef]
- Zhang, G.; Tang, B.; Tang, G. An improved stochastic subspace identification for operational modal analysis. Measurement 2012, 45, 1246–1256. [Google Scholar] [CrossRef]
- Chao, S.-H.; Loh, C.-H.; Weng, J.-H. Application of higher order SVD to vibration-based system identification and damage detection. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems; International Society for Optics and Photonics: Bellingham, WA, USA, 2012; Volume 8345, p. 834525. [Google Scholar] [CrossRef]
- Döhler, M.; Andersen, P.; Mevel, L. Operational modal analysis using a fast stochastic subspace identification method. In Topics in Modal Analysis I; Springer: New York, NY, USA, 2012; Volume 5, pp. 19–24. [Google Scholar]
- Hong, A.L.; Ubertini, F.; Betti, R. New Stochastic Subspace Approach for System Identification and Its Application to Long-Span Bridges. J. Eng. Mech. 2013, 139, 724–736. [Google Scholar] [CrossRef]
- Basseville, M.; Mevel, L.; Goursat, M. Statistical model-based damage detection and localization: Subspace-based residuals and damage-to-noise sensitivity ratios. J. Sound Vib. 2004, 275, 769–794. [Google Scholar] [CrossRef] [Green Version]
- Yu, D.-J.; Ren, W.-X. EMD-based stochastic subspace identification of structures from operational vibration measurements. Eng. Struct. 2005, 27, 1741–1751. [Google Scholar] [CrossRef]
- Zhang, Z.; Fan, J.; Hua, H. Simulation and experiment of a blind subspace identification method. J. Sound Vib. 2008, 311, 941–952. [Google Scholar] [CrossRef]
- Carden, E.P.; Brownjohn, J.M.W. Fuzzy Clustering of Stability Diagrams for Vibration-Based Structural Health Monitoring. Comput. Civ. Infrastruct. Eng. 2008, 23, 360–372. [Google Scholar] [CrossRef]
- Balmès, E.; Basseville, M.; Bourquin, F.; Mevel, L.; Nasser, H.; Treyssède, F. Merging sensor data from multiple temperature scenarios for vibration monitoring of civil structures. Struct. Heal. Monit. 2008, 7, 129–142. [Google Scholar] [CrossRef] [Green Version]
- Basseville, M.; Bourquin, F.; Mevel, L.; Nasser, H.; Treyssède, F. Handling the temperature effect in vibration monitoring: Two subspace-based analytical approaches. J. Eng. Mech. 2010, 136, 367. [Google Scholar] [CrossRef] [Green Version]
- Ren, W.X.; Lin, Y.Q.; Fang, S.E. Structural damage detection based on stochastic subspace identification and statistical pattern recognition: I. Theory. Smart Mater. Struct. 2011, 20, 115009. [Google Scholar] [CrossRef]
- Lin, Y.Q.; Ren, W.X.; Fang, S.E. Structural damage detection based on stochastic subspace identification and statistical pattern recognition: II. Experimental validation under varying temperature. Smart Mater. Struct. 2011, 20, 115010. [Google Scholar] [CrossRef]
- Li, Z.; Chang, C.C. Tracking of structural dynamic characteristics using recursive stochastic subspace identification and instrumental variable technique. J. Eng. Mech. 2011, 138, 591–600. [Google Scholar] [CrossRef]
- Loendersloot, R.; Schiphorst, F.B.A.; Basten, T.G.H.; Tinga, T. Application of SHM Using an Autonomous Sensor Network; DEStech Publications, Inc: Lancaster, PA, USA, 2013. [Google Scholar]
- Miguel, L.F.F.; Lopez, R.H.; Miguel, L.F.F. A hybrid approach for damage detection of structures under operational conditions. J. Sound Vib. 2013, 332, 4241–4260. [Google Scholar] [CrossRef]
- Chao, S.-H.; Loh, C.-H.; Tseng, M.-H. Structural damage assessment using output-only measurement: Localization and quantification. J. Intell. Mater. Syst. Struct. 2013, 25, 1097–1106. [Google Scholar] [CrossRef]
- Reynders, E.; Maes, K.; Lombaert, G.; De Roeck, G. Uncertainty quantification in operational modal analysis with stochastic subspace identification: Validation and applications. Mech. Syst. Signal Process. 2016, 66, 13–30. [Google Scholar] [CrossRef]
- Ozcelik, O.; Misir, I.S.; Amaddeo, C.; Yucel, U.; Durmazgezer, E. Modal Identification Results of Quasi-statically Tested RC Frames at Different Damage Levels. In Topics in Modal Analysis; Springer: Cham, Switzerland, 2015; Volume 10, pp. 215–226. [Google Scholar]
- Magalhães, F.; Reynders, E.; Cunha, Á.; De Roeck, G. Online automatic identification of modal parameters of a bridge using the p-LSCF method. In Proceedings of the IOMAC, Ancona, Italy, 4–6 May 2009. [Google Scholar]
- Wang, S.Q.; Zhang, Y.T.; Feng, Y.X. Comparative study of output-based modal identification methods using measured signals from an offshore platform. In ASME 2010 29th International Conference on Ocean, Offshore and Arctic Engineering; American Society of Mechanical Engineers: New York, NY, USA, 2010; pp. 561–567. [Google Scholar]
- Moaveni, B.; He, X.; Conte, J.P.; Restrepo, J.I.; Panagiotou, M. System identification study of a 7-story full-scale building slice tested on the UCSD-NEES shake table. J. Struct. Eng. 2010, 137, 705–717. [Google Scholar] [CrossRef] [Green Version]
- Cunha, A.; Caetano, E.; Ribeiro, P.; Müller, G. Vibration-based SHM of a centenary bridge: A comparative study between two different automated OMA techniques. Preservation 2011, 1, 12. [Google Scholar]
- Ceravolo, R.; Abbiati, G. Time domain identification of structures: Comparative analysis of output-only methods. J. Eng. Mech. 2012, 139, 537–544. [Google Scholar] [CrossRef]
- Sohn, H. A Bayesian Probabilistic Approach to Damage Detection for Civil Structures. Dep. Civ. Environ. Eng. 1998. [Google Scholar]
- Peeters, B.; De Roeck, G. Reference-based stochastic subspace identification for output-only modal analysis. Mech. Syst. Signal Process. 1999, 13, 855–878. [Google Scholar] [CrossRef] [Green Version]
- Pridham, B.A.; Wilson, J.C. A study of damping errors in correlation-driven stochastic realizations using short data sets. Probabilistic Eng. Mech. 2003, 18, 61–77. [Google Scholar] [CrossRef]
- Pan, Q. System identification of constructed civil engineering structures and uncertainty. Ph.D. Thesis, Drexel University, Philadelphia, PA, USA, 2007. [Google Scholar]
- Benveniste, A.; Mevel, L. Nonstationary consistency of subspace methods. Autom. Control IEEE Trans. 2007, 52, 974–984. [Google Scholar] [CrossRef] [Green Version]
- Reynders, E.; Pintelon, R.; De Roeck, G. Uncertainty bounds on modal parameters obtained from stochastic subspace identification. Mech. Syst. Signal Process. 2008, 22, 948–969. [Google Scholar] [CrossRef]
- Brasiliano, A.; Doz, G.; Brito, J.L.; Pimentel, R. Role of non-metallic components on the dynamic behavior of composite footbridges. In Proceedings of the Third International Conference–Footbridges, Porto, Portugal, 2–4 July 2008; pp. 501–522. [Google Scholar]
- Alıcıoğlu, B.; Luş, H. Ambient vibration analysis with subspace methods and automated mode selection: Case studies. J. Struct. Eng. 2008, 134, 1016–1029. [Google Scholar] [CrossRef]
- Marchesiello, S.; Bedaoui, S.; Garibaldi, L.; Argoul, P. Time-dependent identification of a bridge-like structure with crossing loads. Mech. Syst. Signal Process. 2009, 23, 2019–2028. [Google Scholar] [CrossRef]
- Balmès, É.; Basseville, M.; Mevel, L.; Nasser, H. Handling the temperature effect in vibration monitoring of civil structures: A combined subspace-based and nuisance rejection approach. Control Eng. Pract. 2009, 17, 80–87. [Google Scholar]
- Wang, J.; Sano, A.; Chen, T.; Huang, B. Identification of Hammerstein systems without explicit parameterisation of non-linearity. Int. J. Control 2009, 82, 937–952. [Google Scholar] [CrossRef]
- Magalhães, F.; Cunha, Á.; Caetano, E.; Brincker, R. Damping estimation using free decays and ambient vibration tests. Mech. Syst. Signal Process. 2010, 24, 1274–1290. [Google Scholar] [CrossRef] [Green Version]
- Döhler, M.; Reynders, E.; Magalhaes, F.; Mevel, L.; De Roeck, G.; Cunha, A. Pre-and post-identification merging for multi-setup OMA with covariance-driven SSI. In Dynamics of Bridges; Springer: New York, NY, USA, 2011; Volume 5, pp. 57–70. [Google Scholar]
- Carden, E.P.; Mita, A. Challenges in developing confidence intervals on modal parameters estimated for large civil infrastructure with stochastic subspace identification. Struct. Control Heal. Monit. 2011, 18, 53–78. [Google Scholar] [CrossRef]
- Döhler, M.; Mevel, L. Modular subspace-based system identification from multi-setup measurements. IEEE Trans. Automat. Contr. 2012, 57, 2951–2956. [Google Scholar] [CrossRef]
- Döhler, M.; Lam, X.-B.; Mevel, L. Uncertainty quantification for modal parameters from stochastic subspace identification on multi-setup measurements. Mech. Syst. Signal Process. 2013, 36, 562–581. [Google Scholar] [CrossRef]
- Loh, C.H.; Chen, M.C. Modeling of environmental effects for vibration-based shm using recursive stochastic subspace identification analysis. In Key Engineering Materials; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2013; Volume 558, pp. 52–64. [Google Scholar]
- Brehm, M.; Zabel, V.; Bucher, C. Optimal reference sensor positions using output-only vibration test data. Mech. Syst. Signal Process. 2013, 41, 196–225. [Google Scholar] [CrossRef]
- Cara, F.J.; Juan, J.; Alarcón, E.; Reynders, E.; De Roeck, G. Modal contribution and state space order selection in operational modal analysis. Mech. Syst. Signal Process. 2013, 38, 276–298. [Google Scholar] [CrossRef] [Green Version]
- Ashari, A.E.; Mevel, L. Auxiliary input design for stochastic subspace-based structural damage detection. Mech. Syst. Signal Process. 2013, 34, 241–258. [Google Scholar] [CrossRef]
- Tondreau, G.; Deraemaeker, A. Numerical and experimental analysis of uncertainty on modal parameters estimated with the stochastic subspace method. J. Sound Vib. 2014, 333, 4376–4401. [Google Scholar] [CrossRef] [Green Version]
- Rainieri, C.; Fabbrocino, G. Influence of model order and number of block rows on accuracy and precision of modal parameter estimates in stochastic subspace identification. Int. J. Lifecycle Perform Eng. 10 2014, 1, 317–334. [Google Scholar] [CrossRef]
- Cho, S.; Park, J.-W.; Sim, S.-H. Decentralized system identification using stochastic subspace identification for wireless sensor networks. Sensors 2015, 15, 8131–8145. [Google Scholar] [CrossRef] [Green Version]
- Markovsky, I. The most powerful unfalsified model for data with missing values. Syst. Control Lett. 2016, 95, 53–61. [Google Scholar] [CrossRef]
- Banfi, L.; Carassale, L. Uncertainties in an Application of Operational Modal Analysis. In Model Validation and Uncertainty Quantification; Springer: Cham, Switzerland, 2016; Volume 3, pp. 107–115. [Google Scholar]
- Spiridonakos, M.D.; Chatzi, E.N.; Sudret, B. Polynomial Chaos Expansion Models for the Monitoring of Structures under Operational Variability. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2016, 2, B4016003. [Google Scholar] [CrossRef]
- Huynh, T.C.; Park, J.H.; Kim, J.T. Structural identification of cable-stayed bridge under back-to-back typhoons by wireless vibration monitoring. Measurement 2016, 88, 385–401. [Google Scholar] [CrossRef]
- Li, D.; Ren, W.-X.; Hu, Y.-D.; Yang, D. Operational modal analysis of structures by stochastic subspace identification with a delay index. Struct. Eng. Mech. 2016, 59, 187–207. [Google Scholar] [CrossRef]
- Pepe, M.; Costantino, D.; Restuccia Garofalo, A. An Efficient Pipeline to Obtain 3D Model for HBIM and Structural Analysis Purposes from 3D Point Clouds. Appl. Sci. 2020, 10, 1235. [Google Scholar] [CrossRef] [Green Version]
- Kovačević, S.M.; Bačić, M.; Stipanović, I.; Gavin, K. Categorization of the Condition of Railway Embankments Using a Multi-Attribute Utility Theory. Appl. Sci. 2019, 9, 5089. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Ding, Y.; Sun, P.; Zhao, H.; Geng, F. Modeling of Temperature Time-Lag Effect for Concrete Box-Girder Bridges. Appl. Sci. 2019, 9, 3255. [Google Scholar] [CrossRef] [Green Version]
- Vanlanduit, S.; Parloo, E.; Cauberghe, B.; Guillaume, P.; Verboven, P. A robust singular value decomposition for damage detection under changing operating conditions and structural uncertainties. J. Sound Vib. 2005, 284, 1033–1050. [Google Scholar] [CrossRef]
- Naseralavi, S.S.; Salajegheh, E.; Fadaee, M.J.; Salajegheh, J. A novel sensitivity-based method for damage detection of structures under unknown periodic excitations. J. Sound Vib. 2014, 333, 2776–2803. [Google Scholar] [CrossRef]
- Döhler, M.; Hille, F. Subspace-based damage detection on steel frame structure under changing excitation. In Structural Health Monitoring; Springer: Cham, Switzerland, 2014; Volume 5, pp. 167–174. [Google Scholar]
- Banan, M.R.; Mehdi-Pour, Y. Detection and assessment of damage in 2D structures using measured modal response. J. Sound Vib. 2007, 306, 803–817. [Google Scholar] [CrossRef]
- Siegert, D.; Döhler, M.; Mekki OBen Mevel, L.; Goursat, M.; Toutlemonde, F. Vibration monitoring of a small span composite bridge. In Structural Dynamics; Springer: New York, NY, USA, 2011; Volume 3, pp. 53–61. [Google Scholar]
- Huang, M.C.; Wang, Y.P.; Chang, M.L. Damage Detection of Structures Identified with Deterministic-Stochastic Models Using Seismic Data. Sci. World J. 2014, 2014. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Lynch, J.P. Subspace system identification of support excited structures-part II: Gray-box interpretations and damage detection. Earthq. Eng. Struct. Dyn. 2012, 41, 2253–2271. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.P.; Lin, Y.T.; Huang, G. Damage Localization of Output-Only Frame Systems Using Stochastic Subspace Identification. Adv. Mater. Res. 2012, 3, 1352–1359. [Google Scholar] [CrossRef]
- Moaveni, B.; Stavridis, A.; Shing, P.B. System identification of a three-story infilled RC frame tested on the UCSD-NEES shake table. In Dynamics of Civil Structures; Springer: New York, NY, USA, 2011; Volume 4, pp. 135–143. [Google Scholar]
- Weng, J.H.; Loh, C.H.; Yang, J.N. Experimental Study of Damage Detection by Data-Driven Subspace Identification and Finite-Element Model Updating. J. Struct. Eng. 2009, 135, 1533–1544. [Google Scholar] [CrossRef]
- Karami, K.; Akbarabadi, S. Developing a Smart Structure Using Integrated Subspace-Based Damage Detection and Semi-Active Control. Comput. Civ. Infrastruct. Eng. 2016, 31, 887–903. [Google Scholar] [CrossRef]
- Belleri, A.; Moaveni, B.; Restrepo, J.I. Damage assessment through structural identification of a three-story large-scale precast concrete structure. Earthq. Eng. Struct. Dyn. 2014, 43, 61–76. [Google Scholar] [CrossRef]
- Shinagawa, Y.; Mita, A. Verification of structural health assessment method using full-scale collapse test of four-story steel building. In Key Engineering Materials; Trans Tech Publications Ltd.: Stäfa, Switzerland, 2013; pp. 174–183. [Google Scholar] [CrossRef]
- Zhou, W.; Li, H.; Mevel, L.; Döhler, M.; Lam, X.B.; Mao, C.; Ou, J. Seismic Damage Assessment for a Residential Masonry Building Using Aftershock Monitoring of Wenchuan Earthquake. In Proceedings of the 24th International Conference on Noise and Vibration Engineering (ISMA2010), Leuven, Belgium, 20 September 2010; pp. 773–782. [Google Scholar]
- Yoshimoto, R.; Mita, A.; Okada, K. Damage detection of base-isolated buildings using multi-input multi-output subspace identification. Earthq. Eng. Struct. Dyn. 2005, 34, 307–324. [Google Scholar] [CrossRef]
- Allahdadian, S.; Ventura, C.E.; Andersen, P.; Mevel, L.; Dohler, M. Sensitivity Evaluation of Subspace-Based Damage Detection Method to Different Types of Damage. In Structural Health Monitoring and Damage Detection; Springer: Cham, Switzerland, 2015; pp. 11–18. [Google Scholar] [CrossRef] [Green Version]
- Dohler, M.; Hille, F.; Mevel, L.; Rucker, W. Structural health monitoring with statistical methods during progressive damage test of S101 Bridge. Eng. Struct. 2014, 69, 183–193. [Google Scholar] [CrossRef] [Green Version]
- Deraemaeker, A.; Reynders, E.; De Roeck, G.; Kullaa, J. Vibration-based structural health monitoring using output-only measurements under changing environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef] [Green Version]
- Hu, W.H.; Moutinho, C.; Caetano, E.; Magalhaes, F.; Cunha, A. Continuous dynamic monitoring of a lively footbridge for serviceability assessment and damage detection. Mech. Syst. Signal Process. 2012, 33, 38–55. [Google Scholar] [CrossRef]
- Loh, C.-H.H.; Chao, S.-H.H. Centralized vs. Pattern-level Feature Extraction for Structural Damage Detection. Theor. Appl. Mech. 2014, 79, 479–489. [Google Scholar] [CrossRef] [Green Version]
- Mevel, L.; Goursat, M. Stochastic subspace-based structural identification and damage detection and localisation - Application to the Z24 bridge benchmark. Mech. Syst. Signal Process. 2003, 17, 143–151. [Google Scholar] [CrossRef]
- Kullaa, J. Damage detection of the Z24 bridge using control charts. Mech. Syst. Signal Process. 2003, 17, 163–170. [Google Scholar] [CrossRef]
- Reynders, E.; Wursten, G.; De Roeck, G. Output-only structural health monitoring in changing environmental conditions by means of nonlinear system identification. Struct. Heal. Monit. Int. J. 2014, 13, 82–93. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Mahowald, J.; Maas, S.; Golinval, J.-C. Use of time-and frequency-domain approaches for damage detection in civil engineering structures. Shock Vib. 2014, 2014. [Google Scholar] [CrossRef]
- Cruz, P.J.S.; Salgado, R. Performance of Vibration-Based Damage Detection Methods in Bridges. Comput. Civ. Infrastruct. Eng. 2009, 24, 62–79. [Google Scholar] [CrossRef]
- Nigro, M.B.; Pakzad, S.N.; Dorvash, S. Localized structural damage detection: A change point analysis. Comput. Civ. Infrastruct. Eng. 2014, 29, 416–432. [Google Scholar] [CrossRef]
- Döhler, M.; Andersen, P.; Mevel, L. Variance computation of modal parameter estimates from UPC subspace identification. Irnia 2017, 16, 416–432. [Google Scholar]
- Zhou, Y.; Prader, J.; Weidner, J.; Moon, F.; Aktan, A.E.; Zhang, J.; Yi, W.J. Structural Identification Study of a Steel Multi-Girder Bridge Based on Multiple Reference Impact Test. Int. Symp. Innov. Sustain. Struct. Civ. Eng. 2013, 12, 315–356. [Google Scholar]
- Hu, W.-H.; Cunha, Á.; Caetano, E.; Magalhães, F.; Moutinho, C. LabVIEW toolkits for output-only modal identification and long-term dynamic structural monitoring. Struct. Infrastruct. Eng. 2010, 6, 557–574. [Google Scholar] [CrossRef]
- Chang, M.; Pakzad, S.N.; Leonard, R. Modal identification using smit. In Topics on the Dynamics of Civil Structures; Springer: New York, NY, USA, 2012; Volume 1, pp. 221–228. [Google Scholar]
- Goursat, M.; Mevel, L. COSMAD: Identification and diagnosis for mechanical structures with Scilab. In Proceedings of the 2008 IEEE International Conference on Computer-Aided Control Systems, San Antonio, TX, USA, 3–5 September 2008; pp. 353–358. [Google Scholar]
- Hoofar, S.; Hooman, S.; Norhisham, B.; Heidarrezaei, M.; Koloor, S.S.R.; Petru, M. Vehicle-assisted techniques for health monitoring of bridges. Sensors (Basel) 2020. (Under review). [Google Scholar]
- Shokravi, H.; Shokravi, H.; Bakhary, N.; Heidarrezaei, M.; Koloor, S.R.K.; Petru, M. A review on vehicle classification methods and the potential of using smart-vehicle-assisted techniques. Sensors (Basel) 2020. (under review). [Google Scholar]
| Used Polynomials | Name of Model |
|---|---|
| , | ARX |
| , , | Auto-Regressive Moving Average with eXogenous variable (ARMAX) |
| , | ARMA |
| , , | Auto-Regressive Auto-Regressive with eXogenous input (ARARX) |
| Method/Reference | Test Model | Damage Feature | Pattern Recognition |
|---|---|---|---|
| AR [72] | Progressive failure test of retrofitted reinforced concrete bridge column | AR coefficients | X-bar control chart |
| AR-ARX [73] | Laboratory-scale 8- DOF mass-spring system | Residual error between prediction and reference signal | Multi-paradigm statistical pattern recognition |
| ARMAV [74] | Numerical model of a simply supported beam and a real-size steel-quake structure | Changes in natural frequency | Confidence interval and normal distribution of random variables |
| AR-ARX [75] | A simulated three-story frame structure | Residual errors | Sequential Probability Ratio Test (SPRT) |
| VFAR [76] | Numerical simulations of a six-story shear building and a three-span pre-stressed box-girder bridge | Natural frequency and damping ratio | - |
| VBAR [77] | Numerical model of a lumped mass system and experimental model of a steel cantilever beam | Natural frequency | - |
| ARMAV [78] | Steel-quake structure | Natural frequencies and damping ratio | - |
| TV-ARMAV [79] | Supported beam with a moving mass | Natural frequencies and mode shapes and damping ratio | - |
| ARMA [80] | Analytical and experimental results of the ASCE benchmark structure | First three AR components | Multi-paradigm statistical signal processing approach combined with the pattern classification |
| ARMA [81] | IASC–ASCE four-story experimental benchmark structure, Z24 bridge and the Malaysia–Singapore Second Link Bridge | Normalized AR coefficient | T-test statistical control chart |
| ARMA [82] | Simulated ASCE benchmark structure | GMM | Mahalanobis criterion function |
| ARIMA [83] | Data from Malaysia-Singapore Second Link bridge | Coefficients of the ARIMA model | Statistical outlier detection |
| TARMA [84] | Laboratory-scale steel beam with a moving mass | Natural frequencies | - |
| Method/Reference | Damage Feature | Pattern Recognition | Test Model | Specification |
|---|---|---|---|---|
| SSI-DATA [94] | Eigensolutions | Statistical local approach | Analytical model | Application of a combined SSI |
| SSI-DATA [95] | Residual error | Statistical process control | Aircraft model and real bridge structure | Kalman model is extracted to represent the reference state of the structure. |
| Null-space based algorithm [96] | Residue matrix of orthonormality between subspaces | Statistical process control | Aircraft model and steel lighting device | Subspace analysis of the Hankel matrices is used for extracting features. |
| CSI/ref [97] | Modal parameters | - | Z24 bridge benchmark structure | Stabilization diagram is adopted for post processing of modal data. |
| McKelvey FD SSI [98] | Modal parameters | - | Uncontrolled cantilever plate | Natural frequency was predicted with an average error of 3.2% and damping ratio had an average error of 2.8% |
| KPCA subspace based damage detection [99] | Subspace angles | Through mapping the Subspace angles | A beam with non-linear stiffness | KPCA performs damage detection problem without modal identification. |
| CC-SSI [100] | Modal parameters | - | Ariane 5 launch vehicle | Clear results even in the case of non-stationary data obtained using this algorithm |
| RSSI [101] | Modal parameters | - | 3-story steel frame and 2-story reinforced concrete frame | In this method the SVD algorithm is replaced by an advanced algorithm to update LQ decomposition. |
| Improved SSI [102] | Modal parameters | - | A numerical example of 7 DOF and an experimental model of Chaotianmen bridge | Less computing time due to not having QR decomposition CH matrix is constructed as a replacement for Hankel matrix. Spurious modes are removed using the model similarity index |
| SSA [103] | Subspace-based and nullspace-based damage indices | SVD for change-point detection | 6-story steel frame | SSA algorithm uses SVD for change-point detection |
| Fast CC-SSI [104] | Modal parameters | - | Operational data from a ship | Fast multi-order computation |
| ECCA-based SSI algorithm [105] | Modal parameters | - | FE model and experimental wind tunnel bridge model | Enhanced results are achieved for weakly excited modes and noisy response signals |
| Method/Reference | Damage Feature | Pattern Recognition | Test Model | Specification |
|---|---|---|---|---|
| SSI-COV [106] | Subspace residual | Sensitivity analysis | Numerical analysis | Damage localization using the FE model |
| EMD-SSI-COV [107] | Intrinsic mode functions | Sifting process | Beichuan arch bridge | Capable of dealing with non-stationary signals |
| BSSI-COV [108] | Curvature evolution index | Stabilization diagram | Numerical simulation of an 7-DOF MSD model | Suitable for identifying weakly excited modes |
| SSI-COV [109] | Natural frequencies | Fuzzy clustering | Z24 Bridge and Republic Plaza Office Tower | No need for mode shape data |
| SSI-COV [110] | Residual of the observability null-space | Averaging operation | FE model of a bridge deck and laboratory test of a clamped beam within a climatic chamber | Temperature effect is evaluated using an averaging operation |
| SSI-COV [111] | Subspace residual | test | Workbench and instrumented beam | Handling the temperature effect is a target in this paper |
| SSI-COV [112,113] | State space matrices | Mahalanobis and Euclidean distance decision functions | Two simulated beam model, a laboratory-scale reinforced concrete beam and a full-scale arch bridge structure | The method was capable of locating damage in beam structures. |
| Recursive SSI-COV-IV [114] | Modal parameters | - | Numerical models of a Single Degree of Freedom (SDOF) structure and an ASCE benchmark steel frame structure | Model identification was conducted for a system with time-varying measurement noise |
| RD–SSIcov [115] | Modal parameters | Modal strain energy method | Numerical model and a small scale wind turbine tower | The RD method was selected in this study for its noise reduction capabilities. |
| SSI-COV [116] | Modal parameters | Local optimization methods of NMA, GA, HS and PSO | Numerical examples and a laboratory model of cantilever beams | The model is appropriate to handle incomplete measurement data and truncated mode shapes |
| >SSI-COV [117] | >Curvature change, novelty index and PCA-SSA (for localization) modal updating and stiffness reduction (for quantification) | >Novelty analysis | >Laboratory-scale bridge foundation scouring | >Detection, localization and quantification was conducted in a unified and online recursive subspace algorithm |
| SSI-COV [118] | Eigenfrequencies, damping ratios and mode shapes | Stabilization diagram | Experimental models of a damaged pre-stressed concrete bridge and a mid-rise building | Uncertainty quantification and effect of different setups in modal parameters was evaluated in this study |
| Reference | Identification Method | Advantages and Drawbacks |
|---|---|---|
| Magalhães et al. [55] | SSI | ● Generally, there was a good agreement between the obtained modal frequencies and mode shape in all algorithms, however the damping ratio shows the most significant scatter. ● The PP method is an appropriate technique for modal identification of closely spaced modes. ● SSI and FDD is a more appropriate choice for modal identification where closely spaced frequencies are not of the same type (e.g., bending or torsion). ● PP and FDD are not suitable tools for identification of the modal parameters in cable-stayed bridges. Further analysis must be undertaken to successfully discriminate the vibrational influence of the cables from the global bridge frequencies. ● The FDD and SSI yielded unreliable results for the second pair of closely spaced frequencies due to the coincidence of the modes and coupling effect in ambient excitation. ● Estimation of damping ratios with wind-induced excitation has shown a significant level of scatter. Further research on ambient vibration testing is needed to approach a reliable identification of damping coefficients. ● All the above-mentioned algorithms require human judgment during implementation. The user defined parameters for the SSI, FDD and PP are system order, singular values, and global modes, respectively. |
| PP | ||
| FDD | ||
| Magalhães et al. [120] | SSI-COV | ● Performance of both SSI-COV and p-LSCF was found to be good in the identification of natural frequencies and mode shapes. ● It is demonstrated that p-LSCF can provide better estimation for the daily variations of damping coefficients compared to SSI. |
| p-LSCF | ||
| Wang et al. [121] | SSI | ● All of the modal identification methods perform well when the responses are exposed to noise. ● Model order is an important parameter in extracting correct modal parameters in all methods. ● Significant errors are observed in the damping coefficient when system order varies. ● Damping coefficient is sensitive to noise pollution, specifically for the first mode. ● More stable results for modal identification were obtained by the SSI method in numerical simulations. However, the ERA method outperforms other algorithms for field testing. ● ARMA shows the worst results for both field and numerical experiments. |
| ERA | ||
| ARMA | ||
| ITD | ||
| Moaveni et al. [122] | MNExT-ERA | Comparing output-only methods of SSI-DATA, MNExT-ERA and EFDD, it can be inferred that: ● The identified natural frequencies using these methods display good agreement in each damage scenario. ● The identified damping coefficient shows larger variability but still in a reasonable range. |
| SSI-DATA | ||
| EFDD | ● Lower damping ratios are obtained through FDD than the results identified using SSI-DATA and MNExT-ERA. ● The identified mode shapes using SSI-DATA were confirmed to be the most reliable among all methods. | |
| DSI | Comparing input-output methods of DSI, OKID-ERA, and GRA, the following were observed: ● The identified mode-shapes in all of the above-mentioned algorithms are close to the actual mode shape of the structure. ● In general, the calculated mode shapes by the input-output methods are more accurate than those obtained from output-only methods. ● The mode-shape parameters obtained from the GRA appear to be in good agreement with the actual mode shapes of the structure. | |
| OKID-ERA | ||
| GRA | ||
| Cunha et al. [123] | SSI-COV | ● The same result in terms of damage detection was obtained using both the SSI-COV and FDD procedures. ● In terms of modal parameters, perfect results were extracted through using both methods. |
| FDD | ||
| Liu et al. [54] | SSI and ERA | ● Both the ERA and SSI methods are accurate and provide stable results for modal parameters. The methods are extremely sensitive to the size of the Hankel matrix. ● The work burden of the algorithms is large and usually needs to perform multiple analyses. |
| PolyMAX | ● The PolyMAX and PolyLSCF methods are fast but the operator needs to have a high qualification. ● The algorithm is sensitive to the size of the Hankel matrix and sometimes needs to perform multiple analyses. | |
| PPM | ● PPM is a simple and less demanding algorithm. ● The algorithm can identify modal parameters in the pre-defined frequency range. | |
| PZM | ● PZM and PolyLSCF are basically similar and the obtained results can complement each other. ● PZM uses a non-power spectrum for modal frequencies and damping. | |
| EFDD and FSDD | ● EFDD and FSDD are fast and easy for modal parameter identification under ambient excitation. ● The estimation precisions in these methods depend on the accuracy of the power spectral density. ● Both methods are sensitive to noise and leakage error. | |
| WT | ● The accuracy of the WT is relatively high. ● The WT is not conducive to the real-time monitoring due to analysis load. | |
| Kim and Lynch [53] | SSI | ● Similar performance was confirmed for the SSI and FDD methods. ● The FDD method slightly suffered from resolution problems due to the limited number of data points. ● Though SSI has no resolution problems, more scattered data are generated when dealing with output-only modal analysis. |
| FDD | ||
| Ceravolo and Abbiati [124] | SSI-DATA | ● All three output-only methods of SSI-DATA, AR and ERA/RDS show high robustness to modal frequency estimation in non-stationary conditions. ● By using the same methods, damping estimates were very scattered. ● The estimation error of modal frequency in all methods remained less than 1.5%. ● The error in estimating damping ratio ranged from 15% (in SSI) to 50% (in AR). |
| AR | ||
| ERA/RDS |
| Reference | Method | Concern |
|---|---|---|
| Peeters and De Roeck [126] | SSI | Dealing with the sensor data of different measurement setups. |
| Pridham and Wilson [127] | Correlation-driven subspace algorithm | The effect of sample size and the dimension of the Hankel matrix on the estimated damping coefficient |
| Pan [128] | - | Discriminates the effects of epistemic uncertainty |
| Benveniste and Mevel [129] | SSI | Consistency of the subspace algorithm against non-stationarities in the measurement data |
| Reynders et al. [130] | SSI | Removing bias errors in ambient vibrations |
| Brasiliano et al. [131] | SSI-COV and SSI-DATA | Effect of non-structural elements in the vibrational behavior of bridge structures. |
| Alıcıoğlu & Luş [132] | SSI-COV and SSI-DATA techniques through BR and CVA. | The effect of structural complexity and ambient conditions on modal identification. |
| Marchesiello et al. [133] | ST-SSI | Time-variant identification |
| Balmès et al. [134] | Extended SSI-COV-based | Handling temperature effect in the identified modal parameters. |
| Wang et al. [135] | SSI together with ARX | Damage detection of Hammerstein systems or non-linearity introduced to a linear dynamic system through piece-wise constant inputs |
| Magalhães et al. [136] | EFDD and SSI-COV | Quality of the extracted damping ratios considering the proximity of natural frequencies, non-proportional damping and accuracy of the identification algorithms |
| Döhler et al. [137] | SSI-COV | Multiple non-simultaneously recorded measurement setups. |
| Carden and Mita [138] | A combined SSI-DATA method and first order perturbation technique | The challenges faced in extracting the accurate confidence interval of modal parameters in civil engineering structures. |
| Döhler and Mevel [139] | SSI- a modular and scalable approach | Merging sensor data by applying a modular approach. |
| Döhler et al. [140] | First-order SSI method perturbation analysis | Evaluation of the statistical uncertainty in a multi-setup configuration |
| Loh and Chen [141] | Hybrid RSSI-COV, NLPCA and AANN | Distinguishing the damage abnormality from those caused by environmental and operational variations |
| Brehm et al. [142] | Power spectral amplitudes and FE model | Determination of the optimum position of the reference sensor |
| Cara et al. [143] | Kalman filter SSI algorithm | Contribution of the modal parameters in each mode to the recorded measurement data. |
| Ashari and Mevel [144] | SSI-based algorithm | Injecting auxiliary input to extract the unexcited modes |
| Tondreau and Deraemaeker, [145] | Monte-Carlo and SSI | Introducing uncertainty into an FE model |
| Rainieri and Fabbrocino [146] | SSI | Influence of the system order and number of block rows in identification accuracy |
| Cho et al. [147] | SDSI | Implementation of VDD using wireless sensor networks |
| Markovsky [148] | SSI | Influence of missing measurement data in dynamic system |
| Banfi & Carassale [149] | SSI, SRA and FDD | Effect of uncertainty in determining modal parameters |
| Spiridonakos et al. [150] | PCE | Humidity and temperature effects |
| Huynh et al. [151] | A combined SSI algorithm and short-time Fourier transform | Structural analysis of a cable-stayed bridge under typhoons with various wind speeds. |
| Ren et al. [152] | Improved SSI algorithm | Eliminating spurious modes caused by non-white noise |
| Reference | Applied Damage Detection Technique | Test Structure | Damage Configuration | Damage Identification Results |
|---|---|---|---|---|
| Vanlanduit et al. [156] | Subspace theory and RSVD | Laboratory-scale aluminum beam | (1) 30% and 50% sew cut in the middle (2) A beam with fatigue crack under several geometrical and damping conditions. | Reliable results were obtained by applying the introduced RSVD method. |
| Naseralavi et al. [157] | Theory of subspaces and Kernel parallelization | Three simulations of 1D and 2D case studies | Reduction in Young’s modulus ranging from 10% to 30% correlated with the extent of the damage | Most single and multiple damage scenarios |
| Döhler and Hille [158] | Subspace-based | (1) Numerical simulations (2) A 1D steel frame structure | The crack-like damage simulated by the loosened 3 to 7 number of bolts, which correlates with a reduction of bending stiffness from 3% to 30%, respectively. | All damage cases were clearly detected under variable excitation using the new test method |
| Banan and Mehdi-Pour, [159] | Concept of subspace rotation and Monte Carlo simulation | A simulation model of a braced-frame structure | Single damage case with a 25%, 50%, and 95% reduction in Young’s Modulus | Damages were detected at noise ratios less than 5% but for a noise ratio of 20%, the results were unreliable for all damage rates. |
| Reference | Applied Damage Detection Technique | Test Structure | Damage Configuration | Damage Identification Results |
|---|---|---|---|---|
| Siegert et al. [160] | Statistical subspace-based algorithm | Laboratory-scale composite bridge deck | 40% reduction of the Young modulus | Algorithm can successfully detect the damages of the structure investigated |
| Li and Chang [114] | SSI and IV | Numerical model of a four-story, ASCE benchmark steel frame | A damage case of 30% reduction in the stiffness of the first story | Application of the technique tracking damages in the presence of measurement noise was successful. |
| Huang et al. [161] | SSI and DLV | Numerical model and laboratory-scale of a five-story steel frame | Damage scenarios with single and two damage case inflicted on the first second, third and fourth stories’ columns | (1) Poor results were recorded for multiple damage cases. (2) The obtained result for the ill-conditioned counterpart was effective. |
| Kim and Lynch [162] | SSI algorithms | Laboratory scale of a single-bay six-story steel frame structure | Six damage cases comprised of sew cuttings of 3, 6 and 9 cm of the columns on the first and second floors | All damage in the structure was easy to identify using the proposed algorithm even in the presence of noise. |
| Wang et al. [163] | SSI and DLV | Five-story shear frame structure with diagonal bracings. | Damage conditions simulated by partially removing some of the bracings | The proposed algorithm for damage localization was successful |
| Moaveni et al. [164] | Deterministic-stochastic subspace identification | Laboratory-scale, three-story, two-bay, infilled RC | Progressive damage induced by shaking table experiencing scaled earthquake records. | Natural frequencies decrease with increase in damage level during the test experiment |
| Weng et al. [165] | SI and model updating | Six-story steel frame structure and a two-story RC frame. | (1) Loosening the connection bolts in single and multiple damage case in 2nd, 4th and 6th stories. (2) by progressive damage through shaking table in a RC frame. | The method was capable of detecting, localizing and quantifying the damage in both steel and concrete frames. |
| Karami and Akbarabadi [166] | Active control strategy and SSI | Numerical model of a 5 story and a 20 story shear building | Reduction in the stories’ lateral stiffness ranged from 10 to 50% | The algorithm can detect damages accurately. |
| Belleri et al. [167] | Combined deterministic-stochastic subspace identification | Real-size three-story half-scale precast concrete building | Base excitation leading to loss of stiffness, cracks, and failure of the connections | Damage reduces natural frequencies and increases the damping ratios |
| Shinagawa and Mita [168] | Subspace identification | Full-scale four-story steel building | Collapse test. | Strong correlation between the extracted features with structural damage was observed. |
| Zhou et al. [169] | Subspace-based methods | A six-story residential building | More than 20 earthquake aftershocks recorded after instrumentation | Results of damage detection were not very reliable for earthquake induced excitation |
| Yoshimoto et al. [170] | MIMO SSI method and sub-structuring | An existing 7-story base-isolated building. | Stiffness reduction in the stories | The estimated damage of the stories correlates with the reduction ratio. |
| Reference | Applied Damage Detection Technique | Test Structure | Damage Configuration | Damage Identification Results |
|---|---|---|---|---|
| Allahdadian et al. [171] | SSDD and test | Reibersdorf Bridge | Damage simulated in girder, column, bearing, deck and cap beam with the ratios varied between 20%, 40% and 80%. | Unable to detect minor damage with a ratio of 20% |
| Dohler et al. [172] | Statistics-based subspace and test | S101 Bridge | Progressive damage test including cutting column, column settlement, horizontal crack in column, settling of bridge deck, and cutting pre-stress tendons. | (1) All steps of the column settlement and uplifting were clearly visible (2) Cutting of the pre-stressing tendons was not detectable. |
| Deraemaeker et al. [173] | Automated SSI and Shewhart-T control charts | Numerical model of a 3 span bridge | Four damage scenarios simulated by stiffness reduction in three different locations. | Proposed method was capable of detecting damage scenarios |
| Hu et al. [174] | SSI-COV and PCA algorithm | Pedro e Ines footbridge | Several realistic damage scenarios of 5%, 10%, 15%, 20% and 30% reduction of model spring constants | The method was capable of detecting all damage scenarios |
| Loh and Chao [175] | SSI-COV and MSSA | Laboratory-scale bridge | Displacement and lowering of a pier due to scouring | Localization and quantification were successful |
| Mevel and Goursat [176] | SSI | Z24 Bridge | Pier settlement of 20mm and 80 mm. | The efficiency of the proposed method was confirmed |
| Lin et al. [113] | Statistics-based SSI | (1) Laboratory-sale pre-stressed RC beams (2) a full-scale RC arch bridge | Gradually releasing the pre-stressed tendon from 17% to 73% | Algorithm was successful in detecting damage |
| Kullaa [177] | Subspace and stabilization diagram and control chart | Z24 Bridge | Pier settlements of 40mm and 95mm | Multivariate control charts have better performance in damage detection compared to univariate methods |
| Reynders, and De Roeck [178] | SSI algorithm and KPCA | Z24 | Pier settlement, tilt of foundation, concrete spalling, landslide of abutment, failure of concrete hinge, failure of anchor heads and rupture of tendons were introduced to the structure | The proposed algorithm was capable of detecting imperfection in most cases |
| Nguyen et al. [179] | NSA and EPCA | Numerical model of Champangshiehl Bridge | Several intentionally created cuttings in pre-stressed tendons | The obtained result was encouraging. |
| Reference | Software | Analysis Tool | Environment | Purpose |
|---|---|---|---|---|
| Döhler et al. [182] | ARTeMIS | CC-SSI | - | Modal identification |
| Y. Zhou et al. [183] | ModalVIEW | SSI, RPF and LSCF | LabVIEW | Modal identification |
| Hu et al. [184] | SMI | EFDD | LabVIEW | Modal identification |
| Hu et al. [184] | CSMI | PP, FDD and SSI | LabVIEW | Modal identification |
| Goursat & Mevel [186] | COSMAD | SSI-COV | Scilab | Modal identification |
| Chang et al. [185] | SMIT | SSI, auto-regressive-based methods and realization-based algorithms | MATLAB | SHM |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shokravi, H.; Shokravi, H.; Bakhary, N.; Rahimian Koloor, S.S.; Petrů, M. Health Monitoring of Civil Infrastructures by Subspace System Identification Method: An Overview. Appl. Sci. 2020, 10, 2786. https://doi.org/10.3390/app10082786
Shokravi H, Shokravi H, Bakhary N, Rahimian Koloor SS, Petrů M. Health Monitoring of Civil Infrastructures by Subspace System Identification Method: An Overview. Applied Sciences. 2020; 10(8):2786. https://doi.org/10.3390/app10082786
Chicago/Turabian StyleShokravi, Hoofar, Hooman Shokravi, Norhisham Bakhary, Seyed Saeid Rahimian Koloor, and Michal Petrů. 2020. "Health Monitoring of Civil Infrastructures by Subspace System Identification Method: An Overview" Applied Sciences 10, no. 8: 2786. https://doi.org/10.3390/app10082786
APA StyleShokravi, H., Shokravi, H., Bakhary, N., Rahimian Koloor, S. S., & Petrů, M. (2020). Health Monitoring of Civil Infrastructures by Subspace System Identification Method: An Overview. Applied Sciences, 10(8), 2786. https://doi.org/10.3390/app10082786








