Dynamic Event-Triggered Time-Varying Formation Control of Second-Order Dynamic Agents: Application to Multiple Quadcopters Systems

Abstract

This paper investigates the problem of the time-varying formation control of a second-order dynamic agent based on a distributed dynamic event-triggered algorithm. In this problem, each agent can exchange the information of its position and velocity with its neighbors via limited communication ability. Our approach provides a new dynamic event triggering mechanism to reduce the number of triggering times while maintaining satisfactory control performance. Further, a novel Lyapunov function is proposed to guarantee that the group of agents asymptotically tracks the desired time-varying formation trajectory. The practical applicability of the event triggering mechanism is also indicated by excluding the Zeno behavior in the proposed control algorithm. Finally, the validity and effectiveness of the proposed method are demonstrated via illustrative examples of the time-varying formation flight for six quadcopters.

1. Introduction

One of the most common animal habits that efficiently yields undeniable outcomes in nature is cooperative work. For example, a swarm of birds has a V-shaped flight formation to reduce the induced drag and to increase their range [1]; ants maintain a separation distance to search for food optimally; and herbivores collectively migrate to defend against any predators in wild areas. Encouraged by these biological tactics of a group of multiple creatures, multi-agent systems (MASs) have attracted intense attention because of the vast number of applications in many aspects. They are moderately useful to carry out a range of different assignments, such as irrigating large agricultural areas, monitoring in the military, investigating and locating lost objects in inaccessible zones, and maintaining undersea oil pipelines [2,3,4]. In recent years, the formation control problem of MASs, whose purpose is to steer multiple objects in a network to achieve and maintain their predefined geometric pattern in their states, has increasingly fascinated the scientific community. Because of many versatile and helpful applications in real life, there have been several fruitful results in studies focusing on unmanned aerial vehicles (UAVs), ground mobile robots, autonomous underwater vehicles, and multisensor networks [5,6,7,8]. Based on the types of sensed and controlled variables of the probed systems in MASs, an excellent survey paper with the topics of the formation problem categorized as position-based, displacement-based, and distance-based control is [9] (and see the references therein). The above-mentioned studies preferred to employ the first approach rather than the others.

Multiple mechanical systems are mostly offered as a distributed control structure due to the limited computation and communication resources. Because each individual system in multi-agent systems possesses many sensors such as real-time kinematic-global positioning system (RTK-GPS), inertial measurement unit (IMU), WiFi, telemetry, and radio receiver, the whole of the investigated system can also be considered as a multi-sensor network system. In practice, each agent in a multi-sensor network commonly has limited energy resources and often broadcasts its own sampled data to task manager nodes through a communication network [10,11,12,13]. Additionally, there is a restricted capability of data transmission in the network system bandwidth. It is clear that using common estimators in the majority of experimental devices, e.g., the Kalman filter and the extended Kalman filter, which require a large amount of system state information, would be unpractical. Moreover, approaches based on consensus and formation algorithms are also unpractical because they require a massive capability of communication among agents and a large amount of energy expenditures in the multi-sensor network. To alleviate the waste of energy consumption reasonably, efficiently making use of these resources plays an important role in cyber-physical system design. By applying most of the conventional control techniques to the distributed algorithm, it is assumed that each agent state feedback controller periodically executes and does not depend on whether system states are updated; its neighborhood information is completely exchanged. This implementation method may cause unnecessary work in hardware devices while there are many other required assignments, leading to overloads and network congestion. Due to some drawbacks of these existing schemes, many scientists in the cybernetics community have tended to research event-triggered control system design.

Recent years have witnessed a growth of results regarding event-triggered control for a single-agent system [14,15,16] before this concept was originally extended to propose a control structure for MASs [17]. The core idea of the event-triggered control is that controllers or actuators are solely updated when some specific events occur rather than after the elapse of a fixed amount of time [16]. It can be clearly detailed that the system inputs remain unchanged between two consecutive triggering times, which are determined by the aforementioned events, i.e., the events may be considered as a threshold and constructed by tracking errors. A key issue fascinating the scientific community to date is how to propose a triggering rule that moderately reduces the number of triggering times while maintaining satisfactory control performance and excluding the Zeno behavior, which means infinite numbers of triggering times in a finite time interval [18]. The authors in [19] proposed an aperiodic sampled-data formation protocol for MAS, in which each agent solely exchanges its information with its neighbors at a specific discrete time. In the continuous control system design, instead of using the static event-triggered rule, a dynamic event-triggered control that has evident merits in lessening the risk of network congestion has been considered attractive in many recent studies (see [20,21,22,23] and the references therein). In [24], a dynamic event triggering mechanism was proven to have a minimum triggering time that was greater than that of the static counterpart, leading to a reduction in redundant workloads and network congestion. Based on the dynamic triggering rule for the distributed formation control, the authors in [25] proposed an event-triggered communication mechanism to achieve a fixed formation of multiple ground robots. The study [26] presented a dynamic and a self event-triggered control for one-integrator MASs to achieve an average consensus, where the Zeno behavior was excluded. By considering an agent as a leader, second-order MASs that used event-sampling schemes achieved a consensus problem based on a leader-follower protocol in [27]. These existing results somehow can be enriched by expanding with the time-varying formation control of multi-agent systems.

Motivated by the above observations, this paper proposes a dynamic event-triggered control algorithm for the time-varying formation of multi-agent systems. The dedicated algorithm guarantees that the group of agents is capable of tracking the desired time-varying formation, as well as significantly reducing the number of trigger times in each agent in comparison with that of the conventional continuous control algorithm. In our approach, the control synthesis is based on a new control Lyapunov function such that each agent possesses a distributed controller and an event triggering mechanism, leading to the exponential asymptotic convergence of the formation tracking errors. Additionally, the new triggering mechanism is designed to exclude the Zeno behavior. To summarize, our main contributions can be highlighted as follows:

(1)

A distributed dynamic event-triggered time-varying formation control algorithm is proposed for a group of agents, in which each agent includes position and attitude dynamics. To the best of our knowledge, comparatively little progress has been made towards time-varying formation control with a dynamic event triggering mechanism.

(2)

In the control design for the systems, one of the most challenging problems is that the distributed property is a compulsory requirement in both controllers and event triggering mechanisms. Based on a new control Lyapunov function, a state feedback controller and a dynamic event triggering mechanism are proposed. As a result, the proposed control law guarantees that the group of agents asymptotically tracks the desired formation trajectory. Finally, the performance of the proposed controller is illustrated via an example of quadcopter formation control.

(3)

Another challenging problem arises from the time-varying formation control. It is worth noting that the control inputs depend not only on the states of the agent, but also the desired formation trajectory, which makes our approach different from the existing approaches reported in [16,17,24,25,26]. In this context, our approach ensures the exclusion of the Zeno behavior to avoid the accumulation of triggering instants as time goes to infinity. These results guarantee the practical feasibility of the proposed method.

Notation: The notations $X\ge Y$ and $X>Y$ mean that $X-Y$ is positive semi-definite and positive definite, respectively. The following notations and symbols will be used throughout this paper. ${\mathbb{R}}_{+}$ denotes the set of real positive numbers; ${\mathbb{R}}^n$ and ${\mathbb{R}}^{n\times m}$ stand for sets of real n-dimensional vectors and n-row m-column matrices, respectively; $I_n$ is the $n\times n$ identity matrix; and ${\lambda }_{min}\left\{W\right\}$ $\left({\lambda }_{max}\left\{W\right\}\right)$ represents the minimum (maximum) eigenvalue of matrix W. Next, ${\mathbf{1}}_n$ is used for the vector having n elements equal to one, and ${\parallel x\parallel }_2=\sqrt{x^{T}x}$ stands for the length of the vector in Euclidean space. Additionally, we have the following notations: $c\varphi =cos\left(\varphi \right(t\left)\right)$, $s\varphi =sin\left(\varphi \right(t\left)\right)$, $c\theta =cos\left(\theta \right(t\left)\right)$, $s\theta =sin\left(\theta \right(t\left)\right)$, $c\psi =cos\left(\psi \right(t\left)\right)$, $s\psi =sin\left(\psi \right(t\left)\right)$, and

$$\begin{array}{c}\hfill \mathit{diag}\left(w_1,w_2,\dots ,w_n\right)=\left[\begin{array}{cccc}{w}_1& 0& \dots & 0\\ 0& w_2& \dots & 0\\ ⋮& \ddots & \ddots & ⋮\\ 0& 0& \dots & w_n\end{array}\right].\end{array}$$

2. Preliminaries

2.1. Algebraic Graph Theory

Let $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$ be a weighted digraph with the set of vertices $\mathcal{V}=\{1,2,\dots ,N\}$, the set of edges $\mathcal{E}\subseteq \mathcal{V}\times \mathcal{V}$, and the weighted adjacency matrix $\mathcal{A}=\left[a_{ij}\right]$. For any $(i,j)\in \mathcal{E},i\ne j$, the element of the weight adjacency matrix $a_{ij}$ is positive if vertices ith and jth can communicate with each other, while $a_{ij}=0$ in the cases of $(i,j)\notin \mathcal{E}$ or $i=j$. The in-degree of vertex i is denoted as $de{g}_i^{in}={\sum }_{j=1}^n{a}_{ij}$, and the degree matrix of graph $\mathcal{G}$ is defined as $\mathcal{D}=\mathit{diag}\left(de{g}_1^{in},de{g}_2^{in},\dots ,de{g}_N^{in}\right)$. The Laplacian matrix is defined as $\mathcal{L}=\left[{\ell }_{ij}\right]=\mathcal{D}-\mathcal{A}$. Further, $\mathcal{G}$ is called an undirected graph if and only if $\mathcal{A}$ is a symmetric matrix. An edge of the undirected graph $\mathcal{G}$ is denoted by an unordered pair $(i,j)\in \mathcal{E}$. The undirected graph is connected if there exists at least a path between any pair of vertices. The set of all neighbors of the vertex i is denoted as ${\mathcal{N}}_i=\{j\in \mathcal{V}:(i,j)\in \mathcal{E}\}$.

Lemma 1 ([28]).

If a graph $\mathcal{G}$ is connected, then its Laplacian matrix $\mathcal{L}$ is positive semidefinite. Moreover, $x^T\mathcal{L}x=0$ if and only if $x=a{\mathbf{1}}_n$ for some $a\in \mathbb{R}$.

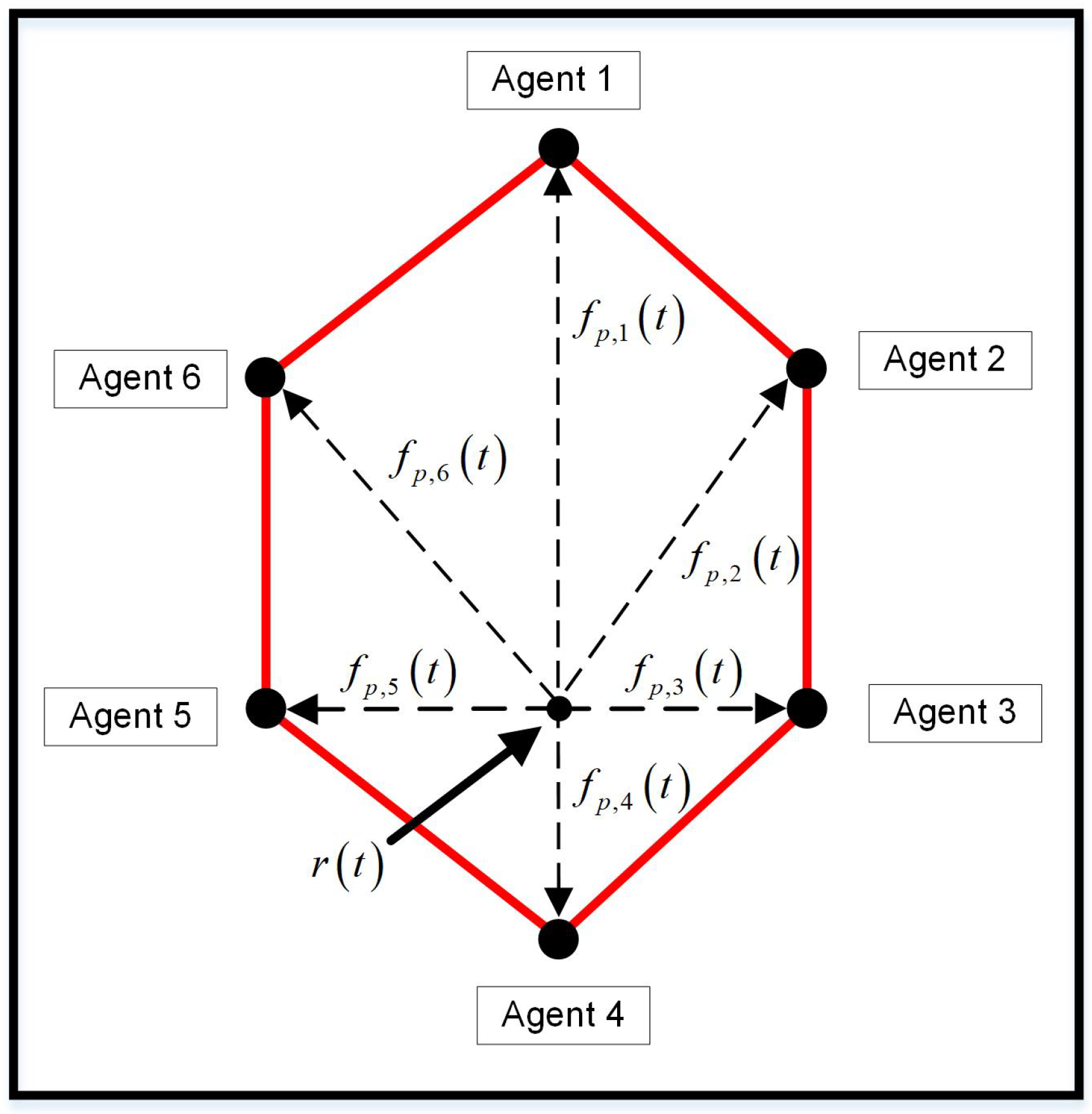
2.2. Formation Description

In this note, the multi-agent system is considered as the undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathcal{A})$, in which each agent is a vertex in $\mathcal{V}$. Additionally, a pair $(i,j)\in \mathcal{E}$ implies that the ith agent can simultaneously receive/transmit its state information from/to the jth agent. From our control objectives, the group of N agents is navigated by a proposed control algorithm to reach an anticipated formation. Generally, a formation of the multiple agents is considered as a geometric shape in three-dimensional space that satisfies some prescribed constraints achieved and preserved by the group of agents.

The formation control survey in [9] reported various formation representations, such as distance-based, displacement-based, and position-based formations. In this paper, let us define a reference trajectory of the formation $r\left(t\right):{\mathbb{R}}_{+}\to {\mathbb{R}}^n$ and a formation shape vector of the ith agent $f_{p,i}\left(t\right):{\mathbb{R}}_{+}\to {\mathbb{R}}^n$, as seen in Figure 1. Additionally, $f_{p,i}\left(t\right)$ are continuously twice differentiable functions, i.e., $f_{v,i}\left(t\right)={\dot{f}}_{p,i}\left(t\right)$, $f_{a,i}\left(t\right)={\ddot{f}}_{p,i}\left(t\right)$, and $\parallel f_{a,i}\left(t\right)\parallel <{\varpi }_{fa}$, where ${\varpi }_{fa}$ is a positive constant. Furthermore, in the group, at least one agent knows the reference trajectory of the formation $r\left(t\right)$, and the ith agent only knows its position in the formation via $f_{p,i}\left(t\right)$. Let ${\delta }_i=1$ if the ith agent knows $r\left(t\right)$ and ${\delta }_i=0$ otherwise. Let us consider that $r\left(t\right)$ satisfies the following:

$$\begin{array}{c}\hfill \dot{r}\left(t\right)=v_0,\end{array}$$

(1)

where $v_0\in {\mathbb{R}}^n$ is the constant reference velocity of the formation.

Let us consider time-varying formation control for N second-order agents, each of which has the following dynamics:

$$\begin{array}{c}\left\{\begin{array}{c}{\dot{p}}_i\left(t\right)=v_i\left(t\right),\hfill \\ {\dot{v}}_i\left(t\right)=u_i\left(t\right).\hfill \end{array}\right.\hfill \end{array}$$

(2)

where $i\in \mathcal{V}=\{1,2,\dots ,N\}$ begin the set of all agents and $p_i\left(t\right),v_i\left(t\right)\in {\mathbb{R}}^n$ stand for the state of agent ith with control input $u_i\left(t\right)$.

Definition 1.

The multiple agents (2) are said to achieve the state formation specified by the vectors $f_{p,i}\left(t\right)$, $i\in \mathcal{V}$ for any given bounded initial states if:

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\left(p_i\left(t\right)-f_{p,i}\left(t\right)-r\left(t\right)\right)=0,i\in \mathcal{V}.\end{array}$$

(3)

Lemma 2.

By letting $\Delta =\mathit{diag}\left({\delta }_1,{\delta }_2,\dots ,{\delta }_N\right)\in {\mathbb{R}}^{N\times N}$, if the graph $\mathcal{G}$ is undirected and strongly connected, the matrices $\mathcal{L}+\Delta$ and $\mathcal{M}=(\mathcal{L}+\Delta )\otimes I_n$ are symmetric positive-definite.

Proof of Lemma 2.

Let us recall Lemma 1. The Laplacian symmetric matrix $\mathcal{L}$ is semi-positive definite, in that there is only one zero eigenvalue and the rest are positive. $x^T\mathcal{L}x=0$ iff $x=a{\mathbf{1}}_n$, $a\in \mathbb{R}$, while $x^T\mathcal{L}x>0$ for any $x\ne 0\in {\mathbb{R}}^N$. Moreover, from the previously-defined matrix $\Delta$ with ${\delta }_i\in \left\{0,1\right\}$, $\left(i\in \mathcal{V}\right)$, because it is assumed that there is at least one ${\delta }_i=1$, $x^T\Delta x>0$ for any $x=a{\mathbf{1}}_n$, $a\ne 0$. Therefore, it is clear that $x^T\left(\mathcal{L}+\Delta \right)x>0$ for any $x\ne 0\in {\mathbb{R}}^N$, leading to $\left(\mathcal{L}+\Delta \right)>0$. Furthermore, it is obvious that the matrix $\mathcal{M}$ is symmetric by taking the Kronecker product of the symmetric $\left(\mathcal{L}+\Delta \right)$ and the identity matrix. Let us consider the vector $\xi ={\left[{\xi }_1^T,{\xi }_2^T,\dots ,{\xi }_n^T\right]}^T\in {\mathbb{R}}^{nN}$, in which ${\xi }_1$, ${\xi }_2$,…, ${\xi }_n$$\in {\mathbb{R}}^N$, and $\xi \ne 0$:

$$\begin{array}{cc}\hfill {\xi }^T\mathcal{M}\xi & =\left[{\xi }_1^T\left(\mathcal{L}+\Delta \right),{\xi }_2^T\left(\mathcal{L}+\Delta \right),\dots ,{\xi }_n^T\left(\mathcal{L}+\Delta \right)\right]\xi \hfill \\ \hfill & ={\xi }_1^T\left(\mathcal{L}+\Delta \right){\xi }_1+{\xi }_2^T\left(\mathcal{L}+\Delta \right){\xi }_2+\cdots +{\xi }_n^T\left(\mathcal{L}+\Delta \right){\xi }_n.\hfill \end{array}$$

(4)

Because matrix $\left(\mathcal{L}+\Delta \right)>0$ and there is at least one element in vectors ${\xi }_i$$\left(i\in \mathbb{N}\right)$ that is not equal to zero, Equation (4) implies that ${\xi }^T\mathcal{M}\xi >0$ for any $\xi \ne 0\in {\mathbb{R}}^{nN}$. □

Remark 1.

In the case of more complicated trajectories, it is possible to divide them into a sequence of desired points that describe the desired position of the formation. Hence, the reference trajectory of the multi-agent system can be established by combining many straight lines connecting two consecutive points in the sequence, i.e., each straight line is considered as a constant velocity represented in (1).

3. Main Results

This section proposes a distributed dynamic event-triggered control law for each agent such that it achieves the predefined formation of the multi-agent system and avoids the continuous exchange of information among agents and the Zeno behavior. For convenience, let us define the following:

$$\begin{array}{cc}\hfill {\eta }_{p,i}\left(t\right)& =p_i\left(t\right)-f_{p,i}\left(t\right),{\eta }_{v,i}\left(t\right)=v_i\left(t\right)-f_{v,i}\left(t\right),\hfill \\ \hfill {\mathit{\eta }}_p\left(t\right)& ={\left[{\eta }_{p,1}^T\left(t\right),{\eta }_{p,2}^T\left(t\right),\dots ,{\eta }_{p,N}^T\left(t\right)\right]}^T,\hfill \\ \hfill {\mathit{\eta }}_v\left(t\right)& ={\left[{\eta }_{v,1}^T\left(t\right),{\eta }_{v,2}^T\left(t\right),\dots ,{\eta }_{v,N}^T\left(t\right)\right]}^T.\hfill \end{array}$$

(5)

3.1. Dynamic Event Triggering Mechanism

Let us consider the multi-agents given in (2) with the undirected strongly connected graph $\mathcal{G}$ and take ${\left\{t_{k_i+1}^i\right\}}_{k_i=1}^{\infty }$ as the triggering time sequence of the ith agent. Each element $t_{k_i}^i$ stands for a triggering time at which the ith agent can take its information $p_i(t_{k_i}^i)$, $v_i(t_{k_i}^i)$, the last information $p_i(t_{k_j}^j)$, $v_i(t_{k_j}^j)$ of its neighbors, and $r(t_{k_i}^i)$ of formation trajectory $r\left(t\right)$. It is worth noting that the communication between two consecutive ith and jth agents only occurs at their triggering time. Hence, to reduce the number of communication times, our goal in this part is to find a mechanism for each agent that can properly determine the triggering time. Suppose that the first triggering time corresponds to initial state $t_1^i=0$; the ith agent determines its triggering time sequence as follows:

$$\begin{array}{c}{t}_1^i=0,\hfill \\ t_{k_i+1}^i=\underset{r>t_{k_i}^i}{min}\left\{r\in {\mathbb{R}}_{+}:{\sigma }_i{\chi }_i\left(r\right)+{\widehat{\chi }}_i\left(r\right)\le 0\right\},\hfill \end{array}$$

(6)

where:

$$\begin{array}{c}{\widehat{\chi }}_i\left(t\right)=\gamma {\theta }_p\parallel z_{p,i}\left(t\right){\parallel }_2^2+{\theta }_v\parallel z_{v,i}\left(t\right){\parallel }_2^2-{\left(\gamma z_{p,i}\left(t\right)+z_{v,i}\left(t\right)\right)}^T{q}_i\left(t\right),\hfill \end{array}$$

(7)

$$\begin{array}{c}{q}_i\left(t\right)={\gamma }_p\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left({\tilde{\eta }}_{p,i}\left(t\right)-{\tilde{\eta }}_{p,j}\left(t\right)\right)+{\gamma }_v\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left({\tilde{\eta }}_{v,i}\left(t\right)-{\tilde{\eta }}_{v,j}\left(t\right)\right)-{\gamma }_v{\delta }_i{\tilde{\eta }}_{v,i}\left(t\right)-{\gamma }_p{\delta }_i{\tilde{e}}_p\left(t\right)+{\tilde{f}}_{a,i}\left(t\right),\hfill \end{array}$$

(8)

$$\begin{array}{c}{z}_{p,i}\left(t\right)={\delta }_i\left({\eta }_{p,i}\left(t\right)-r\left(t\right)\right)-\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left({\eta }_{p,i}\left(t\right)-{\eta }_{p,j}\left(t\right)\right),\hfill \end{array}$$

(9)

$$\begin{array}{c}{z}_{v,i}\left(t\right)={\delta }_i\left({\eta }_{v,i}\left(t\right)-v_0\right)-\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left({\eta }_{v,i}\left(t\right)-{\eta }_{v,j}\left(t\right)\right),\hfill \\ {\tilde{\eta }}_{p,i}\left(t\right)={\eta }_{p,i}(t_{k_i}^i)-{\eta }_{p,i}\left(t\right),\hfill \\ {\tilde{\eta }}_{v,i}\left(t\right)={\eta }_{v,i}(t_{k_i}^i)-{\eta }_{v,i}\left(t\right),\hfill \\ \tilde{r}\left(t\right)=r(t_{k_i}^i)-r\left(t\right),\hfill \\ {\tilde{e}}_p\left(t\right)={\tilde{\eta }}_{p,i}\left(t\right)-\tilde{r}\left(t\right),\hfill \\ {\tilde{f}}_{a,i}\left(t\right)=f_{a,i}(t_{k_i}^i)-f_{a,i}\left(t\right),t\in \left[t_{k_i}^i,t_{k_i+1}^i\right),\hfill \end{array}$$

(10)

and the internal dynamic variable ${\chi }_i\left(t\right)$ with ${\chi }_i\left(0\right)>0$ is given as follows:

$$\begin{array}{c}\hfill {\dot{\chi }}_i\left(t\right)=-{\beta }_i{\chi }_i\left(t\right)+{\widehat{\chi }}_i\left(t\right),\end{array}$$

(11)

where ${\beta }_i,{\sigma }_i,\gamma ,{\gamma }_p,{\gamma }_v,{\theta }_p$, and ${\theta }_v\in {\mathbb{R}}_{+}$.

Remark 2.

In the conventional event triggering mechanism, the triggering condition was constructed from the current and latest triggered states, e.g., in this case, the system states will be triggered when ${\widehat{\chi }}_i\left(t\right)\le 0$ occurs instead of (6). Thus, it is also known as the static event-triggered controller [16]. According to [24], the static event-triggered controller guarantees the asymptotic stability of the system, as well as excluding the Zeno behavior phenomenon. In this study, the dynamic triggering law has been enriched with the time-varying formation control of the multi-agent system.

3.2. Distributed Formation Protocol

From the proposed dynamic event triggering mechanism, we then present a control law of each agent based on its neighborhood position and velocity with the formation description. The distributed formation control input between two consecutive triggering times of the ith agent is given by the following:

$$\begin{array}{cc}\hfill u_i\left(t\right)={\gamma }_p& \sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left({\eta }_{p,i}(t_{k_i}^i)-{\eta }_{p,j}(t_{k_j}^j)\right)+{\gamma }_v\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left({\eta }_{v,i}(t_{k_i}^i)-{\eta }_{v,j}(t_{k_j}^j)\right)\hfill \\ \hfill & -{\gamma }_p{\delta }_i\left({\eta }_{p,i}(t_{k_i}^i)-r(t_{k_i}^i)\right)-{\gamma }_v{\delta }_i\left({\eta }_{v,i}(t_{k_i}^i)-v_0\right)+f_{a,i}(t_{k_i}^i),\hfill \end{array}$$

(12)

for all $t\in \left[t_{k_i}^i,t_{k_i+1}^i\right)$, where $f_{a,i}\left(t\right)={\dot{f}}_{v,i}\left(t\right)$, ${\gamma }_p,{\gamma }_v\in {\mathbb{R}}_{+}$, and $t_{k_j}^j$ is the last triggering time of the jth agent. Additionally, when $t>t_{k_i}^i$, $t_{k_i+1}^i$ can be determined from the dynamic event triggering mechanism (6). Hence, each agent takes into account the last updated value of each of its neighbors in its control law. Further, the control law of the ith agent is updated both at its own event times $t_0^i,t_1^i,\dots ,t_{k_i}^i,\dots$ and at the event times of its neighbors $t_0^j,t_1^j,\dots$, $t_{k_j}^j,\dots ,j\in {\mathcal{N}}_i$. It should be noted that the definition of $t_{k_j}^j$ implies that ${\eta }_{p,j}(t_{k_j}^j)={\eta }_{p,j}\left(t\right)+{\tilde{\eta }}_{p,j}\left(t\right)$ and ${\eta }_{v,j}(t_{k_j}^j)={\eta }_{v,j}\left(t\right)+{\tilde{\eta }}_{v,j}\left(t\right)$. Then, the closed loop error dynamics of the ith agent is given as follows:

$$\begin{array}{cc}\hfill {\dot{e}}_{p,i}\left(t\right)=& e_{v,i}\left(t\right),\hfill \\ \hfill {\dot{e}}_{v,i}\left(t\right)=& {\gamma }_p\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left(e_{p,i}\left(t\right)-e_{p,j}\left(t\right)\right)+{\gamma }_p\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left({\tilde{\eta }}_{p,i}\left(t\right)-{\tilde{\eta }}_{p,j}\left(t\right)\right)+{\gamma }_v\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left(e_{v,i}\left(t\right)-e_{v,j}\left(t\right)\right)\hfill \\ \hfill & +{\gamma }_v\sum _{j\in {\mathcal{N}}_i}{\ell }_{ij}\left({\tilde{\eta }}_{v,i}\left(t\right)-{\tilde{\eta }}_{v,j}\left(t\right)\right)-{\gamma }_p{\delta }_i\left(e_{p,i}\left(t\right)+{\tilde{\eta }}_{p,i}\left(t\right)-{\tilde{r}}_i\left(t\right)\right)-{\gamma }_v{\delta }_i\left(e_{v,i}\left(t\right)+{\tilde{\eta }}_{v,i}\left(t\right)\right)\hfill \\ \hfill & +f_{a,i}(t_{k_i}^i)-f_{a,i}\left(t\right),t\in \left[t_{k_i}^i,t_{k_i+1}^i\right),\hfill \end{array}$$

(13)

where $e_{p,i}\left(t\right)={\eta }_{p,i}\left(t\right)-r\left(t\right)$, $e_{v,i}\left(t\right)={\eta }_{v,i}\left(t\right)-v_0$, and ${\tilde{r}}_i\left(t\right)=r(t_{k_i}^i)-r\left(t\right)$. From (13), the closed loop error dynamics of N agents follows:

$$\begin{array}{cc}\hfill {\dot{\mathit{e}}}_p\left(t\right)& ={\mathit{e}}_v\left(t\right),\hfill \\ \hfill {\dot{\mathit{e}}}_v\left(t\right)& =-{\gamma }_p\mathcal{M}{\mathit{e}}_p\left(t\right)-{\gamma }_v\mathcal{M}{\mathit{e}}_v\left(t\right)+{\tilde{\mathit{f}}}_a\left(t\right)-{\gamma }_p\mathcal{M}{\tilde{\mathit{\eta }}}_p\left(t\right)-{\gamma }_v\mathcal{M}{\tilde{\mathit{\eta }}}_v\left(t\right)+{\gamma }_p(\Delta \otimes I_n)\tilde{\mathit{r}}\left(t\right),\hfill \end{array}$$

(14)

where:

$$\begin{array}{c}{\mathit{e}}_p\left(t\right)={\left[e_{p,1}^T\left(t\right),e_{p,2}^T\left(t\right),\dots ,e_{p,N}^T\left(t\right)\right]}^T,{\mathit{e}}_v\left(t\right)={\left[e_{v,1}^T\left(t\right),e_{v,2}^T\left(t\right),\dots ,e_{v,N}^T\left(t\right)\right]}^T,\hfill \\ {\tilde{\mathit{f}}}_a\left(t\right)={\left[f_{a,1}^T\left(t_{k_1}^1\right)-f_{a,1}^T\left(t\right),f_{a,2}^T\left(t_{k_2}^2\right)-f_{a,2}^T\left(t\right),\dots ,f_{a,N}^T\left(t_{k_N}^N\right)-f_{a,N}^T\left(t\right)\right]}^T,\hfill \\ {\tilde{\mathit{\eta }}}_p\left(t\right)={\left[{\tilde{\eta }}_{p,1}^T\left(t\right),{\tilde{\eta }}_{p,2}^T\left(t\right),\dots ,{\tilde{\eta }}_{p,N}^T\left(t\right)\right]}^T,{\tilde{\mathit{\eta }}}_v\left(t\right)={\left[{\tilde{\eta }}_{v,1}^T\left(t\right),{\tilde{\eta }}_{v,2}^T\left(t\right),\dots ,{\tilde{\eta }}_{v,N}^T\left(t\right)\right]}^T.\hfill \\ \tilde{\mathit{r}}\left(t\right)={\left[{\tilde{r}}_1^T\left(t\right),{\tilde{r}}_2^T\left(t\right),\dots ,{\tilde{r}}_N^T\left(t\right)\right]}^T.\hfill \end{array}$$

The following theorem presents the control synthesis conditions formulated in terms of linear matrix inequalities.

Theorem 1.

Consider the multi-agent system (2). Suppose that the graph $\mathcal{G}$ is undirected and strongly connected; there exist positive scalar coefficients γ, ${\gamma }_p$, ${\gamma }_v$, ${\theta }_p$, and ${\theta }_v$ such that:

$$\begin{array}{c}0<{\gamma }_p-{\theta }_p,\hfill \end{array}$$

(15)

$$\begin{array}{c}0<\left({\gamma }_v-{\theta }_v\right){\mathcal{M}}^2-\gamma \mathcal{M},\hfill \end{array}$$

(16)

$$\begin{array}{c}0<\left({\gamma }_p+{\gamma }_v\gamma \right){\mathcal{M}}^2-{\gamma }^2\mathcal{M}.\hfill \end{array}$$

(17)

Then, under the control law (12) and the dynamic event triggering mechanism (6), the closed loop system (14) is exponentially asymptotically stable, and there is no Zeno behavior.

Proof of Theorem 1.

From (6), it is obvious that ${\sigma }_i{\chi }_i\left(t\right)+{\widehat{\chi }}_i\left(t\right)>0$ for all $t\in \left[t_{k_i}^i,t_{k_i+1}^i\right)$. Then, (11) offers ${\dot{\chi }}_i\left(t\right)>-{\beta }_i{\chi }_i\left(t\right)-{\sigma }_i{\chi }_i\left(t\right)$. By using the comparison lemma in, e.g., [29], pp. 102–103, one has:

$$\begin{array}{c}\hfill {\chi }_i\left(t\right)>{\chi }_i\left(0\right)e^{-\left({\beta }_i+{\sigma }_i\right)t}.\end{array}$$

(18)

Because of ${\beta }_i,{\sigma }_i\in {\mathbb{R}}_{+}$, and ${\chi }_i\left(0\right)>0$, it can be derived that ${\chi }_i\left(t\right)>0$. By utilizing Schur’s complement, the condition (17) and Lemma 2 ensure that:

$$\begin{array}{c}\hfill \mathbb{P}=\left[\begin{array}{cc}({\gamma }_p+{\gamma }_v\gamma ){\mathcal{M}}^2& \gamma \mathcal{M}\\ \gamma \mathcal{M}& \mathcal{M}\end{array}\right]>0.\end{array}$$

(19)

Next, let us take a Lyapunov function candidate as follows:

$$\begin{array}{cc}\hfill V\left(t\right)=& \frac{1}{2}{\overline{\mathit{e}}}^T\left(t\right)\mathbb{P}\overline{\mathit{e}}\left(t\right)+\sum _{i=1}^N{\chi }_i\left(t\right),\hfill \end{array}$$

(20)

where $\overline{\mathit{e}}\left(t\right)={\left[{\mathit{e}}_p^T\left(t\right),{\mathit{e}}_v^T\left(t\right)\right]}^T$. The time-derivative of $V\left(t\right)$ along with the solution of (14) is given by:

$$\begin{array}{cc}\hfill \dot{V}\left(t\right)& =({\gamma }_p+{\gamma }_v\gamma ){\mathit{e}}_p^T\left(t\right){\mathcal{M}}^2{\mathit{e}}_v\left(t\right)+\gamma {\mathit{e}}_v^T\left(t\right)\mathcal{M}{\mathit{e}}_v\left(t\right)+\gamma {\mathit{e}}_p^T\left(t\right)\mathcal{M}{\dot{\mathit{e}}}_v\left(t\right)+{\mathit{e}}_v^T\left(t\right)\mathcal{M}{\dot{\mathit{e}}}_v\left(t\right)+\sum _{i=1}^N{\dot{\chi }}_i\left(t\right)\hfill \\ \hfill & =-{\gamma }_p\gamma {\mathit{e}}_p^T{\mathcal{M}}^2{\mathit{e}}_p\left(t\right)-{\mathit{e}}_v^T\left(t\right)({\gamma }_v{\mathcal{M}}^2-\gamma \mathcal{M}){\mathit{e}}_v\left(t\right)-{\left(\gamma {\mathit{e}}_p\left(t\right)+{\mathit{e}}_v\left(t\right)\right)}^T\mathcal{M}({\gamma }_p(\mathcal{L}\otimes I_n){\tilde{\mathit{\eta }}}_p\left(t\right)\hfill \\ \hfill & \hspace{1em}+{\gamma }_v\mathcal{M}{\tilde{\mathit{\eta }}}_v\left(t\right)+{\gamma }_p(\Delta \otimes I_n){\tilde{\mathit{e}}}_p\left(t\right)-{\tilde{\mathit{f}}}_a\left(t\right))+\sum _{i=1}^N{\dot{\chi }}_i\left(t\right),\hfill \end{array}$$

(21)

where ${\tilde{\mathit{e}}}_p\left(t\right)={\tilde{\mathit{\eta }}}_p\left(t\right)-\tilde{\mathit{r}}\left(t\right)$. We remark that $e_{p,i}\left(t\right)$ and $e_{p,i}\left(t\right)$ are only available in the ith agent if ${\delta }_i=1$. Thus, let ${\mathit{z}}_p\left(t\right)={\left[z_{p,1}^T\left(t\right),z_{p,2}^T\left(t\right),\dots ,z_{p,N}^T\left(t\right)\right]}^T$, ${\mathit{z}}_v\left(t\right)={\left[z_{v,1}^T\left(t\right),z_{v,2}^T\left(t\right),\dots ,z_{v,N}^T\left(t\right)\right]}^T$. From (9) and (10), it can be established that:

$$\begin{array}{c}\hfill {\mathit{z}}_p\left(t\right)=\mathcal{M}{\mathit{e}}_p\left(t\right),{\mathit{z}}_v\left(t\right)=\mathcal{M}{\mathit{e}}_v\left(t\right).\end{array}$$

(22)

Additionally, by letting $\mathit{q}\left(t\right)=\left[q_1^T\left(t\right),q_2^T\left(t\right),\dots ,q_N^T\left(t\right)\right]$, it can be derived from (8) that:

$$\begin{array}{cc}\hfill \mathit{q}\left(t\right)& =-{\gamma }_p(\mathcal{L}\otimes I_n){\tilde{\mathit{\eta }}}_p\left(t\right)-{\gamma }_v\mathcal{M}{\tilde{\mathit{\eta }}}_v\left(t\right)-{\gamma }_p(\Delta \otimes I_n){\tilde{\mathit{e}}}_p\left(t\right)+{\tilde{\mathit{f}}}_a\left(t\right).\hfill \end{array}$$

(23)

From (9) and (10), (21) can be rewritten as:

$$\begin{array}{cc}\dot{V}\left(t\right)=& -\gamma ({\gamma }_p-{\theta }_p){\mathit{e}}_p^T\left(t\right){\mathcal{M}}^2{\mathit{e}}_p\left(t\right)-{\mathit{e}}_v^T\left(t\right)\left(({\gamma }_v-{\theta }_v){\mathcal{M}}^2-\gamma \mathcal{M}\right){\mathit{e}}_v\left(t\right)-\gamma {\mathit{z}}_p^T\left(t\right)\left({\theta }_p{\mathit{z}}_p\left(t\right)-\mathit{q}\left(t\right)\right)\hfill \\ & -{\mathit{z}}_v^T\left(t\right)\left({\theta }_v{\mathit{z}}_v\left(t\right)-\mathit{q}\left(t\right)\right)+\sum _{i=1}^N{\dot{\chi }}_i\left(t\right).\hfill \end{array}$$

(24)

Further, by substituting the dynamic event-triggered law (6), (7), and (23) into (24), it can be established:

$$\begin{array}{ccc}\hfill \dot{V}\left(t\right)& =& -\gamma ({\gamma }_p-{\theta }_p){\mathit{e}}_p^T\left(t\right){\mathcal{M}}^2{\mathit{e}}_p\left(t\right)-{\mathit{e}}_v^T\left(t\right)\left(({\gamma }_v-{\theta }_v){\mathcal{M}}^2-\gamma \mathcal{M}\right){\mathit{e}}_v\left(t\right)\hfill \\ \hfill & & -\sum _{i=1}^N{\widehat{\chi }}_i+\sum _{i=1}^N\left(-{\beta }_i{\chi }_i\left(t\right)+{\widehat{\chi }}_i\left(t\right)\right)\hfill \\ \hfill & =& -{\overline{\mathit{e}}}^T\left(t\right)\mathbb{M}\overline{\mathit{e}}\left(t\right)-\sum _{i=1}^N{\beta }_i{\chi }_i\left(t\right),\hfill \end{array}$$

(25)

where:

$$\begin{array}{c}\hfill \mathbb{M}=\left[\begin{array}{cc}\gamma ({\gamma }_p-{\theta }_p){\mathcal{M}}^2& 0\\ 0& ({\gamma }_v-{\theta }_v){\mathcal{M}}^2-\gamma \mathcal{M}\end{array}\right].\end{array}$$

By invoking the conditions (15) and (16), the matrix $\mathbb{M}$ is positive definite. From the fact that $\mathbb{M}\ge \frac{{\lambda }_{min}\left(\mathbb{M}\right)}{{\lambda }_{max}\left(\mathbb{P}\right)}\mathbb{P}$ where $\mathbb{P}$ is also a positive definite matrix, let us select:

$$\begin{array}{cc}\hfill \kappa =& min\left\{\frac{2{\lambda }_{min}\left(\mathbb{M}\right)}{{\lambda }_{max}\left(\mathbb{P}\right)},{\beta }_1,\dots ,{\beta }_N\right\}.\hfill \end{array}$$

Then, (25) offers:

$$\begin{array}{c}\hfill \dot{V}\left(t\right)\le -\kappa V\left(t\right),\end{array}$$

(26)

for $\forall t\ge 0$. Therefore, by applying the comparison lemma again to Inequality (26), one has:

$$\begin{array}{c}\hfill \frac{1}{2}{\overline{\mathit{e}}}^T\left(t\right)\mathbb{P}\overline{\mathit{e}}\left(t\right)<V\left(t\right)\le V\left(0\right)e^{-\kappa t}.\end{array}$$

(27)

Next, we are going to prove that there is no Zeno behavior in the proposed dynamic event triggering mechanism. By using a contradiction, let us assume that there exists Zeno behavior for at least the ith agent, which implies there exists $0<\mathcal{T}<\infty$ such that:

$$\begin{array}{c}\hfill \underset{k_i\to \infty }{lim}{t}_{k_i}^i=\mathcal{T}.\end{array}$$

(28)

Then, there exist $\epsilon \in {\mathbb{R}}_{+}$ and $N\left(\epsilon \right)\in \mathbb{N}$ such that:

$$\begin{array}{c}\hfill t_{k_i}^i\in [\mathcal{T}-\epsilon ,\mathcal{T}),\forall k_i\ge N\left(\epsilon \right).\end{array}$$

(29)

In other words, from (27), there exist positive constants ${\varpi }_{p,i}$ and ${\varpi }_{v,i}$ such that $\parallel e_{p,i}\left(t\right){\parallel }_2\le {\varpi }_{p,i}$, $\parallel e_{v,i}\left(t\right){\parallel }_2\le {\varpi }_{v,i}$, and subsequently, $\parallel {\tilde{e}}_{p,i}\left(t\right){\parallel }_2\le 2{\varpi }_{p,i}$, $\parallel {\tilde{e}}_{v,i}\left(t\right){\parallel }_2\le 2{\varpi }_{v,i}$, for all $t\in \left[0,\mathcal{T}\right)$. Then, $\parallel u_i\left(t\right)\parallel \le {\varpi }_{u,i}$, with ${\varpi }_{u,i}={\gamma }_p\left(2{\ell }_{ii}+{\delta }_i\right){\varpi }_{p,i}+{\gamma }_v\left(2{\ell }_{ii}+{\delta }_i\right){\varpi }_{v,i}+{\varpi }_{fa}$. Let us consider the following conditions in $t\in [t_{N\left(\epsilon \right)},\mathcal{T})$:

$$\begin{array}{c}\hfill {\widehat{\chi }}_i\left(t\right)\ge -{\sigma }_i{\chi }_i\left(0\right)e^{-\left({\beta }_i+{\sigma }_i\right)t}.\end{array}$$

(30)

From (18), the condition (30) guarantees ${\sigma }_i{\chi }_i\left(t\right)+{\widehat{\chi }}_i\left(t\right)>0$, which can be obtained from (6). Further, because of the boundedness of $u_i\left(t\right)$, ${\chi }_i\left(t\right)$ and ${\widehat{\chi }}_i\left(t\right)$ are continuous differentiable functions. By invoking the mean value theorem for $h_i\left(\tau \right)={\sigma }_i{\chi }_i\left(\tau \right)+{\widehat{\chi }}_i\left(\tau \right)$ in $[t_{N\left(\epsilon \right)}^i,t]$, there exists $c\in \left(t_{N\left(\epsilon \right)}^i,t\right)$ such that:

$$\begin{array}{c}\frac{h_i\left(t\right)-h_i\left(t_{N\left(\epsilon \right)}^i\right)}{t-t_{N\left(\epsilon \right)}^i}=\frac{h_i\left(t\right)}{t-t_{N\left(\epsilon \right)}^i}=h_i^{\prime }\left(c\right),\hfill \end{array}$$

(31)

where $h_i^{\prime }\left(c\right)=\frac{d{h}_i\left(\tau \right)}{d\tau }{|}_{\tau =c}$. From (31), we have $h^{\prime }\left(c\right)\left(t-t_{N\left(\epsilon \right)}^i\right)>{\widehat{\chi }}_i\left(t\right)$. Then, let ${\alpha }_i={sup}_{\tau \in (t_{N\left(\epsilon \right)}^i,t)}\left|h_i^{\prime }\left(\tau \right)\right|$. It can be said that the condition (29) is ensured by:

$$\begin{array}{c}\hfill t-t_{N\left(\epsilon \right)}^i<\frac{{\sigma }_i}{{\alpha }_i}{\chi }_i\left(0\right)e^{-\left({\beta }_i+{\sigma }_i\right)t},\end{array}$$

(32)

for $t\in \left[t_{N\left(\epsilon \right)}^i,{\widehat{t}}_{N\left(\epsilon \right)+1}^i\right)$.

Now, let us consider a static event-triggered law ${\left\{{\widehat{t}}_k^i\right\}}_{N\left(\epsilon \right)}^{\infty }$ with ${\widehat{t}}_{N\left(\epsilon \right)}^i=t_{N\left(\epsilon \right)}^i$ that guarantees the condition (32). Because (32) is a sufficient condition of (6), one has:

$$\begin{array}{cc}\hfill t_{N\left(\epsilon \right)+1}^i-t_{N\left(\epsilon \right)}^i& \ge {\widehat{t}}_{N\left(\epsilon \right)+1}^i-t_{N\left(\epsilon \right)}^i\hfill \\ \hfill & =\frac{{\sigma }_i}{{\alpha }_i}{\chi }_i\left(0\right)e^{-\left({\beta }_i+{\sigma }_i\right){\widehat{t}}_{N\left(\epsilon \right)+1}^i}\hfill \\ \hfill & \ge \frac{{\sigma }_i}{{\alpha }_i}{\chi }_i\left(0\right)e^{-\left({\beta }_i+{\sigma }_i\right)\mathcal{T}}.\hfill \end{array}$$

(33)

By taking $\epsilon =\frac{{\sigma }_i}{{\alpha }_i}{\chi }_i\left(0\right)e^{-\left({\beta }_i+{\sigma }_i\right)\mathcal{T}}$, this implies that (33) contradicts (29). Therefore, the aforementioned Zeno behavior is eliminated in the proposed approach.

Consequently, it can be seen from (27) that the formation tracking error $\overline{\mathit{e}}\left(t\right)$ exponentially asymptotically converges to the origin. In general, the proposed distributed control law navigates the group of agents to track the predefined formation. Further, the internal dynamics (11) is also asymptotically stable. □

Remark 3.

Intuitively, from (30), we can conclude that the larger initial values ${\chi }_i\left(0\right)$ result in a larger inter-event time. Further, one can obtain from proof of Theorem 1 that there always exists the static event trigger ${\widehat{\chi }}_i\left(t\right)\le 0$ that has inter-event time larger than the dynamic event triggering mechanism.

Remark 4.

In the following, let us provide a discussion on the choice of parameters in order to tune the behaviors of the considered system. While γ solely guarantees the existence of ${\gamma }_p,{\gamma }_v,{\theta }_v$ and does not impact the performance of the system, the others influence the inter-event time and a decay rate κ of the Lyapunov function (26). Actually, because $\mathcal{M}$ in (16) and (17) absolutely depends on the network topology of the considered multi-agent system, we should firstly choose γ, ${\gamma }_p,{\gamma }_v$, and ${\theta }_v$ to satisfy (16) and (17). After selecting ${\sigma }_i$ in the proposed triggering law (6), ${\beta }_i$ and ${\theta }_p$ are possibly adjusted to compromise the decay rate of the Lyapunov function (26) and the value of the minimum inter-event time.

Remark 5.

Obviously, because the system requires extensive communication among agents, communication delays and package losses clearly affect the performance of the system. In this note, we studied the application of multi-agent systems to a multiple quadcopter system. Due to the much larger dynamics of mechanical systems, compared with that of communication, it can be assumed that there is ideal information transmission among agents. On the other hand, there have been several studies [20,30,31,32] addressing these aforementioned problems in consensus multi-agent systems. Thus, we leave these as future research into the formation control of multi-quadcopter systems.

4. Application to Multiple Quadcopter Systems

In several special cases of the formation control of MASs, a predefined spot of each agent can be considered as a time-varying function, leading to time-varying formation control. The formation shape established by each time-varying agent position is able to be flexibly changed in many different real applications, such as obstacle avoidance and the cooperative work in carrying payloads. Quadcopters, which are one of the most active classes of UAVs, have two pairs of motors to adjust their altitude and attitude. The reasons why quadcopters have been widely researched in many recent studies are that their practical models shrink in experiments for safety, and they have enough actuators to control their rigid body states including position and orientation [33,34,35,36]. In considering the formation control of multiple quadcopters, each agent can be treated as a point-mass system, and the outer loop dynamic model is described as a second-order dynamics.

To verify the proposed method in the control of the multi-agent system, the simulation results of six unmanned aerial vehicles (quadcopters) with the dynamic event-triggered controllers were carried out. The investigated systems were able to form an anticipated shape and asymptotically track a predefined trajectory. In this scenario, each tracking reference of the ith quadcopter was a combination of the predefined formation flight trajectory $r\left(t\right)$ and the individual time-varying position in the formation $f_{p,i}\left(t\right)$. It was supposed that $r\left(t\right)$ was only available to the first quadcopter, while the others did not know $r\left(t\right)$, and all quadcopters possessed their time-varying position $f_{p,i}\left(t\right)$. The proposed algorithm will be applied to the outer loop (double integrator) (2) before calculating the thrust force and the desired attitude for the inner loop (40). By making use of the lower controller in the inner loop, the thrust force $U_{1i}\left(t\right)$ and rotation moments $U_{2i}\left(t\right),U_{3i}$(t), and $U_{4i}\left(t\right)$ control each quadcopter system modeled in (37) and (39). Following the predefined formation flight, the proposed control algorithm and dynamic event-triggered mechanism were designed to guarantee the exponential convergence of formation tracking errors.

4.1. Quadcopter Dynamics

Let us take into account the ith individual quadcopter with body frame ${\left\{Oxyz\right\}}_B$, position $p_i\left(t\right)=[p_{x,i}\left(t\right),p_{y,i}\left(t\right),$ $p_{z,i}\left(t\right){]}^T\in {\mathbb{R}}^3$, and velocity $v_i\left(t\right)={\left[v_{x,i}\left(t\right),v_{y,i}\left(t\right),v_{z,i}\left(t\right)\right]}^T\in {\mathbb{R}}^3$ in the Earth-fixed frame ${\left\{Oxyz\right\}}_E$. To be specific, the plus-configuration setup and all parameters of the ith quadcopter are presented in Figure 2 and

Table 1. The quadcopter parameters.

Definition	Symbol	Unit
Mass of quadcopter	$m_i$	kg
Gravitational accelerator	g	m·${\mathrm{s}}^{-2}$
Arm length	$l_i$	m
Thrust coefficient	$b_i$	N·${\mathrm{s}}^2·$${\mathrm{rad}}^{-2}$
Drag coefficient	$d_i$	N·${\mathrm{s}}^2·$${\mathrm{rad}}^{-2}$
Moment of inertia along x-axis	${\mathcal{I}}_{x,i}$	kg·${\mathrm{m}}^2$
Moment of inertia along y-axis	${\mathcal{I}}_{y,i}$	kg·${\mathrm{m}}^2$
Moment of inertia along z-axis	${\mathcal{I}}_{z,i}$	kg·${\mathrm{m}}^2$

, respectively. In addition, ${\varphi }_i\left(t\right)$, ${\theta }_i\left(t\right)$, and ${\psi }_i\left(t\right)$ denote the roll, pitch, and yaw angle in the Earth-fixed frame, while ${\nu }_{p,i}\left(t\right)$, ${\nu }_{q,i}\left(t\right)$, and ${\nu }_{r,i}\left(t\right)$ stand for the angular rates in the body frame obtained from an attached inertial measurement unit (IMU) in the quadcopter. By setting each rotor speed ${\omega }_{ki}\left(t\right)$ for $k=\{1,2,3,4\}$ with thrust $b_i$ and drag coefficients $d_i$, the allocation control is given by Equation (34), in which $U_{1i}\left(t\right)$ generates a lift force, while the others create rotation moments.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{U}_{1i}\left(t\right)=b_i\left({\omega }_{1i}^2\left(t\right)+{\omega }_{2i}^2\left(t\right)+{\omega }_{3i}^2\left(t\right)+{\omega }_{4i}^2\left(t\right)\right),\hfill \\ U_{2i}\left(t\right)=b_i{l}_i\left(-{\omega }_{2i}^2\left(t\right)+{\omega }_{4i}^2\left(t\right)\right),\hfill \\ U_{3i}\left(t\right)=b_i{l}_i\left({\omega }_{1i}^2\left(t\right)-{\omega }_{3i}^2\left(t\right)\right),\hfill \\ U_{4i}\left(t\right)=d_i{l}_i\left(-{\omega }_{1i}^2\left(t\right)+{\omega }_{2i}^2\left(t\right)-{\omega }_{3i}^2\left(t\right)+{\omega }_{4i}^2\left(t\right)\right),\hfill \end{array}\right.\end{array}$$

(34)

The rotation matrix $R_B^E\left({\varphi }_i\left(t\right),{\theta }_i\left(t\right),{\psi }_i\left(t\right)\right)$ from the body to the Earth-fixed frame:

$$\begin{array}{c}\hfill R_B^E\left({\varphi }_i\left(t\right),{\theta }_i\left(t\right),{\psi }_i\left(t\right)\right)=\left[\begin{array}{ccc}c{\psi }_{i}c{\theta }_i& c{\psi }_{i}s{\theta }_{i}s{\varphi }_i-s{\psi }_{i}c{\varphi }_i& c{\psi }_{i}s{\theta }_{i}c{\varphi }_i+s{\psi }_{i}s{\varphi }_i\\ s{\psi }_{i}c{\theta }_i& s{\psi }_{i}s{\theta }_{i}s{\varphi }_i+c{\psi }_{i}c{\varphi }_i& s{\psi }_{i}s{\theta }_{i}c{\varphi }_i-c{\psi }_{i}s{\varphi }_i\\ -s{\theta }_i& c{\theta }_{i}s{\varphi }_i& c{\theta }_{i}c{\varphi }_i\end{array}\right],\end{array}$$

(35)

As a result, the angular rates ${\nu }_{p,i}\left(t\right)$, ${\nu }_{q,i}\left(t\right)$, and ${\nu }_{r,i}\left(t\right)$ in the body frame can be transformed from the Euler angle rate in the Earth-fixed frame:

$$\begin{array}{c}\left[\begin{array}{c}{\nu }_{p,i}\left(t\right)\\ {\nu }_{q,i}\left(t\right)\\ {\nu }_{r,i}\left(t\right)\end{array}\right]=\left[\begin{array}{ccc}1& 0& -s{\theta }_i\\ 0& c{\varphi }_i& s{\varphi }_{i}c{\theta }_i\\ 0& -s{\varphi }_i& c{\varphi }_{i}c{\theta }_i\end{array}\right]\left[\begin{array}{c}\dot{{\varphi }_i}\left(t\right)\\ \dot{{\theta }_i}\left(t\right)\\ \dot{{\psi }_i}\left(t\right)\end{array}\right].\hfill \end{array}$$

(36)

By using the Euler–Lagrange equations, the quadcopter dynamics model is given as:

$$\begin{array}{c}\left[\begin{array}{c}{\ddot{p}}_{x,i}\left(t\right)\\ {\ddot{p}}_{y,i}\left(t\right)\\ {\ddot{p}}_{z,i}\left(t\right)\end{array}\right]=-G+\frac{U_{1i}\left(t\right)}{m_i}\left[\begin{array}{c}c{\psi }_{i}s{\theta }_{i}c{\varphi }_i+s{\psi }_{i}s{\varphi }_i\\ s{\psi }_{i}s{\theta }_{i}c{\varphi }_i-c{\psi }_{i}s{\varphi }_i\\ c{\theta }_{i}c{\varphi }_i\end{array}\right],\hfill \end{array}$$

(37)

$$\begin{array}{c}\left[\begin{array}{c}{U}_{2i}\left(t\right)\\ U_{3i}\left(t\right)\\ U_{4i}\left(t\right)\end{array}\right]={\mathcal{I}}_{B,i}\left[\begin{array}{c}{\dot{\nu }}_{p,i}\left(t\right)\\ {\dot{\nu }}_{q,i}\left(t\right)\\ {\dot{\nu }}_{r,i}\left(t\right)\end{array}\right]+\left[\begin{array}{c}{\nu }_{p,i}\left(t\right)\\ {\nu }_{q,i}\left(t\right)\\ {\nu }_{r,i}\left(t\right)\end{array}\right]\times \left({\mathcal{I}}_{B,i}\left[\begin{array}{c}{\nu }_{p,i}\left(t\right)\\ {\nu }_{q,i}\left(t\right)\\ {\nu }_{r,i}\left(t\right)\end{array}\right]\right),\hfill \end{array}$$

(38)

where “×” denotes the cross product, $G={[0,0,g]}^T$, and ${\mathcal{I}}_{B,i}=\mathit{diag}\left({\mathcal{I}}_{x,i},{\mathcal{I}}_{y,i},{\mathcal{I}}_{z,i}\right)$ is the tensor matrix of this system. By substituting (36) into (38), the dynamic equations of the quadcopter attitude ith can be obtained:

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\ddot{\varphi }}_i\left(t\right)\\ {\ddot{\theta }}_i\left(t\right)\\ {\ddot{\psi }}_i\left(t\right)\end{array}\right]={\mathcal{J}}_i^{-1}\left(\left[\begin{array}{c}{U}_{2i}\left(t\right)\\ U_{3i}\left(t\right)\\ U_{4i}\left(t\right)\end{array}\right]-{\mathcal{C}}_i\left[\begin{array}{c}{\dot{\varphi }}_i\left(t\right)\\ {\dot{\theta }}_i\left(t\right)\\ {\dot{\psi }}_i\left(t\right)\end{array}\right]\right),\end{array}$$

(39)

where ${\mathcal{J}}_i$ and ${\mathcal{C}}_i\in {\mathbb{R}}^{3\times 3}$ can be found in Appendix A. Inspired by the studies [6,7,27,36,37,38,39,40], where the control of a quadcopter can be separated into inner (39) and outer loop (37) paradigms, this paper proposes a control structure, in which the outer control loop of each quadcopter guarantees the formation tracking in the group of quadcopters by adjusting the reference attitude. Additionally, the inner loop was designed such that the actual attitude tracked its reference generated by the outer loop. In the scope of this work, we were mainly devoted to designing the dynamic event-triggered formation control of the outer loop. Therefore, for the formation control problem, each quadcopter could be regarded as a point-mass, and its dynamics could be described by a second-order control system, which can be derived from Equation (37) as follows: where $u_i\left(t\right)=A_i\left(t\right){\tau }_i\left(t\right)-G$ and:

$$\begin{array}{c}\hfill A_i\left(t\right)=\frac{1}{m_i}\left[\begin{array}{ccc}c{\psi }_i& -s{\psi }_i& 0\\ s{\psi }_i& c{\psi }_i& 0\\ 0& 0& 1\end{array}\right],{\tau }_i\left(t\right)=\left[\begin{array}{c}{\tau }_{x,i}\left(t\right)\\ {\tau }_{y,i}\left(t\right)\\ {\tau }_{z,i}\left(t\right)\end{array}\right]=\left[\begin{array}{c}{U}_{1i}\left(t\right)c{\varphi }_{i}s{\theta }_i\\ -U_{1i}\left(t\right)s{\varphi }_i\\ U_{1i}\left(t\right)c{\varphi }_{i}c{\theta }_i\end{array}\right].\end{array}$$

It can be seen that the desired attitude is generated for the inner loop as follows:

$$\begin{array}{c}{U}_{1i}\left(t\right)=\sqrt{{\tau }_{x,i}{\left(t\right)}^2+{\tau }_{y,i}{\left(t\right)}^2+{\tau }_{z,i}{\left(t\right)}^2},\hfill \\ {\varphi }_i\left(t\right)=arcsin\frac{-{\tau }_{y,i}\left(t\right)}{U_{1i}\left(t\right)},{\theta }_i\left(t\right)=arctan\frac{{\tau }_{x,i}\left(t\right)}{{\tau }_{z,i}\left(t\right)}.\hfill \end{array}$$

(40)

Remark 6.

Most of the computational devices in quadcopter systems are developed by using the Robot Operating System (ROS), which is a set of software libraries and tools for building robot applications. In addition, these devices typically are a combination of a companion computer and an IMU, as shown in [41,42,43]. For the companion computer, each system can communicate with others and do its individual tasks to meet the formation flight requirements. Figure 3 illustrates our algorithm where the companion computer covers the formation control law, the event triggering condition, and the wireless communication. By following this procedure, the thrust force $U_{1,i}\left(t\right)$ and desired roll, pitch, and yaw angle are calculated in the companion computer before being published to the inner loop. It can be assumed that the attitude is able to track immediately the desired one in the inner loop (refer to [33,34,35,44,45,46]).

4.2. Numerical Simulation Results

The parameter values of each quadcopter based on the F450 frame are given in

Table 2. The quadcopter parameter values in the simulation.

Definition	Value	Unit
Mass of quadcopter	$m_i=1.568$	kg
Gravitational accelerator	$g=9.8$	m·${\mathrm{s}}^{-2}$
Arm length	$l_i=0.25$	m
Thrust coefficient	$b_i=7.73\times {10}^{-6}$	N·${\mathrm{s}}^2·$${\mathrm{rad}}^{-2}$
Drag coefficient	$d_i=1.28\times {10}^{-7}$	N·${\mathrm{rad}}^{-2}$
Moment of inertia along x-axis	${\mathcal{I}}_{x,i}=0.0119$	kg·${\mathrm{m}}^2$
Moment of inertia along y-axis	${\mathcal{I}}_{y,i}=0.0119$	kg·${\mathrm{m}}^2$
Moment of inertia along z-axis	${\mathcal{I}}_{z,i}=0.0223$	kg·${\mathrm{m}}^2$

[33], and each quadcopter’s initial states were chosen such that they lied outside their predefined spots in the formation to validate the proposed algorithm strongly: $p_1\left(0\right)={\left[0,2,0\right]}^T$, $p_2\left(0\right)={\left[1.5,1,0\right]}^T$, $p_3\left(0\right)={\left[1.5,0,0\right]}^T$, $p_4\left(0\right)={\left[0,-1,0\right]}^T$, $p_5\left(0\right)={\left[-1,0,0\right]}^T$, and $p_6\left(0\right)={\left[-1,1.5,0\right]}^T$ (m). The formation shape is defined by a regular hexagon with the length of the sides $d_0=3$m. It is easily seen that $f_{p,1d}={\left[0,3d_0/2,0\right]}^T$, $f_{p,2d}={\left[d_0\sqrt{3}/2,d_0,0\right]}^T$, $f_{p,3d}={\left[d_0\sqrt{3}/2,0,0\right]}^T$, $f_{p,4d}={\left[0,-d_0/2,0\right]}^T$, $f_{p,5d}={\left[-d_0\sqrt{3}/2,0,0\right]}^T$, and $f_{p,6d}={\left[-d_0\sqrt{3}/2,d_0,0\right]}^T$ (m). Each ith quadcopter time-varying spot can be set as $f_{p,i}\left(t\right)=f_{p,id}\left(1-\exp \left(-10t\right)\right)$, $\left(i\in \mathbb{S}\right)$. Additionally, based on Theorem 1, all coefficients are selected as: $\gamma =0.2$, ${\gamma }_v=3$, ${\gamma }_p=2$, ${\theta }_v=1.3$, ${\theta }_p=1.3$, ${\beta }_i=5$, $\sigma =0.2$, ${\chi }_i\left(0\right)=10$ $\left(i\in \mathbb{S}\right)$, ${\delta }_1=1$, and ${\delta }_j=0$ $(j\in \mathbb{S},j\ne 1)$. The reference velocity is set as $v_0={\left[1,1,2\right]}^T$. Furthermore, a connected network of six quadcopters is considered with the Laplacian matrix:

$$\begin{array}{c}\hfill \mathcal{L}=\left[\begin{array}{cccccc}2& -1& 0& 0& 0& -1\\ -1& 2& -1& 0& 0& 0\\ 0& -1& 2& -1& 0& 0\\ 0& 0& -1& 2& -1& 0\\ 0& 0& 0& -1& 2& -1\\ -1& 0& 0& 0& -1& 2\end{array}\right],\end{array}$$

(41)

where each quadcopter communicates with its two neighbors, e.g., the first quadcopter exchanges its information with the second and sixth quadcopters.

Figure 4a–c shows six different dotted color lines describing the tracking errors of the quadcopters projected on the x-, y-, and z- axes, respectively. The initial state of each quadcopter was arranged outside its desired position in the formation to demonstrate our method strongly. By using the cascade control structure, the actual attitude of each quadcopter automatically tracked its desired value generated by the outer loop. Hence, although the reference attitude of each quadcopter remained unchanged between two consecutive triggering times, the formation tracking errors of each quadcopter were almost smooth. Based on Theorem 1, it was proven that the investigated system asymptotically achieved the predefined time-varying formation flight as time went to infinity. It can be seen that these figures confirmed the asymptotic convergence of the closed loop system at the origin from the eighth second, leading to the achievement of the time-varying formation flight for the six quadcopter system. Figure 5a illustrates the overall formation flight for the probed system within ten seconds of simulation. By using dotted blue lines to mark the shape of the six quadcopters at times T = 0, T = 2, T = 5, and T = 10 (s), the transition of the time-varying formation is easily observed in three-dimensional space. Additionally, by projecting into the $xy$-plane, the position snapshots of the time-varying formation flight are shown in Figure 5b. Beginning from an arbitrary hexagon at T = 0 s, they almost reached the predefined regular hexagon at T = 5 s after magnifying their shape at T = 2 s. Finally, the predefined regular hexagon was totally achieved at T = 10 s.

As mentioned in [24], the minimum execution time of the proposed method was greater than that of the static law. However, we could not say anything about the total triggering times for these two algorithms. These times could be computed in the simulations of two cases, i.e., using the proposed and static triggering laws for the same scenario of the formation flight within 10 s of simulation. The figures for the triggering times of these two laws are reported in

Table 3. Comparison of the number of triggering times of the proposed dynamic and static event-triggered algorithms in 10 s.

Quad. No.	1st	2nd	3rd	4th	5th	6th
Dynamics	124	107	104	102	108	115
Statics	247	300	274	226	233	336

. There was a significant reduction in the input update times of the dynamics compared with the statics. It can be seen that by using the proposed method, the triggering times were almost half or one-third that of the conventional scheme. There were dissimilar decreases in the triggering times of all quadcopters because of their different initial tracking errors. In other words, since the reference trajectory of the formation $r\left(t\right)$ was only available to the first quadcopter, the value of its triggering times was slightly greater than that for the others. To be specific, in comparison with periodical sampling where the sampling rate was around 20 to 100 Hz for the outer control loop (10–50 ms for the sampling time) due to GPS sensor, our algorithm provided less triggered times (number of sampling times). As can be shown in Table 3, it took 124 to 115 sampling times for 10 s in the outer control loop (the minimum interval time was approximately 50 ms). It should be noted that fewer sampling times possibly brought twofold beneficial effects. The first one was the decrease of computational burden in the inner loop controller. The other one was that the transmission times between each pair of connected quadcopters and the required sampling rate of its GPS sensors were reduced. By marking “*” when events occurred in each quadcopter in Figure 6, not only was it proven in Theorem 1, but also the total corresponding triggering times of each quadcopter were shown to guarantee once again that the Zeno behavior was excluded.

As mentioned in Remark 1, we verified our proposed control algorithm for more general reference trajectories, including multiple straight lines. The following simulation result for the case reference trajectory $r\left(t\right)$ with five straight lines was established to demonstrate the effectiveness of our method. In more detail, the reference velocity could be chosen as: $v_0\left(t\right)={\left[0.8,0.5,1.5\right]}^T$$t\in \left[0,10\right)$, $v_0\left(t\right)={\left[0.6,0.3,1.5\right]}^T$ $t\in \left[10,30\right)$, $v_0\left(t\right)={\left[1,-0.2,1.5\right]}^T$ $t\in \left[30,50\right)$, $v_0\left(t\right)={\left[0.3,-0.2,1.5\right]}^T$ $t\in \left[50,70\right)$, and $v_0\left(t\right)={\left[-0.4,-0.4,1.5\right]}^T$ $t\in \left[70,100\right]\left(\mathrm{s}\right)$. The formation flight of the probed system tracking the multiple straight lines trajectory is shown in three-dimensional space in Figure 7a. To achieve the asymptotic stability of the closed loop system clearly, Figure 8a–c illustrates the tracking errors of the corresponding quadcopters with multiple line trajectories. Although there were sudden changes of the reference velocities at times $T=10$ s, $T=30$ s, $T=50$ s, and $T=70$ s, the tracking errors of the considered system along the x-, y-, and z-axes asymptotically converged to the origin. The snapshots of the six quadcopters’ position projected on the $xy$-plane at times $T=10$ s, $T=30$ s, $T=50$ s, $T=70$ s, and $T=100$ s are illustrated in Figure 7b. It was clear that the formation of the six-quadcopter system still kept its shape as a regular hexagon despite the transitions of the reference velocities.

5. Conclusions

In this paper, the time-varying distributed formation control of a multi-agent system via limited communication was studied. The proposed aperiodic sampling law based on the dynamic event-triggered algorithm possibly alleviated the computational burden in the inner loop controller, as well as the requirements of the sampling rate of the sensors. When it comes to multiple mechanical systems, the distributed protocol has been widely utilized to remove centralized tasks at a ground station. Many works such as computation, communication, and control input update need to be executed in each agent. Further, in case each agent shares a mutual remote sensor system, the fixed base station periodically transmits numerous preprocessing data to all agents. To decrease burdens of each agent significantly, we proposed the event triggering mechanism to determine the next actions in each agent. Instead of executing inputs after the elapsing of a periodic fixed time, the devoted algorithm solely updates the next inputs when the constructed events occur. Moreover, by establishing the new control Lyapunov function, the considered multi-agent system not only exponentially asymptotically achieved the predefined time-varying formation, but also completely excluded the Zeno behavior, which allowed the practical ability of this method. As a result, our algorithm was capable of guaranteeing a satisfactory system, as well as addressing practical problems. In future work, we plan to study the switching topology and/or collision avoidance among a group of quadcopters. Another interesting topic is to consider communication delays and packet losses on the formation flight of multiple quadcopter systems.