Robust Structural Damage Detection Using Analysis of the CMSE Residual’s Sensitivity to Damage
Abstract
:1. Introduction
2. Theoretical Background
2.1. CMSE Method
2.2. ITR Method
3. Robust Damage Identification Scheme
4. Numerical Simulation
4.1. Description of the Truss Structure
4.2. Damage Cases
4.3. Robustness Performance Investigation
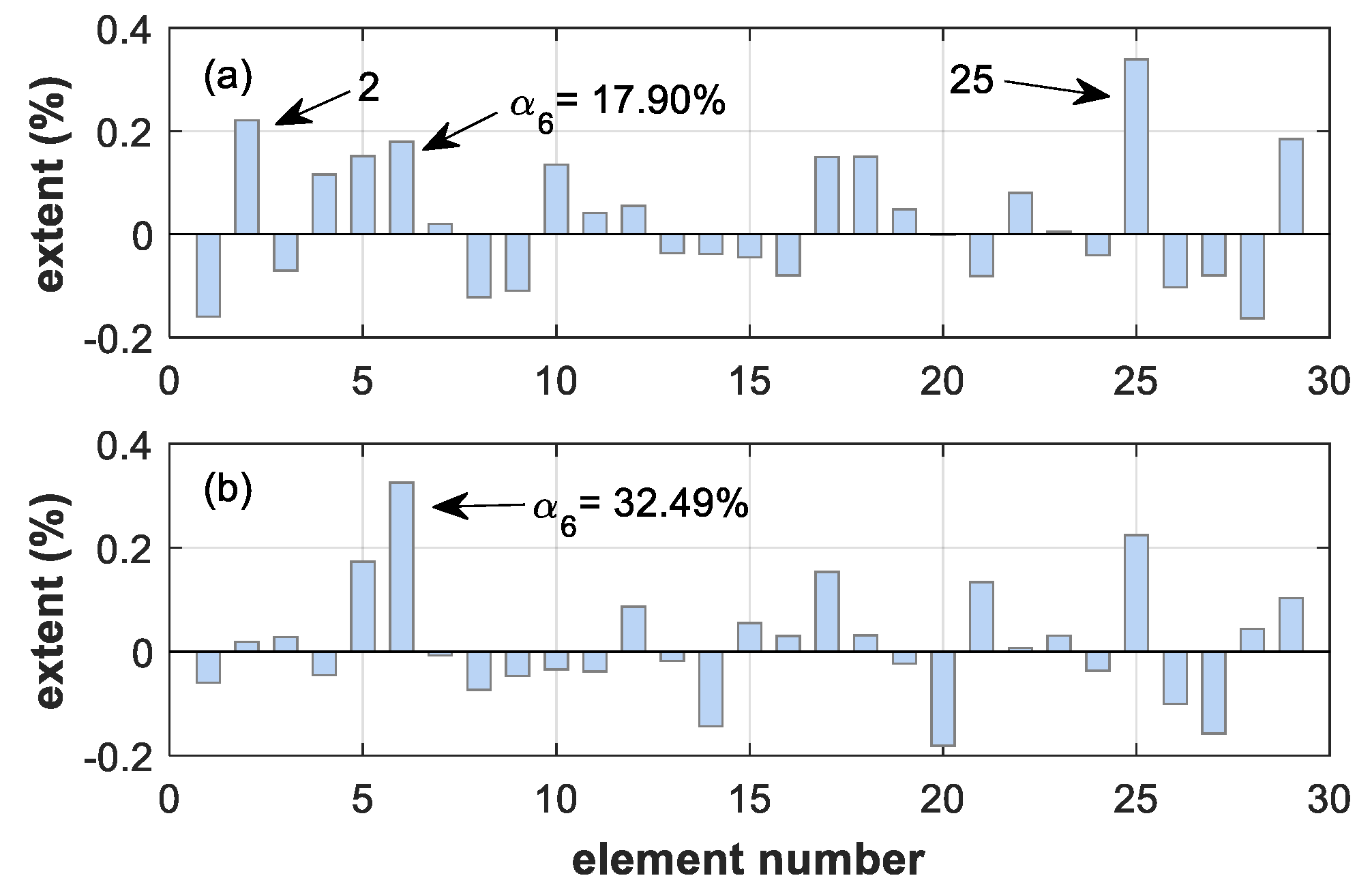
4.3.1. Effects of Damage Location
4.3.2. Effects of Damage Level
5. Experimental Validation
5.1. Description of the Beam Structure
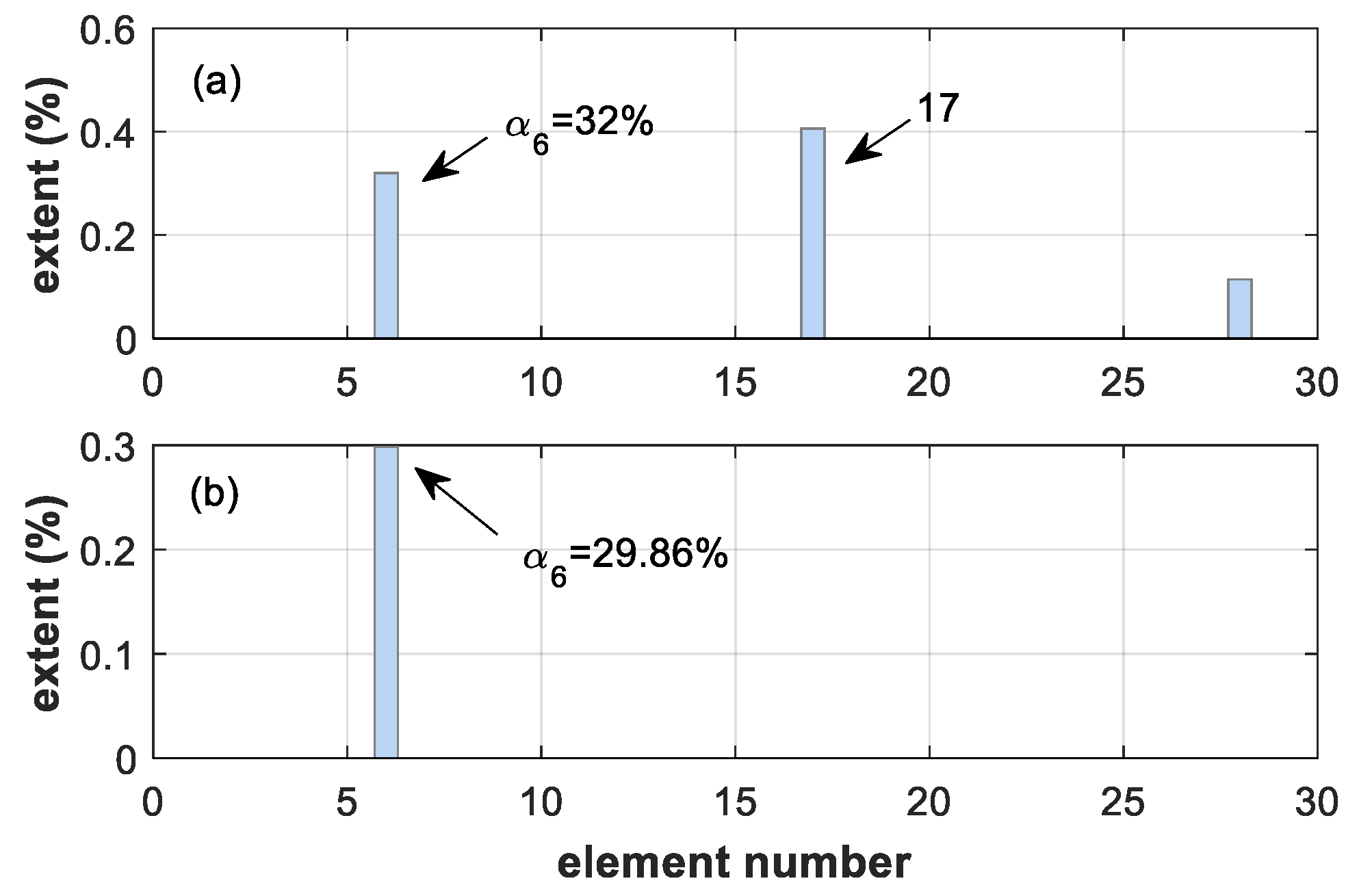
5.2. Results and Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Flynn, E.B.; Todd, M.D. A Bayesian approach to optimal sensor placement for structural health monitoring with application to active sensing. Mech. Syst. Signal Process. 2010, 24, 891–903. [Google Scholar] [CrossRef]
- Pérez, J.E.R.; Rodríguez, R.; Vázquez-Hernández, A.O. Damage detection in offshore jacket platforms with limited modal information using the damage submatrices method. Mar. Struct. 2017, 55, 78–103. [Google Scholar] [CrossRef]
- Oliveira, G.; Magalhães, F.; Cunha, Á.; Caetano, E. Vibration-based damage detection in a wind turbine using 1 year of data. Struct. Control Health Monit. 2018, 25, e2238. [Google Scholar] [CrossRef]
- Soman, R.; Mieloszyk, M.; Ostachowicz, W. A two-step damage assessment method based on frequency spectrum change in a scaled wind turbine tripod with strain rosettes. Mar. Struct. 2018, 61, 419–433. [Google Scholar] [CrossRef]
- Chaabane, M.; Mansouri, M.; Ben Hamida, A.; Nounou, H.; Nounou, M. Multivariate statistical process control-based hypothesis testing for damage detection in structural health monitoring systems. Struct. Control Health Monit. 2019, 26, e2287. [Google Scholar] [CrossRef] [Green Version]
- Ding, Z.H.; Li, J.; Hao, H. Structural damage identification using improved Jaya algorithm based on sparse regularization and Bayesian inference. Mech. Syst. Signal Process. 2019, 132, 211–231. [Google Scholar] [CrossRef]
- Wang, S.Q.; Wang, H.Y.; Xu, M.Q.; Guo, J. Identifying the presence of structural damage: A statistical hypothesis testing approach combined with residual strain energy. Mech. Syst. Signal Process. 2020, 140, 106655. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Structural damage localization from modal strain energy change. J. Eng. Mech. 2000, 218, 1216–1223. [Google Scholar] [CrossRef]
- Zhu, H.P.; Xu, Y.L. Damage detection of mono-coupled periodic structures based on sensitivity analysis of modal parameters. J. Sound Vib. 2005, 285, 365–390. [Google Scholar] [CrossRef]
- Hu, S.L.J.; Wang, S.Q.; Li, H.J. Cross-Modal Strain Energy Method for Estimating Damage Severity. J. Eng. Mech. 2006, 132, 429–437. [Google Scholar]
- Zhan, J.W.; Xia, H.; Chen, S.Y.; Roeck, G.D. Structural damage identification for railway bridges based on train-induced bridge responses and sensitivity analysis. J. Sound Vib. 2011, 330, 757–770. [Google Scholar] [CrossRef]
- Zheng, Z.D.; Lu, Z.R.; Chen, W.H.; Liu, J.K. Structural damage identification based on power spectral density sensitivity analysis of dynamic responses. Comput. Struct. 2015, 146, 176–184. [Google Scholar] [CrossRef]
- Golub, G.; Hansen, P.; O’Leary, D. Tikhonov regularization and total least squares. J. Matrix Anal. Appl. 1999, 21, 185–194. [Google Scholar] [CrossRef] [Green Version]
- Calvetti, D.; Morigi, S.; Reichel, L.; Sgallari, F. Tikhonov regularization and the L-curve for large discrete ill-posed problems. J. Comput. Appl. Math. 2000, 123, 423–446. [Google Scholar] [CrossRef] [Green Version]
- Hansen, P.C. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve. SIAM Rev. 1992, 34, 561–580. [Google Scholar] [CrossRef]
- Zhang, C.D.; Xu, Y.L. Comparative studies on damage identification with Tikhonov regularization and sparse regularization. Struct. Control Health Monit. 2016, 23, 560–579. [Google Scholar] [CrossRef]
- Entezami, A.; Shariatmadar, H.; Sarmadi, H. Structural damage detection by a new iterative regularization method and an improved sensitivity function. J. Sound Vib. 2017, 399, 285–307. [Google Scholar] [CrossRef]
- Fan, X.; Li, J.; Hao, H.; Ma, S. Identification of Minor Structural Damage Based on Electromechanical Impedance Sensitivity and Sparse Regularization. J. Aerosp. Eng. 2018, 31, 04018061. [Google Scholar] [CrossRef]
- Weber, B.; Paultre, P.; Proulx, J. Structural damage detection using nonlinear parameter identification with Tikhonov regularization. Struct. Control Health Monit. 2007, 14, 406–427. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Entezami, A.; Sarmadi, H. A sensitivity-based finite element model updating based on unconstrained optimization problem and regularized solution methods. Struct. Control Health Monit. 2020, 27, e2481. [Google Scholar] [CrossRef]
- Yan, G.; Sun, H.; Büyüköztürk, O. Impact load identification for composite structures using Bayesian regularization and unscented Kalman filter. Struct. Control Health Monit. 2017, 24, e1910. [Google Scholar] [CrossRef]
- Björck, Å. A bidiagonalization algorithm for solving large and sparse ill-posed systems of linear equations. BIT Numer. Math. 1988, 28, 659–670. [Google Scholar] [CrossRef]
- Golub, G.H.; Heath, M.; Wahba, G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter. Technometrics 1979, 21, 215–223. [Google Scholar] [CrossRef]
- Wang, S.Q.; Xu, M.Q.; Xia, Z.P.; Li, Y.C. A novel Tikhonov regularization-based iterative method for structural damage identification of offshore platforms. J. Mar. Sci. Technol. 2019, 24, 575–592. [Google Scholar] [CrossRef]
- Carden, E.P.; Fanning, P. Vibration Based Condition Monitoring: A Review. Struct. Health Monit. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Yan, Y.J.; Cheng, L.; Wu, Z.Y.; Yam, L.H. Development in Vibration-Based Structural Damage Detection Technique. Mech. Syst. Signal Process. 2007, 21, 2198–2211. [Google Scholar] [CrossRef]
- Fan, W.; Qiao, P.Z. Vibration-based Damage Identification Methods: A Review and Comparative Study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Dessi, D.; Camerlengo, G. Damage identification techniques via modal curvature analysis: Overview and comparison. Mech. Syst. Signal Process. 2015, 52, 181–205. [Google Scholar] [CrossRef]
- Wang, S.Q.; Xu, M.Q. Modal Strain Energy-based Structural Damage Identification: A Review and Comparative Study. Struct. Eng. Int. 2019, 29, 234–248. [Google Scholar] [CrossRef]
- Xu, M.Q.; Wang, S.Q.; Jiang, Y.F. Iterative two-stage approach for identifying structural damage by combining the modal strain energy decomposition method with the multiobjective particle swarm optimization algorithm. Struct. Control Health Monit. 2019, 26, e2301. [Google Scholar] [CrossRef]
- Wang, S.Q.; Li, H.J.; Hu, S.L.J. Cross Modal Strain Energy Method for Damage Localization and Severity Estimation. In Proceedings of the ASME 2007 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, CA, USA, 10–15 June 2007; pp. 245–249. [Google Scholar]
- Yan, W.J.; Ren, W.X. A direct algebraic method to calculate the sensitivity of element modal strain energy. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 694–710. [Google Scholar] [CrossRef]
- Lee, I.W.; Jung, G.H. An efficient algebraic method for the computation of natural frequency and mode shape sensitivities—Part I. Distinct natural frequencies. Comput. Struct. 1997, 62, 429–435. [Google Scholar] [CrossRef]
- Messina, A.; Williams, E.J.; Contursi, T. Structural damage detection by a sensitivity and statistical-based method. J. Sound Vib. 1998, 216, 791–808. [Google Scholar] [CrossRef]
- Juang, J.N.; Pappa, R.S. An eigensystem realization algorithm for modal parameter identification and model reduction. J. Guid. Control Dyn. 1985, 8, 620–627. [Google Scholar] [CrossRef]
- Guyan, R.J. Reduction of stiffness and mass matrices. AIAA J. 1965, 3, 380. [Google Scholar] [CrossRef]
- Bertsimas, D.; King, A.; Mazumder, R. Best Subset Selection via a Modern Optimization Lens. Mathematics 2016, 44, 813–852. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Tibshirani, R.J. Extended Comparisons of Best Subset Selection, Forward Stepwise Selection, and the Lasso. arXiv 2017, arXiv:1707.08692. [Google Scholar]
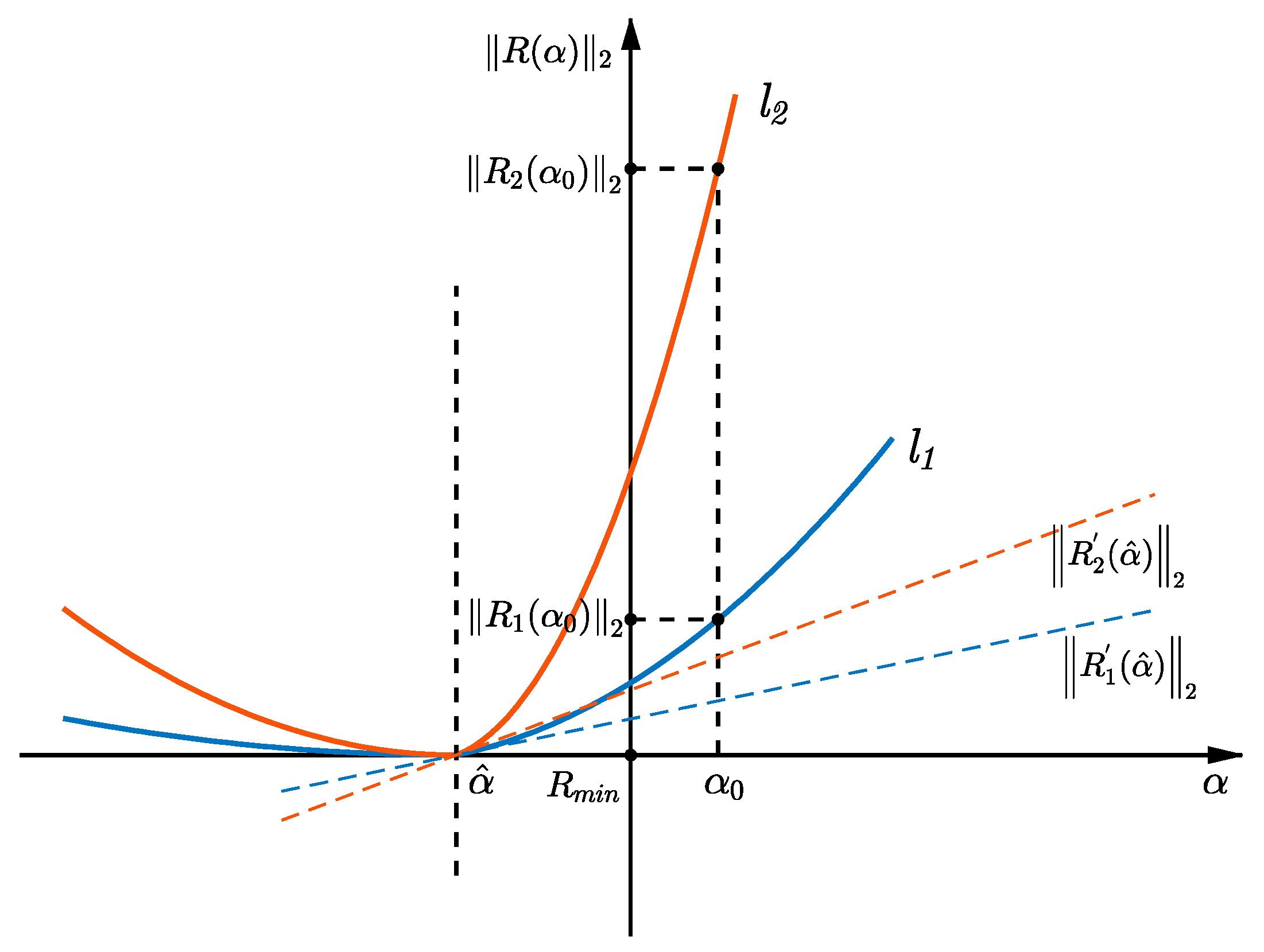


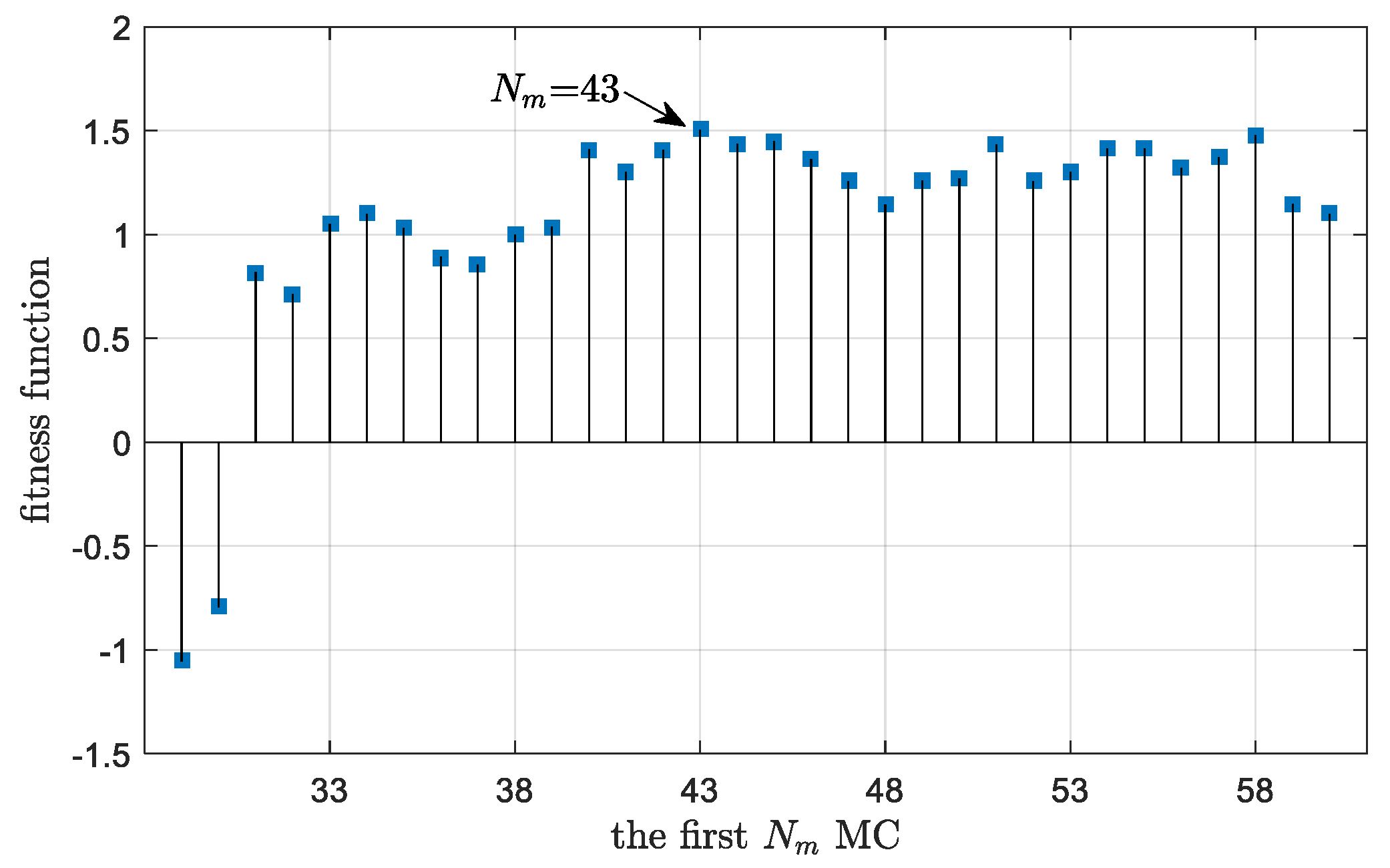

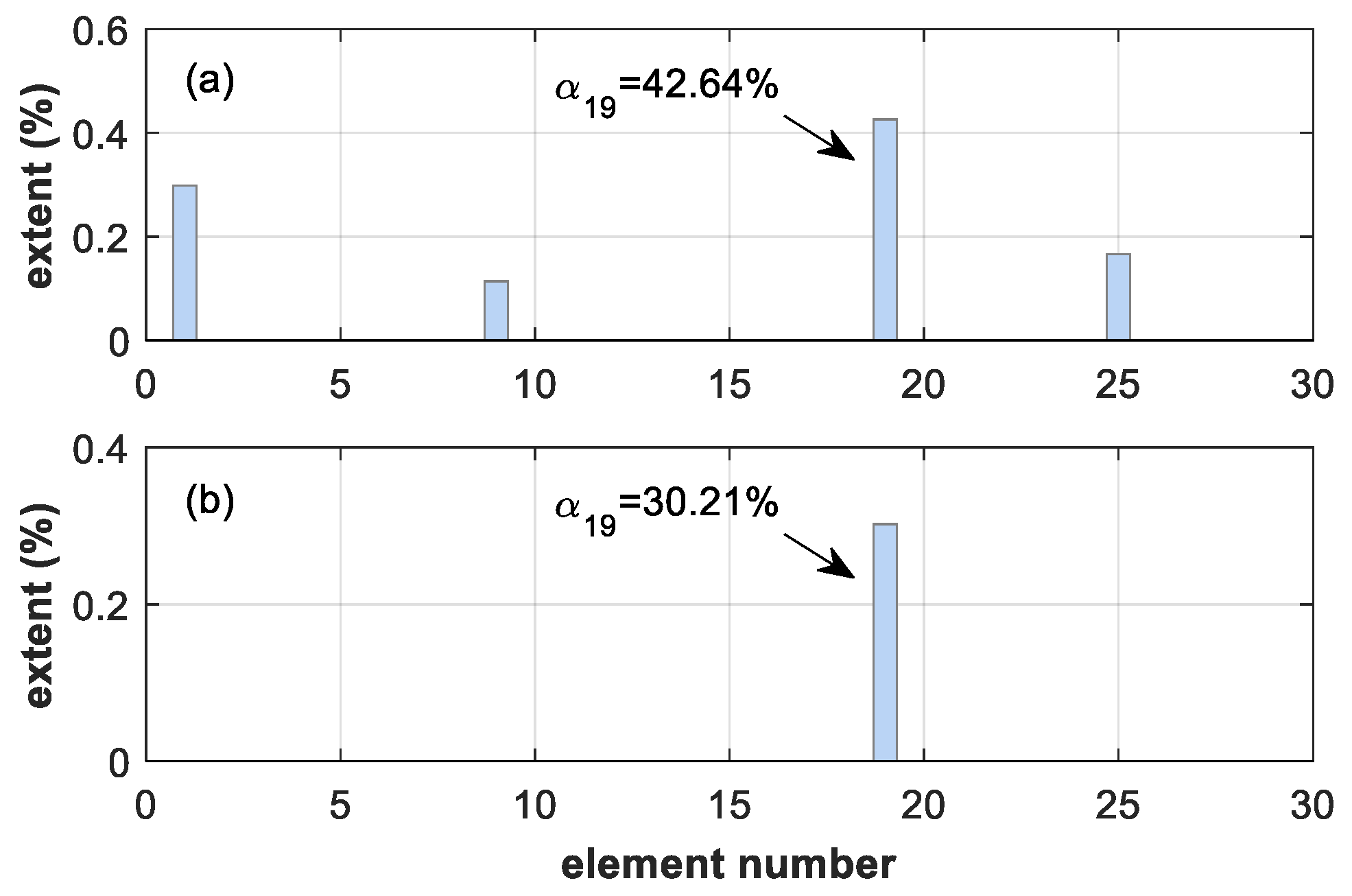



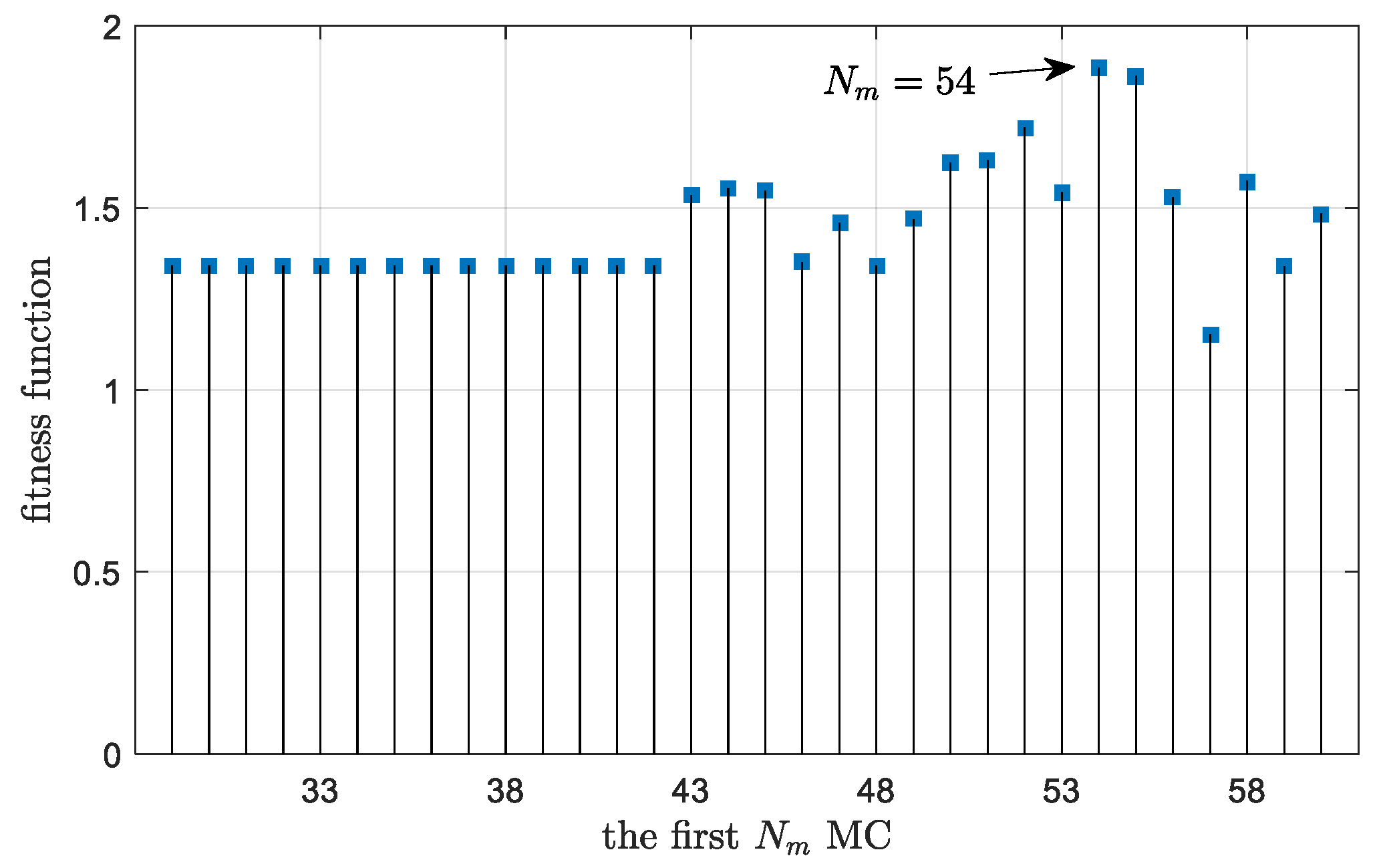
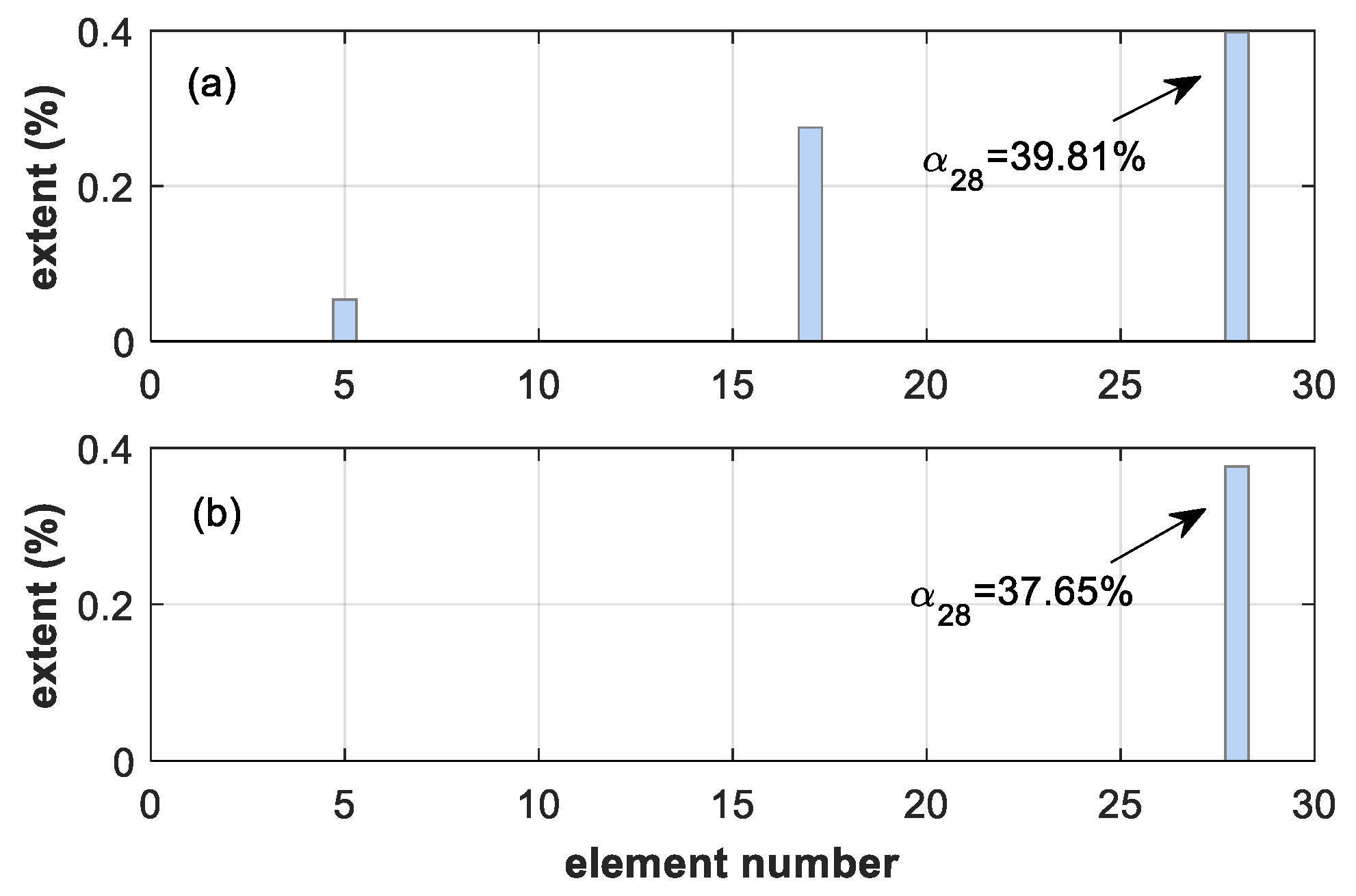
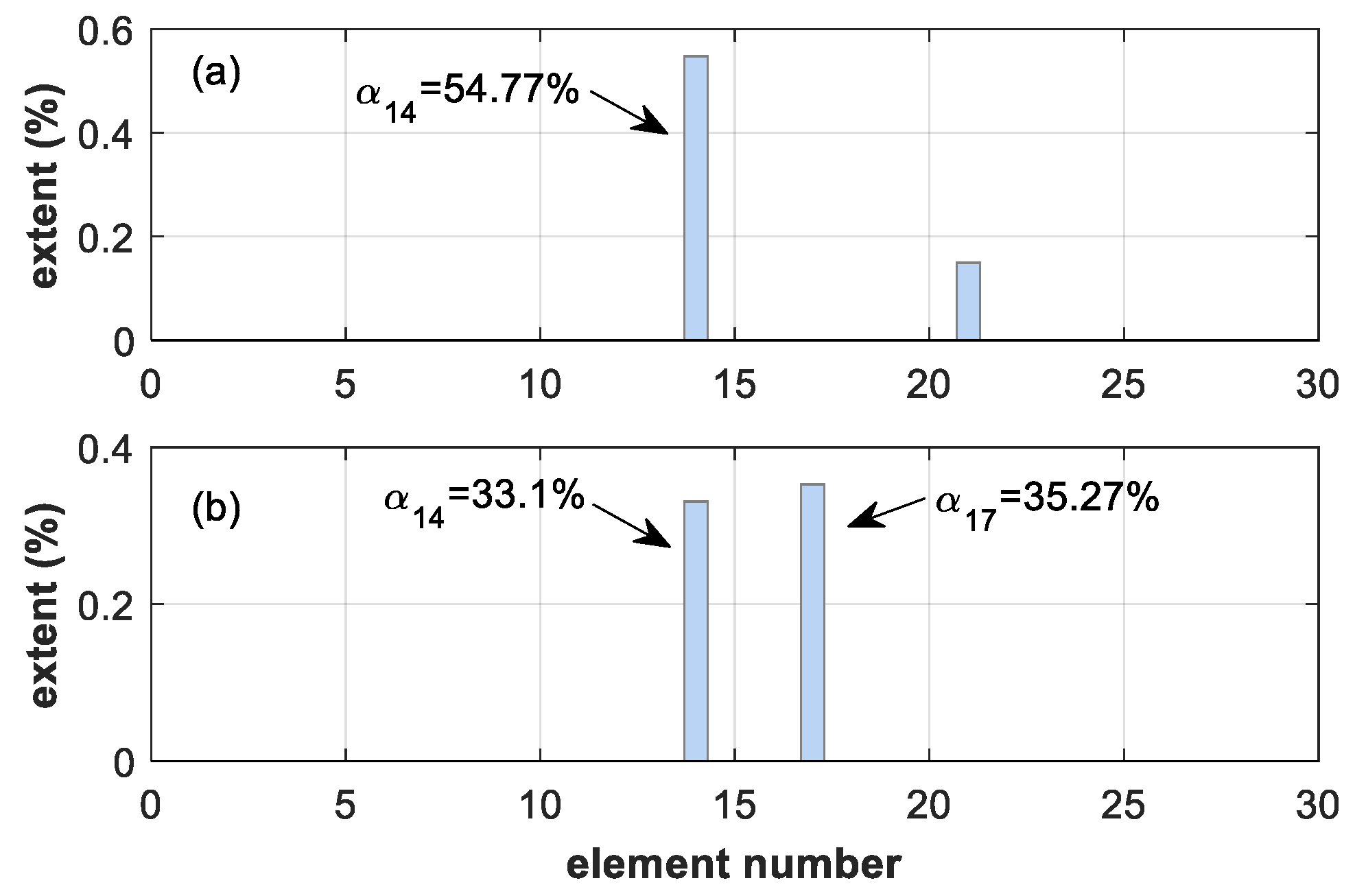

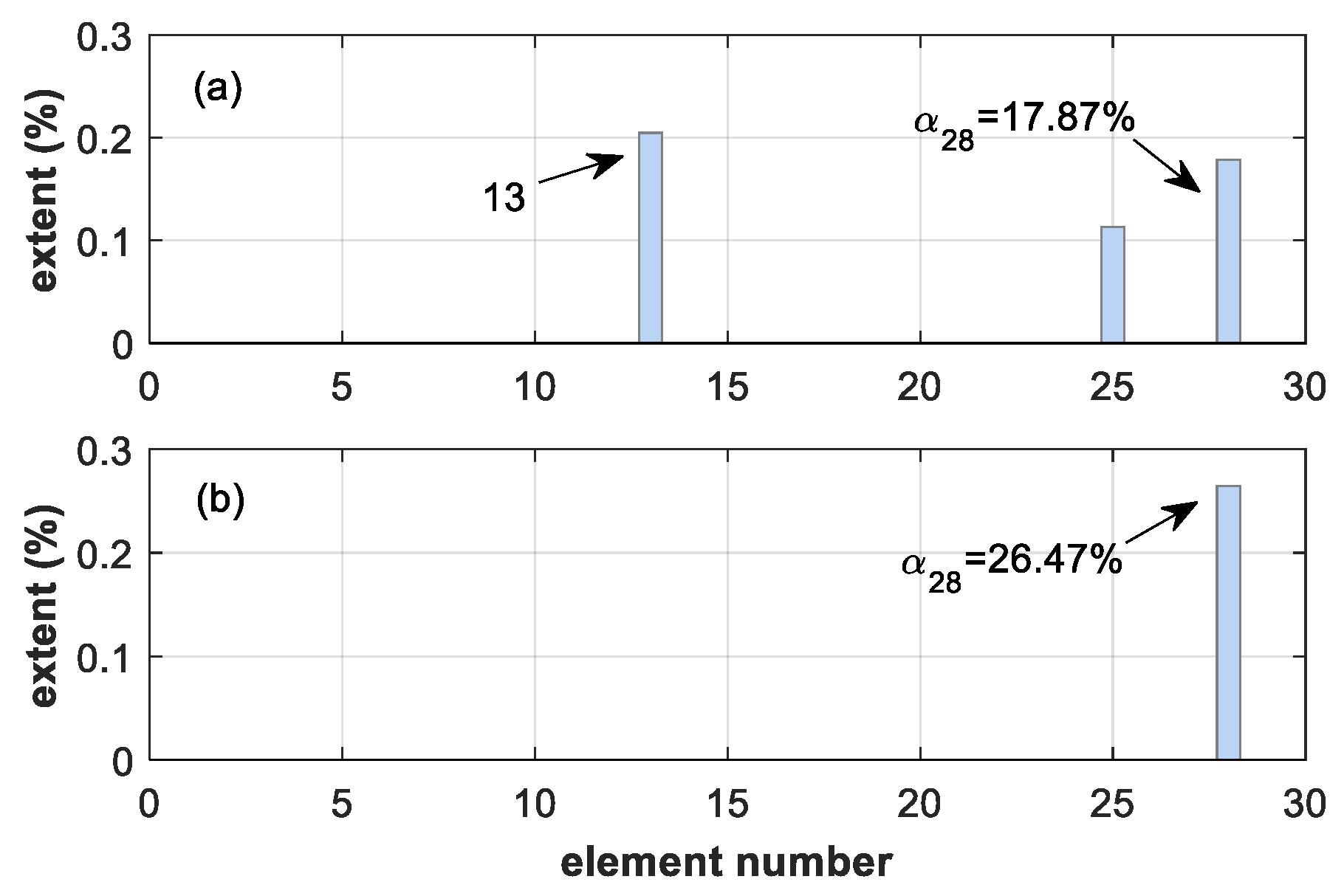
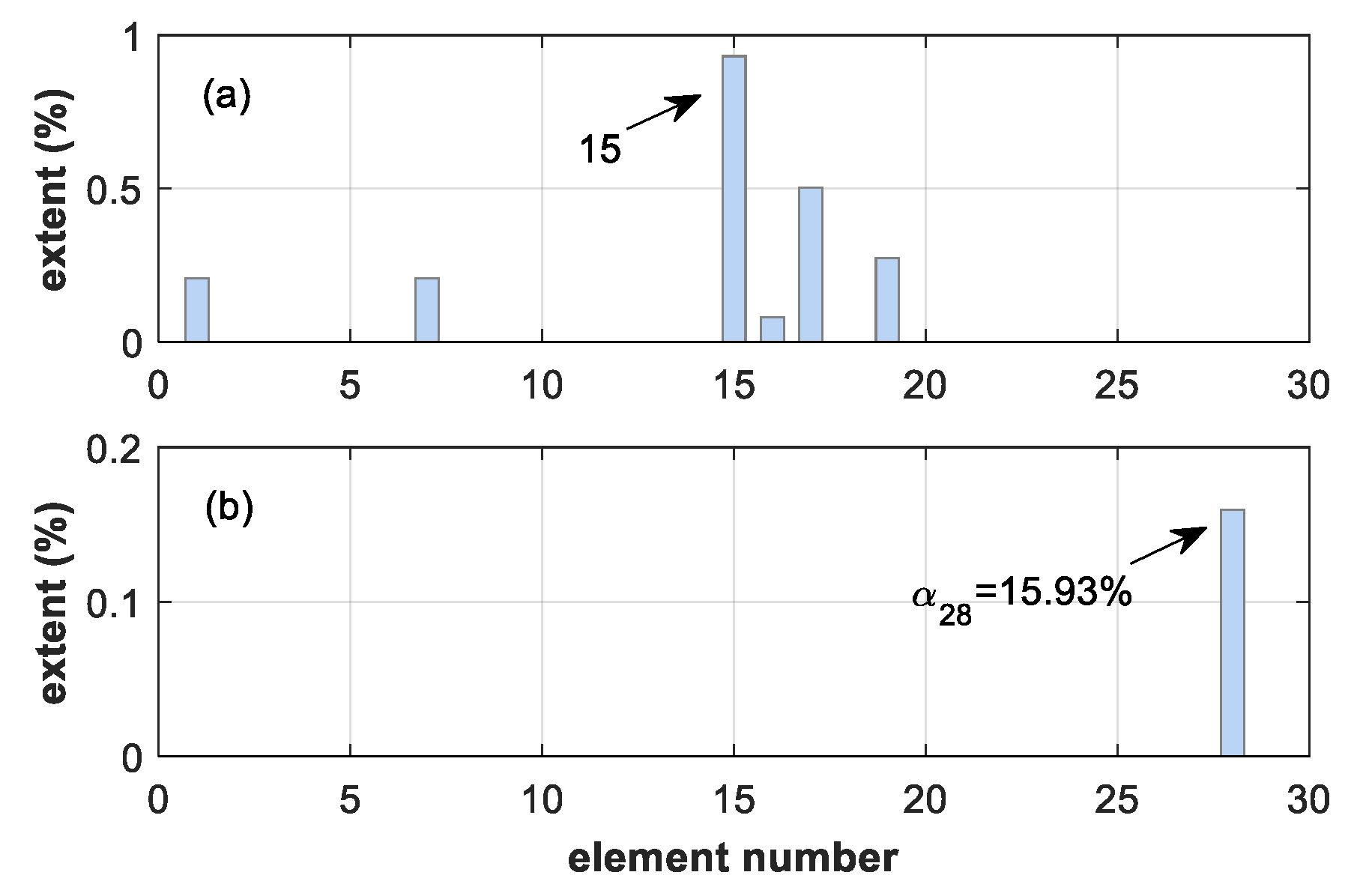


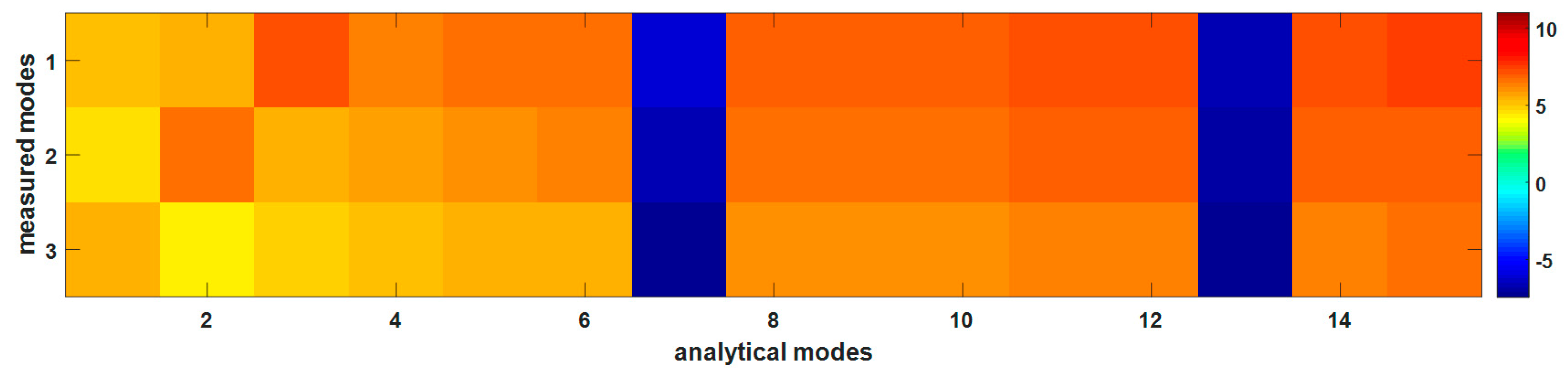
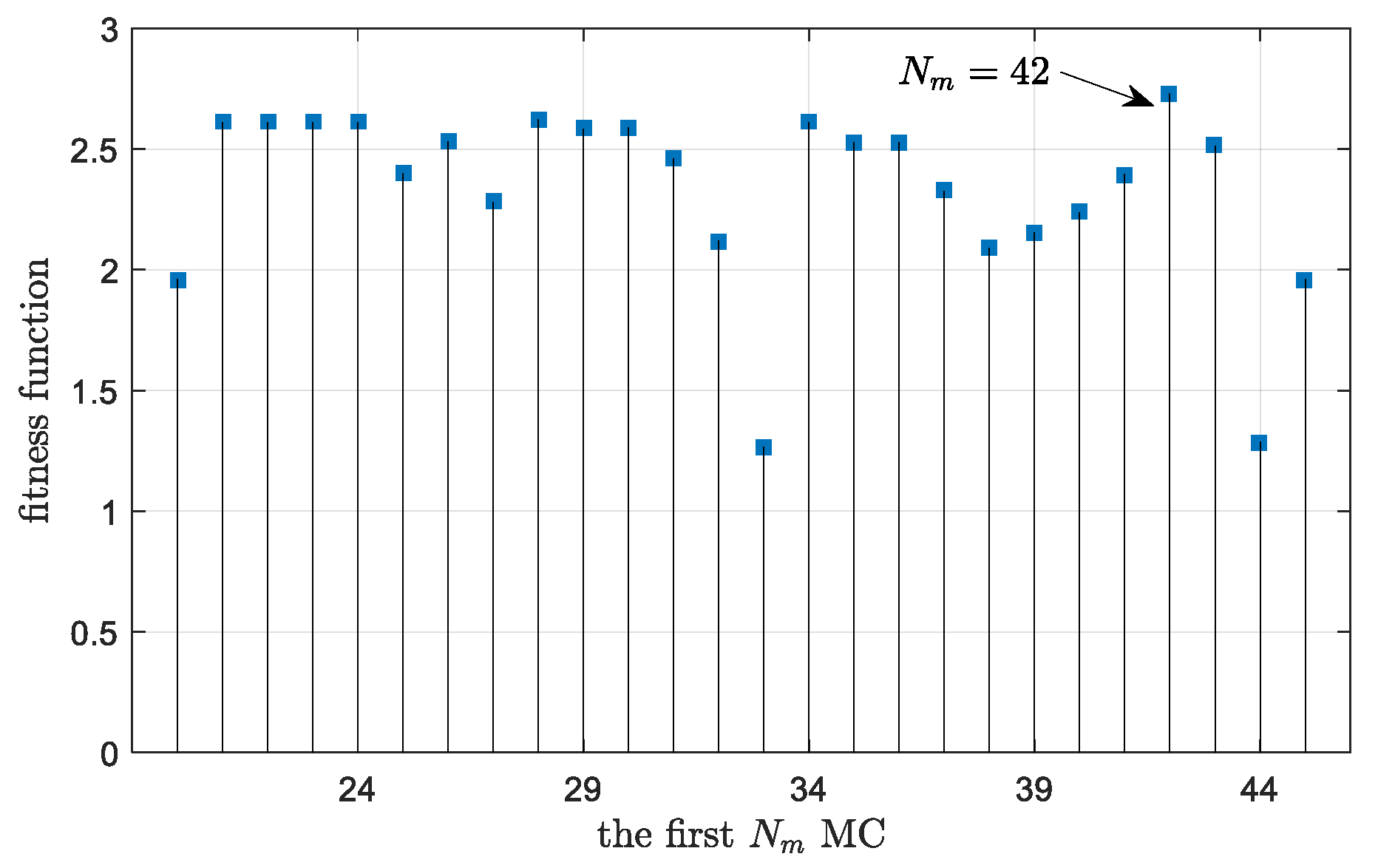
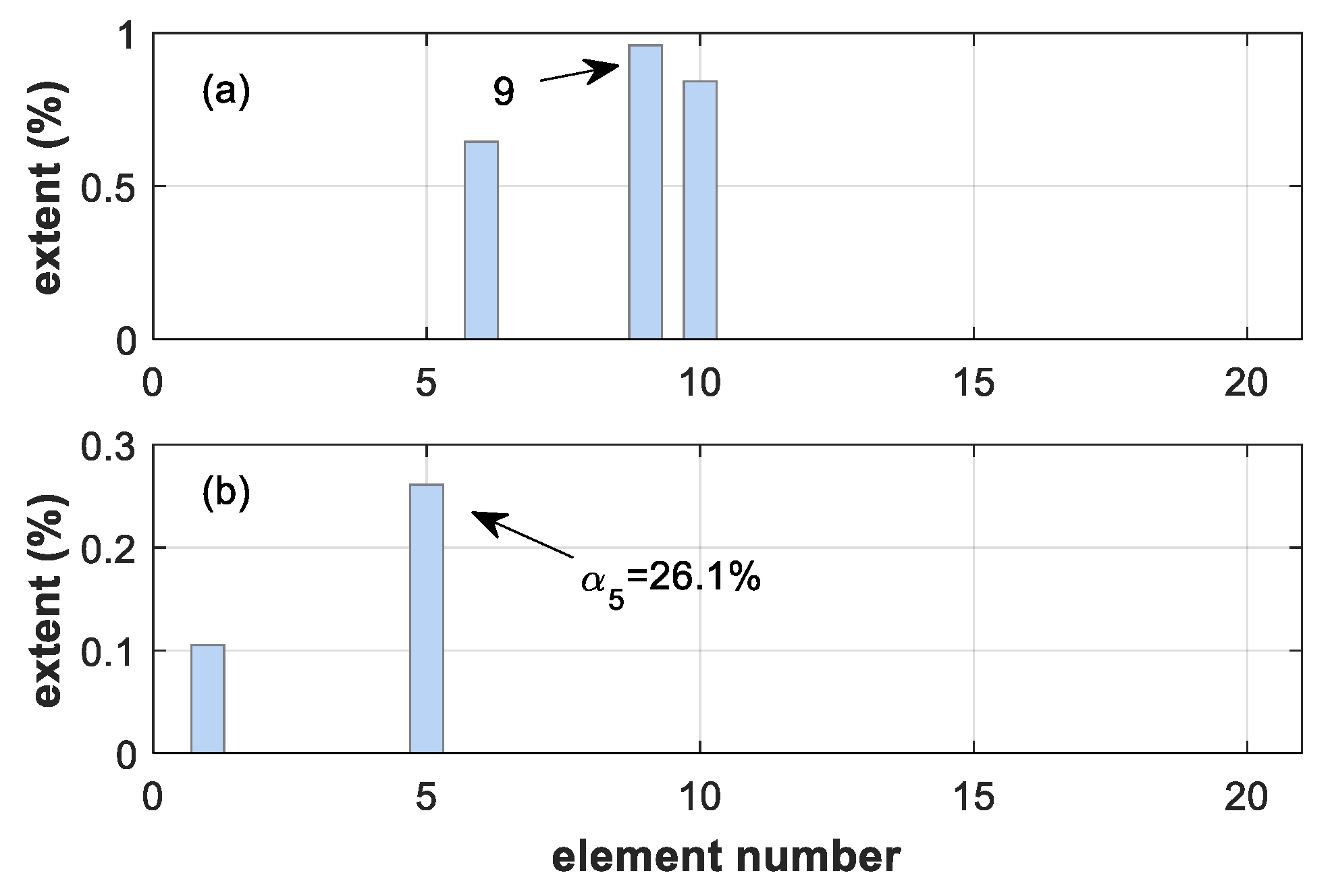

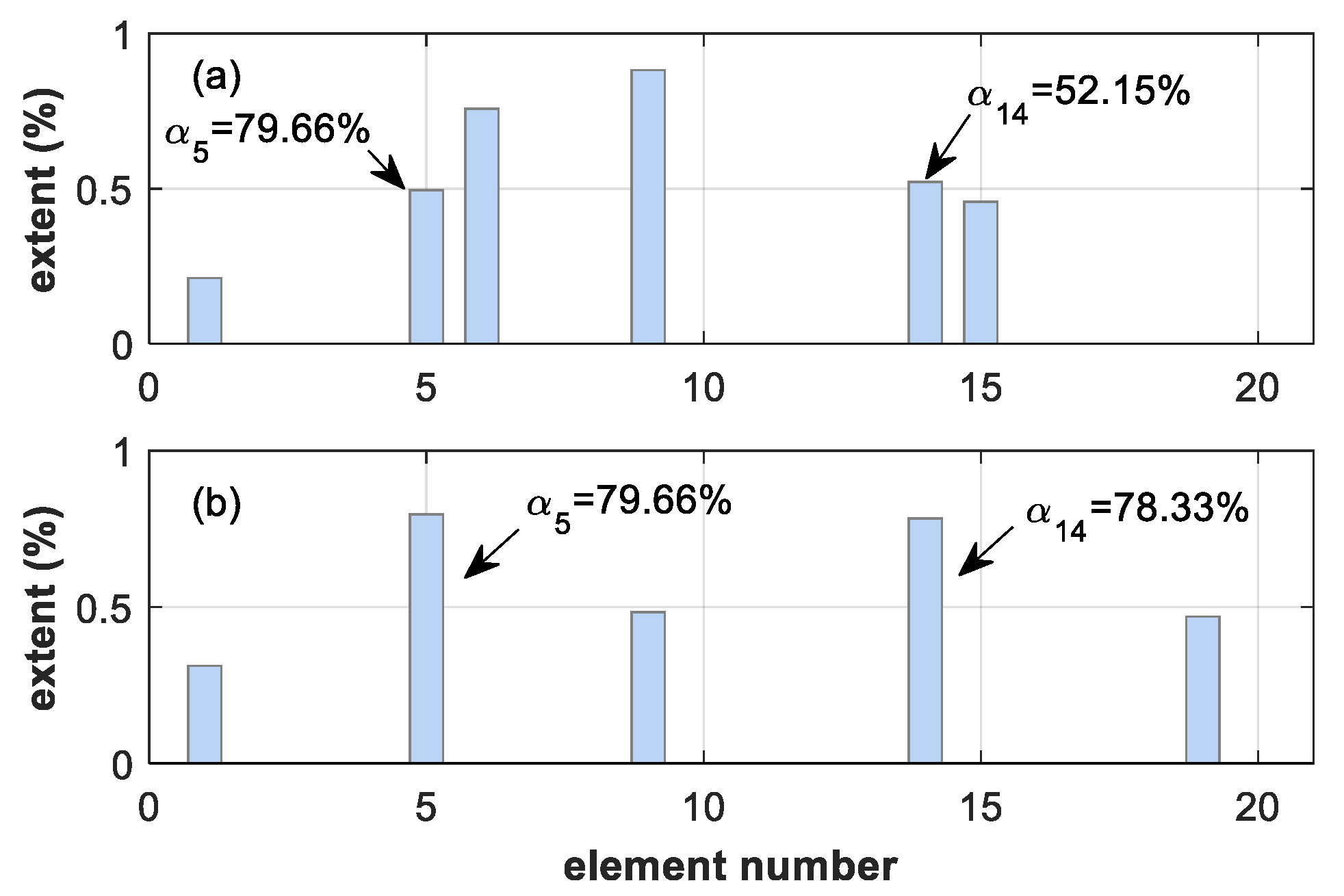
| Damage Case | Location | Extent | Natural Frequencies (Hz) | ||
|---|---|---|---|---|---|
| 1st | 2nd | 3rd | |||
| Baseline | N/A | N/A | 13.878 | 22.257 | 23.832 |
| A | 6 | 30% | 13.845 | 22.074 | 23.634 |
| B | 19 | 30% | 13.877 | 21.996 | 23.740 |
| C | 28 | 30% | 13.701 | 22.166 | 23.601 |
| D | 14, 17 | 30%, 30% | 13.837 | 21.946 | 23.761 |
| E | 28 | 20% | 13.774 | 22.202 | 23.686 |
| F | 28 | 10% | 13.832 | 22.232 | 23.763 |
| Damage Case | Original System | Reduced System | ||
|---|---|---|---|---|
| A | 60 | 126.36 | 35 | 95.92 |
| B | 60 | 126.79 | 40 | 28.23 |
| C | 60 | 128.45 | 54 | 22.31 |
| D | 60 | 123.86 | 45 | 55.15 |
| Damage Case | Original System | Reduced System | ||
|---|---|---|---|---|
| E | 60 | 126.30 | 56 | 36.61 |
| F | 60 | 124.03 | 40 | 25.71 |
| Case | Location | Extent | Natural Frequencies (Hz) | ||
|---|---|---|---|---|---|
| 1st | 2nd | 3rd | |||
| Undamaged | N/A | N/A | 5.524 | 34.711 | 97.200 |
| I | 5 | 1/4 thickness | 5.473 | 34.768 | 96.874 |
| II | 5 | 1/2 thickness | 5.299 | 34.755 | 95.089 |
| III | 5 and 14 | 1/2 and 1/2 thickness | 5.289 | 33.837 | 91.485 |
| Data Type | Natural Frequencies (Hz) | MACs | ||||
|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 1st | 2nd | 3rd | |
| Measured | 5.524 | 34.711 | 97.200 | 0.999 | 0.997 | 0.998 |
| Analytical | 5.523 | 34.644 | 97.079 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, M.; Wang, S.; Guo, J.; Li, Y. Robust Structural Damage Detection Using Analysis of the CMSE Residual’s Sensitivity to Damage. Appl. Sci. 2020, 10, 2826. https://doi.org/10.3390/app10082826
Xu M, Wang S, Guo J, Li Y. Robust Structural Damage Detection Using Analysis of the CMSE Residual’s Sensitivity to Damage. Applied Sciences. 2020; 10(8):2826. https://doi.org/10.3390/app10082826
Chicago/Turabian StyleXu, Mingqiang, Shuqing Wang, Jian Guo, and Yingchao Li. 2020. "Robust Structural Damage Detection Using Analysis of the CMSE Residual’s Sensitivity to Damage" Applied Sciences 10, no. 8: 2826. https://doi.org/10.3390/app10082826
APA StyleXu, M., Wang, S., Guo, J., & Li, Y. (2020). Robust Structural Damage Detection Using Analysis of the CMSE Residual’s Sensitivity to Damage. Applied Sciences, 10(8), 2826. https://doi.org/10.3390/app10082826




