Low-Frequency Vibration and Radiation Performance of a Locally Resonant Plate Attached with Periodic Multiple Resonators

Abstract

The low-frequency vibration and radiation performance of a locally resonant (LR) plate with periodic multiple resonators is studied in this paper, with both infinite and finite structure properties examined. For the finite cases, taking the LR plate attached with two periodic arrays of resonators as an example, the forced vibration response and the radiation efficiency are theoretically derived by adopting a general model with elastic boundary conditions. Through a comparison with the band structures calculated by the plane-wave-expansion method, it shows that the band gaps in the infinite LR plate are in good agreement with the vibration-attenuation bands in the finite LR plate, no matter what boundary conditions are applied to the latter. In contrast to the vibration reduction in the band gaps, the radiation efficiency of the finite LR plate is sharply increased in the band-gap frequency ranges. Furthermore, the acoustic power radiated from the finite LR plate can be seriously affected by its boundary conditions. For the LR plate with greater constraints, the acoustic power is reduced in the band-gap frequency ranges, while that from the one with fully free boundary conditions is increased. When further considering the damping loss factors of the resonators, the attenuation performance can be improved for both the vibration and radiation of the LR plate.

1. Introduction

Owing to the band-gap property, periodic structures have attracted a great deal of interest over the past several decades. Periodic beams [1] and stiffened plates [2] are used widely in engineering, while the band gaps are mostly limited to mid-and-high frequency ranges due to the Bragg scattering mechanism [3,4], which requires the structure period to be of the same order as the wavelength of the band-gap frequency. Since the locally resonant (LR) mechanism was proposed by Liu et al. [5], the study of periodic structures based on the LR mechanism (e.g., phononic crystals [6,7], acoustic metamaterials [8,9], etc.) has been increased. They are usually manufactured by adding arrays of resonant microstructures periodically into/onto the structures to suppress flexural wave propagation. It is considered as an efficient method to achieve the low-frequency band gaps. Xiao et al. [10] studied the propagation of flexural waves in an LR thin plate made of a two-dimensional periodic array of one type of resonator attached on a thin homogeneous plate. Qian and Shi [11] extended the traditional plane-wave-expansion (PWE) method to calculate the band structures of the “spring-mass” simplified model and the “spring-torsional spring-mass” simplified model of LR plate systems, where the effect of the viscidity is also considered. Nouh et al. [12,13] presented the vibration characteristic of metamaterial beams and plates manufactured out of assemblies of periodic elements with built-in local resonances. Wang et al. [14] proposed a meta-plate model by periodically attaching high-static-low-dynamic-stiffness resonators onto the thin plate to attenuate very low-frequency flexural waves. To broaden the bandwidths, many researchers investigated the band gaps in periodic structures with multiple local resonators. Flexural wave propagation in locally resonant beams with multiple periodic arrays of attached spring-mass resonators was studied by Xiao et al. [15], showing that much broader band gaps can be achieved by applying damped resonators. Wang et al. [16] studied a homogeneous damped plate with parallel attached resonators on both surfaces, from which two band gaps were generated to improve the band-gap performance. Wang et al. [17] investigated wave propagation and power flow in an acoustic metamaterial plate with a lateral local resonance attachment, where two band gaps can be formed by tuning the parameters of the vertical spring-mass and the lateral spring-mass. A chiral-lattice-based elastic metamaterial beam with multiple resonators was numerically and experimentally studied for the broadband vibration suppression by utilizing their individual band gaps by Zhu et al. [18]. Zhou et al. [19] realized multi-low-frequency band gaps in beams by using the mechanism of multiple resonators containing negative-stiffness. Ma et al. [20] studied the band-gap properties of a periodic vibration suppressor composed of a bottom spring-mass oscillator with multiple secondary oscillators with an arbitrary degree of freedom. Qin and Sheng [21] developed the theory of the PWE method to calculate the band structures of the LR plate attached with multiple spring-mass resonators, which is applied in this paper. It was also concluded that the spring damping characteristic can assist in attenuating the vibration responses outside the band-gap frequency ranges.

At present, most studies were focused on dynamic behavior based on band-gap properties. It is generally accepted that vibration attenuation leads to noise reduction. Since the band gaps affect the flexural wave propagation, it is expected that the vibro-acoustic radiation from the LR plate can also be suppressed, especially in the low-frequency range. Acoustic radiation from the LR plate-like structures has been investigated by several researchers. Claus et al. [22] investigated the acoustic radiation efficiency of local resonance-based band-gap materials in both infinite structures and corresponding finite structures, with a specific focus on the radiation efficiency variation affected by the correlation between the resonant frequency and the critical frequency of the plate. It was first found that the band-gap property may increase the radiation efficiency of the LR plate. Song et al. [23] investigated the suppression of vibration and acoustic radiation in a sandwich plate through the use of a periodic design by the finite-element method (FEM). Guo et al. [24] derived the average radiation efficiency of a sandwich plate with periodically inserted LR resonators theoretically. Recently, Jung et al. [25,26] used the LR band gaps to increase the efficiency of sound radiation employing defect modes on a phononic crystal. Although research has been conducted focusing on acoustic radiation in LR structures, more studies can be done to further obtain valuable acoustical characteristics of the LR structure in the low-frequency range.

In this paper, the low-frequency vibration and radiation performance of the LR plate attached with periodic multiple resonators is studied. Following the introduction, the theoretical models are built for the forced response and the total radiation efficiency of the finite LR plate in Section 2. A general model of the boundary conditions is adopted by using linear and torsional springs for the finite LR plate. In Section 3, the band-gap property in the infinite LR plate and vibration attenuation in its finite counterpart are discussed. Furthermore, the acoustic radiation from the finite LR plate is analyzed, with a focus on the effect of the boundary conditions of the plate itself and the damping characteristic of the resonators on the acoustic radiation property. Finally, the conclusions are summarized in Section 4. The theory built in this paper and the corresponding findings can guide the multi-band-gap design of the LR plate for noise control.

2. Model and formulations

2.1. Forced Response of the Finite LR Plate with Elastic Boundary Conditions

In this subsection, the displacement is derived by solving the forced response of the LR plate with elastic boundary conditions. Shown in Figure 1 is a finite rectangular LR plate with multiple spring-mass resonators periodically attached on the base plate, of which all four edges are applied with elastic boundary conditions. The base plate has dimensions of thickness $h_p$, length $a$, and width $b$, and material parameters of Young’s modulus $E$, Possion’s ratio $\nu$, and mass density ${\rho }_p$. A harmonic point force $F_0{e}^{j\omega t}$ is applied at the position of $\left(x_0,y_0\right)$ on the base plate. The differential equation of motion for a forced vibration of the base plate is given by:

$$D{\nabla }^{4}w\left(x,y\right)-{\rho }_p{h}_p{\omega }^{2}w\left(x,y\right)=F,$$

(1)

where $D=E{h}_p^3/12\left(1-{\nu }^2\right)$ is the bending stiffness of the plate, ${\nabla }^4={\partial }^4/\partial x^4+2{\partial }^4/\partial x^2\partial y^2+{\partial }^4/\partial y^4$, and $F$ includes both the external force and the forces from the resonators.

In the case of the LR plate attached with two periodic resonators of $(m_{R1},k_{R1})$ and $(m_{R2},k_{R2})$ along the $x-$direction, $F$ can be expressed as:

$$F=F_0\delta \left(x-x_0\right)\delta \left(y-y_0\right)+{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{F}_{1st}\delta \left(x-x_{1s}\right)\delta \left(y-y_t\right)}}+{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{F}_{2st}\delta \left(x-x_{2s}\right)\delta \left(y-y_t\right)}},$$

(2)

where $F_0$ is the amplitude of the external force and $\delta \left(x-x_0\right)\delta \left(y-y_0\right)$ is the 2-D Dirac delta function. On the base plate $2S\times T$ resonators are attached. The terms $F_{1st}$ and $F_{2st}$ are the amplitudes of forces from the vibrating resonators of $(m_{R1},k_{R1})$ and $(m_{R2},k_{R2})$, respectively. The terms $\left(x_{1s},y_t\right)$ and $\left(x_{2s},y_t\right)$ represent the coordinates of the individuals in both kinds, where $s$ ($s\in \left[0,S\right]$) is an odd number, $t$ ($t\in \left[0,T\right]$) is an integer, and $x_{2s}=x_{1s}+a_L$.

The transverse displacement of a thin rectangular plate can be expressed as [27,28]:

$$w\left(x,y\right)={\displaystyle \sum _{m=0}^{\infty }{\displaystyle \sum _{n=0}^{\infty }{A}_{mn}\cos \left({\lambda }_{am}x\right)\cos \left({\lambda }_{bn}y\right)}}+{\displaystyle \sum _{l=1}^4\left({\xi }_b^l\left(y\right){\displaystyle \sum _{m=0}^{\infty }{c}_m^l\cos \left({\lambda }_{am}x\right)}+{\xi }_a^l\left(x\right){\displaystyle \sum _{n=0}^{\infty }{d}_n^l\cos \left({\lambda }_{bn}y\right)}\right).}$$

(3)

Let the infinite series be truncated to $m=M$ and $n=N$ in the following calculation, and then Equation (3) can be written as:

$$w\left(x,y\right)={\displaystyle \sum _{m=0}^M{\displaystyle \sum _{n=0}^N{A}_{mn}\cos \left({\lambda }_{am}x\right)\cos \left({\lambda }_{bn}y\right)}}+{\displaystyle \sum _{l=1}^4\left({\xi }_b^l\left(y\right){\displaystyle \sum _{m=0}^M{c}_m^l\cos \left({\lambda }_{am}x\right)}+{\xi }_a^l\left(x\right){\displaystyle \sum _{n=0}^N{d}_n^l\cos \left({\lambda }_{bn}y\right)}\right)},$$

(4)

where ${\lambda }_{am}=m\pi /a$ and ${\lambda }_{bn}=n\pi /b$. The terms $A_{mn}$, $c_m^l$, and $d_n^l$ are unknown expansion coefficients that need to be determined by both boundary equations and governing differential equations. The terms ${\xi }_a^l\left(x\right)$ and ${\xi }_b^l\left(y\right)$ are given in the form of trigonometric functions and are defined as:

$$\{\begin{array}{l}{\mathsf{\xi }}_a\left(x\right)={\left[\begin{array}{cccc}{\xi }_a^1\left(x\right)& {\xi }_a^2\left(x\right)& {\xi }_a^3\left(x\right)& {\xi }_a^4\left(x\right)\end{array}\right]}^T=A_a{\phi }_a,\\ {\mathsf{\xi }}_b\left(y\right)={\left[\begin{array}{cccc}{\xi }_b^1\left(y\right)& {\xi }_b^2\left(y\right)& {\xi }_b^3\left(y\right)& {\xi }_b^4\left(y\right)\end{array}\right]}^T=A_b{\phi }_b\end{array},$$

(5)

where $A_a$ and $A_b$ are two arbitrary $4\times 4$ matrixes of full rank, and:

$$\{\begin{array}{l}{\phi }_a={\left[\begin{array}{cccc}\sin \left(\pi x/2a\right)& \cos \left(\pi x/2a\right)& \sin \left(3\pi x/2a\right)& \cos \left(3\pi x/2a\right)\end{array}\right]}^T,\\ {\phi }_b={\left[\begin{array}{cccc}\sin \left(\pi y/2b\right)& \cos \left(\pi y/2b\right)& \sin \left(3\pi y/2b\right)& \cos \left(3\pi y/2b\right)\end{array}\right]}^T\end{array}$$

(6)

The first- to fourth-order derivatives used in the boundary equations and governing differential equations can be determined as:

$$\{\begin{array}{l}{\xi }_a{}^{\left(1\right)}\left(x\right)=A_a{B}_{a1}{B}_{a0}{\mathit{\phi }}_a,{\xi }_a{}^{\left(2\right)}\left(x\right)=A_a{B}_{a2}{\mathit{\phi }}_a,{\xi }_a{}^{\left(3\right)}\left(x\right)=A_a{B}_{a3}{B}_{a0}{\mathit{\phi }}_a,{\xi }_a{}^{\left(4\right)}\left(x\right)=A_a{B}_{a4}{\mathit{\phi }}_a,\\ {\xi }_b{}^{\left(1\right)}\left(y\right)=A_b{B}_{b1}{B}_{b0}{\mathit{\phi }}_b,{\xi }_b{}^{\left(2\right)}\left(y\right)=A_b{B}_{b2}{\mathit{\phi }}_b,{\xi }_b{}^{\left(3\right)}\left(y\right)=A_b{B}_{b3}{B}_{b0}{\mathit{\phi }}_b,{\xi }_b{}^{\left(4\right)}\left(y\right)=A_b{B}_{b4}{\mathit{\phi }}_b\end{array},$$

(7)

where the matrixes $B_{a0}$, $B_{a1}$, $B_{a2}$, $B_{a3}$, $B_{a4}$, $B_{b0}$, $B_{b1}$, $B_{b2}$, $B_{b3}$, and $B_{b4}$ are defined in Equation (A1) in Appendix A.

To make the separation of variables in Equation (4) possible, ${\phi }_a$ and ${\phi }_b$ need to be expanded in the form of cosine series as:

$${\phi }_a={\displaystyle \sum _{m=0}^M{\tau }_m\cos \left({\lambda }_{am}x\right)},{\phi }_b={\displaystyle \sum _{n=0}^N{\tau }_n\cos \left({\lambda }_{bn}y\right)},$$

(8)

where ${\tau }_m={\left[\begin{array}{cccc}{\tau }_m^1& {\tau }_m^2& {\tau }_m^3& {\tau }_m^4\end{array}\right]}^T$ and ${\tau }_n={\left[\begin{array}{cccc}{\tau }_n^1& {\tau }_n^2& {\tau }_n^3& {\tau }_n^4\end{array}\right]}^T$, which are defined in Equation (A3) in Appendix A. Hence, Equation (5) can be further expressed as:

$${\xi }_a{}^{\left(i\right)}\left(x\right)={\displaystyle \sum _{m=0}^M{\alpha }_{im}\cos \left({\lambda }_{am}x\right)},{\xi }_b{}^{\left(i\right)}\left(y\right)={\displaystyle \sum _{n=0}^N{\beta }_{in}\cos \left({\lambda }_{bn}y\right)},$$

(9)

where the superscript of ${}^{\left(i\right)}$ means the $i^{\mathrm{th}}$ derivative and $i=0,1,2,3,4$. The terms ${\alpha }_{im}={\left[\begin{array}{cccc}{\alpha }_{im}^1& {\alpha }_{im}^2& {\alpha }_{im}^3& {\alpha }_{im}^4\end{array}\right]}^T$ and ${\mathit{\beta }}_{in}={\left[\begin{array}{cccc}{\beta }_{in}^1& {\beta }_{in}^2& {\beta }_{in}^3& {\beta }_{in}^4\end{array}\right]}^T$ are $4\times 1$ column vectors, given by:

$$\{\begin{array}{l}{\mathit{\alpha }}_{0m}={\mathit{A}}_a{\mathit{\tau }}_m,{\alpha }_{1m}={\mathit{A}}_a{\mathit{B}}_{a1}{\mathit{B}}_{a0}{\mathit{\tau }}_m,{\mathit{\alpha }}_{2m}={\mathit{A}}_a{\mathit{B}}_{a2}{\mathit{\tau }}_m,{\mathit{\alpha }}_{3m}={\mathit{A}}_a{\mathit{B}}_{a3}{\mathit{B}}_{a0}{\mathit{\tau }}_m,{\mathit{\alpha }}_{4m}={\mathit{A}}_a{\mathit{B}}_{a4}{\mathit{\tau }}_m,\\ {\mathit{\beta }}_{0n}={\mathit{A}}_b{\mathit{\tau }}_n,{\mathit{\beta }}_{1n}={\mathit{A}}_b{\mathit{B}}_{b1}{\mathit{B}}_{b0}{\mathit{\tau }}_n,{\mathit{\beta }}_{2n}={\mathit{A}}_b{\mathit{B}}_{b2}{\mathit{\tau }}_n,{\mathit{\beta }}_{3n}={\mathit{A}}_b{\mathit{B}}_{b3}{\mathit{B}}_{b0}{\mathit{\tau }}_n,{\mathit{\beta }}_{4n}={\mathit{A}}_b{\mathit{B}}_{b4}{\mathit{\tau }}_n\end{array}$$

(10)

The base plate is elastically restrained on four edges bearing the shear forces and bending moments balanced by the linear and torsional springs. The boundary conditions of the base plate can be expressed by:

$$\{\begin{array}{l}{k}_{x0}w\left(0,y\right)={Q_x|}_{x=0},K_{x0}\frac{\partial w}{\partial x}\left(0,y\right)={-M_x|}_{x=0},k_{xa}w\left(a,y\right)={-Q_x|}_{x=a},K_{xa}\frac{\partial w}{\partial x}\left(a,y\right)={M_x|}_{x=a},\\ k_{y0}w\left(x,0\right)={Q_y|}_{y=0},K_{y0}\frac{\partial w}{\partial y}\left(x,0\right)={-M_y|}_{y=0},k_{yb}w\left(x,b\right)={-Q_y|}_{y=0},K_{yb}\frac{\partial w}{\partial y}\left(x,b\right)={M_y|}_{y=b}\end{array}$$

(11)

where $k_{x0}$, $k_{xa}$, $k_{y0}$, and $k_{yb}$ are the linear spring stiffnesses, and $K_{x0}$, $K_{xa}$, $K_{y0}$, and $K_{yb}$ are the torsional spring stiffnesses. The bending moments $M_x$ and $M_y$, and the so-called effective shear forces $Q_x$ and $Q_y$, are defined in Equation (A4) in Appendix A. Substituting Equation (4) into Equation (11) and applying the orthogonality of trigonometric functions give:

$$\{\begin{array}{l}{\displaystyle \sum _{l=1}^4{\displaystyle \sum _{m=0}^M{g}_{i,1}{c}_m^l}}+{\displaystyle \sum _{l=1}^4{g}_{i,2}{d}_n^l}={\displaystyle \sum _{m=0}^M{g}_{i,3}{A}_{mn}}\left(n=0,1,\cdots ,N,i=1,2,3,4\right),\\ {\displaystyle \sum _{l=1}^4{g}_{i,1}{c}_m^l}+{\displaystyle \sum _{l=1}^4{\displaystyle \sum _{n=0}^N{g}_{i,2}{d}_n^l}}={\displaystyle \sum _{n=0}^N{g}_{i,3}{A}_{mn}}\left(m=0,1,\cdots ,M,i=5,6,7,8\right)\end{array},$$

(12)

where $g_{i,1}$, $g_{i,2}$, and $g_{i,3}$ are given by Equation (A5) in Appendix A. Equation (12) represents $4\left(M+1\right)+4\left(N+1\right)$ boundary equations, and they can be rewritten in a matrix form as:

$$\mathit{H}\mathit{p}=\mathit{Q}\mathit{a},$$

(13)

where $\mathit{H}$ and $\mathit{Q}$ are coefficient matrixes represented with the elements $g_{i,1}$, $g_{i,2}$, and $g_{i,3}$. The terms $\mathit{p}$ and $\mathit{a}$ are defined as:

$$\begin{array}{ll}\mathit{p}=[c_0^1,& c_1^1,\cdots ,c_M^1,c_0^2,c_1^2,\cdots ,c_M^2,c_0^3,c_1^3,\cdots ,c_M^3,c_0^4,c_1^4,\cdots ,c_M^4,\\ & {d_0^1,d_1^1,\cdots ,d_N^1,d_0^2,d_1^2,\cdots ,d_N^2,d_0^3,d_1^3,\cdots ,d_N^3,d_0^4,d_1^4,\cdots ,d_N^4]}^T,\end{array}$$

(14)

$$\mathit{a}={\left[A_{00},A_{01},\cdots ,A_{0N},A_{10},A_{11},\cdots ,A_{1N},\cdots ,A_{mn},\cdots ,A_{M0},A_{M1},\cdots ,A_{MN}\right]}^T,$$

(15)

respectively. Thus, $p$ can be expressed by $a$, namely:

$$\mathit{p}={\mathit{H}}^{-1}\mathit{Q}\mathit{a}.$$

(16)

In Equation (4), a total of $\left(M+1\right)\left(N+1\right)+4\left(M+1\right)+4\left(N+1\right)$ unknown expansion coefficients can be obtained. Except for $4\left(M+1\right)+4\left(N+1\right)$ boundary equations supported by Equation (13), $\left(M+1\right)\left(N+1\right)$ governing differential equations are provided in the following. Furthermore, express the force terms found in Equation (2) in Fourier series with a cosine form as:

$$F^{\prime }\delta \left(x-x^{\prime }\right)\delta \left(y-y^{\prime }\right)={\displaystyle \sum _{m=0}^M{\displaystyle \sum _{n=0}^N{F}_{mn}\cos \left({\lambda }_{am}x\right)\cos \left({\lambda }_{bn}y\right)}},$$

(17)

where $F_{mn}$ is the modal force. By using the orthogonality of trigonometric functions, multiplying $\cos \left({\lambda }_{am}x\right)\cos \left({\lambda }_{bn}y\right)$ on both sides of Equation (17), and integrating in the area of $\left(x,y\right)\in \left(\left[0,a\right]\times \left[0,b\right]\right)$, $F_{mn}$ can be given by:

$$F_{mn}=\frac{F^{\prime }}{L_{am}{L}_{bn}}\cos \left({\lambda }_{am}{x}^{\prime }\right)\cos \left({\lambda }_{bn}{y}^{\prime }\right),$$

(18)

where $L_{am}=\{\begin{array}{ll}a,& m=0\\ a/2,& m\ne 0\end{array}$ and $L_{bn}=\{\begin{array}{ll}b,& n=0\\ b/2,& n\ne 0\end{array}$.

Hence, the external force in Equation (2) can be expressed as:

$$F_0\delta \left(x-x_0\right)\delta \left(y-y_0\right)={\displaystyle \sum _{m=0}^M{\displaystyle \sum _{n=0}^N{F}_{mn0}\cos \left({\lambda }_{am}x\right)\cos \left({\lambda }_{bn}y\right)}},$$

(19)

where $F_{mn0}=\left(F_0/L_{am}{L}_{bn}\right)\cos \left({\lambda }_{am}{x}_0\right)\cos \left({\lambda }_{bn}{y}_0\right)$.

When considering the damping characteristic of the springs, the force equilibrium equation of both kinds of resonators can be written as:

$$m_{Ri}{\ddot{w}}_{Rist}+k_{Ri}\left(1+j{\eta }_{Ri}\right)\left[w_{Rist}-w\left(x_{is},y_t\right)\right]=0,i=1,2,$$

(20)

where ${\eta }_{Ri}$ is the damping loss factor of the spring damper, and then the displacements of two kinds of resonators can be expressed by:

$$w_{Rist}=\frac{k_{Ri}\left(1+j{\eta }_{Ri}\right)}{k_{Ri}\left(1+j{\eta }_{Ri}\right)-{\omega }^2{m}_{Ri}}w\left(x_{is},y_t\right),i=1,2.$$

(21)

Thus, $F_{ist}$ in Equation (2) are given by:

$$F_{ist}=-m_{Ri}{\ddot{w}}_{Rist}=Z_{Ri}\left(\omega \right)w\left(x_{is},y_t\right),i=1,2,$$

(22)

where $Z_{Ri}\left(\omega \right)=\frac{{\omega }^2{m}_{Ri}{k}_{Ri}\left(1+j{\eta }_{Ri}\right)}{k_{Ri}\left(1+j{\eta }_{Ri}\right)-{\omega }^2{m}_{Ri}}$. The substitution of $F_{ist}\delta \left(x-x_{is}\right)\delta \left(y-y_t\right)$ into Equation (17) gives:

$$F_{ist}\delta \left(x-x_{is}\right)\delta \left(y-y_t\right)={\displaystyle \sum _{m=0}^M{\displaystyle \sum _{n=0}^N{F}_{mn}{}_{ist}\cos \left({\lambda }_{am}x\right)\cos \left({\lambda }_{bn}y\right)}},i=1,2,$$

(23)

where $F_{mn}{}_{ist}=\left(F_{ist}/L_{am}{L}_{bn}\right)\cos \left({\lambda }_{am}{x}_{is}\right)\cos \left({\lambda }_{bn}{y}_t\right)$.

Substituting Equations (4), (9), (19), and (23) into Equation (1) derives equations written in a matrix form as:

$$\left(\mathit{R}\mathit{a}+\mathit{S}\mathit{p}\right)-{\omega }^2\left(\mathit{Z}\mathit{a}+\mathit{T}\mathit{p}\right)-\left[\mathit{U}\left(\omega \right)\mathit{a}+\mathit{V}\left(\omega \right)\mathit{p}\right]=\mathit{F},$$

(24)

where $\mathit{F}={\left[\cdots ,F_{mn0}+{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T\left(F_{mn}{}_{1st}+F_{mn}{}_{2st}\right)}},\cdots \right]}_{\left(M+1\right)\left(N+1\right)\times 1}^T$. The coefficient matrixes $\mathit{R}$, $\mathit{S}$, $\mathit{Z}$, $\mathit{T}$, $\mathit{U}\left(\omega \right)$, and $\mathit{V}\left(\omega \right)$ are defined in Equations (A6)–(A10) in Appendix A.

The substitution of Equation (16) makes Equation (24) be expressed as:

$$\left[\mathit{K}-{\omega }^2\mathit{M}-\mathit{W}\left(\omega \right)\right]\mathit{a}=\mathit{F},$$

(25)

where $\mathit{K}=\mathit{R}+\mathit{S}{\mathit{H}}^{-1}\mathit{Q}$, $\mathit{M}=\mathit{Z}+\mathit{T}{\mathit{H}}^{-1}\mathit{Q}$, and $\mathit{W}\left(\omega \right)=\mathit{U}\left(\omega \right)+\mathit{V}\left(\omega \right){\mathit{H}}^{-1}\mathit{Q}$.

For a given frequency $\omega$, by solving Equation (25), the coefficient vector $\mathit{a}$ can be achieved, and then $\mathit{p}$ can be determined by Equation (16). The transverse displacement of the base plate can be further obtained by Equation (4).

2.2. Wavenumber Domain Approach for the Total Radiation Efficiency of the Finite LR Plate

A finite LR plate with elastic boundary conditions is embedded in an infinite rigid baffle, as shown in Figure 2. As the acoustic medium is air in this paper, the effect of the fluid load is ignored.

A harmonic motion at the arbitrary frequency $\omega$ is assumed. The radiated pressure $p\left(x,y,z\right)$ satisfies the Helmholtz equation:

$$\left({\nabla }^2+k^2\right)p\left(x,y,z\right)=0,$$

(26)

where ${\nabla }^2={\partial }^2/\partial x^2+{\partial }^2/\partial y^2$, $k=\omega /c_0$, and $c_0$ is the speed of sound. The propagation of acoustic pressure in a plane, harmonic, bending wave in 3-D space can be represented as:

$$p\left(x,y,z,t\right)=\tilde{p}{e}^{-j{k}_{x}x-j{k}_{y}y-j{k}_{z}z}{e}^{j\omega t},$$

(27)

where $k_x^2+k_y^2+k_z^2=k^2$. Substituting Equation (27) into the momentum equation:

$$\frac{\partial p}{\partial z}+{\rho }_0\frac{\partial v}{\partial t}=0,$$

(28)

Yields:

$$p\left(x,y,z\right)=\frac{{\rho }_0{c}_{0}k}{k_z}v\left(x,y,z\right),$$

(29)

where $v\left(x,y,z\right)$ is the particle velocity in air, and ${\rho }_0$ is the air density. By using the spatial Fourier transform as:

$$P\left(k_x,k_y,z\right)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }p\left(x,y,z\right)e^{-j{k}_{x}x-j{k}_{y}y}dxdy}},$$

(30)

$$V\left(k_x,k_y,z\right)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }v\left(x,y,z\right)e^{-j{k}_{x}x-j{k}_{y}y}dxdy}},$$

(31)

Equation (29) can be written as:

$$P\left(k_x,k_y,z\right)=Z_a\left(k_x,k_y\right)V\left(k_x,k_y,z\right),$$

(32)

where $Z_a\left(k_x,k_y\right)$ is the acoustic impedance, expressed as:

$$Z_a\left(k_x,k_y\right)=\pm \{\begin{array}{l}\frac{{\rho }_0{c}_{0}k}{\sqrt{k^2-k_x^2-k_y^2}},k_x^2+k_y^2<k^2\\ j\frac{{\rho }_0{c}_{0}k}{\sqrt{k_x^2+k_y^2-k^2}},k_x^2+k_y^2>k^2\end{array}.$$

(33)

Considering the radiation of the air-plate interface, if $V\left(k_x,k_y,z=0\right)$ is known, the upper surface pressure $P\left(k_x,k_y,z=0\right)$ can be derived. The term $V\left(k_x,k_y,z=0\right)$ can be determined by the base plate velocity $v\left(x,y\right)$, which can be acquired by multiplying $w\left(x,y\right)$ by $j\omega$.

For the baffled LR plate under harmonic excitation, the total acoustic power can be calculated by integrating the acoustic intensity over the plate-baffle plane, i.e., $z=0$, expressed as:

$$W=\frac{1}{2}\mathrm{Re}\left\{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }p\left(x,y\right)v^{*}\left(x,y\right)dxdy}}\right\},$$

(34)

where the superscript of ^* means a complex conjugate.

The inverse Fourier transforms of $p\left(x,y\right)$ and $v\left(x,y\right)$ are represented as:

$$p\left(x,y\right)=\frac{1}{4{\pi }^2}{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }P\left(k_x,k_y\right)e^{j{k}_{x}x+j{k}_{y}y}d{k}_{x}d{k}_y}},$$

(35)

$$v\left(x,y\right)=\frac{1}{4{\pi }^2}{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }V\left(k_x,k_y\right)e^{j{k}_{x}x+j{k}_{y}y}d{k}_{x}d{k}_y}},$$

(36)

respectively, and substituting them into Equation (34) gives:

$$W=\frac{1}{32{\pi }^4}\mathrm{Re}\left\{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }P\left(k_x,k_y\right)e^{j{k}_{x}x+j{k}_{y}y}d{k}_{x}d{k}_y\times {\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{V}^{*}\left(k_x{}^{\prime },k_y{}^{\prime }\right)e^{-j{k}_x{}^{\prime }x-j{k}_y{}^{\prime }y}d{k}_x{}^{\prime }d{k}_y{}^{\prime }}}dxdy}}}}\right\}$$

(37)

By changing the order of integration and firstly performing the integration over $x$ and $y$, the Dirac delta function is obtained, namely:

$${\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{e}^{j\left(k_x-k_x{}^{\prime }\right)x}{e}^{j\left(k_y-k_y{}^{\prime }\right)y}dxdy}}=4{\pi }^2\delta \left(k_x-k_x{}^{\prime }\right)\delta \left(k_y-k_y{}^{\prime }\right).$$

(38)

The substitution of Equation (32) into Equation (37) derives:

$$W=\frac{1}{8{\pi }^2}\mathrm{Re}\left\{{\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }{Z}_a\left(k_x,k_y\right)\times {\left|V\left(k_x,k_y\right)\right|}^{2}d{k}_{x}d{k}_y}}\right\}.$$

(39)

It should be noted that only the wavenumber components $k_x$ and $k_y$ satisfying $k_x^2+k_y^2<k^2$ contribute to an effective acoustic radiation. The range of integration can be limited, and Equation (39) can be expressed as:

$$W=\frac{1}{8{\pi }^2}\mathrm{Re}\left\{{\displaystyle {\int }_{-k}^k{\displaystyle {\int }_{-\sqrt{k^2-k_y^2}}^{\sqrt{k^2-k_y^2}}{Z}_a\left(k_x,k_y\right)\times {\left|V\left(k_x,k_y\right)\right|}^{2}d{k}_{x}d{k}_y}}\right\}.$$

(40)

The substitution of $V\left(k_x,k_y\right)$ calculated by Equation (31) into Equation (40) can acquire $W$. Therefore, the radiation efficiency of the LR plate can be derived by:

$${\sigma }_{rad}=\frac{W}{\frac{1}{2}{\rho }_0{c}_{0}ab\langle {\left|v\right|}^2\rangle },$$

(41)

where $\langle {\left|v\right|}^2\rangle$ is the mean square velocity averaged over the plate surface.

3. Examples and Discussion

In Section 3, the band-gap properties in the infinite LR plate are acquired by the theory in reference [21], and the vibration and radiation responses in the finite LR plate are obtained by the theory in Section 2.1 and Section 2.2. Examples of the LR plate with two resonators in each periodic element (TRIEPE LR plate) are focused on, for a low-frequency vibro-acoustic performance. In the following examples, the base plate is made of steel with a material density ${\rho }_p=7800{\mathrm{kg}/\mathrm{m}}^3$, Young’s modulus $E=2.1\times {10}^{11}\mathrm{Pa}$, Poisson’s ratio $\nu =0.3$, and damping loss factor ${\eta }_p=0.001$. The thickness of the plate is set as $h_p=0.003\mathrm{m}$ and the lattice constant $a_L=0.05\mathrm{m}$.

3.1. Band-Gap Property and Vibration Attenuation

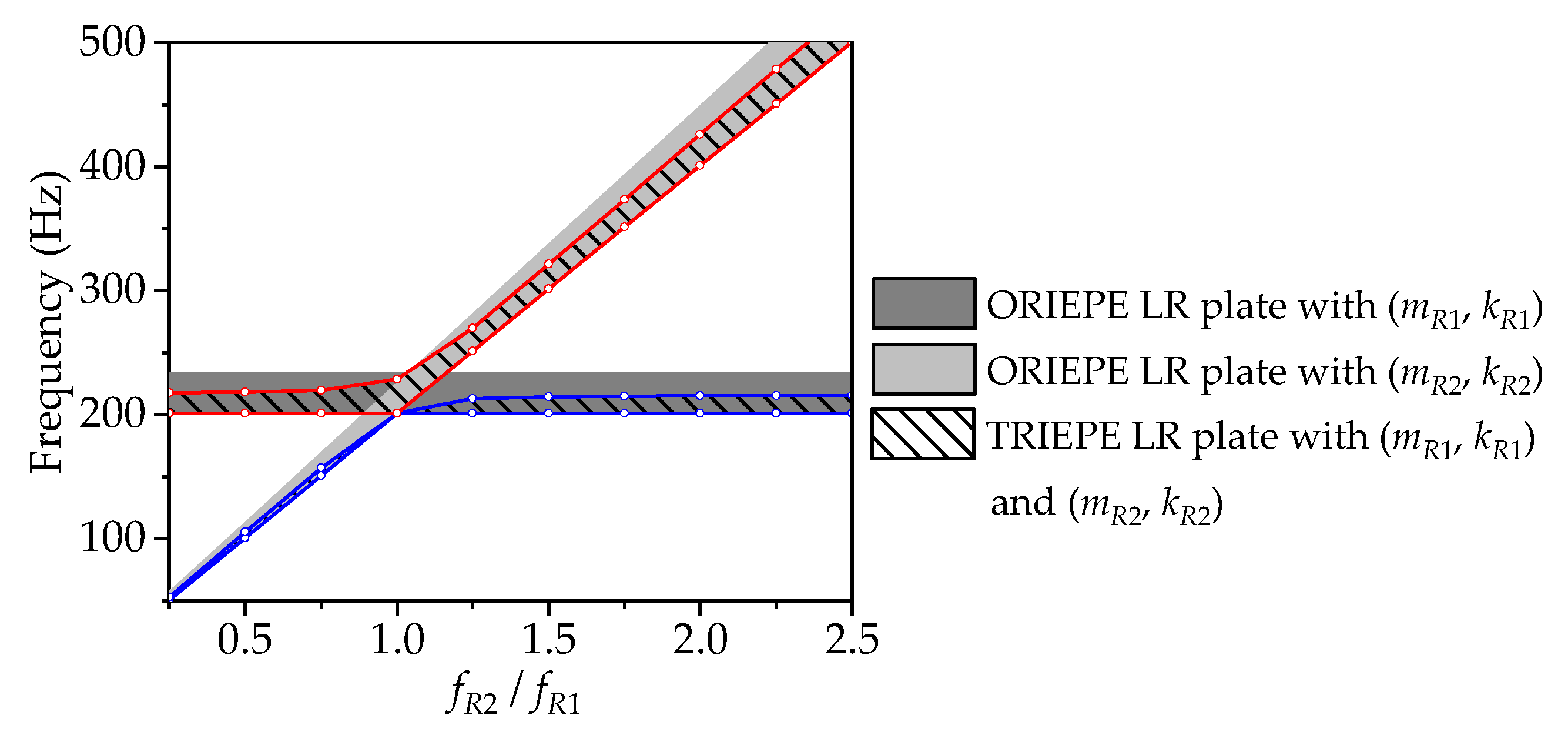
It should be noted that introducing a new type of resonator will affect the original band-gap frequency range in the LR plate with one resonator in each periodic element (ORIEPE LR plate), which is related to the spring-mass parameters of the new resonators. Thus, the effect of the ratio between the resonant frequencies on the band-gap frequency range is studied first of all. Since the complete band gaps are closely related to the LR mechanism in the LR plate system, directional band gaps are not considered in this paper. Shown in Figure 3 are the trends of two band-gap frequency ranges versus $f_{R2}/f_{R1}$ in the TRIEPE LR plate with resonators $(m_{R1},k_{R1})$ and $(m_{R2},k_{R2})$, with the resonant frequencies of $f_{R1}$ and $f_{R2}$, respectively. The band-gap frequency ranges in the two corresponding ORIEPE LR plates are also shown in Figure 3 for comparison. The parameters $m_{R1}=0.020\mathrm{kg}$, $k_{R1}=3.2\times {10}^4\mathrm{N}/\mathrm{m}$, $f_{R1}=201\mathrm{Hz}$, and $m_{R2}=0.014\mathrm{kg}$ are kept unchanged, while $f_{R2}/f_{R1}$ is varied by changing $k_{R2}$.

It can be seen in Figure 3 that the single band gap in the ORIEPE LR plate with $(m_{R1},k_{R1})$ is 201–233 Hz, as shown in the dark grey shaded area. The light grey shaded area shows that, within the frequency range of 0–500 Hz, with the increase of $f_{R2}/f_{R1}$, both the lower and upper frequencies of the single band gap in the ORIEPE LR plate with $(m_{R2},k_{R2})$ keep increasing, and the lower frequency is very close to the resonant frequency $f_{R2}$. When $f_{R2}/f_{R1}=1$, the lower frequencies of the two single band gaps are totally the same, while the difference between $m_{R1}$ and $m_{R2}$ makes the upper frequencies 233 Hz and 224 Hz, respectively, which means the resonator mass plays an important part in the determination of the upper frequency. Furthermore, it can be seen that the lower frequencies of the two single band gaps in both ORIEPE LR plates almost coincide with those of the two band gaps in the TRIEPE LR plate, while the band gaps in the former cases cover those in the latter case. In the TRIEPE LR plate with both $(m_{R1},k_{R1})$ and $(m_{R2},k_{R2})$, when $f_{R2}/f_{R1}<1$, the band gap formed by the resonance of $(m_{R2},k_{R2})$ is the 1st band gap. The 1st band gap is getting narrower as $f_{R2}$ approaches $f_{R1}$, and meanwhile the 2nd band gap is getting wider. When $f_{R2}/f_{R1}=1$, the original 1st band gap vanishes and only one band gap exists. As $f_{R2}/f_{R1}$ continues increasing, two band gaps reappear, while the band gap formed by the resonance of $(m_{R2},k_{R2})$ turns into the 2nd band gap. The bandwidth of the 1st band gap is not changed after a slight increase, and the bandwidth of the 2nd band gap keeps increasing after a decrease.

Shown in Figure 4 are the total bandwidths of the band gaps in three corresponding LR plates when $f_{R2}$ is below 500 Hz. The bandwidth of the band gap in the ORIEPE LR plate with $(m_{R1},k_{R1})$ is 32 Hz. With the increase of $f_{R2}/f_{R1}$, the bandwidth in the ORIEPE LR plate with $(m_{R2},k_{R2})$ has a nearly linear increase, which makes its bandwidth curve intersect with that in the ORIEPE LR plate with $(m_{R1},k_{R1})$ when $f_{R2}/f_{R1}$ reaches a certain value. Moreover, the curve of the total bandwidth of the two band gaps in the TRIEPE LR plate seems positively proportional to $f_{R2}/f_{R1}$ with a lower slope than that in the ORIEPE LR plate with $(m_{R2},k_{R2})$. Interestingly, three bandwidth curves intersect at $f_{R2}/f_{R1}\approx 1.4$, where the total bandwidths are all 32 Hz. With the exception of this point, the bandwidth in the TRIEPE LR plate stays between the bandwidths in both ORIEPE LR plates below 500 Hz.

It can be seen that when aiming to achieve a new low-frequency band gap, the introduction of the new periodic resonators might make the total bandwidth decrease in the TRIEPE LR plate. Appropriate spring-mass parameters for both kinds of resonators could make the total bandwidth not be greatly affected. Hence, the chosen parameters of the periodic element of the TRIEPE LR plate in this paper are given in

Table 1. Parameters of the periodic element and the details of the base plate in the finite locally resonant plate with two resonators in each periodic element.

Symbol	Description	Value
$m_{R1}$	Mass of the resonator $(m_{R1},k_{R1})$	$0.020\mathrm{kg}$
$k_{R1}$	Spring stiffness of the resonator $(m_{R1},k_{R1})$	$3.2\times {10}^4\mathrm{N}/\mathrm{m}$
$m_{R2}$	Mass of the resonator $(m_{R2},k_{R2})$	$0.014\mathrm{kg}$
$k_{R2}$	Spring stiffness of the resonator $(m_{R2},k_{R2})$	$5\times {10}^4\mathrm{N}/\mathrm{m}$
$a_L$	Lattice constant	$0.05\mathrm{m}$
$h_p$	Thickness of the base plate	$0.003\mathrm{m}$
$a$	Length of the finite base plate	$0.8\mathrm{m}$
$b$	Width of the finite base plate	$0.5\mathrm{m}$
$F_0$	Amplitude of excitation force	$1\mathrm{N}$
$\left(x_0,y_0\right)$	Force position on the finite base plate	$\left(0.1\mathrm{m},0.1\mathrm{m}\right)$

, together with the details of the finite base plate. In the following analysis, the parameters are kept unchanged unless otherwise stated.

As illustrated in Section 2.1, the four boundaries of the plate are supported by a linear spring with stiffness $k$ and a torsional spring with stiffness $K$. The free, simply supported, and clamped boundary conditions can be simulated by using specific stiffness values of $k$ and $K$: the free boundary condition can be expressed when $k=0$ and $K=0$; the simply supported boundary condition can be expressed when $k$ tends to infinity and $K=0$; and the clamped boundary condition can be expressed when both $k$ and $K$ tend to infinity. The variation of the boundary conditions can result in the difference in the vibration response and acoustic performance [29,30]. In this paper, three kinds of different boundary conditions are applied to the plate, including fully free boundary conditions (‘FFFF’), fully simply supported boundary conditions (‘SSSS’), and fully clamped boundary conditions (‘CCCC’).

Before the analysis of the vibration attenuation property of the LR plate, taking the SSSS boundary condition as an example, the theory to simulate the vibration response in this paper is examined by using the FEM software of Ansys. The comparisons are shown in Figure 5a–c, respectively for the bare plate, the mass-loaded (ML) plate, and the LR plate. The ML plate indicates the plate periodically attached with point masses, for which the plate, the lattice constant, and the loaded masses are all identical to those of the LR plate. The above theory is also appropriate for the ML plate via replacing Equation (21) by $w_{Rist}=w\left(x_{is},y_t\right)$. Good agreements can be found between the root-mean-square velocities (RMSVs) averaged over the whole surface calculated by the theory and FEM, which validates the correctness of the theory in this paper.

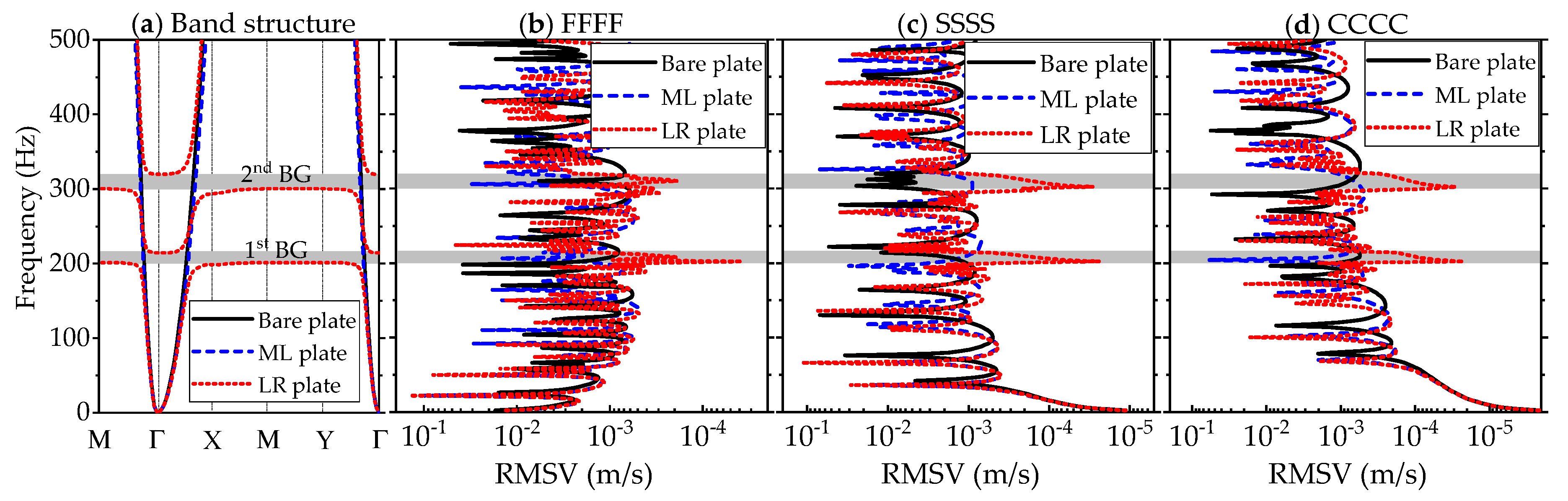
Shown in Figure 6a are the band structure curves of the infinite bare plate, the infinite LR plate, and the infinite ML plate. The RMSVs averaged over the whole plate surface of the bare plate, the LR plate, and the ML plate, for the cases of various boundary conditions, are shown in Figure 6b–d. In the range of 0–500 Hz, the band gaps induced by the LR effect are labeled in Figure 6a, with band-gap frequency ranges of 201–215 Hz and 300–320 Hz, where no waves propagate. The two ranges correspond to the resonant frequencies of two kinds of resonators, i.e., $f_{R1}=201\mathrm{Hz}$ and $f_{R2}=300\mathrm{Hz}$. It can also be seen that, for the bare plate and the ML plate, waves are allowed at any frequency. The comparison between the band structures in Figure 6a and the vibration results in Figure 6b–d basically show a good coincidence between the band gaps of the infinite LR plate and the vibration attenuation bands of its finite counterpart, no matter what boundary conditions are applied to the finite plate. In the band-gap frequency ranges, the vibration of the finite LR plate is attenuated when compared with those of the bare plate and the ML plate.

As illustrated above, the ML plate and the LR plate have the same weight, heavier than the bare plate. From Figure 6b–d, it is obvious that the first few modal frequencies of the bare plate are a little larger than those of the ML plate and the LR plate. Except for the effect on the structural vibration, the weight also affects the acoustic behavior [22]. Thus, only the ML plate is considered for comparison below.

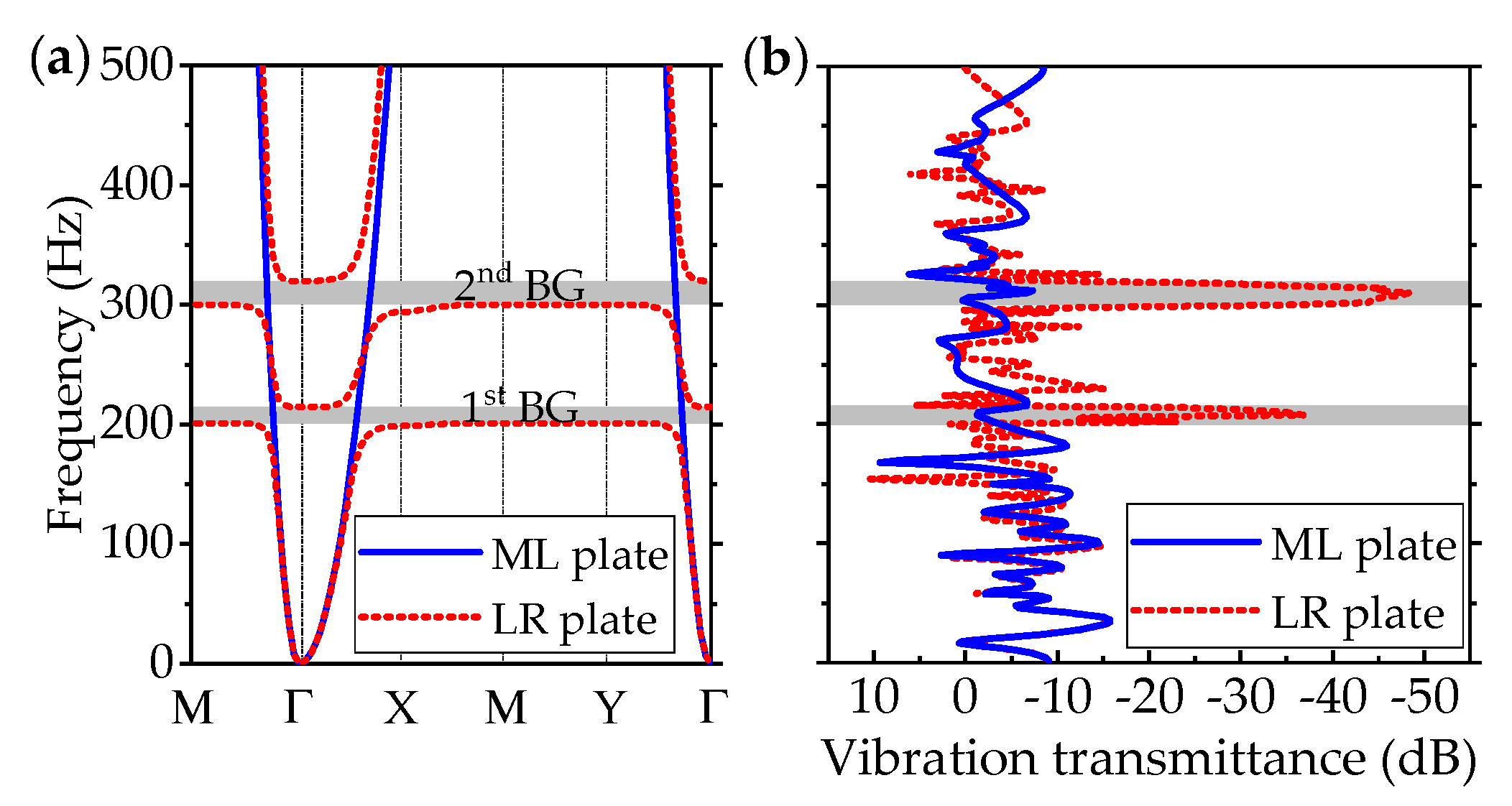
It is noted that the RMSV results in Figure 6b–d are all averaged over the whole plate surface, which makes the vibration attenuation in the LR plates not very obvious at some frequencies in two band gaps, especially for the FFFF boundary conditions in Figure 6b. In the finite LR plates, the vibration attenuation in the band-gap frequency ranges is usually evaluated by the vibration transmittance. With the band structure curves of the infinite ML and LR plates shown in Figure 7a for comparison, Figure 7b shows the vibration transmittances of the finite ML and LR plates with FFFF boundary conditions. The vibration transmittance is given by $T=20\log 10\left|v_{res}/v_{ext}\right|$, where the RMSVs averaged over the area of $0<x<0.1 \mathrm{m}$ and $0.5 \mathrm{m}<x<0.6 \mathrm{m}$ within the base plate surface are chosen as $v_{ext}$ and $v_{res}$, respectively. From the comparison between the vibration transmittances of the ML and LR plates, it can be seen that the flexural waves in the LR plate can be dramatically suppressed in the band-gap frequency ranges, better revealing its band-gap property. Figure 8a,b shows the displacement profiles of the LR plate at 202 Hz and 310 Hz, respectively within two band gaps. It can be seen that, with the exception of the area around the force position, the excited responses over almost the whole surface of the LR plate are significantly suppressed at the two frequencies.

For all of the above results of the LR plates, the damping characteristic of the resonators is not considered, while it could broaden the vibration attenuation band outside the band-gap frequency ranges [21]. Shown in Figure 9a–c are the RMSVs averaged over the whole surface of the FFFF ML plate and the FFFF LR plate with the ${\eta }_{R1}$ and ${\eta }_{R2}$ values of the resonators varying separately and simultaneously. When applying the damping loss factors to the resonator springs, it has little effect on the RMSV in a lower frequency range under 150 Hz in this case. With ${\eta }_{R2}$ kept as zero and ${\eta }_{R1}$ varied by 0, 0.05, and 0.1, the attenuation band covering the 1st band-gap frequency range becomes wider, though the RMSV in the original 1st band-gap frequency range is increased. Meanwhile, the RMSV within the 2nd band-gap frequency range changes little, as shown in Figure 9a. Figure 9b shows an analogous effect in the case where ${\eta }_{R1}$ is zero and ${\eta }_{R2}$ is varied by 0, 0.05, and 0.1. With the damping loss factor increasing simultaneously, as shown in Figure 9c, the RMSV is decreased between the two band-gap frequency ranges, and a much wider attenuation band appears covering them. Moreover, the RMSV curves become smoother in the higher frequency range with the application of the resonator damping. It is revealed that a better attenuation performance can be achieved in the LR plate with multiple resonators when further considering their damping characteristic.

3.2. Acoustic Radiation Property of the Finite LR Plate

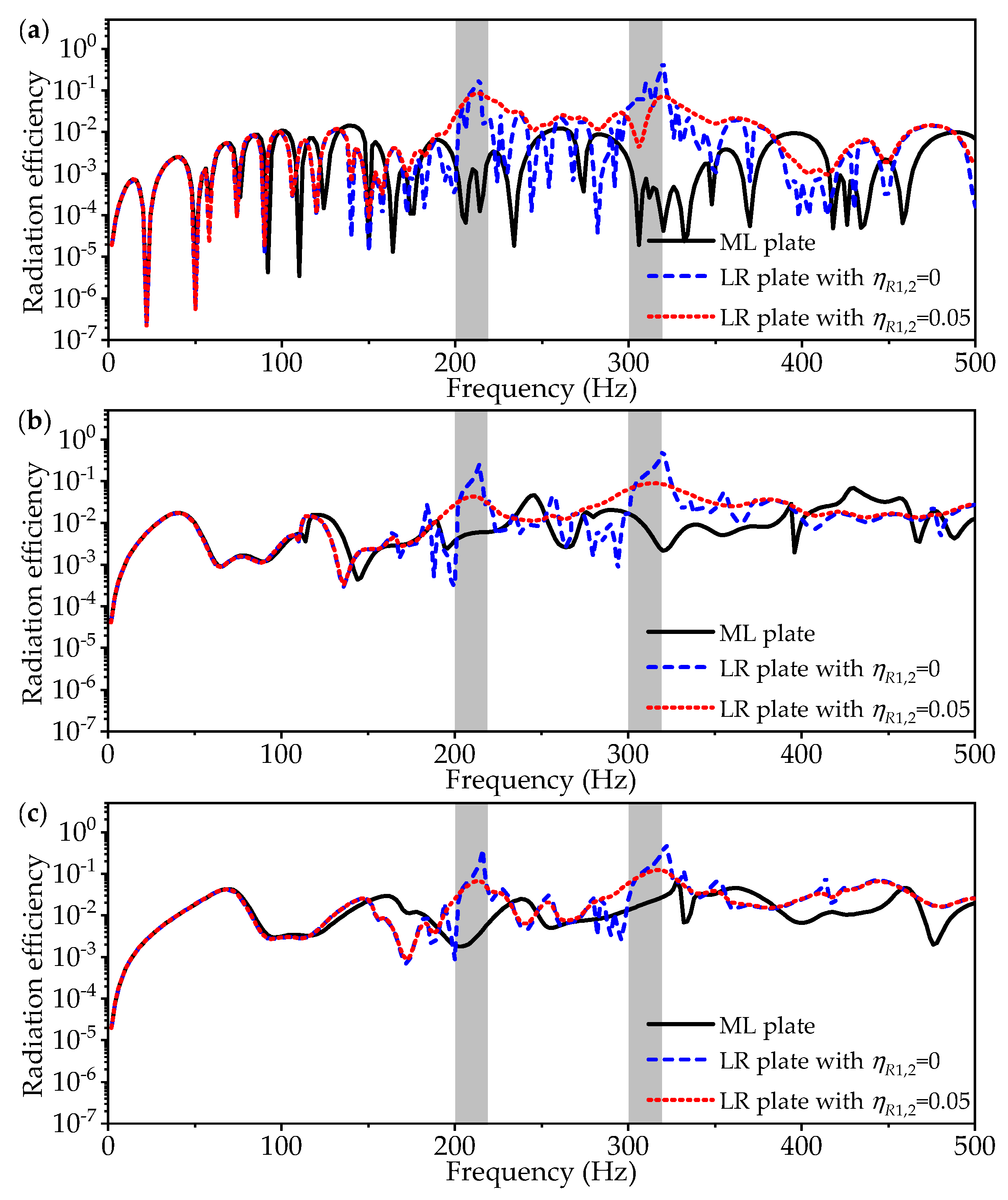
As derived in Section 2.1 and Section 2.2, the theory in this paper can calculate the radiation efficiencies of the finite LR plate with various boundary conditions. Figure 10a–c gives the radiation efficiencies of the FFFF, SSSS, and CCCC plates, including the results of the ML plate, the LR plates with undamped resonators, and the LR plate with damped resonators of ${\eta }_{R1,2}=0.05$. It is not difficult to observe that more peaks and dips appear in the curves of the RMSV and the radiation efficiency of the FFFF plates in 0–500 Hz, than in those in the case of greater constraints, such as the SSSS and CCCC boundary conditions simulated in this paper. Moreover, the modal frequencies shift to higher frequencies when more constraints are applied to the plate boundaries; for instance, the 1st modal frequencies of the LR plates with FFFF, SSSS, and CCCC boundary conditions are respectively 22 Hz, 36 Hz, and 69 Hz in this paper. As for the radiation efficiency, it can be easily seen from Figure 10a–c that, in contrast to the vibration attenuation in the two band-gap frequency ranges, the radiation efficiency has been obviously increased in both bands compared with the results of the ML plates. When the resonators are damped, the curves become smoother than those in the undamped case from below the lower frequency of the 1st band gap, while the acoustic radiation is still high in the band-gap frequency ranges in each case.

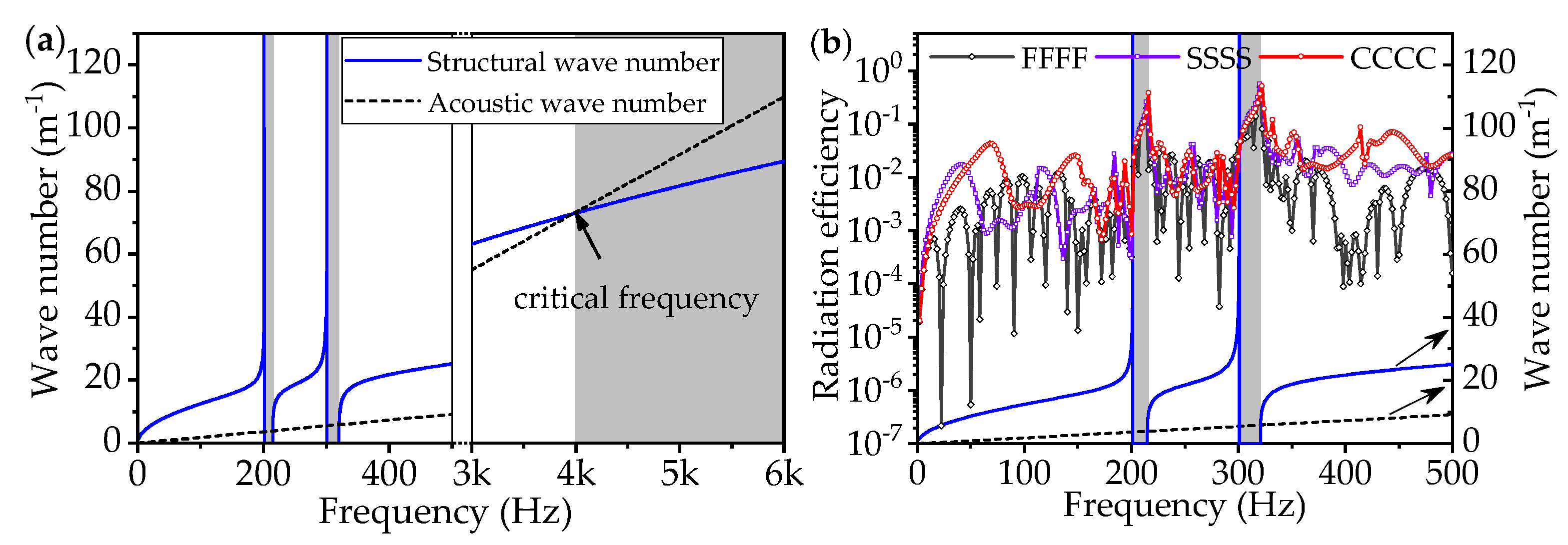
It is known that the acoustic radiation from the infinite bare plate is effective only above the critical frequency [31] where the acoustic wave number exceeds the structural wave number. For its finite counterpart, though its acoustic power can effectively radiate in the whole frequency range, the radiation efficiency reaches the highest at the critical frequency and tends to unity above the critical frequency. Based on this relationship, the structural and acoustic wave numbers of the infinite LR plate are then calculated. In an infinite LR plate with the wave vector $\mathit{k}=\left(k_x,k_y\right)$, the displacement function can be assumed as:

$$w\left(x,y\right)=W{e}^{-j{k}_{x}x}{e}^{-j{k}_{y}y}$$

(42)

The substitution of Equation (42) into the governing equation of the infinite LR plate:

$$\left(D{\nabla }^4-{\omega }^2{\rho }_p{h}_p\right)w\left(\mathit{r}\right)={\displaystyle \sum _{i=1}^2{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{t=1}^T{F}_{ist}\delta \left(x-x_{is}\right)\delta \left(y-y_t\right)}}},$$

(43)

Yields:

$$\left[\begin{array}{ccc}D{k}_p^4-{\omega }^2{\rho }_p{h}_p& -\frac{{\omega }^2{m}_{R1}}{2a_L^2}& -\frac{{\omega }^2{m}_{R2}}{2a_L^2}{e}^{j{k}_x{a}_L}\\ -k_{R1}& k_{R1}-{\omega }^2{m}_{R1}& 0\\ -k_{R2}{e}^{-j{k}_x{a}_L}& 0& k_{R2}-{\omega }^2{m}_{R2}\end{array}\right]\left[\begin{array}{c}W\\ w_{R1}\\ w_{R2}\end{array}\right]=\mathbf{0},$$

(44)

where $k_P=\sqrt{k_x^2+k_y^2}$ is the structural wave number. To obtain the non-zero displacement responses of the base plate and the resonators, the matrix determinant of Equation (44) should equal zero, and then the structural and acoustic wave numbers can be obtained.

The structural and acoustic wave numbers of the infinite LR plate are compared in 0–500 Hz and 3–6 kHz, where the effective radiation frequency ranges are shaded, as shown in Figure 11a. It can be seen that, besides the range where the infinite LR plate radiates sound effectively above the critical frequency of about 4 kHz, the acoustic wave number also exceeds the structural wave number in the two additional bands of 201–215 Hz and 300–320 Hz. The two bands coincide well with the band gaps, which means that the acoustic radiation from the infinite LR plate is effective in the band-gap frequency ranges. Therefore, the acoustic radiation from the finite LR plate of identical resonator parameters can reach a high effectiveness in the band-gap frequency ranges, as expressly shown in Figure 11b. It can be seen that the radiation efficiencies of the finite FFFF, SSSS, and CCCC LR plates are sharply increased in two band-gap frequency ranges. Furthermore, by comparing the results of three different LR plates, the results behave almost the same and closer to unity in the band-gap frequency ranges. However, at most frequencies in 0–500 Hz, the greater the boundary conditions are, the higher the radiation efficiency of the LR plate is in this case.

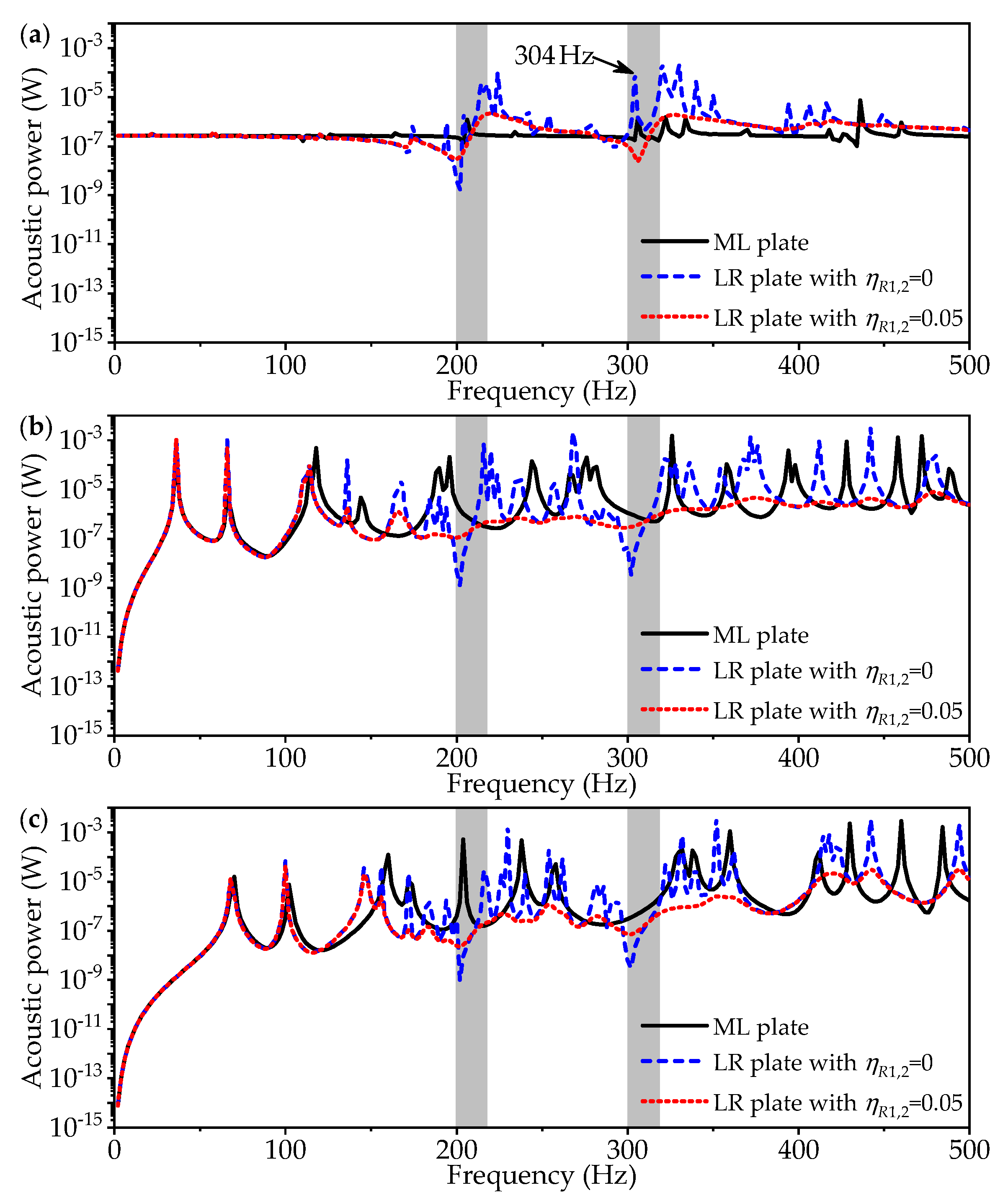
Figure 12a–c shows the acoustic power radiated from the finite ML and LR plates with FFFF, SSSS, and CCCC boundary conditions. It can be observed from the comparison between Figure 12a and Figure 12b (or Figure 12c) that the acoustic behavior behaves quite different when no constraints are applied to the plate. It has been explained in reference [29] that the acoustic power in the low-frequency range radiated from the FFFF bare plate is mainly dominated by three rigid body modes. The rigid body motion and rotation of the FFFF plate make the first few flexural modes inefficiently radiating ones, and then the acoustic power at these modal frequencies is not highlighted, unlike the results of the finite plates with higher constraints. As shown in Figure 12a, the acoustic power radiated from the ML plate is almost constant below 200 Hz in this case. For the LR plate, the radiated power is approximate to that from the ML plate in 0–100 Hz and is decreased below the lower frequency of the 1st band gap, while it turns out to be increased at a certain frequency within the band gap. A similar phenomenon is found around the 2nd band-gap frequency range.

For the LR plates with greater constraints, such as the SSSS and CCCC boundary conditions considered in this paper, it is expected that the acoustic power is decreased in the band-gap frequency ranges, as shown in Figure 12b,c. It can be concluded that, although the radiation efficiency of the LR plate with greater constraints, is increased in the band-gap frequency ranges, due to the good performance of the vibration attenuation the acoustic power is reduced much in the same bands. Moreover, when considering the damping characteristic of the resonators, the acoustic power curve becomes smooth from below the lower frequency of the 1st band gap. Although the degree of acoustic power reduction in the band-gap frequency ranges is weakened, the attenuation band of acoustic radiation is broadened.

It can be seen that the application of the periodic resonators on the FFFF base plate cannot be a good noise-control method in this case, especially in and above the band gap frequency ranges. In fact, it can be understood from the vibration profile shown in Figure 13a that the vigorously vibrating FFFF ML plate at the two frequencies may not radiate much sound power due to radiation cancellation from the uniform distribution of anti-phase regions. Conversely, though the vibration over the whole surface of the FFFF LR plate is not strong, as shown in Figure 13b, the acoustic power radiated from the vibrating area near the excitation can be very high when no cancellation exists.

However, when considering the damping loss factors of the resonators, the high acoustic power radiated from the FFFF LR plate can be decreased. The vibration profile of the FFFF LR plate with damped resonators is shown in Figure 14. It can be seen that the LR plate with undamped resonators in Figure 13b vibrates vigorously near the excitation and hardly over the other surface. When replaced by damped resonators, the response of the FFFF LR plate is suppressed in the region where it is originally vibrating strongly, as shown in Figure 14, and thus the radiated power is reduced. This is why the acoustic power radiated from the LR plate with undamped resonators is peculiarly high and decreased greatly after considering the damping characteristic of the resonators at 304 Hz, as shown in Figure 12a.

Overall, the acoustic power radiated from the plates is related to their boundary conditions. For the FFFF ML plate, the radiation cancellation could appear more easily in a wide frequency range, and the plate radiates sound weakly. However, for the FFFF LR plate without good radiation cancellation, despite a lower RMSV in the band-gap frequency ranges, the higher radiation efficiency will translate to a higher acoustic power. In other cases where the base plate has greater constraints, such as the SSSS and CCCC LR plates in the manuscript, even though the radiation efficiency is higher in the band-gap frequency ranges, a lower RMSV will lead to a lower acoustic power.

4. Conclusions

In this paper, the low-frequency vibration and radiation performance of an LR plate is analyzed. The theoretical model is established for the band structures of the infinite LR plate with periodic multiple resonators. Taking the finite LR plate attached with two periodic arrays of resonators as an example, the forced vibration response and the radiation efficiency of the finite LR plate are derived, by adopting a general model with elastic boundary conditions.

First, we discuss the impact of the parameter of the ratio between the resonant frequencies of two resonators on the band-gap frequency ranges. The band-gap width in the TRIEPE LR plate stays between those in both corresponding ORIEPE LR plates. By using the proper spring-mass parameters, the band structures of the infinite bare, ML, and LR plates and the RMSVs of their finite FFFF, SSSS, and CCCC counterparts are calculated. The comparison shows a good coincidence between the band gaps in the infinite LR plate and the vibration attenuation bands in the finite LR plate, no matter what boundary conditions are applied to the latter. A better vibration attenuation performance can be achieved when further considering the damping characteristic of the resonators.

In contrast to the obvious decrease of the RMSV, the radiation efficiency of the finite LR plate has been sharply increased in the band-gap frequency ranges compared with the ML plate. By comparing the structural and acoustic wavenumbers, it can be seen that the acoustic radiation from the infinite LR plate is effective in the band gaps, and correspondingly that its finite counterpart can radiate sound highly effectively in the band-gap frequency ranges. Moreover, the acoustic power radiated from the finite LR plate around the band-gap frequencies may be seriously affected by its boundary conditions. The acoustic power radiated from the FFFF LR plate could be increased in the band-gap frequency ranges due to no effective cancellation of radiation from the strongly vibrating area near the excitation. However, for the LR plate with greater constraints, such as the SSSS and CCCC boundary conditions considered in this paper, the acoustic power is decreased in the band-gap frequency ranges. When further considering the damping characteristic of the resonators, a better vibration attenuation performance can result in the improvement of a radiation reduction around and above the band-gap frequencies.