Temperature Effects on Vibration-Based Damage Detection of a Reinforced Concrete Slab
Abstract
:1. Introduction
2. RC Slab and Vibration Testing
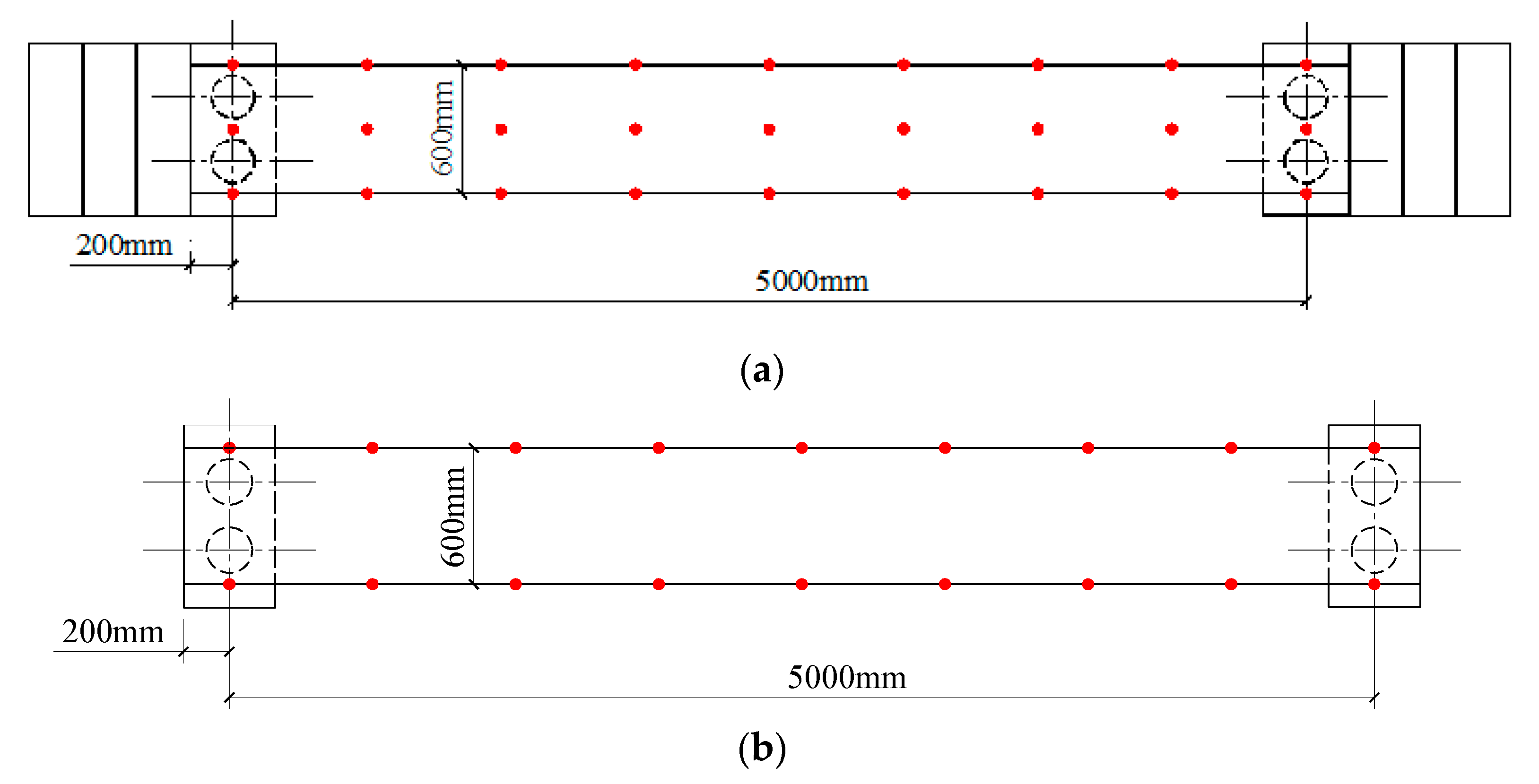
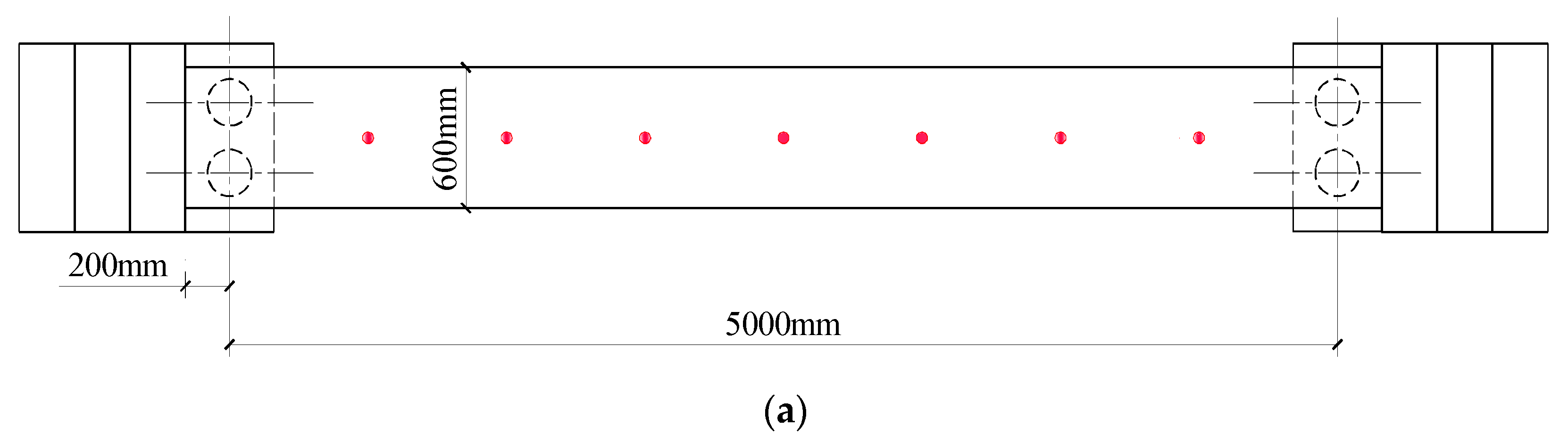
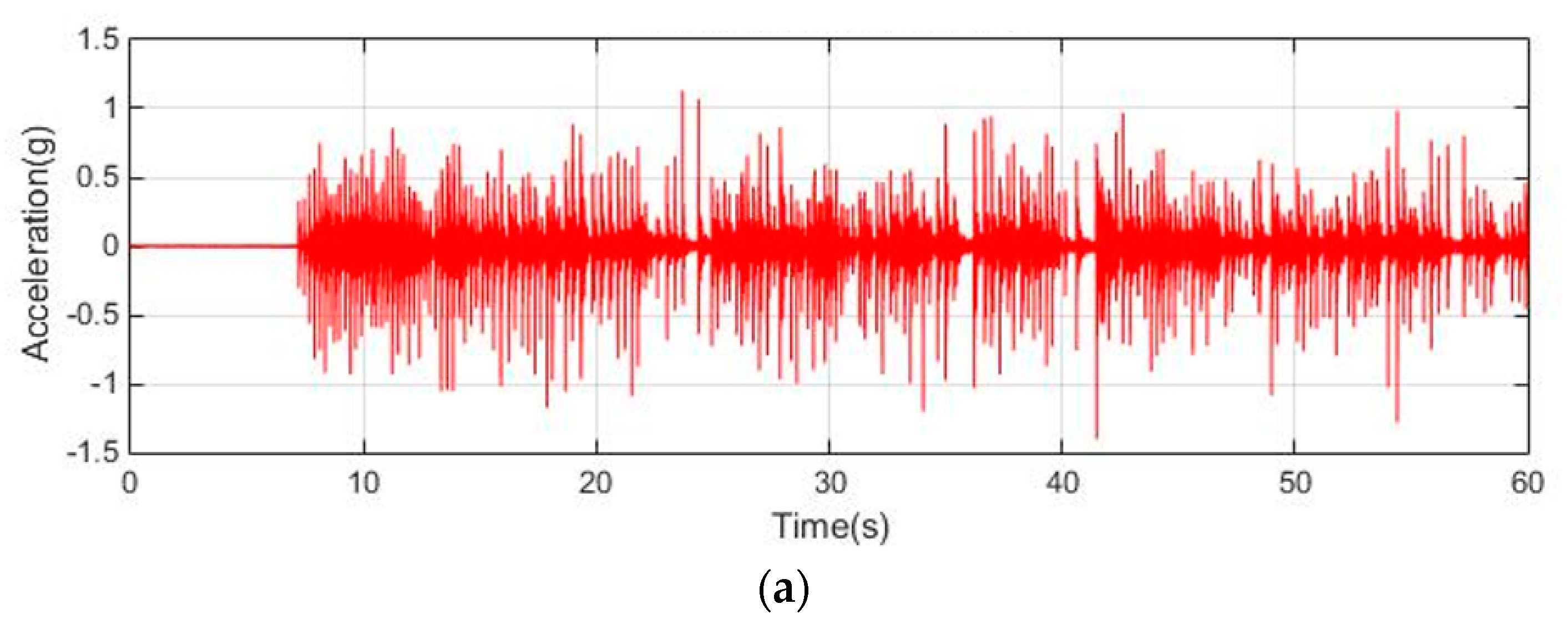
2.1. Testing Setup
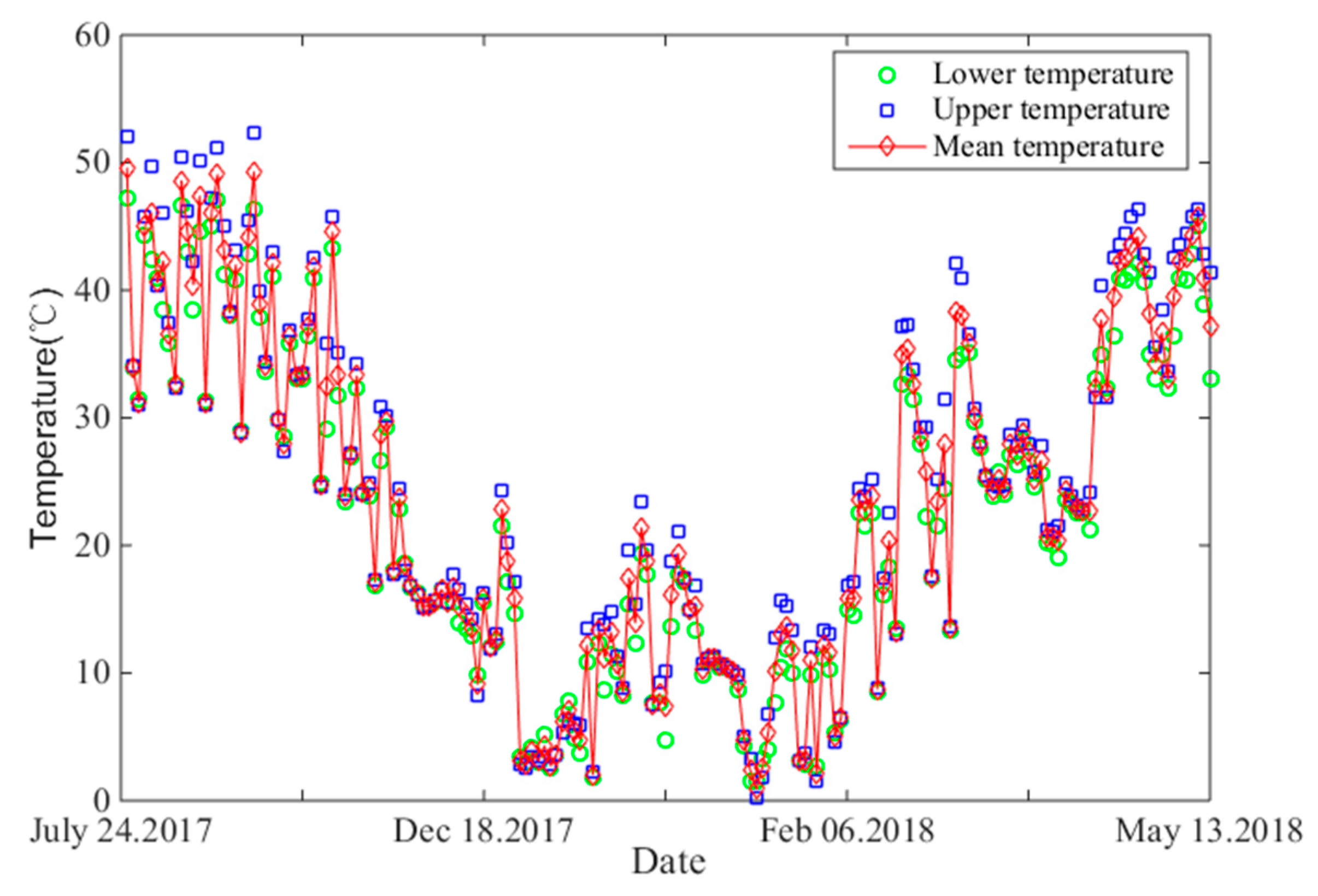
2.2. Variations of Natural Frequencies
2.3. Variation of Damping Ratios
2.4. Variation of MAC
3. Mathematical Model
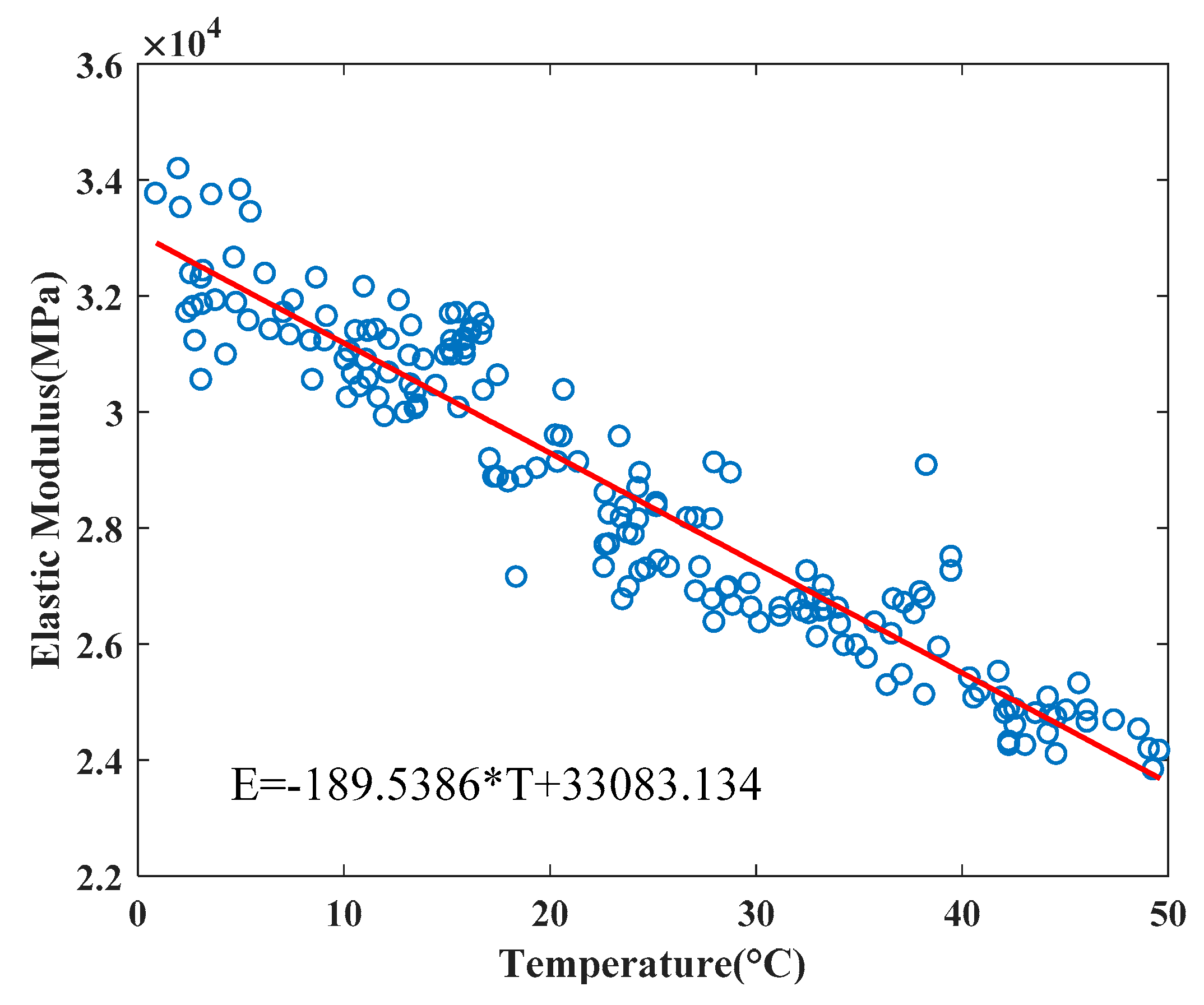
3.1. Theoretical Derivation
3.2. Simple Linear Regression Model
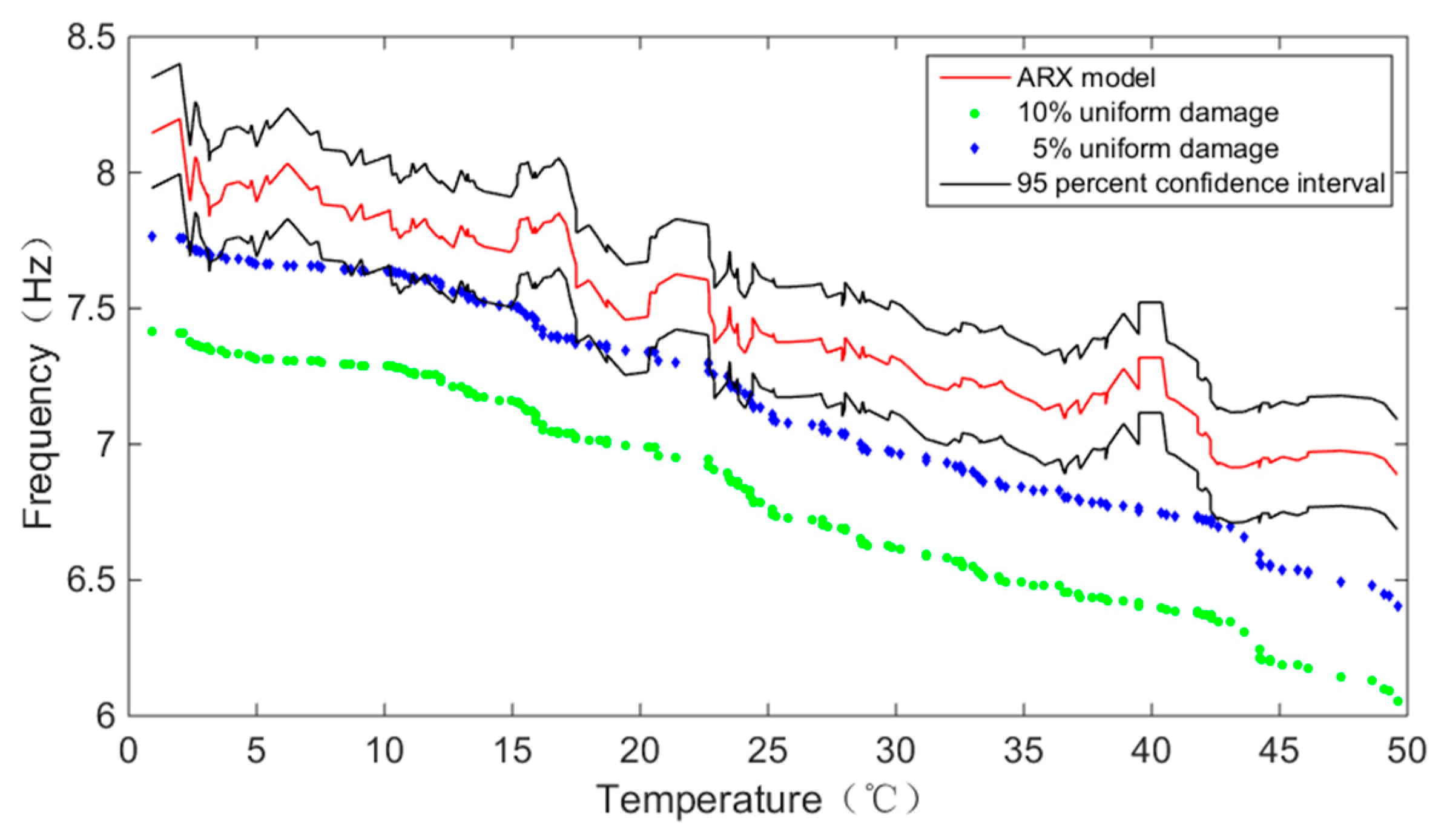
3.3. ARX Model
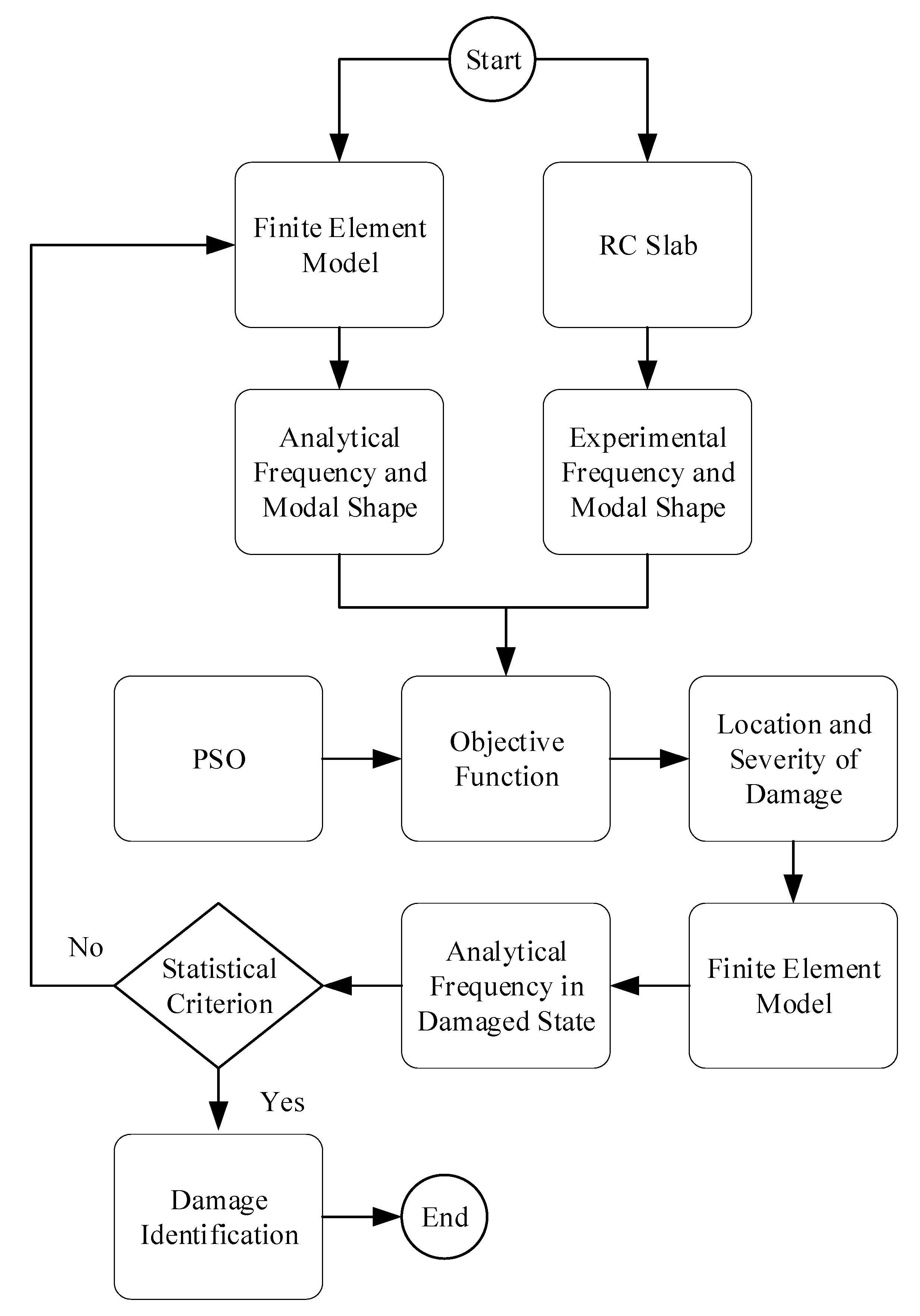
4. Damage Identification in Test Structure
4.1. Statistical Criterion
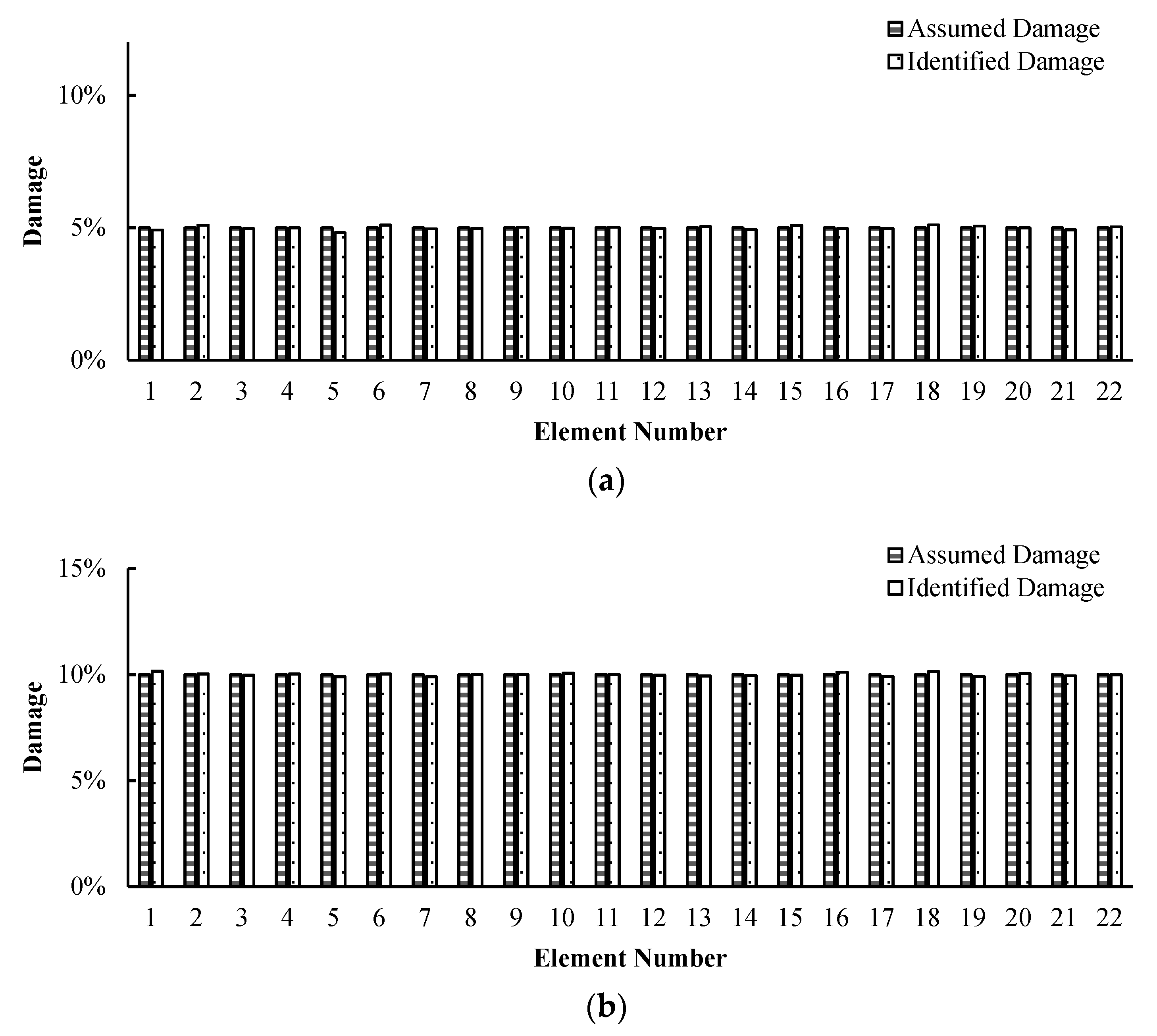
4.2. Damage Identification Considering Temperature Variations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Adedayo, R.A.; Fauzi, Z.; Sathyajith, M. Sustainable energy towards air pollution and climate change mitigation. J. Environ. Eng. Landsc. 2020, 260, 109978. [Google Scholar]
- Cotana, F.; Vittori, S.; Marseglia, G.; Medaglia, C.M.; Coccia, V.; Petrozzi, A.; Nicolini, A.; Cavalaglio, G. Pollutant emissions of a biomass gasifier inside a multifuel energy plant. Atmos. Pollut. Res. 2019, 10, 2000–2009. [Google Scholar] [CrossRef]
- Marseglia, G.; Medaglia, C.M.M.; Petrozzi, A. Experimental tests and modeling on a CHP biomass plant. J. Energ. 2019, 12, 2615. [Google Scholar]
- Manni, M.; Coccia, V.; Nicolini, A.; Marseglia, G.; Petrozzi, A. Towards Zero Energy Stadiums: The Case Study of the Dacia Arena in Udine, Italy. Energies 2018, 11, 2396. [Google Scholar] [CrossRef] [Green Version]
- Requena-Garcia-Cruz, M.-V.; Morales-Esteban, A.; Durand-Neyra, P.; Estêvão, J. An index-based method for evaluating seismic retrofitting techniques. Application to a reinforced concrete primary school in Huelva. PLoS ONE 2019, 14, e0215120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marseglia, G.; Rivieccio, E.; Medaglia, C.M. The dynamic role of Italian energy strategies in the worldwide scenario. Kybernetes 2019, 48, 636–649. [Google Scholar] [CrossRef]
- Moaveni, B.; Behmanesh, I. Effects of changing ambient temperature on finite element model updating of the Dowling Hall Footbridge. Eng. Struct. 2012, 43, 58–68. [Google Scholar] [CrossRef]
- Moorty, S.; Roeder, C.W. Temperature?Dependent Bridge Movements. J. Struct. Eng. 1992, 118, 1090–1105. [Google Scholar] [CrossRef]
- Liang, Y.; Li, N.; Song, G.; Li, H. Damage Diagnosis under Environmental and Operational Variations Using Improved Restoring Force Method. Earth Space 2014 2015, 690–702. [Google Scholar] [CrossRef]
- Del Grosso, A.; Lanata, F. A long-term static monitoring experiment on R.C. beams: Damage identification under environmental effect. Struct. Infrastruct. Eng. 2013, 10, 911–920. [Google Scholar] [CrossRef]
- Li, J.; Law, S.; Hao, H. Improved damage identification in bridge structures subject to moving loads: Numerical and experimental studies. Int. J. Mech. Sci. 2013, 74, 99–111. [Google Scholar] [CrossRef] [Green Version]
- Yarnold, M.; Moon, F. Temperature-based structural health monitoring baseline for long-span bridges. Eng. Struct. 2015, 86, 157–167. [Google Scholar] [CrossRef]
- Chang, K.-C.; Kim, C.-W.; Kawatani, M. Feasibility investigation for a bridge damage identification method through moving vehicle laboratory experiment. Struct. Infrastruct. Eng. 2013, 10, 328–345. [Google Scholar] [CrossRef] [Green Version]
- Doebling, S.; Farrar, C.; Prime, M.; Shevitz, D. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review; Los Alamos National Lab: Los Alamos, NM, USA, 1996. [CrossRef] [Green Version]
- Doebling, S.W.; Farrar, C.R.; Prime, M. A Summary Review of Vibration-Based Damage Identification Methods. Shock. Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef] [Green Version]
- Hao, H.; Xia, Y. Vibration-based Damage Detection of Structures by Genetic Algorithm. J. Comput. Civ. Eng. 2002, 16, 222–229. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Preumont, A. Vibration based damage detection using large array sensors and spatial filters. Mech. Syst. Signal Process. 2006, 20, 1615–1630. [Google Scholar] [CrossRef] [Green Version]
- Boonlong, K. Vibration-Based Damage Detection in Beams by Cooperative Coevolutionary Genetic Algorithm. Adv. Mech. Eng. 2014, 6, 624949. [Google Scholar] [CrossRef] [Green Version]
- Nandan, H.; Singh, M.P. Effects of thermal environment on structural frequencies: Part II—A system identification model. Eng. Struct. 2014, 81, 491–498. [Google Scholar] [CrossRef]
- Alampalli, S. Influence of in-service environment on modal parameters//Proceedings-SPIE The International Society For Optical Engineering. SPIE Int. Soc. Opt. 1998, 1, 111–116. [Google Scholar]
- Peeters, B.; Maeck, J.; De Roeck, G. Vibration-based damage detection in civil engineering: Excitation sources and temperature effects. Smart Mater. Struct. 2001, 10, 518–527. [Google Scholar] [CrossRef]
- Zhao, J.; DeWolf, J.T. Dynamic Monitoring of Steel Girder Highway Bridge. J. Bridg. Eng. 2002, 7, 350–356. [Google Scholar] [CrossRef]
- Xu, Z.-D.; Wu, Z. Simulation of the Effect of Temperature Variation on Damage Detection in a Long-span Cable-stayed Bridge. Struct. Health Monit. 2007, 6, 177–189. [Google Scholar] [CrossRef]
- Martins, N.; Caetano, E.; Diord, S.; Magalhães, F. Cunha, Álvaro Dynamic monitoring of a stadium suspension roof: Wind and temperature influence on modal parameters and structural response. Eng. Struct. 2014, 59, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Gül, M.; Zhu, H.-P. Vibration-Based Structural Damage Identification under Varying Temperature Effects. J. Aerosp. Eng. 2018, 31, 04018014. [Google Scholar] [CrossRef]
- Jin, C.; Jang, S.; Sun, X.; Li, J.; Christenson, R. Damage detection of a highway bridge under severe temperature changes using extended Kalman filter trained neural network. J. Civ. Struct. Health Monit. 2016, 6, 545–560. [Google Scholar] [CrossRef]
- Jiao, Y.; Liu, H.; Cheng, Y.; Wang, X.; Gong, Y.; Song, G. Fuzzy Neural Network-Based Damage Assessment of Bridge under Temperature Effect. Math. Probl. Eng. 2014, 2014, 1–9. [Google Scholar] [CrossRef]
- Ni, Y.-Q.; Hua, X.; Fan, K.; Ko, J. Correlating modal properties with temperature using long-term monitoring data and support vector machine technique. Eng. Struct. 2005, 27, 1762–1773. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W.; Cornwell, P.J. Variability of Modal Parameters Measured on the Alamosa Canyon Bridge; Los Alamos National Lab: Los Alamos, NM, USA, 1996.
- Sohn, H.; Dzwonczyk, M.; Straser, E.G. An experimental study of temperature effect on modal parameters of the Alamosa Canyon Bridge. J. Earthq. Eng. Struct. D 1999, 28, 879–897. [Google Scholar] [CrossRef]
- Xia, Y.; Hao, H.; Zanardo, G.; Deeks, A. Long term vibration monitoring of an RC slab: Temperature and humidity effect. Eng. Struct. 2006, 28, 441–452. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Jiao, Y. Effect of Temperature Variation on Modal Frequency of Reinforced Concrete Slab and Beam in Cold Regions. Shock. Vib. 2016, 2016, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.-D.; Yi, T.-H. A Summary Review of Correlations between Temperatures and Vibration Properties of Long-Span Bridges. Math. Probl. Eng. 2014, 2014, 1–19. [Google Scholar] [CrossRef]
- Giorgio, I.; Scerrato, D. Multi-scale concrete model with rate-dependent internal friction. Eur. J. Environ. Civ. Eng. 2016, 21, 821–839. [Google Scholar] [CrossRef]
- Scerrato, D.; Giorgio, I.; Madeo, A.; Limam, A.; Darve, F. A simple non-linear model for internal friction in modified concrete. Int. J. Eng. Sci. 2014, 80, 136–152. [Google Scholar] [CrossRef] [Green Version]
- Ewins, D.J. Modal Testing—Theory, Practice and Application; Research Studies Press Ltd.: Hertfordshire, UK, 2000. [Google Scholar]
- Baldwin, R.; North, M.A. A stress-strain relationship for concrete at high temperatures. Mag. Concr. Res. 1973, 25, 208–212. [Google Scholar] [CrossRef]
- Blevins, R.D.; Plunkett, R. Formulas for Natural Frequency and Mode Shape. J. Appl. Mech. 1980, 47, 461–462. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y. MATLAB Solution of Control Mathematical Problem; Tsinghua University Press: Beijing, China, 2007. (In Chinese) [Google Scholar]
- Andreaus, U.; Baragatti, P. Experimental damage detection of cracked beams by using nonlinear characteristics of forced response. Mech. Syst. Signal Process. 2012, 31, 382–404. [Google Scholar] [CrossRef]
- Placidi, L.; Barchiesi, E.; Misra, A. A strain gradient variational approach to damage: A comparison with damage gradient models and numerical results. Math. Mech. Complex Syst. 2018, 6, 77–100. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle Swarm Optimisation. SSRN Electron. J. 2007, 4, 1942–1948. [Google Scholar] [CrossRef]
- Huang, M.; Lei, Y.; Cheng, S. Damage identification of bridge structure considering temperature variations based on particle swarm optimization—Cuckoo search algorithm. Adv. Struct. Eng. 2019, 22, 3262–3276. [Google Scholar] [CrossRef]


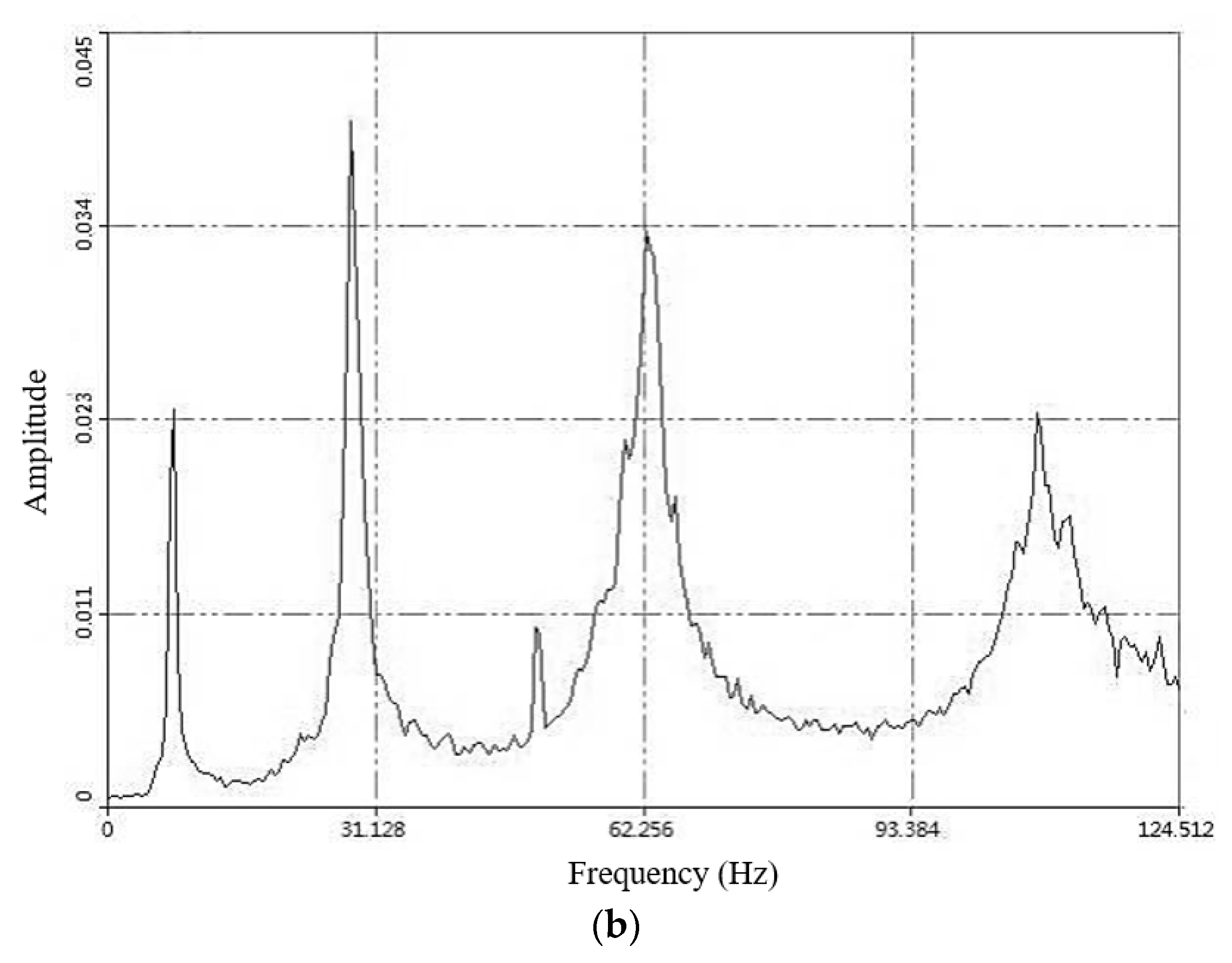



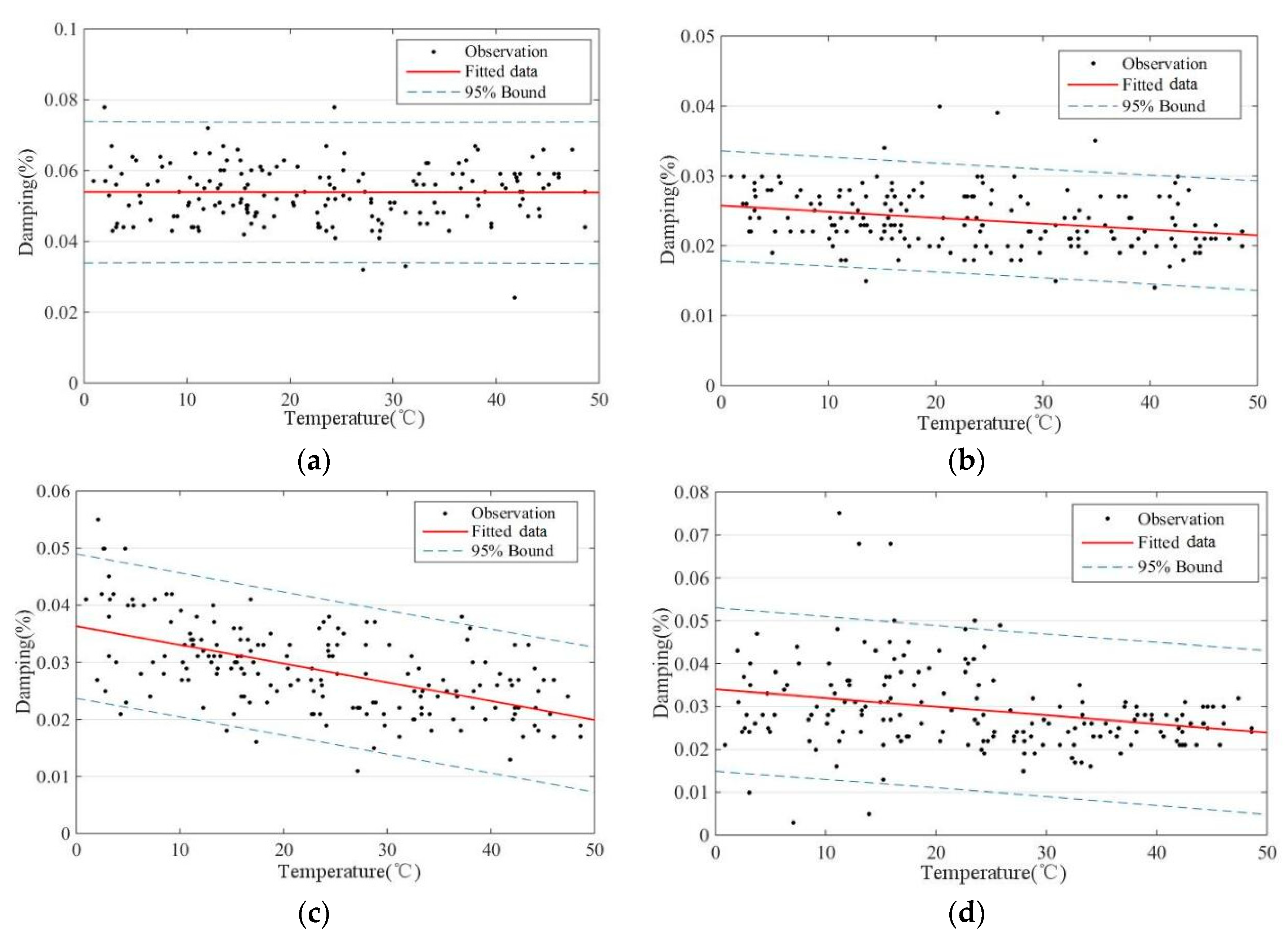
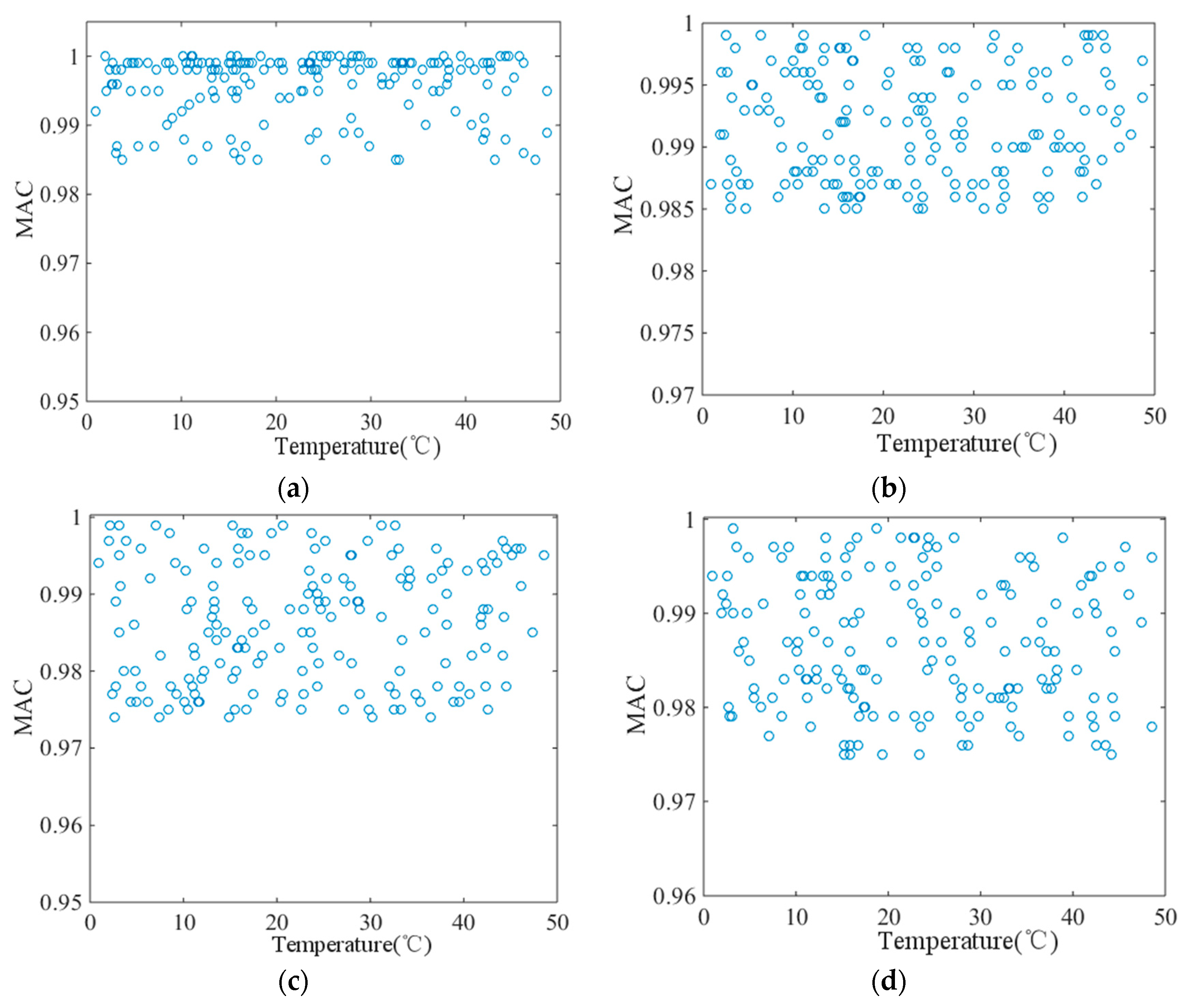


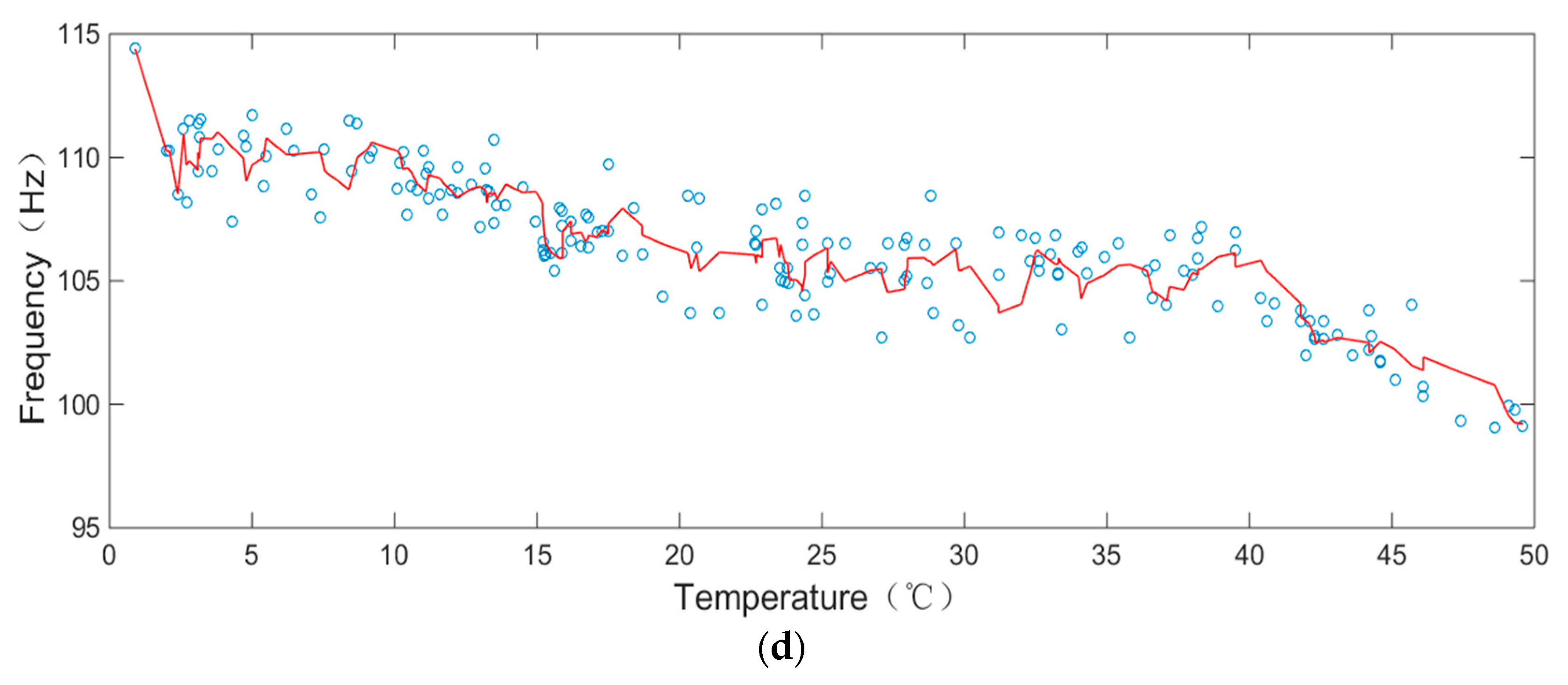

| Mode | Minimum/Hz | Maximum/Hz | Error/% |
|---|---|---|---|
| 1st | 6.884 | 8.198 | 16.52 |
| 2nd | 26.093 | 29.467 | 11.45 |
| 3rd | 58.292 | 65.764 | 11.36 |
| 4th | 99.051 | 114.398 | 13.42 |
| Mode | K | b |
|---|---|---|
| 1st | −0.025 | 8.081 |
| 2nd | −0.0429 | 28.955 |
| 3rd | −0.1222 | 64.572 |
| 4th | −0.1955 | 114.398 |
| Model | 1st Mode | 2nd Mode | 3rd Mode | 4th Mode |
|---|---|---|---|---|
| ARX model | 0.0104 | 0.0882 | 0.561 | 1.812 |
| LR model | 0.0119 | 0.0969 | 0.568 | 2.1904 |
| Damage Case | Lower Bound of the Interval | Upper Bound of the Interval | The First Analytical Frequency | Determination of Damage |
|---|---|---|---|---|
| 5% uniform damage (20 °C) | 7.266 | 7.672 | 7.34 | Damaged |
| 10%uniform damage (20 °C) | 6.99 | Damaged |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Huang, M.; Gu, J. Temperature Effects on Vibration-Based Damage Detection of a Reinforced Concrete Slab. Appl. Sci. 2020, 10, 2869. https://doi.org/10.3390/app10082869
Wang Z, Huang M, Gu J. Temperature Effects on Vibration-Based Damage Detection of a Reinforced Concrete Slab. Applied Sciences. 2020; 10(8):2869. https://doi.org/10.3390/app10082869
Chicago/Turabian StyleWang, Zhenpeng, Minshui Huang, and Jianfeng Gu. 2020. "Temperature Effects on Vibration-Based Damage Detection of a Reinforced Concrete Slab" Applied Sciences 10, no. 8: 2869. https://doi.org/10.3390/app10082869
APA StyleWang, Z., Huang, M., & Gu, J. (2020). Temperature Effects on Vibration-Based Damage Detection of a Reinforced Concrete Slab. Applied Sciences, 10(8), 2869. https://doi.org/10.3390/app10082869






