Influences of Material Variations of Functionally Graded Pipe on the Bree Diagram
Abstract
:1. Introduction
2. Mathematical Formulations for Cyclic Plasticity Constitutive Model
3. The Problem Definition
3.1. Gradation Relations
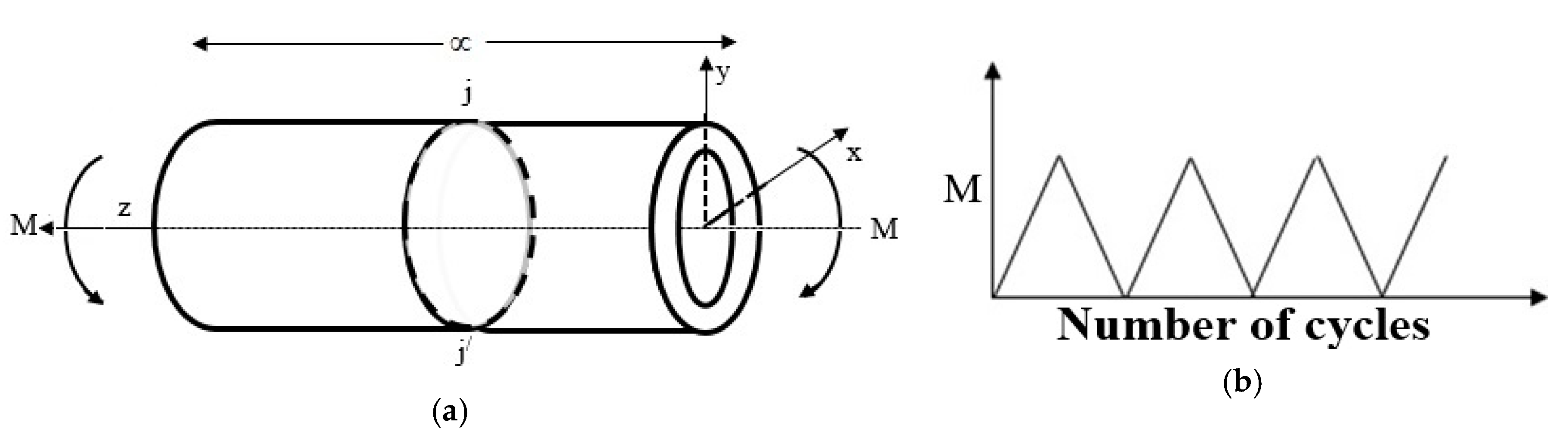
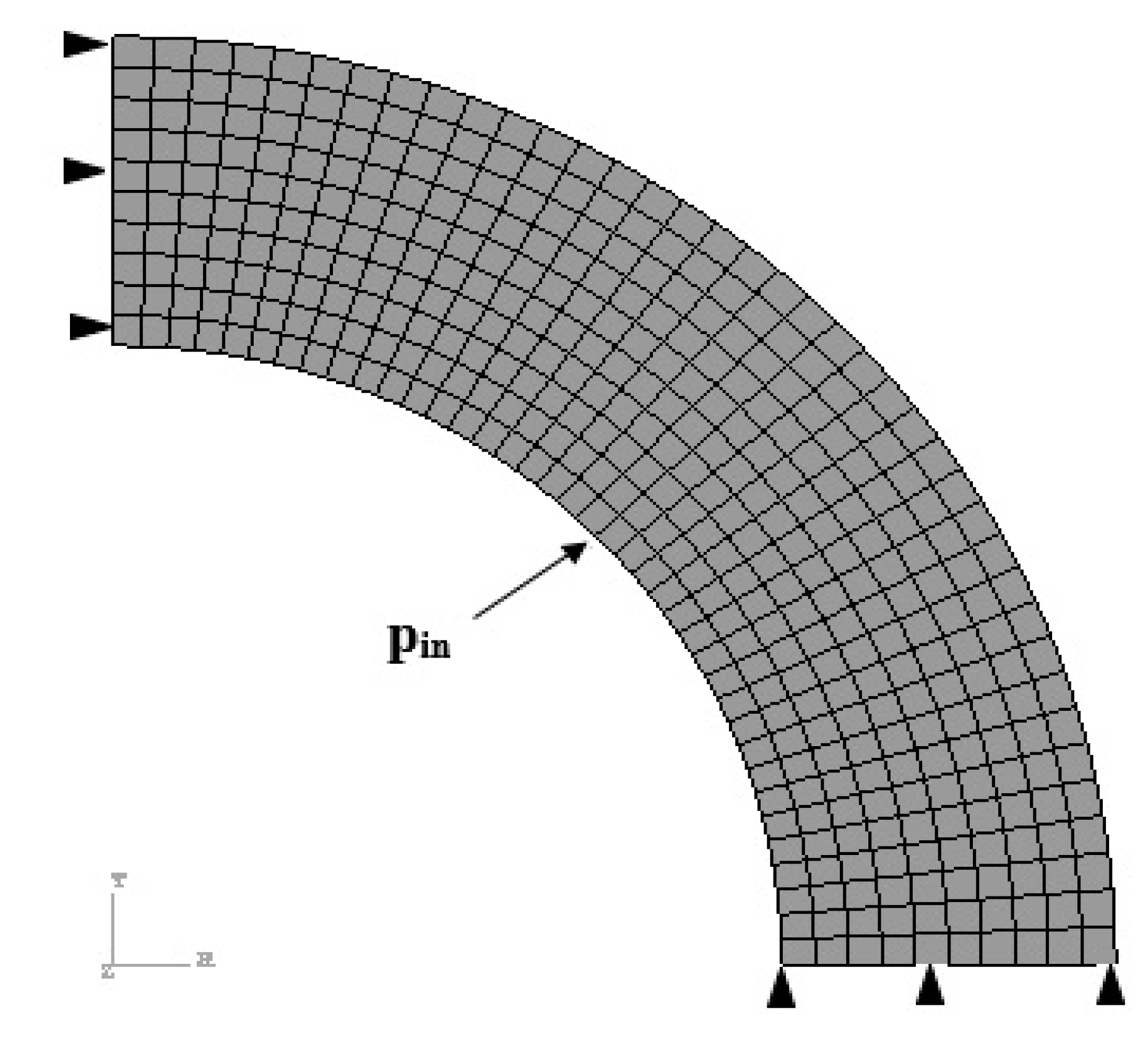
3.2. Internally Pressurized FGM Cylindrical Pipe Submitted to Cyclic Bending
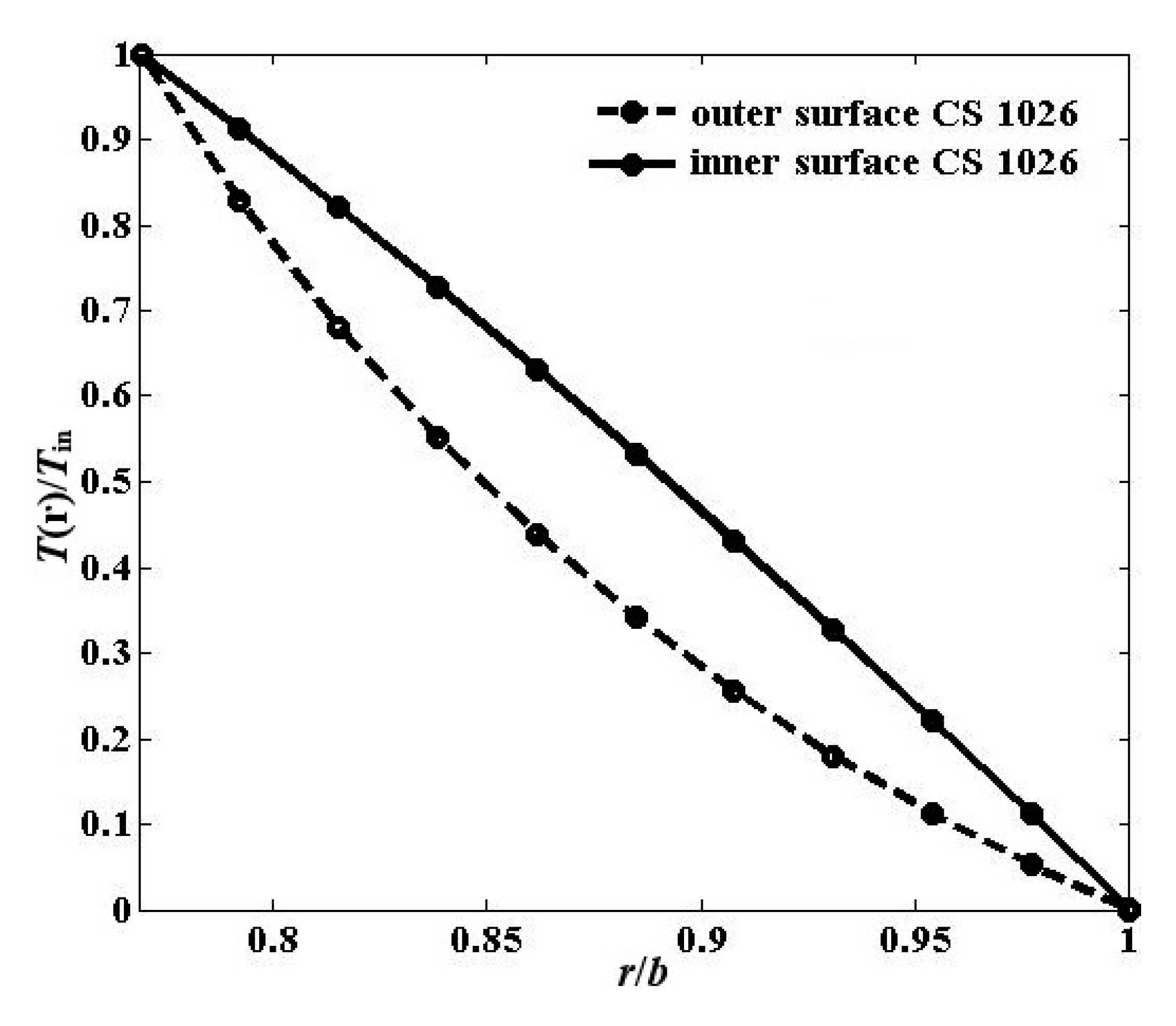
3.3. Internally Pressurized FGM Pipe under Cyclic Temperature Difference through Thickness
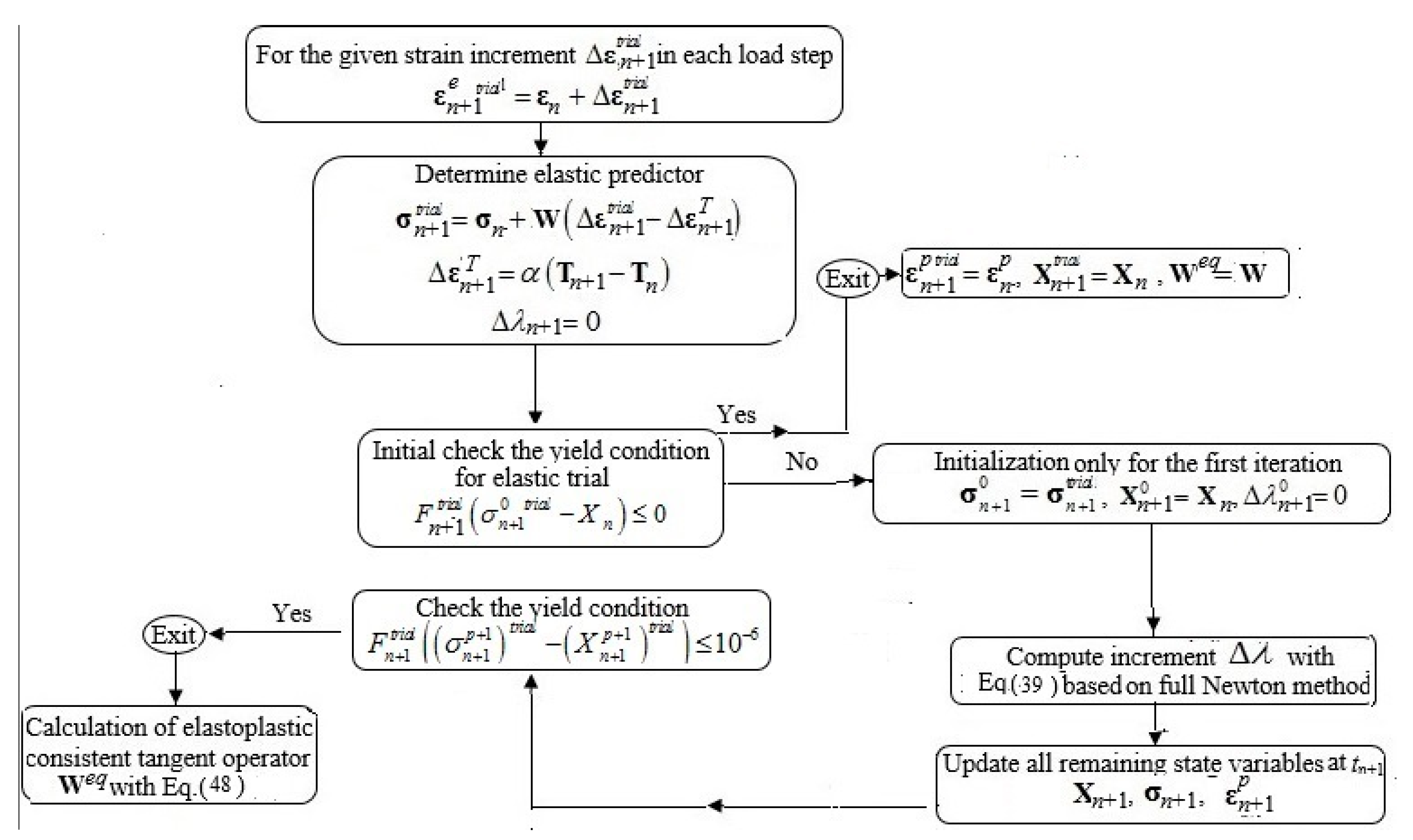
4. Integration Algorithm
5. Numerical Results
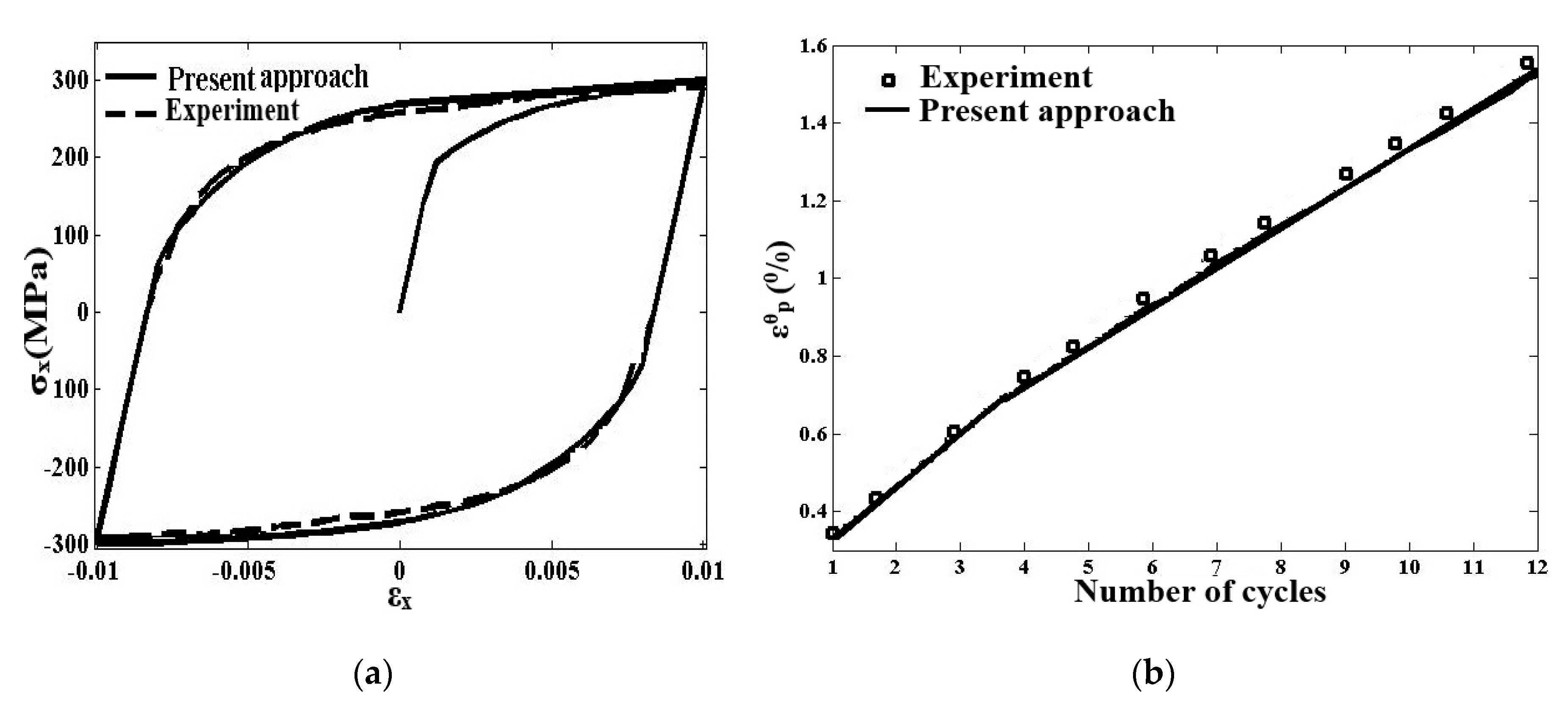
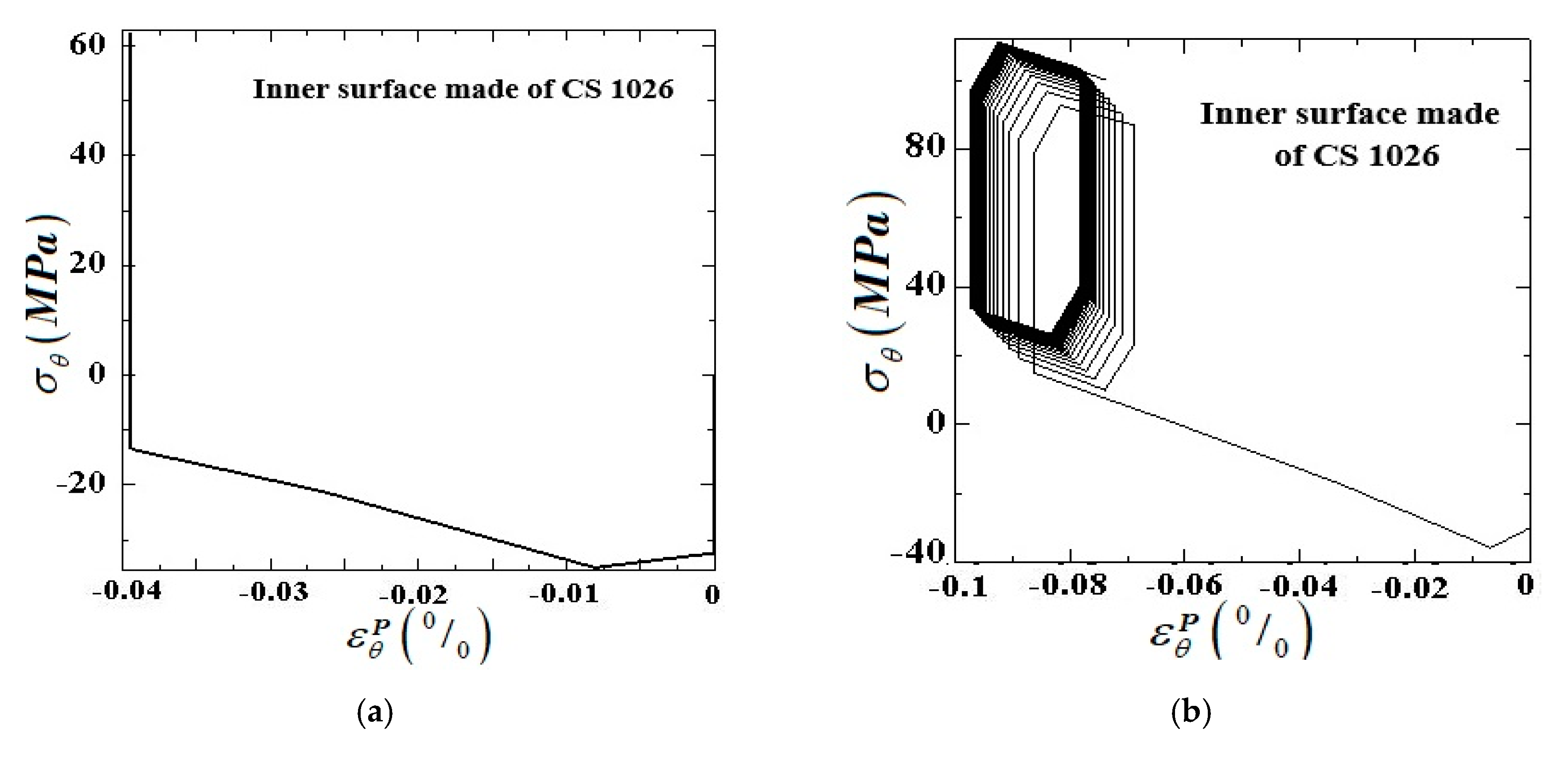
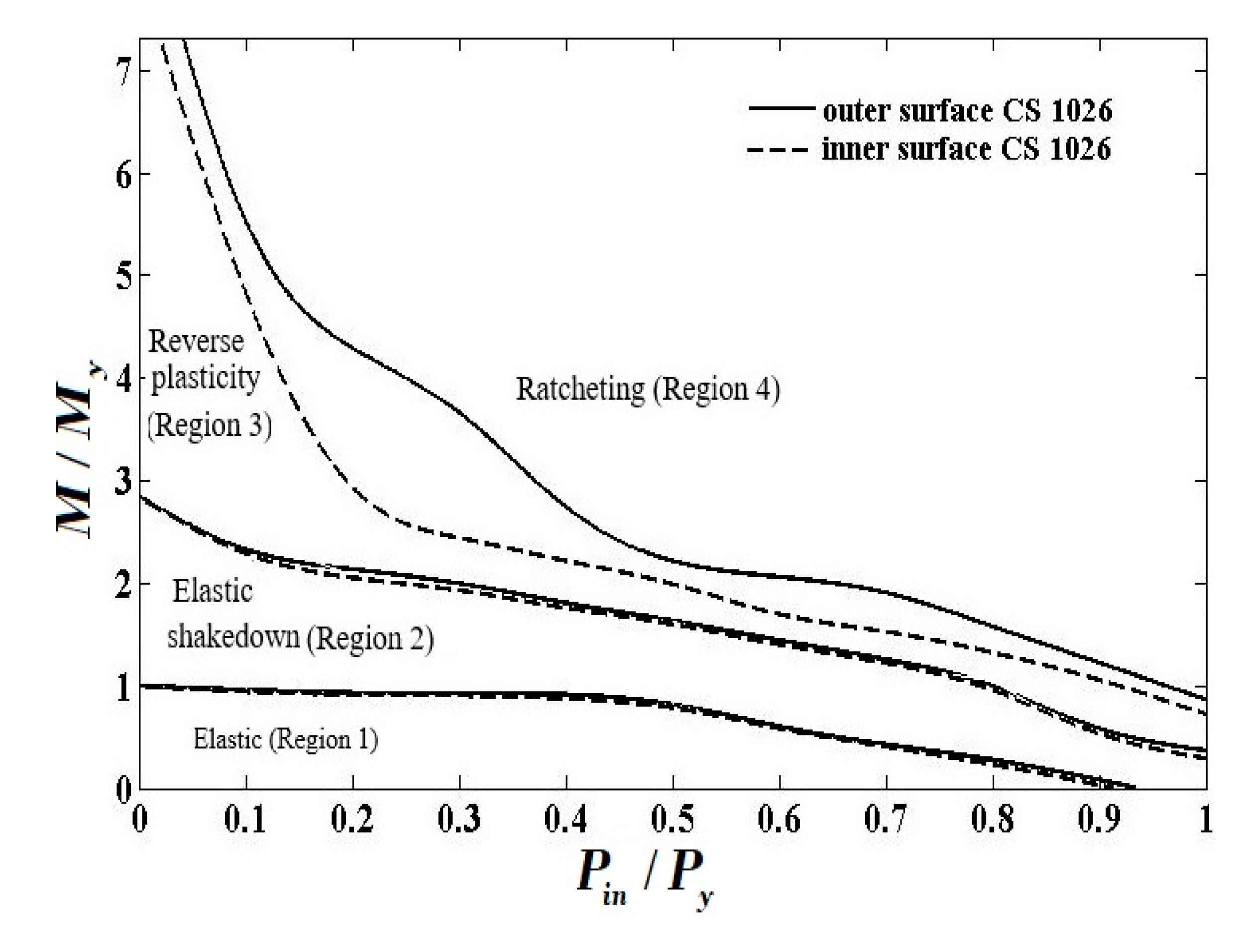
5.1. Internally Pressurized FGM Pipe under Cyclic Bending Moment
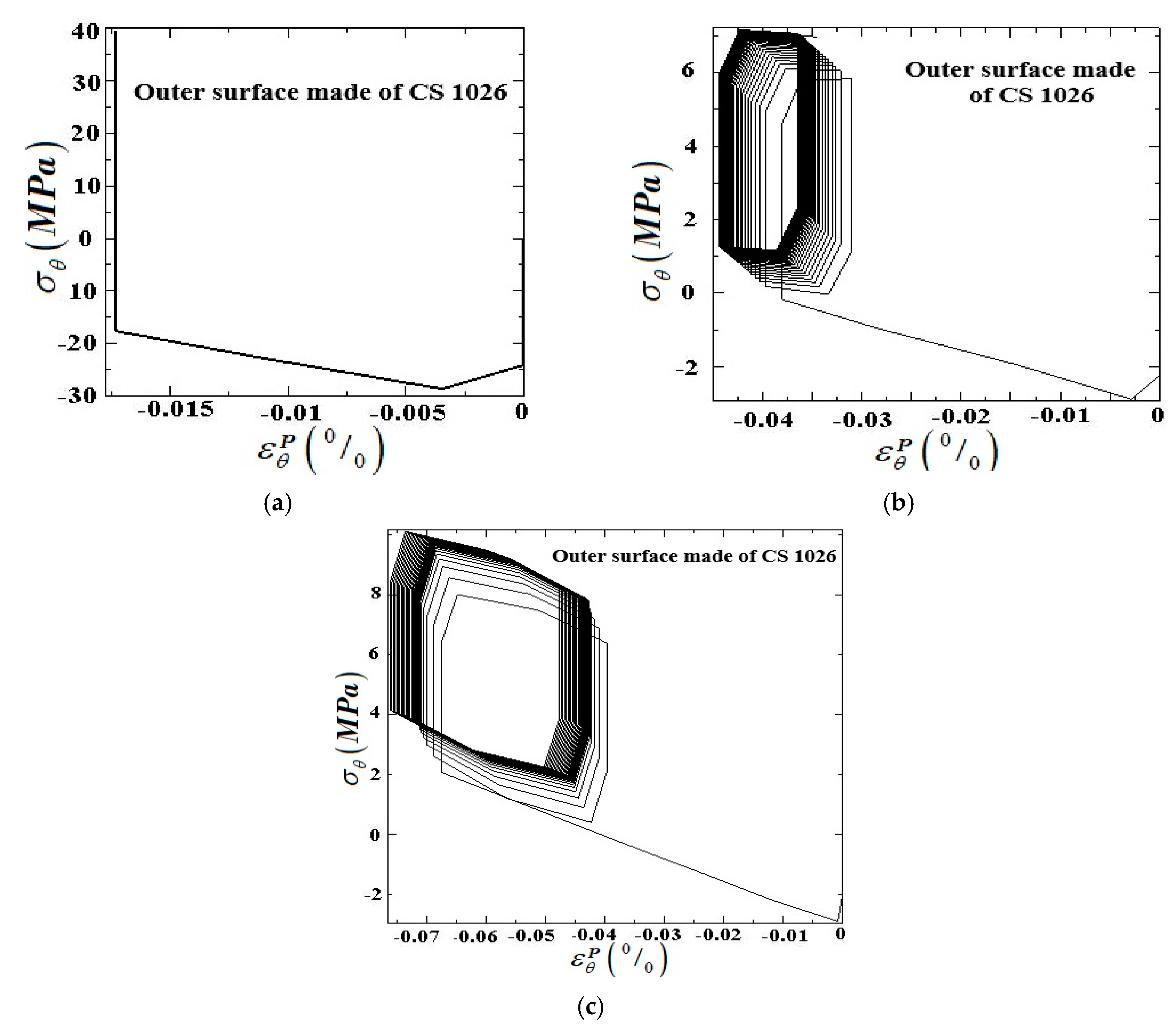
5.2. The Numerical Results of Internally Pressurized FG Pipe under Cyclic through the Thickness Temperature Gradient
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Back stress rate | Poisson’s ratio | ν | |
| Bending moment | M | Plastic multiplier rate | |
| Chaboche material parameters | and | Rates of stress | |
| Coefficient of thermal expansion | Thermal conductivity | ||
| Deviatoric back stress increment | Thermal strain rate | ||
| Deviatoric stress | Total rates of strain, elastic, thermal and plastic strains | , , , | |
| Equivalent plastic strain rate | Trial variables | ||
| Internal pressure | Pin | Yield stress | |
| FGM grading indexes | mi | Yield bending moment | |
| Fourth-order stiffness tensor | Yield pressure, temperature | py, Ty | |
| Outer and inner surfaces temperature | Tout, Tin | Young’s modulus | E0 |
| Inertia moment | Inner and outer radii of FGM pipe | a, b |
References
- Armstrong, P.J.; Frederick, C.O. A Mathematical Representation of the Multiaxial Bauschinger Effect; Central Electricity Generating Board and Berkeley: London, UK, 1966. [Google Scholar]
- Chaboche, J. On some modifications of kinematic hardening to improve the description of ratchetting effects. Int. J. Plast. 1991, 7, 661–678. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.-D. Kinematic hardening rules with critical state of dynamic recovery, part I: Formulation and basic features for ratchetting behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- McDowell, D. Stress state dependence of cyclic ratchetting behavior of two rail steels. Int. J. Plast. 1995, 11, 397–421. [Google Scholar] [CrossRef]
- Jiang, Y.; Sehitoglu, H. Modeling of Cyclic Ratchetting Plasticity, Part I: Development of Constitutive Relations. J. Appl. Mech. 1996, 63, 720–725. [Google Scholar] [CrossRef]
- Abdel-Karim, M.; Ohno, N. Kinematic hardening model suitable for ratchetting with steady-state. Int. J. Plast. 2000, 16, 225–240. [Google Scholar] [CrossRef]
- Chen, X.; Jiao, R.; Kim, K.S. On the Ohno—Wang kinematic hardening rules for multiaxial ratcheting modeling of medium carbon steel. Int. J. Plast. 2005, 21, 161–184. [Google Scholar] [CrossRef]
- Rahman, S.M.; Hassan, T.; Corona, E. Evaluation of cyclic plasticity models in ratcheting simulation of straight pipes under cyclic bending and steady internal pressure. Int. J. Plast. 2008, 24, 1756–1791. [Google Scholar] [CrossRef]
- Wang, L.; Chen, G.; Zhu, J.; Sun, X.; Mei, Y.; Ling, X.; Chen, X. Bending ratcheting behavior of pressurized straight Z2CND18.12N stainless steel pipe. Struct. Eng. Mech. 2014, 52, 1135–1156. [Google Scholar] [CrossRef]
- Rokhgireh, H.; Nayebi, A. Cyclic uniaxial and multiaxial loading with yield surface distortion consideration on prediction of ratcheting. Mech. Mater. 2012, 47, 61–74. [Google Scholar] [CrossRef]
- Duarte, A.P.C.; Silva, B.A.P.; Silvestre, N.; De Brito, J.; Julio, E.; Castro, J. Experimental study on short rubberized concrete-filled steel tubes under cyclic loading. Compos. Struct. 2016, 136, 394–404. [Google Scholar] [CrossRef]
- Ahmadzadeh, G.; Varvani-Farahani, A.; Varvani-Farahani, A. A kinematic hardening rule to investigate the impact of loading path and direction on ratcheting response of steel alloys. Mech. Mater. 2016, 101, 40–49. [Google Scholar] [CrossRef]
- Chen, H.; Ure, J.; Li, T.; Chen, W.; MacKenzie, N. Shakedown and limit analysis of 90° pipe bends under internal pressure, cyclic in-plane bending and cyclic thermal loading. Int. J. Press. Vessel. Pip. 2011, 88, 213–222. [Google Scholar] [CrossRef] [Green Version]
- Mattos, H.D.C.; Peres, J.M.; Melo, M.A.C. Ratcheting behaviour of elasto-plastic thin-walled pipes under internal pressure and subjected to cyclic axial loading. Thin Walled Struct. 2015, 93, 102–111. [Google Scholar] [CrossRef]
- Amirpour, M.; Das, R.; Bickerton, S. An elasto-plastic damage model for functionally graded plates with in-plane material properties variation: Material model and numerical implementation. Compos. Struct. 2017, 163, 331–341. [Google Scholar] [CrossRef]
- Eraslan, A.N.; Akış, T. Plane strain analytical solutions for a functionally graded elastic–plastic pressurized tube. Int. J. Press. Vessel. Pip. 2006, 83, 635–644. [Google Scholar] [CrossRef]
- Mukhtar, F.M.; Al-Gadhib, A.H. Collocation Method for Elastoplastic Analysis of a Pressurized Functionally Graded Tube. Arab. J. Sci. Eng. 2014, 39, 7701–7716. [Google Scholar] [CrossRef]
- Peng, X.; Zheng, H.; Hu, N.; Fang, C. Static and kinematic shakedown analysis of FG plate subjected to constant mechanical load and cyclically varying temperature change. Compos. Struct. 2009, 91, 212–221. [Google Scholar] [CrossRef]
- Farhatnia, F.; Babaei, J.; Foroudastan, R. Thermo-Mechanical Nonlinear Bending Analysis of Functionally Graded Thick Circular Plates Resting on Winkler Foundation Based on Sinusoidal Shear Deformation Theory. Arab. J. Sci. Eng. 2017, 43, 1137–1151. [Google Scholar] [CrossRef]
- Zhang, L.; Xuewu, L. Buckling and vibration analysis of functionally graded magneto-electro-thermo-elastic circular cylindrical shells. Appl. Math. Model. 2013, 37, 2279–2292. [Google Scholar] [CrossRef]
- Loghman, A.; Arani, A.G.; Amir, S.; Vajedi, A. Magnetothermoelastic creep analysis of functionally graded cylinders. Int. J. Press. Vessel. Pip. 2010, 87, 389–395. [Google Scholar] [CrossRef]
- Behravan-Rad, A. Thermo-elastic analysis of functionally graded circular plates resting on a gradient hybrid foundation. Appl. Math. Comput. 2015, 256, 276–298. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Wang, Q.; Zhou, J. Asymptotic analysis of thermoelastic response in functionally graded thin plate subjected to a transient thermal shock. Compos. Struct. 2016, 139, 233–242. [Google Scholar] [CrossRef] [Green Version]
- Sadrabadi, S.A.; Rahimi, G.; Citarella, R.; Karami, J.S.; Sepe, R.; Esposito, R. Analytical solutions for yield onset achievement in FGM thick walled cylindrical tubes undergoing thermomechanical loads. Compos. Part B Eng. 2017, 116, 211–223. [Google Scholar] [CrossRef]
- De Souza Neto, E.A.; Peric, D.; Owen, D.R. Computational Methods for Plasticity: Theory and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Chaboche, J. Time-independent constitutive theories for cyclic plasticity. Int. J. Plast. 1986, 2, 149–188. [Google Scholar] [CrossRef]
- Chaboche, J. Constitutive equations for cyclic plasticity and cyclic viscoplasticity. Int. J. Plast. 1989, 5, 247–302. [Google Scholar] [CrossRef]
- Nayebi, A.; Sadrabadi, S.A. FGM elastoplastic analysis under thermomechanical loading. Int. J. Press. Vessel. Pip. 2013, 111, 12–20. [Google Scholar] [CrossRef]
- Mahbadi, H.; Eslami, M. Cyclic loading of thick vessels based on the Prager and Armstrong–Frederick kinematic hardening models. Int. J. Press. Vessel. Pip. 2006, 83, 409–419. [Google Scholar] [CrossRef]
- Peng, X.; Li, X.-F. Thermoelastic analysis of a cylindrical vessel of functionally graded materials. Int. J. Press. Vessel. Pip. 2010, 87, 203–210. [Google Scholar] [CrossRef]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Hassan, T.; Kyriakides, S. Ratcheting in cyclic plasticity, part I: Uniaxial behavior. Int. J. Plast. 1992, 8, 91–116. [Google Scholar] [CrossRef]
- Mahmoudi, A.-H.; Pezeshki-Najafabadi, S.; Badnava, H. Parameter determination of Chaboche kinematic hardening model using a multi objective Genetic Algorithm. Comput. Mater. Sci. 2011, 50, 1114–1122. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehditabar, A.; Ansari Sadrabadi, S.; Sepe, R.; Armentani, E.; Walker, J.; Citarella, R. Influences of Material Variations of Functionally Graded Pipe on the Bree Diagram. Appl. Sci. 2020, 10, 2936. https://doi.org/10.3390/app10082936
Mehditabar A, Ansari Sadrabadi S, Sepe R, Armentani E, Walker J, Citarella R. Influences of Material Variations of Functionally Graded Pipe on the Bree Diagram. Applied Sciences. 2020; 10(8):2936. https://doi.org/10.3390/app10082936
Chicago/Turabian StyleMehditabar, Aref, Saeid Ansari Sadrabadi, Raffaele Sepe, Enrico Armentani, Jason Walker, and Roberto Citarella. 2020. "Influences of Material Variations of Functionally Graded Pipe on the Bree Diagram" Applied Sciences 10, no. 8: 2936. https://doi.org/10.3390/app10082936
APA StyleMehditabar, A., Ansari Sadrabadi, S., Sepe, R., Armentani, E., Walker, J., & Citarella, R. (2020). Influences of Material Variations of Functionally Graded Pipe on the Bree Diagram. Applied Sciences, 10(8), 2936. https://doi.org/10.3390/app10082936









