1. Introduction
Distributed photovoltaics (PV) currently constitute roughly half of the global PV solar energy installed capacity [
1]. The advantage of distributed energy is the generation of electricity right at the consumer location. Distributed PV is a general term for locally generated electricity in an urban environment, and building-integrated photovoltaics (BIPV) are a subcategory. Rooftops may provide a large amount of empty space that can reduce the use of dedicated land for large PV plant installations [
2]. PV fields are usually designed with multiple collector rows. The row-to-row distance is an important parameter of the PV field design. The distance may be determined by maintenance requirements, by the amount of allowed percent of shading, or by a customary rule.
Rooftop and ground PV systems usually adopt different row-to-row distances, because rooftops are usually limited in area and these systems are therefore densely designed. Photovoltaic collectors in the second and subsequent rows, in a multiple-row deployment of PV fields, are subject to mutual shading, and hence generate reduced electric energy. The amount of shading depends on roof and collector geometric parameters. Shading causes uneven distribution of the incident solar radiation on the PV modules, resulting in the formation of steps across the I–V characteristics. Articles that include analytical expressions for shading on PV collectors in solar fields are mentioned in [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19]. Shadow analysis and its effect on solar PV systems for flat-plate collectors was started early by [
3] and followed by [
6,
7,
8]. References [
10,
11,
12,
13,
14] also calculate the shading losses. With the wide broadening of PV plants across the world, authors recently returned to deal with the shading losses of PV systems [
15,
16,
17,
18,
19].
Mathematical expressions were developed in [
15] for the distance between PV rows on horizontal and sloping grounds, facing north-south and east-west directions. A method to calculate the minimum distance between the rows to avoid the effect of shadings is developed in [
16]. In [
17] the coordinates of the shadow on solar collectors are determined for horizontal, step-like, and inclined solar fields. The calculation of row spacing was developed in [
18] using a vector analysis method for PV systems on horizontal and non-horizontal planes, and then comparing this method with a ray tracing shadow software package. No equations for shadow height and length, nor shadow losses, are explicitly mentioned in this reference. The distance from a building object to the PV array was calculated in [
19], based on the Solo Pro software simulation tool; however, no mathematical expressions for the shading were specified. The references [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18] deal with analytical expressions for the spacing between rows for PV systems deployed on the ground, the exception is reference [
19].
The main objective of the present study is to develop mathematical expressions for distances from objects, like walls and fences encountered on rooftops, to PV collectors deployed on horizontal, sloped, and saw-tooth roofs affecting shading losses. The expressions for distances may be used for predesigns of PV systems, for designing PV systems, and for analyzing systems that are already in operation. The last section studies the optimal inclination and azimuth angles on triangular sloped rooftops. The literature on shading on PV systems concentrates on distances between collector rows deployed on the ground, but it does not address shading and distances from protruding objects encountered on rooftops. The aim of the present study is to deal with this subject.
2. Shading by Obscuring Objects
PV collectors that are deployed on rooftops may be obscured by objects such as adjacent PV collectors, walls, and fences. The shadow cast by these objects decreases the amount of incident radiation on the PV modules. The methodology for calculating the shading is based on references [
3] and [
4].
2.1. Shading by Walls
Figure 1 depicts an inclined collector
with an angle
behind a south facing wall of height
. Based on [
4], Appendix A, and after some mathematical manipulations, the shadow height is given by:
where
Therefore,
where
is the sun elevation angle,
is the sun azimuth, and
is the collector azimuth angle with respect to south, (+) eastward, and (−) westward. We denote:
For , the shadow is eastward and for , the shadow is westward.
The shadow length is
, where
In the case of a saw-tooth roofs (see
Figure 2), the shadow height and length, respectively, are obtained by setting
and replacing
with
in Equations (3) and (6):
An inclined roof may contain modules placed flush along the roof width for which Equations (7) and (8) apply.
In the case of saw-tooth roofs in
Figure 3, the height
in
Figure 2 is replaced with
(see Equations (7) and (8)), obtaining the shadow height and length on the collector
:
The distance from the wall (see
Figure 2) and the beginning of where the deployment starts at the bottom of the first collector, is determined by the shadow height
(see Equation (7) and
Figure 4), at noon (
) on the winter solstice [
20]:
where
is the site latitude and
.
The distance from the wall becomes:
2.2. Numerical Results—Distance from Wall – Figure 4
Figure 5 shows the relationship between the distance
and the inclination angle
of the saw-tooth plane for different wall heights
based on Equation (12).
Shorter distances are needed from walls and fences to the PV collectors for steeper inclined roofs.
2.3. Numerical Results—Distance from Wall – Figure 3
Figure 6 shows the relationship between the distance
and the inclination angle
for a saw- tooth plane for different wall heights,
,
m,
applying Equation (9).
Larger distances are required for higher walls.
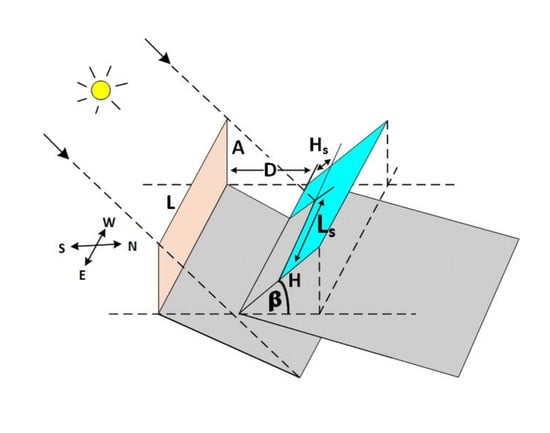
3. Fence Shading
Figure 7 shows an inclined collector with an angle
facing south and a vertical fenced wall
oriented with an azimuth
with respect to E-W direction. The shadow cast by the fence on the collector is developed in [
4], Appendix B, providing expressions for the shadow angle
and the length
. For a vertical wall with an angle
with respect to the E-W collector direction, the shadow angle
and the distance
respectively become:
Therefore, the shaded area is:
To reduce the shading on the collectors, the collectors are shifted away from the fence by a distance
. The shadow length becomes (see Equation (14)),
Numerical Results—Distance From Fence
The distance from the north-south vertical fence to the collector row is determined by the shaded area (see Equation (16)), i.e., by the shading losses.
Figure 8 depicts the annual percentage energy shading losses with the distance
from the fence for several heights
(see
Figure 7), for collector width
, collector length
, latitude
, and inclination angle
.
Figure 8 pertains to a PV system bounded by two north-south vertical fences, one to the east and the second to the west of the collectors. If, for example, one agrees to accept a loss of
in direct beam radiation, one may place the collectors
away from a fence of height
.
The shading losses decrease with an increase in the distance from obscuring objects; however, higher obscuring objects increase the shading losses.
4. Distance between Collector Rows
The shadow height
and the length
are developed in [
4] for horizontal and inclined planes. In this section the distance between the collector rows is determined. The distance is calculated, based on the customary approach, by the shadow length on December 21, at noon [
20]. One may obtain for an inclined plane, see
Figure 9, the following distance:
where
For a horizontal plane .
Numerical Results—Distance between Rows
Figure 10 shows the relationship between the distance
and the inclination angle
of the plane for collector width
and inclination angles
Shorter row-to-row distances between the PV collectors are needed for steeper inclined roofs, and larger collector inclination angles require larger row-to-row distances.
5. Sloped Rooftops
Photovoltaic modules may be installed in multiple rows on sloped rooftops. Rooftops may be oriented at any azimuth.
Figure 11 shows a PV system installed on a rooftop facing west with a slope
and roof width
(one side). The distance between the rows is denoted by
and the row inclination angle is
with respect to the roof plane. To fully utilize the roof width, the modules are rotated with an angle
with respect to the roof length, creating a shift
between the rows, the amount of which is given by:
where
is the width of the PV modules.
Given
and
, one may calculate the optimal angles
and
to obtain the maximum annual incident irradiation per unit area on the PV module, based on the solar radiation data at a given location. The optimization was performed for
,
rows,
, latitude
, and for roof slopes
to
with increments of
for two cases: (a) optimal
and
, and (b) optimal
for
(rows pointing due south for comparison). Mutual shading between rows was taken into account. The results are shown in
Table 1.
The left column indicates the roof slope
, the second column is the optimal inclination angle
of the PV modules with respect to the roof plane, the third column indicates the rotation angle
of the rows relative to the roof length, and the fourth row is the annual global incident irradiation per square meter
. For comparison, the optimization was also carried out for PV rows facing south (
). The fifth column is the optimal inclination angle, the six column is the annual global incident irradiation per unit area, and the last column is the percentage difference between the two cases calculated by
.
Table 1 reveals that almost no gain in incident irradiation is obtained by rotating the rows on sloped roofs for
; however, a gain of about
may be obtained by pointing the rows south-east with an angle
.
Remark: Because of asymmetry in the solar radiation at the location, the optimal azimuth angle of the PV rows on a horizontal plane is positive, i.e., pointing to the south-west by .
6. Discussion
Rooftops are usually limited in area, and therefore the deployment of PV collectors on rooftops is densely designed. In addition, rooftops may contain objects obscuring the PV collectors, such as fences, walls, and other protruding objects. Mutual shading by collectors and shading by obscuring objects on the collectors reduce the direct beam incident radiation, and hence impair the generated energy of the PV system. Therefore, estimating the tolerated shading losses has to be taken into account in the design of the PV systems on rooftops. Consequently, the approach of designing PV systems on rooftops may be different than that for large PV systems on the ground. The present study deals mainly with the distance between the obscuring objects, like walls and fences, and the PV collectors encountered on different roof types affecting shading losses. These expressions may as well be applied to ground PV systems. The expressions for the appropriate distances may also be incorporated into optimization algorithms for optimized PV system designs. Literature on the shading of PV systems concentrate on mutual shading and the distances between the collector rows deployed on the ground, but they do not address shading and the distances from protruding objects encountered on rooftops. The present study focuses mainly on the distances from walls and fences.
7. Conclusions
The deployment of PV collectors on rooftops may encounter shading by adjacent collectors and by obscuring structures on the rooftops, resulting in a reduction in the generated electric energy. Increasing the row distance between the collector rows or increasing the distance from the obscuring structures (walls and fences) to reduce or avoid shading may not be an option because of limited rooftop area. The present study develops mainly analytical expressions for distances between walls and fences and PV collector rows for horizontal, inclined, and saw-tooth roofs. These expressions may also be applied to PV fields on the ground. Based on
Figure 5,
Figure 6,
Figure 8 and
Figure 10, the following conclusions may be drawn: (1) Shorter row-to-row distances between the PV collectors are needed for steeper inclined roofs. (2) Larger collector inclination angles require larger row-to-row distances. (3) Shorter distances are needed from walls and fences to the PV collectors for steeper inclined roofs; however, higher walls and fences require larger distances. (4) Shading losses decrease with an increase in the distance from obscuring objects; however, higher obscuring objects increase the shading losses. On fenced roofs, the shadow on the collectors depends on the fence height and azimuth, on the distance between the collectors and the fence, and on the collectors’ inclination angle. Higher annual incident irradiation may be obtained on sloped triangular roofs for PV modules deployed with angles pointing south-east and south-west, rather than due south.