A Novel Fast Terminal Sliding Mode Tracking Control Methodology for Robot Manipulators

Featured Application

Featured Application: This paper proposed the control synthesis, which can be performed in the trajectory tracking control for various robot manipulators as well as in other mechanical systems, the control of the higher-order system, several uncertain nonlinear systems, or chaotic systems.

Abstract

This paper comes up with a novel Fast Terminal Sliding Mode Control (FTSMC) for robot manipulators. First, to enhance the response, fast convergence time, against uncertainties, and accuracy of the tracking position, the novel Fast Terminal Sliding Mode Manifold (FTSMM) is developed. Then, a Supper-Twisting Control Law (STCL) is applied to combat the unknown nonlinear functions in the control system. By using this technique, the exterior disturbances and uncertain dynamics are compensated more rapidly and more correctly with the smooth control torque. Finally, the proposed controller is launched from the proposed sliding mode manifold and the STCL to provide the desired performance. Consequently, the stabilization and robustness criteria are guaranteed in the designed system with high-performance and limited chattering. The proposed controller runs without a precise dynamic model, even in the presence of uncertain components. The numerical examples are simulated to evaluate the effectiveness of the proposed control method for trajectory tracking control of a 3-Degrees of Freedom (DOF) robotic manipulator.

1. Introduction

Robots are gradually replacing people in the fields of social life, manufacturing, exploring, and performing complex tasks. In order to improve productivity, product quality, system reliability, electronics, measurement, and mechanical systems of robotic systems, more advanced designs are required. Therefore, this leads to an increase in the complexity of the structural and mathematical model when there is an additional occurrence of uncertain components.

Sliding Mode Control (SMC) [1,2,3,4,5,6,7,8,9,10,11,12,13,14] is capable of handling high non-linearity and external noise when it possesses outstanding features such as fast response, and robustness towards the existing uncertainties. However, the chattering problem in the SMC causes oscillations in the control input system leading to vibrations in the mechanical system, heat, and even causing instability. Furthermore, the SMC does not yield convergence in a defined period and provides a slow convergence time when it uses a linear sliding manifold. As a result of the linear sliding manifold, the SMC only ensures asymptotic convergence [15]. Therefore, in case that the pressure of a large control force is unavailable, the asymptotic stability status is less likely to converge fast with high-precision control. Terminal Sliding Mode Control (TSMC) [16,17] is proposed to solve convergence problems in finite time, enhancing the transient performance. However, in several situations, TSMC does not offer the desired performance with initial state variables far from the equilibrium point. Additionally, it has not solved the chattering and slow convergence, as well as creating a new problem that is the singularity phenomenon.

To resolve the issues of SMC and TSMC in a synchronized manner, Nonsingular Fast Terminal Sliding Mode Control (NFTSMC) has been evolved successfully in robotic systems [10,12,18,19,20,21,22,23,24]. It thoroughly solves the problems, including singularity, convergence in finite-time, and slow convergence. Unfortunately, the chattering has not yet been addressed as these controllers still use a robust reaching control law to deal with uncertain components, and also require the upper limit value of unknown components. For chattering, many solutions have been proposed that can be mentioned, such as the Boundary Layer Method (BLM) [6,25,26], the Adaptive Super-Twisting Method (ASTM) [27], the Second-Order SMC (SOSMC) or the Third-Order SMC (TOSMC) [28,29,30,31], the Full-Order SMC (FOSMC) [32,33,34,35], and the Fuzzy-SMC (F-SMC) [5,36,37,38]. For the requirement of the upper limit value of unknown components, many control methods were based on a combination of Neural Networks (NNs), Fuzzy Logic Systems (FLSs), or Adaptive Control Laws (ALCs) with NFTSMC. Although the behavior of unknown components can be well learned by NNs or FLSs. However, it increases the complexity of the control method design because there are more parameters to be adjusted. ACLs are more applicable than the other two methods because they use simple and effective updating rules.

Based on the mentioned analysis, our paper attempts to propose an advanced Fast Terminal Sliding Mode Control (FTSMC) with contributions for robot manipulators: (1) inherits the benefits of the FTSMC and Supper-Twisting Control Law (STCL) in the characteristics of robustness towards the existing uncertainties, finite-time convergence, singularity elimination, estimation capability, and good transient performance; (2) proposes a new Fast Terminal Sliding Mode Manifold (FTSMM) and provides sufficient evidence of finite-time convergence; (3) further improves the precision in the trajectory tracking control; (4) the control torque commands are smooth with less oscillation.

The rest of our paper has the following arrangement. The issue statements are outlined in Section 2. Section 3 presents a synthesis of the designed controller. Continued after Section 3, simulation examples are conducted to assess the influence of the designed controller for a 3-Degrees of Freedom (DOF) robot manipulator in Section 4. Its control performance was then evaluated along with the performance of different control algorithms, including SMC and NFTSMC. Section 5 presents some noteworthy conclusions.

2. Issue Description

Consider the dynamic equation of robot manipulators without the loss of generality:

$$M\left(\theta \right)\ddot{\theta }+Q\left(\theta ,\dot{\theta }\right)\dot{\theta }+G\left(\theta \right)+f_r\left(\dot{\theta }\right)+{\delta }_d\left(t\right)=\tau$$

(1)

where $\theta ={\left[\begin{array}{ccc}{\theta }_1,& \dots ,& {\theta }_n\end{array}\right]}^T\in R^{n\times 1}$, $\dot{\theta }={\left[\begin{array}{ccc}{\dot{\theta }}_1,& \dots ,& {\dot{\theta }}_n\end{array}\right]}^T\in R^{n\times 1}$, and $\ddot{\theta }={\left[\begin{array}{ccc}{\ddot{\theta }}_1,& \dots ,& {\ddot{\theta }}_n\end{array}\right]}^T\in R^{n\times 1}$ declare the position angle vector, the velocity angle vector, and the acceleration angle vector, respectively. $M\left(\theta \right)=\widehat{M}\left(\theta \right)+\Delta M\left(\theta \right)\in R^{n\times n}$ declares the real inertia matrix, $Q\left(\theta ,\dot{\theta }\right)=\widehat{Q}\left(\theta ,\dot{\theta }\right)+\Delta Q\left(\theta ,\dot{\theta }\right)\in R^{n\times n}$ declares the real Coriolis and centrifugal force matrix, and $G\left(\theta \right)=\widehat{G}\left(\theta \right)+\Delta G\left(\theta \right)\in R^{n\times n}$ represents the real gravitational matrix. $\widehat{M}\left(\theta \right)\in R^{n\times n}$ declares the estimated inertia matrix, $\widehat{Q}\left(\theta ,\dot{\theta }\right)\in R^{n\times n}$ represents the estimated Coriolis and centrifugal force matrix, and $\widehat{G}\left(\theta \right)\in R^{n\times n}$ declares the estimated gravitational matrix. $f_r\left(\dot{\theta }\right)\in R^{n\times 1}$ and ${\delta }_d\left(t\right)\in R^{n\times 1}$ declare the friction vector and disturbance vector, respectively. $\Delta M\left(\theta \right)\in R^{n\times n}$ and $\Delta Q\left(\theta ,\dot{\theta }\right)\in R^{n\times n}$ are the errors of the real dynamic model.

Consequently, the real dynamic equation of robot manipulators is achieved as:

$$\widehat{M}\left(\theta \right)\ddot{\theta }+\widehat{Q}\left(\theta ,\dot{\theta }\right)\dot{\theta }+\widehat{G}\left(\theta \right)+\Delta U=\tau$$

(2)

The lumped uncertain component $\Delta u$ in Equation (2) is given as:

$$\Delta u=\Delta M\left(\theta \right)\ddot{\theta }+\Delta Q\left(\theta ,\dot{\theta }\right)\dot{\theta }+\Delta G\left(\theta \right)+f_r+{\delta }_d\left(t\right)$$

(3)

Accordingly, the robotic dynamic in Equation (1) is reorganized as:

$$\ddot{\theta }=\widehat{M}{}^{-1}\left(\theta \right)\tau -{\widehat{M}}^{-1}\left(\theta \right)\left[\widehat{Q}\left(\theta ,\dot{\theta }\right)\dot{\theta }+\widehat{G}\left(\theta \right)\right]- {\widehat{M}}^{-1}\left(\theta \right)\Delta u$$

(4)

Then, the dynamic Equation (4) can be transferred into the following state-space form as:

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=\Pi \left(x,t\right)+\Phi \left(x,t\right)u+D\left(\theta ,\Delta u\right)\end{array}$$

(5)

where, we set $u=\tau$ as the control input and $x={\left[x_1,x_2\right]}^T$ as the state vector in which $x_1,x_2$ correspond to $\theta ,\dot{\theta }\in R^{n\times 1}$. $\Pi \left(x,t\right)=-{\widehat{M}}^{-1}\left(\theta \right)\left[\widehat{Q}\left(\theta ,\dot{\theta }\right)\dot{\theta }+\widehat{G}\left(\theta \right)\right]$, $\Phi \left(x,t\right)={\widehat{M}}^{-1}\left(\theta \right)$, and $D\left(\theta ,\Delta U\right)=- {\widehat{M}}^{-1}\left(\theta \right)\Delta u$.

The control target of the system is to further increase the response speed and accuracy of the trajectory tracking control for robot manipulators, even if the effects of uncertain dynamics and external perturbations are valid. First, to enhance the response, fast convergence time against uncertainties, and accuracy of the tracking position, the novel FTSMM is developed. Then, STCL is applied to combat the unknown nonlinear functions in the control system. By using this combined technique, the exterior disturbances and uncertain dynamics will be compensated more rapidly and more correctly with the smooth control torque. Finally, the designed controller is launched from the proposed sliding mode manifold and the STCL to obtain the control efficiency.

3. Main Results

The position control error and the velocity control error on each joint are, respectively, defined as follows:

$$x_{ei}=x_{1i}-x_{di}$$

(6)

$$x_{dei}=x_{2i}-{\dot{x}}_{di};i=1,\dots n$$

(7)

where $x_d\in R^{n\times 1}$ represents the angle of the expected position.

3.1. The Designed FTSMM

To enhance the response, fast convergence time, and accuracy of the tracking position, the novel FTSMM is developed as follows:

$$s_i=x_{dei}+\frac{2{\gamma }_1}{1+e^{-{\mu }_1\left(\left|x_{ei}\right|-\varphi \right)}}{x}_{ei}+\frac{2{\gamma }_2}{1+e^{{\mu }_2\left(\left|x_{ei}\right|-\varphi \right)}}{\left|x_{ei}\right|}^{\alpha }\mathrm{sgn}\left(x_{ei}\right)$$

(8)

where $s_i$ is the proposed sliding mode manifold, ${\gamma }_1,{\gamma }_2,{\mu }_1,{\mu }_2$ are the positive constants, $0<\alpha <1$, and $\varphi ={\left(\frac{{\gamma }_2}{{\gamma }_1}\right)}^{1/\left(1-\alpha \right)}$.

Based on the SMC, when the control errors operate in the sliding mode, the following constrain is satisfied [1]:

$$\begin{array}{l}{s}_i=0;\\ {\dot{s}}_i=0\end{array}$$

(9)

From condition in Equation (9), it is pointed out that:

$$x_{dei}=-\frac{2{\gamma }_1}{1+e^{-{\mu }_1\left(\left|x_{ei}\right|-\varphi \right)}}{x}_{ei}-\frac{2{\gamma }_2}{1+e^{{\mu }_2\left(\left|x_{ei}\right|-\varphi \right)}}{\left|x_{ei}\right|}^{\alpha }\mathrm{sgn}\left(x_{ei}\right)$$

(10)

Remark 1.

When the control error of  $\left|x_{ei}\right|$ is much greater than $\varphi$, the first component of Equation (10) offers the role of providing a quick convergence rate and the second component has a smaller role. Contrariwise, when the control error of $\left|x_{ei}\right|$ is much smaller than $\varphi$, the second component of Equation (10) offers a greater role than the first one.

The following theorem is launched to guarantee that convergence takes place within the defined time.

Theorem 1.

Let us consider dynamic of Equation (10).  $x_{ei}=0$ is defined as the equilibrium point and the state variables of the dynamic of Equation (10), including $x_{ei}$ and $x_{dei}$ stabilize to zero in finite-time.

Proof. 

To validate the correctness of Theorem 1, the Lyapunov function candidate is proposed as follows:

$$L_1=0.5x_{ei}^2,$$

(11)

and its time derivative is

$$\begin{array}{l}{\dot{L}}_1=x_{ei}{x}_{dei}\\ =-\frac{2{\gamma }_1}{1+e^{-{\mu }_1\left(\left|x_{ei}\right|-\varphi \right)}}{x}_{ei}^2-\frac{2{\gamma }_2}{1+e^{{\mu }_2\left(\left|x_{ei}\right|-\varphi \right)}}{\left|x_{ei}\right|}^{\alpha +1}\mathrm{sgn}\left(x_{ei}\right)\\ <0\end{array}$$

(12)

It is shown that ${\dot{L}}_1<0$, hence, $x_{ei}$ and $x_{dei}$ concentrate on the equilibrium state in finite time.

When $\left|x_{ei}\left(0\right)\right|>\varphi$, the sliding motion consists of two phases:

The first phase: $x_{ei}\left(0\right)\to \left|x_{ei}\right|=\varphi$, the first component of Equation (10) offers the role of providing a quick convergence rate and the second component has a smaller role.

$$\begin{array}{l}{\displaystyle \underset{0}{\overset{t_1}{\int }}dt={\displaystyle \underset{\varphi }{\overset{x_{ei}\left(0\right)}{\int }}\frac{1}{\frac{2{\gamma }_1}{1+e^{-{\mu }_1\left(\left|x_{ei}\right|-\varphi \right)}}{x}_{ei}+\frac{2{\gamma }_2}{1+e^{{\mu }_2\left(\left|x_{ei}\right|-\varphi \right)}}{\left|x_{ei}\right|}^{\alpha }}d\left(\left|x_{ei}\right|\right)}}\\ <{\displaystyle \underset{\varphi }{\overset{x_{ei}\left(0\right)}{\int }}\frac{1}{{\gamma }_1\left|x_{ei}\right|}d\left(\left|x_{ei}\right|\right)}=\frac{\ln \left(\left|x_{ei}\left(0\right)\right|\right)-\ln \left(\varphi \right)}{{\gamma }_1}\end{array}$$

(13)

The second phase: $\left|x_{ei}\right|=\varphi \to x_{ei}=0$, the second component of Equation (10) offers a role greater than the first one.

$$\begin{array}{l}{\displaystyle \underset{0}{\overset{t_2}{\int }}dt}={\displaystyle \underset{0}{\overset{\varphi }{\int }}\frac{1}{\frac{2{\gamma }_1}{1+e^{-{\mu }_1\left(\left|x_{ei}\right|-\varphi \right)}}{x}_{ei}+\frac{2{\gamma }_2}{1+e^{{\mu }_2\left(\left|x_{ei}\right|-\varphi \right)}}{\left|x_{ei}\right|}^{\alpha }}d\left(\left|x_{ei}\right|\right)}\\ <{\displaystyle \underset{0}{\overset{\varphi }{\int }}\frac{1}{{\gamma }_2{\left|x_{ei}\right|}^{\alpha }}d\left(\left|x_{ei}\right|\right)}=\frac{1}{{\gamma }_2\left(1-\alpha \right)}{\left|\varphi \right|}^{1-\alpha }\end{array}$$

(14)

The total time of the sliding motion phase is defined as:

$$T_s=t_1+t_2<\frac{\ln \left(\left|x_{ei}\left(0\right)\right|\right)-\ln \left(\varphi \right)}{{\gamma }_1}+\frac{1}{{\gamma }_2\left(1-\alpha \right)}{\left|\varphi \right|}^{1-\alpha }$$

(15)

The state variable of the dynamic in Equation (10) converges to sliding manifold ($s\left(0\right)\to 0$) within the defined time $T_r$, which was pointed out in [8]. Therefore, the total time for stability on the sliding manifold is computed as:

$$T\le T_r+T_s$$

(16)

3.2. The Designed Control Methodology

Let us take the time derivative of Equation (8):

$$\begin{array}{l}\dot{s}={\dot{x}}_{de}+\frac{2{\gamma }_1}{1+e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}}{x}_{de}+\frac{2{\gamma }_1{\mu }_1{x}_{de}\mathrm{sgn}\left(x_e\right)e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}}{{\left(1+e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}\right)}^2}{x}_e\\ +\frac{2{\gamma }_2\alpha }{1+e^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}}{\left|x_e\right|}^{\alpha -1}{x}_{de}-\frac{2{\gamma }_2{\mu }_2{x}_{de}{e}^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}}{{\left(1+e^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}\right)}^2}{\left|x_e\right|}^{\alpha }\end{array}$$

(17)

With ${\dot{x}}_{de}={\ddot{x}}_2-{\ddot{x}}_d$, the time derivation of Equation (17) gets along with the system in Equation (5) as follows:

$$\begin{array}{l}\dot{s}=\Pi \left(x,t\right)+\Phi \left(x,t\right)u+D\left(\theta ,\Delta u\right)-{\ddot{x}}_d+\frac{2{\gamma }_1}{1+e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}}{x}_{de}+\frac{2{\gamma }_1{\mu }_1{x}_{de}\mathrm{sgn}\left(x_e\right)e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}}{{\left(1+e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}\right)}^2}{x}_e\\ +\frac{2{\gamma }_2\alpha }{1+e^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}}{\left|x_e\right|}^{\alpha -1}{x}_{de}-\frac{2{\gamma }_2{\mu }_2{x}_{de}{e}^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}}{{\left(1+e^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}\right)}^2}{\left|x_e\right|}^{\alpha }\end{array}$$

(18)

In order to facilitate controller design, there is the following assumption:

Assumption 1.

The lumped uncertain terms, $D\left(\theta ,\Delta u\right)=\left[D_1\left(\theta ,\Delta u\right),\dots ,D_n\left(\theta ,\Delta u\right)\right]$, need to satisfy the following standard condition:

$$\Vert D_i\left(\theta ,\Delta u\right)\Vert \le K_i{\left|s_i\right|}^{\frac{1}{2}};i=1,\dots ,n$$

(19)

where$K_i>0$.

In order to achieve the stabilization target of the robot system, the following control action is proposed:

$$u=-{\Phi }^{-1}\left(x,t\right)\left(u_{eq}+u_r\right).$$

(20)

Here, it should be noted that the $u_{eq}$ is designed as:

$$\begin{array}{l}{u}_{eq}=\Pi \left(x,t\right)-{\ddot{x}}_d+\frac{2{\gamma }_1}{1+e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}}{x}_{de}+\frac{2{\gamma }_1{\mu }_1{x}_{de}\mathrm{sgn}\left(x_e\right)e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}}{{\left(1+e^{-{\mu }_1\left(\left|x_e\right|-\varphi \right)}\right)}^2}{x}_e\\ +\frac{2{\gamma }_2\alpha }{1+e^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}}{\left|x_e\right|}^{\alpha -1}{x}_{de}-\frac{2{\gamma }_2{\mu }_2{x}_{de}{e}^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}}{{\left(1+e^{{\mu }_2\left(\left|x_e\right|-\varphi \right)}\right)}^2}{\left|x_e\right|}^{\alpha }\end{array}$$

(21)

and $u_r$ is designed as:

$$\begin{array}{l}{u}_r={\Sigma }_1{\left|s\right|}^{\frac{1}{2}}\mathrm{sgn}\left(s\right)+\eta \\ \dot{\eta }=-{\Sigma }_2\mathrm{sgn}\left(s\right)\end{array}$$

(22)

where ${\Sigma }_1=diag\left({\Sigma }_{11},\dots ,{\Sigma }_{1n}\right)$ and ${\Sigma }_2=diag\left({\Sigma }_{21},\dots ,{\Sigma }_{2n}\right)$. ${\Sigma }_{1i}$ and ${\Sigma }_{2i}$ are assigned to satisfy the following relationship [8]:

$$\{\begin{array}{l}{\Sigma }_{1i}>2K_i\\ {\Sigma }_{2i}>{\Sigma }_{1i}\frac{5K_i{\Sigma }_{1i}+4K_i^2}{2\left({\Sigma }_{1i}-2K_i\right)}\end{array};i=1,2,\dots ,n$$

(23)

Based on those above statements, the following theorems are written to prove the stability problem.

Theorem 2.

Consider the robot system in Equation (1). If the designed torque actions are proposed for system in Equation (1) as Equations (20)–(22), then $x_{ei}$ and $x_{dei}$ stabilize to zero in finite time. That means that robot system in Equation (1) runs in a stable mode.

Proof. 

Applying control torque in Equation (20)–(22) to Equation (19) gains:

$$\{\begin{array}{l}\dot{s}=D\left(\theta ,\Delta u\right)-{\Sigma }_1{\left|s\right|}^{1/2}\mathrm{sgn}\left(s\right)-\eta \\ \dot{\eta }=-{\Sigma }_2\mathrm{sgn}\left(s\right)\end{array}$$

(24)

Based on the assumption in Equation (19), and the selection condition of the sliding gains in Equation (23), it can be verified that the sliding manifold and its time derivative will converge to zero in finite time. Now, considering one of the elements in Equation (24) as follows:

$$\{\begin{array}{l}{\dot{s}}_i=D_i\left(\theta ,\Delta u\right)-{\Sigma }_{1i}{\left|s_i\right|}^{1/2}\mathrm{sgn}\left(s_i\right)-{\eta }_i\\ {\dot{\eta }}_i=-{\Sigma }_{2i}\mathrm{sgn}\left(s_i\right)\end{array}$$

(25)

The following Lyapunov function is defined for the system in Equation (25):

$$L_2={\sigma }^T\Gamma \sigma$$

(26)

Here, $\sigma ={\left[s_i^{1/2},{\lambda }_i\right]}^T$, $\Gamma =\frac{1}{2}\left[\begin{array}{cc}\begin{array}{c}4{\Sigma }_{2i}+{\Sigma }_{1i}^2\\ -{\Sigma }_{1i}\end{array}& \begin{array}{c}-{\Sigma }_{1i}\\ 2\end{array}\end{array}\right]$. If ${\Sigma }_{2i}>0$, so, according to Rayleigh’s inequality:

$${\lambda }_{\min }(\Gamma ){\Vert \sigma \Vert }^2\le L_2\le {\lambda }_{\max }(\Gamma ){\Vert \sigma \Vert }^2$$

(27)

with ${\Vert \sigma \Vert }^2=\left|s_i\right|+{\eta }_i^2$.

The time derivation of Equation (26) is:

$${\dot{L}}_2=-\frac{1}{{\left|s_i\right|}^{1/2}}{\sigma }^T\Phi \sigma +\frac{1}{{\left|s_i\right|}^{1/2}}\left[D_i\left(\theta ,\Delta u\right),0\right]\Gamma \sigma$$

(28)

with $\Phi =\frac{{\Sigma }_{1i}}{2}\left[\begin{array}{cc}\begin{array}{c}2{\Sigma }_{2i}+{\Sigma }_{1i}^2\\ -{\Sigma }_{1i}\end{array}& \begin{array}{c}-{\Sigma }_{1i}\\ 1\end{array}\end{array}\right]$.

Based on the assumption in Equation (19), we can gain:

$$\begin{array}{l}{\dot{L}}_2\le -\frac{1}{{\left|s_i\right|}^{1/2}}{\sigma }^T\tilde{\Phi }\sigma \\ \le -\frac{1}{{\left|s_i\right|}^{1/2}}{\lambda }_{\min }\left(\tilde{\Phi }\right){\Vert \sigma \Vert }^2\end{array}$$

(29)

where $\tilde{\Phi }=\frac{{\Sigma }_{1i}}{2}\left[\begin{array}{cc}\begin{array}{c}2{\Sigma }_{2i}+{\Sigma }_{1i}^2-\left(4{\Sigma }_{2i}+{\Sigma }_{1i}\right)K_i\\ -\left({\Sigma }_{1i}+2K_i\right)\end{array}& \begin{array}{c}-\left({\Sigma }_{1i}+2K_i\right)\\ 1\end{array}\end{array}\right]$.

$\tilde{\Phi }$ is selected to be greater than zero. Consequently, ${\dot{L}}_2<0$.

Applying the Equation (27) gives:

$${\left|s_i\right|}^{1/2}\le \Vert \sigma \Vert$$

(30)

It follows that:

$${\dot{L}}_2\le \upsilon L_2^{1/2}$$

(31)

with $\upsilon =\frac{{\lambda }_{\min }\left(\tilde{\Phi }\right)}{{\lambda }_{\max }^{1/2}(\Gamma )}$.

According to [8], $s_i$ and ${\dot{s}}_i$ are equal to zero in finite-time ($t_{ri}=2L_2^{1/2}\left(t=0\right)/\upsilon$). Therefore, $s$ and $\dot{s}$ equal to zero in finite time ($T_r={\max }_{i=1,\dots ,n}\left\{t_{ri}\right\}$) and both $x_{ei}$ and $x_{dei}$ also stabilize to equilibrium in finite time ($T\le T_r+T_s$) under the control action in Equation (20)–(22).

4. Numerical Simulation Studies

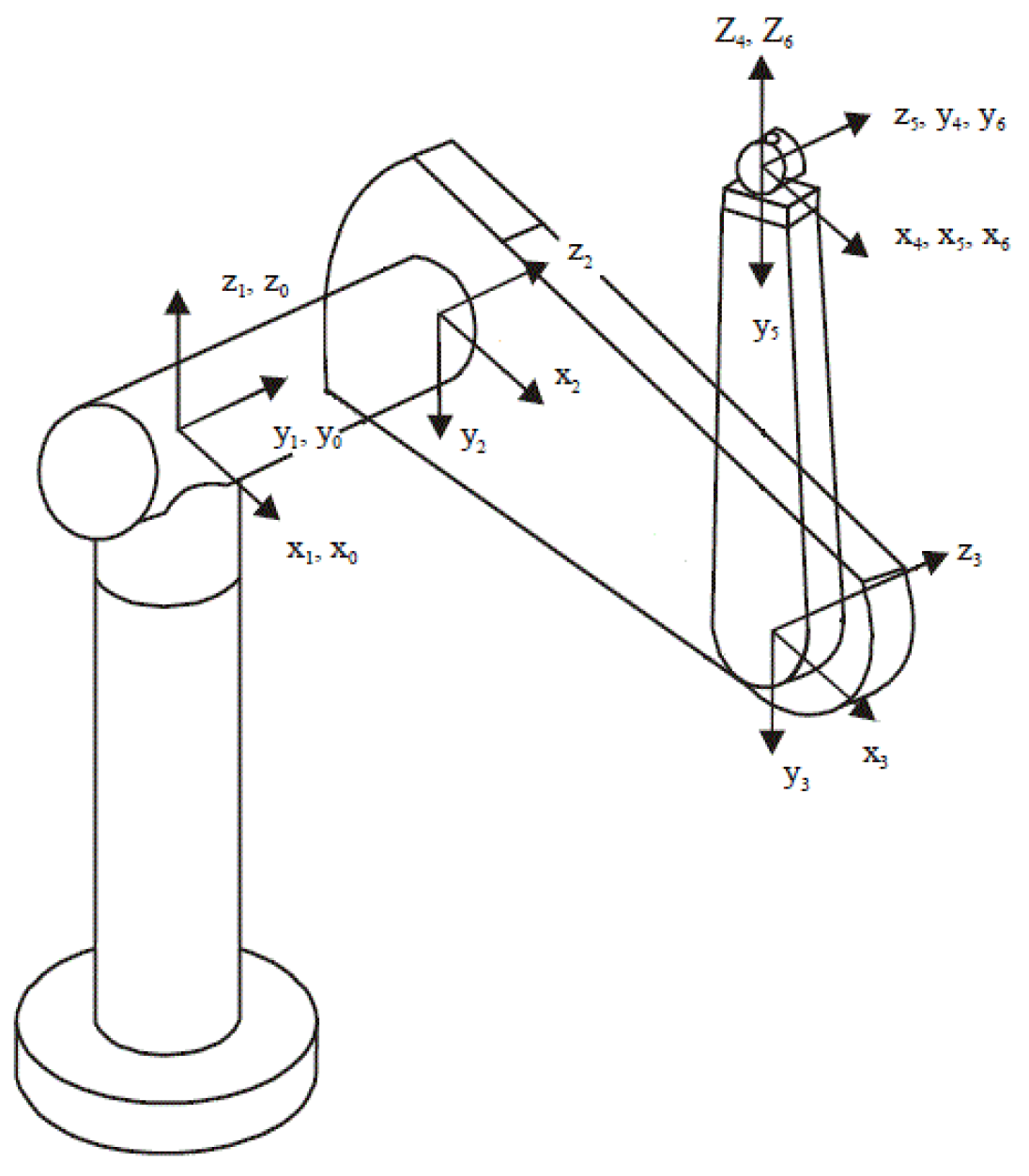
In this numerical example, a 3-DOF PUMA560 robot manipulator (with the first three joints and the last three joints blocked) is adopted. The MATLAB/SIMULINK software (2019a MATLAB Version of The MathWorks, Inc. 3 Apple Hill Drive Natick, MA 01760 USA) was used for all computation, the sampling time was set to 10⁻³ s, and the solver ode3 was used. The kinematic description for the robot system is displayed in Figure 1. The design parameters and dynamic models of the robot system are referenced from the document [39]. There are many essential parameters of a robot that need to be presented. Therefore, to present briefly, the design parameters and dynamic models of the robot system are reported in [39].

To explore the potential of our designed approach, the robot is controlled to follow the designated trajectory configuration at first. Later, its control performance is then evaluated and compared with the performance of different control algorithms, including SMC and NFTSMC. These control methods for comparison are briefly explained as follows:

The normal SMC [14] has the following control torque:

$$u= -\Phi {\left(x,t\right)}^{-1}\left[\Pi \left(x,t\right)+c(x_2-{\dot{x}}_d)-{\ddot{x}}_d+\left(\Sigma +\xi \right)\mathrm{sgn}(s)\right]$$

(32)

where $s=x_{de}+c{x}_e$ is the linear sliding manifold, $c$ is a positive constant.

Further, the NFTSMC [40] has the following control torque:

$$u\left(t\right)= -\Phi {\left(x,t\right)}^{-1}\left[\Pi \left(x,t\right)+\varpi \frac{\mathrm{q}}{l}{x}_{de}^{2-l/q}-{\ddot{x}}_d+\left(\Sigma +\xi \right)\mathrm{sgn}(s)\right]$$

(33)

where $s=x_e+{\varpi }^{-1}{x}_{de}^{l/q}$ is a nonlinear sliding manifold.

The designed parameters of three control methodologies are given in

Table 1. Parameter values for three different control methodologies.

Control Schemes	Parameters	Values
SMC	$\begin{array}{l}c\\ \xi ,\Sigma \end{array}$	$\begin{array}{l}2\\ 0.01,20\end{array}$
NFTSMC	$\begin{array}{l}l,q,\varpi \\ \xi ,\Sigma \end{array}$	$\begin{array}{l}5,3,2\\ 0.01,20\end{array}$
Proposed FTSMC	$\begin{array}{l}{\gamma }_1,{\gamma }_2,{\mu }_1,{\mu }_2\\ \varphi ,\alpha ,{\Sigma }_1,{\Sigma }_2\end{array}$	$\begin{array}{l}1,1,1.2,1.4\\ 1,0.6,40,50\end{array}$

.

The designated trajectory configuration for position tracking when the robot manipulator operates:

$${\theta }_d=\{\begin{array}{l}{\theta }_{d1}=0.6+\cos \left(\frac{t}{6\pi }\right)-1\\ {\theta }_{d2}=-0.6\sin \left(\frac{t}{6\pi }+0.5\pi \right)-1\\ {\theta }_{d3}=0.6+\sin \left(0.2\frac{t}{\pi }+0.5\pi \right)-1\end{array}$$

(34)

Friction and disturbance models are hypothesized to analyze the strong capability of the designed FTSMC. It is not amenable to accurately calculate these friction and disturbance terms; therefore, the physical values of frictions and disturbances are not measured. Therefore, the following friction forces and disturbances were modeled, respectively:

$$f_r\left(\dot{\theta }\right)=\{\begin{array}{l}{f}_{r1}=2.3{\dot{\theta }}_1+2.14\mathrm{sgn}\left(3{\dot{\theta }}_1\right)\\ f_{r2}=4.5{\dot{\theta }}_2+2.35\mathrm{sgn}\left(2{\dot{\theta }}_2\right)\\ f_{r3}=1.7{\dot{\theta }}_3+1.24\mathrm{sgn}\left(2{\dot{\theta }}_3\right)\end{array}$$

(35)

$${\delta }_d\left(t\right)=\{\begin{array}{l}{\delta }_{d1}\left(t\right)=7.6\sin \left({\dot{\theta }}_1\right)\\ {\delta }_{d2}\left(t\right)=6.6\sin \left({\dot{\theta }}_2\right)\\ {\delta }_{d3}\left(t\right)=4.23\sin \left({\dot{\theta }}_3\right)\end{array}$$

(36)

To clearly present the results within the simulation period and to facilitate easier comparison, the averaged tracking error i:

$$E_j=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N\left({\Vert e_j\left(k\right)\Vert }^2\right)}};j=1,2,3$$

(37)

where $Z$ is the number of simulation steps.

To demonstrate the superiority of the designed controller, the average control error is calculated over two different simulation periods (10 s and 30 s).

The averaged tracking errors are reported in

Table 2. The averaged tracking errors under the input of the controllers.

Error Control System	${\mathit{E}}_1\left(10\mathbf{s}\right)$	${\mathit{E}}_2\left(10\mathbf{s}\right)$	${\mathit{E}}_3\left(10\mathbf{s}\right)$	${\mathit{E}}_1\left(30\mathbf{s}\right)$	${\mathit{E}}_2\left(30\mathbf{s}\right)$	${\mathit{E}}_3\left(30\mathbf{s}\right)$
SMC	0.03102	0.01946	0.03113	0.01077	0.00671	0.01082
NFTSMC	0.02322	0.01284	0.02208	0.00774	0.00428	0.00737
Proposed Controller	0.01939	0.01037	0.01793	0.00646	0.00345	0.00597

.

The designated trajectory configuration and real trajectory under three control methods at the first three joints are displayed in Figure 2. It can be seen from Figure 2 that all three controllers appear to have a similar tracking control performance. However, they have different convergence times in the following order: the designed controller has the fastest convergence time among all three control methods, and NFTSMC has faster convergence time than the normal SMC.

Figure 3 and Figure 4 show the position control errors and the velocity control errors, respectively. It can be seen from Figure 3 and Table 2, the position control errors of the designed control scheme are relatively small compared to those of the other control methods, in the order of ${10}^{-7}rad$. The position control errors of the NFTSMC are in the order of ${10}^{-6}rad$. SMC provides the largest position control errors of the three control methods, in the order of ${10}^{-4}rad$.

From Figure 4, it is seen that the designed control method also has the smallest velocity control errors among all the three control methods.

The control torque for all three control manners, including SMC, NFTSMC, and the designed FTSMC, are displayed in Figure 5. It can be recognized from Figure 5, SMC and NFTSMC have discontinuous control torque because of using the high-frequency control law. Meanwhile, the designed system has smooth control torque with a significant elimination of the chattering phenomena. To achieve this goal, the suggested controller applies STCL to substitute the high-frequency control law in removing chattering behavior.

Response time of the sliding mode manifolds, including SMC, NFTSMC, and designed FTSMC, are shown in Figure 6.

5. Conclusions

This paper focuses on designing a novel FTSMC for robot manipulators. In the first step, the novel FTSMM is developed to enhance response capability, fast convergence time, uncertainties opposition, and especially, improve the accuracy of the tracking position. To alleviate unknown nonlinear parameters in the control system, STCL is then applied. Thanks to this valuable technique, exterior disturbances and nonlinear elements are compensated more rapidly and more correctly with the smooth control torque. Finally, combining STCL and our proposed sliding mode manifold, under the flexible controller, the stability and robustness of the control system are guaranteed with high-performance and limited chattering. To evaluate the efficiency, a simulation example is performed for the trajectory tracking control of a 3-DOF robotic manipulator.

From theoretical evidence, simulation results, and a comparison with SMC and NFTSMC, our proposed controller has some of the following contributions: (1) the proposed controller provides finite-time convergence and faster transient performance without singularity problem in controlling; (2) the proposed controller inherits the benefits of the FTSMC and CRCL in the characteristics of robustness towards the existing uncertainties; (3) a new FTSMM was proposed, and evidence of finite-time convergence was sufficiently proved; (4) the precision of the proposed controller was further improved in the trajectory tracking control; (5) the proposed controller shows the smoother control torque commands with lesser oscillation.