Analysis on Tunnel Field-Effect Transistor with Asymmetric Spacer
Abstract
1. Introduction
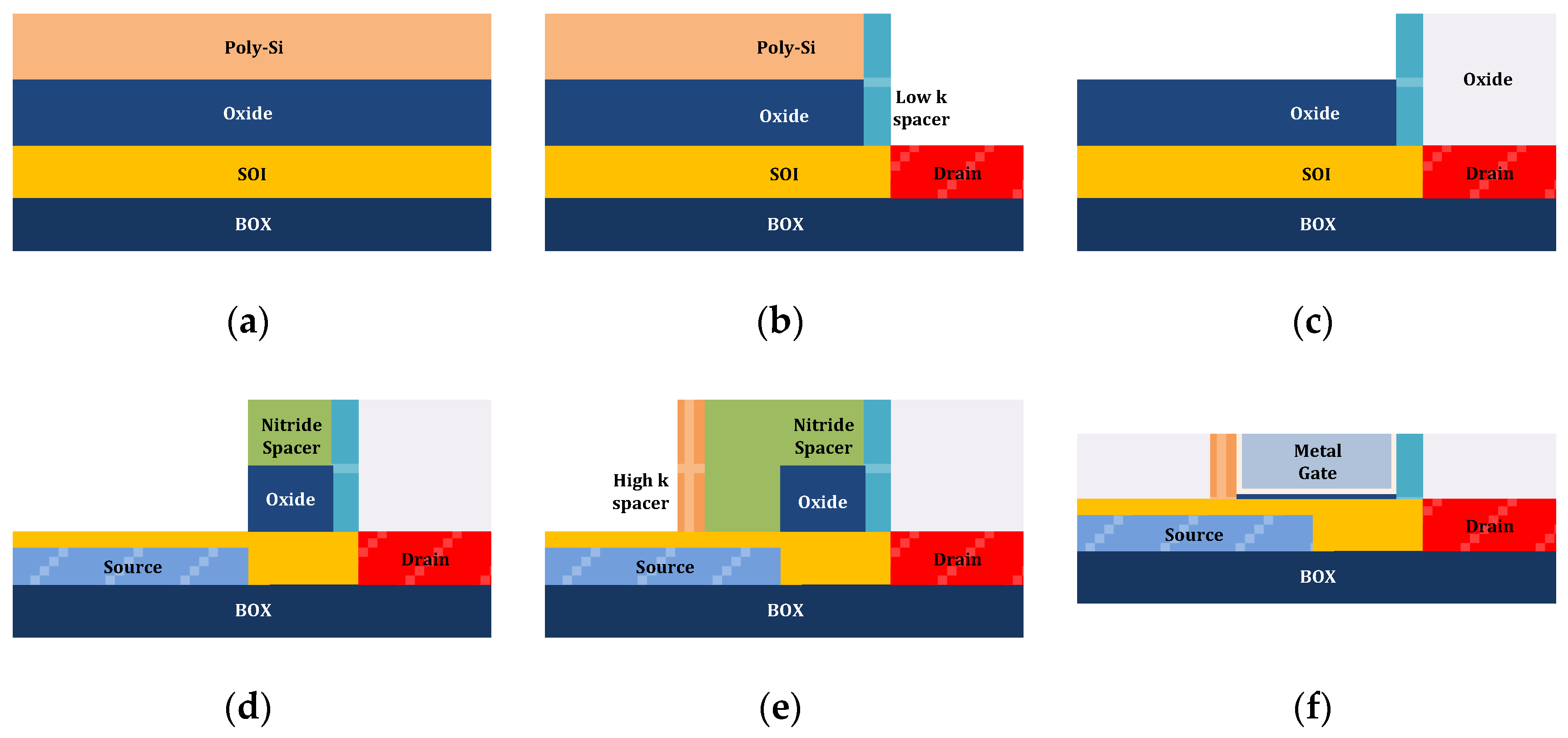
2. Device Structure and Parameters
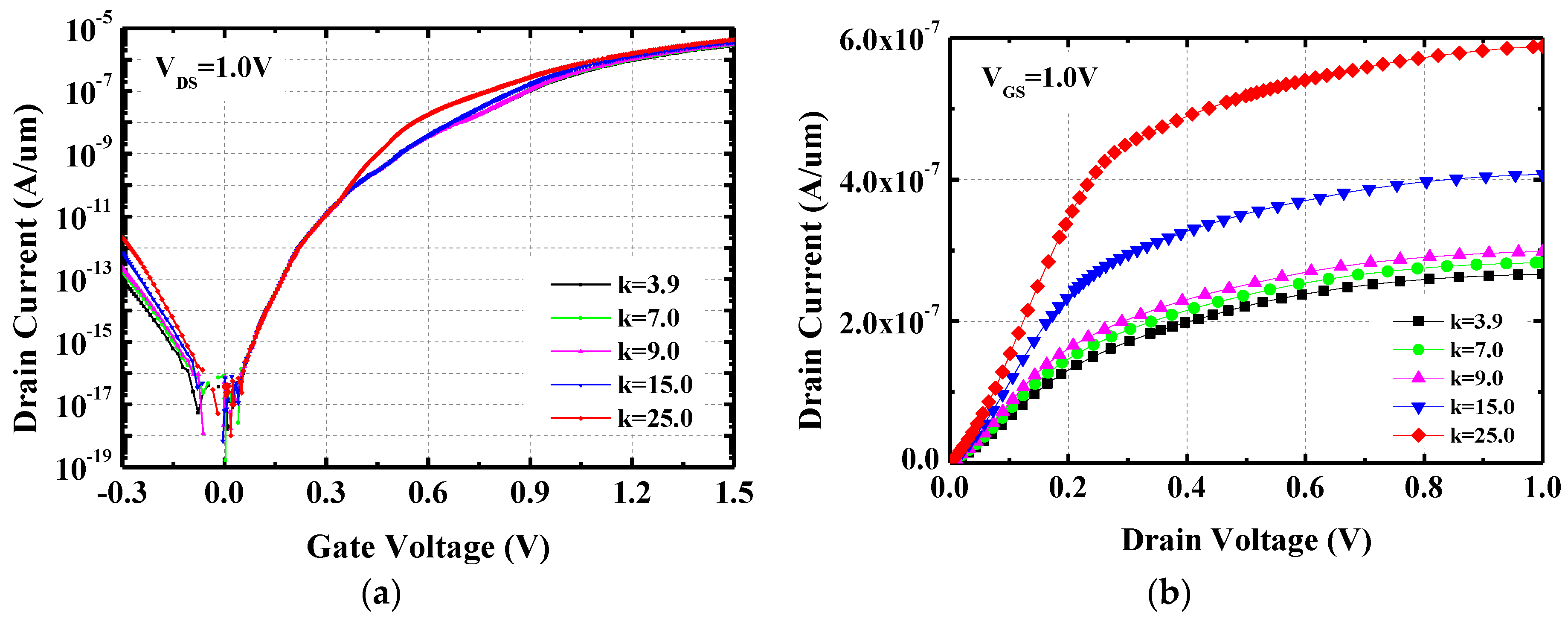
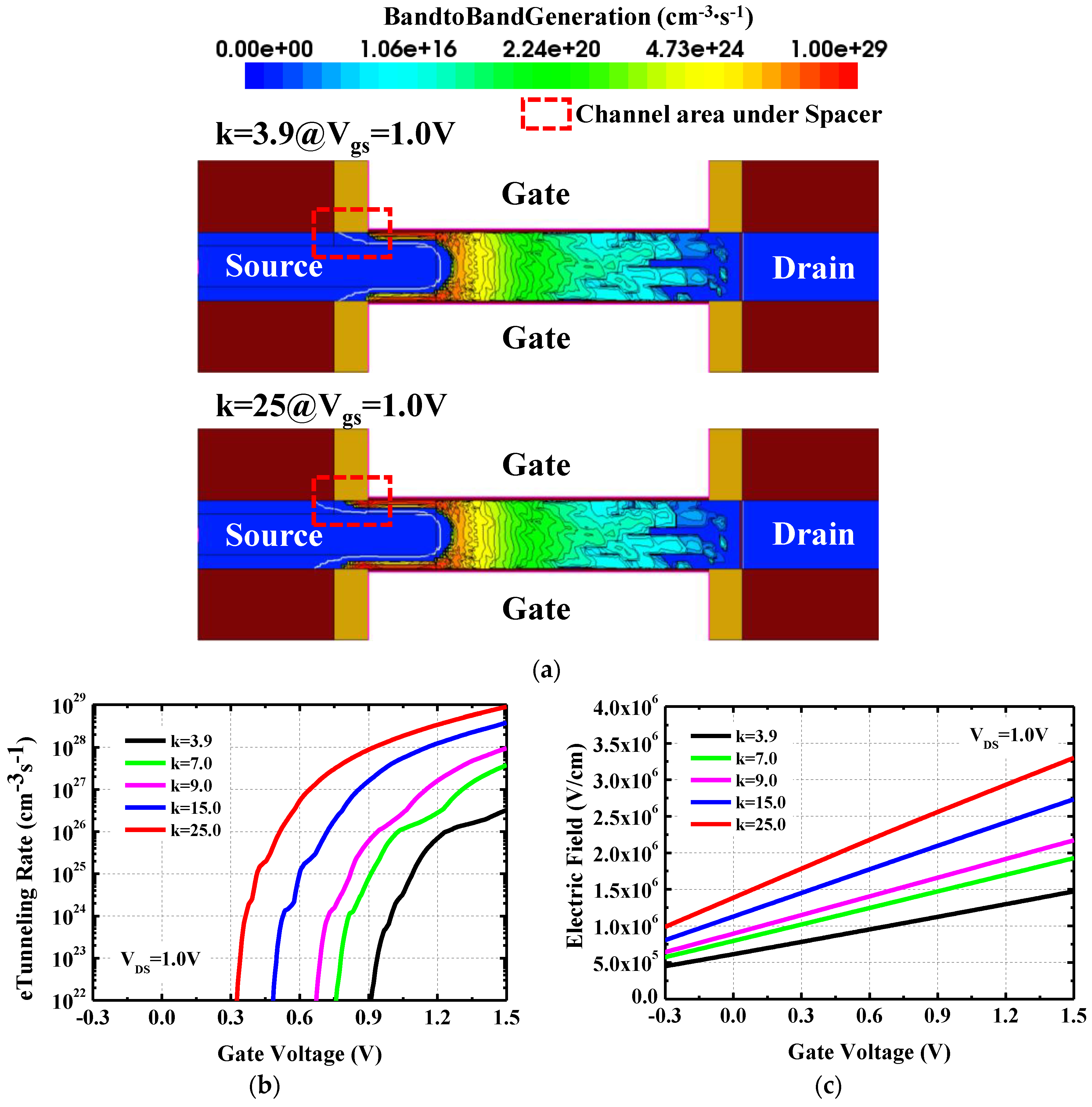
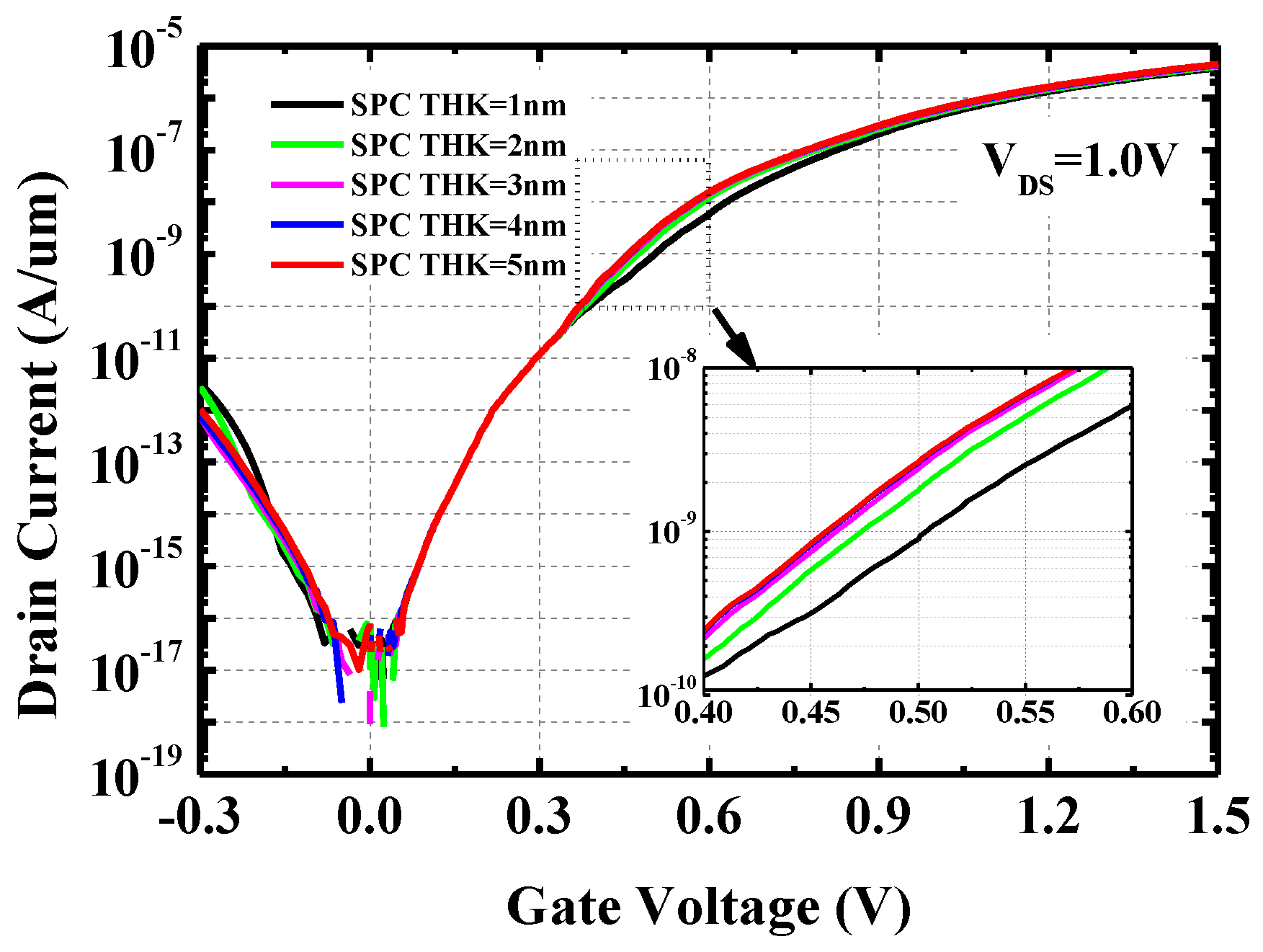
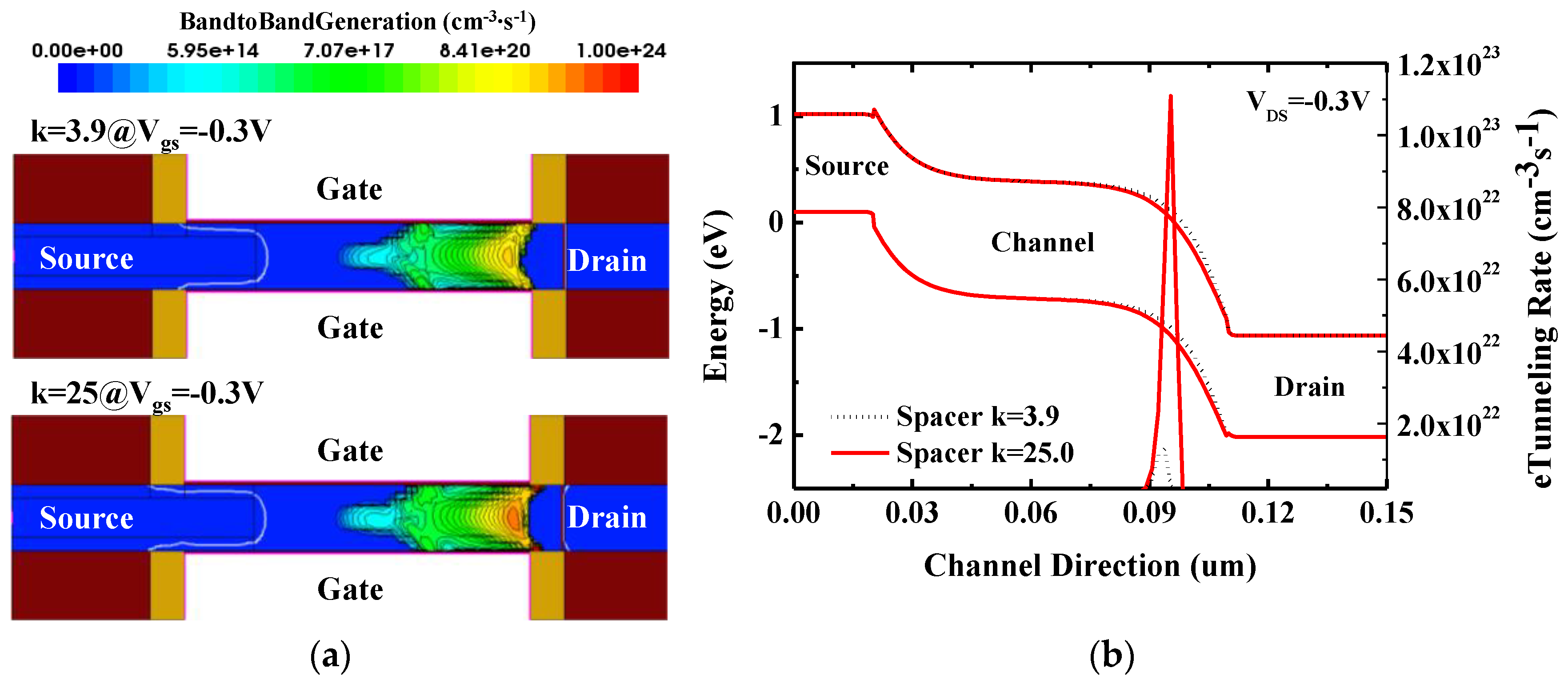
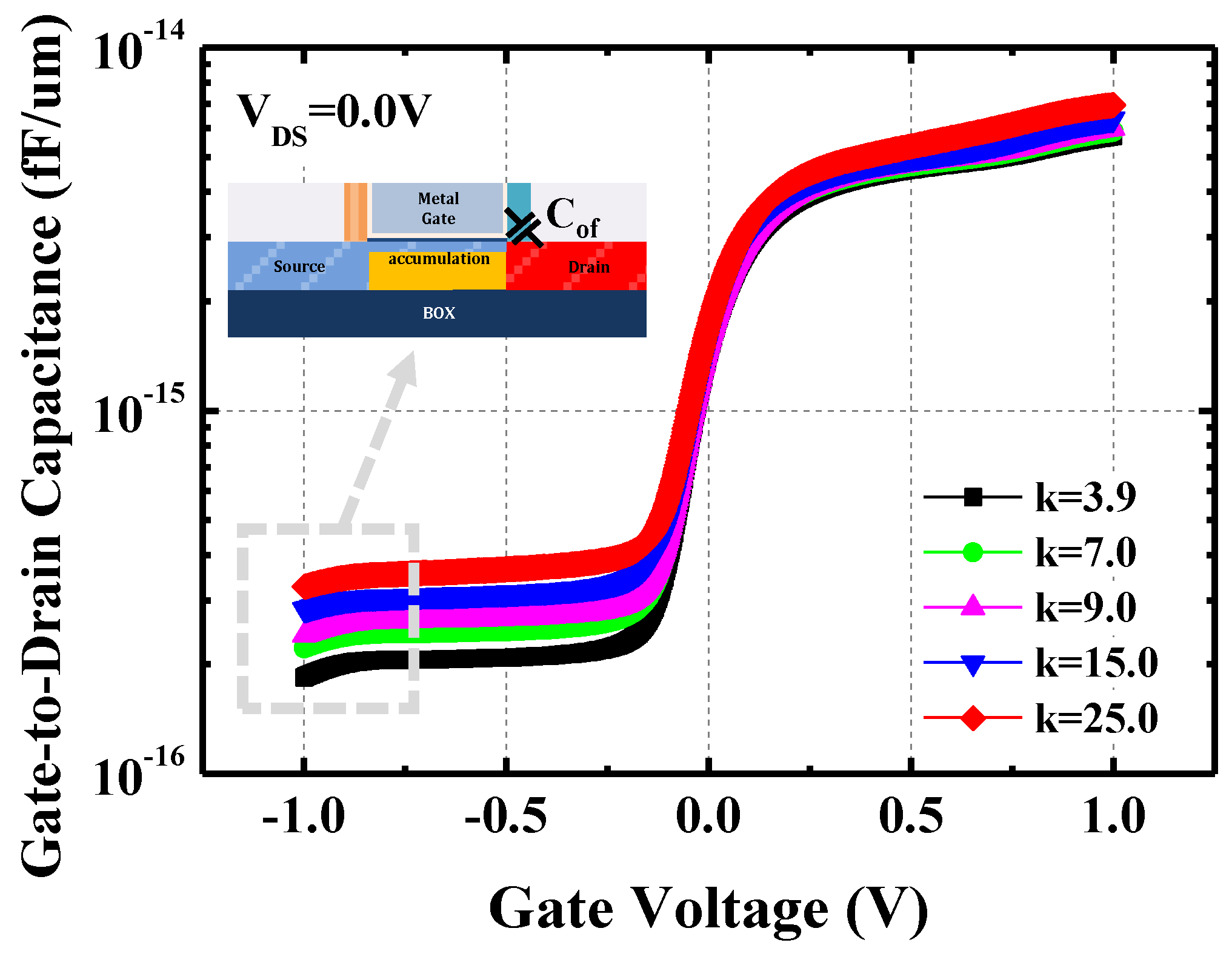
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- White, M.; Chen, Y. Scaled CMOS technology reliability users guide. JPL Publ. 2008, 3, 8. [Google Scholar]
- Razavieh, A.; Zeitzoff, P.; Nowak, E.J. Challenges and Limitations of CMOS Scaling for FinFET and beyond Architectures. IEEE Trans. Nanotechnol. 2019, 18, 999–1004. [Google Scholar] [CrossRef]
- Choi, W.Y.; Park, B.G.; Lee, J.D.; Liu, T.J.K. Tunneling field-effect transistors (TFETs) with subthreshold swing (SS) less than 60 mV/dec. IEEE Electron Device Lett. 2007, 28, 743–745. [Google Scholar] [CrossRef]
- Boucart, K.; Ionescu, A.M. Double-gate tunnel FET with high-κ gate dielectric. IEEE Trans. Electron Devices 2007, 54, 1725–1733. [Google Scholar] [CrossRef]
- Kwon, D.; Cheema, S.; Lin, Y.K.; Liao, Y.H.; Chatterjee, K.; Tan, A.J.; Hu, C.; Salahuddin, S. Near Threshold Capacitance Matching in a Negative Capacitance FET with 1 nm Effective Oxide Thickness Gate Stack. IEEE Electron Device Lett. 2020, 41, 179–182. [Google Scholar] [CrossRef]
- Salahuddin, S.; Datta, S. Use of negative capacitance to provide voltage amplification for low power nanoscale devices. Nano Lett. 2008, 8, 405–410. [Google Scholar] [CrossRef] [PubMed]
- Seabaugh, A.C.; Zhang, Q. Low-voltage tunnel transistors for beyond CMOS logic. Proc. IEEE 2010, 98, 2095–2110. [Google Scholar] [CrossRef]
- Khan, A.I.; Yeung, C.W.; Hu, C.; Salahuddin, S. Ferroelectric negative capacitance MOSFET: Capacitance tuning & antiferroelectric operation. In Proceedings of the Technical Digest - International Electron Devices Meeting, IEDM, Washington, DC, USA, 5–7 December 2011. [Google Scholar]
- Ionescu, A.M.; Riel, H. Tunnel field-effect transistors as energy-efficient electronic switches. Nature 2011, 479, 329–337. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, B.; Akram, M.W. Junctionless tunnel field effect transistor. IEEE Electron Device Lett. 2013, 34, 584–586. [Google Scholar] [CrossRef]
- Kim, H.W.; Kim, J.P.; Kim, S.W.; Sun, M.C.; Kim, G.; Kim, J.H.; Park, E.; Kim, H.; Park, B.G. Schottky barrier tunnel field-effect transistor using spacer technique. J. Semicond. Technol. Sci. 2014, 14, 572–578. [Google Scholar] [CrossRef]
- Avci, U.E.; Morris, D.H.; Young, I.A. Tunnel field-effect transistors: Prospects and challenges. IEEE J. Electron Devices Soc. 2015, 3, 88–95. [Google Scholar] [CrossRef]
- Pahwa, G.; Dutta, T.; Agarwal, A.; Chauhan, Y.S. Physical Insights on Negative Capacitance Transistors in Nonhysteresis and Hysteresis Regimes: MFMIS Versus MFIS Structures. IEEE Trans. Electron Devices 2018, 65, 867–873. [Google Scholar] [CrossRef]
- Bhuwalka, K.K.; Schulze, J.; Eisele, I. Performance enhancement of vertical tunnel field-effect transistor with SiGe in the δp+ layer. Jpn. J. Appl. Phys. Part 1 Regul. Pap. Short Notes Rev. Pap. 2004, 43, 4073–4078. [Google Scholar] [CrossRef]
- Zhang, Q.; Fang, T.; Xing, H.; Seabaugh, A.; Jena, D. Graphene nanoribbon tunnel transistors. IEEE Electron Device Lett. 2008, 29, 1344–1346. [Google Scholar] [CrossRef]
- Jhaveri, R.; Nagavarapu, V.; Woo, J.C.S. Effect of pocket doping and annealing schemes on the source-pocket tunnel field-effect Transistor. IEEE Trans. Electron Devices 2011, 58, 80–86. [Google Scholar] [CrossRef]
- Kim, S.H.; Agarwal, S.; Jacobson, Z.A.; Matheu, P.; Hu, C.; Liu, T.J.K. Tunnel field effect transistor with raised germanium source. IEEE Electron Device Lett. 2010, 31, 1107–1109. [Google Scholar] [CrossRef]
- Choi, W.Y.; Lee, W. Hetero-gate-dielectric tunneling field-effect transistors. IEEE Trans. Electron Devices 2010, 57, 2317–2319. [Google Scholar] [CrossRef]
- Li, R.; Lu, Y.; Zhou, G.; Liu, Q.; Chae, S.D.; Vasen, T.; Hwang, W.S.; Zhang, Q.; Fay, P.; Kosel, T.; et al. AlGaSb/InAs tunnel field-effect transistor with on-current of 78 μaμm at 0.5 v. IEEE Electron Device Lett. 2012, 33, 363–365. [Google Scholar] [CrossRef]
- Abdi, D.B.; Kumar, M.J. In-built N+ Pocket p-n-p-n tunnel field-effect transistor. IEEE Electron Device Lett. 2014, 35, 1170–1172. [Google Scholar] [CrossRef]
- Kim, S.W.; Kim, J.H.; Liu, T.J.K.; Choi, W.Y.; Park, B.G. Demonstration of L-Shaped Tunnel Field-Effect Transistors. IEEE Trans. Electron Devices 2016, 63, 1774–1778. [Google Scholar] [CrossRef]
- Anghel, C.; Hraziia, A.; Gupta, A.; Amara, A.; Vladimirescu, A. 30-nm tunnel FET with improved performance and reduced ambipolar current. IEEE Trans. Electron Devices 2011, 58, 1649–1654. [Google Scholar] [CrossRef]
- Anghel, C.; Chilagani, P.; Amara, A.; Vladimirescu, A. Tunnel field effect transistor with increased on current, low-k spacer and high-k dielectric. Appl. Phys. Lett. 2010, 96, 122104. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Mallik, A. Impact of a spacer dielectric and a gate Overlap/Underlap on the Device Performance of a Tunnel Field-Effect Transistor. IEEE Trans. Electron Devices 2011, 58, 677–683. [Google Scholar] [CrossRef]
- Synopsys, Inc. Sentaurus Device User Guide; Synopsys, Inc.: Mountain View, CA, USA, 2009; Available online: http://www.sentaurus.dsod.pl/manuals/data/sdevice_ug.pdf (accessed on 26 November 2019).
- Kwon, D.W.; Kim, H.W.; Kim, J.H.; Park, E.; Lee, J.; Kim, W.; Kim, S.; Lee, J.H.; Park, B.G. Effects of Localized Body Doping on Switching Characteristics of Tunnel FET Inverters with Vertical Structures. IEEE Trans. Electron Devices 2017, 64, 1799–1805. [Google Scholar] [CrossRef]
- Kane, E.O. Theory of tunneling. J. Appl. Phys. 1961, 32, 83–91. [Google Scholar] [CrossRef]
- Robertson, J. High dielectric constant oxides. EPJ Appl. Phys. 2004, 28, 265–291. [Google Scholar] [CrossRef]
- Mookerjea, S.; Krishnan, R.; Datta, S.; Narayanan, V. On enhanced miller capacitance effect in interband tunnel transistors. IEEE Electron Device Lett. 2009, 30, 1102–1104. [Google Scholar] [CrossRef]
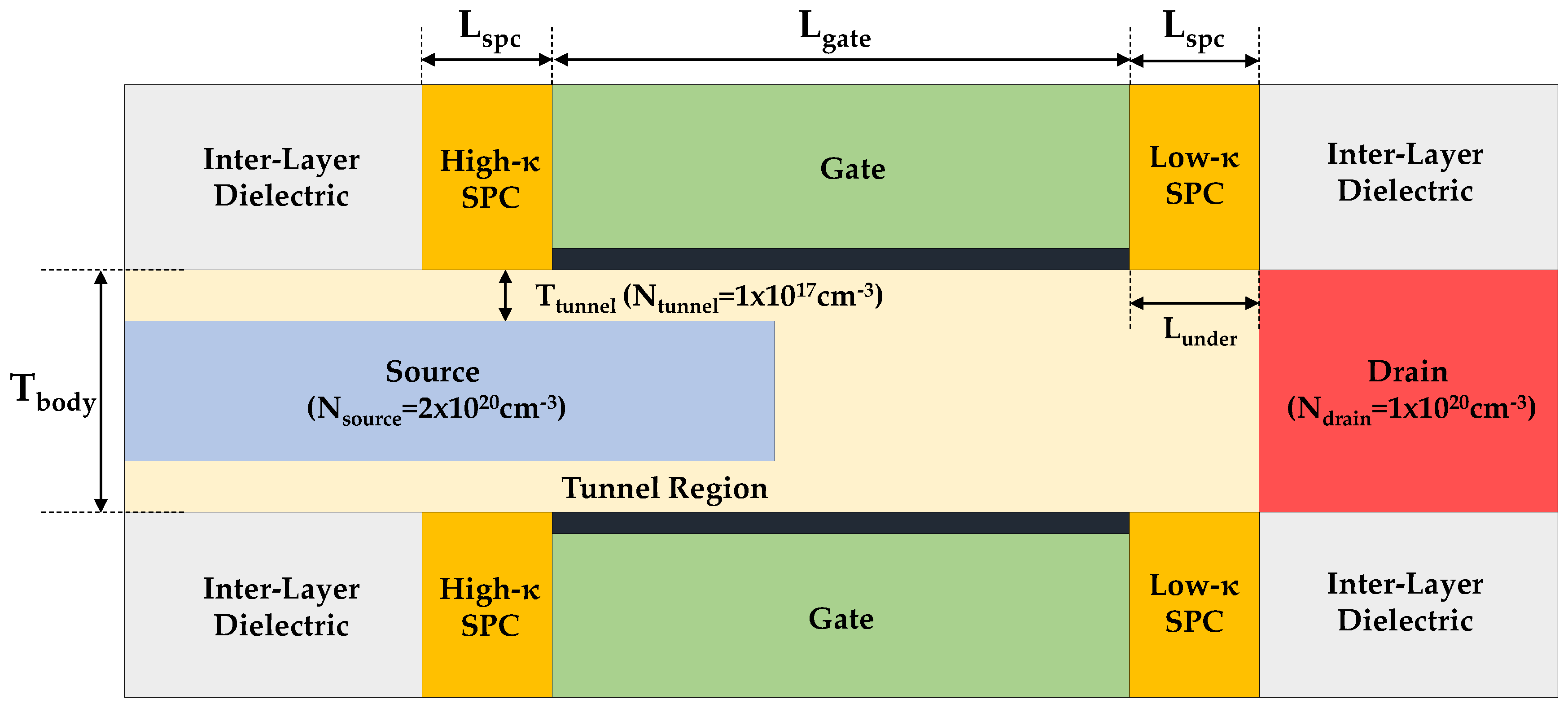

| Definition | Parameter | Value |
|---|---|---|
| Gate Length | Lgate | 100 nm |
| Equivalent Oxide Thickness | Tox | 1 nm |
| Spacer Thickness | Lspc | 0–10 nm |
| Spacer Dielectric Constant | κspc | 3.9–25 |
| Body Thickness | Tbody | 20 nm |
| Tunnel Region Thickness | Ttunnel | 4 nm |
| Drain Underlap Length | Lunder | 10 nm |
| Tunnel Region Doping | Ntunnel | 1 × 1017 cm−3 |
| Source Doping | Nsource | 2 × 1020 cm−3 |
| Drain Doping | Ndrain | 1 × 1020 cm−3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.W.; Kwon, D. Analysis on Tunnel Field-Effect Transistor with Asymmetric Spacer. Appl. Sci. 2020, 10, 3054. https://doi.org/10.3390/app10093054
Kim HW, Kwon D. Analysis on Tunnel Field-Effect Transistor with Asymmetric Spacer. Applied Sciences. 2020; 10(9):3054. https://doi.org/10.3390/app10093054
Chicago/Turabian StyleKim, Hyun Woo, and Daewoong Kwon. 2020. "Analysis on Tunnel Field-Effect Transistor with Asymmetric Spacer" Applied Sciences 10, no. 9: 3054. https://doi.org/10.3390/app10093054
APA StyleKim, H. W., & Kwon, D. (2020). Analysis on Tunnel Field-Effect Transistor with Asymmetric Spacer. Applied Sciences, 10(9), 3054. https://doi.org/10.3390/app10093054




