Coordinated LVRT Control for a Permanent Magnet Synchronous Generator Wind Turbine with Energy Storage System
Abstract
:1. Introduction
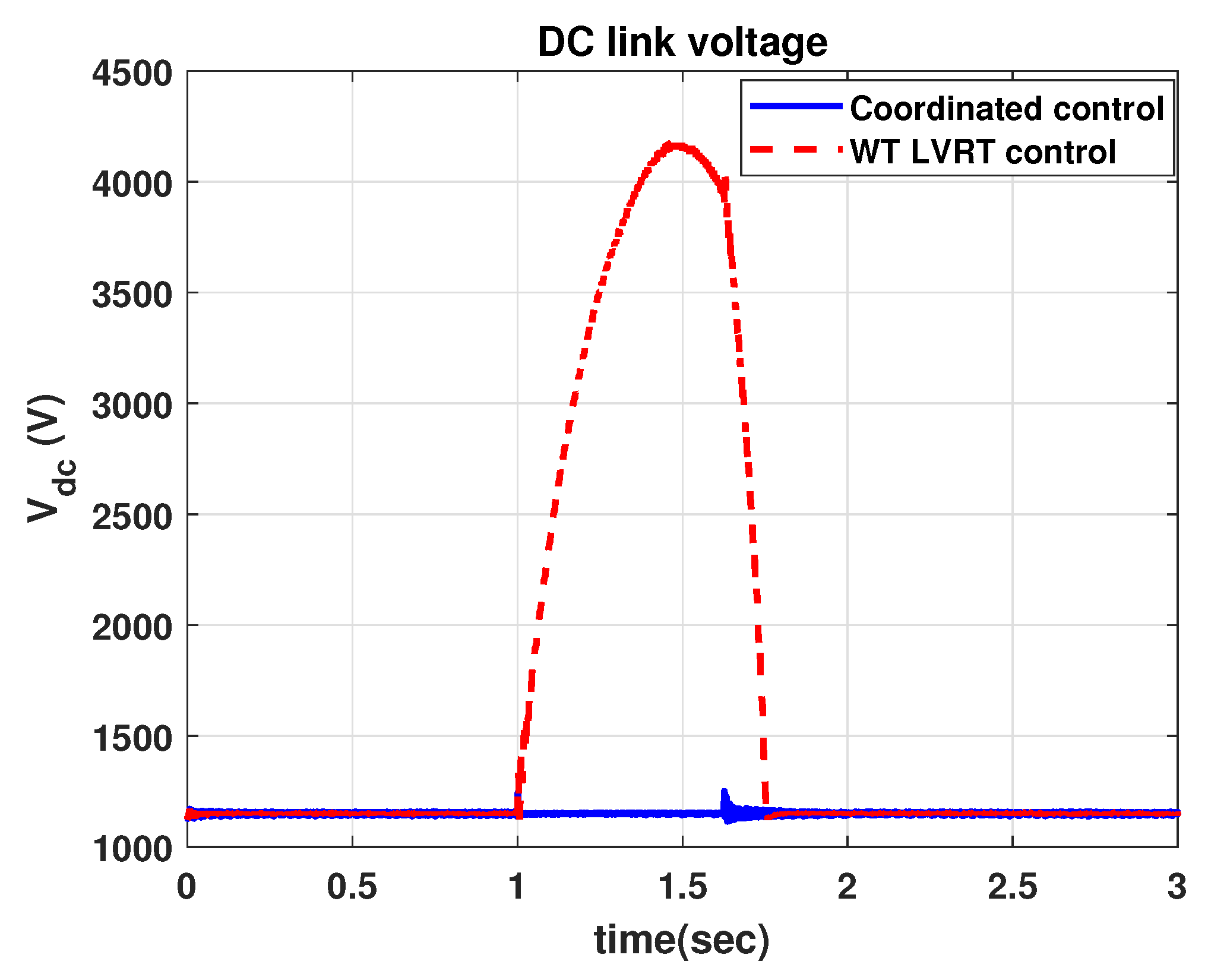
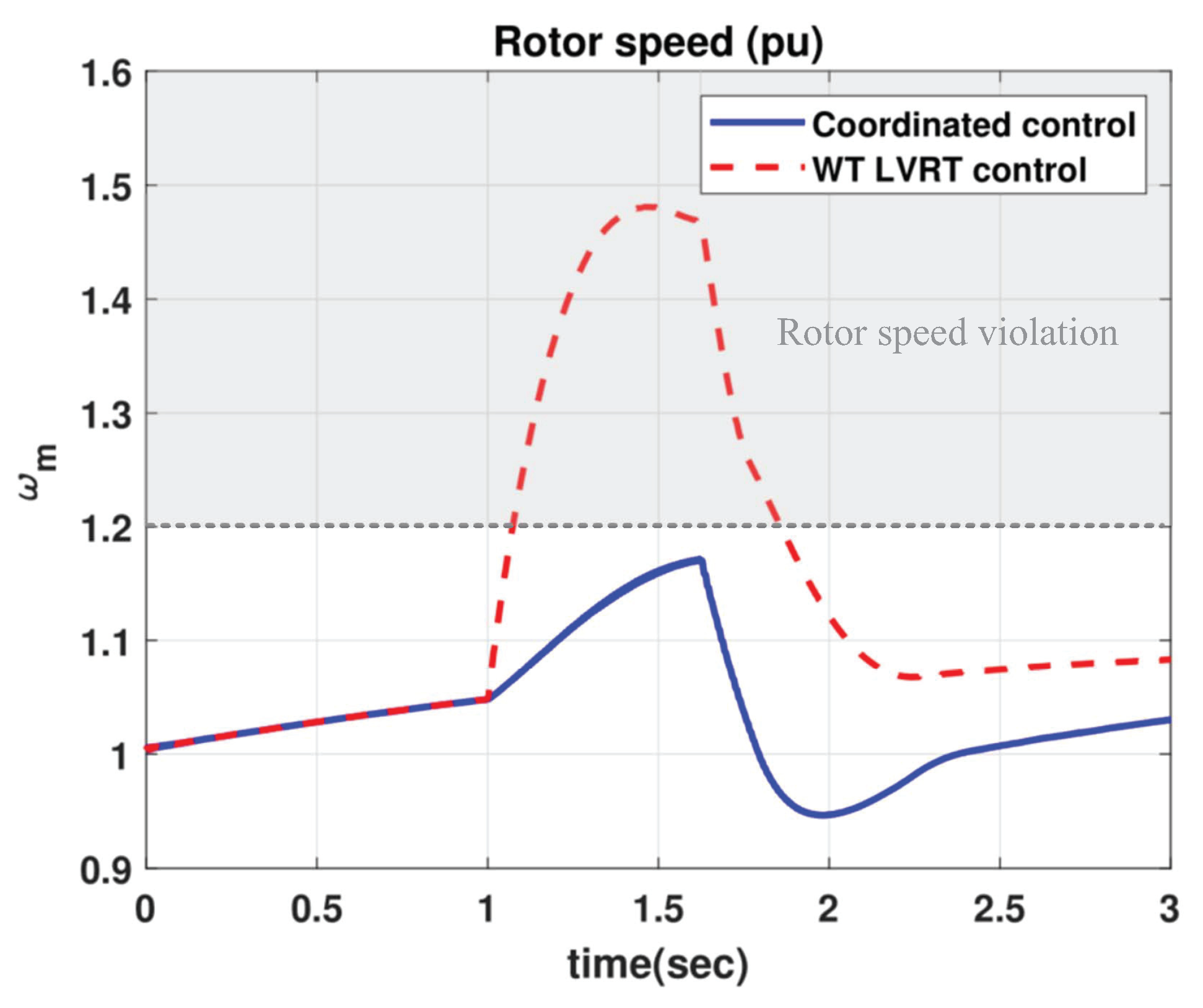
- The proposed method can effectively control both of a WT and an ESS without violation of operational constraints.
- From the proposed method, the stability of the LVRT operation can be improved in any wind speed conditions and it can prevent failures in both a WT and an ESS.
- The proposed method can be applied with previous coordinated control methods by improving its stability.
- No additional device such as chopper is required for achieving stable operation by dissipating power during grid faults.
2. PMSG Wind Power Systems
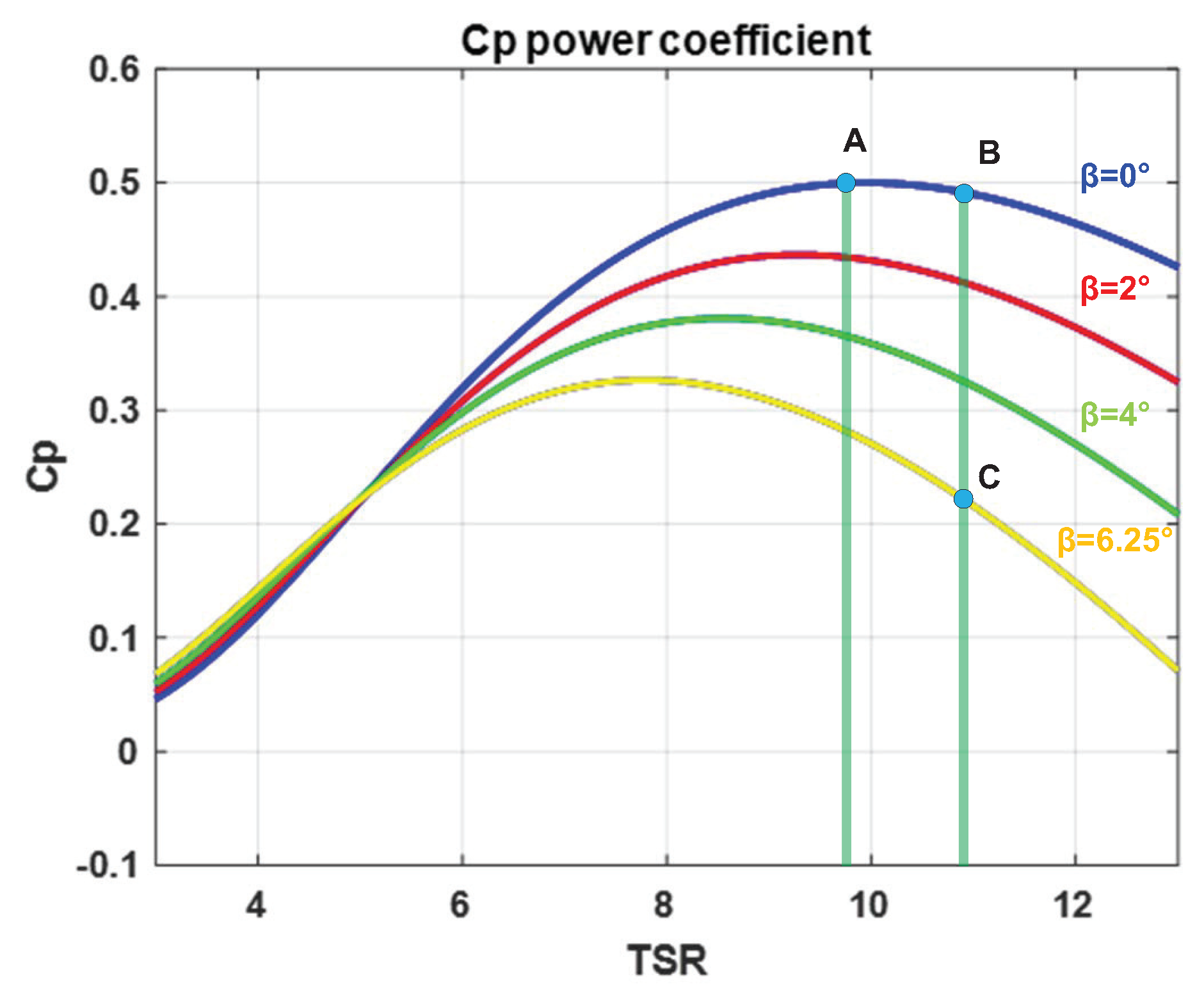
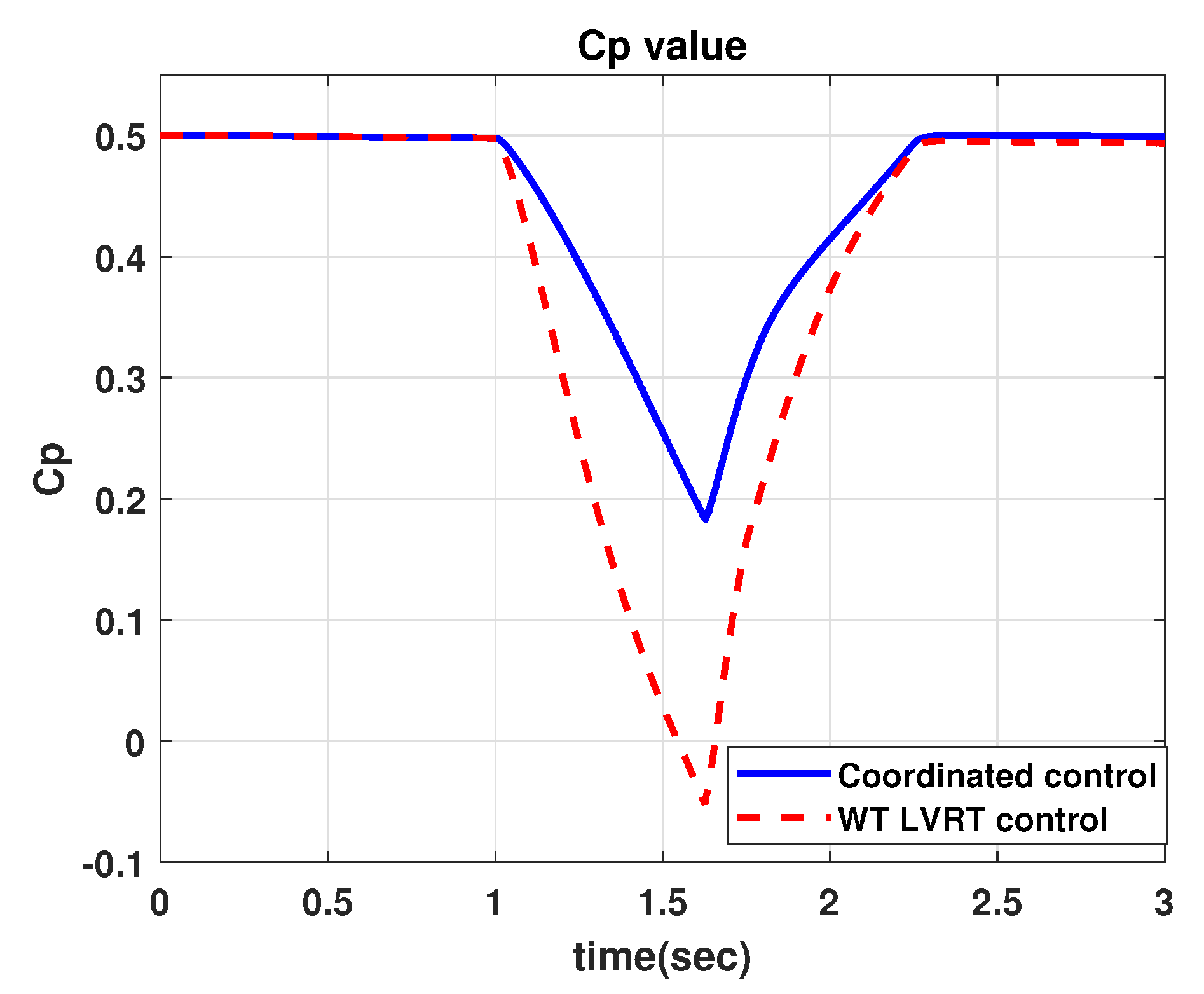
2.1. Mechanical Power of Wind Turbine
2.2. Rotor Side Converter Model
2.3. Grid Side Converter Model
2.4. DC Link Voltage Model
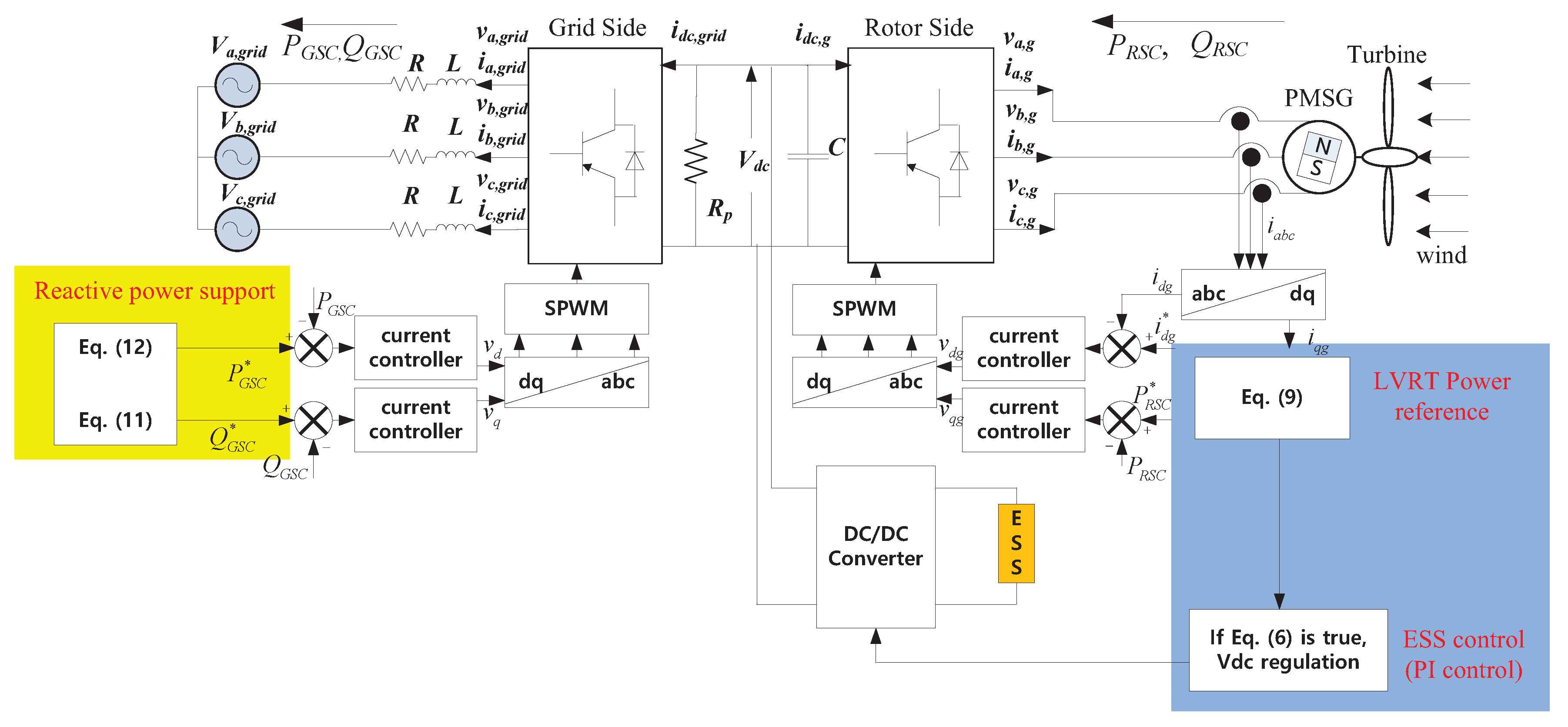
3. Proposed LVRT Control System
3.1. Pitch & Rotor Side Converter Controls
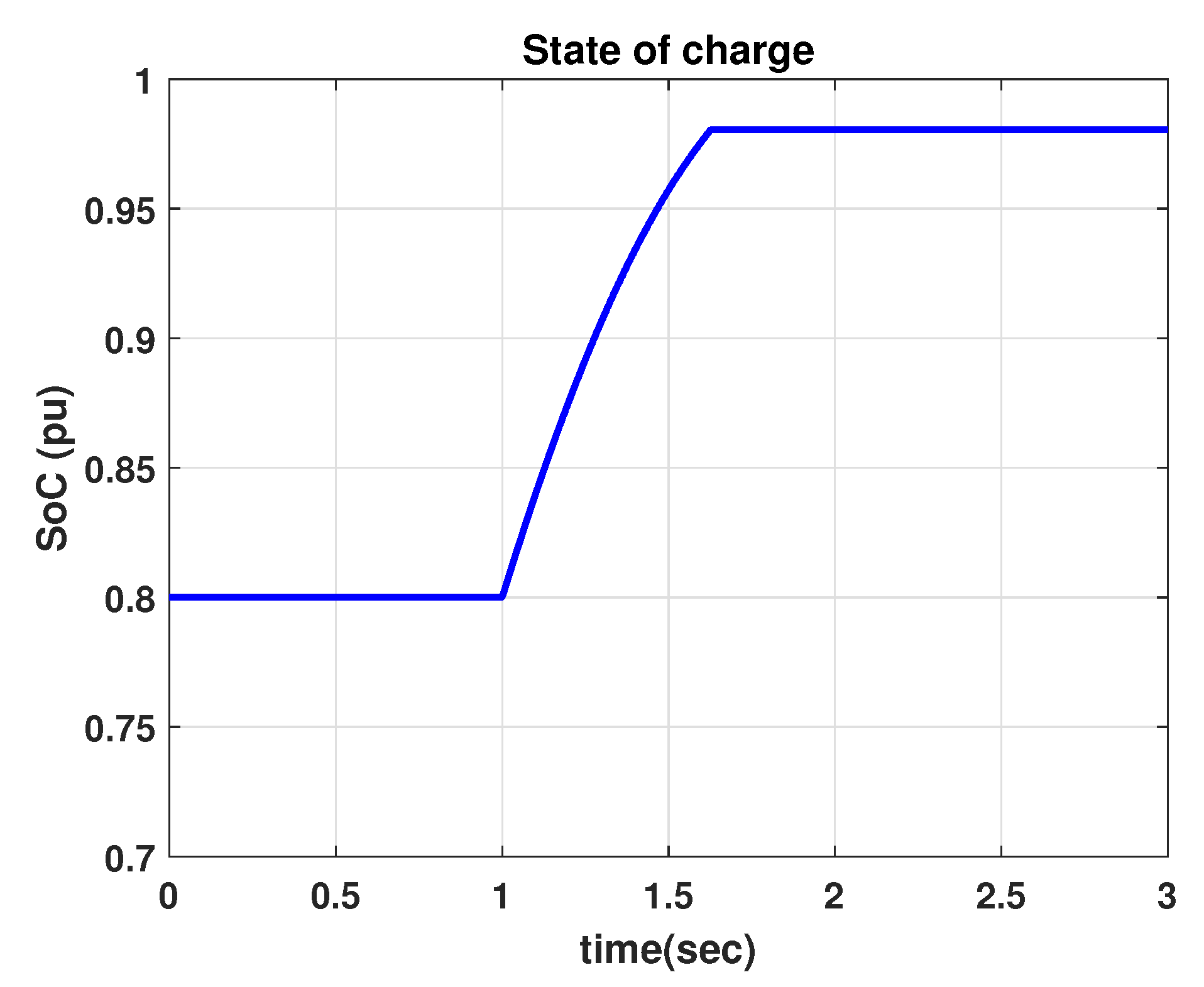
3.2. Grid Side Converter & ESS Control
4. Simulation Result
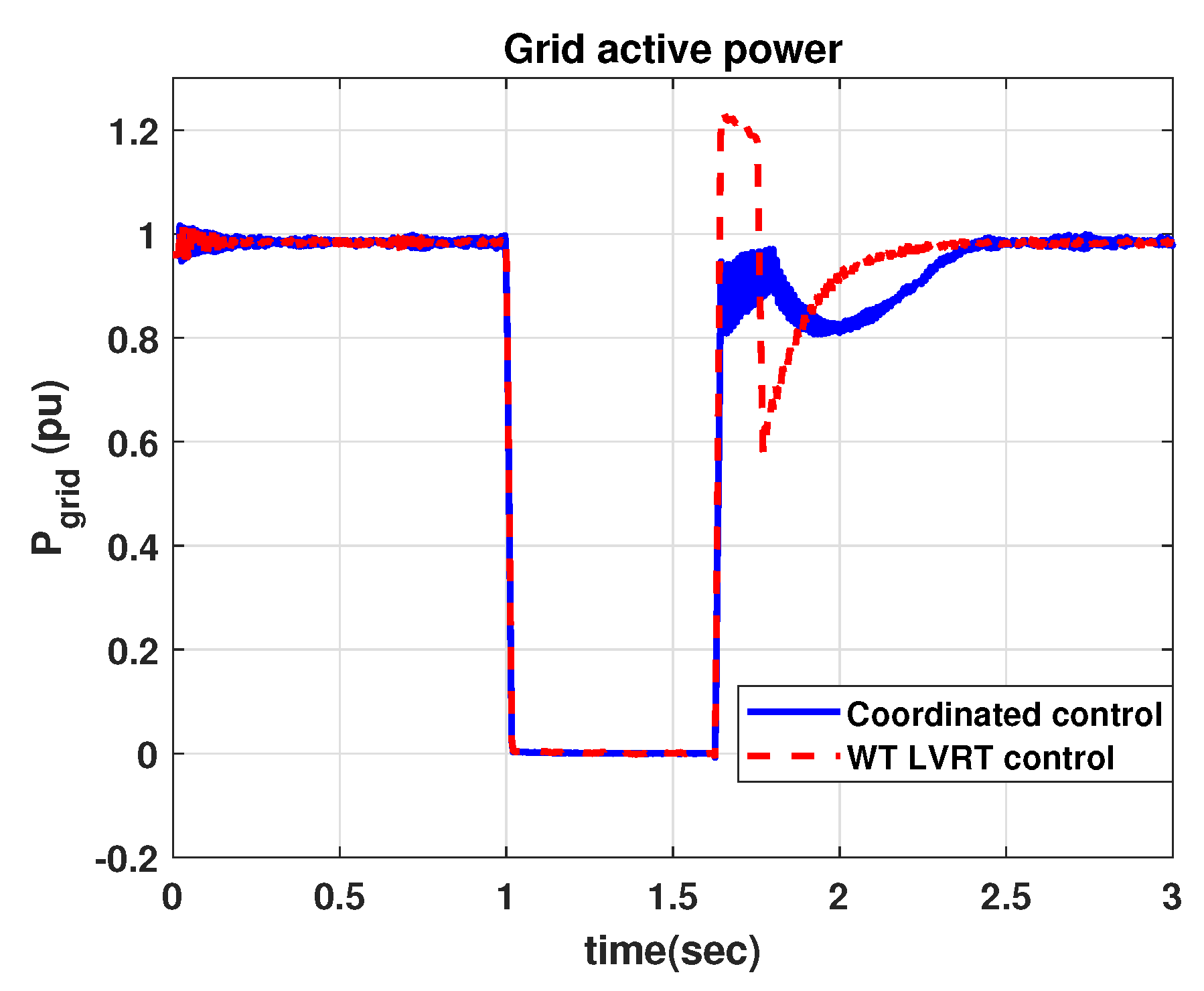
4.1. Comparison with WT LVRT
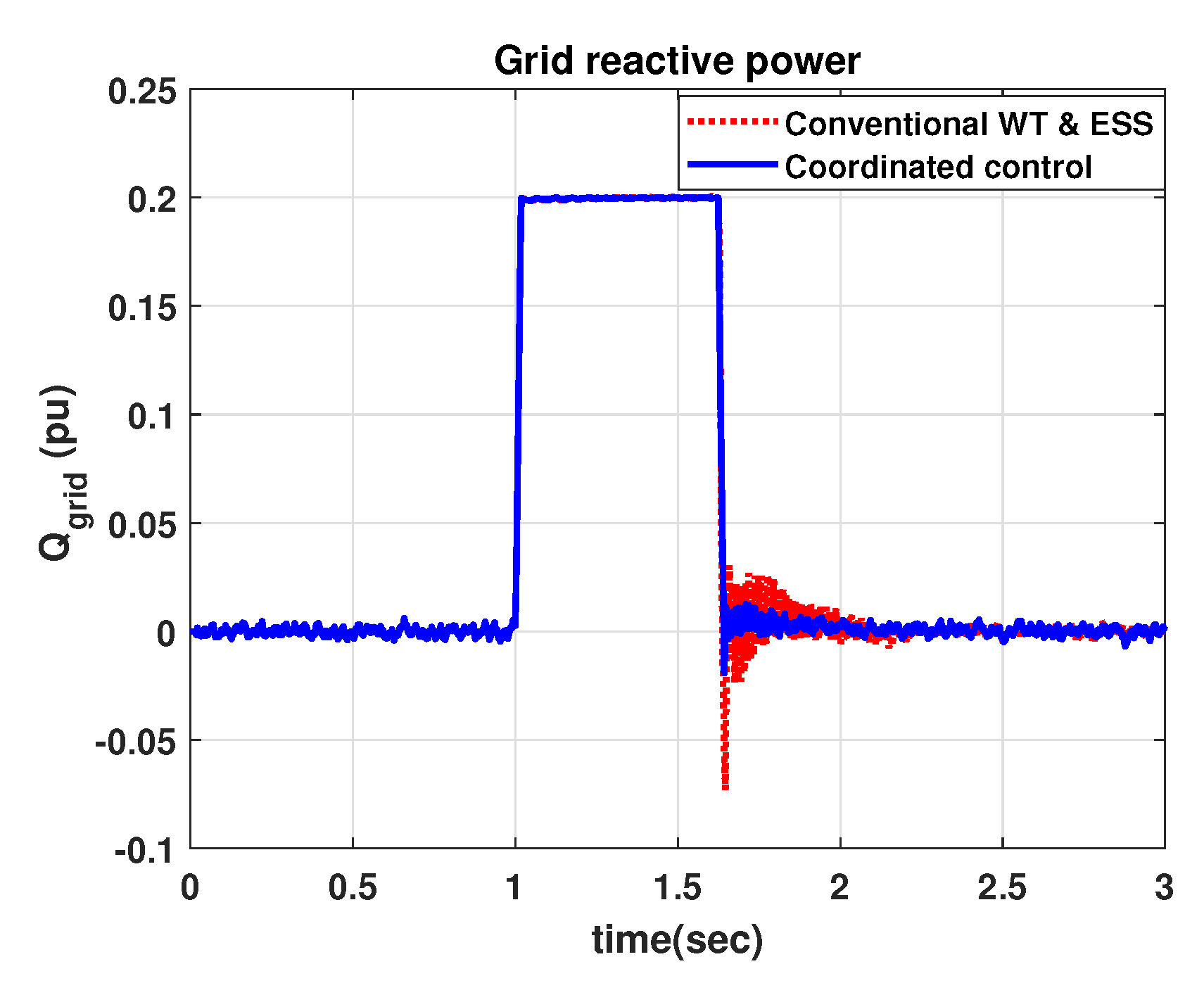
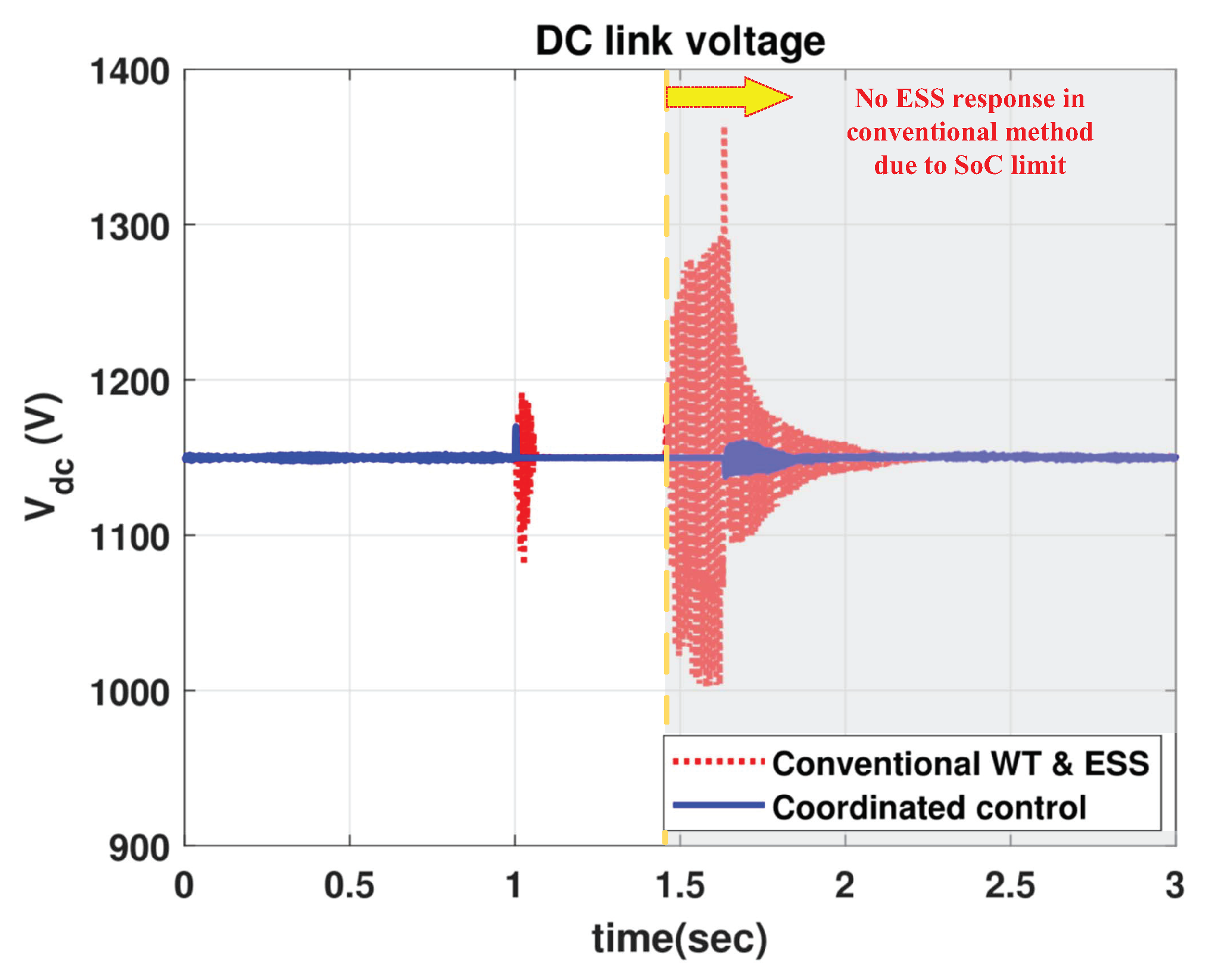
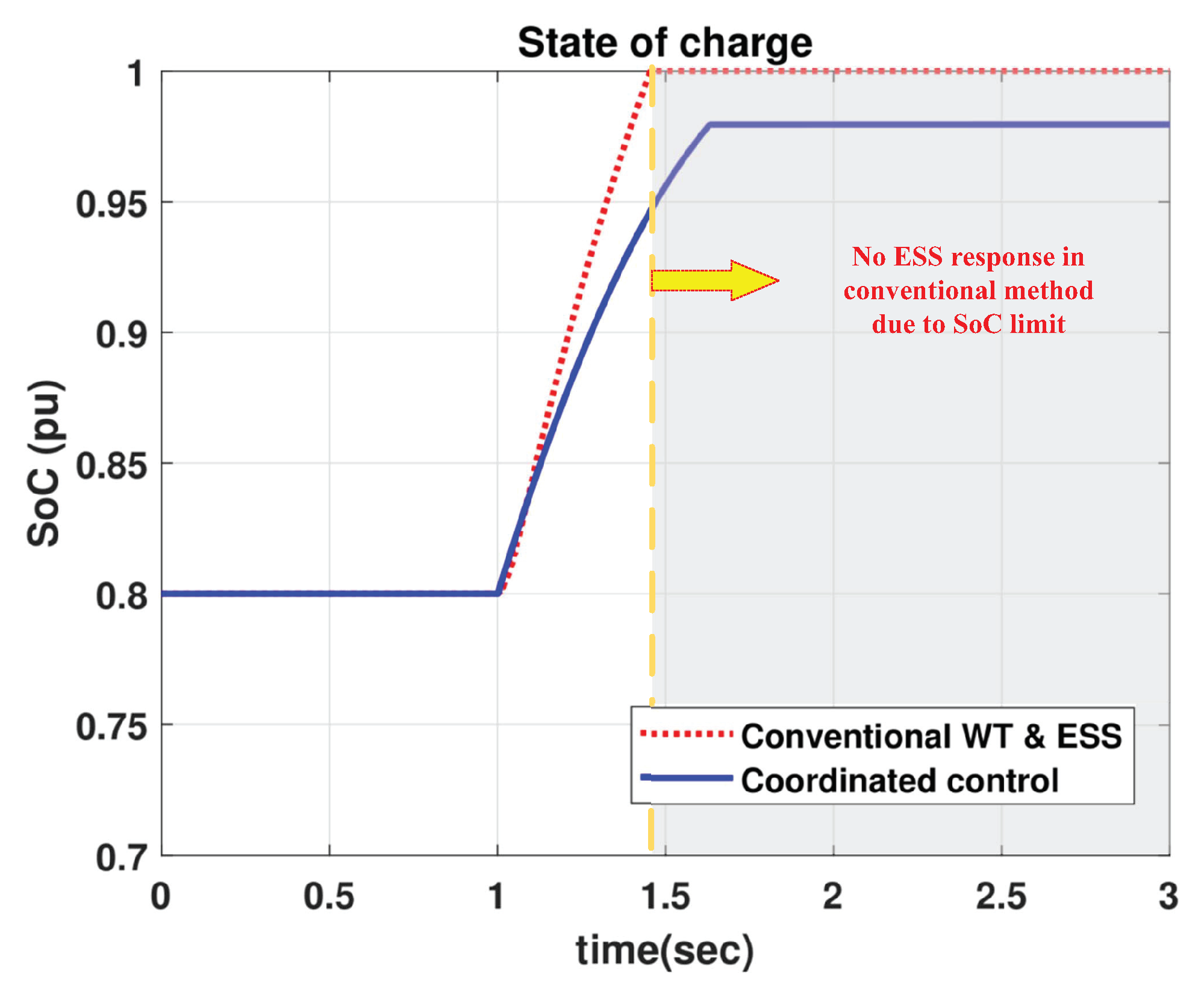
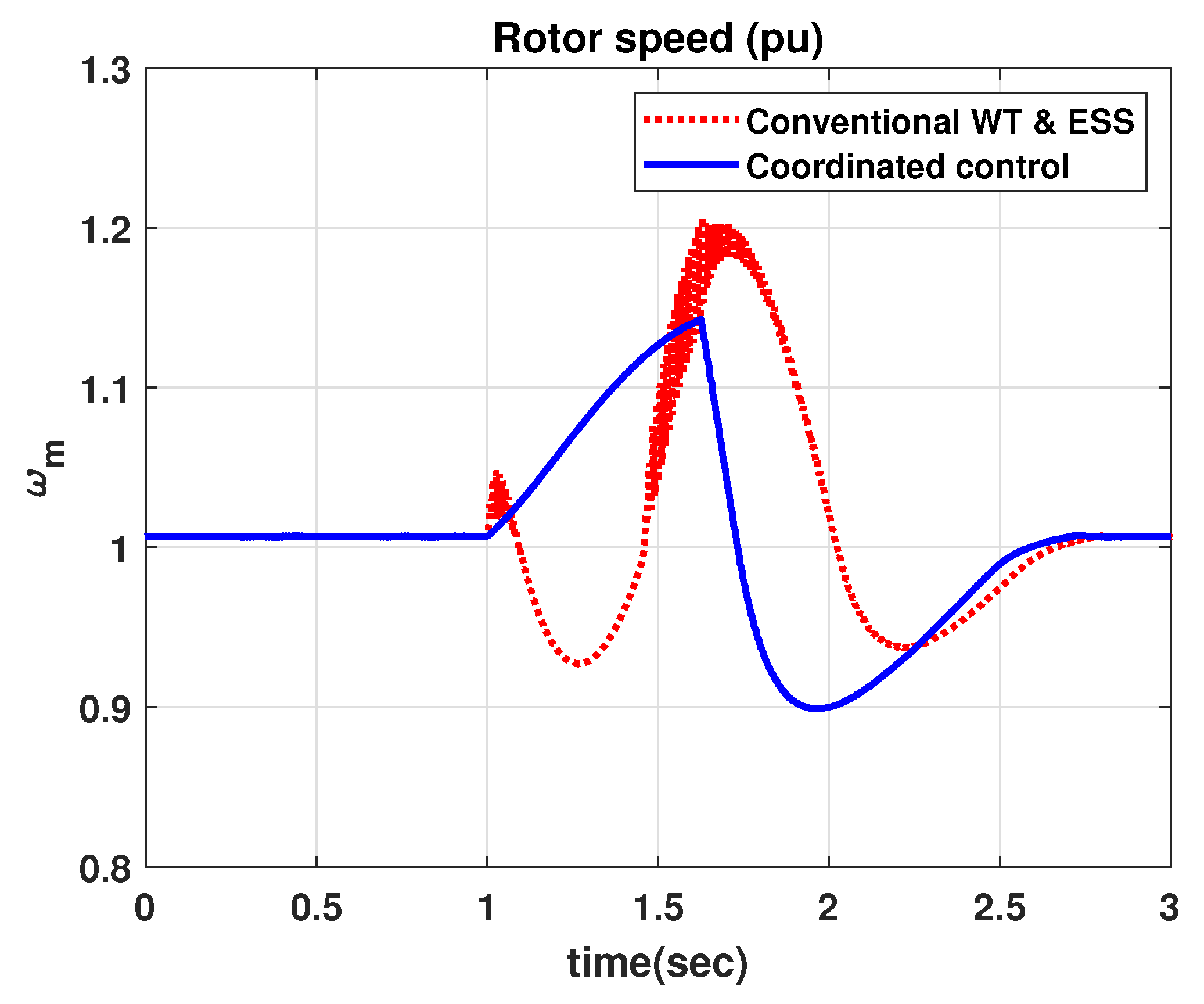
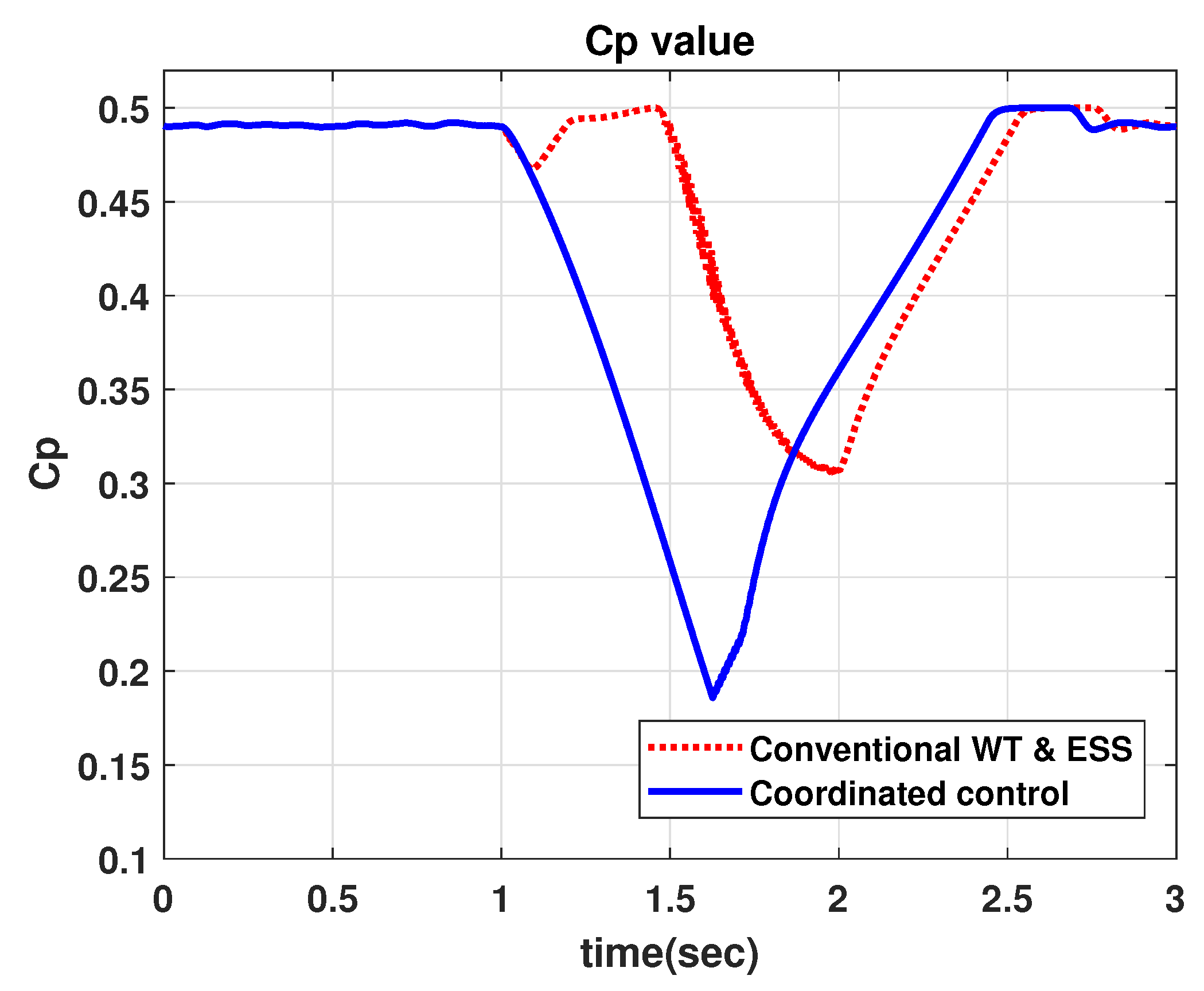
4.2. Comparison with Conventional WT & ESS for LVRT
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| DFIG | Doubly-fed induction generator |
| ESS | Energy storage system |
| GSC | Grid-side converter |
| LVRT | Low-voltage ride through |
| MPPT | Maximum power point tracking |
| PCC | Point of common coupling |
| PI | Proportional-integral |
| PMSG | Permanent magnet synchronous generator |
| RSC | Rotor-side converter |
| SoC | State of charge |
| WP | Wind power |
| WPS | Wind power system |
| WT | Wind turbine |
References
- Chinchilla, M.; Arnaltes, S.; Burgos, J.C. Control of permanentmagnet generators applied to variable-speed wind-energy systems connected to the grid. IEEE Trans. Energy Convers. 2006, 21, 130–135. [Google Scholar] [CrossRef] [Green Version]
- Polinder, H.; Van der Pijl, F.F.A.; Vilder, D.; Tavner, P.J. Comparison of direct-drive and geared generator concepts for wind turbines. IEEE Trans. Energy Convers. 2006, 21, 725–733. [Google Scholar] [CrossRef] [Green Version]
- Gui, Y.; Xiongfei, W.; Heng, W.; Blaabjerg, F. Voltage modulated direct power control for a weak grid-connected voltage source inverters. IEEE Trans. Power Electron. 2019, 34, 11383–11395. [Google Scholar] [CrossRef] [Green Version]
- Gui, Y.; Wang, X.; Blaabjerg, F.; Pan, D. Control of grid-connected voltage-source converters: The relationship between direct-power control and vector-current control. IEEE Ind. Electron. Mag. 2019, 13, 31–40. [Google Scholar] [CrossRef] [Green Version]
- Kim, C.; Gui, Y.; Chung, C.C. Maximum power point tracking of a wind power plant with predictive gradient ascent method. IEEE Trans. Sustain. Energy 2017, 8, 685–694. [Google Scholar] [CrossRef]
- Kim, J.; Muljadi, E.; Gevorgian, V.; Hoke, A. Dynamic capabilities of an energy storage-embedded dfig system. IEEE Trans. Ind. Appl. 2019, 55, 4124–4134. [Google Scholar] [CrossRef]
- Kim, C.; Muljadi, E.; Chung, C.C. Coordinated control of wind turbine and energy storage system for reducing wind power fluctuation. Energies 2018, 11, 52. [Google Scholar] [CrossRef] [Green Version]
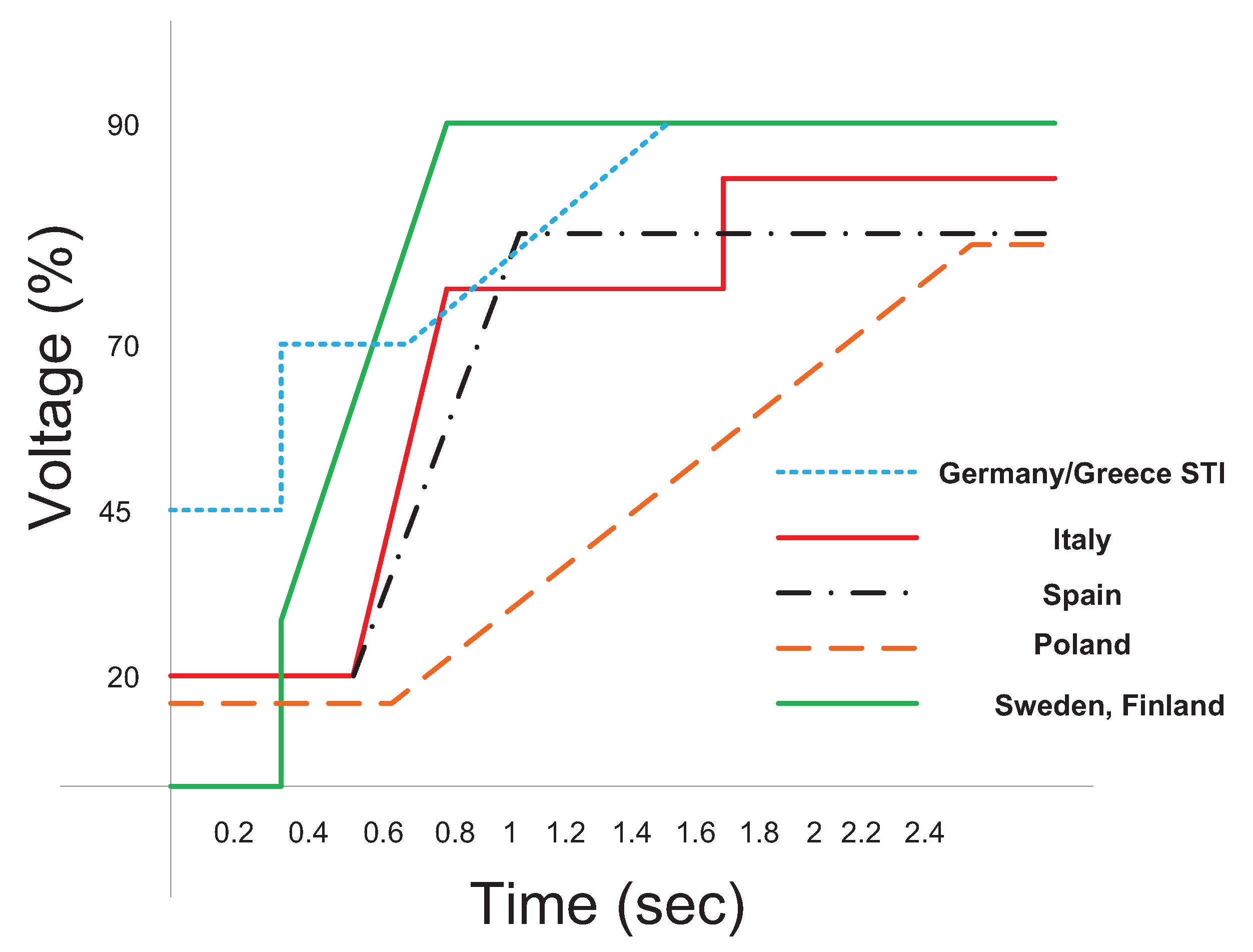
- Tsili, M.; Papathanassiou, S. A review of grid code technical requirements for wind farms. IET Renew. Power Gener. 2009, 3, 308–332. [Google Scholar] [CrossRef]
- Marmouh, S.; Boutoubat, M.; Mokrani, L.; Machmoum, M. A coordinated control and management strategy of a wind energy conversion system for a universal low-voltage ride-through capability. Int. Trans. Electr. Energy Syst. 2019, 29, e12035. [Google Scholar] [CrossRef]
- Mahela, O.P.; Gupta, N.; Khosravy, M.; Patel, N. Comprehensive overview of low voltage ride through methods of grid integrated wind generator. IEEE Access 2019, 7, 99299–99326. [Google Scholar] [CrossRef]
- Saccomando, G.; Svensson, J.; Sannino, A. Improving voltage disturbance rejection for variable-speed wind turbines. IEEE Trans. Energy Convers. 2002, 17, 422–428. [Google Scholar] [CrossRef]
- Mullane, A.; Lightbody, G.; Yacamini, R. Wind-turbine fault ridethrough enhancement. IEEE Trans. Power Syst. 2005, 20, 1929–1937. [Google Scholar] [CrossRef]
- Matas, J.; Castilla, M.; Guerrero, J.M.; Garcia de Vicuna, L.; Miret, J. Feedback linearization of direct-drive synchronous wind-turbines via a sliding mode approach. IEEE Trans. Power Electron. 2008, 23, 1093–1103. [Google Scholar] [CrossRef]
- Kim, C.; Gui, Y.; Chung, C.C. A coordinated lvrt control for pmsg wind turbine. IFAC-PapersOnLine 2017, 50, 8758–8763. [Google Scholar] [CrossRef]
- Conroy, J.F.; Watson, R. Low-voltage ride-through of a full converter wind turbine with permanent magnet generator. IET Renew. Power Gener. 2007, 1, 182–189. [Google Scholar] [CrossRef]
- Alepuz, S.; Calle, A.; Busquets-Monge, S.; Kouro, S.; Wu, B. Use of stored energy in PMSG rotor inertia for low-voltage ride-through in back-to-back NPC converter-based wind power systems. IEEE Trans. Ind. Electron. 2013, 60, 1787–1796. [Google Scholar] [CrossRef]
- Kim, K.-H.; Jeung, Y.-C.; Lee, D.-C.; Kim, H.-G. LVRT scheme of PMSG wind power systems based on feedback linearization. IEEE Trans. Power Electron. 2012, 27, 2376–2384. [Google Scholar] [CrossRef]
- Nasiri, M.; Mobayen, S.; Zhu, Q.M. Super-twisting sliding mode control for gearless pmsg-based wind turbine. Complexity 2019, 2019. [Google Scholar] [CrossRef]
- Abbey, C.; Joos, G. Supercapacitor energy storage for wind energy applications. IEEE Trans. Ind. Appl. 2007, 43, 769–776. [Google Scholar] [CrossRef]
- Wang, W.; Ge, B.; Bi, D.; Qin, M.; Liu, W. Energy storage based LVRT and stabilizing power control for direct-drive wind power system. In Proceedings of the 2010 International Conference on Power System Technology, Hangzhou, China, 24–28 October 2010. [Google Scholar]
- Liu, J.; Wei, Y.; Jiakun, F.; Jinyu, W.; Shijie, C. Stability analysis and energy storage-based solution of wind farm during low voltage ride through. Int. J. Electr. Power Energy Syst. 2018, 3, 75–84. [Google Scholar] [CrossRef]
- Yao, J.; Jiawei, L.; Lisha, G.; Ruikuo, L.; Depeng, X. Coordinated control of a hybrid wind farm with pmsg and fsig during asymmetrical grid fault. Int. J. Electr. Power Energy Syst. 2018, 3, 287–300. [Google Scholar] [CrossRef]
- Li, J.; Wang, N.; Zhou, D.; Hu, W.; Huang, Q.; Chen, Z.; Blaabjerg, F. Optimal reactive power dispatch of permanent magnet synchronous generator-based wind farm considering levelised production cost minimisation. Renew. Energy 2020, 3, 1–12. [Google Scholar] [CrossRef]
- Haque, M.E.; Negnevitsky, M.; Muttaqi, K. A novel control strategy for a variable speed wind turbine with a permanent magnet synchronous generator. In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008. [Google Scholar]
- Nasiri, M.; Milimonfared, J.; Fathi, S.H. A review of low-voltage ride-through enhancement methods for permanent magnet synchronous generator based wind turbines. Renew. Sustain. Energy Rev. 2015, 47, 399–415. [Google Scholar] [CrossRef]






| Parameter | Value | Unit |
|---|---|---|
| Rated power | 1.63 | MW |
| Rated wind speed | 12 | m/s |
| Max. power coeff. | 0.5 | |
| Optimal tip speed ratio | 9.9495 | |
| Blade radius | 33.05 | m |
| Air density | 1.12 | |
| Max. rotor speed | 1.2 | pu |
| DC link voltage | 1150 | V |
| Turbine inertia | 6500 | |
| ESS capacity | 1 | kWh |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Gui, Y.; Zhao, H.; Kim, W. Coordinated LVRT Control for a Permanent Magnet Synchronous Generator Wind Turbine with Energy Storage System. Appl. Sci. 2020, 10, 3085. https://doi.org/10.3390/app10093085
Kim C, Gui Y, Zhao H, Kim W. Coordinated LVRT Control for a Permanent Magnet Synchronous Generator Wind Turbine with Energy Storage System. Applied Sciences. 2020; 10(9):3085. https://doi.org/10.3390/app10093085
Chicago/Turabian StyleKim, Chunghun, Yonghao Gui, Haoran Zhao, and Wonhee Kim. 2020. "Coordinated LVRT Control for a Permanent Magnet Synchronous Generator Wind Turbine with Energy Storage System" Applied Sciences 10, no. 9: 3085. https://doi.org/10.3390/app10093085
APA StyleKim, C., Gui, Y., Zhao, H., & Kim, W. (2020). Coordinated LVRT Control for a Permanent Magnet Synchronous Generator Wind Turbine with Energy Storage System. Applied Sciences, 10(9), 3085. https://doi.org/10.3390/app10093085








