Investigation of Factors Affecting Sensitivity Enhancement of an Optical Fiber Probe for Microstructure Measurement Using Oblique Incident Light
Abstract
:1. Introduction
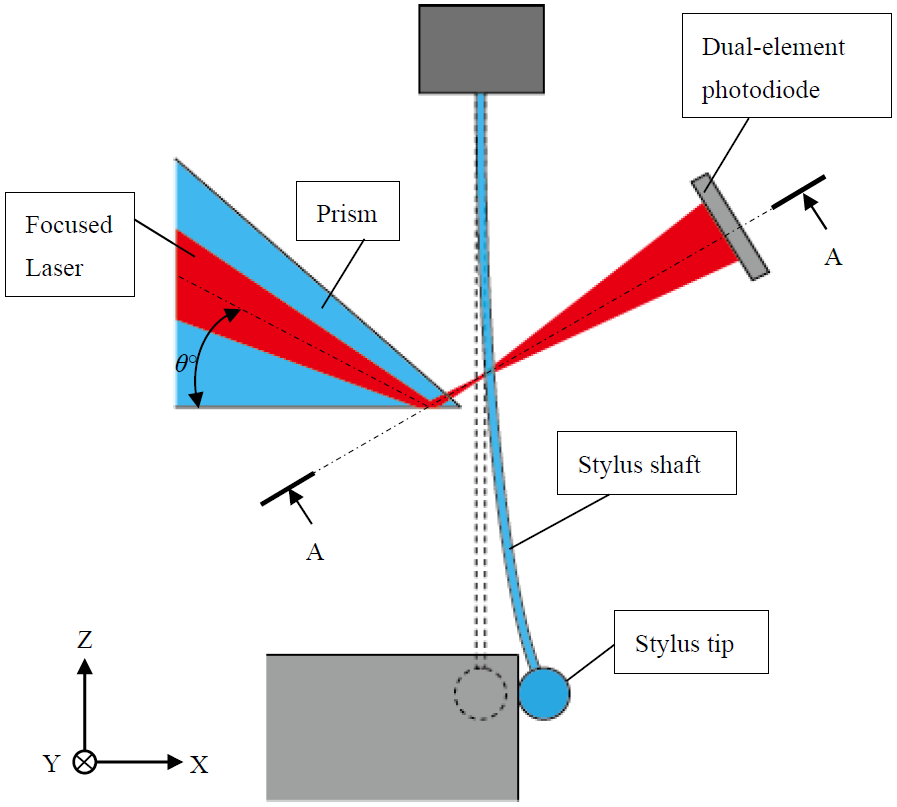
2. Configuration of the Optical Fiber Probe
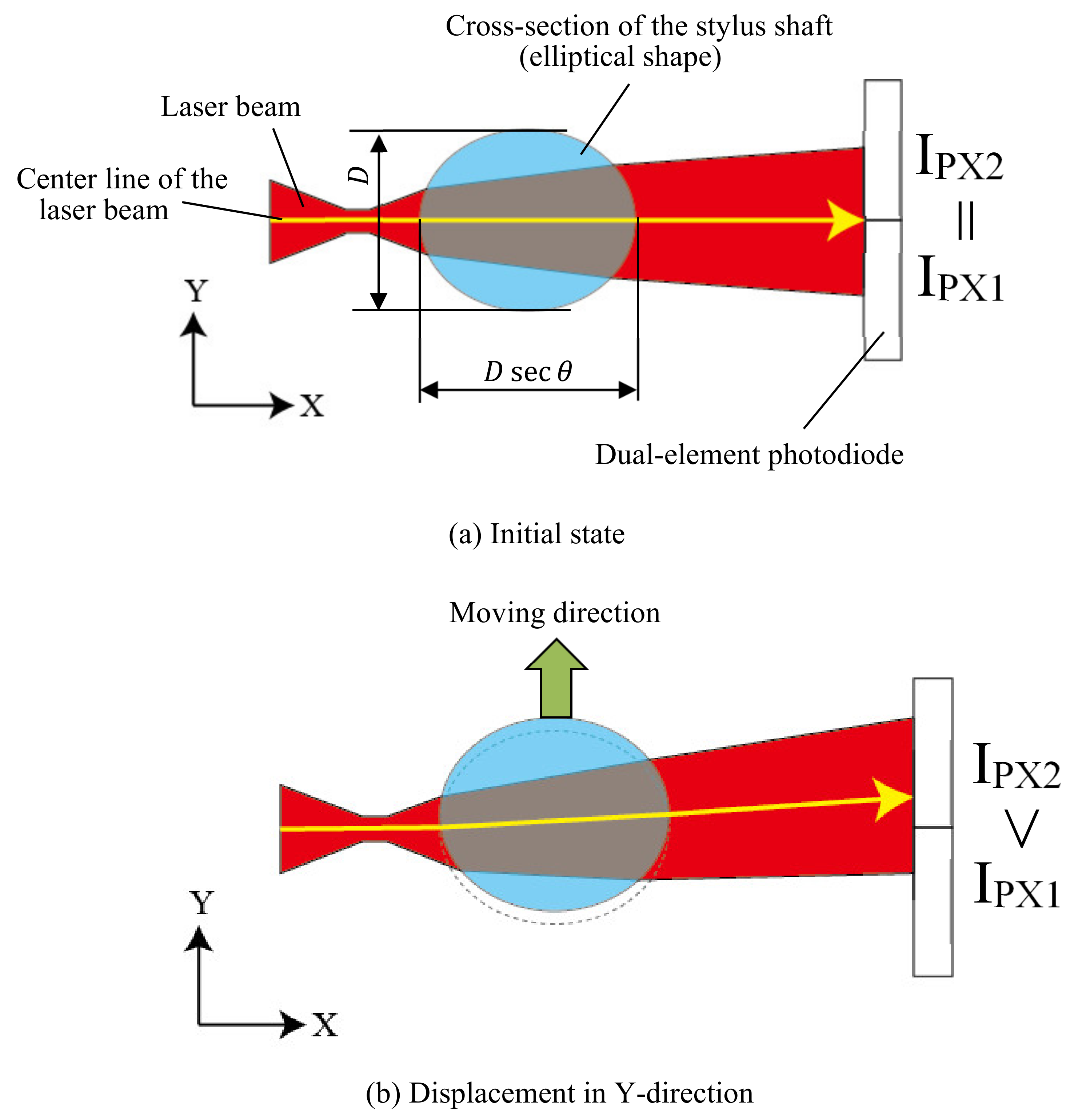
3. Effect of Incident Angle of the Light on the Measurement Sensitivity
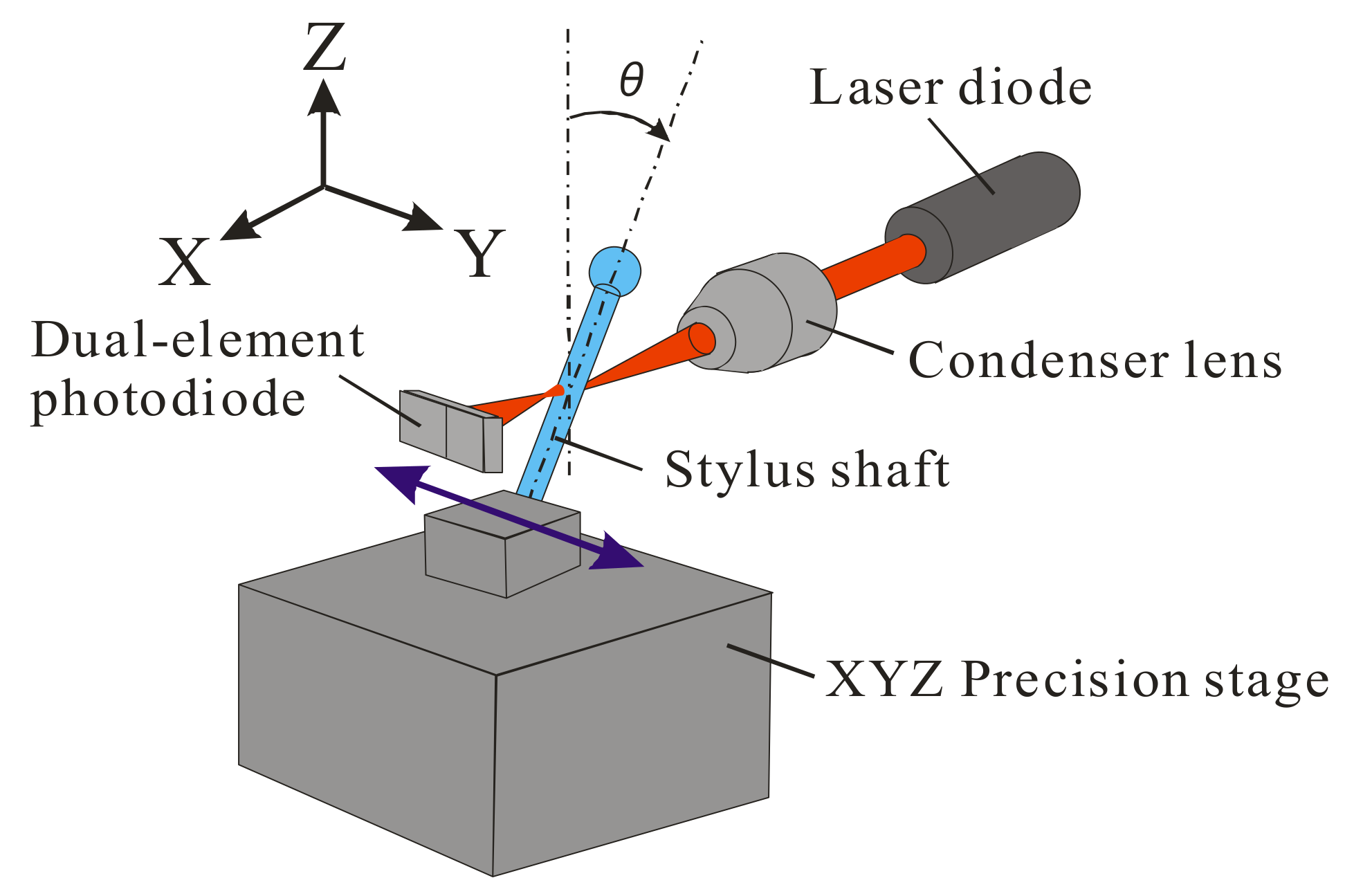
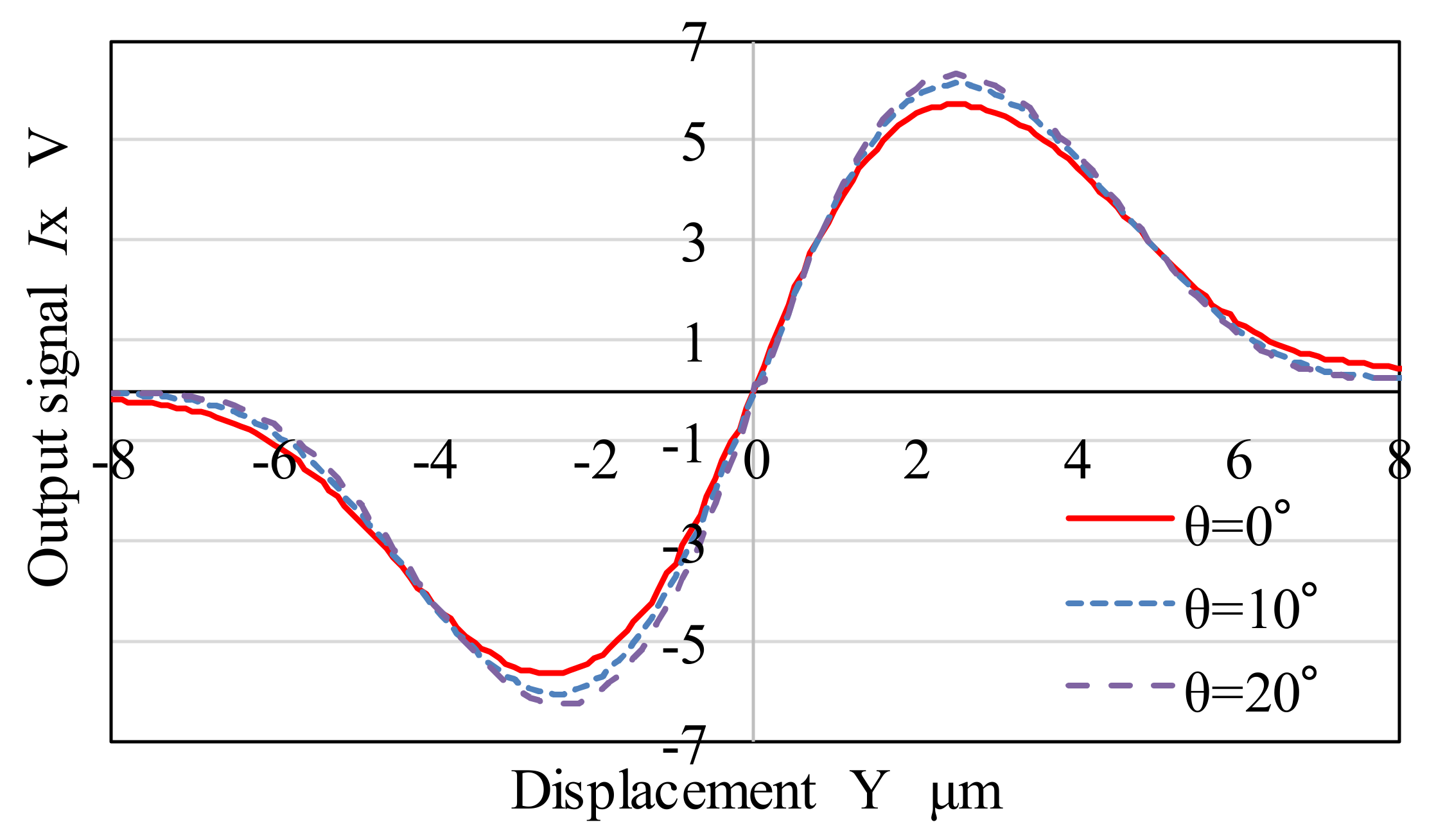
3.1. Experimental Assessment of Sensitivity
3.2. Simulation Assessment of Sensitivity
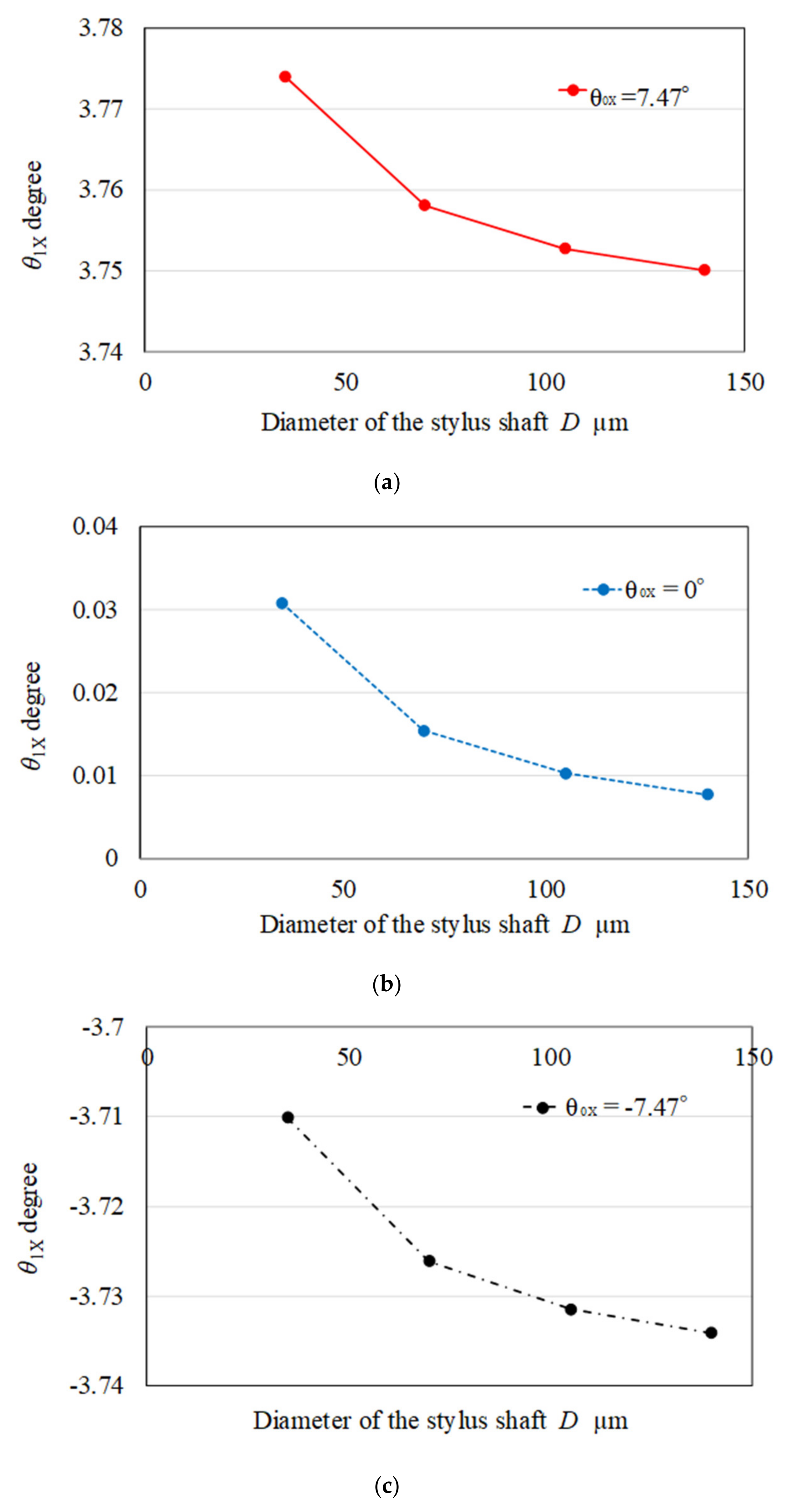
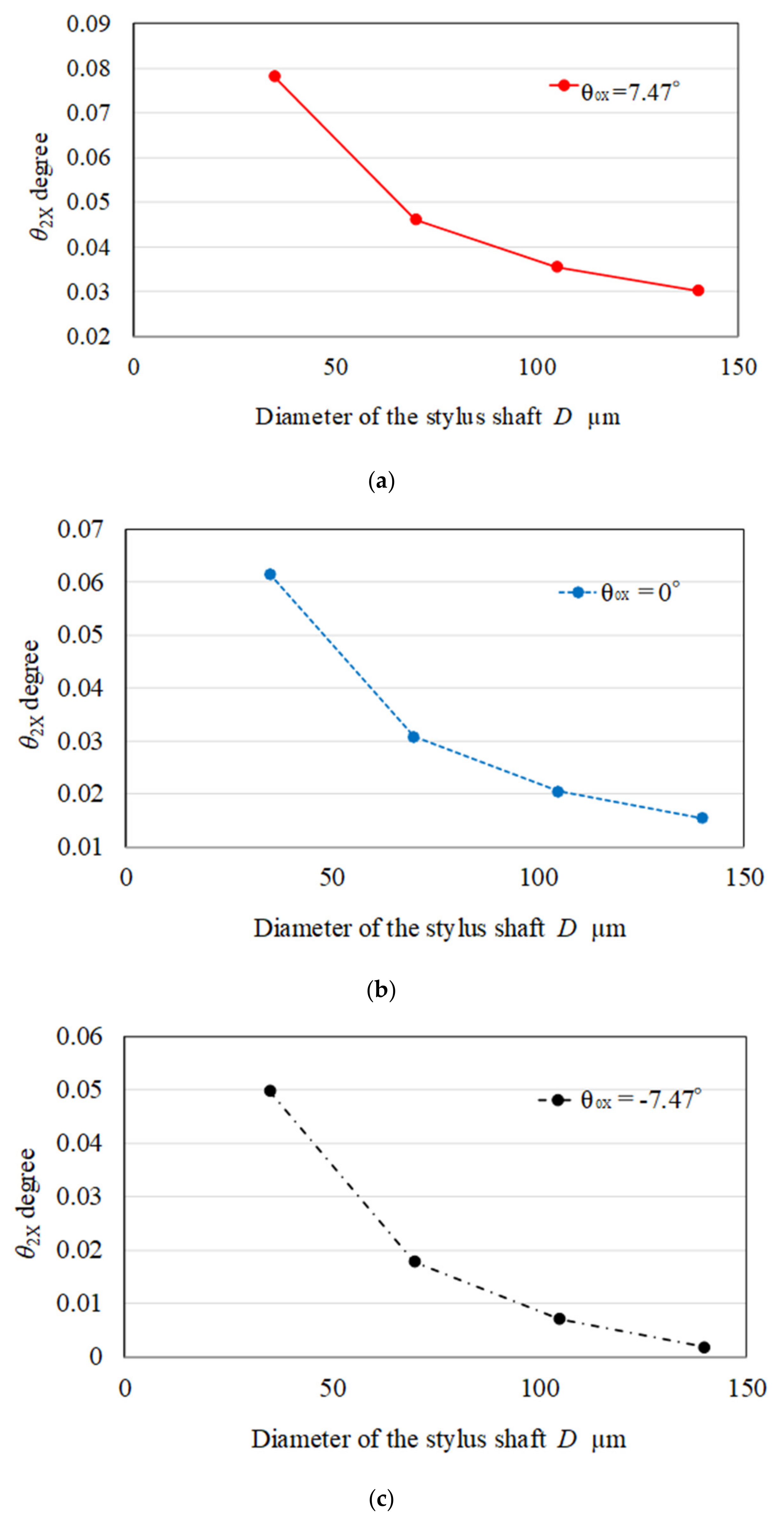
3.3. Discussion Associated with Enhancement of Sensitivity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Albalaihid, K.; Lawes, S.; Kinnell, P. Variable stiffness probing systems for micro-coordinate measuring machines. Precis. Eng. 2016, 43, 262–269. [Google Scholar] [CrossRef] [Green Version]
- Huang, Q.; Chen, C.; Wu, K.; Zhang, L.; Li, R.; Fan, K.-C. A Three-Dimensional Resonant Triggering Probe for Micro-CMM. Appl. Sci. 2017, 7, 403. [Google Scholar] [CrossRef] [Green Version]
- Ito, S.; Kikuchi, H.; Chen, Y.; Shimizu, Y.; Gao, W.; Takahashi, K.; Kanayama, T.; Arakawa, K.; Hayashi, A. A micro-coordinate measurement machine (CMM) for large-scale dimensional measurement of micro-slits. Appl. Sci. 2016, 6, 156. [Google Scholar] [CrossRef] [Green Version]
- Cui, J.; Li, J.; Feng, K.; Tan, J.; Zhang, J. A 3D fiber probe based on orthogonal micro focal-length collimation and fiber Bragg grating. Meas. Sci. Technol. 2016, 27, 074005. [Google Scholar] [CrossRef]
- Muralikrishnan, B.; Stone, J.A.; Stoup, J.R. Fiber deflection probe for small hole metrology. Precis. Eng. 2006, 30, 154–164. [Google Scholar] [CrossRef]
- Takaya, Y.; Michihata, M.; Hayashi, T. Scanning type microrobe for displacement measurement based on standing wave detection using an optically trapped particle. Int. J. Autom. Technol. 2011, 5, 395–402. [Google Scholar] [CrossRef]
- Felix, M.; Alain, K. Development of a 3D-AFM for ture 3D measurements of nanostructures. Meas. Sci. Technol. 2011, 22, 094009. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Sajima, T.; Uchiyama, K.; Yoshida, I.; Hamano, Y.; Honda, H. Development of measurement system for microstructures using an optical fiber probe: Improvement of measurable region and depth. Meas. Sci. Technol. 2020, 31, 075902. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Sajima, T.; Uchiyama, K. Fabrication of an ultra-small-diameter optical fiber probe using an acid-etch technique and a CO2 laser for 3D micro metrology. Int. J. Autom. Technol. 2017, 11, 699–706. [Google Scholar] [CrossRef]
- Murakami, H.; Katsuki, A.; Sajima, T.; Tokuoh, N.; Fukuda, M. Development of a system for 3-D micro metrology using an ultra-small-diameter optical fiber probe. Proc. Am. Soc. Precis. Eng. 2014, 59, 63–66. [Google Scholar]
- Press, W.H. Numerical Recipes in C; Cambridge University Press: Cambridge, UK, 1988; p. 216. [Google Scholar]



| Light Source | Wavelength: 630 nm |
|---|---|
| Diameter of the stylus shaft, D | 70 µm |
| Refractive index of optical fiber (stylus shaft) | 1.457 |
| Length from planes 0 to 1, L0 | 20 µm |
| Length from planes 2 to 3, L1 | 40 mm |
| Numerical aperture of the lens | 0.13 |
| Displacement of the stylus shaft, Y | –8–8 µm |
| Diameter of laser spot, DS | 10 µm |
| Region of the dual-element photodiode | 5 × 10 mm |
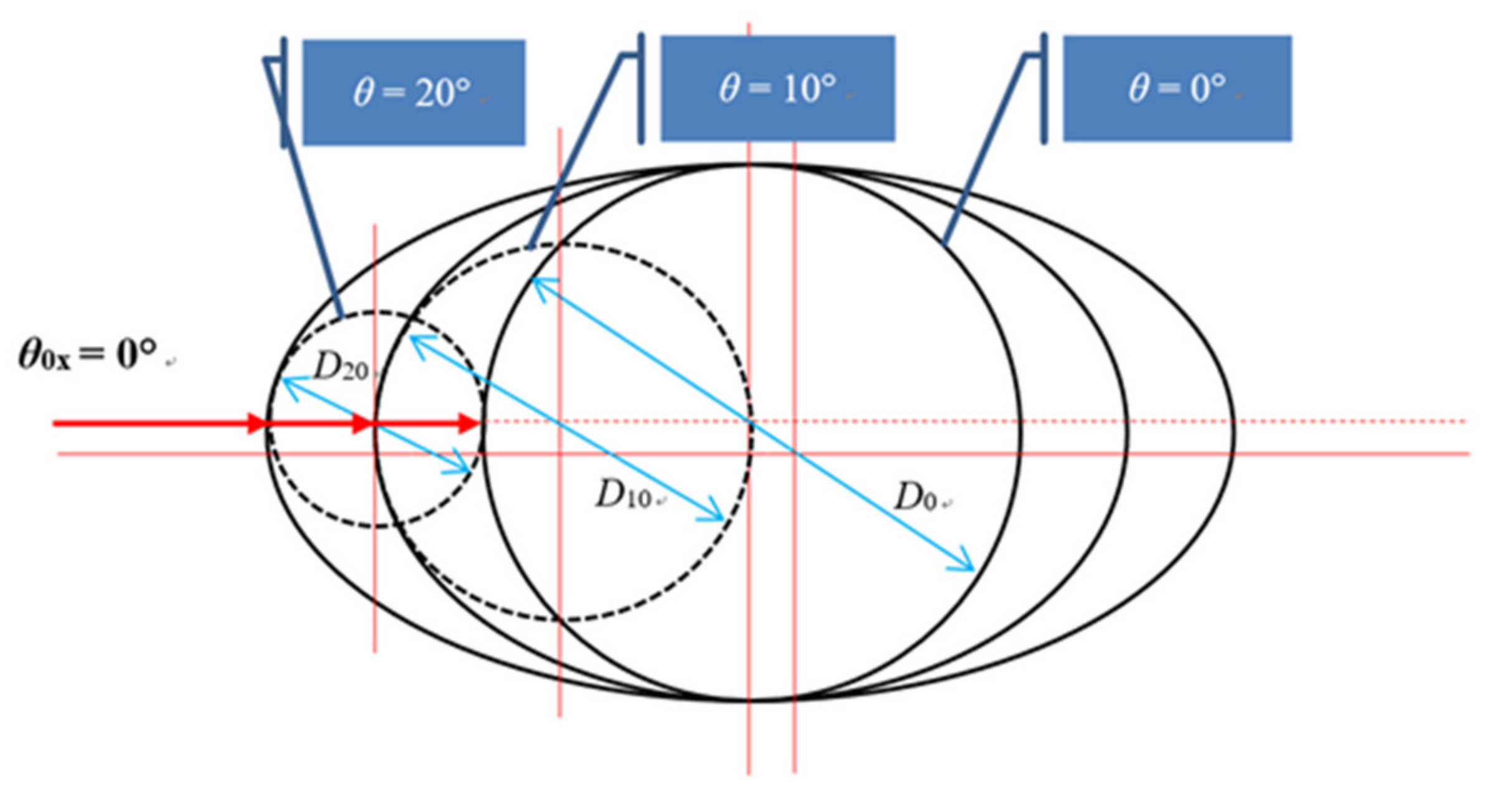
| X, Y, Z: Coordinates Used for Ray-Tracing |
| D: Diameter of the stylus shaft |
| L0, L1: Length from between plane 0 to plane 1, plane 2 to plane 3 |
| n0, n1: Refractive indices of the air and optical fiber (stylus) |
| W1, W2, W3: Heights of laser beam at respective planes |
| , : Inclination angles of rays in the X-direction |
| , : Inclination angles for rays in the Z-direction |
| , : Angles between the normal line at the laser irradiation position of the stylus shaft and X-axis |
| , : Incident angle |
| , : Refracting angle |
| : Length from a laser irradiation position on the surface of the stylus shaft to plane-1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Murakami, H.; Katsuki, A.; Sajima, T.; Uchiyama, K.; Yoshida, I.; Hamano, Y.; Honda, H. Investigation of Factors Affecting Sensitivity Enhancement of an Optical Fiber Probe for Microstructure Measurement Using Oblique Incident Light. Appl. Sci. 2020, 10, 3191. https://doi.org/10.3390/app10093191
Murakami H, Katsuki A, Sajima T, Uchiyama K, Yoshida I, Hamano Y, Honda H. Investigation of Factors Affecting Sensitivity Enhancement of an Optical Fiber Probe for Microstructure Measurement Using Oblique Incident Light. Applied Sciences. 2020; 10(9):3191. https://doi.org/10.3390/app10093191
Chicago/Turabian StyleMurakami, Hiroshi, Akio Katsuki, Takao Sajima, Kosuke Uchiyama, Ichiro Yoshida, Yasuo Hamano, and Hiroshi Honda. 2020. "Investigation of Factors Affecting Sensitivity Enhancement of an Optical Fiber Probe for Microstructure Measurement Using Oblique Incident Light" Applied Sciences 10, no. 9: 3191. https://doi.org/10.3390/app10093191
APA StyleMurakami, H., Katsuki, A., Sajima, T., Uchiyama, K., Yoshida, I., Hamano, Y., & Honda, H. (2020). Investigation of Factors Affecting Sensitivity Enhancement of an Optical Fiber Probe for Microstructure Measurement Using Oblique Incident Light. Applied Sciences, 10(9), 3191. https://doi.org/10.3390/app10093191





