A Comparative Study of Weighting Methods for Local Reference Frame
Abstract
:1. Introduction
- (1)
- When the wights of the distant points in the local neighborhood are too large, the LRF is sensitive to occlusion, clutter, partial overlap, noise, outliers, and keypoint localization error. By contrast, when the wights of the distant points are too small, the LRF is susceptible to noise, varying point density, and keypoint localization error.
- (2)
- The weighting method should be mainly designed to achieve the robustness to noise and keypoint localization error. Then, it should be properly adjusted to get a balanced robustness to noise, keypoint localization error, and shape incompleteness. The robustness to point density variation and outliers should be obtained by extra methods.
- (3)
- No method is generalized, but the GF can always get good performance on different data modalities by changing the value of the Gaussian parameter. Therefore, GF can be regarded as a generalized method.
2. Overview of Five Weighting Methods
3. Evaluation Methodology
3.1. Datasets
3.2. Evaluation Criterion
3.3. Implementation Details
4. Experimental Results and Analysis
4.1. Test on the Six Datasets
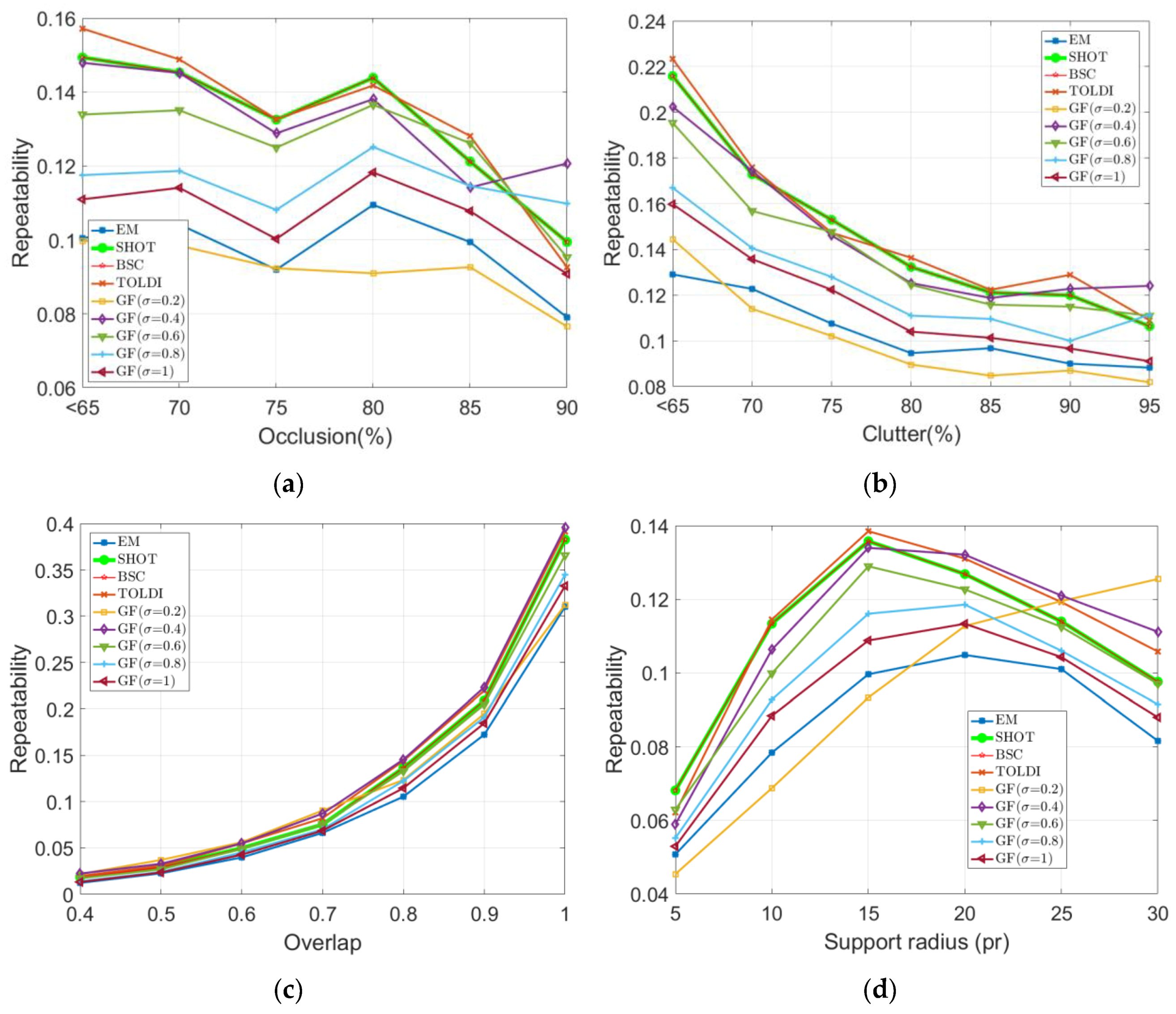
4.2. Repeatability of LRF Under Different Levels of Occlusion, Clutter, and Partial Overlap, as Well as Varying Support Radii
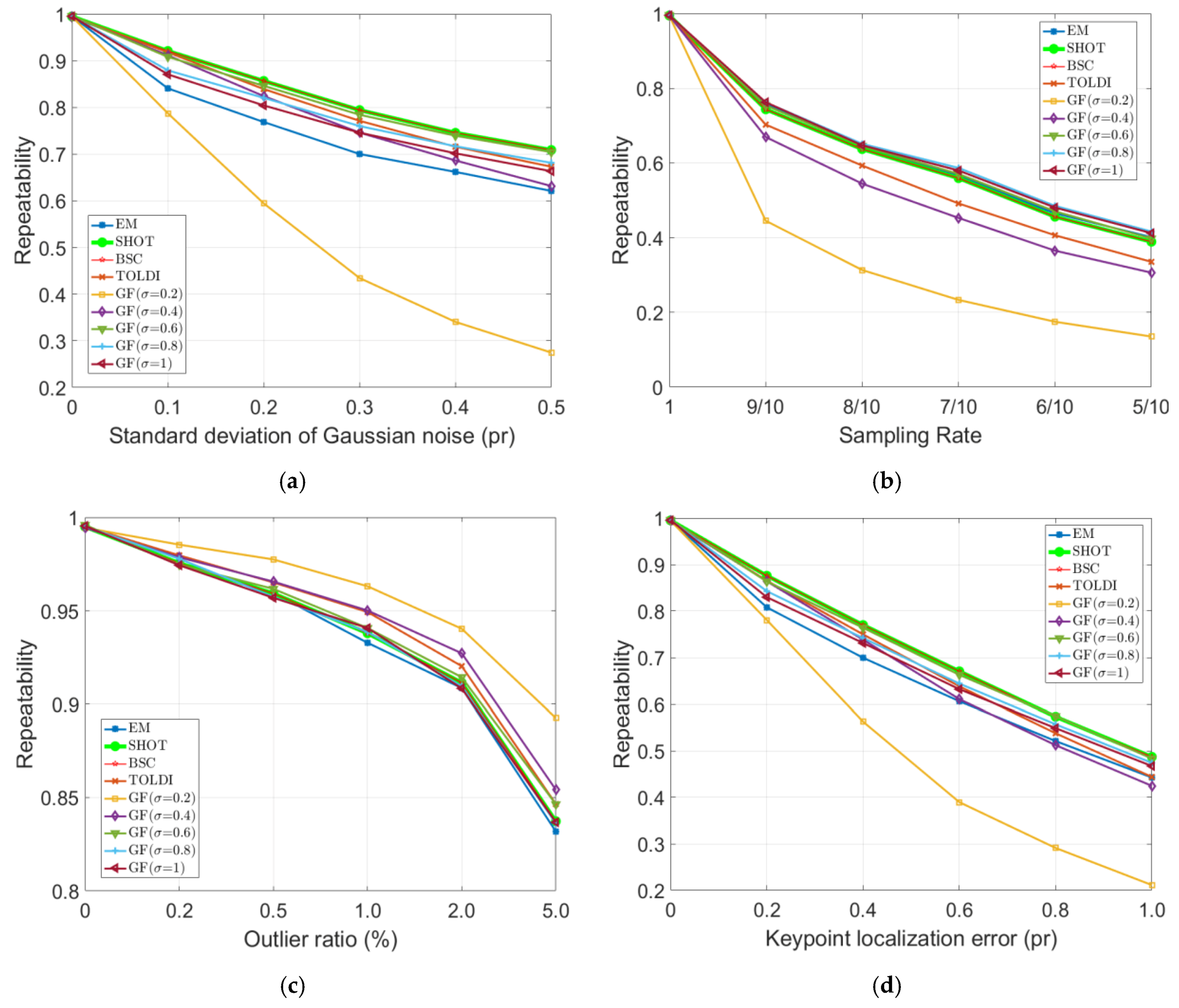
4.3. Repeatability of LRF Under Different Levels of Gaussian Noise, Point Density Variation, Shot Noise, and Keypoint Localization Error
4.4. Comparison of Weights
4.5. Performance Summary and Suggestions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, Y.; Sohel, F.; Bennamoun, M.; Lu, M.; Wan, J. Rotational projection statistics for 3D local surface description and object recognition. Int. J. Comput. Vis. 2013, 105, 63–86. [Google Scholar] [CrossRef] [Green Version]
- Johnson, A.E.; Hebert, M. Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 433–449. [Google Scholar] [CrossRef] [Green Version]
- Lu, M.; Guo, Y.; Zhang, J.; Ma, Y.; Lei, Y. Recognizing objects in 3D point clouds with multi-scale local features. Sensors 2014, 14, 24156–24173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tateno, K.; Tombari, F.; Navab, N. When 2.5D is not enough: Simultaneous reconstruction, segmentation and recognition on dense SLAM. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016. [Google Scholar]
- Dong, Z.; Yang, B.; Liang, F.; Huang, R.; Scherer, S. Hierarchical registration of unordered TLS point clouds based on binary shape context descriptor. ISPRS J. Photogramm. Remote Sens. 2018, 144, 61–79. [Google Scholar] [CrossRef]
- Guo, Y.; Sohel, F.; Bennamoun, M.; Wan, J.; Lu, M. An accurate and robust range image registration algorithm for 3D object modeling. IEEE Trans. Multimed. 2014, 16, 1377–1390. [Google Scholar] [CrossRef]
- Gao, Y.; Dai, Q. View-based 3-D object retrieval: Challenges and approaches. IEEE Multimed. 2014, 21, 52–57. [Google Scholar] [CrossRef]
- Salti, S.; Tombari, F.; Di Stefano, L. On the use of implicit shape models for recognition of object categories in 3D data. In Asian Conference on Computer Vision; Springer: Berlin, Heidelberg, 2011; Volume 6494, pp. 653–666. [Google Scholar]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. 3D Object recognition in cluttered scenes with local surface features: A survey. IEEE Trans. Pattern Anal. Mach. Intell 2014, 36, 2270–2287. [Google Scholar] [CrossRef]
- Yamany, S.M.; Farag, A.A. Free-form surface registration using surface signatures. In Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1098–1104. [Google Scholar]
- Yang, J.; Cao, Z.; Zhang, Q. A fast and robust local descriptor for 3d point cloud registration. Inf. Sci. 2016, 346, 163–179. [Google Scholar] [CrossRef]
- Albarelli, A.; Rodolà, E.; Torsello, A. Fast and accurate surface alignment through an isometry-enforcing game. Pattern Recognit. 2015, 48, 2209–2226. [Google Scholar] [CrossRef]
- Tombari, F.; Salti, S.; Di Stefano, L. Unique signatures of histograms for local surface description. In European Conference on Computer Vision; Springer: Berlin, Heidelberg, 2010; pp. 356–369. [Google Scholar]
- Guo, Y.; Sohel, F.; Bennamoun, M.; Wan, J.; Lu, M. A novel local surface for 3D object recognition under clutter and occlusion. Inf. Sci. 2015, 293, 196–213. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.; Xian, K.; Xiao, Y.; Cao, Z. Rotational contour signatures for both real-valued and binary feature representations of 3D local shape. Comput. Vis. Image Understand. 2017, 160, 133–147. [Google Scholar] [CrossRef]
- Johnson, A.E.; Hebert, M. Surface matching for object recognition in complex three-dimensional scenes. Image Vis. Comput. 1998, 16, 635–651. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3d registration. In Proceedings of the IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Yang, J.; Zhang, Q.; Xiao, Y.; Cao, Z. TOLDI: An effective and robust approach for 3D local shape description. Pattern Recognit. 2017, 65, 175–187. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J.; Kwok, N.M. A comprehensive performance evaluation of 3d local feature descriptors. Int. J. Comput. Vis. 2016, 116, 66–89. [Google Scholar] [CrossRef]
- Yang, J.; Xiao, Y.; Cao, Z. Toward the repeatability and robustness of the local reference frame for 3D shape matching: An evaluation. IEEE Trans. Image Process. 2018, 27, 3766–3781. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J. An integrated framework for 3-D modeling, object detection, and pose estimation from point-clouds. IEEE Trans. Instrum. Meas. 2015, 64, 683–693. [Google Scholar]
- Tombari, F.; Di Stefano, L. Object recognition in 3D scenes with occlusions and clutter by Hough voting. In Proceedings of the 2010 Fourth Pacific-Rim Symposium on Image and Video Technology, Singapore, 14–17 November 2010; pp. 349–355. [Google Scholar]
- Petrelli, A.; Di Stefano, L. Pairwise registration by local orientation cues. Comput. Graph. Forum 2016, 35, 59–72. [Google Scholar] [CrossRef]
- Dong, Z.; Yang, B.; Liu, Y.; Liang, F.; Li, B.; Zang, Y. A novel binary shape context for 3D local surface description. ISPRS J. Photogramm. Remote Sens. 2017, 130, 431–452. [Google Scholar] [CrossRef]
- Petrelli, A.; Di Stefano, L. A repeatable and efficient canonical reference for surface matching. In Proceedings of the 2012 2nd International Conference on 3D Imaging, Modeling, Processing, Visualization & Transmission, Zurich, Switzerland, 13–15 October 2012; pp. 403–410. [Google Scholar]
- Novatnack, J.; Nishino, K. Scale-dependent/invariant local 3D shape descriptors for fully automatic registration of multiple sets of range images. In European Conference on Computer Vision; Springer: Berlin, Heidelberg, 2008; pp. 440–453. [Google Scholar]
- Levin, D. Mesh-Independent surface interpolation. Geometric Modeling for Scientific Visualization. Mathematics and Visualization; Springer: Berlin, Heidelberg, 2004; pp. 37–49. [Google Scholar]
- Tombari, F.; Salti, S.; Di Stefano, L. Performance evaluation of 3D keypoint detectors. Int. J. Comput. Vis. 2013, 102, 198–220. [Google Scholar] [CrossRef]
- Mian, A.; Bennamoun, M.; Owens, R. On the repeatability and quality of keypoints for local feature-based 3D object retrieval from cluttered scenes. Int. J. Comput. Vis. 2010, 89, 348–361. [Google Scholar] [CrossRef] [Green Version]
- Mian, A.S.; Bennamoun, M.; Owens, R. Three-dimensional model based object recognition and segmentation in cluttered scenes. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1584–1601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kammerl, J.; Blodow, N.; Rusu, R.B.; Gedikli, S.; Beetz, M.; Steinbach, E. Real-time compression of point cloud streams. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, 14–18 May 2012; pp. 778–785. [Google Scholar]



| Dataset | Scenario | Challenge | Modality |
|---|---|---|---|
| Retrieval | Retrieval | Gaussian noise and point density variation | LiDAR |
| Laser Scanner | Object recognition | Clutter and occlusion | LiDAR |
| Kinect | Object recognition | Clutter, occlusion and real noise | Kinect |
| Space Time | Object recognition | Clutter, occlusion, real noise, and outliers | Space Time |
| LiDAR Registration | Registration | Self-occlusion and missing regions | LiDAR |
| Kinect Registration | Registration | Self-occlusion, missing regions, and real noise | Kinect |
| Retrieval | Laser Scanner | Kinect | Space Time | LiDAR Registration | Kinect Registration | |
|---|---|---|---|---|---|---|
| EM | 0.4992 | 0.0998 | 0.2040 | 0.2507 | 0.1079 | 0.0949 |
| SHOT | 0.5121 | 0.1360 | 0.1903 | 0.2517 | 0.1330 | 0.0905 |
| BSC | 0.5121 | 0.1360 | 0.1903 | 0.2517 | 0.1330 | 0.0905 |
| TOLDI | 0.4445 | 0.1386 | 0.1605 | 0.2458 | 0.1391 | 0.0792 |
| GF() | 0.1930 | 0.0936 | 0.0468 | 0.2189 | 0.1234 | 0.0350 |
| GF() | 0.4056 | 0.1338 | 0.1414 | 0.2478 | 0.1420 | 0.0751 |
| GF() | 0.5151 | 0.1292 | 0.1965 | 0.2597 | 0.1289 | 0.0935 |
| GF() | 0.5238 | 0.1164 | 0.2008 | 0.2565 | 0.1120 | 0.0960 |
| GF() | 0.5175 | 0.1091 | 0.2028 | 0.2508 | 0.1155 | 0.0956 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tao, W.; Hua, X.; Yu, K.; Wang, R.; He, X. A Comparative Study of Weighting Methods for Local Reference Frame. Appl. Sci. 2020, 10, 3223. https://doi.org/10.3390/app10093223
Tao W, Hua X, Yu K, Wang R, He X. A Comparative Study of Weighting Methods for Local Reference Frame. Applied Sciences. 2020; 10(9):3223. https://doi.org/10.3390/app10093223
Chicago/Turabian StyleTao, Wuyong, Xianghong Hua, Kegen Yu, Ruisheng Wang, and Xiaoxing He. 2020. "A Comparative Study of Weighting Methods for Local Reference Frame" Applied Sciences 10, no. 9: 3223. https://doi.org/10.3390/app10093223
APA StyleTao, W., Hua, X., Yu, K., Wang, R., & He, X. (2020). A Comparative Study of Weighting Methods for Local Reference Frame. Applied Sciences, 10(9), 3223. https://doi.org/10.3390/app10093223







