Design Optimization and Experimental Verification of Permanent Magnet Synchronous Motor Used in Electric Compressors in Electric Vehicles
Abstract
:Featured Application
Abstract
1. Introduction
2. PMSM for Electric Compressor
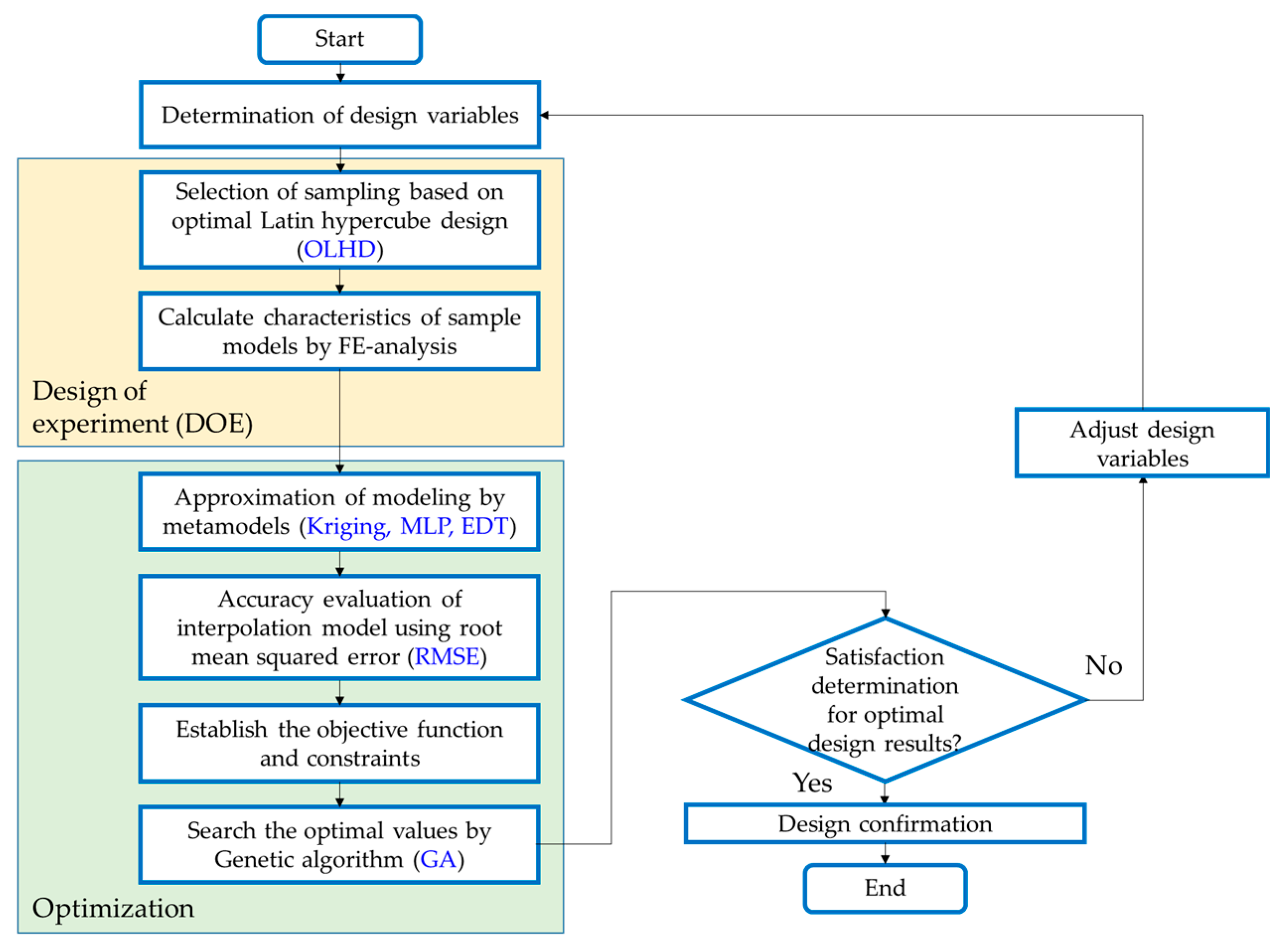
3. Design Optimization
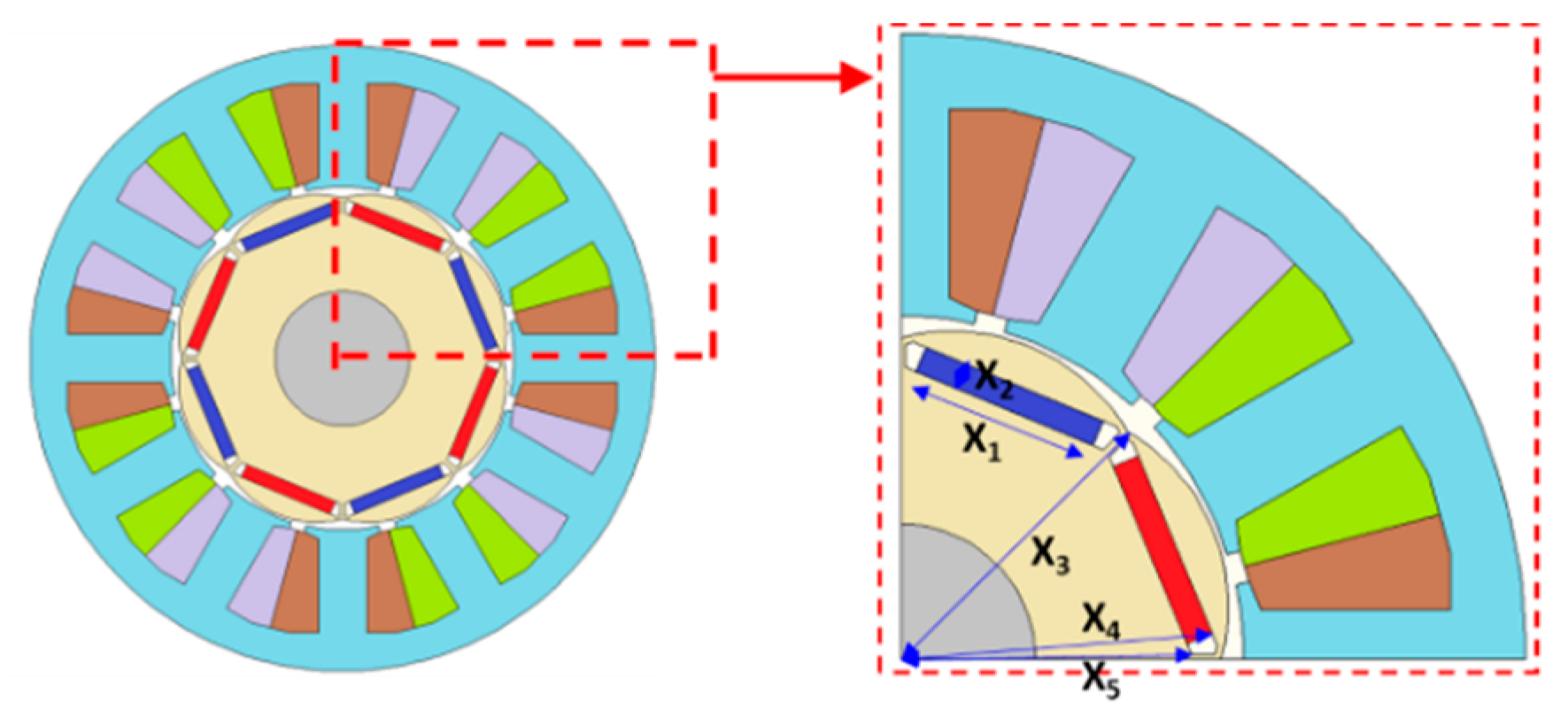
3.1. Rotor Shape Optimization Process
- Objective function:
- Constraints:
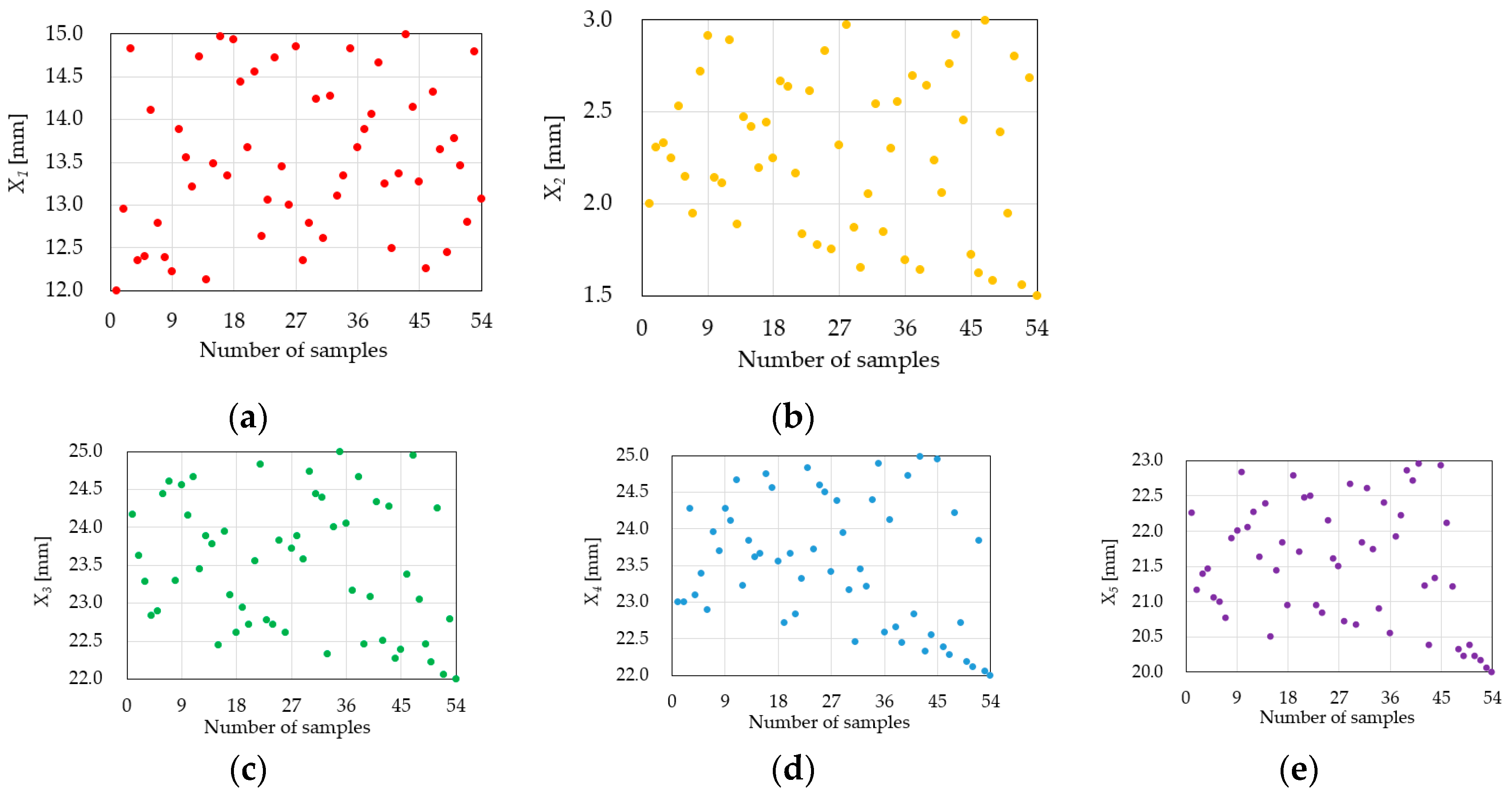
3.2. Design of Experiment
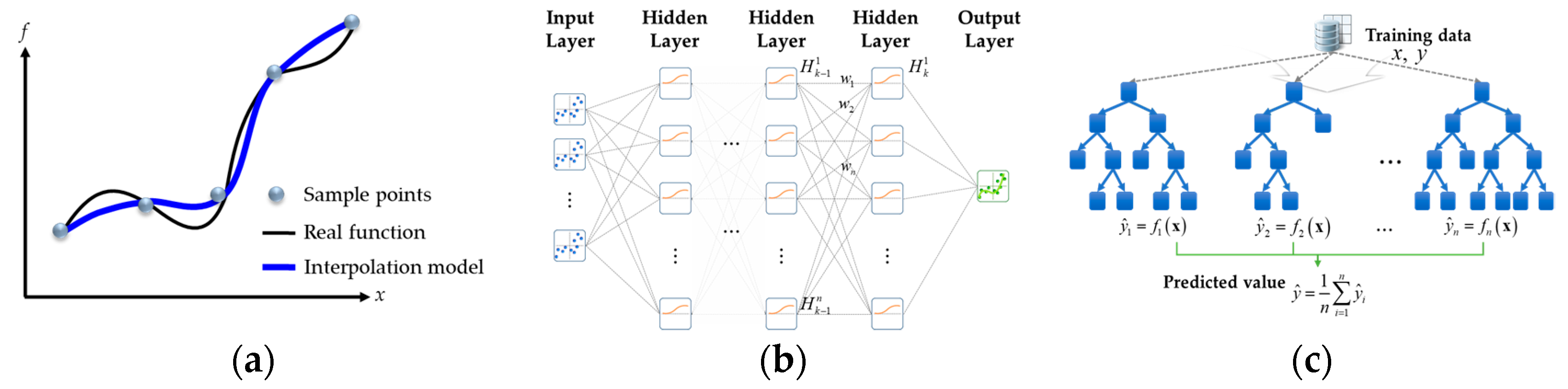
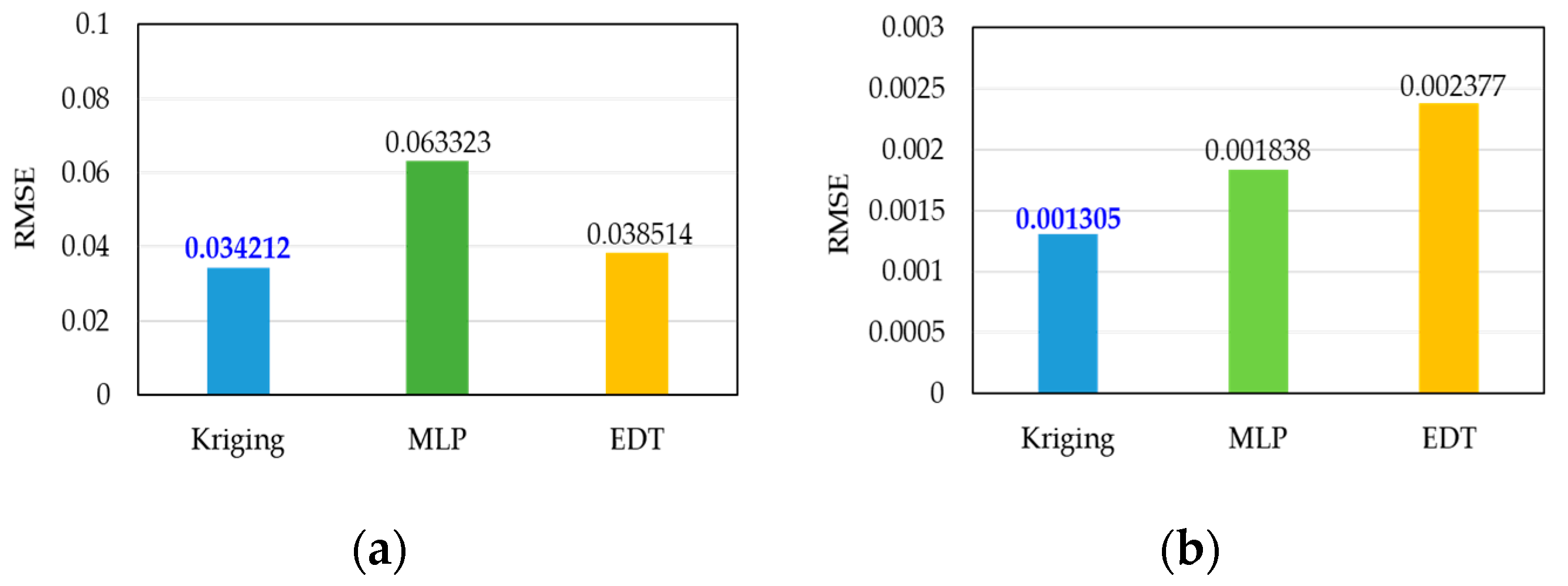
3.3. Metadmodeling
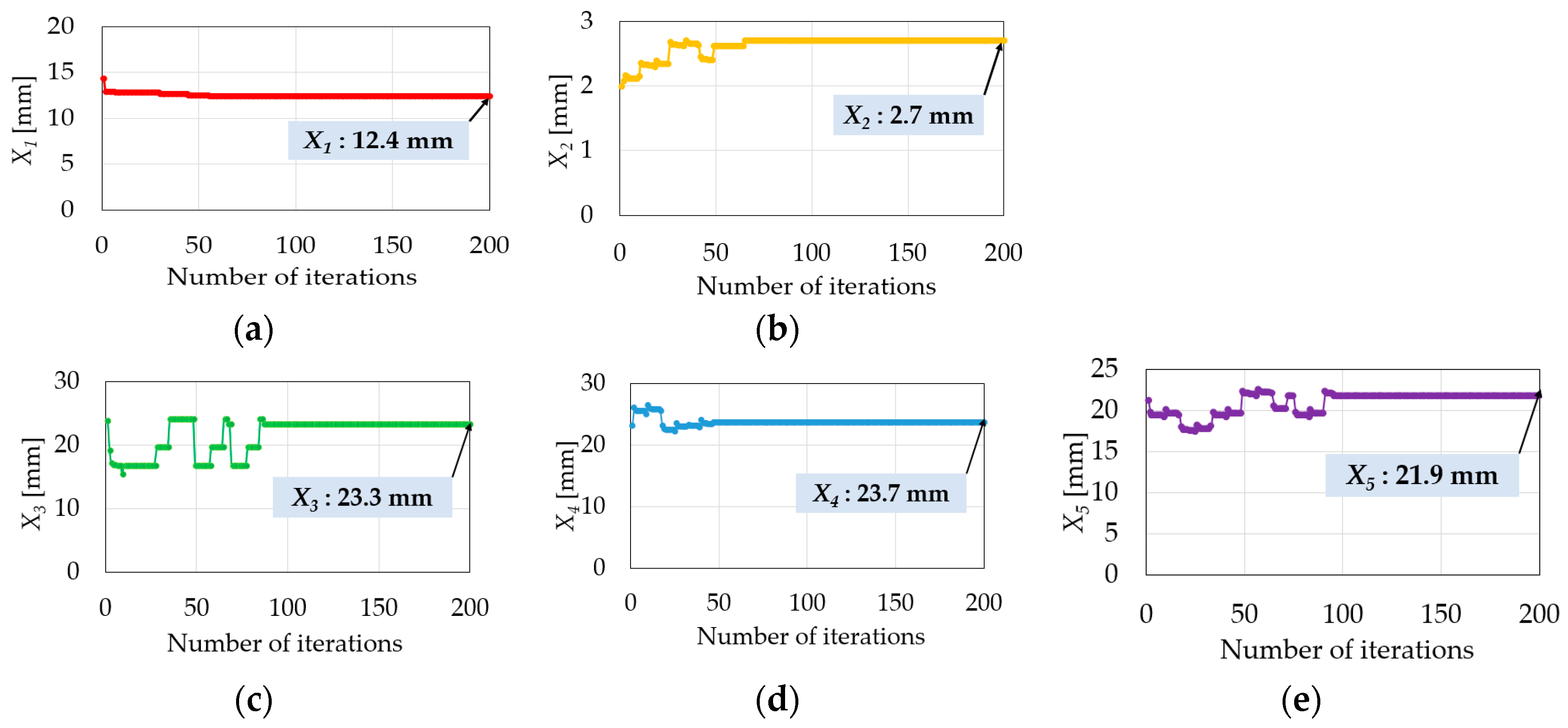
3.4. Global Searching with the GA
4. Verification of Simulations and Experiments
4.1. Simulation Results
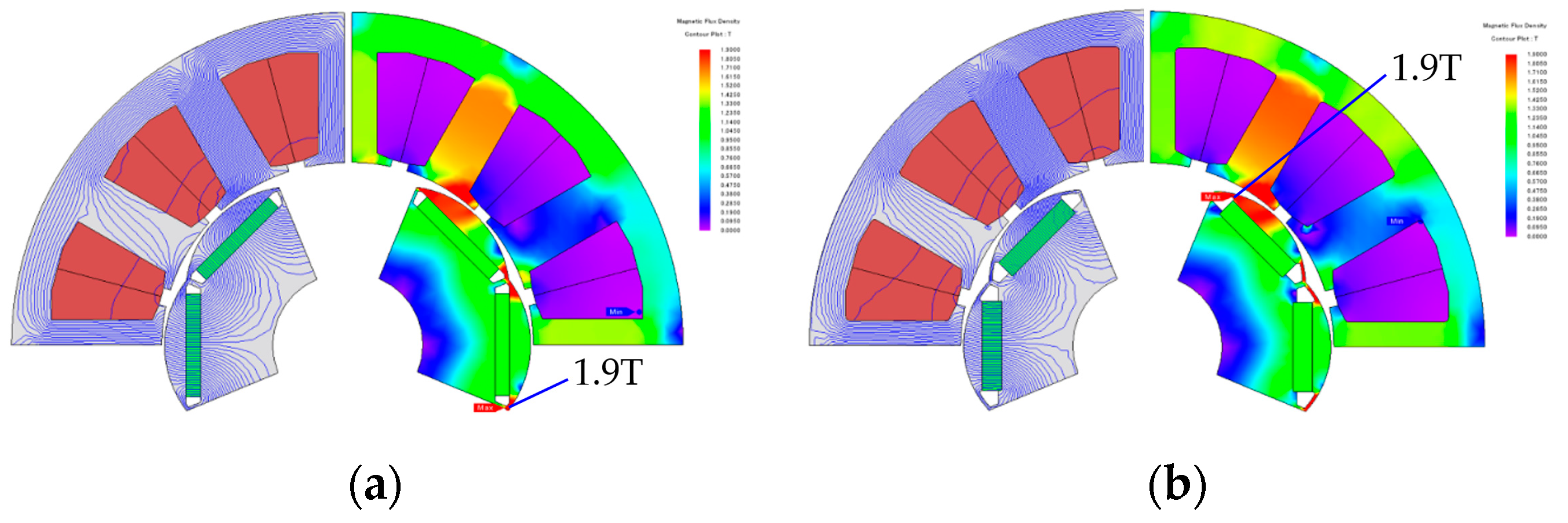
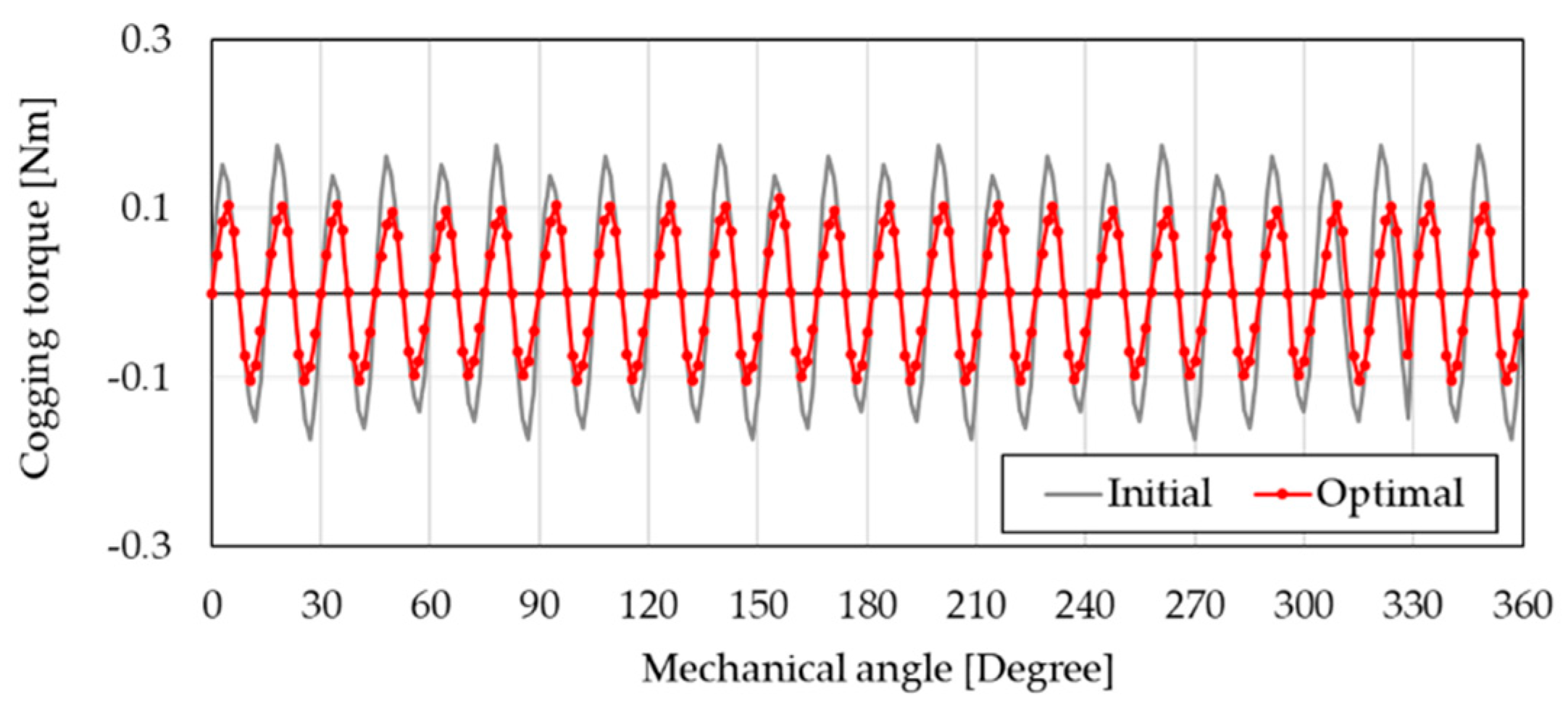
4.1.1. No-Load Analysis
4.1.2. Load Analysis
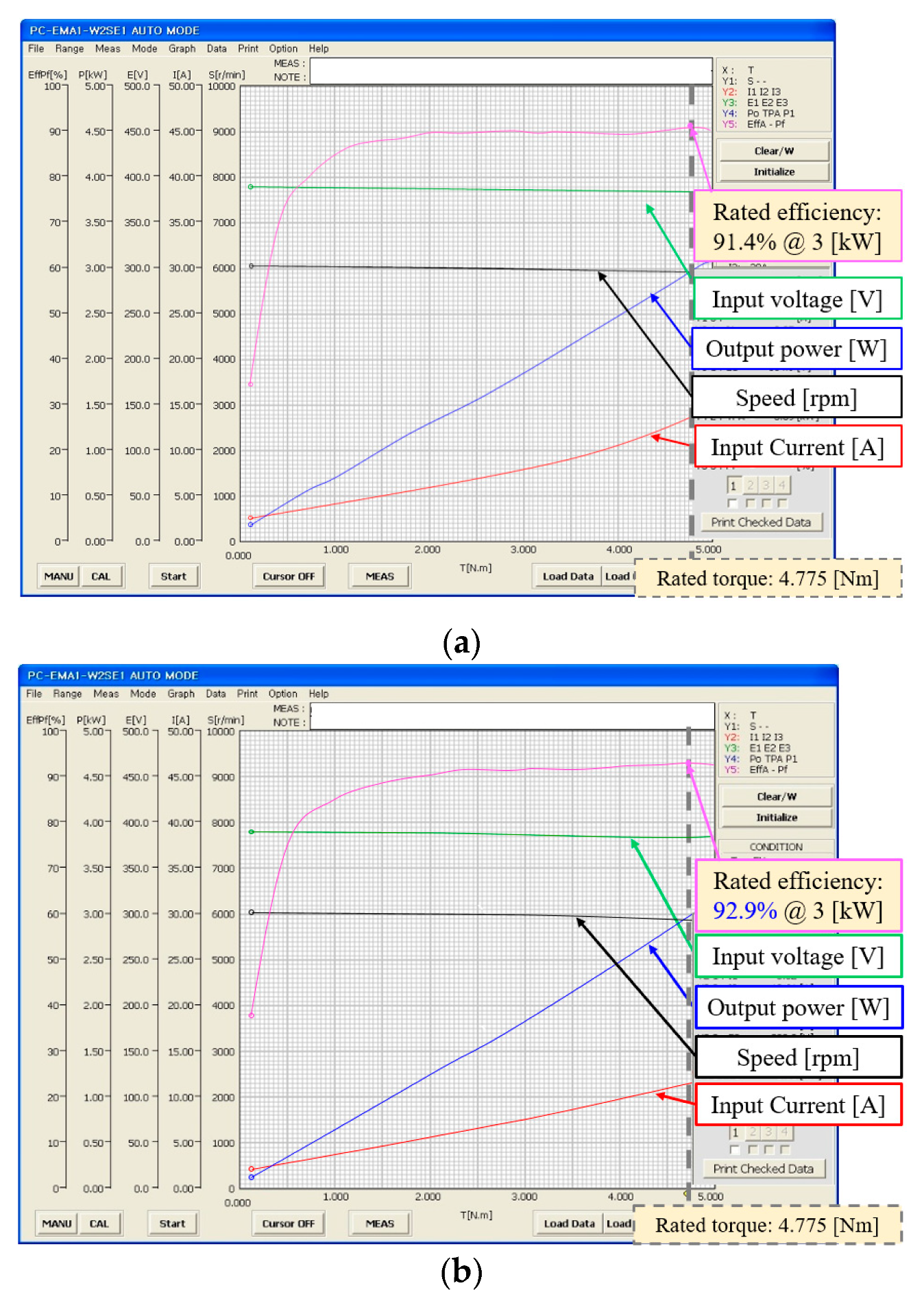
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Number | X1 | X2 | X3 | X4 | X5 | Efficiency (%) | Cogging Torque (Nm) |
|---|---|---|---|---|---|---|---|
| 1 | 12.000 | 2.000 | 24.167 | 22.998 | 22.267 | 91.87 | 0.2746 |
| 2 | 12.956 | 2.306 | 23.625 | 23.000 | 21.166 | 91.91 | 0.2774 |
| 3 | 14.833 | 2.333 | 23.278 | 24.278 | 21.389 | 92.35 | 0.2816 |
| 4 | 12.352 | 2.250 | 22.833 | 23.091 | 21.458 | 92.98 | 0.2939 |
| 5 | 12.400 | 2.528 | 22.889 | 23.389 | 21.056 | 93.21 | 0.2881 |
| 6 | 14.111 | 2.150 | 24.444 | 22.889 | 21.000 | 92.88 | 0.3242 |
| 7 | 12.785 | 1.946 | 24.611 | 23.952 | 20.766 | 92.38 | 0.3438 |
| 8 | 12.380 | 2.720 | 23.300 | 23.700 | 21.900 | 91.55 | 0.2778 |
| 9 | 12.222 | 2.916 | 24.556 | 24.275 | 22.000 | 92.35 | 0.3412 |
| 10 | 13.889 | 2.139 | 24.161 | 24.109 | 22.833 | 91.37 | 0.2751 |
| 11 | 13.558 | 2.111 | 24.670 | 24.662 | 22.056 | 93.06 | 0.2736 |
| 12 | 13.215 | 2.889 | 23.444 | 23.222 | 22.278 | 93.06 | 0.3176 |
| 13 | 14.733 | 1.890 | 23.891 | 23.840 | 21.634 | 91.42 | 0.2765 |
| 14 | 12.122 | 2.472 | 23.778 | 23.611 | 22.389 | 93.44 | 0.3272 |
| 15 | 13.482 | 2.417 | 22.444 | 23.667 | 20.500 | 93.58 | 0.3385 |
| 16 | 14.971 | 2.194 | 23.948 | 24.749 | 21.433 | 93.01 | 0.2761 |
| 17 | 13.347 | 2.444 | 23.111 | 24.555 | 21.833 | 91.11 | 0.2863 |
| 18 | 14.933 | 2.250 | 22.611 | 23.555 | 20.944 | 93.41 | 0.3026 |
| 19 | 14.444 | 2.667 | 22.945 | 22.723 | 22.777 | 92.74 | 0.2855 |
| 20 | 13.668 | 2.639 | 22.722 | 23.667 | 21.704 | 91.51 | 0.2969 |
| 21 | 14.556 | 2.167 | 23.556 | 22.835 | 22.479 | 91.85 | 0.3275 |
| 22 | 12.631 | 1.833 | 24.831 | 23.322 | 22.500 | 93.13 | 0.3438 |
| 23 | 13.055 | 2.611 | 22.778 | 24.833 | 20.947 | 92.96 | 0.2973 |
| 24 | 14.723 | 1.778 | 22.712 | 23.722 | 20.832 | 91.49 | 0.2989 |
| 25 | 13.444 | 2.833 | 23.832 | 24.597 | 22.150 | 91.08 | 0.2779 |
| 26 | 13.000 | 1.750 | 22.608 | 24.500 | 21.611 | 91.12 | 0.3045 |
| 27 | 14.855 | 2.320 | 23.721 | 23.411 | 21.501 | 93.27 | 0.2771 |
| 28 | 12.345 | 2.972 | 23.883 | 24.381 | 20.722 | 91.27 | 0.2774 |
| 29 | 12.784 | 1.872 | 23.575 | 23.942 | 22.667 | 93.41 | 0.2781 |
| 30 | 14.234 | 1.652 | 24.738 | 23.166 | 20.665 | 92.99 | 0.2741 |
| 31 | 12.611 | 2.055 | 24.445 | 22.453 | 21.835 | 92.56 | 0.2737 |
| 32 | 14.278 | 2.540 | 24.388 | 23.444 | 22.611 | 93.34 | 0.2738 |
| 33 | 13.111 | 1.847 | 22.325 | 23.213 | 21.748 | 91.03 | 0.3178 |
| 34 | 13.344 | 2.298 | 24.000 | 24.390 | 20.889 | 93.21 | 0.2965 |
| 35 | 14.834 | 2.556 | 25.000 | 24.885 | 22.407 | 92.97 | 0.2833 |
| 36 | 13.667 | 1.691 | 24.056 | 22.584 | 20.556 | 92.63 | 0.2755 |
| 37 | 13.879 | 2.695 | 23.167 | 24.117 | 21.927 | 93.38 | 0.2829 |
| 38 | 14.056 | 1.639 | 24.666 | 22.662 | 22.216 | 93.67 | 0.2734 |
| 39 | 14.667 | 2.642 | 22.459 | 22.444 | 22.857 | 92.53 | 0.3112 |
| 40 | 13.250 | 2.235 | 23.088 | 24.722 | 22.711 | 93.04 | 0.2836 |
| 41 | 12.489 | 2.057 | 24.331 | 22.832 | 22.958 | 92.83 | 0.2751 |
| 42 | 13.367 | 2.762 | 22.503 | 24.978 | 21.222 | 92.91 | 0.3053 |
| 43 | 14.999 | 2.922 | 24.278 | 22.333 | 20.390 | 92.36 | 0.2941 |
| 44 | 14.145 | 2.452 | 22.271 | 22.553 | 21.333 | 92.61 | 0.2911 |
| 45 | 13.265 | 1.721 | 22.389 | 24.944 | 22.942 | 92.94 | 0.2839 |
| 46 | 12.256 | 1.622 | 23.378 | 22.385 | 22.113 | 92.49 | 0.2781 |
| 47 | 14.325 | 2.996 | 24.944 | 22.278 | 21.218 | 92.33 | 0.2735 |
| 48 | 13.650 | 1.583 | 23.051 | 24.220 | 20.333 | 91.37 | 0.2847 |
| 49 | 12.444 | 2.389 | 22.455 | 22.722 | 20.222 | 92.71 | 0.9267 |
| 50 | 13.777 | 1.944 | 22.222 | 22.192 | 20.389 | 92.21 | 0.3221 |
| 51 | 13.458 | 2.805 | 24.246 | 22.111 | 20.221 | 92.19 | 0.3333 |
| 52 | 12.798 | 1.558 | 22.060 | 23.833 | 20.167 | 93.45 | 0.3445 |
| 53 | 14.795 | 2.685 | 22.794 | 22.056 | 20.056 | 92.15 | 0.2736 |
| 54 | 13.075 | 1.500 | 22.001 | 22.001 | 20.001 | 92.11 | 0.3511 |
References
- Yilmaz, M.; Krein, P.T. Review of battery charger topologies, charging power levels, and infrastructure for plug-in electric and hybrid vehicles. IEEE Trans. Power Electron. 2013, 28, 2151–2169. [Google Scholar] [CrossRef]
- Chukwu, U.C.; Mahajan, S.M. Real-time management of power systems with V2G facility for smart-grid applications. IEEE Trans. Sustain. Energy 2014, 5, 558–566. [Google Scholar] [CrossRef]
- Babin, A.; Rizoug, N.; Mesbahi, T.; Boscher, D.; Hamdoun, Z.; Larouci, C. Total cost of ownership improvement of commercial electric vehicles using battery sizing and intelligent charge method. IEEE Trans. Ind. Appl. 2018, 54, 1691–1700. [Google Scholar] [CrossRef]
- Loiselle-Lapointe, A.; Whittal, I.; Christenson, M. Electric Vehicles: Impacts of Mileage Accumulation and Fast Charging. World Electr. Veh. J. 2016, 8, 249–262. [Google Scholar] [CrossRef] [Green Version]
- De Almeida, A.T.; Ferreira, F.J.; Baoming, G. Beyond Induction Motors—Technology Trends to Move Up Efficiency. IEEE Trans. Ind. Appl. 2013, 50, 2103–2114. [Google Scholar] [CrossRef]
- Yang, Z.; Shang, F.; Brown, I.P.; Krishnamurthy, M. Comparative study of interior permanent magnet, induction, and switched reluctance motor drives for EV and HEV applications. IEEE Trans. Transp. Electrif. 2015, 1, 245–254. [Google Scholar] [CrossRef]
- Lu, C.; Ferrari, S.; Pellegrino, G. Two Design Procedures for PM Synchronous Machines for Electric Powertrains. IEEE Trans. Transp. Electrif. 2017, 4, 98–107. [Google Scholar] [CrossRef] [Green Version]
- Jung, T.-U. Development of Hybrid Electric Compressor Motor Drive System for Hybrid Electrical Vehicles. J. Power Electron. 2009, 9, 960–968. [Google Scholar]
- Jolly, L.; Jabbar, M.A.; Qinghua, L. Design optimization of permanent magnet motors using response surface methodology and genetic algorithms. IEEE Trans. Magn. 2005, 41, 3928–3930. [Google Scholar] [CrossRef]
- Hwang, C.-C.; Cho, Y.H. Effects of leakage flux on magnetic fields of interior permanent magnet synchronous motors. IEEE Trans. Magn. 2001, 37, 3021–3024. [Google Scholar] [CrossRef]
- Ilka, R.; Alinejad-Beromi, Y.; Yaghobi, H. Techno-economic Design Optimisation of an Interior Permanent-Magnet Synchronous Motor by the Multi-Objective Approach. IET Electr. Power Appl. 2018, 12, 972–978. [Google Scholar] [CrossRef]
- Hong, G.; Wei, T.; Ding, X. Multi-objective Optimal Design of Permanent Magnet Synchronous Motor for High Effciency and High Dynamic Performance. IEEE Access 2018, 6, 23568–23581. [Google Scholar] [CrossRef]
- Cho, S.; Jung, K.; Choi, J. Design Optimization of Interior Permanent Magnet Synchronous Motor for Electric Compressors of Air-Conditioning Systems Mounted on EVs and HEVs. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Baek, S. Optimum shape design of a BLDC motor for electric continuous variable valve timing system considering efficiency and torque characteristics. Microsyst. Technol. 2018, 24, 4441–4452. [Google Scholar] [CrossRef]
- Lee, S.; Baek, S. A study on the improvement of the cam phase control performance of an electric continuous variable valve timing system using a cycloid reducer and BLDC motor. Microsyst. Technol. 2020, 26, 59–70. [Google Scholar] [CrossRef]
- Ortega, A.J.P.; Paul, S.; Islam, R.; Xu, L. Analytical model for predicting effects of manufacturing variations on cogging torque in surface-mounted permanent magnet motors. IEEE Trans. Magn. 2016, 52, 3050–3061. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, H.; Meng, G.; Zhou, S.; Cao, Q. Analytical calculation of magnetic field and cogging torque in surface-mounted permanent-magnet machines accounting for any eccentric rotor shape. IEEE Trans. Ind. Electron. 2015, 62, 3438–3447. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.W.; Song, J.Y.; Kim, Y.J.; Jung, S.Y. A Novel Memetic Algorithm Using Modified Particle Swarm Optimization and Mesh Adaptive Direct Search for PMSM Design. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Edhah, S.O.; Alsawalhi, J.Y.; Al-Durra, A.A. Multi-Objective Optimization Design of Fractional Slot Concentrated Winding Permanent Magnet Synchronous Machines. IEEE Access 2019, 7, 162874–162882. [Google Scholar] [CrossRef]
- Chung, S.U.; Kim, J.W.; Chun, Y.D.; Woo, B.C.; Hong, D.K. Fractional Slot Concentrated Winding PMSM with Consequent Pole Rotor for a Low-Speed Direct Drive Reduction of Rare Earth Permanent Magnet. IEEE Trans. Energy Convers. 2015, 30, 103–109. [Google Scholar] [CrossRef]
- Kwon, J.W.; Lee, J.H.; Zhao, W.L.; Kwon, B.I. Flux-Switching Permanent Magnet Machine with Phase-Group Concentrated-Coil Windings and Cogging Torque Reduction Technique. Energies 2018, 11, 2758. [Google Scholar] [CrossRef] [Green Version]
- Yoon, K.-Y.; Baek, S.-W. Robust design optimization with penalty function for electric oil pumps with BLDC motors. Energies 2019, 12, 153. [Google Scholar] [CrossRef] [Green Version]
- Guo, H.; He, H.; Sun, F. A combined cooperative braking model with a predictive control strategy in an electric vehicle. Energies 2013, 6, 6455–6475. [Google Scholar] [CrossRef]
- Ma, P.; Zhou, Y.; Shang, X.; Yang, M. Firing accuracy evaluation of electromagnetic railgun based on multicriteria optimal Latin hypercube design. IEEE Trans. Plasma Sci. 2017, 45, 1503–1511. [Google Scholar] [CrossRef]
- Shin, P.S.; Woo, S.H.; Koh, C.S. An optimal design of large scale permanent magnet pole shape using adaptive response surface method with Latin hypercube sampling strategy. IEEE Trans. Magn. 2009, 45, 1214–1217. [Google Scholar] [CrossRef]
- Zhang, B.S.; Song, B.W.; Mao, Z.Y.; Tian, W.L.; Li, B.Y.; Li, B. Novel parametric modeling method and optimal design for savonius wind turbines. Energies 2017, 10, 301. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.K.; Song, B.W.; Mao, Z.Y.; Tian, W.L. Analysis and optimization of the electromagnetic performance of a novel stator modular ring drive thruster motor. Energies 2018, 11, 1598. [Google Scholar] [CrossRef] [Green Version]
- Gong, J.; Gillon, F.; Canh, J.T.; Xu, Y. Proposal of a Kriging output space mapping technique for electromagnetic design optimization. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, F. Performance study of multilayer perceptrons in a low-cost electronic nose. IEEE Trans. Instrum. Meas. 2014, 36, 1670–1679. [Google Scholar] [CrossRef]
- Franzese, G.; Visintin, M. Probabilistic ensemble of deep Information networks. Entropy 2020, 22, 100. [Google Scholar] [CrossRef] [Green Version]
- Baek, S.; Kwon, B. Optimum design of a single-phase line-start PM motor considering efficiency, maximum torque, and starting torque. IEEE Trans. Magn. 2012, 48, 4850–4859. [Google Scholar] [CrossRef]
- Yan, C.; Zhu, J.; Shen, X.; Fan, J.; Mi, D.; Qian, Z. Ensemble of regression-type and interpolation-type metamodels. Energies 2020, 13, 654. [Google Scholar] [CrossRef] [Green Version]
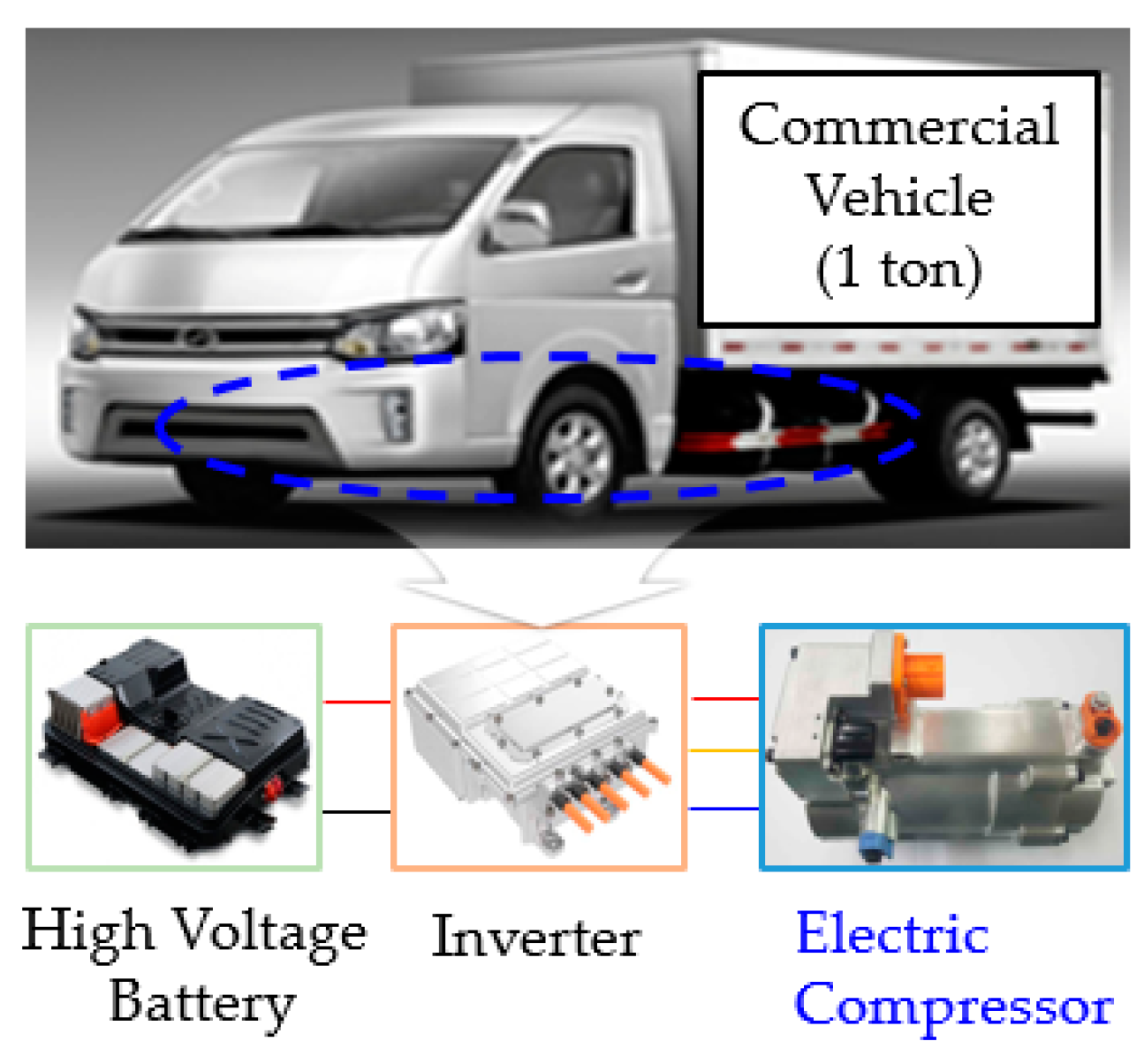
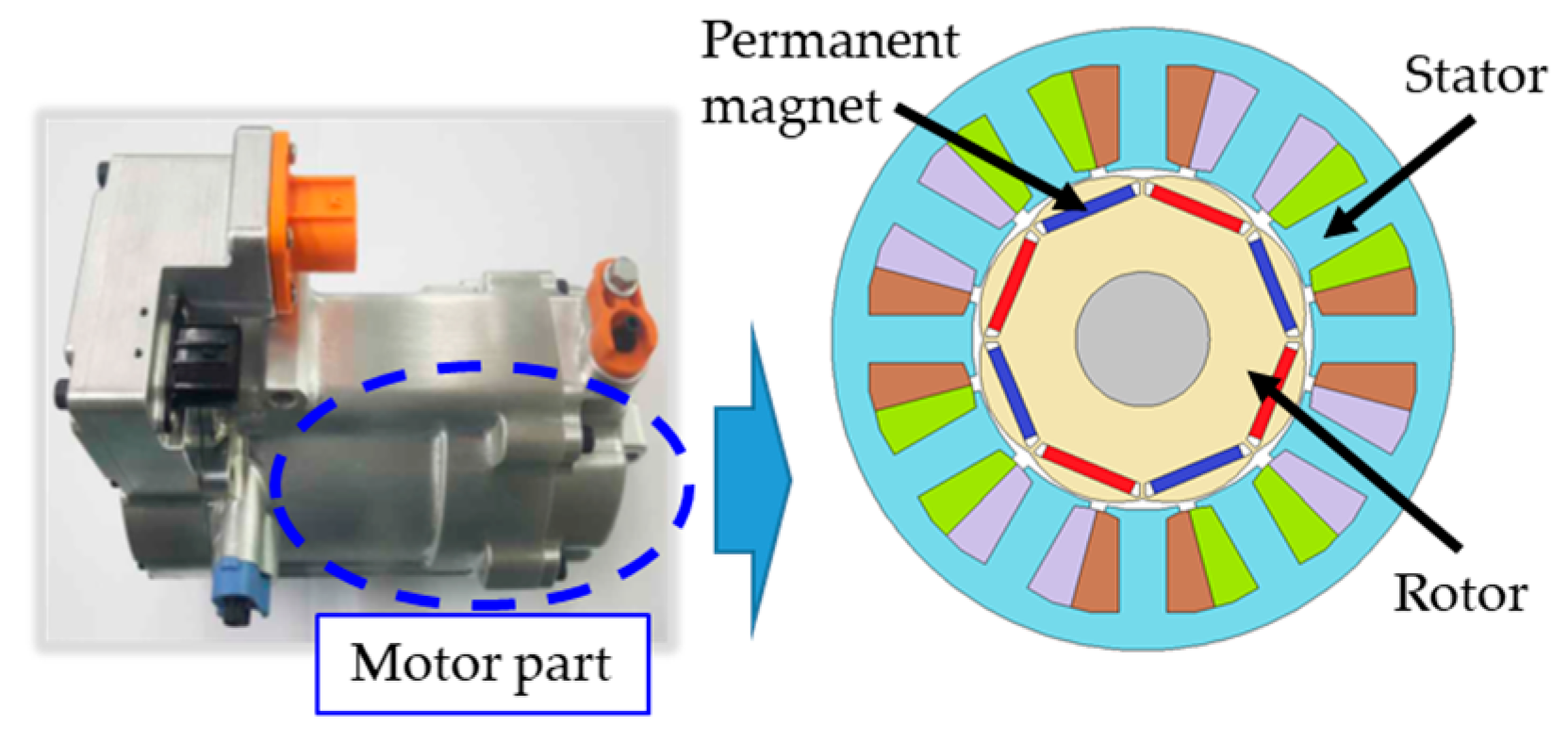
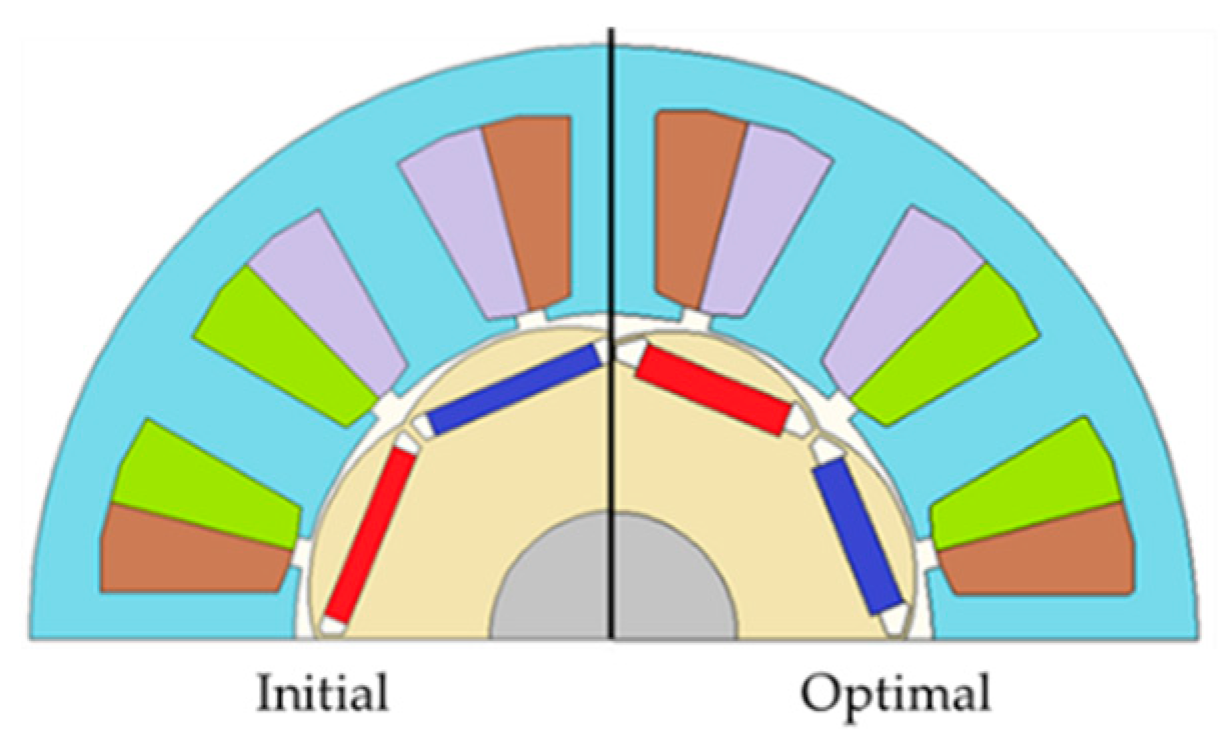
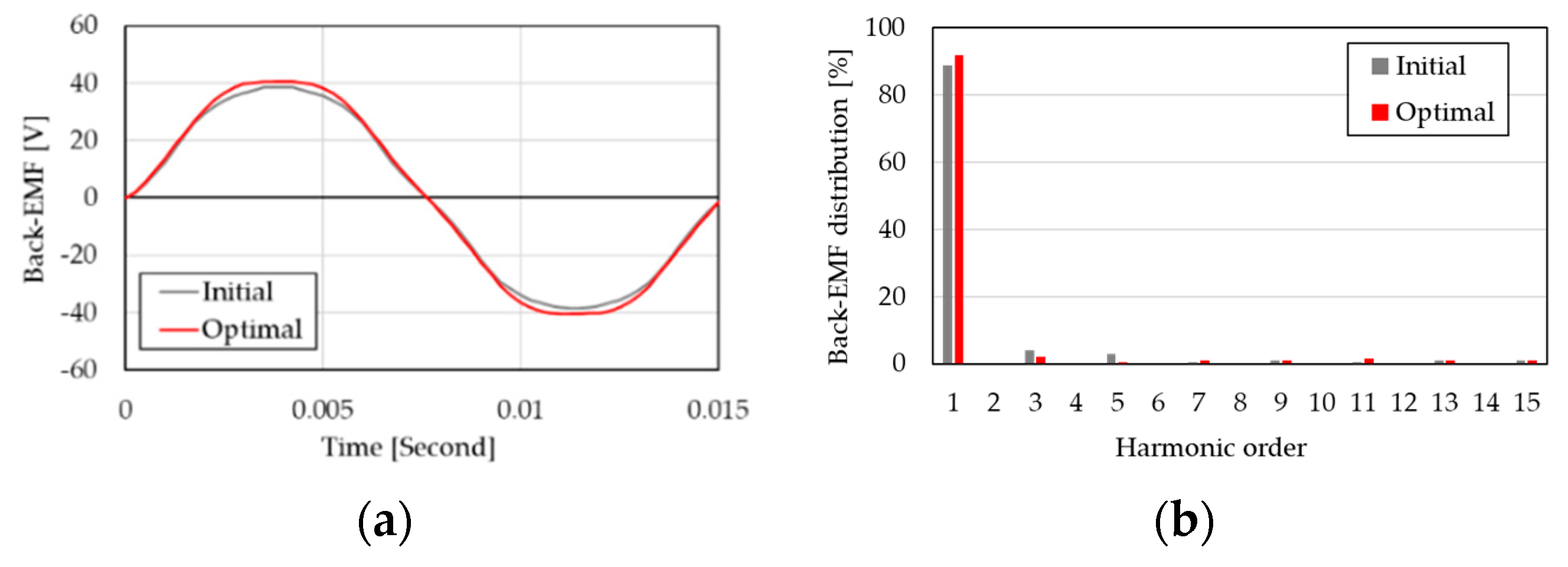
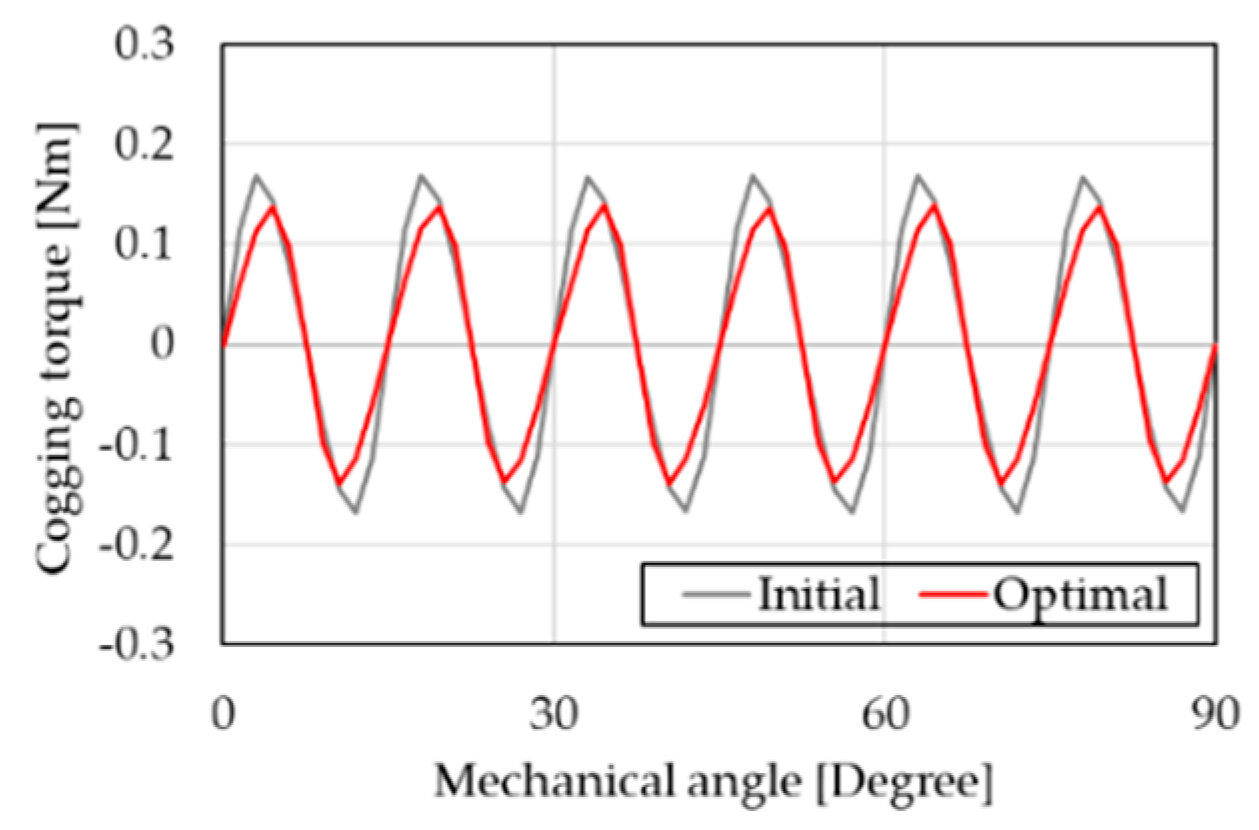
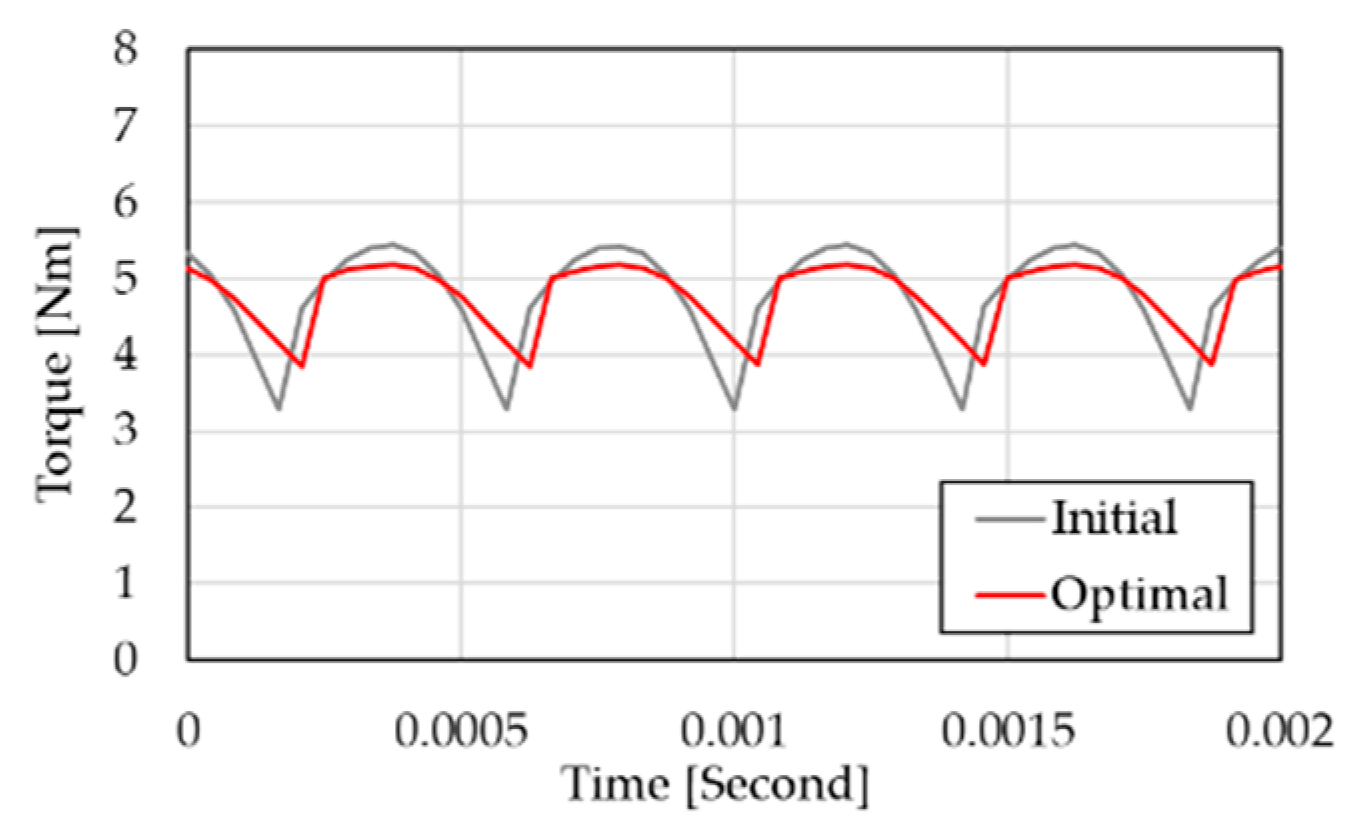


| Items | Unit | Value | |
|---|---|---|---|
| Required specification | Input voltage | V | 380 |
| Rated speed | rpm | 6000 | |
| Rated output power | W | 3000 | |
| Operation frequency | Hz | 400 | |
| Mechanical dimension | Stator’s outer diameter | mm | 93 |
| Stator’s inner diameter | mm | 51 | |
| Rotor’s outer diameter | mm | 50.2 | |
| Shaft diameter | mm | 20 | |
| Air gap length | mm | 0.4 | |
| Stack length | mm | 60 | |
| Electrical dimension | Coil turns | mm | 40 |
| Coil thickness | 0.9 | ||
| Material | Electrical steel | - | 35PN230 |
| Permanent magnet | N42UH | ||
| Characteristics | Back-EMF(@1000rpm) | Vrms | 27.8 |
| Cogging torque(peak to peak) | Nm | 0.3479 | |
| Torque(@rated speed) | Nm | 4.775 | |
| Input current(@rated speed) | Arms | 12.85 | |
| Efficiency(@rated speed) | % | 91.40 | |
| Parameters | Lower (XL) | Upper (XU) | Unit | Remark |
|---|---|---|---|---|
| X1 | 12 | 15 | mm | Magnet length |
| X2 | 1.5 | 3.0 | mm | Magnet width |
| X3 | 22 | 25 | mm | Distance between the center and the inner diameter of rotor |
| X4 | 22 | 25 | mm | Distance between the center and the magnet |
| X5 | 20 | 23 | mm | Distance between the center and the barrier |
| Parameters | Initial | Optimal | Unit |
|---|---|---|---|
| X1 | 14.3 | 12.4 | mm |
| X2 | 2 | 2.7 | mm |
| X3 | 23.8 | 23.3 | mm |
| X4 | 23.2 | 23.7 | mm |
| X5 | 21.3 | 21.9 | mm |
| Items | Initial | Optimal | Unit | |
|---|---|---|---|---|
| Simulation | Rated efficiency | 92.0 | 93.5 | % |
| Cogging torque | 0.3479 | 0.2778 | Nm | |
| Experiment | Rated efficiency | 91.4 | 92.9 | % |
| Cogging torque | 0.2778 | 0.2153 | Nm | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baek, S.-W.; Lee, S.W. Design Optimization and Experimental Verification of Permanent Magnet Synchronous Motor Used in Electric Compressors in Electric Vehicles. Appl. Sci. 2020, 10, 3235. https://doi.org/10.3390/app10093235
Baek S-W, Lee SW. Design Optimization and Experimental Verification of Permanent Magnet Synchronous Motor Used in Electric Compressors in Electric Vehicles. Applied Sciences. 2020; 10(9):3235. https://doi.org/10.3390/app10093235
Chicago/Turabian StyleBaek, Soo-Whang, and Sang Wook Lee. 2020. "Design Optimization and Experimental Verification of Permanent Magnet Synchronous Motor Used in Electric Compressors in Electric Vehicles" Applied Sciences 10, no. 9: 3235. https://doi.org/10.3390/app10093235
APA StyleBaek, S.-W., & Lee, S. W. (2020). Design Optimization and Experimental Verification of Permanent Magnet Synchronous Motor Used in Electric Compressors in Electric Vehicles. Applied Sciences, 10(9), 3235. https://doi.org/10.3390/app10093235





