Study on Passenger Comfort Based on Human–Bus–Road Coupled Vibration
Abstract
1. Introduction
2. Human–Bus–Road Coupled Vibration System
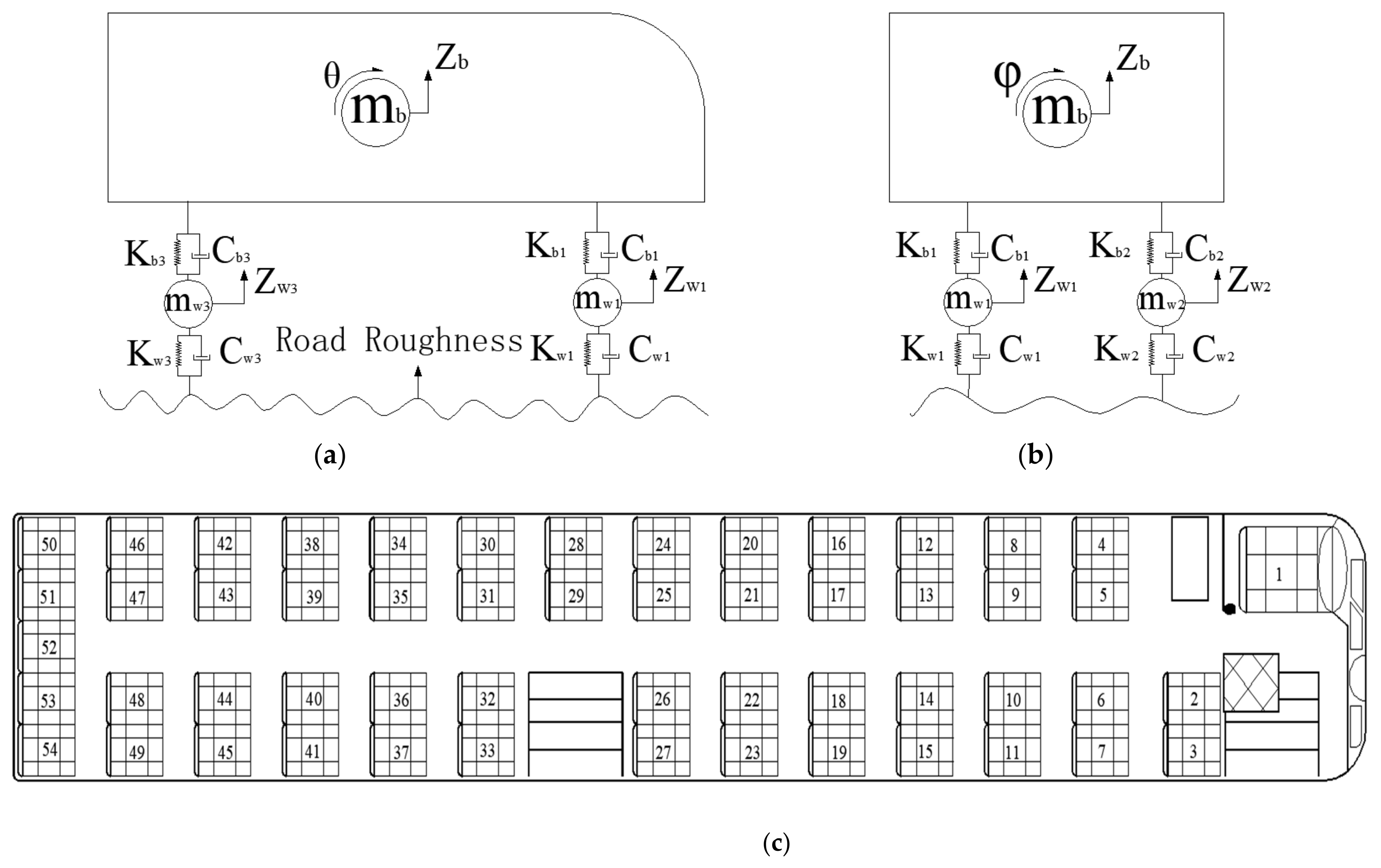
2.1. Human–Bus–Road Model
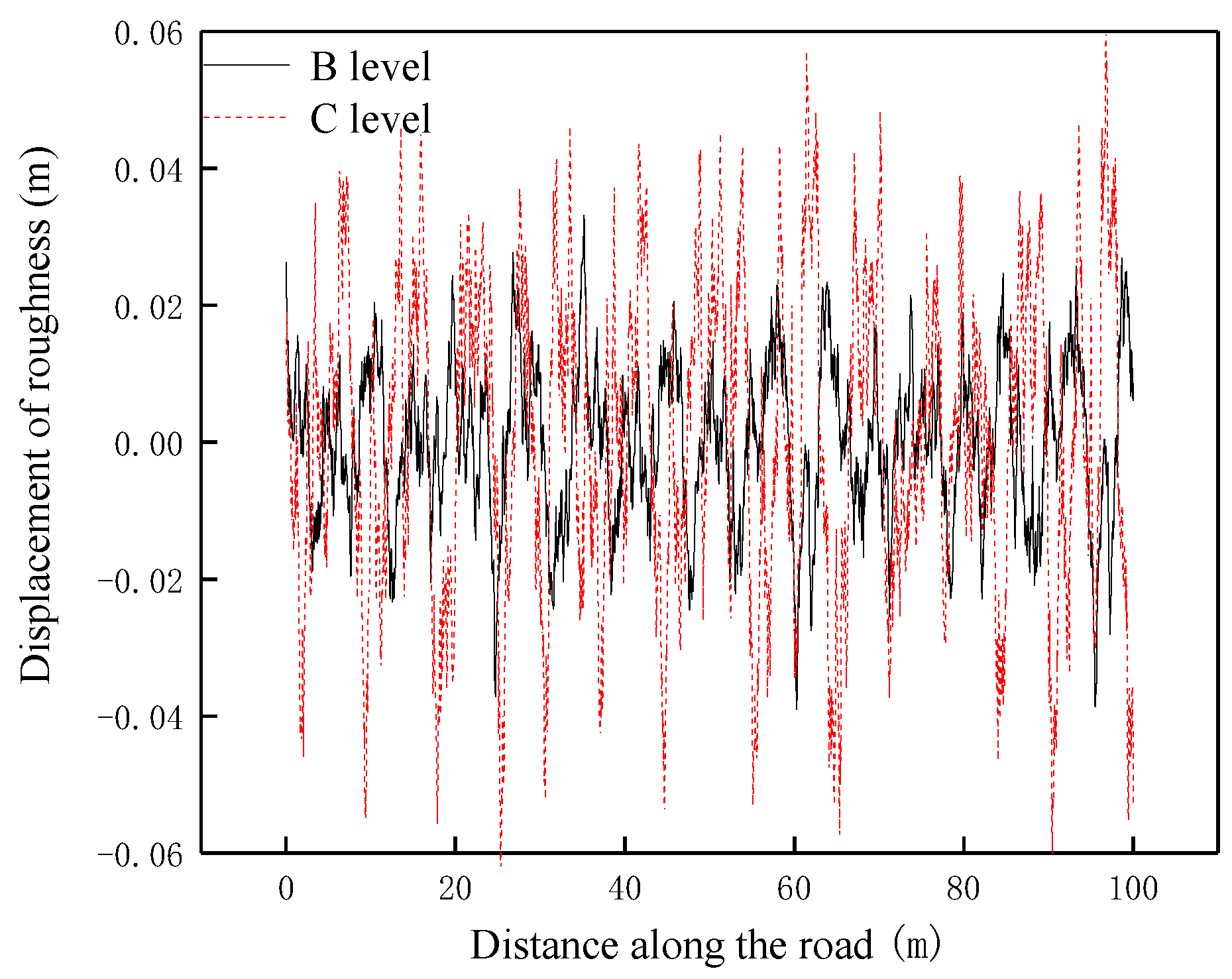
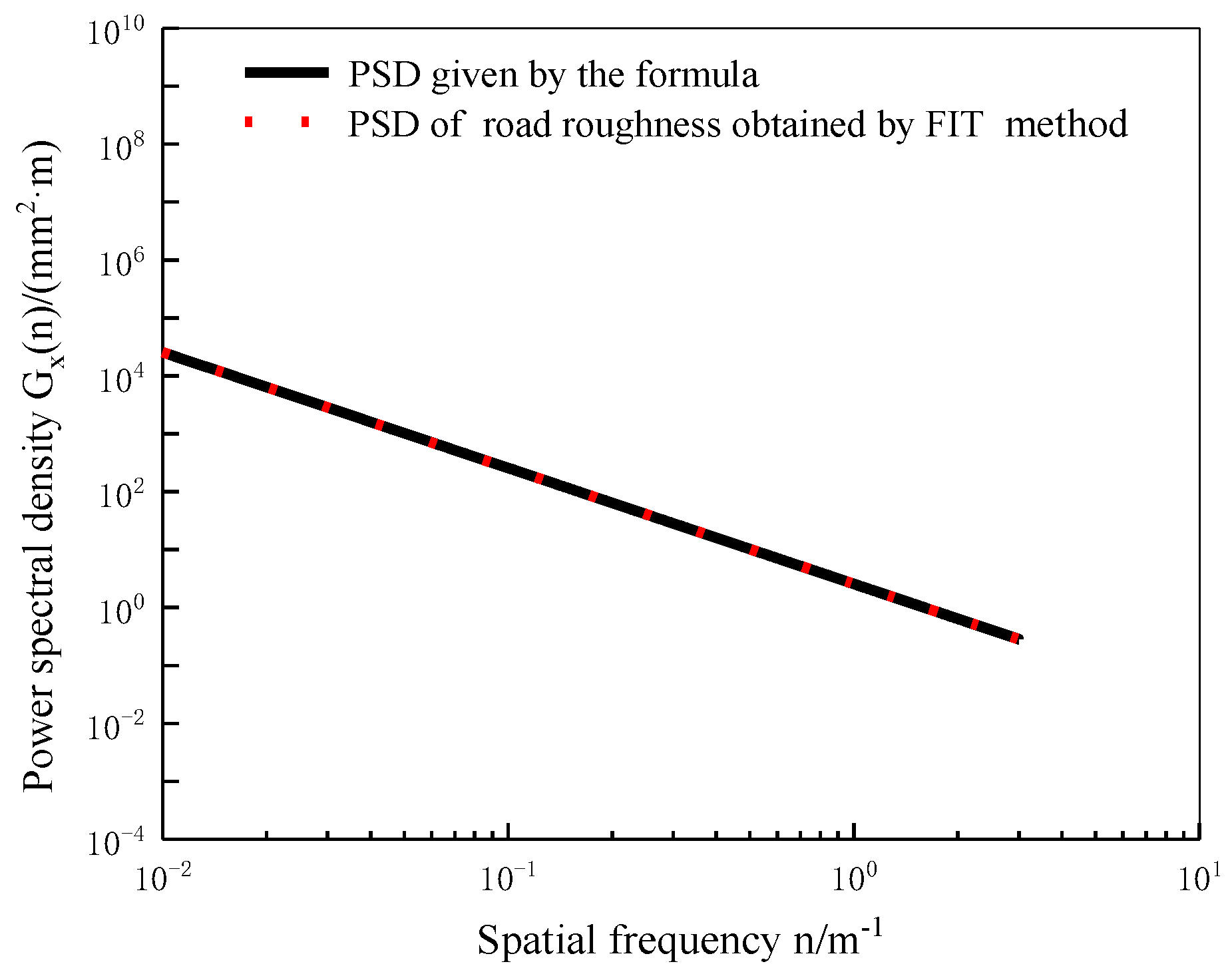
2.1.1. Asphalt Road Model
2.1.2. Road Surface Roughness Condition
2.1.3. 3D Human–Bus Model
2.2. Differential Equations of Human–Bus–Road Coupled Vibration
3. Comfort Evaluation of Human Body
3.1. Calculation of Root Mean Square (RMS) Acceleration
3.2. Comfort Evaluation Based on ISO 2631 Standard
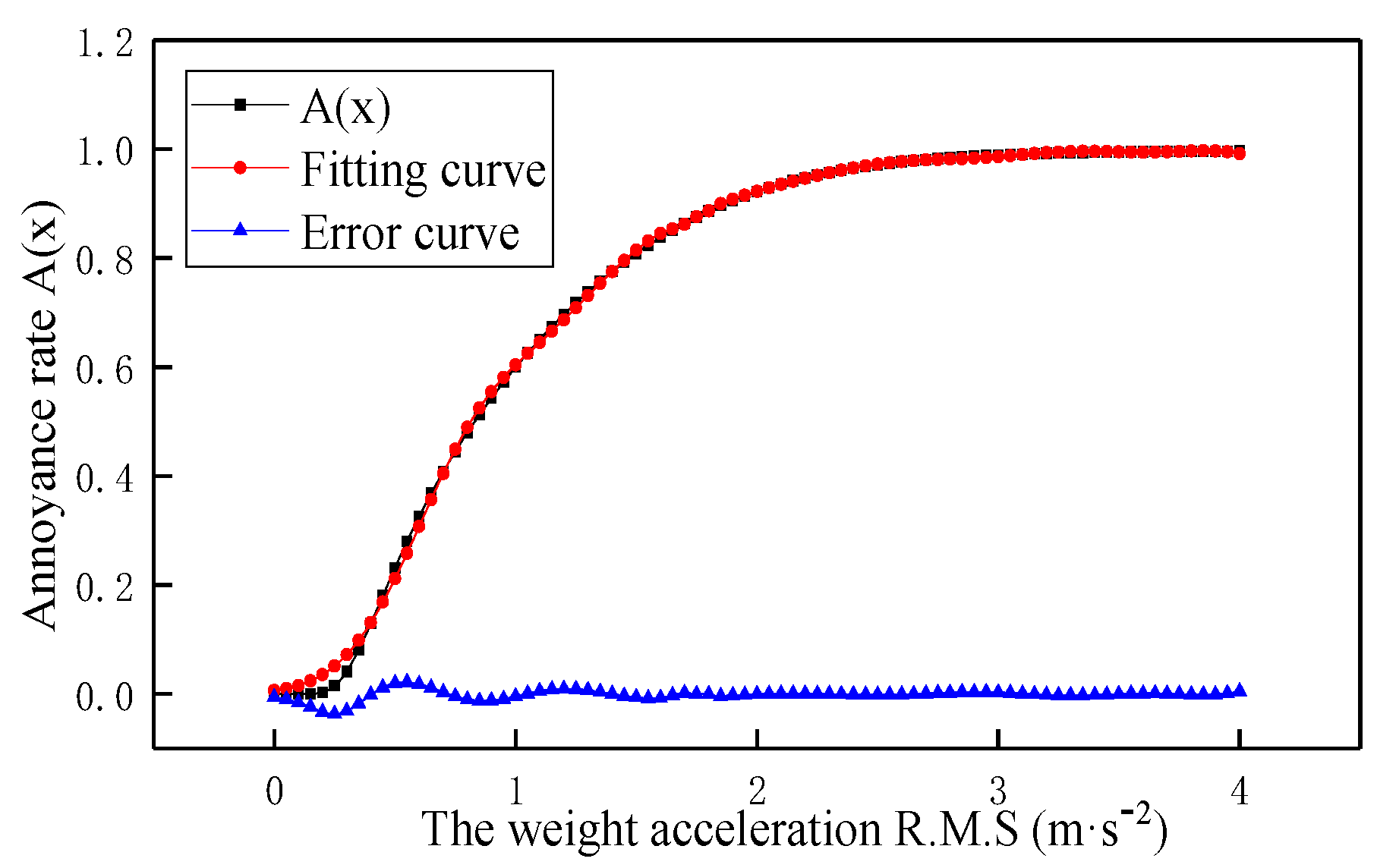
3.3. Comfort Evaluation Based on Annoyance Rate
4. Case Study
4.1. Description of Numerical Example
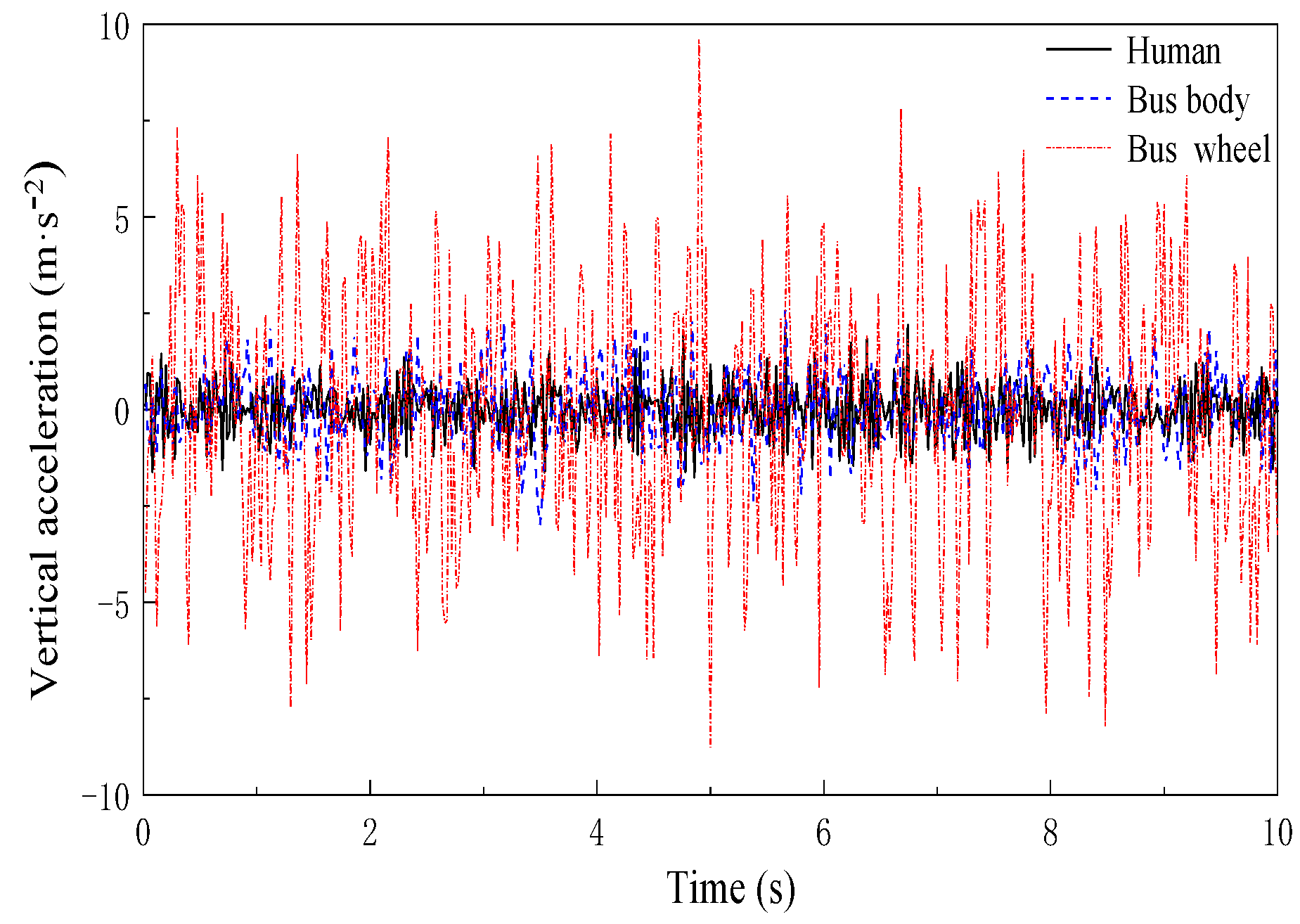
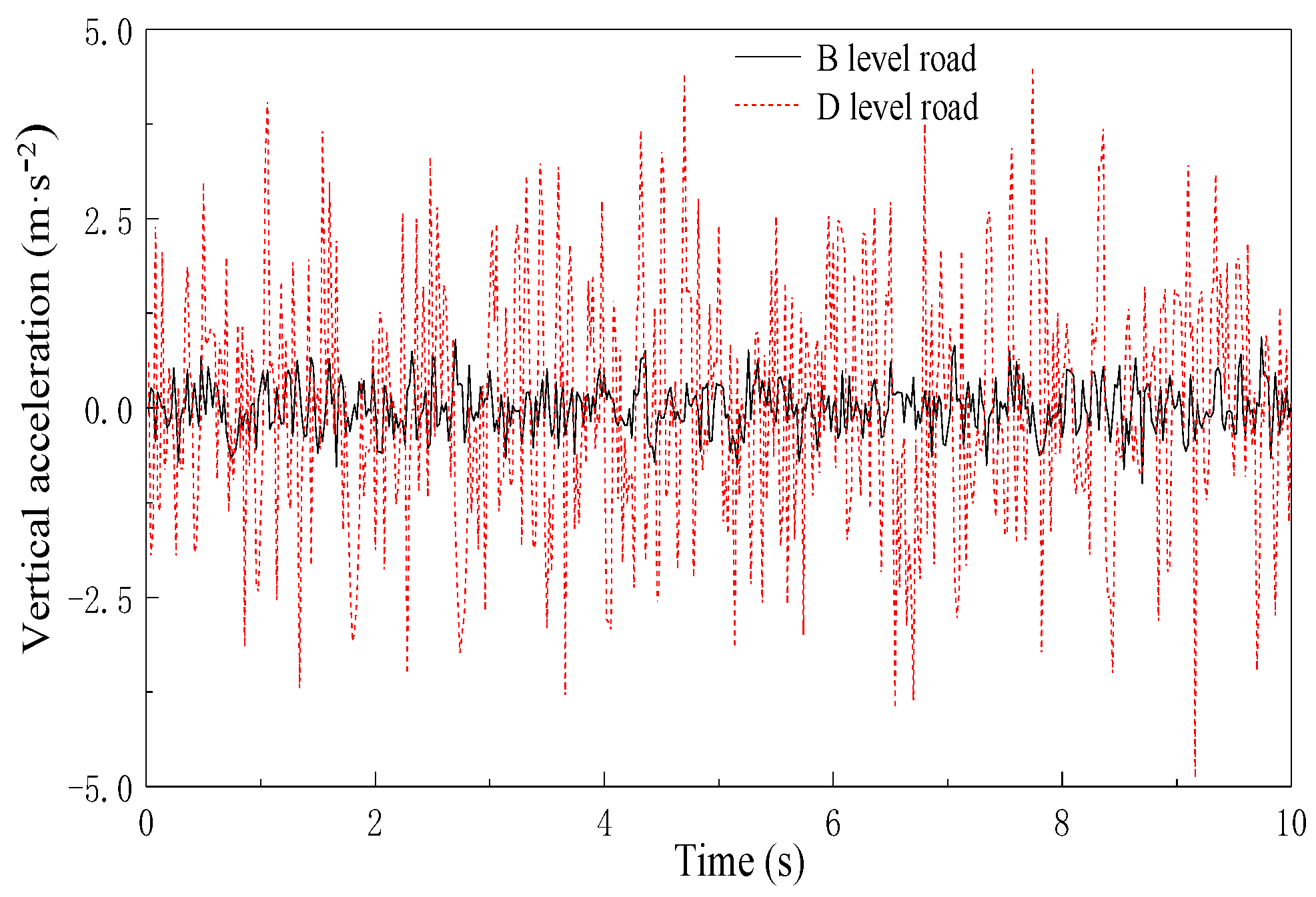
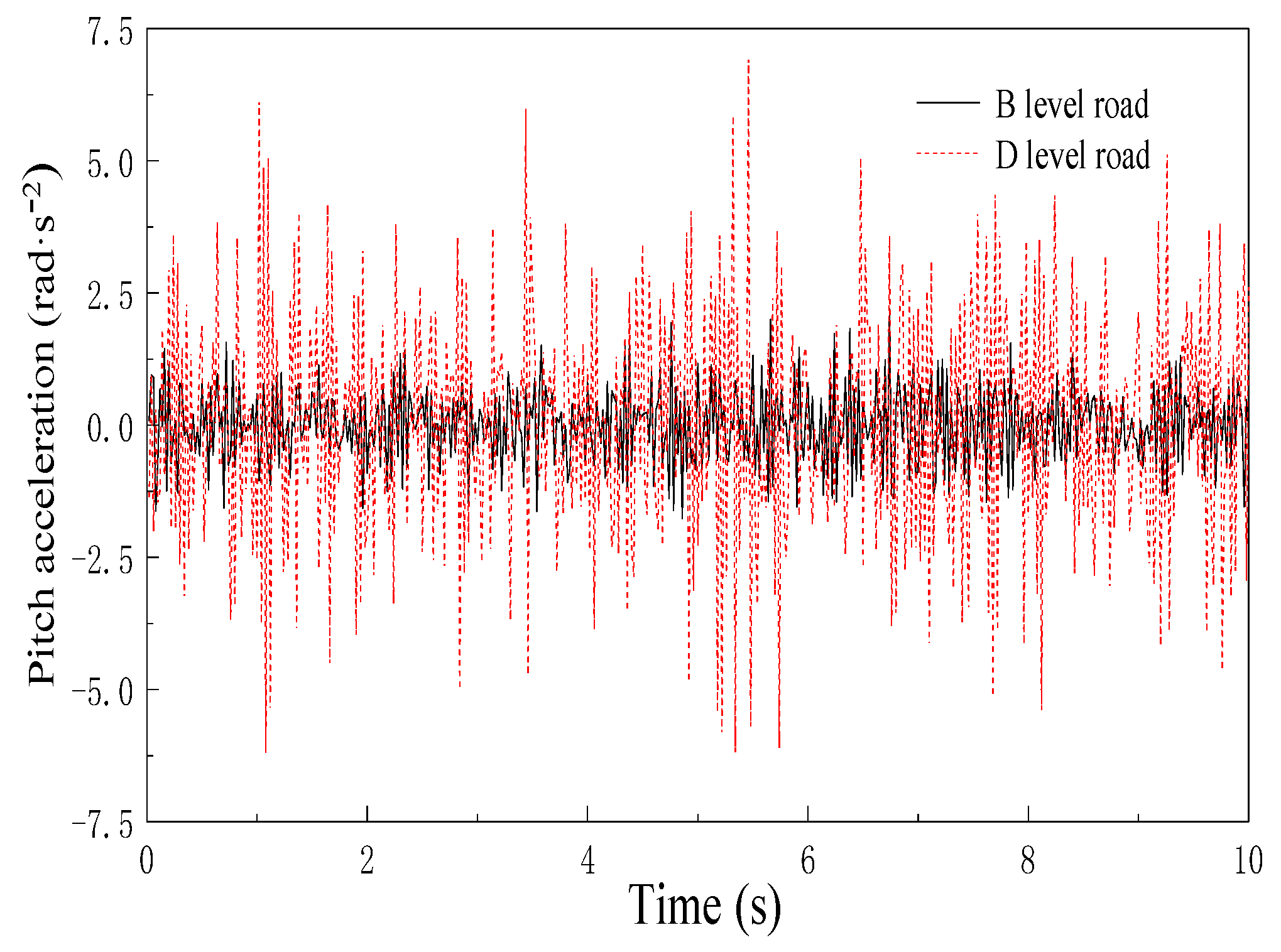
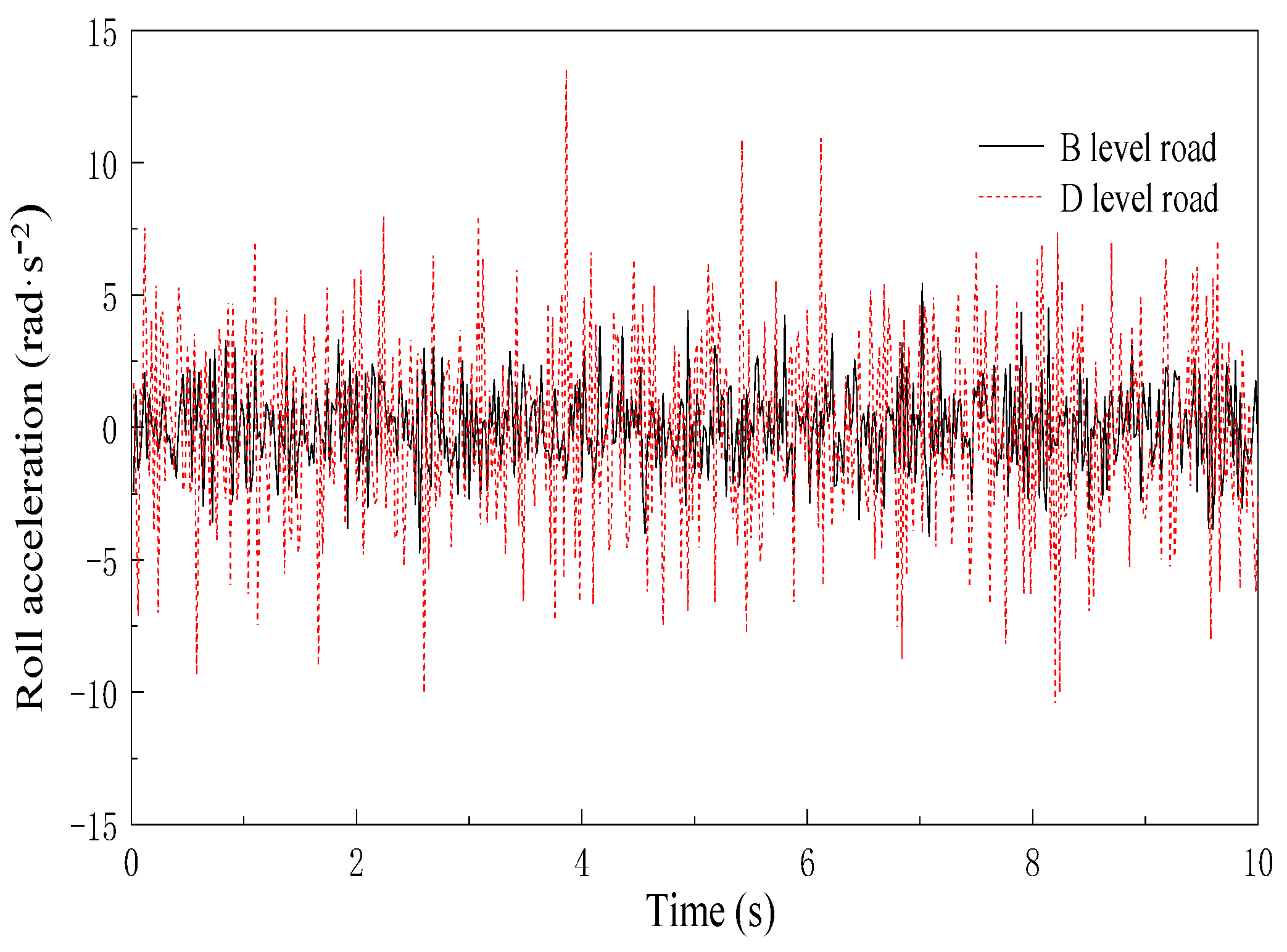
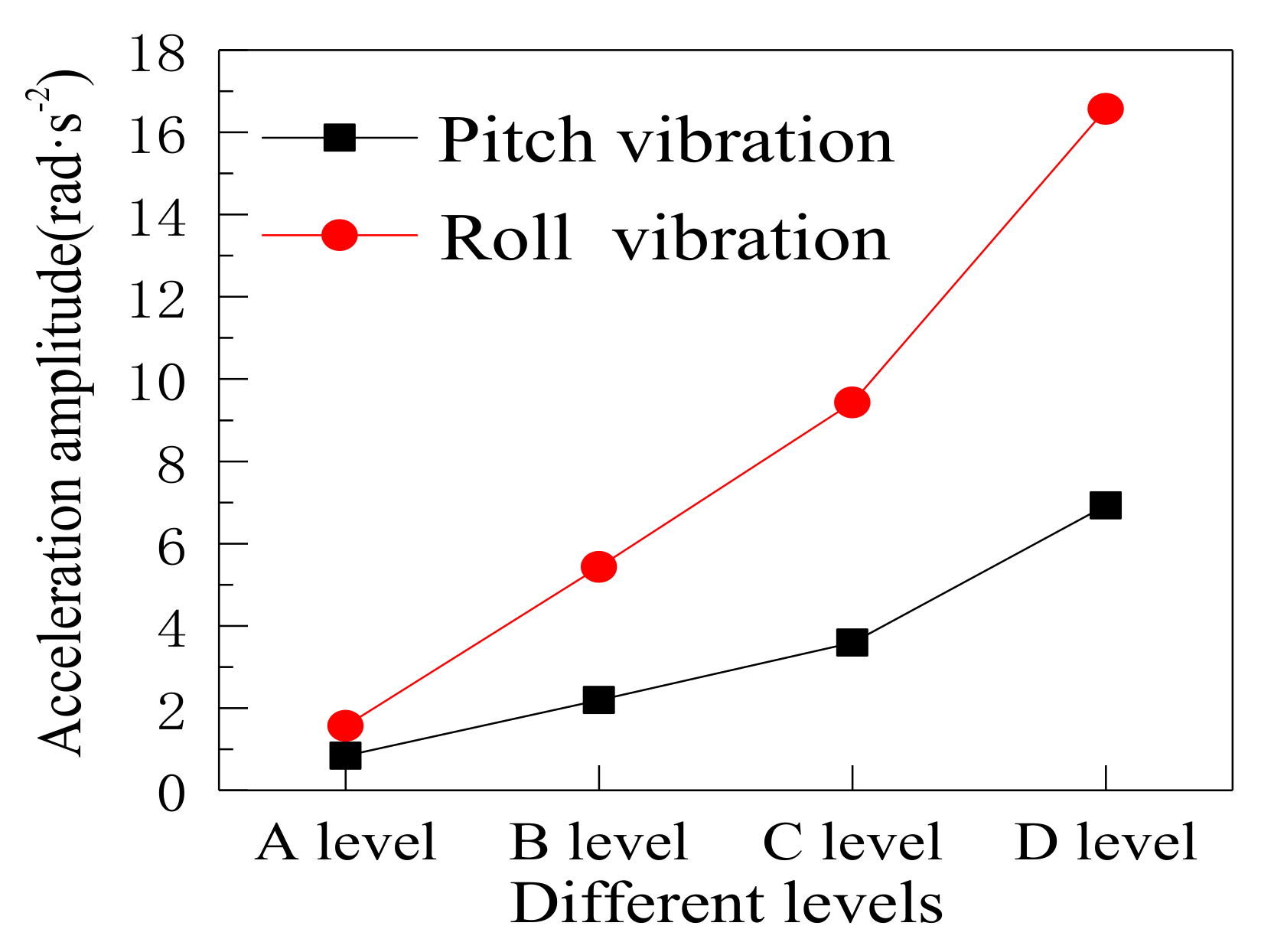
4.2. Dynamic Responses
4.3. Comfort Evaluation
5. Parametric Study
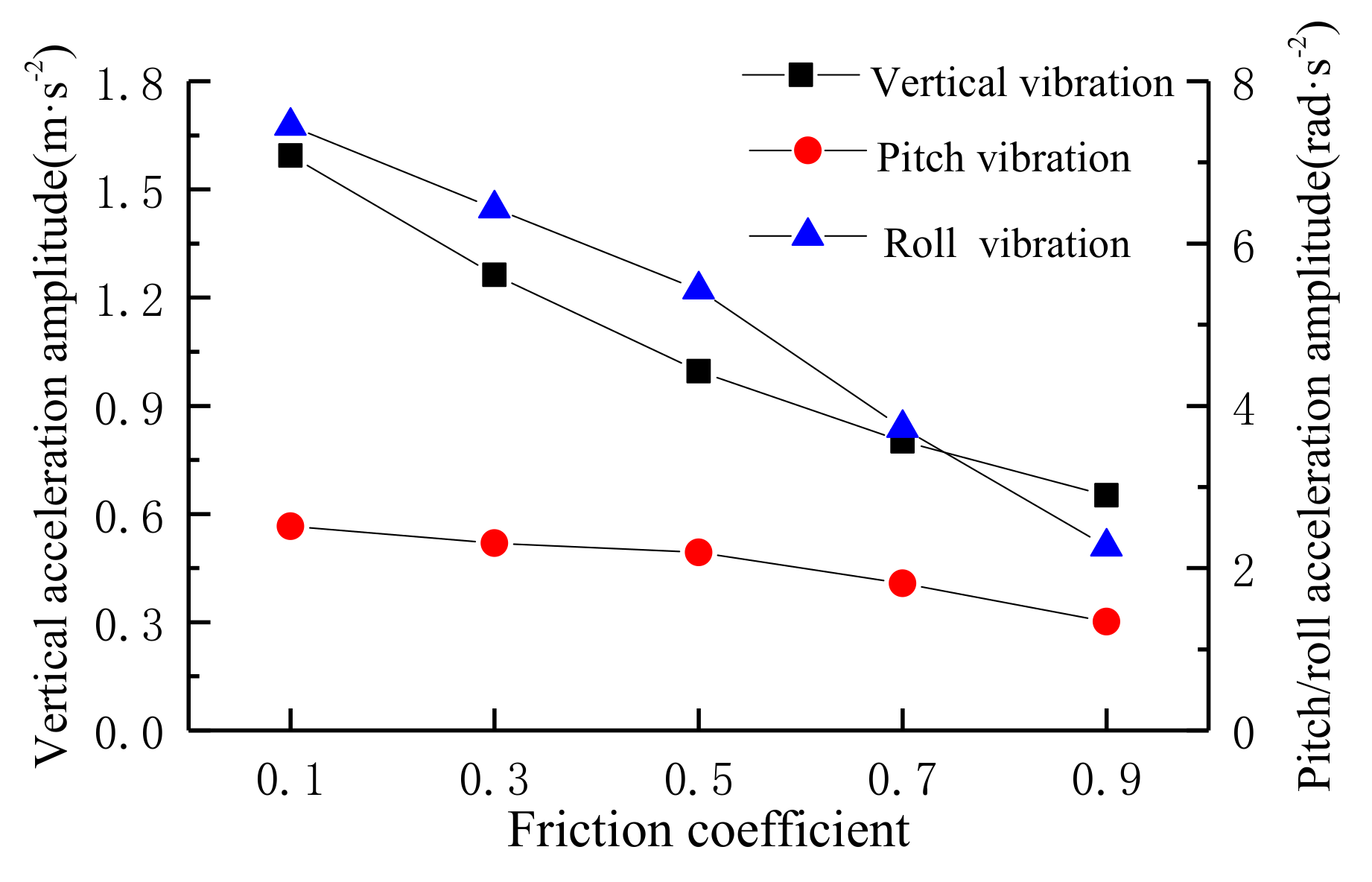
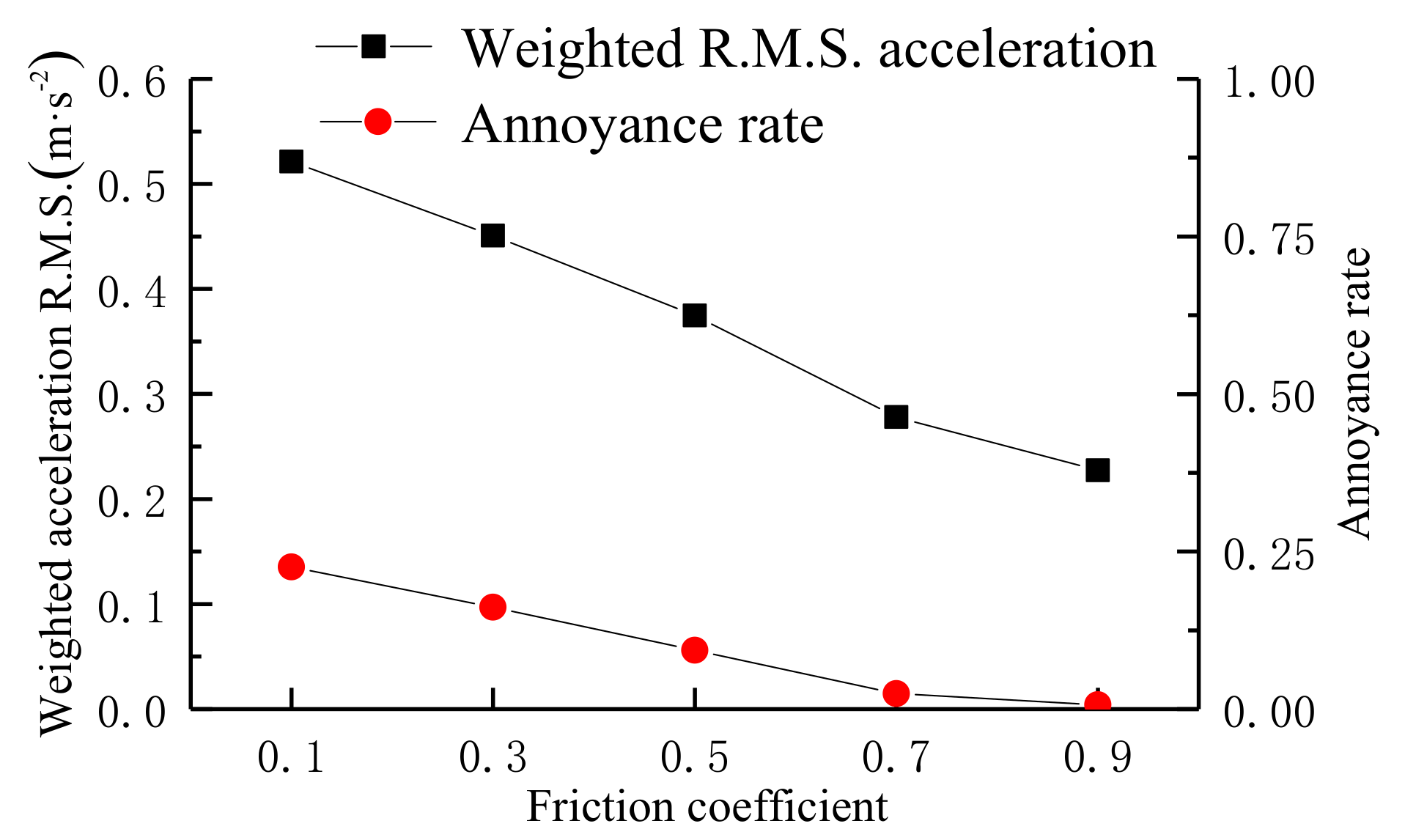
5.1. Effect of Interlayer Bonding Condition of Asphalt Pavement
5.2. Effect of Bus Weight
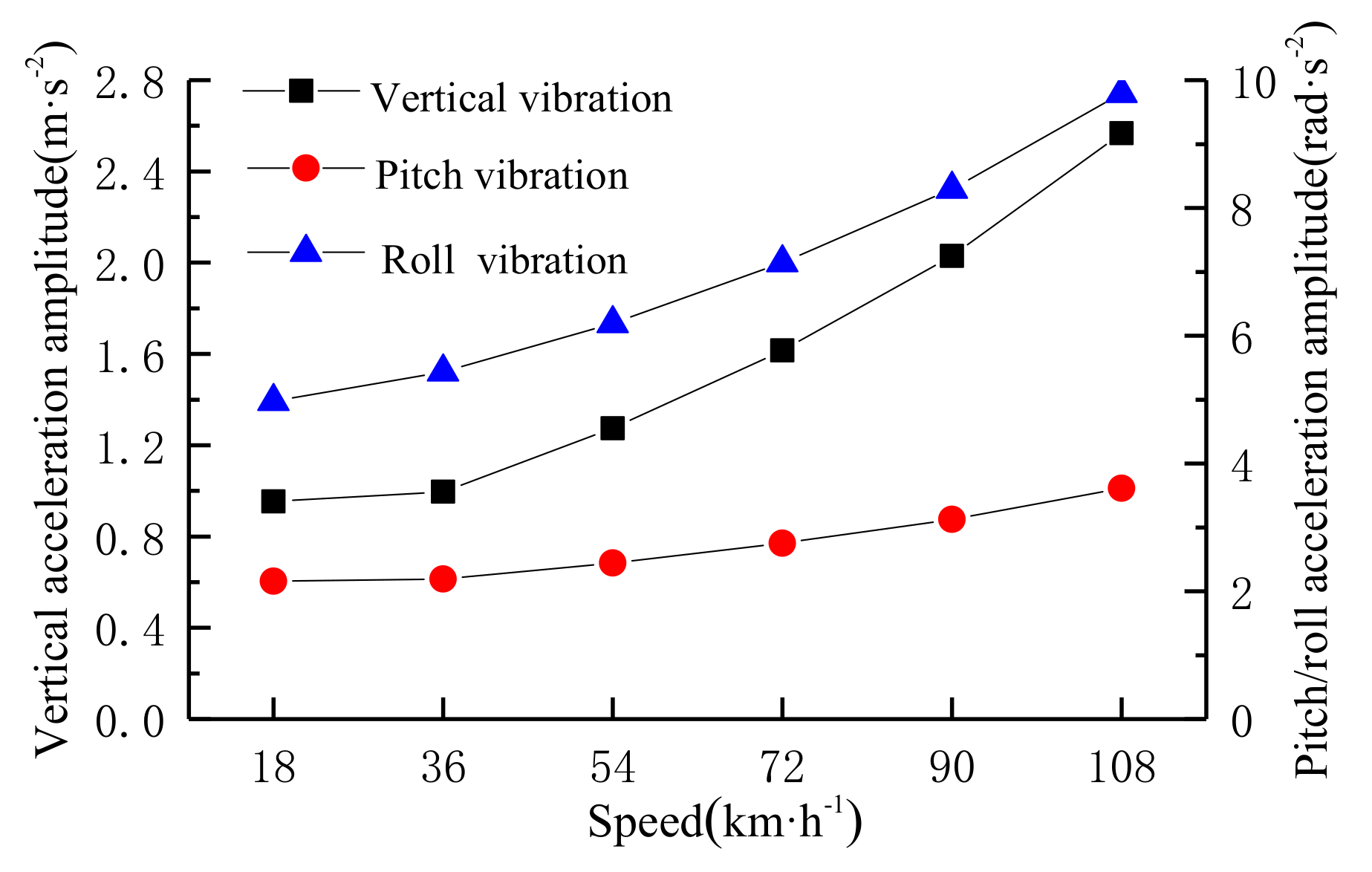
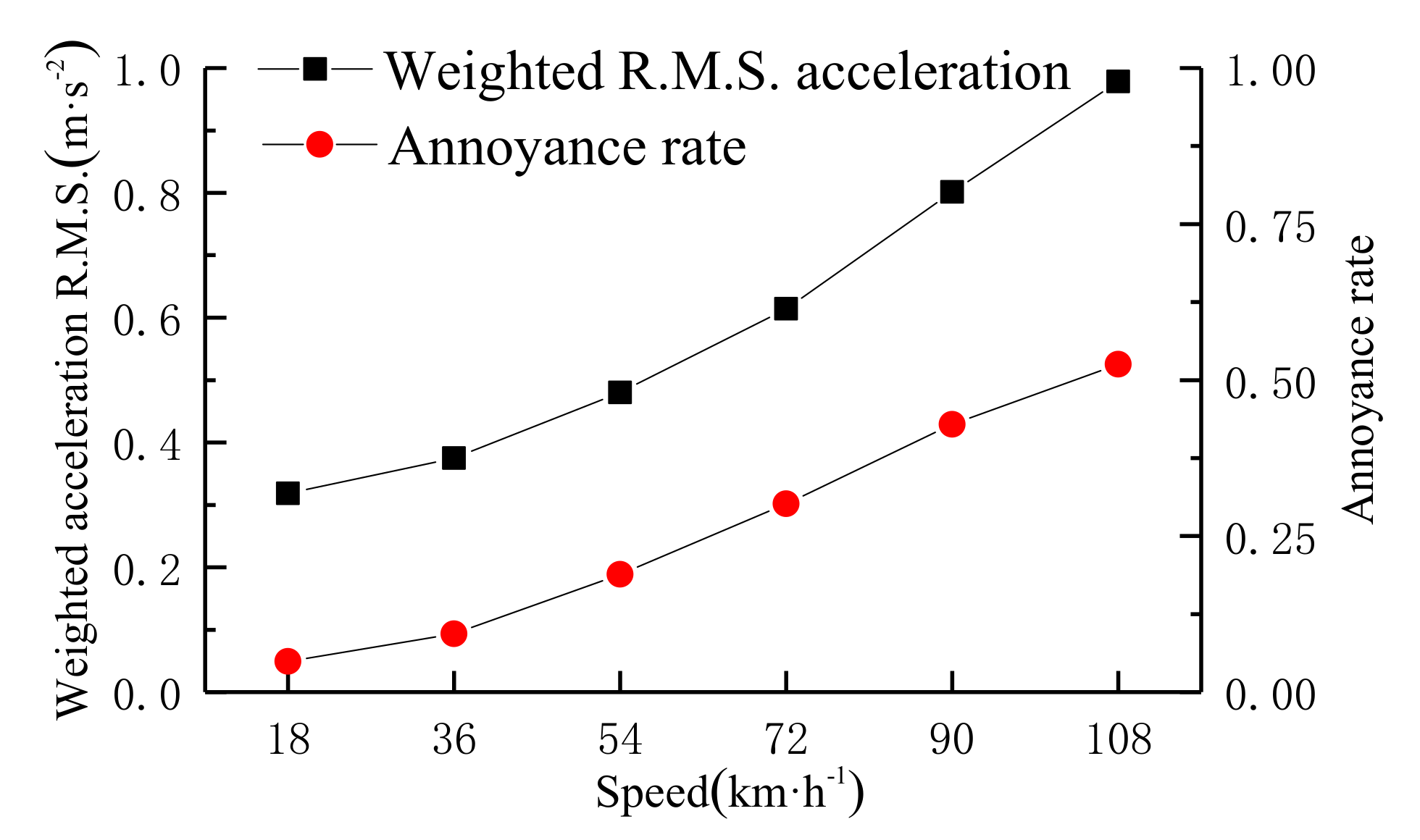
5.3. Effect of Bus Speed
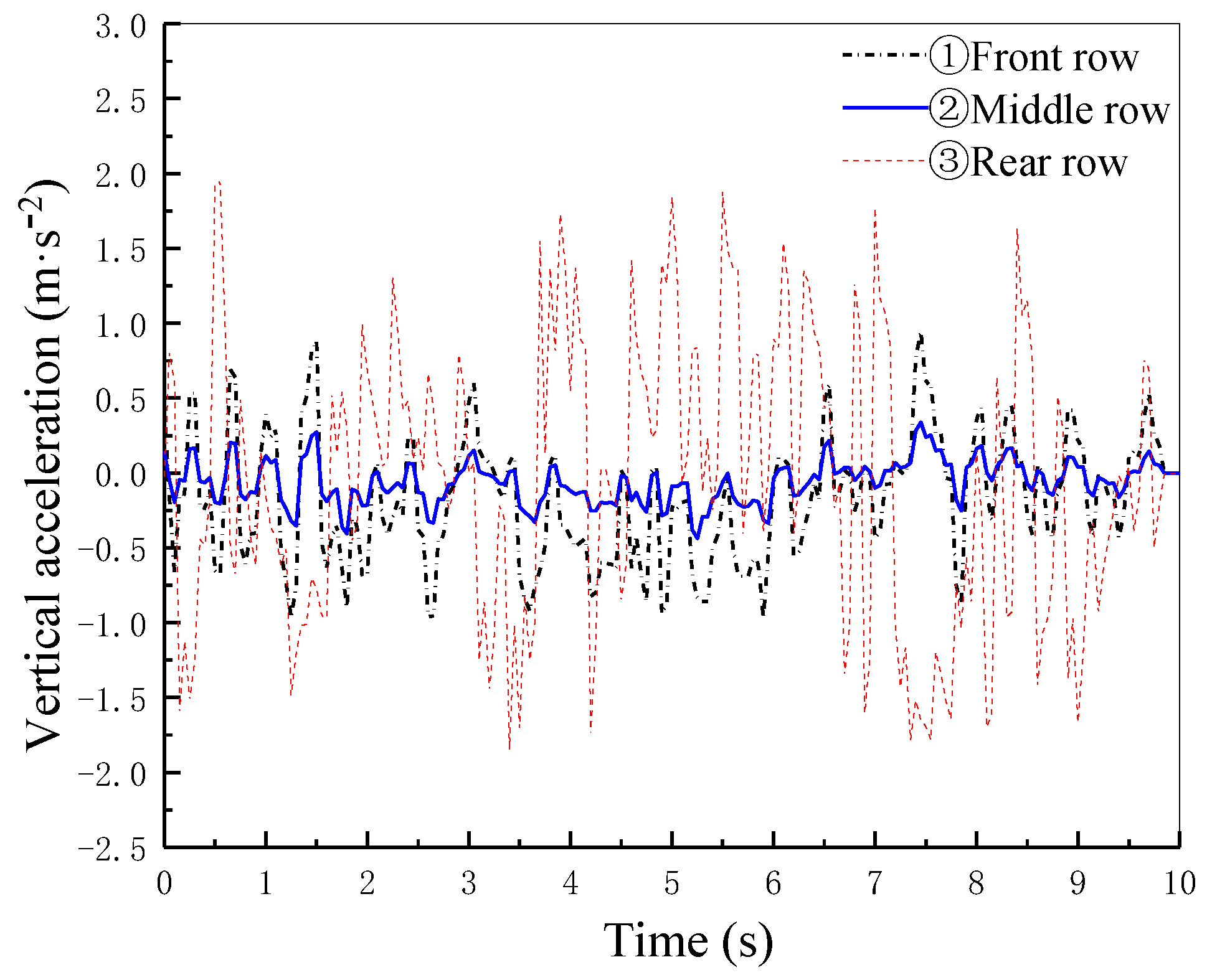
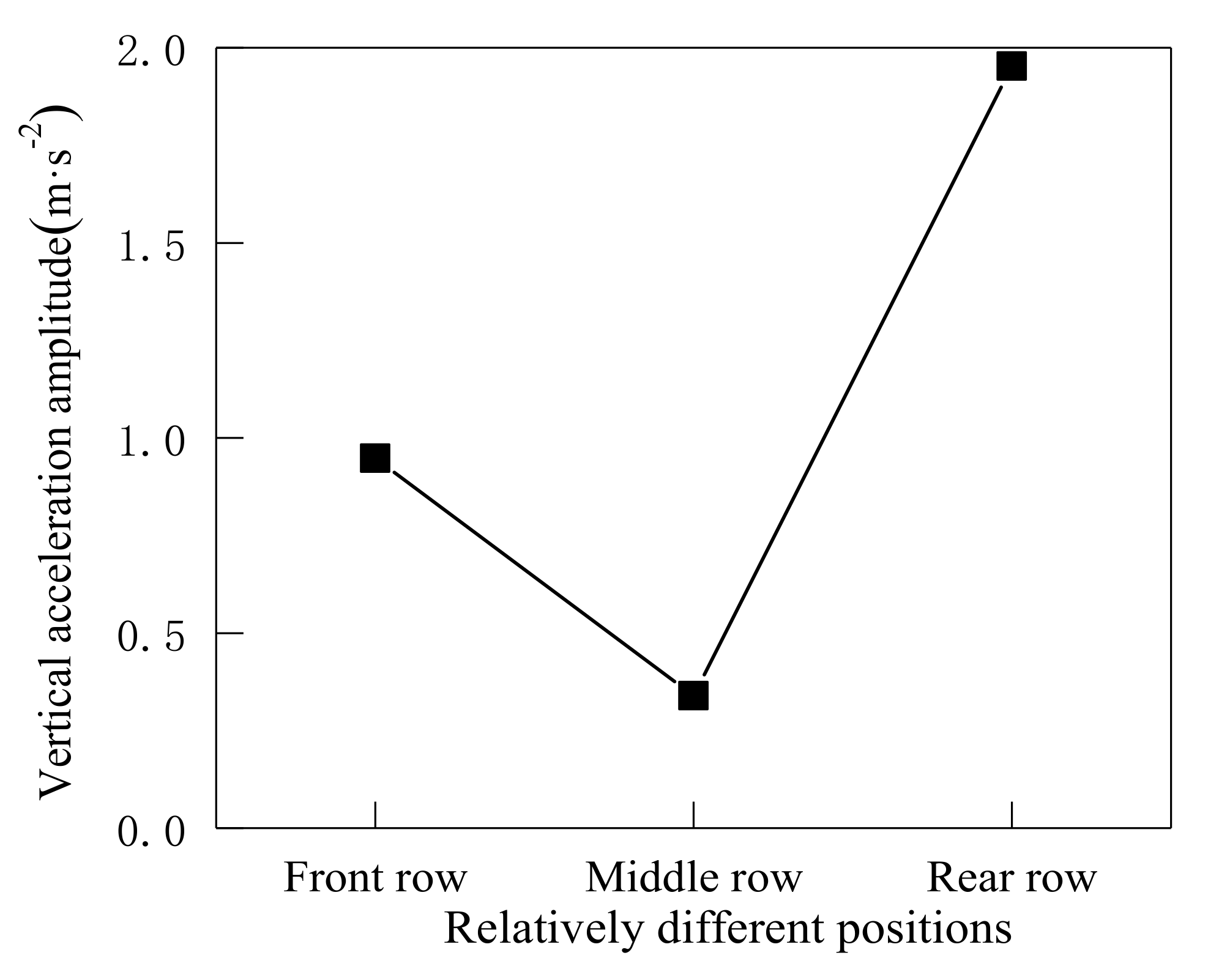
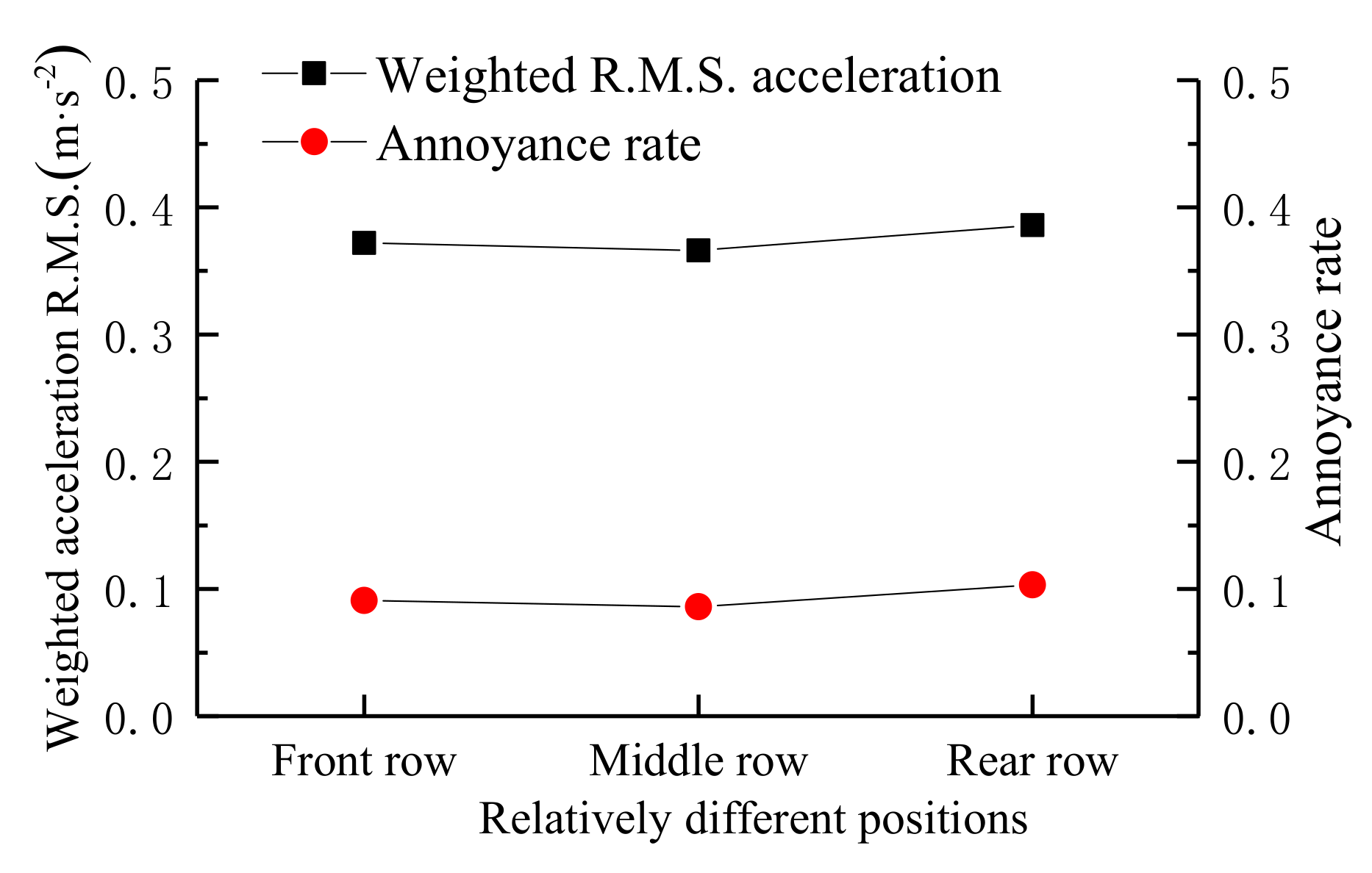
5.4. Effect of Sitting Position
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vishwas, S. Dynamic analysis of rigid pavement with vehicle-pavement interaction. J. Pavement Eng. 2009, 10, 63–72. [Google Scholar]
- Zheng, L.; Hu, Z.; Yao, H.L.; Liu, J. Field evaluation and analysis of road subgrade dynamic responses under heavy duty vehicle. Int. J. Pavement Eng. 2018, 19, 1077–1086. [Google Scholar]
- Auersch, L. The excitation of ground vibration by rail traffic: Theory of vehicle-track-soil interaction and measurements on high-speed lines. J. Sound Vib. 2005, 284, 103–132. [Google Scholar] [CrossRef]
- Carroll, S.P.; Owen, J.S.; Hussein, M.F.M. Experimental identification of the lateral human-structure interaction mechanism and assessment of the inverted-pendulum biomechanical model. J. Sound Vib. 2014, 333, 5865–5884. [Google Scholar] [CrossRef]
- Kim, K.S.; Kim, J.W.; Kim, K.J. Dynamic modeling of seated human body based on measurements of apparent inertia matrix for fore-and-aft/vertical/pitch motion. J. Sound Vib. 2011, 330, 5716–5735. [Google Scholar] [CrossRef]
- Sharma, R.C. Evaluation of Passenger Ride Comfort of Indian Rail and Road Vehicles with ISO 2631-1 Standards Part 1-Mathematical Modelling. Int. J. Veh. Struct. Syst. 2016, 8, 1–6. [Google Scholar] [CrossRef]
- Wang, G.C.; Li, W.S. Analysis of vehicle comfort based on vehicle-bridge coupling vibration. J. Vib. Shock 2016, 35, 224–230. [Google Scholar]
- Wolfgang, R.; Limerick, R.B. Whole-body vibration exposure of haul truck drivers at a surface coal mine. Appl. Ergon. 2014, 45, 1700–1704. [Google Scholar] [CrossRef]
- Duarte, M.L.; Melo, M.G.C. Influence of pavement type and speed on whole body vibration (WBV) levels measured on passenger vehicles. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 3–12. [Google Scholar] [CrossRef]
- Specification for Design of Highway Asphalt Pavement; JTG D50-2017; China Communications Press: Beijing China, 2017.
- John, C.; Zayd, B.G. The Partial Fast Fourier Transform. J. Sci. Comput. 2018, 76, 1578–1593. [Google Scholar]
- Vaibhav, V. Fast inverse nonlinear Fourier transform. Phys. Rev. E 2018, 98, 1–14. [Google Scholar] [CrossRef] [PubMed]
- International Organization for Standardization. Mechanical Vibration-Road Surface Profiles Reporting of Measured Data; ISO 8068: Geneva, Switzerland, 1995. [Google Scholar]
- Deng, L.; Cai, C.S. Development of dynamic impact factor for performance evaluation of existing multi-girder concrete bridges. Eng. Struct. 2010, 32, 21–31. [Google Scholar] [CrossRef]
- Deng, L.; Yan, W.C.; Nie, L. A simple corrosion fatigue design method for bridges considering the coupled corrosion-overloading effect. Eng. Struct. 2019, 178, 309–317. [Google Scholar] [CrossRef]
- Choi, S.B.; Han, Y.M. Vibration control of electrorheological seat suspension with human-body model using sliding mode control. J. Sound Vib. 2007, 303, 391–404. [Google Scholar] [CrossRef]
- Wu, G.Q.; Fan, G.D.; Guo, J.B. Ride comfort evaluation for road vehicle based on rigid-flexible coupling multibody dynamics. Theor. Appl. Mech. Lett. 2013, 3, 013004–013008. [Google Scholar] [CrossRef][Green Version]
- Liu, G.; Lv, Z.R.; Chen, Y.M. Improving Wilson-θ and Newmark-β Methods for Quasi-Periodic Solutions of Nonlinear Dynamical Systems. J. Appl. Math. Phys. 2018, 06, 1625–1635. [Google Scholar] [CrossRef]
- International Organization for Standardization. Mechanical Vibration and Shock-Evaluation of Human Exposure to Whole-body Vibration-part1, General Requirements; ISO 2631-1: Geneva, Switzerland, 1997. [Google Scholar]
- Kong, X.; Cai, C.S.; Hu, J.X. The State-of-the-art on framework of vibration-based structural damage identification for decision making. Appl. Sci. 2017, 7, 497. [Google Scholar] [CrossRef]
- Dóra, H. Calculation model of road traffic noise annoyance rate in urban areas. Pollack Period. 2014, 9, 41–47. [Google Scholar]
- Blair, A.N.; Ayyub, B.M.; Bender, W.J. Fuzzy stochastic risk-based decision analysis with the mobile offshore base as a case study. Mar. Struct. 2001, 14, 69–88. [Google Scholar] [CrossRef]
- Chou, K.C.; Yuan, J. Fuzzy-Bayesian approach to reliability of existing structures. J. Struct. Eng. 1993, 119, 3276–3290. [Google Scholar] [CrossRef]
- Song, Z.G. New Theory of Vibration Comfort Design of Engineering Structures Based on Annoyance Rate Model; Zhejiang University: Hangzhou, China, 2003. [Google Scholar]
- Griffin, M.J.; Whitham, E.M. Individual variability and its effect on subjective and biodynamic response to whole-body vibration. J. Sound Vib. 1978, 58, 239–250. [Google Scholar] [CrossRef]
- Peng, M.J.; Zhao, W.X. Influence of interlayer contact on anti-rutting performance of asphalt pavement. J. Highw. Transp. Res. 2016, 33, 1–6. [Google Scholar]
- GB/T7031-1986, Vehicle Vibration-Describing Method for Road Surface Irregularity; Standards Press of China: Beijing, China, 1987.
- Sekulic´, D. Analysis of vibration effects on the comfort of intercity bus users by oscillatory model with ten degrees of freedom. Appl. Math. Model. 2013, 37, 8629–8644. [Google Scholar] [CrossRef]
- Gao, J.H.; Hou, Z.C.; He, L.; Xia, Q.S. Vertical vibration characteristics of seated human bodies and a biodynamic model with two degrees of freedom. Sci. China Technol. Sci. 2011, 10, 2776–2784. [Google Scholar] [CrossRef]
- Obrien, E.J.; Enright, B. Modeling same-direction two-lane traffic for bridge loading. Struct. Saf. 2011, 33, 296–304. [Google Scholar] [CrossRef]
- Sieniawska, R.; Sniady, P. Life expectancy of highway bridge due to traffic load. J. Sound Vib. 1990, 140, 31–38. [Google Scholar] [CrossRef]







| Weighted RMS Accelerations/m·s−2 | Reactions |
|---|---|
| <0.315 | not uncomfortable |
| 0.315-0.63 | a little uncomfortable |
| 0.5–1 | fairly uncomfortable |
| 0.8–1.6 | uncomfortable |
| 1.25–2.5 | very uncomfortable |
| >2.0 | extremely uncomfortable |
| Structure Layer | Thickness/cm | Elastic Modulus/MPa | Poisson’s Ratio | Density/(kg/m3) | Damping Ratio (ζ) |
|---|---|---|---|---|---|
| Upper layer | 10 | 1400 | 0.25 | 2500 | 0.05 |
| Lower layer | 10 | 1200 | 0.25 | 2500 | 0.05 |
| Base | 20 | 1000 | 0.25 | 2400 | 0.05 |
| Subbase | 20 | 900 | 0.25 | 2300 | 0.05 |
| Soil foundation | 540 | 60 | 0.4 | 1900 | 0.05 |
| Parameters | Description | Values |
|---|---|---|
| elastic-suspended mass of the fully-loaded bus | 15,890 kg | |
| the front axle mass | 746 kg | |
| the rear axle mass | 1355 kg | |
| the suspended mass moment of inertia relative to the x-axis | 13,000 kg·m2 | |
| the suspended mass moment of inertia relative to the y-axis | 150,000 kg·m2 | |
| the front axle moment of inertia relative to the x1 axis | 350 kg·m2 | |
| the rear axle moment of inertia relative to the x2 axis | 620 kg·m2 | |
| single airbag stiffness on the front and the rear axle | 200,000 N/m | |
| single airbag damping on the front and the rear axle | 45,973 Ns/m | |
| single tire stiffness on the front and the rear axle | 1,000,000 N/m | |
| single tire damping on the front and the rear axle | 150 Ns/m |
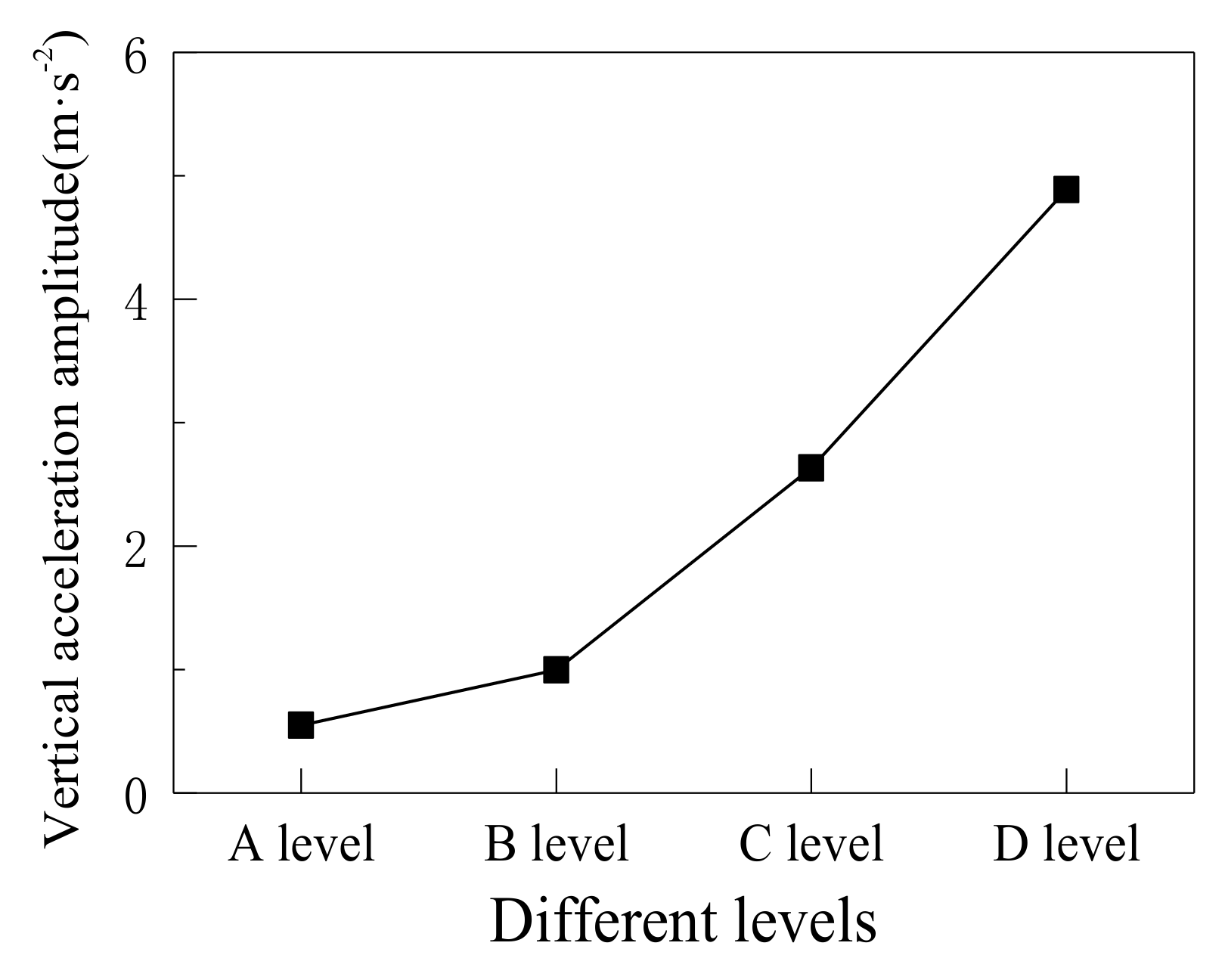
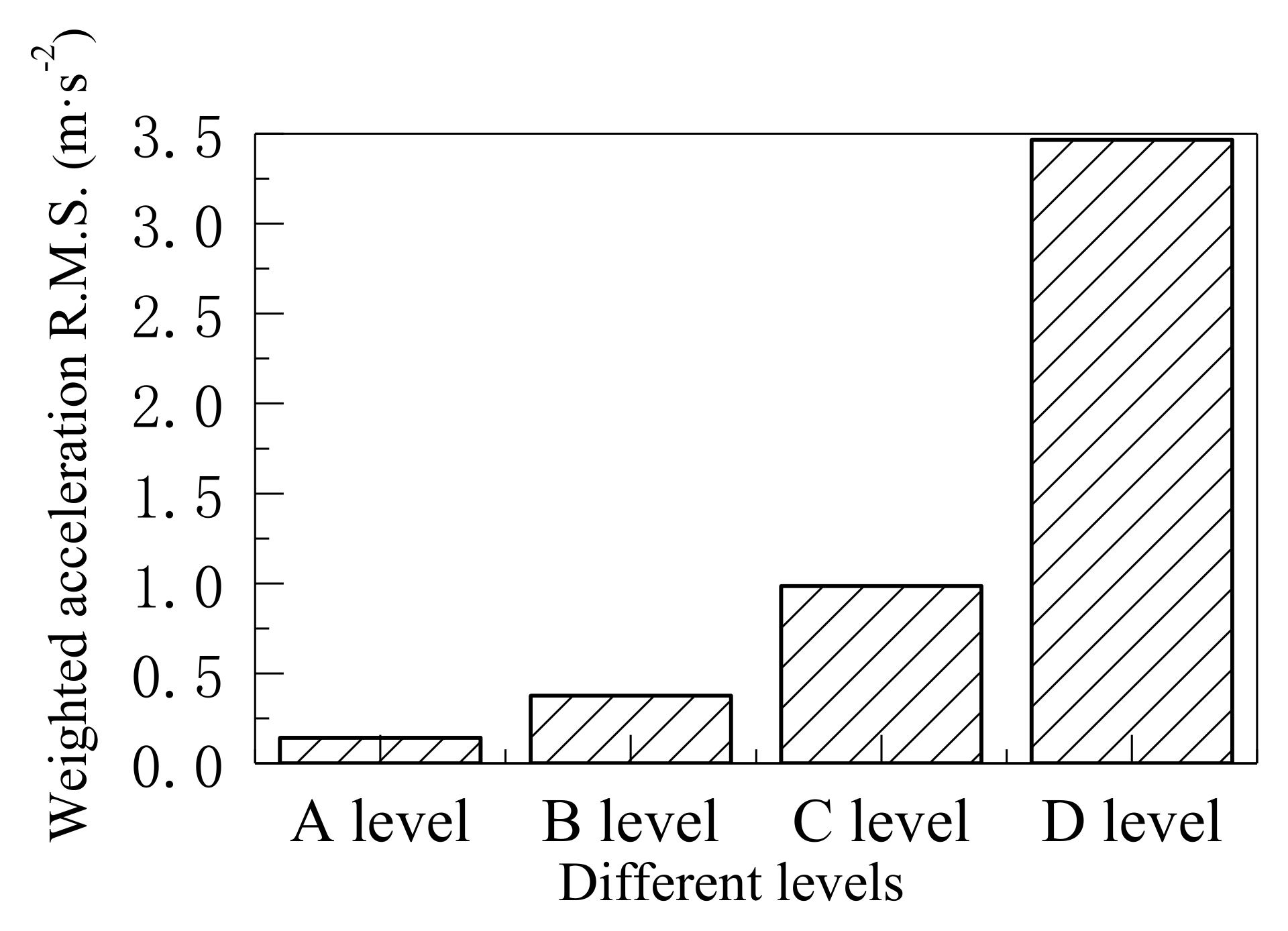
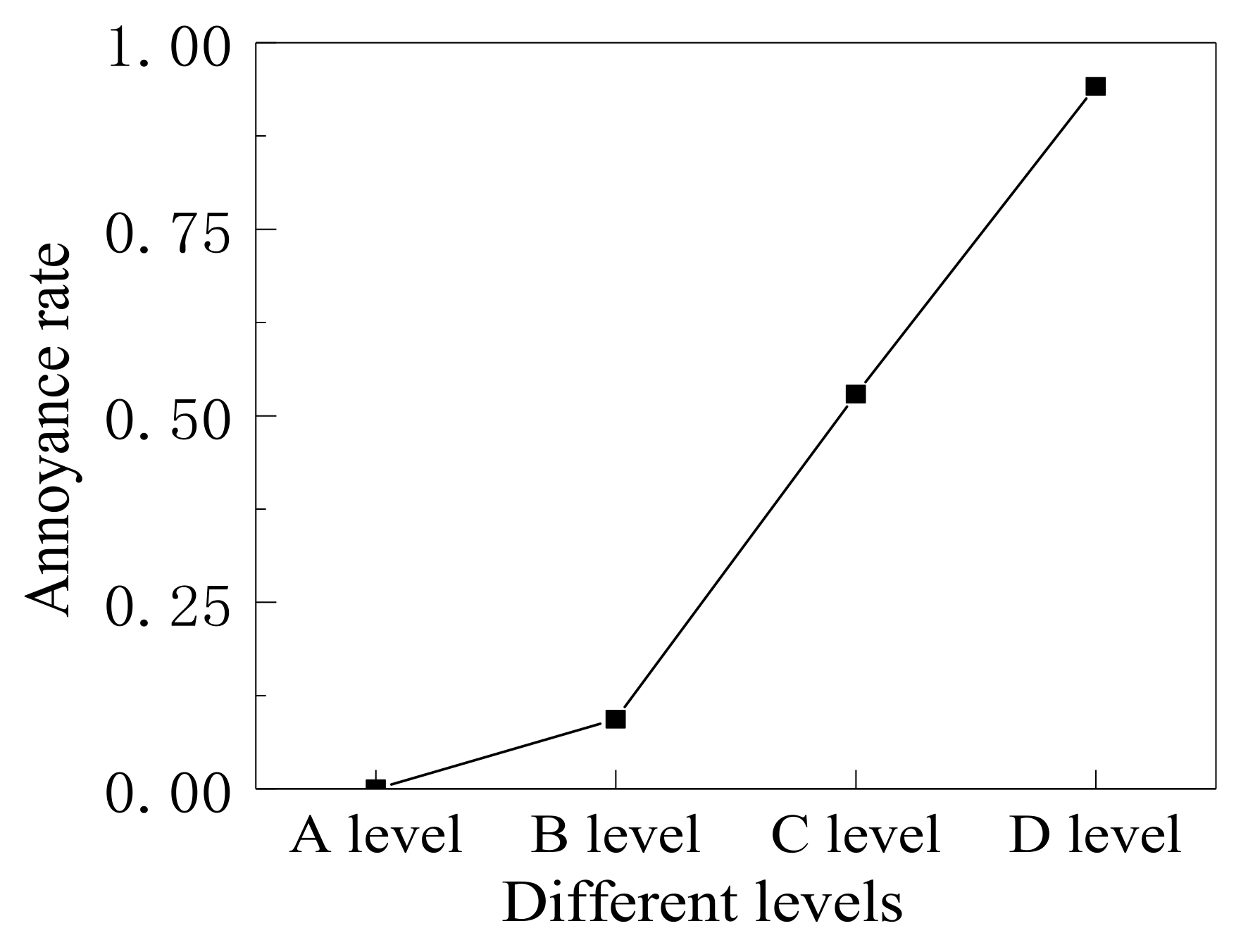
| Road Surface Condition | Weighted RMS Acceleration /m·s−2 | Reactions | Annoyance Rate |
|---|---|---|---|
| A level | 0.1432 | not uncomfortable | 0.0009% |
| B level | 0.3748 | slightly uncomfortable | 9.33% |
| C level | 0.9862 | uncomfortable | 52.90% |
| D level | 3.4663 | extremely uncomfortable | 94.15% |
| Friction Coefficient | Weighted RMS Acceleration /m·s−2 | Reactions | Annoyance Rate |
|---|---|---|---|
| 0.1 | 0.5214 | slightly uncomfortable | 22.54% |
| 0.3 | 0.4507 | slightly uncomfortable | 16.19% |
| 0.5 | 0.3748 | slightly uncomfortable | 9.33% |
| 0.7 | 0.2780 | not uncomfortable | 2.48% |
| 0.9 | 0.2272 | not uncomfortable | 0.69% |
| Weight of Bus/t | Weighted RMS Acceleration /m·s−2 | Reactions | Annoyance Rate |
|---|---|---|---|
| 11.57 | 0.6998 | uncomfortable | 36.38% |
| 13.73 | 0.5032 | slightly uncomfortable | 20.94% |
| 15.89 | 0.3748 | slightly uncomfortable | 9.33% |
| 16.97 | 0.2928 | not uncomfortable | 3.27% |
| 18.05 | 0.2278 | not uncomfortable | 0.71% |
| Speed/km·h−1 | Weighted RMS Acceleration /m·s−2 | Reactions | Annoyance Rate |
|---|---|---|---|
| 18 | 0.3186 | slightly uncomfortable | 4.90% |
| 36 | 0.3748 | slightly uncomfortable | 9.33% |
| 54 | 0.4799 | slightly uncomfortable | 18.85% |
| 72 | 0.6142 | uncomfortable | 30.16% |
| 90 | 0.8015 | extremely uncomfortable | 42.90% |
| 108 | 0.9782 | extremely uncomfortable | 52.51% |
| Ride Location | Weighted RMS Acceleration /m·s−2 | Reactions | Annoyance Rate |
|---|---|---|---|
| Front row | 0.3721 | slightly uncomfortable | 9.09% |
| Middle row | 0.3662 | slightly uncomfortable | 8.59% |
| Rear row | 0.3861 | slightly uncomfortable | 10.31% |
| Parametric | RMS Acceleration | Ratio | Annoyance Rate | Ratio | ||
|---|---|---|---|---|---|---|
| Min | Max | Max/Min | Min | Max | Max/Min | |
| Road roughness | 0.1432 | 3.4663 | 24.2 | 0.0009% | 94.15% | 104,611.1 |
| Interlayer bonding | 0.2272 | 0.5214 | 2.3 | 0.69% | 22.54% | 32.7 |
| Bus weight | 0.2278 | 0.6998 | 3.1 | 0.71% | 36.38% | 51.2 |
| Bus speed | 0.3186 | 0.9782 | 3.1 | 4.90% | 52.51% | 10.7 |
| Sitting Position | 0.3662 | 0.3861 | 1.1 | 8.59% | 10.31% | 1.2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Zhang, J.; Kong, X. Study on Passenger Comfort Based on Human–Bus–Road Coupled Vibration. Appl. Sci. 2020, 10, 3254. https://doi.org/10.3390/app10093254
Wang G, Zhang J, Kong X. Study on Passenger Comfort Based on Human–Bus–Road Coupled Vibration. Applied Sciences. 2020; 10(9):3254. https://doi.org/10.3390/app10093254
Chicago/Turabian StyleWang, Guichun, Jie Zhang, and Xuan Kong. 2020. "Study on Passenger Comfort Based on Human–Bus–Road Coupled Vibration" Applied Sciences 10, no. 9: 3254. https://doi.org/10.3390/app10093254
APA StyleWang, G., Zhang, J., & Kong, X. (2020). Study on Passenger Comfort Based on Human–Bus–Road Coupled Vibration. Applied Sciences, 10(9), 3254. https://doi.org/10.3390/app10093254






