Fault Diagnosis for Wind Turbines Based on ReliefF and eXtreme Gradient Boosting
Abstract
:Featured Application
Abstract
1. Introduction
2. Introduction to the ReliefF and XGBoost Algorithms
2.1. The Principle of the ReliefF Algorithm
2.2. The Principle of the XGBoost Algorithm
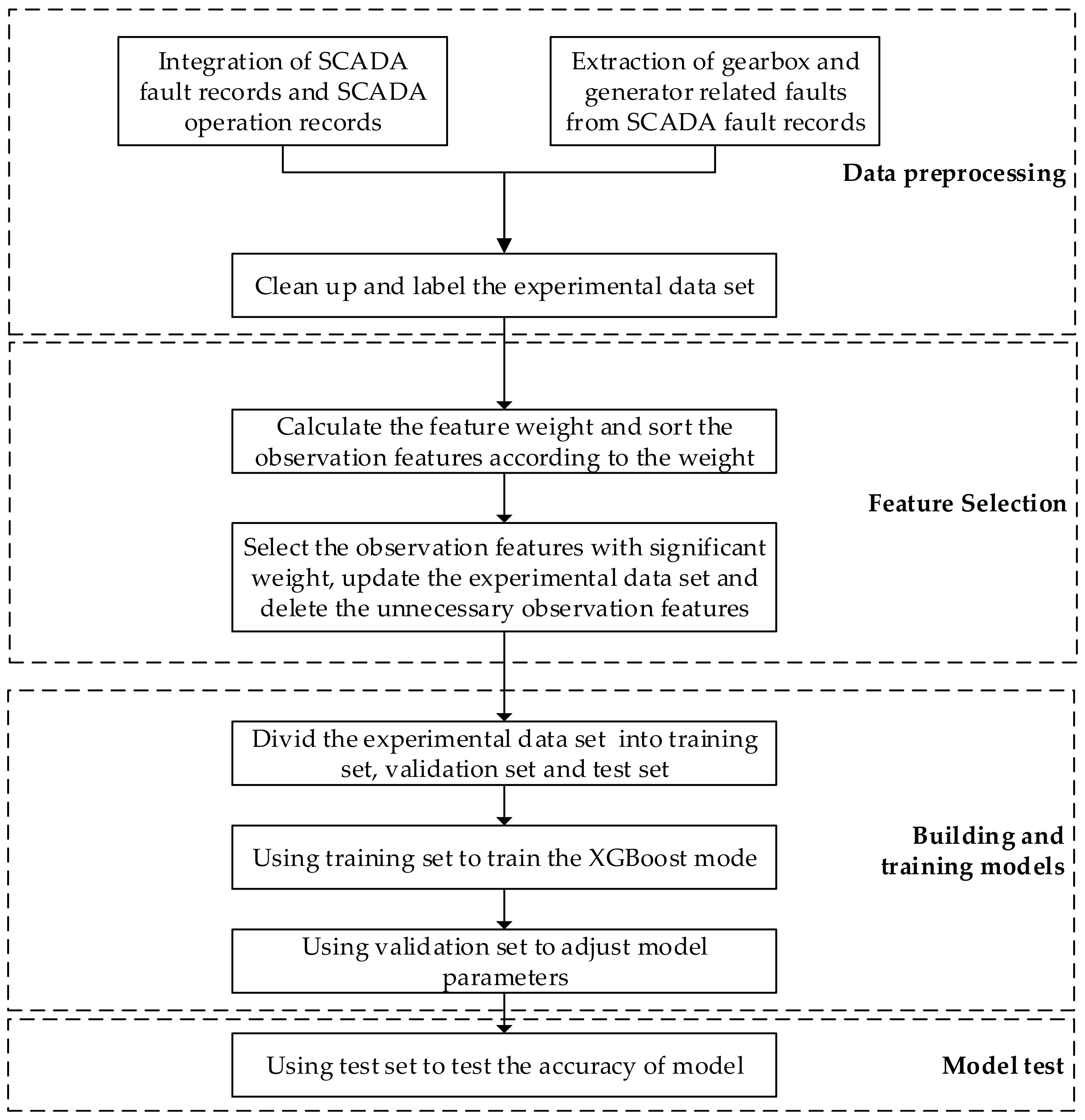
3. Design of Fault Diagnosis Algorithm for Key Parts of Wind Turbine
4. Case Analysis and Result Comparison
4.1. Selecting Characteristic Parameters by ReliefF
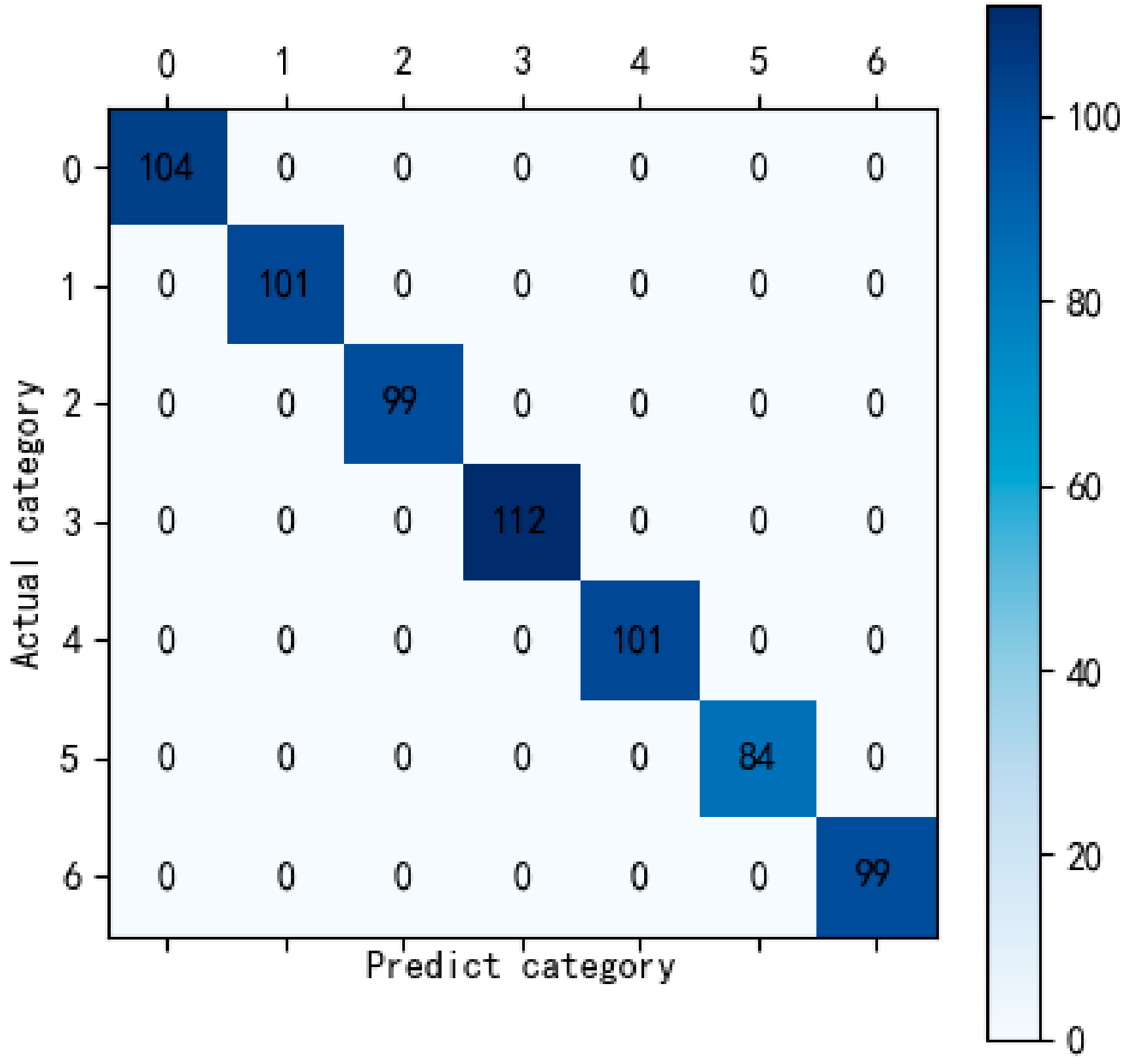
4.2. Fault Identification with XGBoost
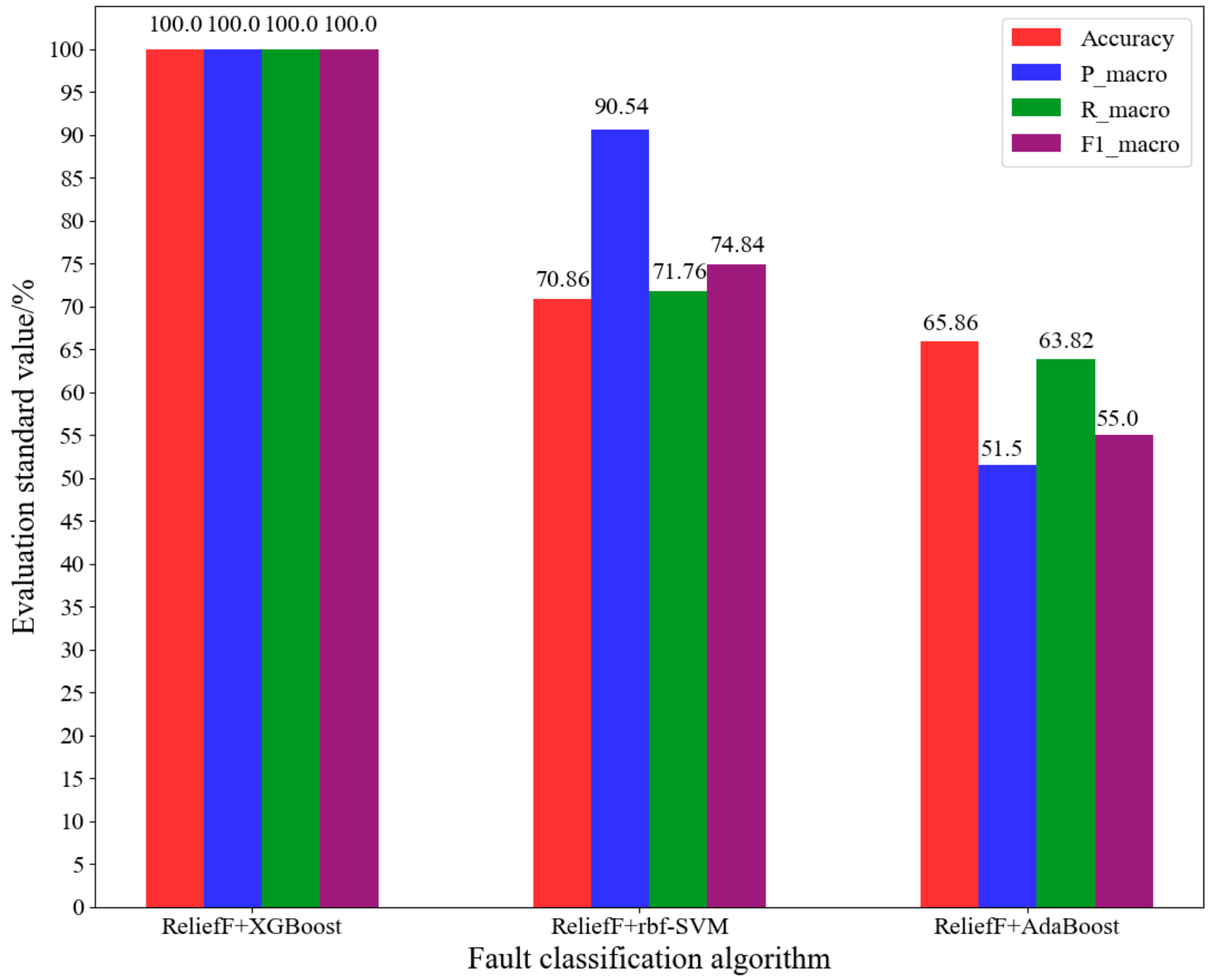
4.3. Comparison of Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiaoli, L.; Chuanglin, F. Wind energy resources distribution and spatial differences of wind power industry in China. In Proceedings of the 2007 Non-Grid-Connected Wind Power Systems—Wind Power Shanghai 2007—Symposium on Non-Grid-Connected Wind Power, NGCWP 2007, Shanghai, China, 2 November 2007; pp. 182–197. [Google Scholar]
- Zhang, Z.; Verma, A.; Kusiak, A. Fault Analysis and Condition Monitoring of the Wind Turbine Gearbox. IEEE Trans. Energy Convers. 2012, 27, 526–535. [Google Scholar] [CrossRef]
- Ribrant, J.; Bertling, L.M. Survey of failures in wind power systems with focus on Swedish wind power plants during 1997–2005. IEEE Trans. Energy Convers. 2007, 22, 167–173. [Google Scholar] [CrossRef]
- Pinar Perez, J.M.; Garcia Marquez, F.P.; Tobias, A.; Papaelias, M. Wind turbine reliability analysis. Renew. Sustain. Energy Rev. 2013, 23, 463–472. [Google Scholar] [CrossRef]
- Spinato, F.; Tavner, P.J.; Van Bussel, G.J.W.; Koutoulakos, E. Reliability of wind turbine subassemblies. Iet Renew. Power Gener. 2009, 3, 387–401. [Google Scholar] [CrossRef] [Green Version]
- McMillan, D.; Ault, G.W. Condition monitoring benefit for onshore wind turbines: Sensitivity to operational parameters. IET Renew. Power Gener. 2008, 2, 60–72. [Google Scholar] [CrossRef]
- Guo, P.; Infield, D.; Yang, X. Wind turbine gearbox condition monitoring using temperature trend analysis. Proc. Chin. Soc. Electr. Eng. 2011, 31, 129–136. [Google Scholar]
- Yin, H.; Jia, R.; Ma, F.; Wang, D. Wind Turbine Condition Monitoring based on SCADA Data Analysis. In Proceedings of the 3rd IEEE Advanced Information Technology, Electronic and Automation Control Conference, IAEAC 2018, Chongqing, China, 12–14 October 2018; pp. 1101–1105. [Google Scholar]
- Gomez, M.J.; Castejon, C.; Corral, E.; Garcia-Prada, J.C. Analysis of the influence of crack location for diagnosis in rotating shafts based on 3 x energy. Mech. Mach. Theory 2016, 103, 167–173. [Google Scholar] [CrossRef]
- Tang, B.; Liu, W.; Song, T. Wind turbine fault diagnosis based on Morlet wavelet transformation and Wigner-Ville distribution. Renew. Energy 2010, 35, 2862–2866. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, X.; Qian, P. Wind Turbine Fault Detection and Identification Through PCA-Based Optimal Variable Selection. IEEE Trans. Sustain. Energy 2018, 9, 1627–1635. [Google Scholar] [CrossRef] [Green Version]
- Ruiz, M.; Mujica, L.E.; Alferez, S.; Acho, L.; Tutiven, C.; Vidal, Y.; Rodellar, J.; Pozo, F. Wind turbine fault detection and classification by means of image texture analysis. Mech. Syst. Signal Process. 2018, 107, 149–167. [Google Scholar] [CrossRef] [Green Version]
- Pozo, F.; Vidal, Y.; Salgado, O. Wind turbine condition monitoring strategy through multiway PCA and multivariate inference. Energies 2018, 11. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Fang, R. An online wind turbine condition assessment method based on SCADA and support vector regression. Autom. Electr. Power Syst. 2013, 37, 7–12. [Google Scholar] [CrossRef]
- Bangalore, P.; Tjernberg, L.B. An artificial neural network approach for early fault detection of gearbox bearings. IEEE Trans. Smart Grid 2015, 6, 980–987. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Long, H.; Xu, J.; Liu, R. Wind Turbine Gearbox Failure Identification with Deep Neural Networks. IEEE Trans. Ind. Inform. 2017, 13, 1360–1368. [Google Scholar] [CrossRef]
- Vidal, Y.; Pozo, F.; Tutiven, C. Wind turbine multi-fault detection and classification based on SCADA data. Energies 2018, 11. [Google Scholar] [CrossRef] [Green Version]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In Proceedings of the European Conference on Machine Learning, ECML 1994, Catania, Italy, 6–8 April 1994; pp. 171–182. [Google Scholar]
- Robnik-ikonja, M.; Kononenko, I. Theoretical and Empirical Analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef] [Green Version]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD 2016, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Kira, K.; Rendell, L.A. Feature selection problem: Traditional methods and a new algorithm. In Proceedings of the Tenth National Conference on Artificial Intelligence—AAAI-92, San Jose, CA, USA, 12–16 July 1992; pp. 129–134. [Google Scholar]
- Xie, Y.; Li, D.; Zhang, D.; Shuang, H. An improved multi-label relief feature selection algorithm for unbalanced datasets. In Proceedings of the 2nd International Conference on Intelligent and Interactive Systems and Applications, IISA 2017, Beijing, China, 17–18 June 2017; pp. 141–151. [Google Scholar]


| Number | Fault Types |
|---|---|
| 1 | Rotor RPM, generator RPM |
| 2 | Excessive speed of rotor |
| 3 | High temperature on generator |
| 4 | High temperature on Gen bear |
| 5 | High temperature on bear |
| 6 | Gear oil radiator overload |
| Fault Types | Fault Code |
|---|---|
| Normal operation | 1 |
| Rotor RPM, generator RPM | 2 |
| Excessive speed of rotor | 3 |
| High temperature on generator | 4 |
| High temperature on Gen bear | 5 |
| High temperature on bear | 6 |
| Gear oil radiator overload | 7 |
| Features | Weights |
|---|---|
| Active setting feedback value | 0.276603 |
| Annual power generation | 0.17884 |
| Blade 1 pitch angle A | 0.177146 |
| Total generating capacity | 0.170743 |
| Gearbox inlet oil pressure | 0.169514 |
| Impeller speed | 0.159299 |
| Generator speed | 0.151687 |
| Ambient temperature | 0.140054 |
| Phase C current at grid side | 0.132598 |
| Phase A current at grid side | 0.13121 |
| Active power | 0.130947 |
| Phase B current at grid side | 0.128243 |
| Fan status reception | 0.120974 |
| Ambient wind direction | 0.096194 |
| Converter coolant inlet temperature | 0.083146 |
| Daily power loss | 0.078387 |
| Power factor | 0.078157 |
| Daily power generation | 0.074917 |
| The temperature of inverter grid-side IGBT | 0.074055 |
| Monthly power generation | 0.072639 |
| Hydraulic system oil temperature V1 | 0.070859 |
| Generator stator winding temperature W1 | 0.068143 |
| Generator stator winding temperature U1 | 0.065242 |
| Generator stator winding temperature V1 | 0.064828 |
| Daily power generation | 0.063899 |
| Generator slip ring temperature | 0.062178 |
| Converter control cabinet temperature | 0.061467 |
| Temperature of reactor 1 at converter grid side | 0.057386 |
| Phase C voltage at grid side | 0.043991 |
| Generator drive side bearing temperature | 0.036021 |
| Frequency | 0.035615 |
| Phase B voltage at grid side | 0.033013 |
| Converter controller temperature | 0.032884 |
| A-phase voltage at grid side | 0.031477 |
| Ambient wind speed | 0.030492 |
| Gearbox high speed bearing temperature | 0.026052 |
| Gearbox oil temperature | 0.021837 |
| Reactive power | 0.007668 |
| The temperature of converter rotor side L1 | 0.006128 |
| The temperature of converter rotor side L3 | 0.005562 |
| The temperature of converter rotor side L2 | 0.005536 |
| Hydraulic system oil pressure | 0.001442 |
| Number | Features |
|---|---|
| 1 | Active setting feedback value |
| 2 | Annual power generation |
| 3 | Blade 1 pitch angle A |
| 4 | Total generating capacity |
| 5 | Gearbox inlet oil pressure |
| 6 | Impeller speed |
| 7 | Generator speed |
| 8 | Ambient temperature |
| 9 | Phase C current at grid side |
| 10 | Phase A current at grid side |
| 11 | Active power |
| 12 | Phase B current at grid side |
| 13 | Fan status reception |
| 14 | Ambient wind direction |
| 15 | Converter coolant inlet temperature |
| 16 | Daily power loss |
| 17 | Power factor |
| 18 | Daily power generation |
| 19 | The temperature of inverter grid-side IGBT |
| 20 | Monthly power generation |
| 21 | Hydraulic system oil temperature V1 |
| 22 | Generator stator winding temperature W1 |
| 23 | Generator stator winding temperature U1 |
| 24 | Daily power generation |
| 25 | Generator slip ring temperature |
| 26 | Converter control cabinet temperature |
| 27 | Temperature of reactor 1 at converter grid side |
| Parameter | Value |
|---|---|
| n estimators | 200 |
| learning rate | 0.12 |
| max dapth | 5 |
| min child weight | 1 |
| objective | Multi:softmax |
| num class | 7 |
| nthread | 4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Z.; Wang, X.; Jiang, B. Fault Diagnosis for Wind Turbines Based on ReliefF and eXtreme Gradient Boosting. Appl. Sci. 2020, 10, 3258. https://doi.org/10.3390/app10093258
Wu Z, Wang X, Jiang B. Fault Diagnosis for Wind Turbines Based on ReliefF and eXtreme Gradient Boosting. Applied Sciences. 2020; 10(9):3258. https://doi.org/10.3390/app10093258
Chicago/Turabian StyleWu, Zidong, Xiaoli Wang, and Baochen Jiang. 2020. "Fault Diagnosis for Wind Turbines Based on ReliefF and eXtreme Gradient Boosting" Applied Sciences 10, no. 9: 3258. https://doi.org/10.3390/app10093258
APA StyleWu, Z., Wang, X., & Jiang, B. (2020). Fault Diagnosis for Wind Turbines Based on ReliefF and eXtreme Gradient Boosting. Applied Sciences, 10(9), 3258. https://doi.org/10.3390/app10093258





