A Power Performance Online Assessment Method of a Wind Turbine Based on the Probabilistic Area Metric
Abstract
1. Introduction
- The probabilistic area metric is used to evaluate the deviations of the probabilistic models of two datasets. In other words, the datasets are transformed into probabilistic models instead of means or variances, and the deviations of the probabilistic models are calculated. The area metric has an obvious advantage in dynamic and stochastic SCADA data mining analysis.
- The assessment method combines physical model analysis and data mining techniques. The assessment result is statistically significant, and it has physical significance and is easy for engineers to understand.
2. Problem Definition
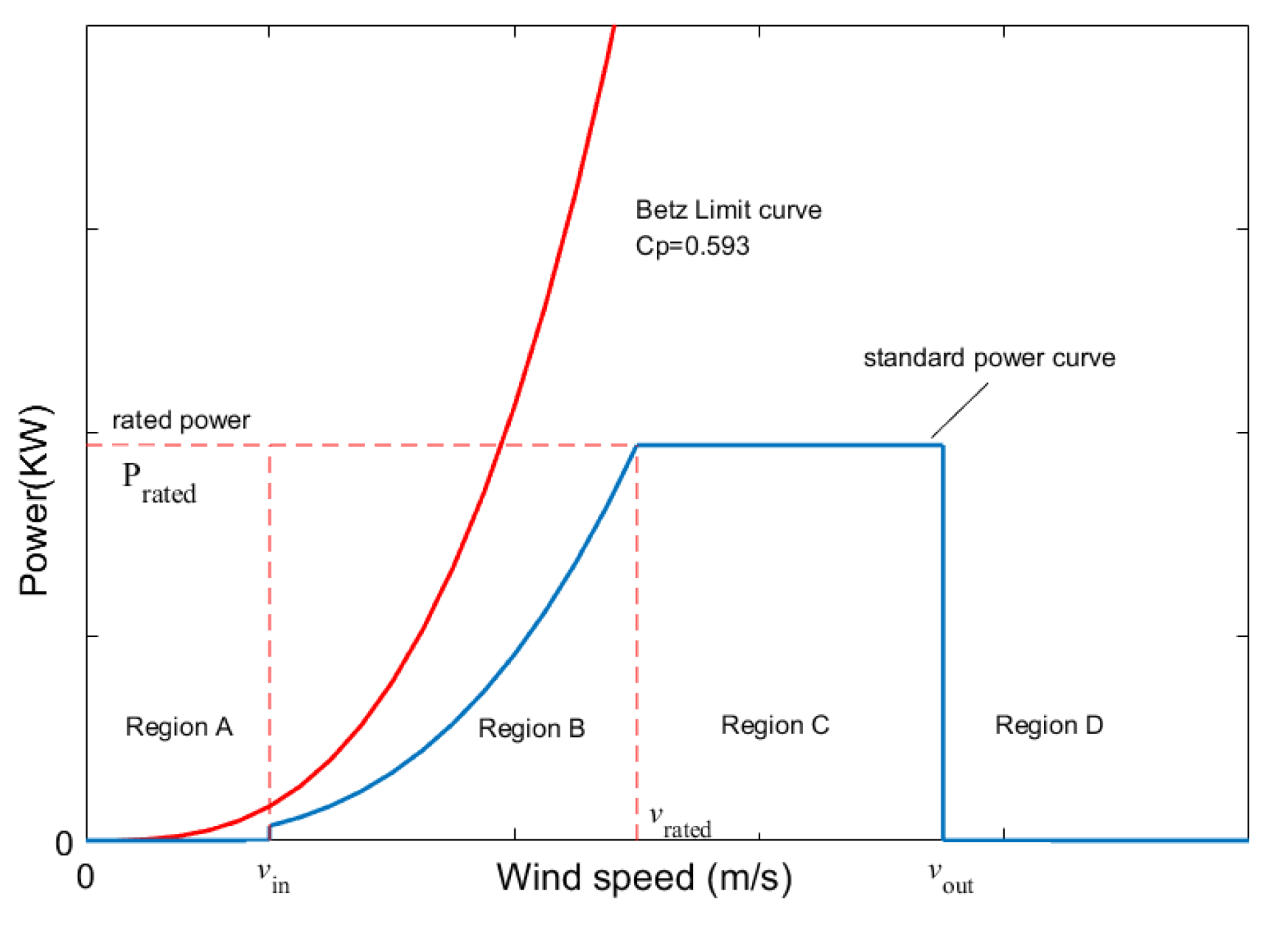
2.1. Power Curves
2.2. Problem Statement and Purpose of Assessment
- (1)
- The evaluation results must accurately indicate the variations between the actual power curve and the baseline power curve.
- (2)
- The method must be robust and unaffected by the presence of outliers.
- (3)
- The method must be able to be implemented simply, and the assessment results must be easy to understand for engineers to understand.
- (4)
- A stable trend of power performance changes must be acquired, as this trend can be used for prediction analysis.
3. Power Performance Assessment Methodology
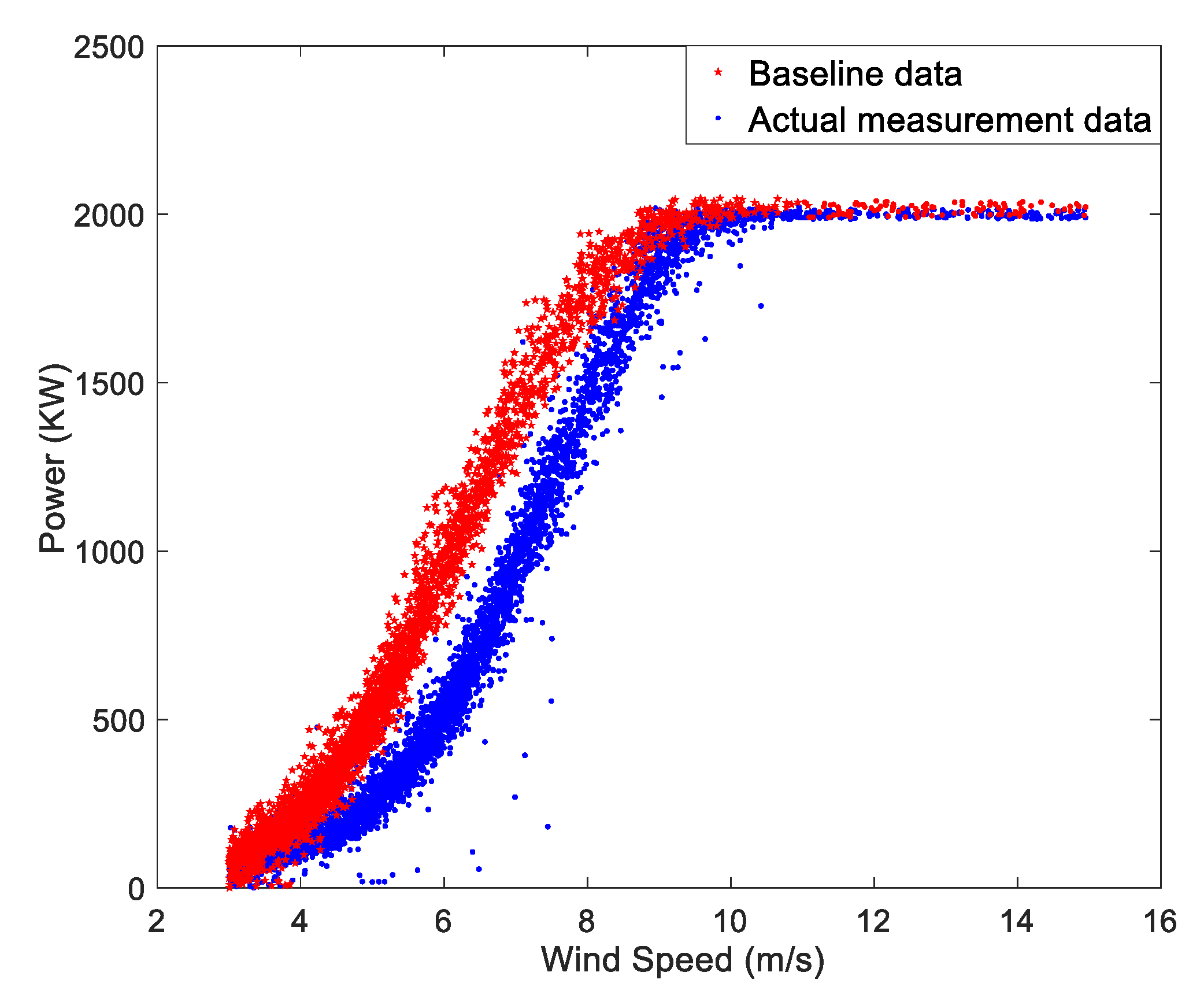
3.1. Baseline Data Selection
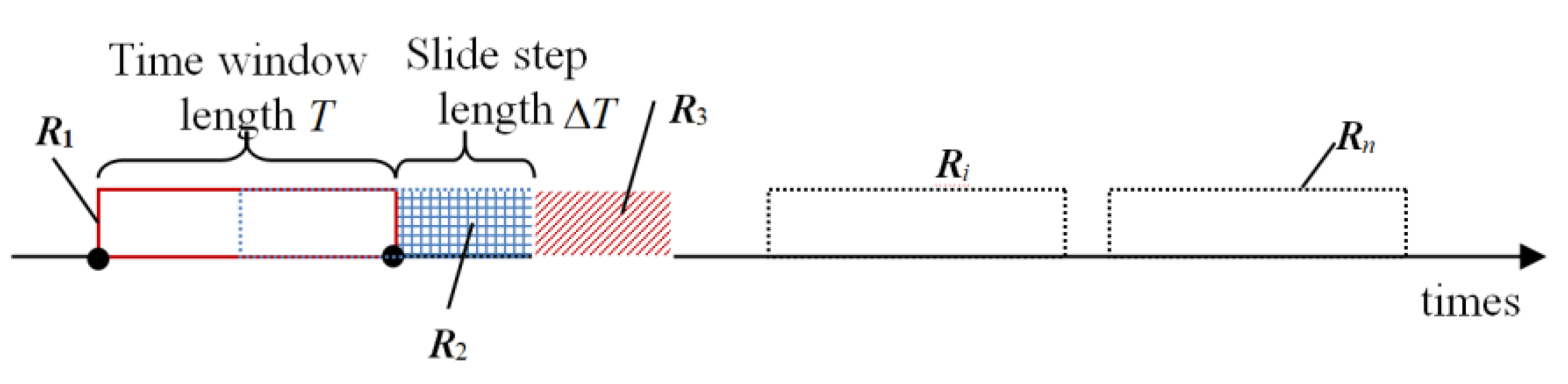
3.2. Preprocessing
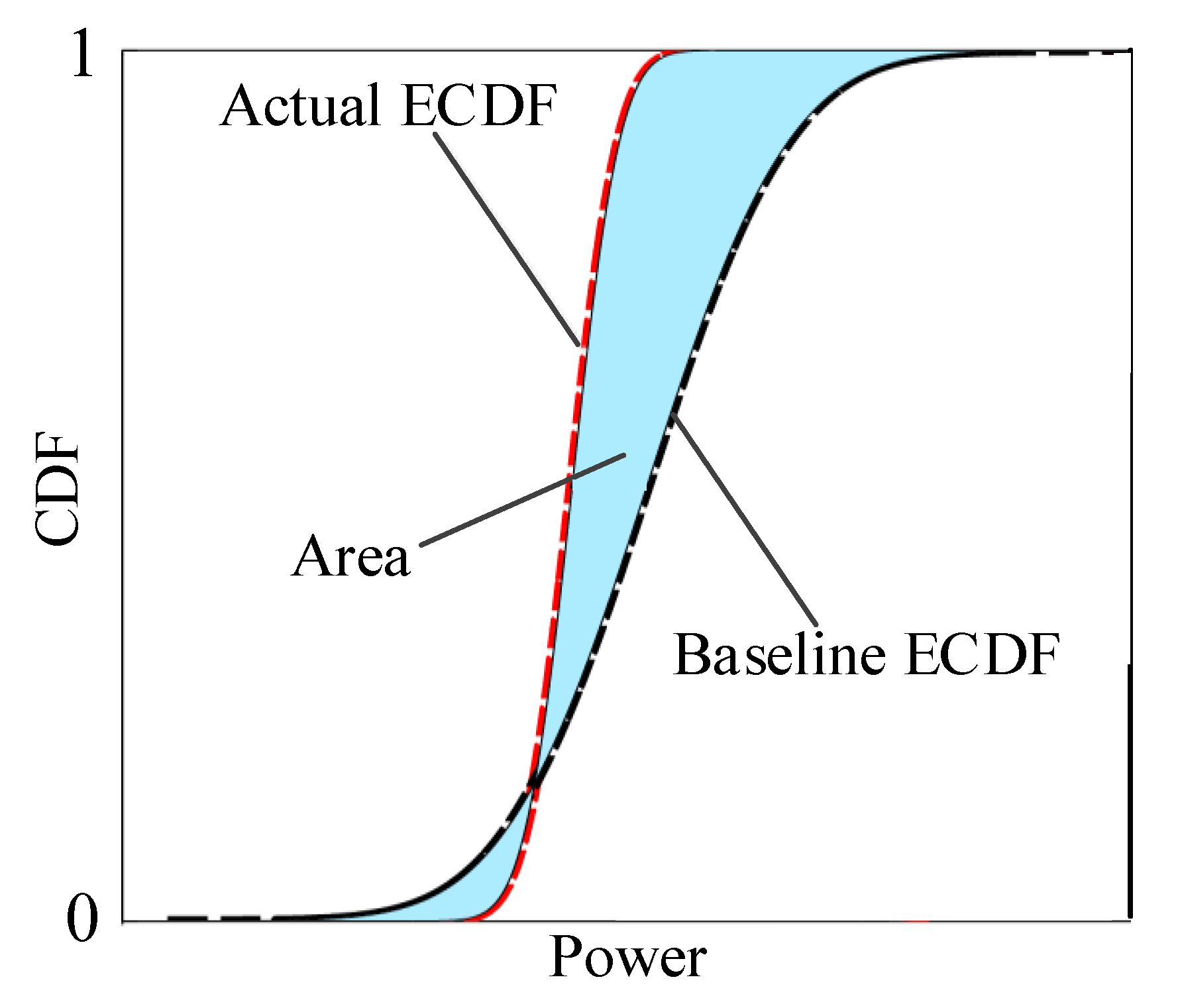
3.3. Health Value Based on the Probabilistic Area Metric
3.3.1. Health Value in the MWPTR
3.3.2. Health Value in the RPOR
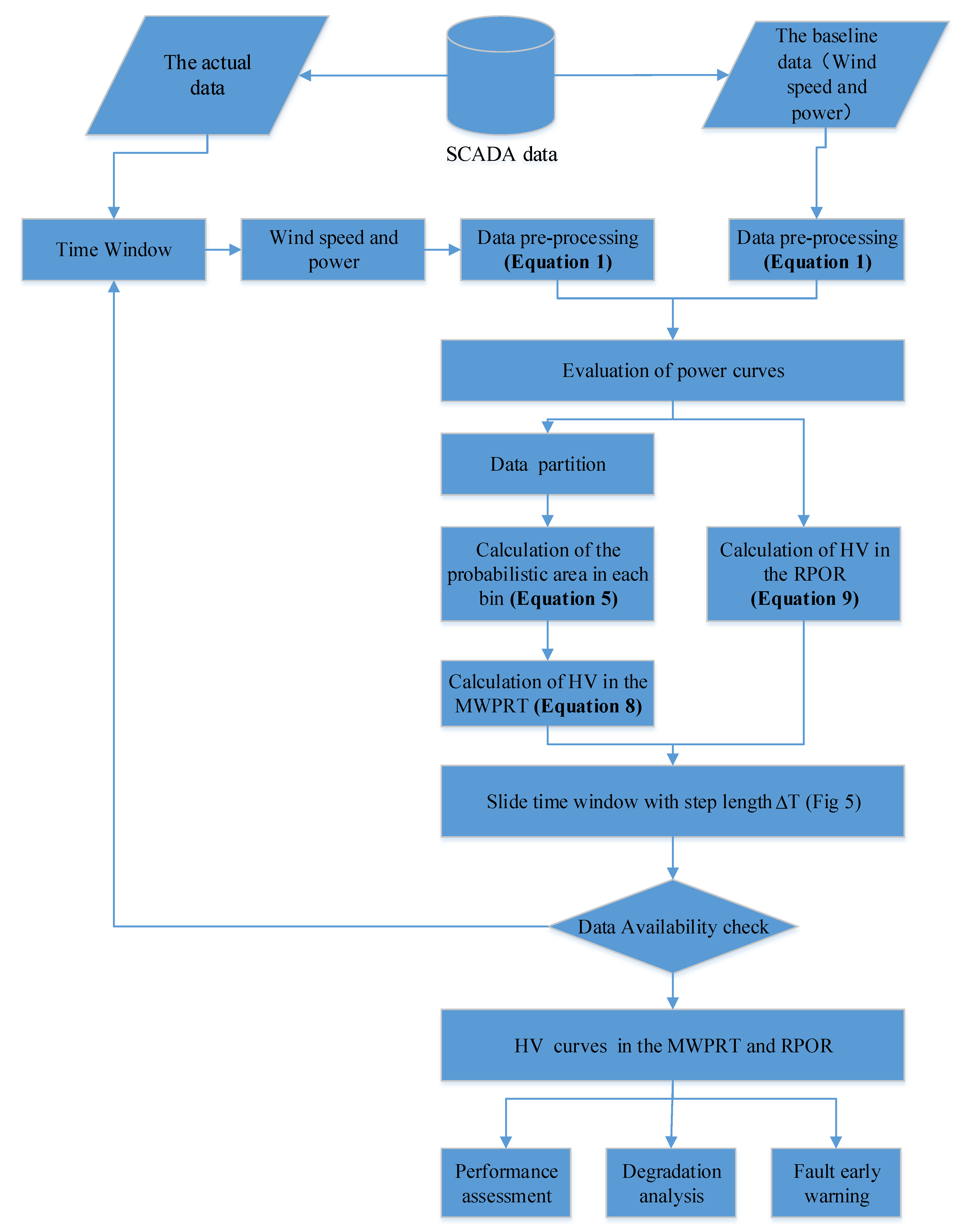
3.4. Calculation Flowchart
4. Verification of Results
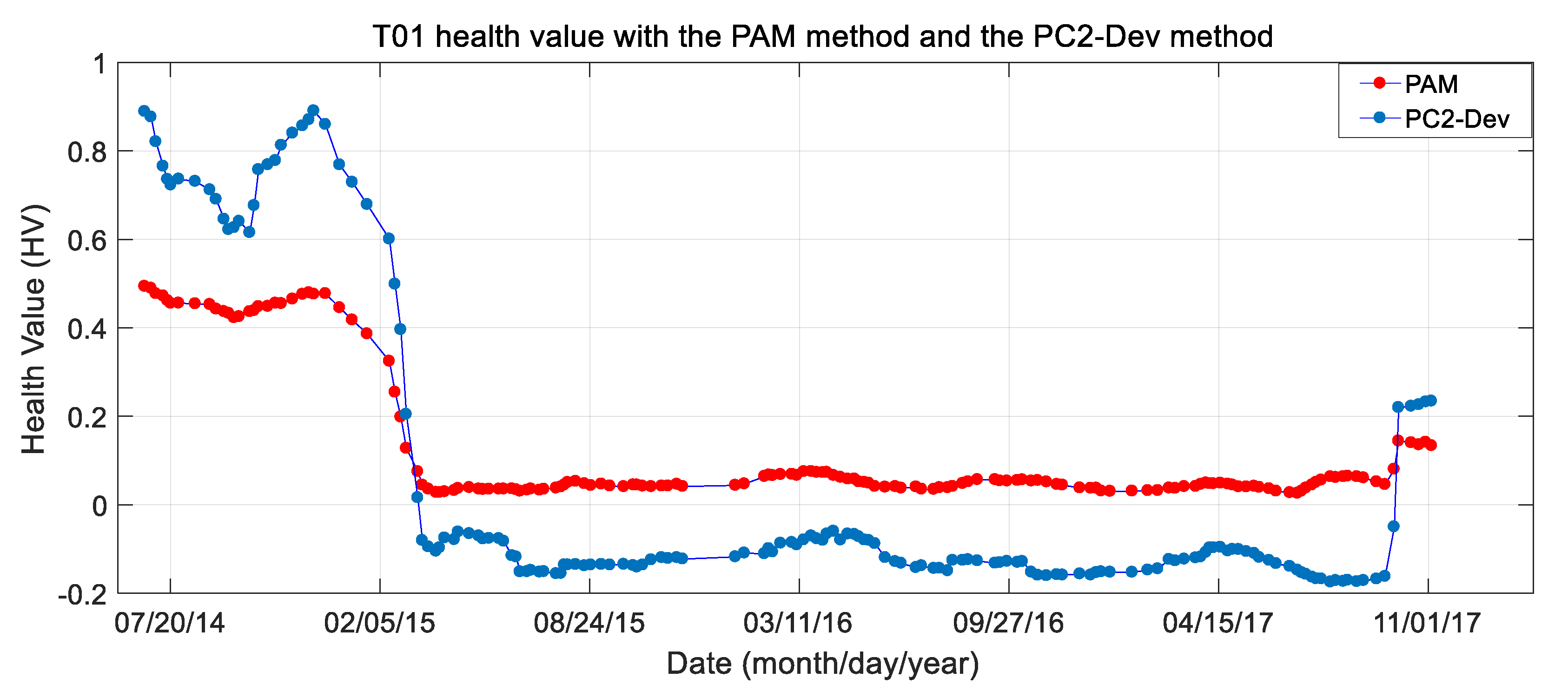
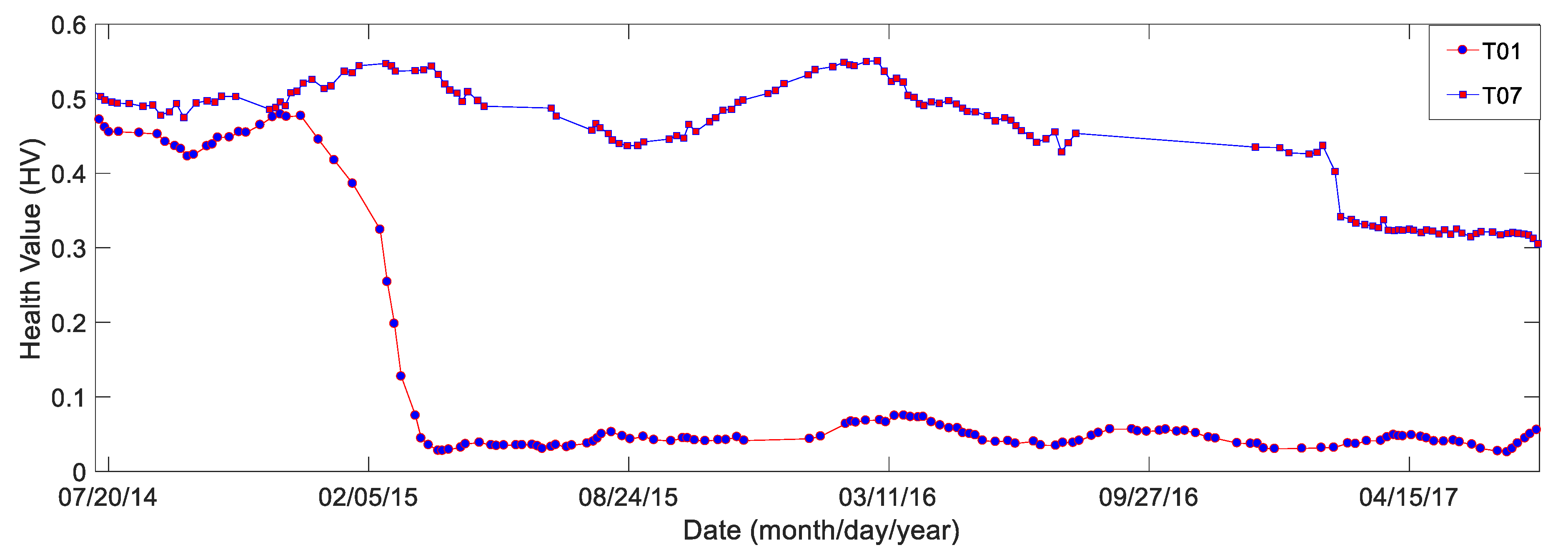
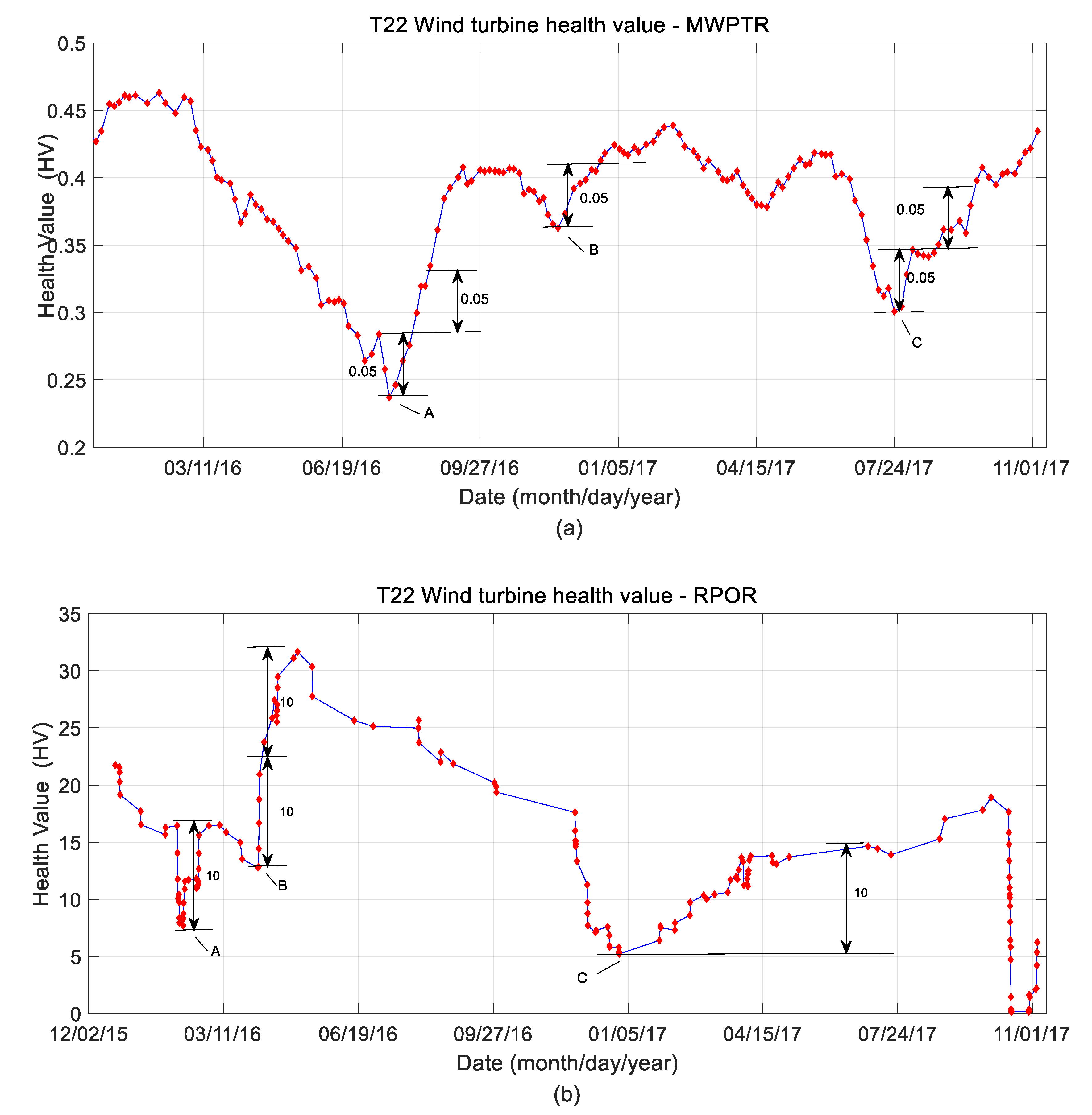
4.1. MWPTR Results
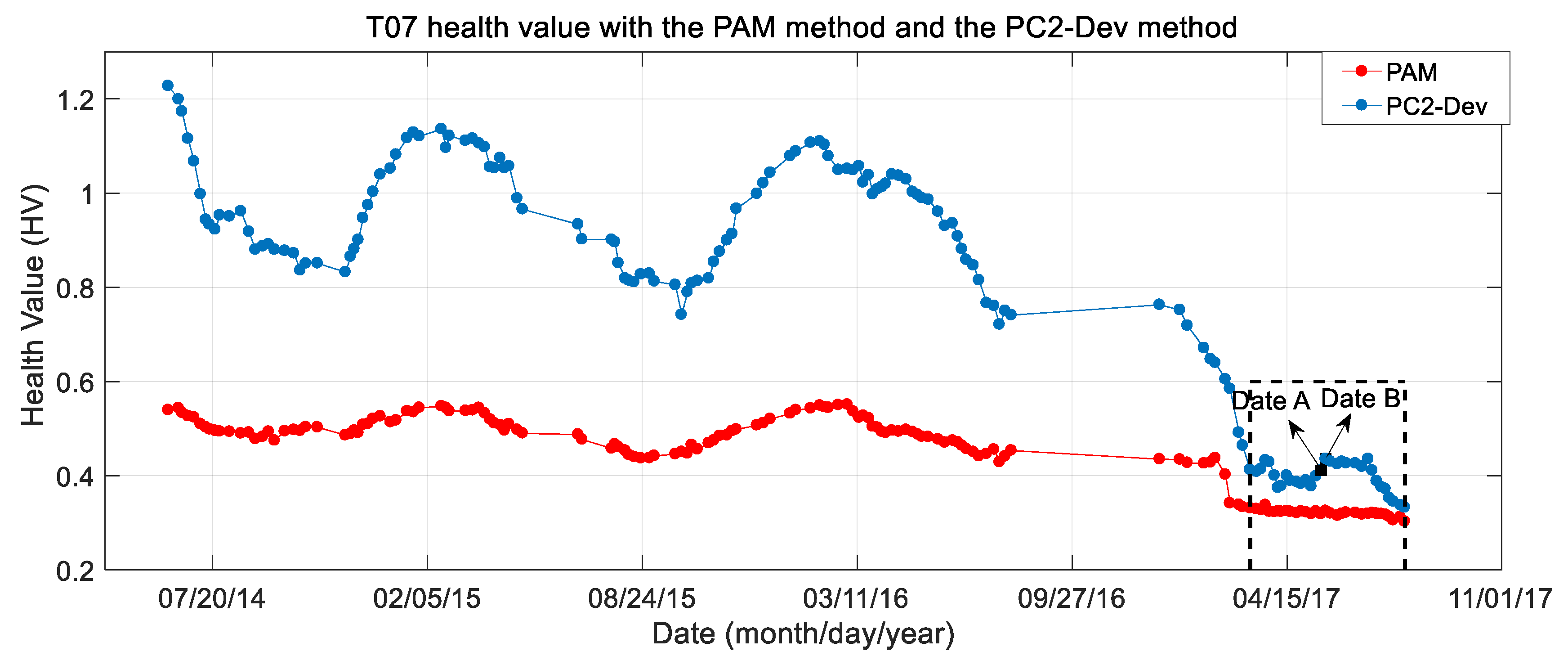
4.2. RPOR Results
5. Potential Implementation
5.1. Performance Optimization
5.2. Degradation Analysis
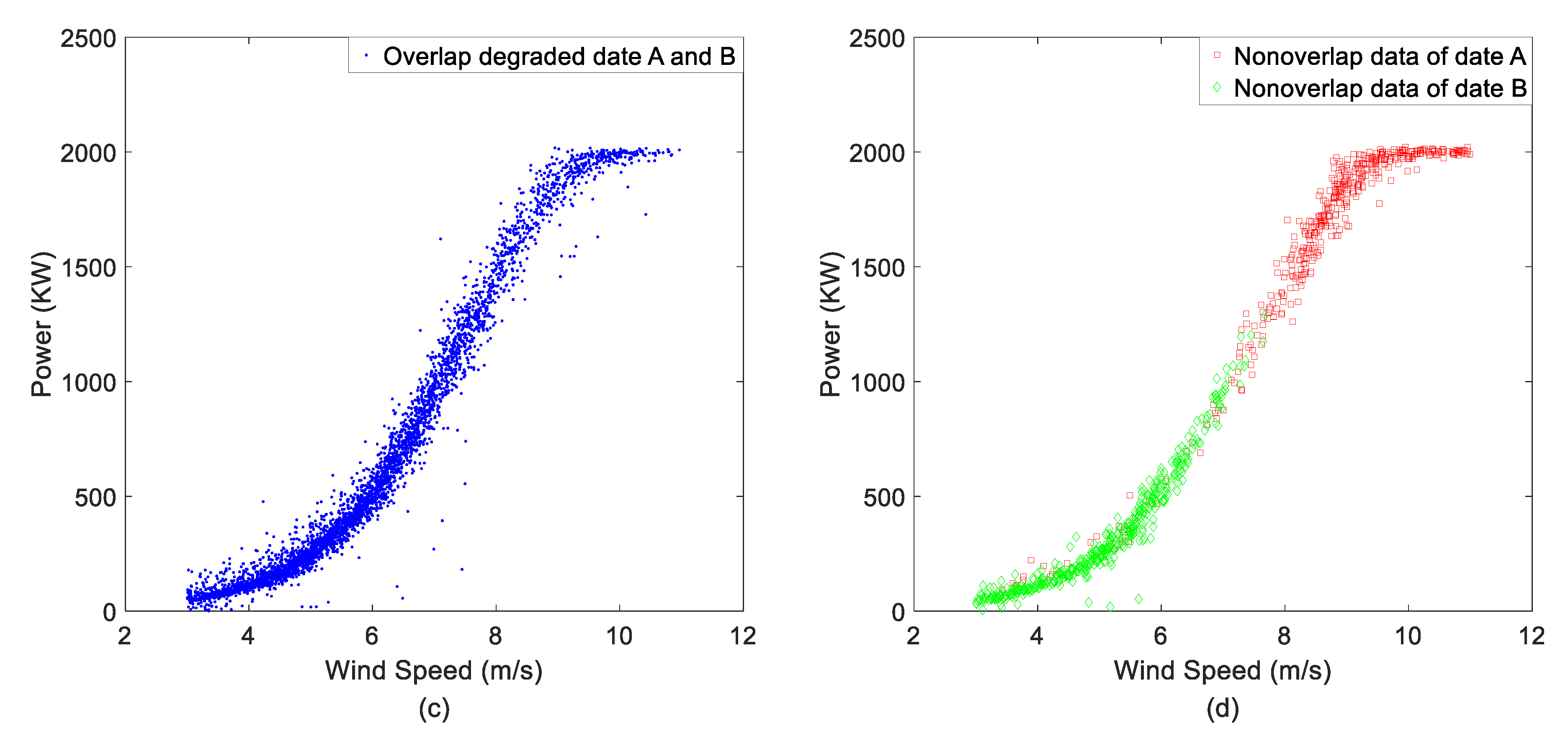
5.3. Condition Pre-Warning
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hameed, Z.; Hong, Y.S.; Cho, Y.M.; Ahn, S.H.; Song, C.K. Condition monitoring and fault detection of wind turbines and related algorithms: A review. Renew. Sustain. Energy Rev. 2009, 13, 1–39. [Google Scholar] [CrossRef]
- Stetco, A.; Dinmohammadi, F.; Zhao, X.; Robu, V.; Flynn, D.; Barnes, M.; Keane, J.; Nenadic, G. Machine learning methods for wind turbine condition monitoring: A review. Renew. Energy 2019, 133, 620–635. [Google Scholar] [CrossRef]
- Gao, Z.; Sheng, S. Real-time monitoring, prognosis, and resilient control for wind turbine systems. Renew. Energy 2018, 116, 1–4. [Google Scholar] [CrossRef]
- Jia, X.; Jin, C.; Buzza, M.; Di, Y.; Siegel, D.; Lee, J. A deviation based assessment methodology for multiple machine health patterns classification and fault detection. Mech. Syst. Signal Process. 2018, 99, 244–261. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Q.C.; Yang, X.B.; Zeng, B. Condition monitoring of wind turbines based on analysis of temperature-related parameters in supervisory control and data acquisition data. Meas. Control 2019. [Google Scholar] [CrossRef]
- Staffell, I.; Green, R. How does wind farm performance decline with age? Renew. Energy 2014, 66, 775–786. [Google Scholar] [CrossRef]
- Roscher, B.; Werkmeister, A.T.; Schelenz, R.; Jacobs, G. Estimation of 1Hz Distribution based on 10min SCADA Data. In Proceedings of the Offshore Wind R&D Conference 2018, Bremerhaven, Germany, 14–16 November 2018. [Google Scholar]
- Li, J.L.; Zhang, X.R.; Zhou, X.; Lu, L.Y. Reliability assessment of wind turbine bearing based on the degradation-Hidden-Markov model. Renew. Energy 2019, 132, 1076–1087. [Google Scholar] [CrossRef]
- Gao, Z.; Ding, S.X.; Cecati, C. Real-time fault diagnosis and fault-tolerant control. IEEE Trans. Ind. Electron. 2015, 62, 3752–3756. [Google Scholar] [CrossRef]
- Gao, Z.; Cecati, C.; Ding, S.X. A survey of fault diagnosis and fault-tolerant techniques-part II: Fault diagnosis with knowledge-Based and hybrid/active approaches. IEEE Trans. Ind. Electron. 2015, 62, 3768–3774. [Google Scholar] [CrossRef]
- IEC, IEC 61400-12-1. Wind Turbines—Part 12-1: Power Performance Measurements of Electricity Producing Wind Turbines; International Electrotechnical Commission: Geneva, Switzerland, 2005. [Google Scholar]
- Taslimi-Renani, E.; Modiri-Delshad, M.; Elias, M.F.M.; Rahim, N.A. Development of an enhanced parametric model for wind turbine power curve. Appl. Energy 2016, 177, 544–552. [Google Scholar] [CrossRef]
- Zhang, F.; Wen, Z.; Liu, D.; Jiao, J.; Wan, H.; Zeng, B. Calculation and Analysis of Wind Turbine Health Monitoring Indicators Based on the Relationships with SCADA Data. Appl. Sci. 2020, 10, 410. [Google Scholar] [CrossRef]
- Lee, J. Measurement of machine performance degradation using a neural network model. Comput. Ind. 1996, 30, 193–209. [Google Scholar] [CrossRef]
- Dai, J.C.; Liu, D.S.; Wen, L.; Long, X. Research on power coefficient of wind turbines based on SCADA data. Renew. Energy 2016, 86, 206–215. [Google Scholar] [CrossRef]
- Park, J.Y.; Lee, J.K.; Oh, K.Y.; Lee, J.S. Development of a novel power curve monitoring method for wind turbines and its field tests. IEEE Trans. Energy Convers. 2014, 29, 119–128. [Google Scholar] [CrossRef]
- Kusiak, A.; Zheng, H.; Song, Z. On-line monitoring of power curves. Renew. Energy 2009, 34, 1487–1493. [Google Scholar] [CrossRef]
- Cambron, P.; Lepvrier, R.; Masson, C.; Tahan, A.; Pelletier, F. Power curve monitoring using weighted moving average control charts. Renew. Energy 2016, 94, 126–135. [Google Scholar] [CrossRef]
- Long, H.; Wang, L.; Zhang, Z.; Song, Z.; Xu, J. Data-Driven Wind Turbine Power Generation Performance Monitoring. IEEE Trans. Ind. Electron. 2015, 62, 6627–6635. [Google Scholar] [CrossRef]
- Guo, P.; Infield, D. Wind Turbine Power Curve Modeling and Monitoring with Gaussian Process and SPRT. IEEE Trans. Sustain. Energy 2018, 11. [Google Scholar] [CrossRef]
- Papatheou, E.; Dervilis, N.; Maguire, A.E.; Campos, C.; Antoniadou, I.; Worden, K. Performance monitoring of a wind turbine using extreme function theory. Renew. Energy 2017, 113, 1490–1502. [Google Scholar] [CrossRef]
- De la Hermosa, R.R.; González-Carrato, R. Wind farm monitoring using Mahalanobis distance and fuzzy clustering. Renew. Energy 2018, 123, 526–540. [Google Scholar]
- Gill, S.; Stephen, B.; Galloway, S. Wind Turbine Condition Assessment through Power Curve Copula Modeling. IEEE Trans. Sustain. Energy 2012, 3, 94–101. [Google Scholar] [CrossRef]
- Marvuglia, A.; Messineo, A. Monitoring of wind farms’ power curves using machine learning techniques. Appl. Energy 2012, 98, 574–583. [Google Scholar] [CrossRef]
- Lapira, E.; Brisset, D.; Ardakani, H.D.; Siegel, D.; Lee, J. Wind turbine performance assessment using multi-regime modeling approach. Renew. Energy 2012, 45, 86–95. [Google Scholar] [CrossRef]
- Skrimpas, G.A.; Sweeney, C.W.; Marhadi, K.S.; Jensen, B.B.; Mijatovic, N.; Holbll, J. Employment of Kernel Methods on Wind Turbine Power Performance Assessment. IEEE Trans. Sustain. Energy 2015, 6, 698–706. [Google Scholar] [CrossRef]
- Jia, X.; Jin, C.; Buzza, M.; Wang, W.; Lee, J. Wind turbine performance degradation assessment based on a novel similarity metric for machine performance curves. Renew. Energy 2016, 99, 1191–1201. [Google Scholar] [CrossRef]
- Dai, J.C.; Yang, W.X.; Cao, J.W.; Liu, D.S.; Long, X. Ageing assessment of a wind turbine over time by interpreting wind farm SCADA data. Renew. Energy 2018, 116, 116,199–208. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.P.; Xu, X. A density-based algorithm for discovering clusters a density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery & Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Daszykowski, M.; Walczak, B.; Massart, D.L. Looking for natural patterns in data: Part 1. Density-based approach. Chemom. Intell. Lab. Syst. 2001, 56, 83–92. [Google Scholar] [CrossRef]
- Daszykowski, M.; Walczak, B.; Massart, D.L. Looking for natural patterns in analytical data. Part 2. Tracing local density with OPTICS. J. Chem. Inf. Comput. Sci. 2016, 42, 500. [Google Scholar] [CrossRef]
- Mahmoud, H.M. Sorting: A Distribution Theory; John Wiley & Sons: Hoboken, NJ, USA, 2000; ISBN 978-04713978-047132710327103. [Google Scholar]



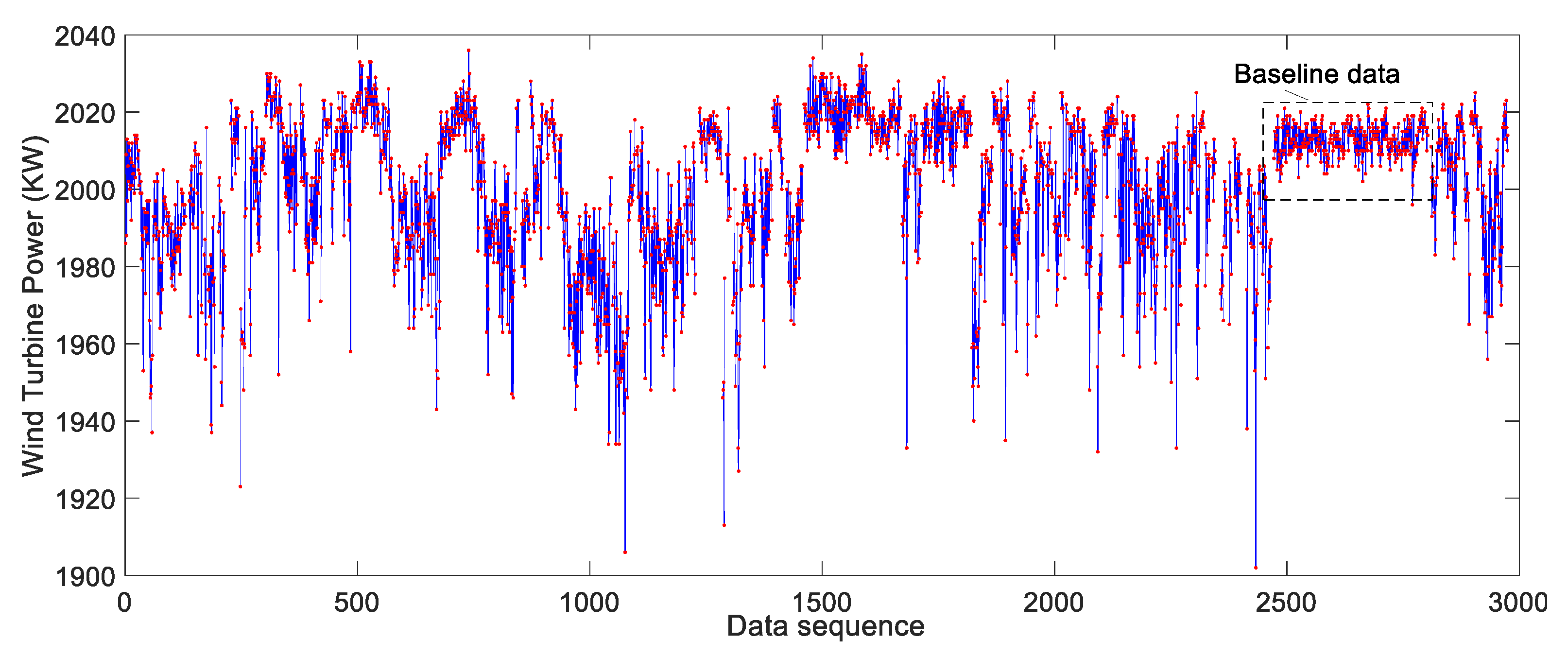
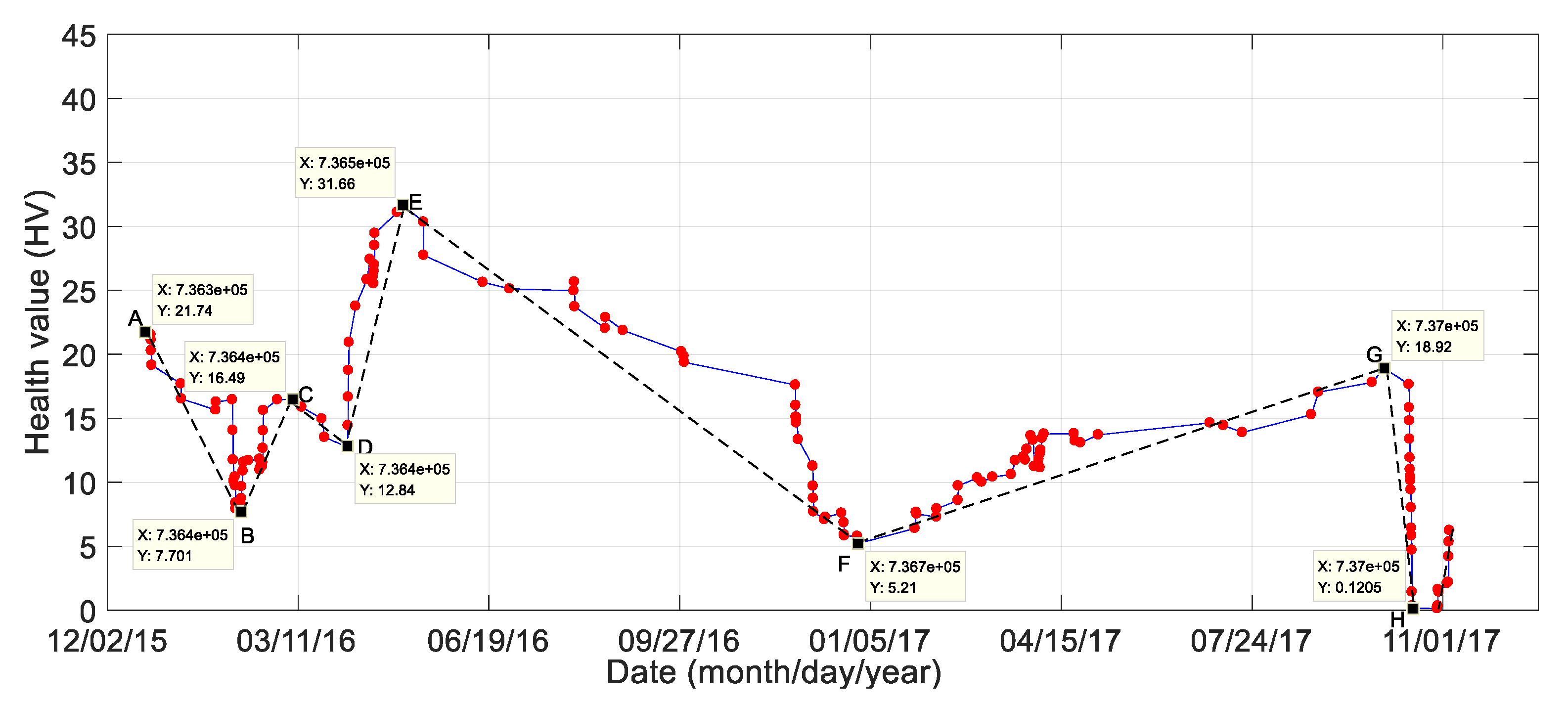
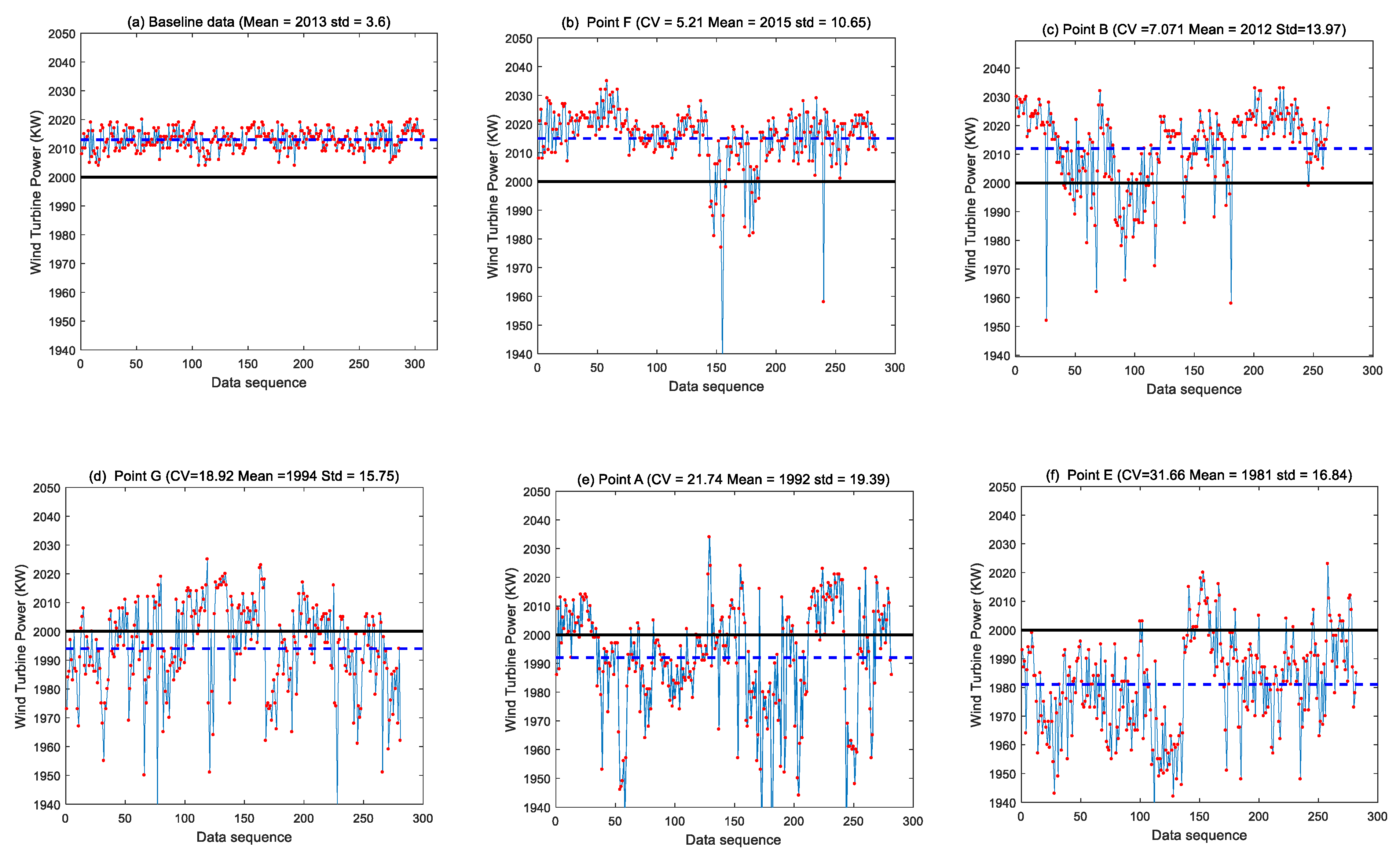
| Date | Health Value | Mean Value (KM) | Standard Deviation (std) |
|---|---|---|---|
| Baseline Data | 0 | 2013 | 3.6 |
| Point F | 5.21 | 2015 | 10.65 |
| Point B | 7.071 | 2012 | 13.97 |
| Point G | 18.92 | 1994 | 15.75 |
| Point A | 21.74 | 1992 | 19.39 |
| Point E | 31.66 | 1981 | 16.84 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Z.; Zhao, Q.; Yang, X.; Zhu, A. A Power Performance Online Assessment Method of a Wind Turbine Based on the Probabilistic Area Metric. Appl. Sci. 2020, 10, 3268. https://doi.org/10.3390/app10093268
Xiao Z, Zhao Q, Yang X, Zhu A. A Power Performance Online Assessment Method of a Wind Turbine Based on the Probabilistic Area Metric. Applied Sciences. 2020; 10(9):3268. https://doi.org/10.3390/app10093268
Chicago/Turabian StyleXiao, Zhao, Qiancheng Zhao, Xuebing Yang, and AnFeng Zhu. 2020. "A Power Performance Online Assessment Method of a Wind Turbine Based on the Probabilistic Area Metric" Applied Sciences 10, no. 9: 3268. https://doi.org/10.3390/app10093268
APA StyleXiao, Z., Zhao, Q., Yang, X., & Zhu, A. (2020). A Power Performance Online Assessment Method of a Wind Turbine Based on the Probabilistic Area Metric. Applied Sciences, 10(9), 3268. https://doi.org/10.3390/app10093268




