Enhancement of a New Methodology Based on the Impulse Excitation Technique for the Nondestructive Determination of Local Material Properties in Composite Laminates

Abstract

A new approach for the nondestructive determination of the elastic properties of composite laminates is presented. The approach represents an improvement of a recently published experimental methodology based on the Impulse Excitation Technique, which allows nondestructively assessing local elastic properties of composite laminates by isolating a region of interest through a proper clamping system. Different measures of the first resonant frequency are obtained by rotating the clamping system with respect to the material orientation. Here, in order to increase the robustness of the inverse problem, which determines the elastic properties from the measured resonant frequencies, information related to the modal shape is retained by considering the effect of an additional concentrated mass on the first resonant frequency. According to the modal shape and the position of the mass, different values of the first resonant frequency are obtained. Here, two positions of the additional mass, i.e., two values of the resonant frequency in addition to the unloaded frequency value, are considered for each material orientation. A Rayleigh–Ritz formulation based on higher order theory is adopted to compute the first resonant frequency of the clamped plate with concentrated mass. The elastic properties are finally determined through an optimization problem that minimizes the discrepancy on the frequency reference values. The proposed approach is validated on several materials taken from the literature. Finally, advantages and possible limitations are discussed.

1. Introduction

Manufacturing defects, low reproducibility of manufacturing process, and in situ material damages due to in service loads are some of the most critical factors that limit the widespread diffusion of composite materials, whose mechanical and weight characteristics are extremely desirable for structural applications. In this context, nondestructive techniques for the determination of the health state of composite components are becoming more and more important. Among the others, thanks to rather simple and rapid testing applications, vibrational methods are increasingly adopted for manufacturing quality control or damage assessment [1,2]. Furthermore, differently from other techniques, such as the micro-computed tomography, these methods are able to quantitatively assess the material properties of a component. Vibrational methods usually adopt an inverse problem formulation that intends to determine the elastic properties from the measured resonant frequencies [3,4,5,6]. In this regard, material constants are calculated through an optimization process based on Finite Element models, Rayleigh–Ritz formulations, and analytical formulas. Four resonant frequencies are usually sufficient to obtain a reasonable set of elastic estimates [7]. The robustness of the assessed elastic properties is a critical aspect of vibrational methods. Therefore, further information is usually considered within the inverse problem, such as the modal shape and/or further frequencies. However, multiple resonant frequencies can be difficult to recognize, while the investigation of the modal shape can require expensive equipment developed for laboratory [8].

Furthermore, vibrational methods usually account for the global response of the component [9]. Thus, the presence of local defects can be concealed or averaged by the global behavior of the component. Indeed, the local assessment of material properties still represents a challenging field [10,11,12]. Recently, a new experimental methodology has been presented that allows nondestructively assessing local elastic properties of composite laminates [13]. The methodology aims to:

(i)

Isolate a region of the component through a specific equipment, which clamps the extremities of the region without damaging the material;

(ii)

Adopt the Impulse Excitation Technique to measure the first resonant frequency of the retained region;

(iii)

Exploit the material anisotropy to obtain at least four different measures of the first resonant frequency, particularly by varying the relative orientation between the clamping system and the material;

(iv)

Assess the elastic properties of the investigated region from the measured resonant frequencies through an optimization process.

The methodology adopts a testing machine to compress two rectangular frames on the plate and isolate the region to investigate. Thus, the use of the testing machine represents a preliminary setup. However, even though this clamping system is not suitable for real-world composite structures, it is particularly useful to investigate the methodology in laboratory testing conditions.

In particular, it was possible to investigate the inverse problem, which intends to assess the elastic properties from the measured first resonant frequencies. The inverse problem can be undetermined, i.e., the measured frequencies can be obtained with multiple sets of elastic estimates. In order to increase the accuracy of the methodology, the number of relative orientations can be increased. Instead, the use of higher mode frequencies is limited by the proximity of the clamped boundaries, whose noninfinite stiffness can consistently affect the result. Indeed, the higher modes increasingly involve in the modal displacement the material in proximity of the clamped boundaries. As a consequence, the effect of the nonfinite stiffness, which is for the first mode as shown in [13], increasingly affects the measurement of the higher resonant frequencies. Furthermore, in order to guarantee the robustness of the methodology, limits on the design domain of the elastic properties, i.e., $E_{11}, E_{22},G_{12}$, and ${\nu }_{12}$, are to be considered, which is undesirable, especially when assessing damage level. Here, the design domain identifies the space where the aforementioned material properties can vary, while the optimization problem minimizes the discrepancy between the measured and the numerical resonant frequencies. Indeed, if the methodology has to be adopted for detecting local material variations, limitations on the material properties can be particularly inconvenient.

In this paper, a new approach based on this experimental methodology is presented, which allows increasing the robustness of the inverse problem. In particular, information related to the modal shape is retained within the inverse problem only by considering the effect of a concentrated mass on the first resonant frequency. The modal shape strictly depends on the material properties and, when dealing with anisotropic material, its isolines are not necessary parallel to the clamped boundaries, as also observed in other works in literature [14,15,16]. It is the case of an orthotropic material whose axes of orthotropy are not parallel to the boundaries. The modal response is here analyzed with the use of a concentrated additional mass, whose effect on the first resonant frequency depends on its position on the plate in accordance with the modal shape. Indeed, according to the modal shape and to the position of the mass, different values of the first resonant frequency are obtained. Here, two positions of the additional mass, i.e., two values of the resonant frequency, in addition to the unloaded resonant frequency of the clamped plate, are considered for each material orientation. Thus, the modal response is accounted within the optimization process, which consistently enhances the sensitivity of the inverse problem to the elastic properties.

A numerical validation of the proposed approach is here performed, which considers materials with different elastic constants. A Rayleigh–Ritz formulation based on higher order theory is adopted to compute the first resonant frequency of the clamped plate loaded by a concentrated mass. The use of Rayleigh–Ritz formulation indeed allows consistently decreasing the computational cost with respect to the finite element-based optimization adopted in [13]. Thus, the Rayleigh–Ritz formulation represents a further step toward the application of the proposed methodology to real-world composite structures. After validating the Rayleigh–Ritz formulation on experimental data taken from the literature, for each retained material, the frequencies are calculated for the different material orientations and mass positions, thus constituting the reference values. Then, the elastic properties are handled as the design variables of an optimization process, which minimizes the discrepancy between the resonant frequency calculated at each iteration and the corresponding reference value. Results show that with the proposed approach, the modal shape can be identified only through a concentrated mass positioned in two different spots, thus avoiding the need for costly equipment. Finally, by accounting for the modal response within the optimization process, the sensitivity of the inverse problem to the elastic properties is particularly enhanced.

2. Methods

This section firstly presents the Rayleigh–Ritz formulation here adopted to calculate the first resonant frequency of clamped laminates loaded by a concentrated mass. Then, the proposed approach for retaining the modal shape through the added mass is detailed.

2.1. Rayleigh–Ritz Formulation

A Rayleigh–Ritz formulation is here presented in order to calculate the first resonant frequency of clamped plates made of laminated composites and loaded by a concentrated mass. A rectangular plate of dimensions $a$ and $b$ and constituted by $N$ orthotropic layers for a total thickness $h$ is considered, as shown in Figure 1.

The displacements in $x$, $y$, and $z$ directions are denoted with $u$, $v$, and $w$, respectively. Thus, the strain energy for the entire laminate is expressed as:

$$U=\frac{1}{2}{{\displaystyle \sum }}_{k=1}^N{{\displaystyle \int }}_{V_k}^{}\underset{\_}{{\epsilon }_k^T}·\underset{\_}{{\sigma }_k}d{V}_k,$$

(1)

where subscript k refers to k-th lamina, $N$ is the total number of layers, $V_k$ is the volume of each lamina, and $\underset{\_}{{\epsilon }_k}$ and $\underset{\_}{{\sigma }_k}$ are the strain and stress vectors at the lamina level.

Due to the presence of the concentrated mass, the kinetic energy is given by the following sum:

$$T=\frac{1}{2}{\displaystyle \sum }_{k=1}^N{{\displaystyle \int }}_{V_k}^{}{\rho }_k\left[{\left(\frac{\delta u}{\delta t}\right)}^2+{\left(\frac{\delta v}{\delta t}\right)}^2+{\left(\frac{\delta w}{\delta t}\right)}^2\right]d{V}_k+\frac{M}{2}\left[{\left(\frac{\delta u_{lm}}{\delta t}\right)}^2+{\left(\frac{\delta v_{lm}}{\delta t}\right)}^2+{\left(\frac{\delta w_{lm}}{\delta t}\right)}^2\right]$$

(2)

where ${\rho }_k$ is the mass density of the k-th lamina and $M$ is the concentrated mass located at $x=l$ and $y=m$. Therefore, for example, $u_{lm}$ indicates the displacement in the x direction in correspondence of the mass location. Here, the effect of the concentrated mass on rotary inertia is neglected, and it is assumed for simplicity that the mass is located on the mid-plane, i.e., at $z=0$.

The Rayleigh–Ritz formulation is here based on the higher-order shear deformation theory for laminated composites proposed by Reddy [17]. According to the Reddy’s theory, the displacements $u$, $v$, and $w$ of an arbitrary point of the plate are represented as

$$\begin{gathered} u\left(x,y,z,t\right)=u_0\left(x,y,t\right)+z{\phi }_x\left(x,y,t\right)-\frac{4·z^3}{3·h^2}\left({\phi }_x\left(x,y,t\right)-\frac{\delta w\left(x,y,t\right)}{\delta x}\right), \\ v\left(x,y,z,t\right)=v_0\left(x,y,t\right)+z{\phi }_y\left(x,y,t\right)-\frac{4·z^3}{3·h^2}\left({\phi }_y\left(x,y,t\right)-\frac{\delta w\left(x,y,t\right)}{\delta y}\right), \\ w\left(x,y,z,t\right)=w_0\left(x,y,t\right), \end{gathered}$$

(3)

where $u_0$, $v_0$, and $w_0$ are the displacements of the mid-plane, and ${\phi }_x$ and ${\phi }_y$ are the rotations around the $x$ and $y$ axes, respectively. Hence, the stress and strain vectors of Equation (1) are $\underset{\_}{{\sigma }_k}={\left[{\sigma }_x,{\sigma }_y,{\sigma }_{xz},{\sigma }_{yz},{\sigma }_{xy}\right]}^T$ and $\underset{\_}{{\epsilon }_k}={\left[{\epsilon }_x,{\epsilon }_y,{\gamma }_{xz},{\gamma }_{yz},{\gamma }_{xy}\right]}^T$, respectively. The congruent equations for each lamina can be written as follows:

$$\underset{\_}{{\epsilon }_k}=B·\underset{\_}{u},$$

(4)

where $\underset{\_}{u}=\left[u_0,v_0,w_0,{\phi }_{0x},{\phi }_{0y}\right]$ and the matrix $B$ is defined as

$$B=\left[\begin{array}{ccccc}\frac{\delta }{\delta x}& 0& -\frac{4z^3{\delta }^2}{3h^2\delta x^2}& \left(z-\frac{4z^3}{3h^2}\right)\frac{\delta }{\delta x}& 0\\ 0& \frac{\delta }{\delta y}& -\frac{4z^3{\delta }^2}{3h^2\delta y^2}& 0& \left(z-\frac{4z^3}{3h^2}\right)\frac{\delta }{\delta y}\\ 0& 0& \left(1-\frac{4z^2}{h^2}\right)\frac{\delta }{\delta y}& 0& \left(1-\frac{4z^2}{h^2}\right)\\ 0& 0& \left(1-\frac{4z^2}{h^2}\right)\frac{\delta }{\delta x}& \left(1-\frac{4z^2}{h^2}\right)& 0\\ \frac{\delta }{\delta y}& \frac{\delta }{\delta x}& -\frac{8z^3{\delta }^2}{3h^2\delta x\delta y}& \left(z-\frac{4z^3}{3h^2}\right)\frac{\delta }{\delta y}& \left(z-\frac{4z^3}{3h^2}\right)\frac{\delta }{\delta x}\end{array}\right].$$

(5)

At the lamina level, the constitutive equations are as usual:

$$\underset{\_}{{\sigma }_k}=D_k·\underset{\_}{{\epsilon }_k},$$

(6)

where $D_k$ is related to the elastic constants through the rotation matrix, as follows:

$$D_k=T_k·Q·T_k^T,$$

(7)

With

$$T_k=\left[\begin{array}{ccccc}{\cos }^2{\theta }_k& {\sin }^2{\theta }_k& 0& 0& -2·\cos {\theta }_k·\sin {\theta }_k\\ {\sin }^2{\theta }_k& {\cos }^2{\theta }_k& 0& 0& 2·\cos {\theta }_k·\sin {\theta }_k\\ 0& 0& \cos {\theta }_k& \sin {\theta }_k& 0\\ 0& 0& -\sin {\theta }_k& \cos {\theta }_k& 0\\ \cos {\theta }_k·\sin {\theta }_k& -\cos {\theta }_k·\sin {\theta }_k& 0& 0& {\cos }^2{\theta }_k-{\sin }^2{\theta }_k\end{array}\right]$$

(8)

and

$$Q=\left[\begin{array}{ccccc}\frac{E_{11}}{\left(1-{\nu }_{12}·{\nu }_{21}\right)}& \frac{{\nu }_{12}·E_{22}}{\left(1-{\nu }_{12}·{\nu }_{21}\right)}& 0& 0& 0\\ \frac{{\nu }_{12}·E_{22}}{\left(1-{\nu }_{12}·{\nu }_{21}\right)}& \frac{E_{22}}{\left(1-{\nu }_{12}·{\nu }_{21}\right)}& 0& 0& 0\\ 0& 0& G_{23}& 0& 0\\ 0& 0& 0& G_{13}& 0\\ 0& 0& 0& 0& G_{12}\end{array}\right].$$

(9)

where, as usual, $E_{11}$ is the Young’s modulus in the longitudinal direction, $E_{22}$ is the Young’s modulus in the transverse direction, $G_{12}$, $G_{13}$, and $G_{23}$ are the shear moduli, and ${\nu }_{12}$ is the Poisson’s ratio. Here, the angle ${\theta }_k$ accounts for both the stacking angle of the lamina and the relative orientations between the clamped boundaries and the material. Furthermore, it is assumed that $G_{13}=G_{23}=G_{12}$. The assumption, for which the three material properties are equal, is certainly coarse for some composite materials as well as it is exact for some others [18,19]. Furthermore, the $G_{23}$ material property cannot be assessed from the measurements of the first resonant frequency. Therefore, it is assumed here that the three properties are equal.

As clamped boundaries do not admit an exact solution, the displacements $u$, $v$, and $w$ are approximated through a set of admissible functions. The plate is firstly assumed to be in harmonic motion, which allows writing the displacement vector $\underset{\_}{u}$ as:

$$\begin{gathered} u_0=U\left(x,y\right)\sin \omega t, \\ {v}_0=V\left(x,y\right)\sin \omega t, \\ {w}_0=W\left(x,y\right)\sin \omega t, \\ {\phi }_x={\mathsf{\Phi }}_x\left(x,y\right)\sin \omega t, \\ {\phi }_y={\mathsf{\Phi }}_y\left(x,y\right)\sin \omega t, \end{gathered}$$

(10)

where $\omega$ is the natural angular frequency. Then, the displacements and rotations are approximated with the following polynomial functions:

$$\begin{gathered} U\left(x,y\right)={{\displaystyle \sum }}_{i=1}^{I_1}{{\displaystyle \sum }}_{j=1}^{J_1}{c}_{ij}^u{\left(\frac{x}{a}\right)}^i{\left(\frac{y}{b}\right)}^j\left(1-\frac{x}{a}\right)\left(1-\frac{y}{b}\right), \\ V\left(x,y\right)={{\displaystyle \sum }}_{i=1}^{I_2}{{\displaystyle \sum }}_{j=1}^{J_2}{c}_{ij}^v{\left(\frac{x}{a}\right)}^i{\left(\frac{y}{b}\right)}^j\left(1-\frac{x}{a}\right)\left(1-\frac{y}{b}\right), \\ W\left(x,y\right)={{\displaystyle \sum }}_{i=2}^{I_3}{{\displaystyle \sum }}_{j=2}^{J_3}{c}_{ij}^w{\left(\frac{x}{a}\right)}^i{\left(\frac{y}{b}\right)}^j{\left(1-\frac{x}{a}\right)}^2{\left(1-\frac{y}{b}\right)}^2, \\ {\mathsf{\Phi }}_x\left(x,y\right)={{\displaystyle \sum }}_{i=1}^{I_4}{{\displaystyle \sum }}_{j=1}^{J_4}{c}_{ij}^{{\phi }_x}{\left(\frac{x}{a}\right)}^i{\left(\frac{y}{b}\right)}^j\left(1-\frac{x}{a}\right)\left(1-\frac{y}{b}\right), \\ {\mathsf{\Phi }}_y\left(x,y\right)={\displaystyle \sum }_{i=1}^{I_5}{\displaystyle \sum }_{j=1}^{J_5}{c}_{ij}^{{\phi }_y}{\left(\frac{x}{a}\right)}^i{\left(\frac{y}{b}\right)}^j\left(1-\frac{x}{a}\right)\left(1-\frac{y}{b}\right) \end{gathered}$$

(11)

Here, the extremities of the summations are considered as $I_1{J}_1=I_2{J}_2=\left(I_3-1\right)\left(J_3-1\right)=I_4{J}_4=I_5{J}_5.$These products define the number of terms n of the polynomials. In particular, parameters I and J represent the grades of the polynomial functions, which are adopted to approximate the modal shape of the resonant frequencies. Finally, substituting Equations (11), (10), (6), and (4) into Equations (1) and (2), the strain and kinetic energies can be written as

$$U=\frac{1}{2}{\left[C\right]}^T\left[K\right]\left[C\right],$$

(12)

$$T=\frac{1}{2}{\omega }^2{\left[C\right]}^T\left[M\right]\left[C\right],$$

where $\left[K\right]$ and $\left[M\right]$ are the stiffness and mass matrices of dimensions $R=I_1{J}_1+I_2{J}_2+\left(I_3-1\right)\left(J_3-1\right)+I_4{J}_4+I_5{J}_5$ and are related to the functions of Equation (11) adopted to describe the displacements field. $\left[C\right]$ is the vector of coefficients, i.e.,:

$${\left[C\right]}^T=\left[c_{11}^u,c_{12}^u,\dots ,c_{I_1{J}_1}^u, c_{11}^v,c_{12}^v,\dots ,c_{I_2{J}_2}^v,c_{11}^w,c_{12}^w,\dots ,c_{I_3{J}_3}^w,c_{11}^{{\phi }_x},c_{12}^{{\phi }_x},\dots ,c_{I_4{J}_4}^{{\phi }_x},c_{I_3{J}_3}^w,c_{11}^{{\phi }_y},c_{12}^{{\phi }_y},\dots ,c_{I_4{J}_4}^{{\phi }_y}\right]$$

(13)

Finally, equaling the strain and kinetic energy, as prescribed by the Rayleigh–Ritz method, the following eigenvalue problem can be written:

$$\left(\left[K\right]-{\omega }^2\left[M\right]\right)\left[C\right]=0,$$

(14)

which allows calculating the resonant frequencies by zeroing the determinant of the matrix. For further details on the matrix elements, the reader can refer to Chen et al. [18].

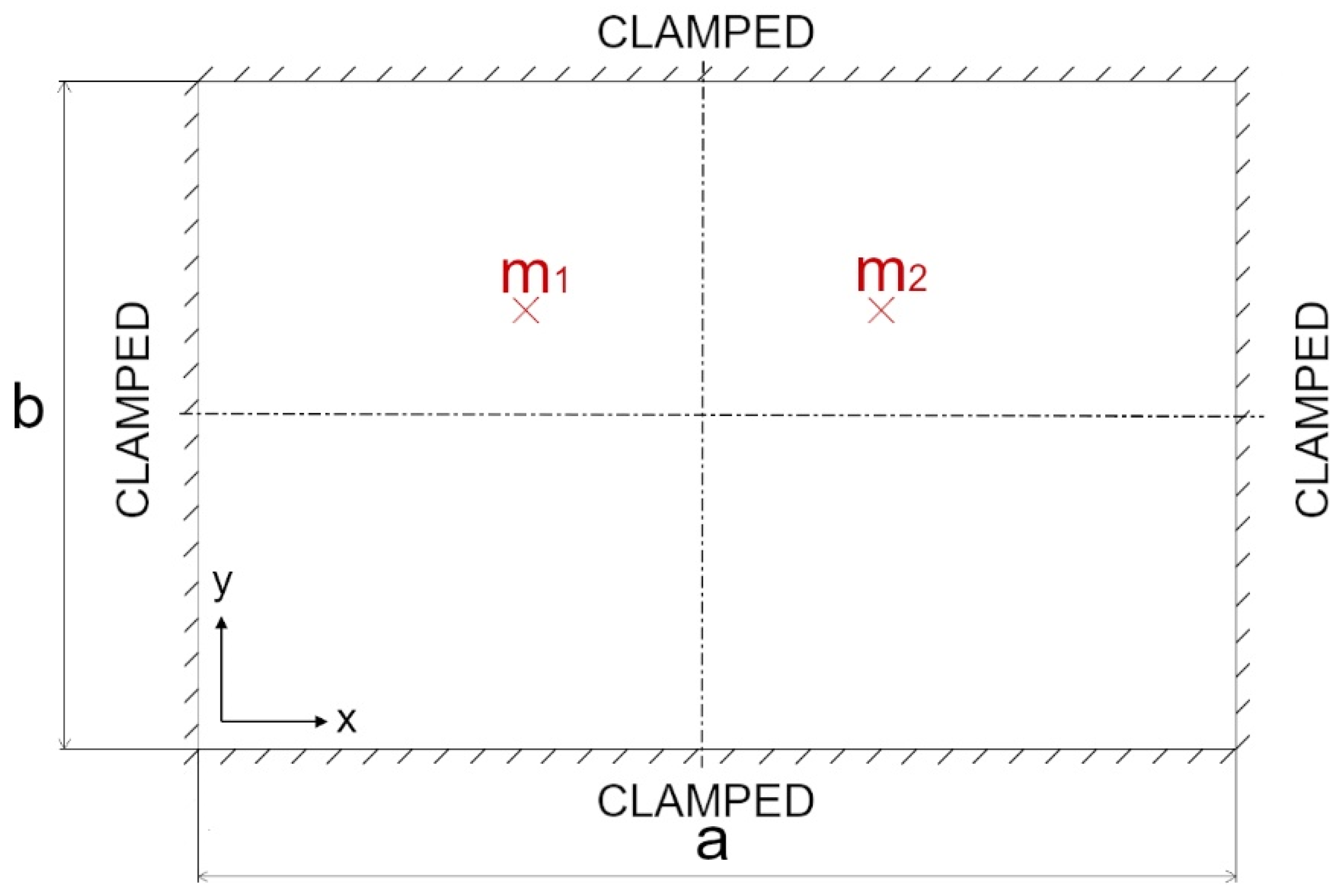
2.2. Modal Shape Information through Mass Position

The proposed approach is based on a recently presented experimental methodology, which allows nondestructively assessing local elastic properties of composite laminates [13]. In particular, the methodology consists of

(i)

Isolating a rectangular region of the component through a specific equipment, which clamps the extremities of the region without damaging the material;

(ii)

Measuring the first resonant frequency of the retained region through the Impulse Excitation Technique;

(iii)

Repeating the frequency measurement after rotating the clamping system with respect to the material. Thus, the material anisotropy is exploited to obtain at least four different measures of the first resonant frequency;

(iv)

Assessing the elastic properties of the investigated region from the measured resonant frequencies through an optimization process.

The methodology assumes that the investigated composite plates are laminates whose stacking sequence is known and whose stacked plies are made of the same material. Thus, the methodology intends to determine the elastic properties at the lamina level.

Figure 2 shows the experimental setup. The boundaries of the retained region are obtained by means of two rectangular frames, which are compressed to the plate through the testing machine equipped with compression blocks. A silicon rubber layer of 0.5 mm has been interposed between the frames and the plate in order to compensate the nonuniform thickness of the composite plate. Indeed, the variation of the thickness can result in a local loss of clamped boundaries, which affects in turn the measured first resonant frequency. Even though the rubber layer decreases the out-of-plane stiffness of the system, results show that the boundaries of the retained region can be approximated with high fidelity as fully clamped.

The inverse problem can be undetermined, i.e., the measured frequencies can be obtained with multiple sets of elastic estimates. In this regard, limits on the design domain of the elastic properties can be considered; however, this is undesirable, especially when assessing damage level. Furthermore, the use of higher mode frequencies is limited by the proximity of the clamped boundaries, which can consistently affect the result. Therefore, in order to increase the accuracy of the methodology, information related to the modal shape can be considered within the optimization problem.

Modal shapes can be investigated through a concentrated mass. Low et al. [20] firstly proposed to move a concentrated mass on the plate and to measure the resultant resonant frequencies. As it is well known, due to the presence of an added mass, the resonant frequencies of the plate decrease. In particular, the reduction of a considered resonant frequency is function of the corresponding modal shape. According to the location of the concentrated mass, the higher the modal displacement in correspondence of the mass position, the lower the resultant resonant frequency. Therefore, by moving a mass on a clamped plate, the first modal shape can be investigated by considering the reduction of the first resonant frequency.

In the case of anisotropic materials, the modal shape is particularly dependent on the elastic parameters. For anisotropic material, the isolines of the modal shape are not necessarily parallel to the clamped boundaries. For instance, it is the case of an orthotropic material whose axes of orthotropy are not parallel to the boundaries. As reported in [13] and as shown in Figure 3, with reference to a unidirectional fiber plate, the first mode shape rotates in accordance with the orientation of the unidirectional reinforcement with respect to the $x$ axis.

In particular, for 0° and 90°, material axes of orthotropy are parallel to the boundaries and so the isolines of the modal shape. Instead, for 30° and 60°, whereas the material anisotropy is enhanced, the isolines are not parallel to the boundaries. This also shows that the modal shape strictly depends on the material properties and on its anisotropy. As the modal shape relates to the material anisotropy, information on the modal shape can be exploited to assess the elastic parameters with increased accuracy and robustness.

To this aim, a concentrated mass can be adopted. Two locations are sufficient to investigate the isolines of the first modal shape and hence the material anisotropy. In particular, the two positions are to be symmetric with respect to one of the axes of symmetry of the rectangle, while not lying on the other axis. For an example of mass locations, the reader can refer to Figure 4.

When the isolines are not parallel to the boundaries, the modal displacement is different in correspondence of the two mass locations. As a consequence, the reduction of the first resonant frequency is different. Instead, when the isolines are parallel to the clamped boundaries, the first resonant frequency equally decreases, as the two mass positions are symmetric with respect to one of the axes of the rectangular plate. Thus, the discrepancy between the reductions of the first resonant frequency due to the two mass locations represents a measure of the material anisotropy.

The methodology presented in [13] is completed as follows:

(i)

Isolate a rectangular region of the component through a specific equipment, which clamps the extremities of the region without damaging the material;

(ii)

Measure the first resonant frequency of the retained region, $f_{ref,i}$, through the Impulse Excitation Technique;

(iii)

Measure the first resonant frequency for each location of the concentrated mass, $f_{ref,m1,i}$ and $f_{ref,m2,i}$;

(iv)

Repeat the frequency measurements after rotating the clamping system with respect to the material;

(v)

Assess the elastic properties of the investigated region from the measured resonant frequencies through an optimization process.

Thus, the information related to the modal shape is accounted within the inverse problem, which can be formulated as follows

$$\begin{array}{c}\underset{\underset{\_}{x}=\left[E_{11},E_{22},G_{12}, {\nu }_{12}\right]}{\min }{\displaystyle \sum }_i\left|\frac{f_{ref,i}-f_i}{f_{ref,i}}\right|+\left|\frac{f_{ref,m1,i}-f_{m1,i}}{f_{ref,m1,i}}\right|+\left|\frac{f_{ref,m2,i}-f_{m2,i}}{f_{ref,m2,i}}\right|\end{array},$$

(15)

where $f_{ref,i}$, $f_{ref,m1,i}$, and $f_{ref,m2,i}$ constitute the reference frequencies for the i-th material orientation, while $f_i$, $f_{m1,i}$, and $f_{m2,i}$ are the values of the first resonant frequencies computed at each iteration of the optimization process.

Here, the reference values $f_{ref,i}$, $f_{ref,m1,i}$, and $f_{ref,m2,i}$ are calculated with the Rayleigh–Ritz method for the considered material. Furthermore, according to the values assumed by the elastic constants at each iteration of the optimization process, the Rayleigh–Ritz method is also used to calculate the three frequencies $f_i$, $f_{m1,i}$, and $f_{m2,i}$ for each material orientation. Thus, the discrepancy between the reference values and the calculated frequencies is minimized by varying the material parameters $\underset{\_}{x}$. Hence, the elastic constants are assessed as the result of the optimization process.

3. Results

The Rayleigh–Ritz formulation is firstly validated on experimental data reported in the literature. Then, the proposed approach is applied on four different laminated composites.

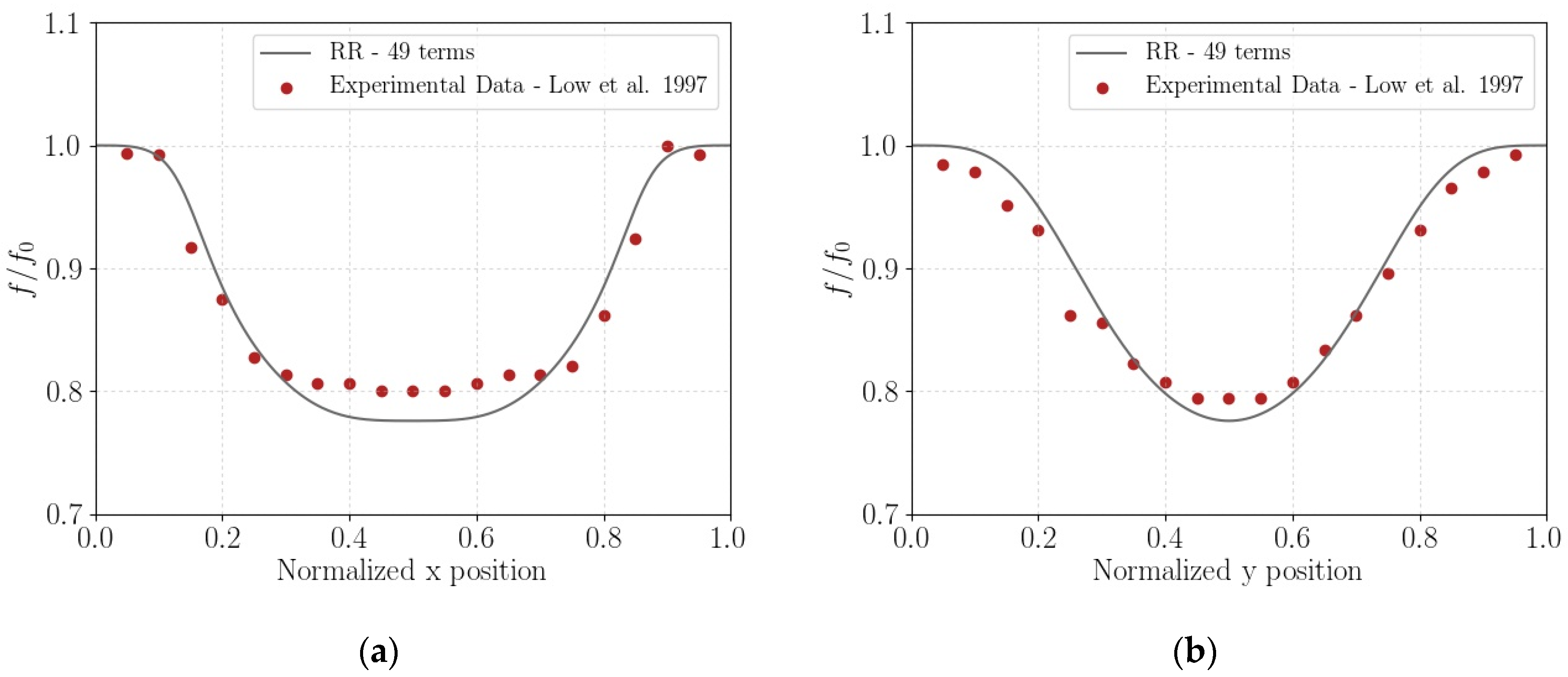
3.1. Validation of the Rayleigh–Ritz Formulation

In order to validate the Rayleigh–Ritz described in Section 2.1, literature data [14,20,21] on clamped plates have been considered. For convergence and validation studies, the comparison concerns six different laminates with unidirectional reinforcement plies. Furthermore, the Rayleigh–Ritz formulation has been validated on the experimental results of an isotropic aluminum plate loaded by a concentrated mass.

In regard to the laminated composites, data and results are taken from Chow et al. [14] and Lam and Chun [21]. In these works, the dimensions of the plates were $a=b=1270$ mm with thickness $h=25.4$ mm. Hence, the plate was relatively thin with the aspect ratio, i.e., the ratio between the in-plane dimension and the thickness, equal to 50. The laminated composites were clamped at the extremities, and the first resonant frequency was acquired.

The laminated composites were constituted by four layers with unidirectional reinforcement and present symmetric stacking sequences ([0°, 0°, 0°, 0°], [15°, −15°, −15°, 15°], [30°, −30°, −30°, 30°], and [45°, −45°, −45°, 45°]), an anti-symmetric stacking sequence ([30°, −30°, 30°, −30°]), and a non-symmetric sequence ([0°, 30°, 60°, 90°]). Material properties of the unidirectional plies are reported in

Table 1. Material properties at ply level.

	${\mathit{E}}_{11} \left[\mathbf{GPa}\right]$	${\mathit{E}}_{22} \left[\mathbf{GPa}\right]$	${\mathit{G}}_{12} \left[\mathbf{GPa}\right]$	${\mathit{\nu }}_{12} [-]$	$\mathit{\rho }[\mathbf{kg}/{\mathbf{m}}^3]$
Unidirectional ply	131.69	8.55	6.76	0.3	1610

with reference to the axes of orthotropy.

Firstly, the convergence study has been addressed. Results of the convergence study are reported in

Table 2. Convergence results of frequency parameter $\lambda$ and comparison to the experimental data presented in the literature - $\lambda ={\left(\frac{\rho h{\omega }^2{a}^4}{D_{11}}\right)}^{\frac{1}{2}}$, $D_{11}=\frac{E_{11}{h}^3}{12\left(1-{\nu }_{12}{\nu }_{21}\right)}$.

Stacking Sequences	Present–36 Terms	Present–49 Terms	Present–64 Terms	Literature Result
[0°, 0°, 0°, 0°]	23.42	23.41	23.41	23.86 1
[15°, −15°, −15°, 15°]	22.89	22.89	22.89	23.29 1
[30°, −30°, −30°, 30°]	21.91	21.90	21.90	22.22 1,2
[45°, −45°, −45°, 45°]	21.44	21.42	21.42	21.75 1
[30°, −30°, 30°, −30°]	21.56	21.56	21.56	21.94 2
[0°, 30°, 60°, 90°]	15.82	15.80	15.80	16.23 2

¹ Chow et al. [14]; ² Lam and Chun [21].

in terms of frequency parameter $\lambda$ for different numbers of terms $n$ of the polynomials in Equation (11). Indeed, as the polynomial degree increases (i.e., the number of terms $n$ increases), the exact solution is better approximated through the Rayleigh–Ritz method. Table 2 shows that the convergence is reached even for $n$= 36. However, for a better approximation, in this paper, a degree of the polynomial equal to 7 has been assumed in the calculations, with the number of terms $n$ equal to 49.

Table 2 also reports a comparison of the results obtained with the formulation proposed in Section 2.1 with those obtained by Chow et al. [14] and Lam and Chun [21] in their works. The discrepancy is very limited. The frequency parameter $\lambda$ calculated through the proposed formulation is always smaller than those calculated in the literature. This is mainly due to the different shear deformation theories. Indeed, the present Rayleigh–Ritz formulation is based on the higher-order shear deformation theory. Instead, the first order shear deformation theory was adopted in the considered works. Indeed, the higher order of the presented formulation increases the compliance of the plates, thus resulting in lower values of the frequency parameter $\lambda$ [18].

The Rayleigh–Ritz formulation has been also validated with respect to the experimental results reported by Low et al. [20], who analyzed the first resonant frequency of a clamped rectangular plate made of aluminum for different positions of a concentrated mass of 96 g. Particularly, the mass was moved along the axes of symmetry of the rectangle, and the resultant first resonant frequency was measured. The clamped plate had dimensions of $a=600$ mm and $b=300$ mm. Therefore, while moving the mass along the x direction, its y coordinate was equal to $\frac{b}{2}=150$ mm. Instead, while moving the mass along the y direction, the x coordinate was 300 mm.

Even though the Rayleigh–Ritz formulation of Section 2.1 is specifically developed for angle-ply laminates, an isotropic material can be considered as a particular case. The longitudinal and transverse Young’s moduli are equal to 69 GPa, as the Young’s modulus of the aluminum plate, while the Poisson’s coefficient is 0.3. Finally, the shear modulus can be related to the Young’s modulus and to the Poisson’s coefficient as usual, $G=E/\left(2\left(1+{\nu }^2\right)\right)$.

Figure 5 shows the comparison of the experimental results with those obtained with the present formulation. Results are reported in normalized form, where $f_0$ is the frequency obtained without the mass loading and the position $x$ and $y$ of the concentrated mass are normalized with respect to $a$ and $b$, respectively. Results of the Rayleigh–Ritz formulation have been obtained by moving the concentrated mass along the plate axes of symmetry with a step of 2 mm and calculating the resultant first resonant frequency. An acceptable agreement is obtained, with the Rayleigh–Ritz formulation able to catch the global trend of the experimental results. Furthermore, it can be appreciated that by moving a mass on the plate and measuring the resultant resonant frequency, the modal shape can be obtained.

3.2. Calculations of the Reference Frequencies

Four different materials are here considered for the validation of the proposed methodology. In addition to the unidirectional ([0°, 0°, 0°, 0°]), the symmetric ([30°, −30°, −30°, 30°]), and the asymmetric materials ([30°, −30°, 30°, −30°]) already presented in Section 3.1, a woven fabric laminate is considered. The woven laminate is also constituted by four layers, with the material properties reported in

Table 3. Material properties at the ply level of the woven fabric.

	${\mathit{E}}_{11} \left[\mathbf{GPa}\right]$	${\mathit{E}}_{22} \left[\mathbf{GPa}\right]$	${\mathit{G}}_{12} \left[\mathbf{GPa}\right]$	${\mathit{\nu }}_{12} [-]$	$\mathit{\rho }[\mathbf{kg}/{\mathbf{m}}^3]$
Woven fabric	59.0	59.0	3.4	0.04	1432.5

with reference to the axes of orthotropy. These materials have been chosen to show the applicability of the proposed approach to the limited selection of laminates, whose stacked plies are made of the same material.

The reference frequencies are here calculated through the Rayleigh–Ritz formulation. Dimensions of the rectangular region are $a=150$ mm and $b=100$ mm, as in the assumption of assessing local elastic properties, according to the methodology described in Section 2.2. The thicknesses of the four laminates are 1 mm for the unidirectional, 1.5 mm for both the symmetric and anti-symmetric laminates, and 2.5 mm for the woven fabric. With respect to the reference axes shown in Figure 1, the mass locations are $\left(x_1,y_1\right)=\left(50, 60\right)$ and $\left(x_2,y_2\right)=\left(100, 60\right)$, which are symmetric with respect to the vertical axis of symmetry of the rectangle. It is worth noting that in order to obtain a measurable discrepancy in the reduction of the first resonant frequency, the two locations must not be located far from the center of the of the plate. The mass is assumed equal to 1 g.

For the unidirectional, the symmetric, and anti-symmetric plates, the reference values have been calculated considering the material orientated at 0°, 30°, 60°, and 90° with respect to the clamped boundaries. For the woven fabric, the assumed rotations are 0°, 15°, 30°, and 45°. Indeed, after 45°, the frequency values are repeated as the longitudinal and transverse Young’s moduli are equal. Results of the reference values of the first resonant frequencies are reported in

Table 4. First resonant frequency values with and without the 1 g mass load of the unidirectional plate ([0°, 0°, 0°, 0°]) for different material orientations.

	0°	30°	60°	90°
$f_{ref}$ [Hz]	505.1	535.5	773.1	948.3
$f_{ref,m1}$ [Hz]	472.3	507.8	720.8	855.2
$f_{ref,m2}$ [Hz]	472.3	494.0	705.9	855.2

,

Table 5. First resonant frequency values with and without the 1 g mass load of the symmetric plate ([30°, −30°, −30°, 30°]) for different material orientations.

	0°	30°	60°	90°
$f_{ref}$ [Hz]	850.2	1117.4	1361.7	1191.8
$f_{ref,m1}$ [Hz]	817.3	1070.3	1283.9	1126.8
$f_{ref,m2}$ [Hz]	808.1	1054.9	1283.2	1136.4

,

Table 6. First resonant frequency values with and without the 1 g mass load of the anti-symmetric plate ([30°, −30°, 30°, −30°]) for different material orientations.

	0°	30°	60°	90°
$f_{ref}$ [Hz]	843.6	931.8	1100.4	1151.4
$f_{ref,m1}$ [Hz]	806.6	894.6	1050.8	1095.5
$f_{ref,m2}$ [Hz]	806.6	885.4	1045.4	1095.5

and

Table 7. First resonant frequency values with and without the 1 g mass load of the woven fabric plate ([0°, 0°, 0°, 0°]) for different material orientations.

	0°	15°	30°	45°
$f_{ref}$ [Hz]	1793.8	1757.9	1686.7	1650.5
$f_{ref,m1}$ [Hz]	1738.0	1702.0	1633.8	1600.5
$f_{ref,m2}$ [Hz]	1738.0	1705.2	1636.6	1600.5

.

As expected, the presence of the concentrated mass reduces the value of the first resonant frequency. Furthermore, when the isolines are parallel to the clamped boundaries, as in the case of the unidirectional laminate with fibers oriented at 0° or at 90° with respect to the clamped boundaries, the first resonant frequency equally decreases for the two mass locations. This is particularly due to the modal shape combined with the choice of the mass positions, which are symmetric with respect to one of the axes of the rectangular plate. Instead, when the isolines are not parallel to the boundaries, the mass affects the first resonant frequency differently in the two locations. As a consequence, the discrepancy between the reductions of the first resonant frequency due to the two mass locations is a measure of the material anisotropy. Furthermore, in regard to the resultant first frequency, it is important to notice that its value is higher for the mass disposed in the first position. Indeed, the modal shape follows the rotations of the material with respect to the clamped boundaries.

Furthermore, the discrepancy between the first resonant frequencies for the two mass positions is inversely proportional to the mass of the concentrated mass, while it is enhanced by the thickness of the laminate. An added mass reduces the resonant frequencies, and higher values of concentrated mass lead to higher reduction of the resonances, thus flattening any discrepancy. On the contrary, the thickness plays a key role in the bending stiffness of the laminate, which in turn affects the resonant frequency. As the thickness increases, the first resonant frequencies for the two mass spots proportionally increase and so does the discrepancy. It is the case of the woven laminate, whose anisotropy is particularly limited but still recognizable, as shown in Table 7.

Finally, it can be argued that as the material properties do not change after a rotation of 90° for the unidirectional reinforcement laminates or 45° in the case of woven fabric, further information can be considered within the optimization process without the need of other replications of the first resonant frequency measure. In particular, in the case of unidirectional reinforced laminates, the results obtained for 30° and 60° are respectively equal to those obtained for rotations equal to 150° and 120°, respectively. However, the results obtained with the concentrated mass must be switched, as the modal shape follows the rotations of the material with respect to the clamped boundaries. The same can be applied to the woven fabric, thus extending the acquired information to the range 45°–90°. This provides further information to the optimization process, which can further increase its robustness.

3.3. Optimization Results

Material properties for the four considered materials are determined through Equation (15). The Nelder–Mead zero-order algorithm has been considered for the optimization process [22]. As the algorithm can fail in reaching the optimal solution, several repetitions of the optimizations have been performed. In particular, the result of an optimization process has been used as a starting point for the next. After few iterations, the algorithm was able to reach the optimal solution.

Table 8. Optimized material properties at ply level for each material.

	${\mathit{E}}_{11} \left[\mathbf{GPa}\right]$	${\mathit{E}}_{22} \left[\mathbf{GPa}\right]$	${\mathit{G}}_{12} \left[\mathbf{GPa}\right]$	${\mathit{\nu }}_{12} [-]$
Unidirectional [0°, 0°, 0°, 0°]	131.72	8.56	6.74	0.29
Symmetric [30°, −30°, −30°, 30°]	131.7	8.55	6.75	0.29
Anti-symmetric [30°, −30°, 30°, −30°]	131.7	8.55	6.75	0.30
Woven fabric	59.0	59.0	3.4	0.04

reports the elastic constants calculated through Equation (15) for each analyzed material.

The difficulty in reaching an optimal solution was mainly due to the limited dependency of the first resonance frequency on the Poisson’s coefficient ${\nu }_{12}$ and on the shear modulus $G_{12}$. Indeed, the first resonant frequency of a clamped composite plate particularly depends on the longitudinal and transverse Young’s moduli. In this regard, the rectangular shape of the analyzed region enhances the sensitivity of the first resonant frequency on the elastic properties in the direction of the short edge of the rectangle, i.e., the transverse direction [13].

Indeed, the dependency of the inverse problem on the shear modulus and on the Poisson’s coefficient represents a critical aspect, particularly when the elastic properties are calculated considering only the first resonant plate without disposing the mass load. In this case, limits on the design domain are necessary. Instead, by considering further information related to the modal shape, the optimization is able to catch all the four elastic constants without the need of limiting the domain of the elastic properties. This is particularly useful when damage level, i.e., residual elastic properties, are to be assessed. Indeed, in order to guarantee the robustness of the methodology, limits on the design domain of the elastic properties, i.e., $E_{11},E_{22},G_{12}$, and ${\nu }_{12}$, were considered in [13]. This is particularly undesirable if the methodology has to be adopted for detecting local material variations. The results of the optimization problem can be constrained by the limits of the design domain, i.e., the space where the aforementioned material properties can vary, and, in the end, be wrong. Furthermore, as shown in Table 8, even though the objective function of Equation (15) is equal to zero, very limited discrepancies from the nominal values are obtained. Only the shear modulus and the Poisson’s ratio are slightly different from the nominal values of Table 1 and Table 2, with discrepancies lower than 0.3% for the shear modulus and 3% for the Poisson’s ratio.

By way of example, the optimization has been also performed without retaining the modal shape information for the symmetric and anti-symmetric stacked laminates. The results are reported in

Table 9. Optimized material properties at the ply level and relative errors for the symmetric and anti-symmetric laminates without considering the modal shape information.

	${\mathit{E}}_{11}$$\left[\mathbf{GPa}\right] - {\mathit{\epsilon }}_{\mathit{r}\mathit{e}\mathit{l}}$	${\mathit{E}}_{22}$$\left[\mathbf{GPa}\right] - {\mathit{\epsilon }}_{\mathit{r}\mathit{e}\mathit{l}}$	${\mathit{G}}_{12}$$\left[\mathbf{GPa}\right] - {\mathit{\epsilon }}_{\mathit{r}\mathit{e}\mathit{l}}$	${\mathit{\nu }}_{12}$$[-] - {\mathit{\epsilon }}_{\mathit{r}\mathit{e}\mathit{l}}$
Symmetric [30°, −30°, −30°, 30°]	132.0%–0.24%	8.55%–0.0%	7.586%–12.2%	0.129%–57%
Anti-symmetric [30°, −30°, 30°, −30°]	132.5%–0.615%	8.85%–3.51%	7.2%–6.51%	0.073%–76%

with relative errors with respect to the elastic properties of Table 1. It is worth noting that even though the resultant first resonant frequencies without mass load for the different material orientations are those reported in the first line of Table 5 and Table 6, respectively, the relative errors can be very high. This particularly shows that the inverse problem can be undetermined, i.e., multiple solutions are allowable. Furthermore, the limited dependency of the first resonant frequency of a clamped plate on the shear modulus and on the Poisson’s ratio is evident. A decrease of the Poisson’s ratio seems to be compensated by an increase of the shear modulus. Furthermore, the errors on these properties can affect in turn the determination of the Young’s modulus in the transverse direction. Instead, the Young’s modulus in the longitudinal direction is assessed with very limited discrepancy.

By comparing the results obtained in Table 8 and Table 9, it is clear that by increasing the amount of information retained within the optimization problem, the two low-influencing material parameters, i.e., $G_{12}$ and ${\nu }_{12}$, can be correctly assessed. The proposed approach intends to retain the modal shape within the optimization process. In particular, the modal shape is simply identified through the use of a concentrated mass positioned in two different points. In accordance with the methodology described in [13], other possibilities to increase the number of information retained in the optimization problem as well as its robustness, could consist of:

(i)

Increasing the number of relative orientations between the clamping system and the plate;

(ii)

Considering higher modes, with the limitations described in the introduction of this paper.

Finally, it is worth noting that as shown in Table 8, even in the numerical analysis here pursued with the further information of the modal shape, the shear modulus and the Poisson’s ratio can still present very limited discrepancies with respect to the nominal values. The sensitivity of the first resonant frequency on these parameters is low but not null. Therefore, by increasing the information retained within the optimization problem, the allowable solutions of the inverse problem accordingly decrease, thus allowing to also estimate the two low-influencing parameters with very limited discrepancy.

4. Conclusions

In this paper, a new approach for the nondestructive determination of the elastic properties of composite laminates is presented. The approach represents an enhancement of a recently presented experimental methodology. The experimental methodology is based on the Impulse Excitation Technique and allows nondestructively assessing local elastic properties of composite laminates by isolating a region of interest through a proper clamping system. In order to take into account the material anisotropy, different measures of the first resonant frequency are obtained by rotating the clamping system with respect to the material orientation. The methodology particularly refers to laminated composites, whose stacked plies are made of the same material.

As the inverse problem, which intends to assess the elastic properties (i.e., $E_{11},E_{22},G_{12}$, and ${\nu }_{12}$) from the measured first resonant frequencies, can be undetermined, further information are required within the optimization process. Apart from the obvious solution of increasing the number of relative orientations between the clamping system and the plate, the use of higher modes is limited by the noninfinite stiffness of the clamped boundaries, which could affect in turn the measure of the resonant frequencies.

The proposed approach intends to increase the number of the retained information and therefore the accuracy of the methodology by identifying the modal shape of the clamped plate. In particular, a concentrated mass has been exploited, whose effect on the first resonant frequency depends on its position on the plate in accordance with the modal shape. According to the location of the concentrated mass, the higher the modal displacement in correspondence of the mass position, the lower the resultant resonant frequency. Only two mass positions, i.e., two measures of the first resonant frequency, are sufficient to investigate the modal shape, as the reduction of the first resonant frequency is different for the two mass spots. Particularly, mass locations have to be symmetric with respect to one of the axes of symmetry of the rectangle, while not lying on the other axis. In turn, the modal shape is a function of the material properties, which allows increasing the accuracy and the robustness of the optimization problem.

A numerical validation of the proposed approach is performed, which considers four different laminated composites, particularly a unidirectional, a symmetric angle-ply, an anti-symmetric angle-ply, and a woven fabric. A Rayleigh–Ritz formulation based on higher order shear deformation theory is adopted to compute the first resonant frequency of the clamped plate loaded by a concentrated mass. Indeed, the use of the Rayleigh–Ritz formulation allows consistently decreasing the computational cost with respect to the finite element-based optimization adopted in [13]. Thus, the Rayleigh–Ritz formulation represents a further step toward the application of the proposed methodology to real-world composite structures. The Rayleigh–Ritz formulation is firstly validated with experimental data taken from the literature and then, for each retained material, it is used to calculate the frequencies for the different material orientations and mass positions, which constitute the reference values. Then, the elastic properties are handled as the design variables of the optimization process, which minimizes the discrepancy between the resonant frequency calculated at each iteration and the corresponding reference value.

The results show that according to the material orientation, the mass differently affects the first resonant frequency in two locations. When dealing with anisotropic materials, the isolines of the modal shape are not parallel to the clamped boundaries, as in the case of an orthotropic material whose axes of orthotropy are not parallel to the boundaries. Particularly, in the case of the unidirectional laminate, the modal shape follows the rotation of the material with respect to the clamped boundaries. Hence, the discrepancy between the reductions of the first resonant frequency for the two mass spots is a measure of the material anisotropy. Thus, information related to the modal shape can be obtained only through a concentrated mass, without the need for expensive equipment. Furthermore, results show that by increasing the number of information, particularly by retaining the modal shape, the accuracy in the assessment of the four elastic properties is increased. In particular, it is shown that even in the numerical analysis here pursued with the further information of the modal shape, the shear modulus and the Poisson’s ratio can still present very limited discrepancies with respect to the nominal values. In particular, these are 0.3% for the shear modulus and 3% for the Poisson’s ratio. Instead, when the information related to the modal shape is not accounted, the discrepancies reach the values of 12% for the shear modulus and 76% for the Poisson’s ratio. Indeed, the sensitivity of the first resonant frequency on these parameters is low but not null. Therefore, by increasing the information retained within the optimization problem, the allowable solutions of the inverse problem accordingly decrease, thus allowing also estimating the two low-influencing parameters with very limited discrepancy. Thus, the optimization is able to catch all the four elastic constants for all the considered materials without the need of limiting the domain of the elastic properties. The promising results of this study can increase the robustness of the previously described experimental methodology for the nondestructive, quantitative, and local assessment of damage level, i.e., of residual elastic properties, in composite laminates. The local characterization of the health state of composite components allows evaluating the quality of a manufacturing process or damages due to in-service loads with consistently enhanced confidence.