One-Dimensional Consolidation of Multi-Layered Unsaturated Soil with Impeded Drainage Boundaries
Abstract
:1. Introduction
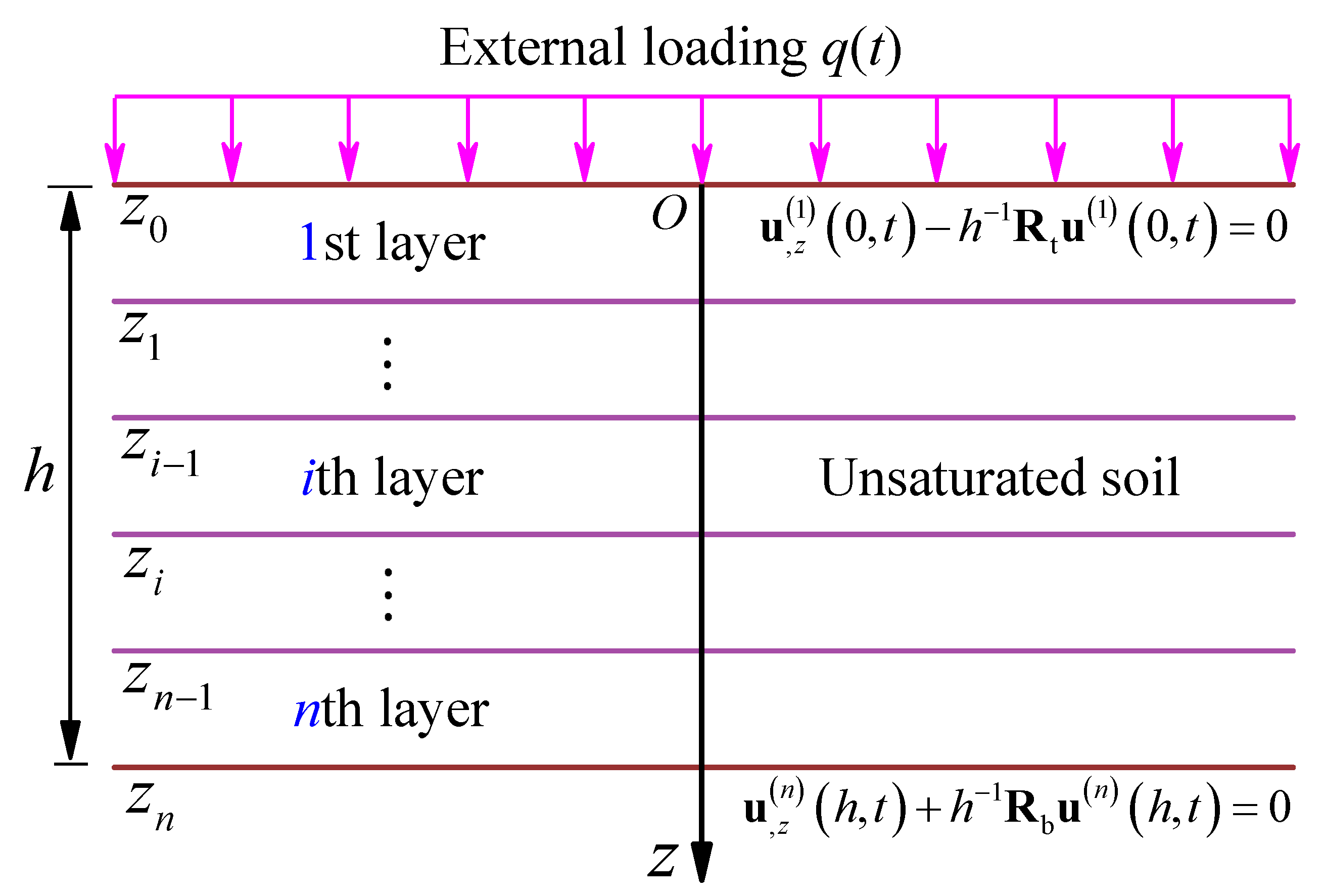
2. Problem Description
2.1. Governing Equations
2.2. Solution Conditions
3. Solution Formulations
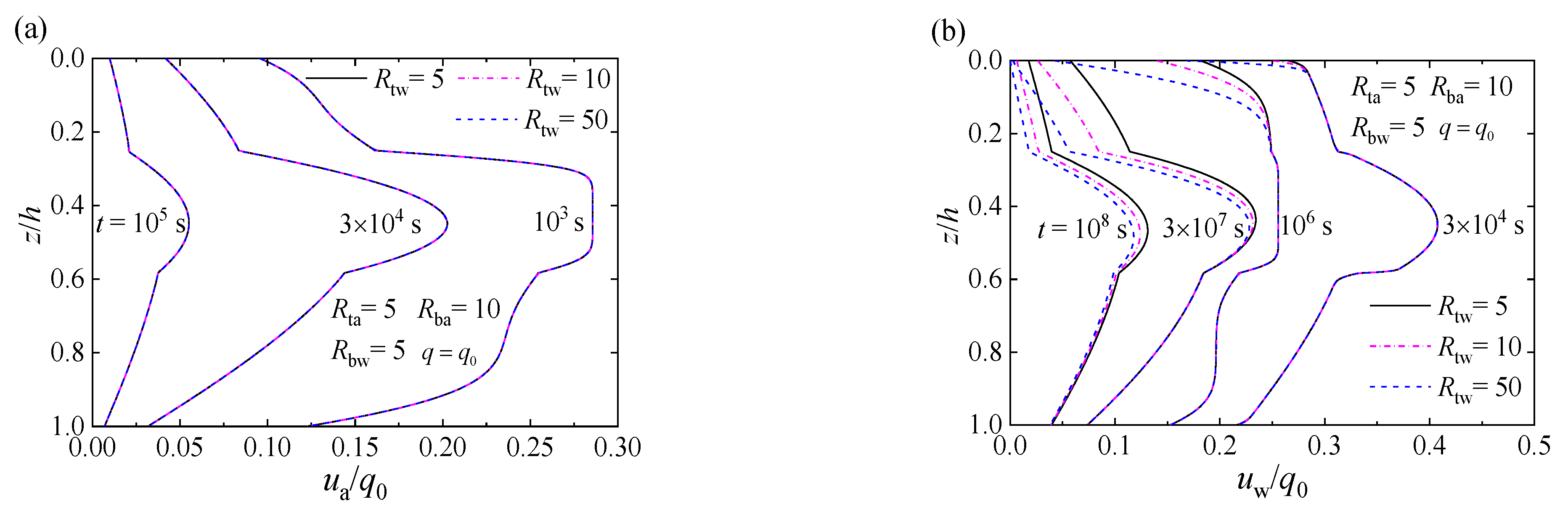
4. Verifications and Examples
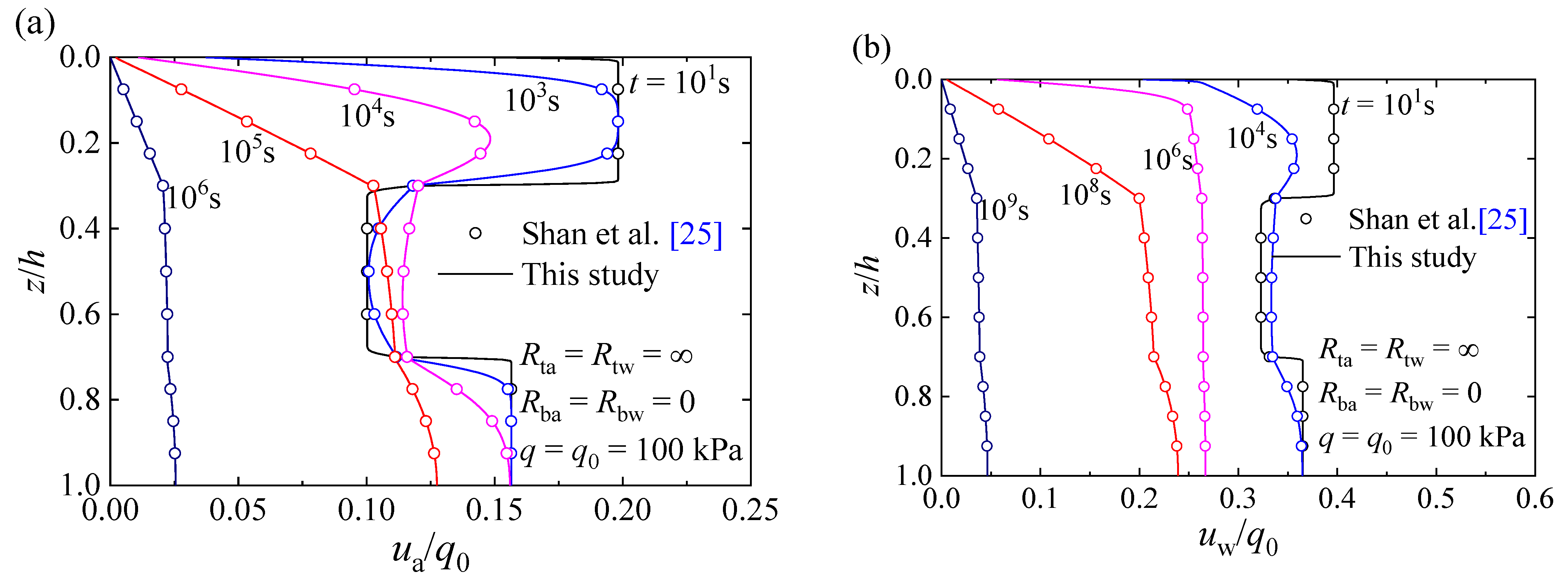
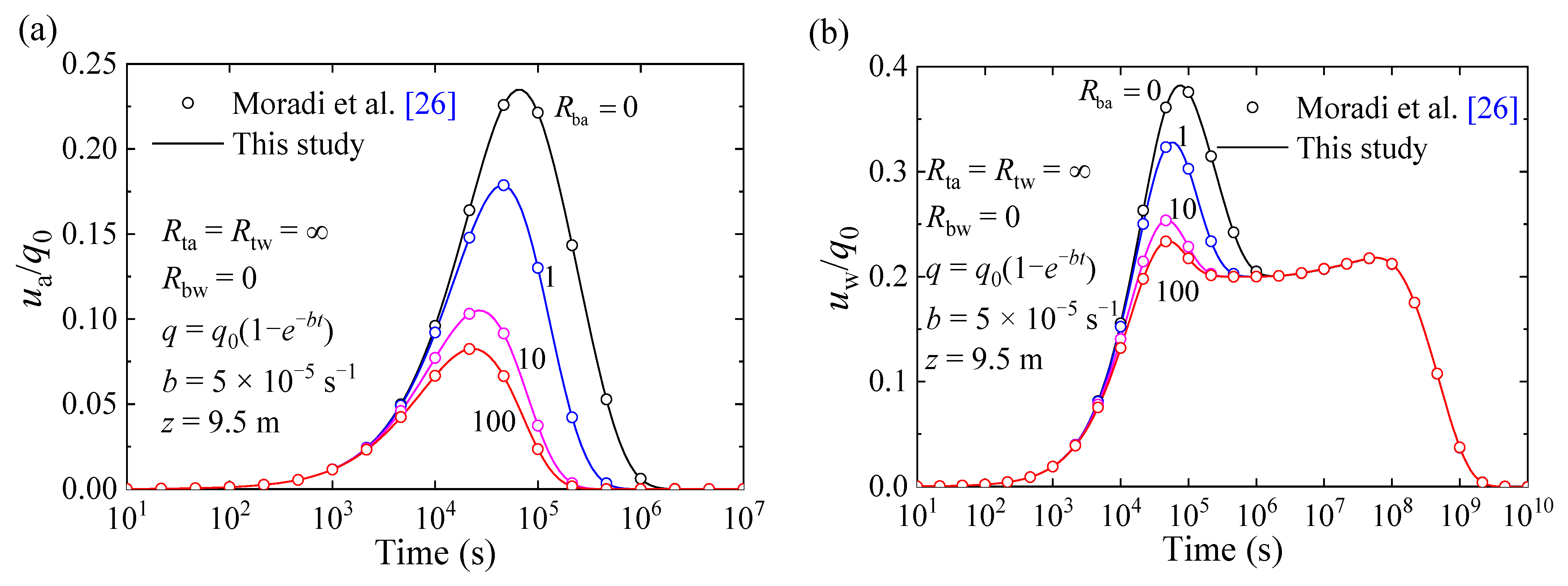
4.1. Verifications
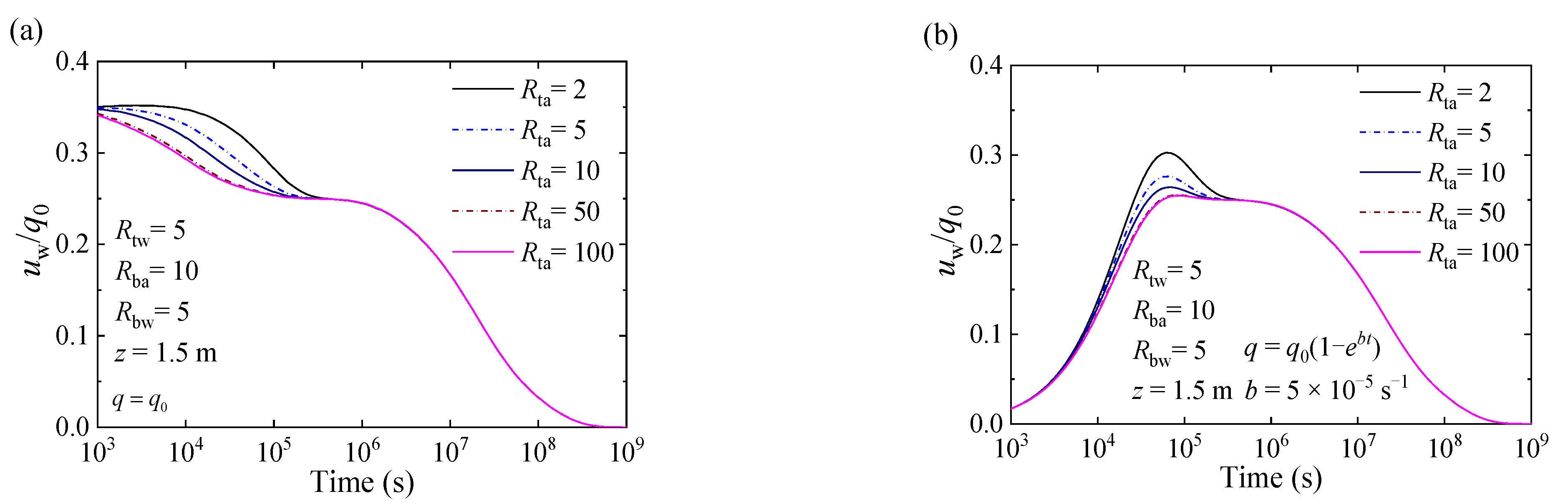
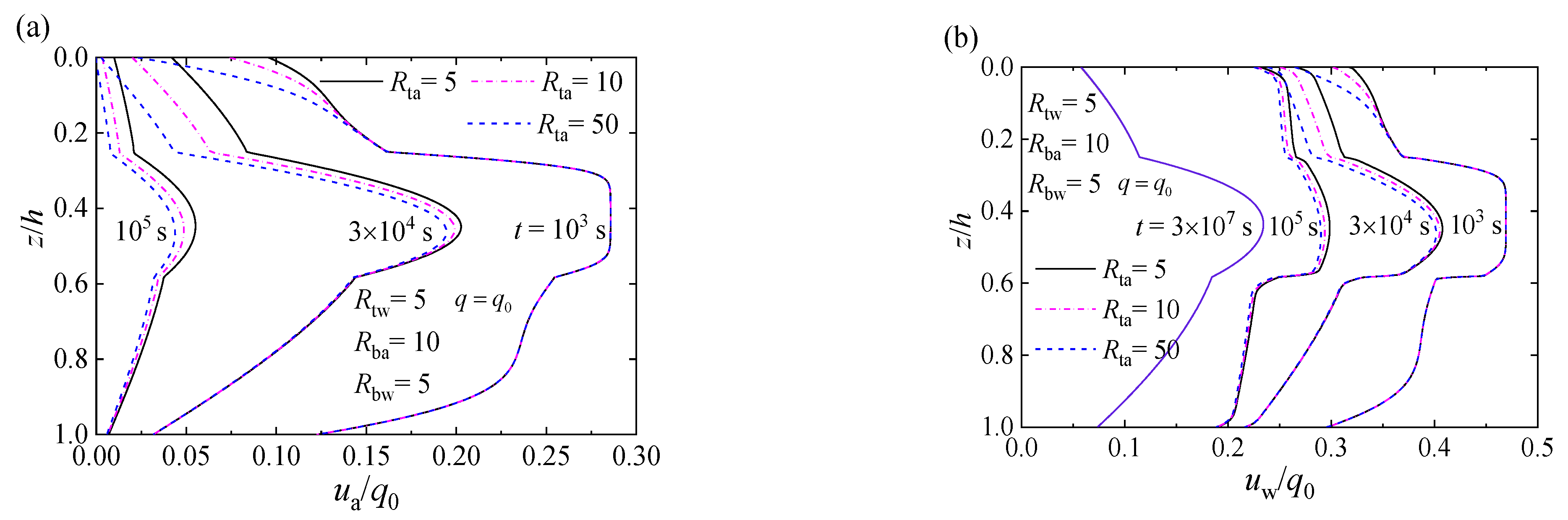
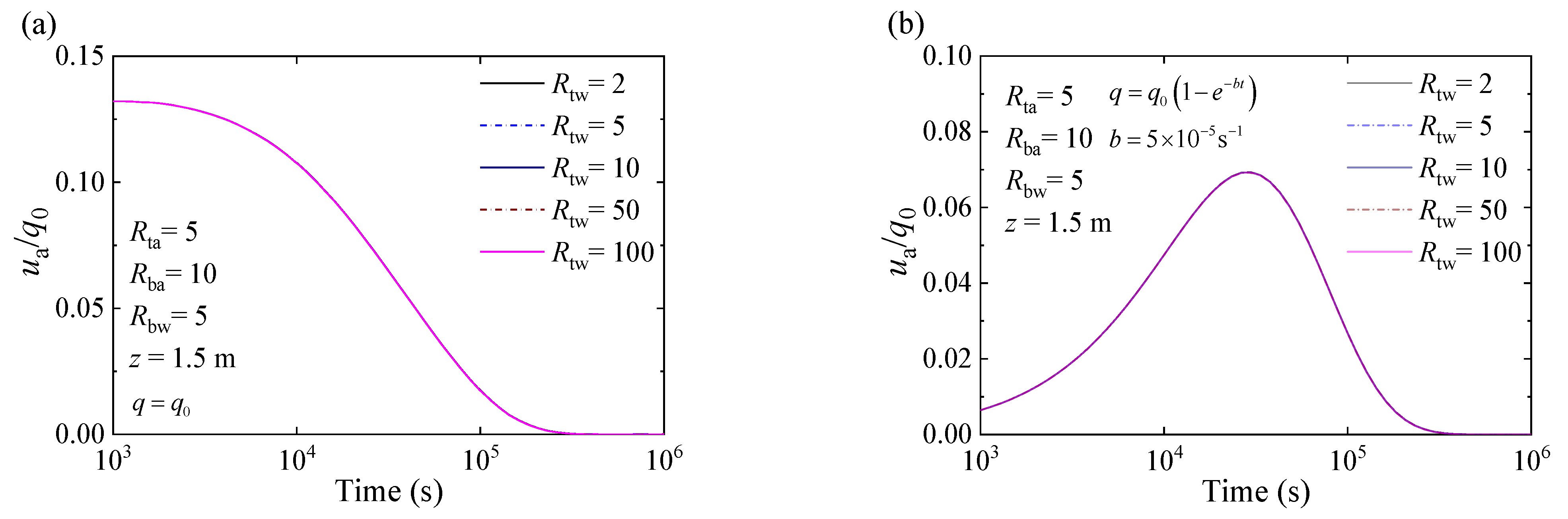
4.2. Worked Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Fredlund, D.G.; Rahardjo, H. Soil Mechanics for Unsaturated Soils; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Jommi, C. General report of TC 106: Unsaturated soils. In Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering: Challenges and Innovations in Geotechnique, Paris, France, 2–6 September 2013; pp. 1061–1068. [Google Scholar]
- Zhou, W.-H.; Zhao, L.-S.; Garg, A.; Yuen, K.-V. Generalized Analytical Solution for the Consolidation of Unsaturated Soil under Partially Permeable Boundary Conditions. Int. J. Géoméch. 2017, 17, 04017048. [Google Scholar] [CrossRef]
- Alonso, E.E.; Gens, A.; Josa, A. A constitutive model for partially saturated soils. Géotechnique 1990, 40, 405–429. [Google Scholar] [CrossRef] [Green Version]
- Rojas, E.; Chavez, O. Volumetric behavior of unsaturated soils. Can. Geotech. J. 2013, 50, 209–222. [Google Scholar] [CrossRef]
- Skutnik, Z.; Lendo-Siwicka, M.; Garbulewski, K. Assessment of the cv coefficient for unsaturated Warsaw Clay. In Proceedings of the 5th International Conference on Unsaturated Soils, Barcelona, Spain, 6–8 September 2010; pp. 371–380. [Google Scholar]
- Scott, R.F. Principles of Soil Mechanics; Addison Wesley: New York, NY, USA, 1963; pp. 270–280. [Google Scholar]
- Barden, L. Consolidation of Compacted and Unsaturated Clays. Géotechnique 1965, 15, 267–286. [Google Scholar] [CrossRef]
- Ho, L.; Fatahi, B.; Khabbaz, H. Analytical solution for one-dimensional consolidation of unsaturated soils using eigenfunction expansion method. Int. J. Numer. Anal. Methods Géoméch. 2014, 38, 1058–1077. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Hasan, J.U. One-dimensional consolidation theory: Unsaturated soils. Can. Geotech. J. 1979, 16, 521–531. [Google Scholar] [CrossRef] [Green Version]
- Fredlund, D.G.; Rahardjo, H.; Fredlund, M.D. Unsaturated Soil Mechanics in Engineering Practice; John Wiley and Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Dakshanamurthy, V.; Fredlund, D.G. Moisture and air flow in an unsaturated soil. In Proceedings of the 4th International Conference on Expansive Soils, Denver, CO, USA, 16–18 June 1980; Volume 1, pp. 514–532. [Google Scholar]
- Dakshanamurthy, V.; Fredlund, D.G.; Rahardjo, H. Coupled three-dimensional consolidation theory of unsaturated porous media. In Proceedings of the 5th International Conference on Expansive Soils, Adelaide, Australia, 21–23 May 1984; pp. 99–103. [Google Scholar]
- Qin, A.F.; Sun, D.A.; Tan, Y.W. Analytical solution to one-dimensional consolidation in unsaturated soils under loading varying exponentially with time. Comput. Geotech. 2010, 37, 233–238. [Google Scholar] [CrossRef]
- Ho, L.; Fatahi, B. One-Dimensional Consolidation Analysis of Unsaturated Soils Subjected to Time-Dependent Loading. Int. J. Géoméch. 2015, 16, 04015052. [Google Scholar] [CrossRef]
- Zhou, W.-H.; Zhao, L.-S.; Li, X.-B. A simple analytical solution to one-dimensional consolidation for unsaturated soils. Int. J. Numer. Anal. Methods Géoméch. 2014, 38, 794–810. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.; Qin, A. General semi-analytical solutions to one-dimensional consolidation for unsaturated soils. Appl. Math. Mech. 2017, 38, 831–850. [Google Scholar] [CrossRef]
- Xie, K.-H.; Xie, X.-Y.; Gao, X. Theory of one dimensional consolidation of two-layered soil with partially drained boundaries. Comput. Geotech. 1999, 24, 265–278. [Google Scholar] [CrossRef]
- Mesri, G. One-dimensional consolidation of a clay layer with impeded drainage boundaries. Water Resour. Res. 1973, 9, 1090–1093. [Google Scholar] [CrossRef]
- Cai, Y.-Q.; Liang, X.; Wu, S.-M. One-dimensional consolidation of layered soils with impeded boundaries under time-dependent loadings. Appl. Math. Mech. 2004, 25, 937–944. [Google Scholar] [CrossRef]
- Gray, H. Simultaneous consolidation of contiguous layers of unlike compressible soils. Transact. ASCE 1945, 110, 1327–1356. [Google Scholar]
- Zhou, W.-H.; Zhao, L.-S. One-Dimensional Consolidation of Unsaturated Soil Subjected to Time-Dependent Loading with Various Initial and Boundary Conditions. Int. J. Géoméch. 2014, 14, 291–301. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.; Li, L.; Li, P.; Xu, Y. Semi-analytical solutions to one-dimensional consolidation for unsaturated soils with symmetric semi-permeable drainage boundary. Comput. Geotech. 2017, 89, 71–80. [Google Scholar] [CrossRef]
- Wang, L.; Sun, D.; Qin, A.F.; Xu, Y.F. Semi-analytical solution to one-dimensional consolidation for unsaturated soils with semi-permeable drainage boundary under time-dependent loading. Int. J. Numer. Anal. Met. 2017, 41, 1636–1655. [Google Scholar] [CrossRef]
- Shan, Z.; Ling, D.; Ding, H. Analytical solution for the 1D consolidation of unsaturated multi-layered soil. Comput. Geotech. 2014, 57, 17–23. [Google Scholar] [CrossRef]
- Moradi, M.; Keshavarz, A.; Fazeli, A. One dimensional consolidation of multi-layered unsaturated soil under partially permeable boundary conditions and time-dependent loading. Comput. Geotech. 2019, 107, 45–54. [Google Scholar] [CrossRef]
- Bert, C.W.; Malik, M. Differential Quadrature Method in Computational Mechanics: A Review. Appl. Mech. Rev. 1996, 49, 1–28. [Google Scholar] [CrossRef]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer Science & Business Media: London, UK, 2012; pp. 121–140. [Google Scholar]
- Crump, K.S. Numerical Inversion of Laplace Transforms Using a Fourier Series Approximation. J. ACM 1976, 23, 89–96. [Google Scholar] [CrossRef]
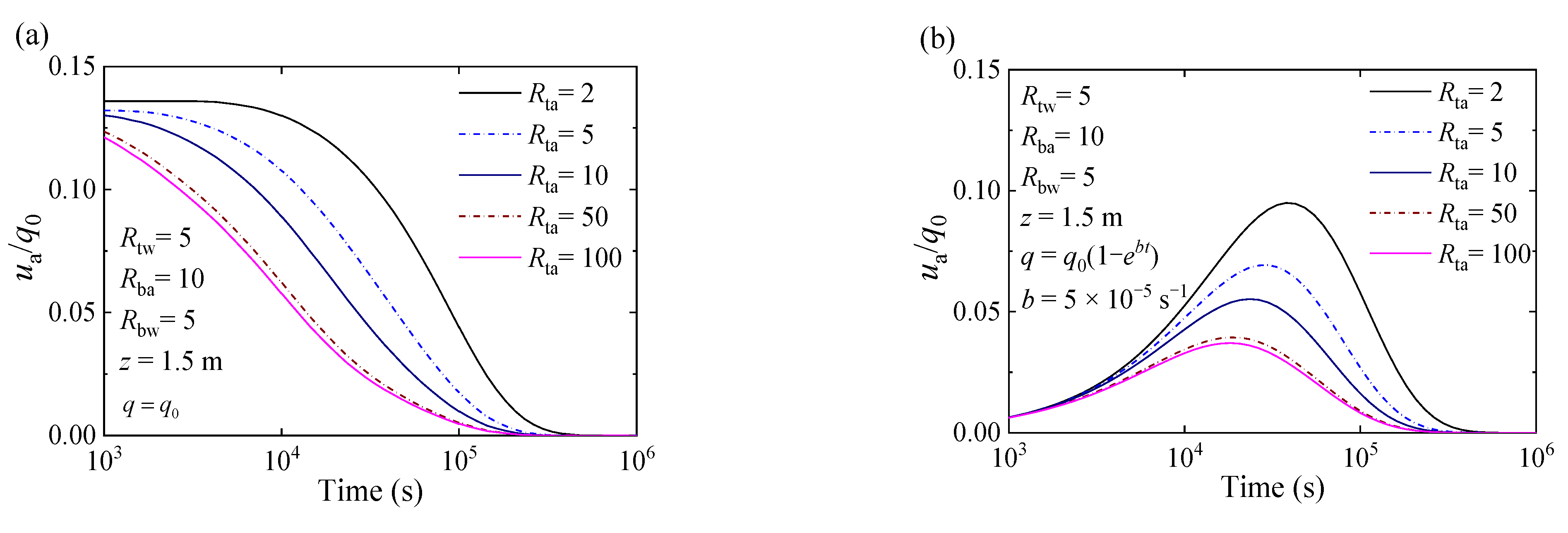

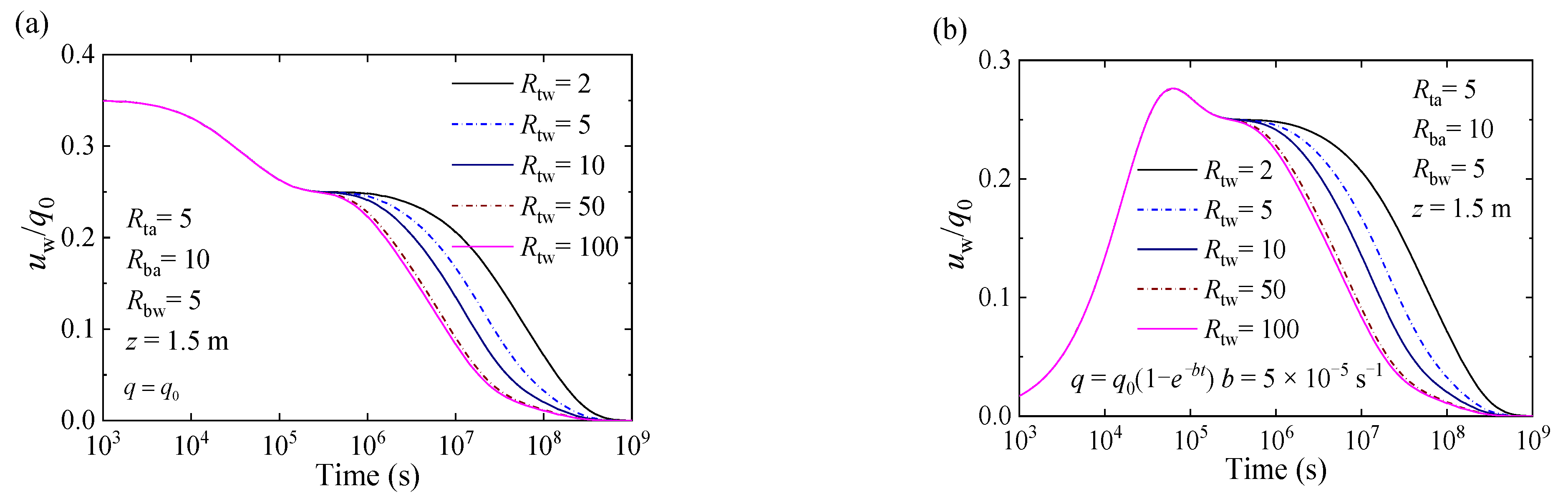

| Case No. | Layer No. | hi(m) | kw | ka | Sr | n0 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| (×10−4 kPa−1) | (×10−9 m/s) | |||||||||
| I Shan et al. (2014) | 1 | 3 | −2.5 | −1.0 | −0.5 | −2.0 | 0.1 | 1 | 0.8 | 0.45 |
| 2 | 4 | −2.5 | −1.0 | −0.5 | −2.0 | 1 | 10 | 0.6 | 0.5 | |
| 3 | 3 | −2.5 | −1.0 | −0.5 | −2.0 | 0.1 | 1 | 0.7 | 0.4 | |
| II Moradi et al. (2019) | 1 | 3 | −2.5 | −1.0 | −0.5 | −2.0 | 1 | 10 | 0.7 | 0.5 |
| 2 | 4 | −3.5 | −1.0 | −0.65 | −2.5 | 0.1 | 1 | 0.8 | 0.4 | |
| 3 | 5 | −1.5 | −0.5 | −0.3 | −1.5 | 0.5 | 5 | 0.9 | 0.45 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Kang, J.; Lv, C.; Huang, M. One-Dimensional Consolidation of Multi-Layered Unsaturated Soil with Impeded Drainage Boundaries. Appl. Sci. 2021, 11, 133. https://doi.org/10.3390/app11010133
Zhou S, Kang J, Lv C, Huang M. One-Dimensional Consolidation of Multi-Layered Unsaturated Soil with Impeded Drainage Boundaries. Applied Sciences. 2021; 11(1):133. https://doi.org/10.3390/app11010133
Chicago/Turabian StyleZhou, Suhua, Jiatao Kang, Chang Lv, and Minghua Huang. 2021. "One-Dimensional Consolidation of Multi-Layered Unsaturated Soil with Impeded Drainage Boundaries" Applied Sciences 11, no. 1: 133. https://doi.org/10.3390/app11010133





