Effect of Burner Operation on the Catalyst Tube Lifetime of a Steam Methane Reformer: A Numerical Study
Abstract
:1. Introduction
2. Numerical Methodologies
2.1. Numerical Methods and Physical Models
- N = number of chemical species in the system
- = stoichiometric coefficient for reactant i in reaction r
- = stoichiometric coefficient for product i in reaction r
- μi = species i
- = forward rate constant for reaction r
- = backward rate constant for reaction r
- = molar concentration of species j in reaction r (kgmol/m3)
- = rate exponent for reactant species j in reaction r
- = rate exponent for product species j in reaction r
- Γ = net effect of third bodies on the reaction rate
- Ar = pre-exponential factor (consistent units)
- βr = temperature exponent (dimensionless)
- Er = activation energy for the reaction (J/kgmol)
- R = universal gas constant (J/kgmol-K)
- Kr = the equilibrium constant for the rth reaction, is computed fromwhere patm denotes the atmospheric pressure (101,325 Pa). The term in the exponential function denotes the change in Gibbs free energy and its components are expressed aswhere and denote the standard-state entropy and standard-state enthalpy (heat of formation), respectively.
- Yp is the mass fraction of any product, P
- YR is the mass fraction of a particular reactant, R
- A is an empirical constant equal to 4.0
- B is an empirical constant equal to 0.5
2.2. Numerical Setup
- (1)
- At the Symmetry planes, the symmetric boundary conditions are used.
- (2)
- At walls, standard wall function is applied.
- (3)
- At the burner inlets, i.e., fuel and flue gas inlets, the real operating conditions used by a petrochemical corporation are adopted, includingQ (Flowrate in the radial direction): 139,710 m3/hrT (Temperature): 673.15 KPgauge (gauge Pressure): 1.04544 × 104 N/m2Species mole fraction, includingH2 (Hydrogen): 0.0816CH4 (Methane): 0.0474N2 (Nitrogen): 0.49057O2 (Oxygen): 0.12818CO2 (Carbon dioxide): 0.25225
- (4)
- At the burner exits, i.e., fuel and flue gas exits, the diffusion flux in the outflow direction is zero for all flow variables, and the conservation of mass should be satisfied.
- (5)
- At the inlets of the catalyst tubes, the real operating conditions used by a petrochemical corporation are adopted, includingQ (Flowrate in the axial direction): 24,740 m3/hrT (Temperature): 912.75 KPgauge (gauge Pressure): 2.1658 × 106 N/m2Species mole fraction, includingCH4 (Methane): 0.2029H2O (Steam): 0.6H2 (Hydrogen): 0.12855CO2 (Carbon dioxide): 0.06565CO (Carbon Monoxide): 0.00145N2 (Nitrogen): 0.00145
- (6)
- At the exits of the catalyst tubes, the diffusion flux in the outflow direction is zero for all flow variables, and the conservation of mass should be satisfied.
- (7)
- At the inlets of the burners or the catalyst tubes, the turbulence kinetic energy is assumed to be 10% of the inlet mean flow kinetic energy. The turbulence dissipation rate is calculated from:where l is connected with the hydraulic diameter, L, by l = 0.07 L.
3. Results and Discussions
3.1. Validation of the Numerical Methodologies
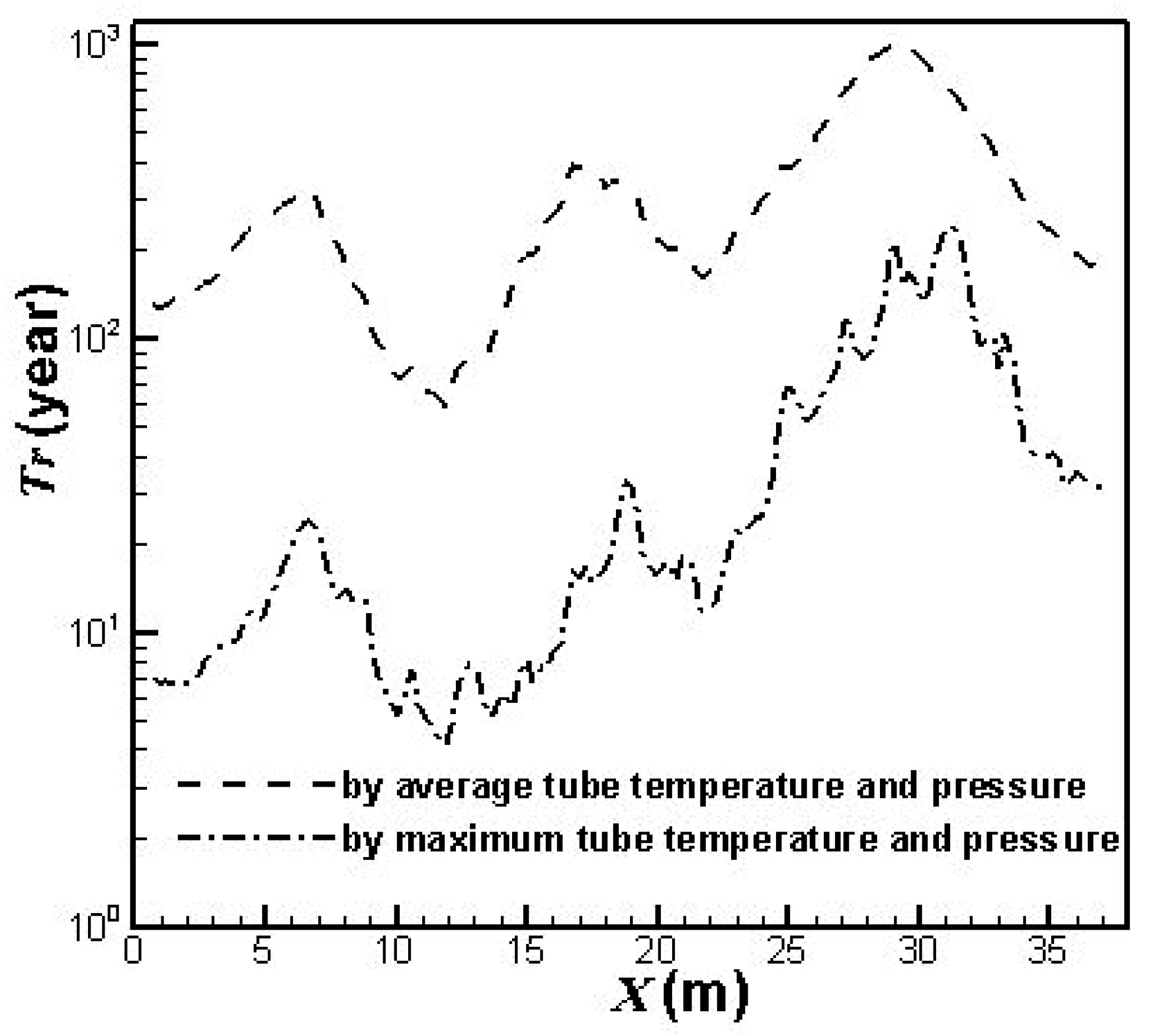
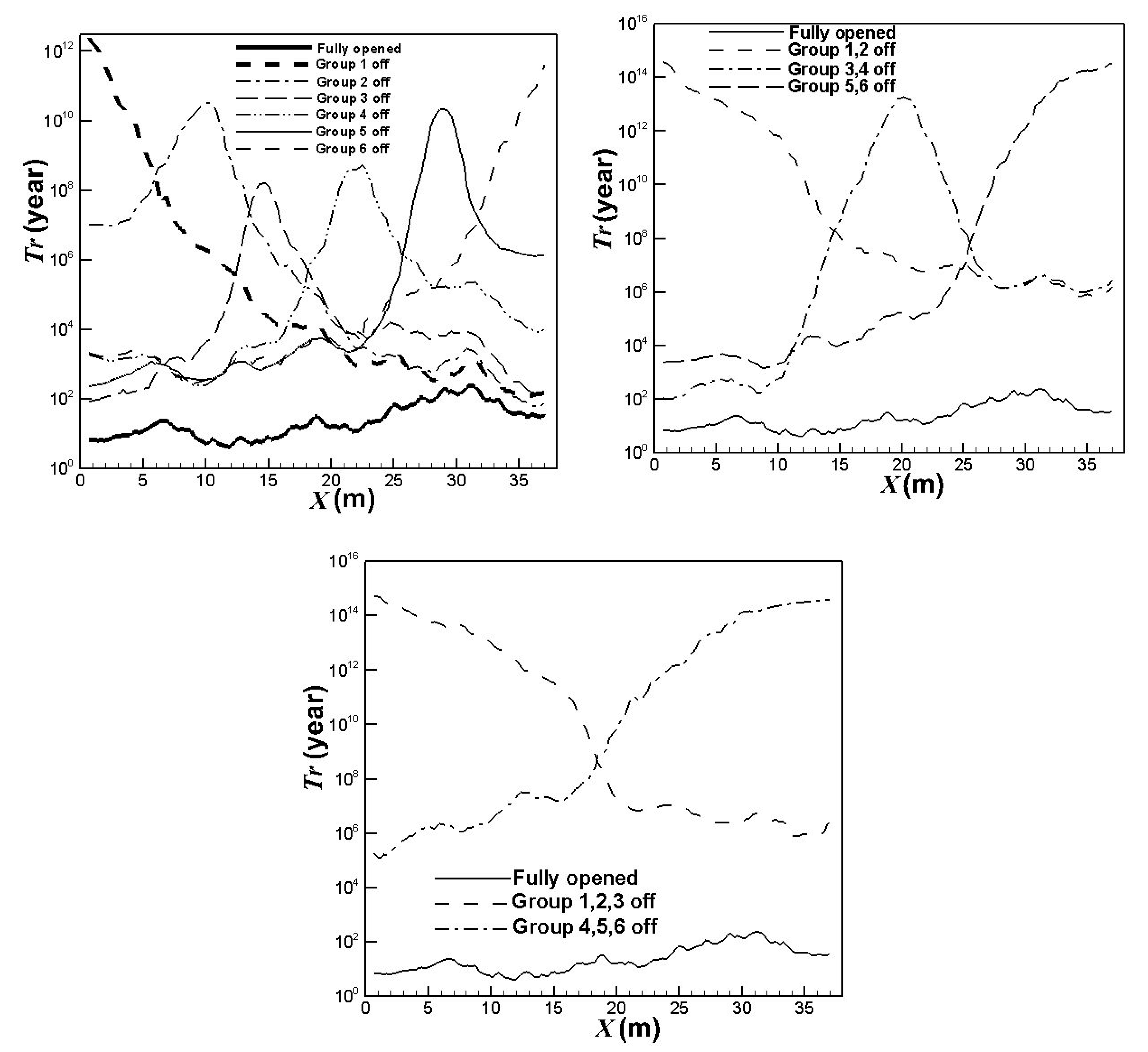
3.2. Lifetime Estimate of the Prototype Reformer
- T represents temperature (K),
- tr represents stress-rupture time (hr),
- C represents a constant, usually of the order 20.
- S represents the stress inside the catalyst tube,
- Do represents the catalyst tube outside diameter,
- t represents the catalyst tube thickness.
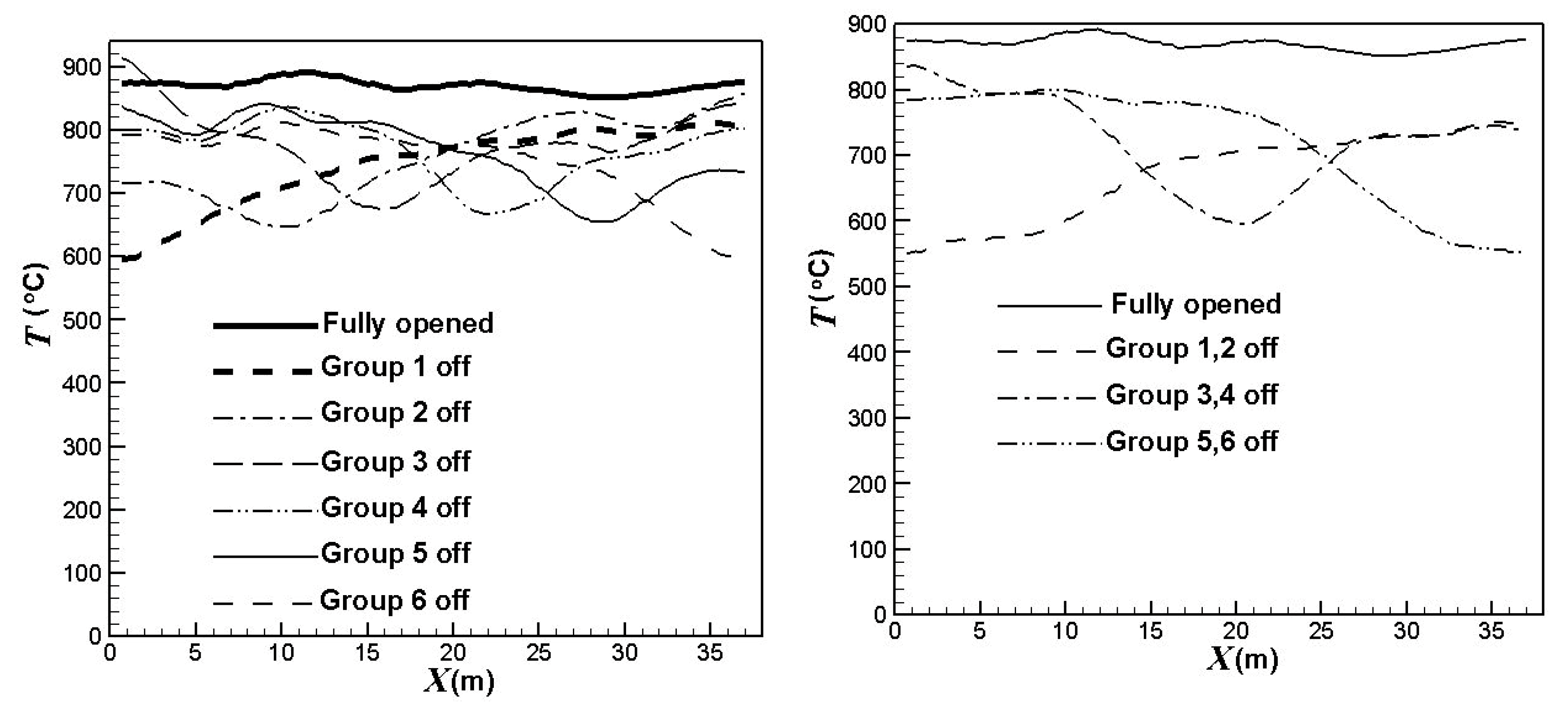
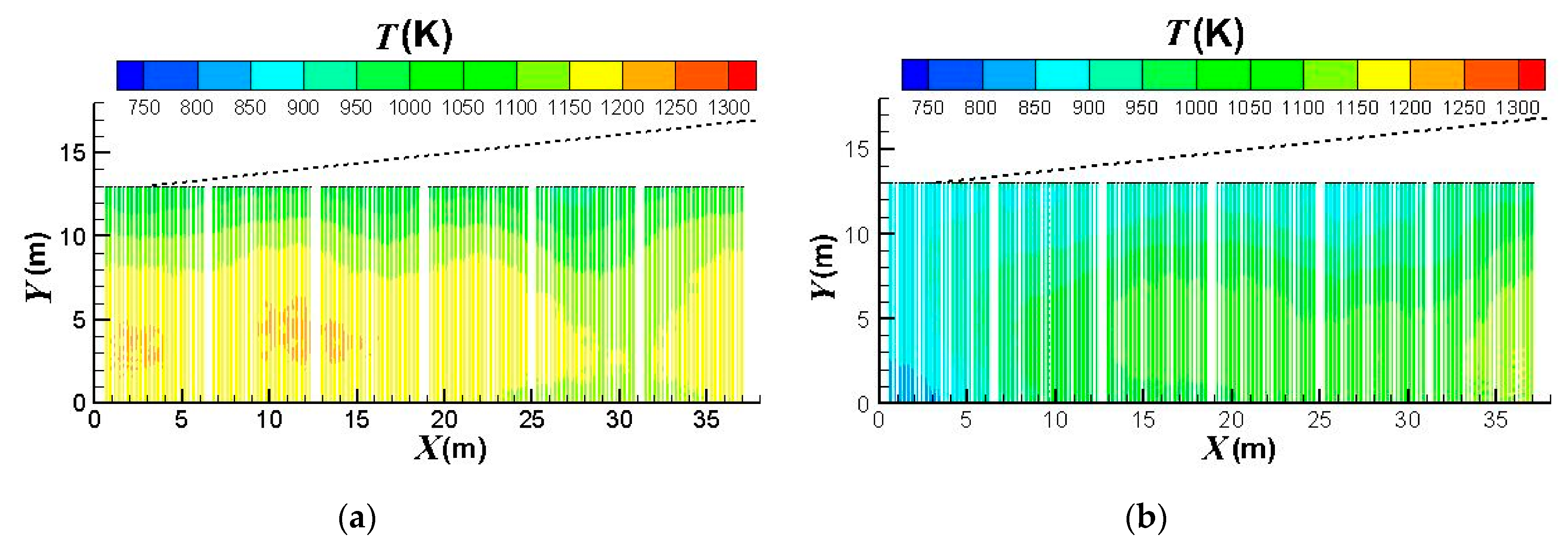
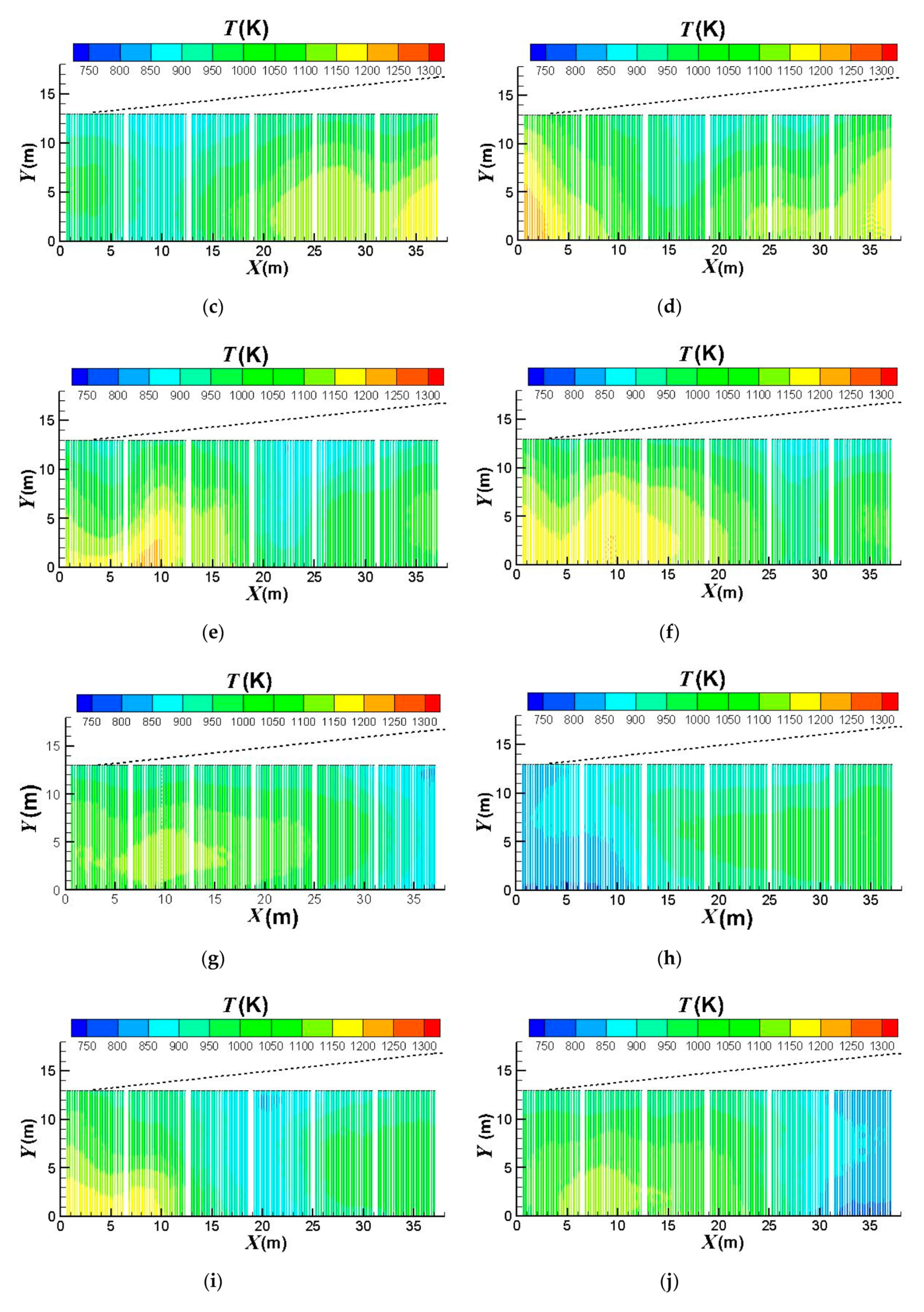
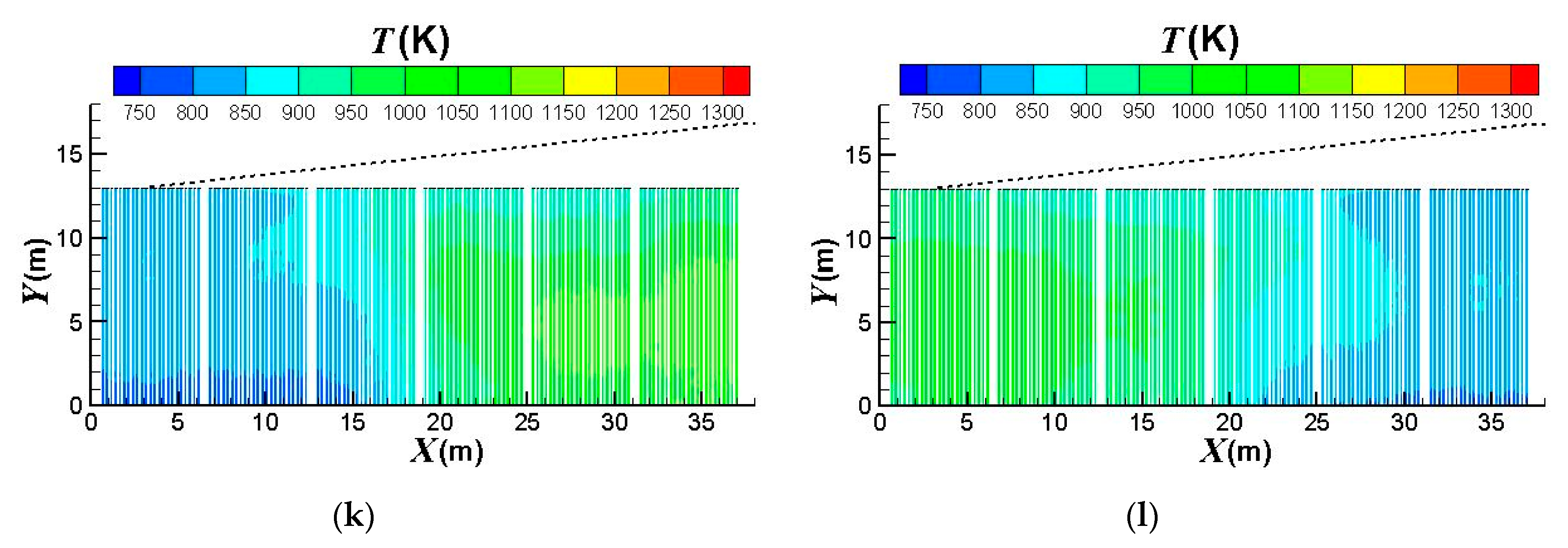
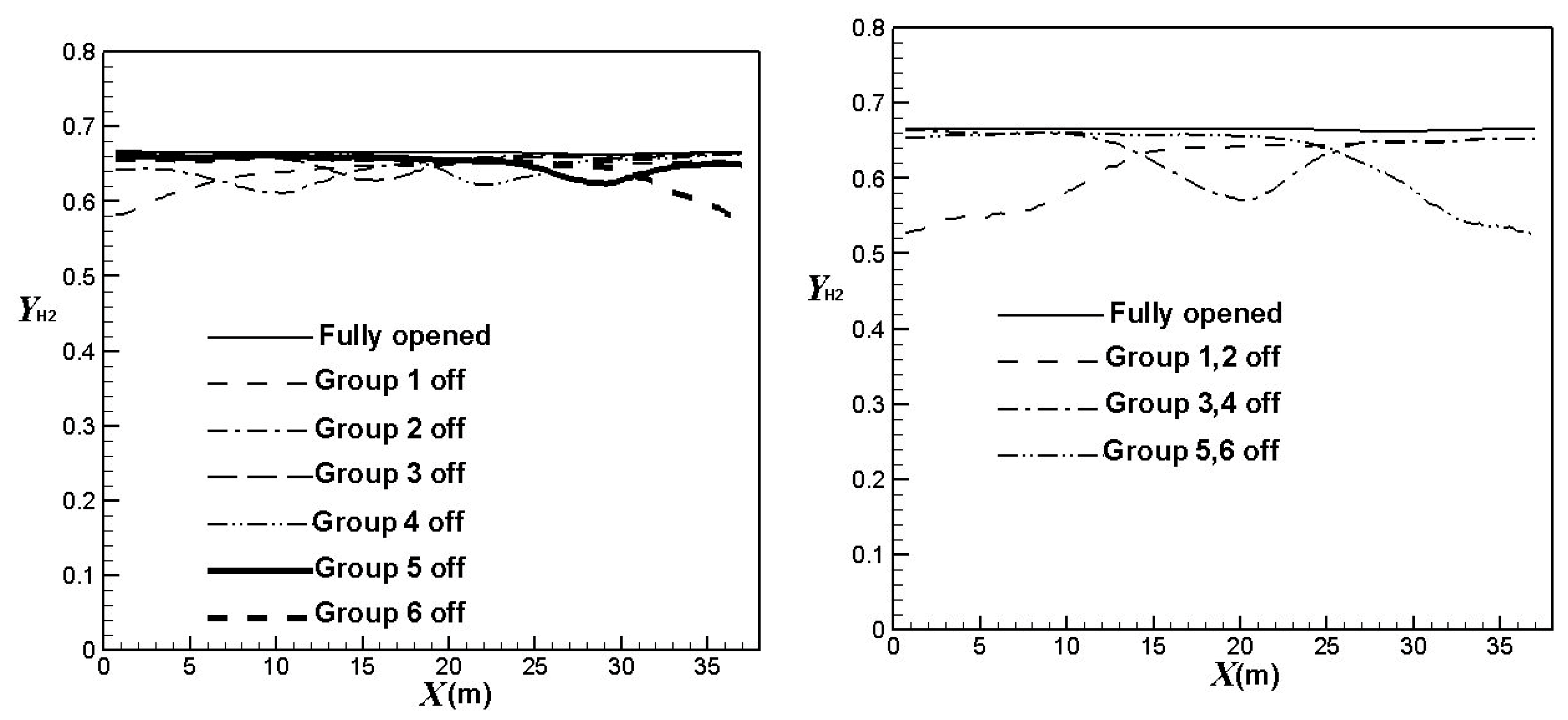
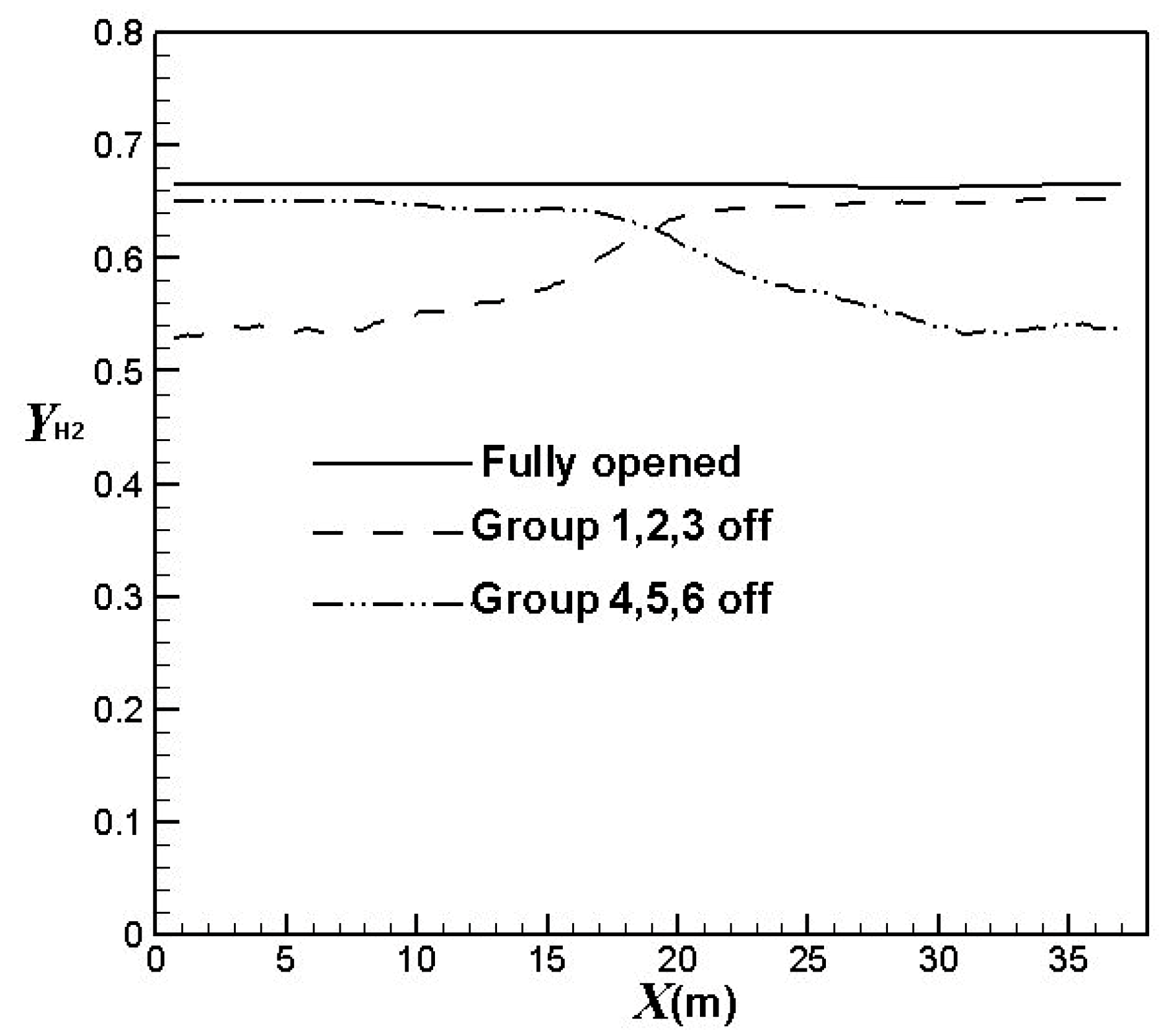
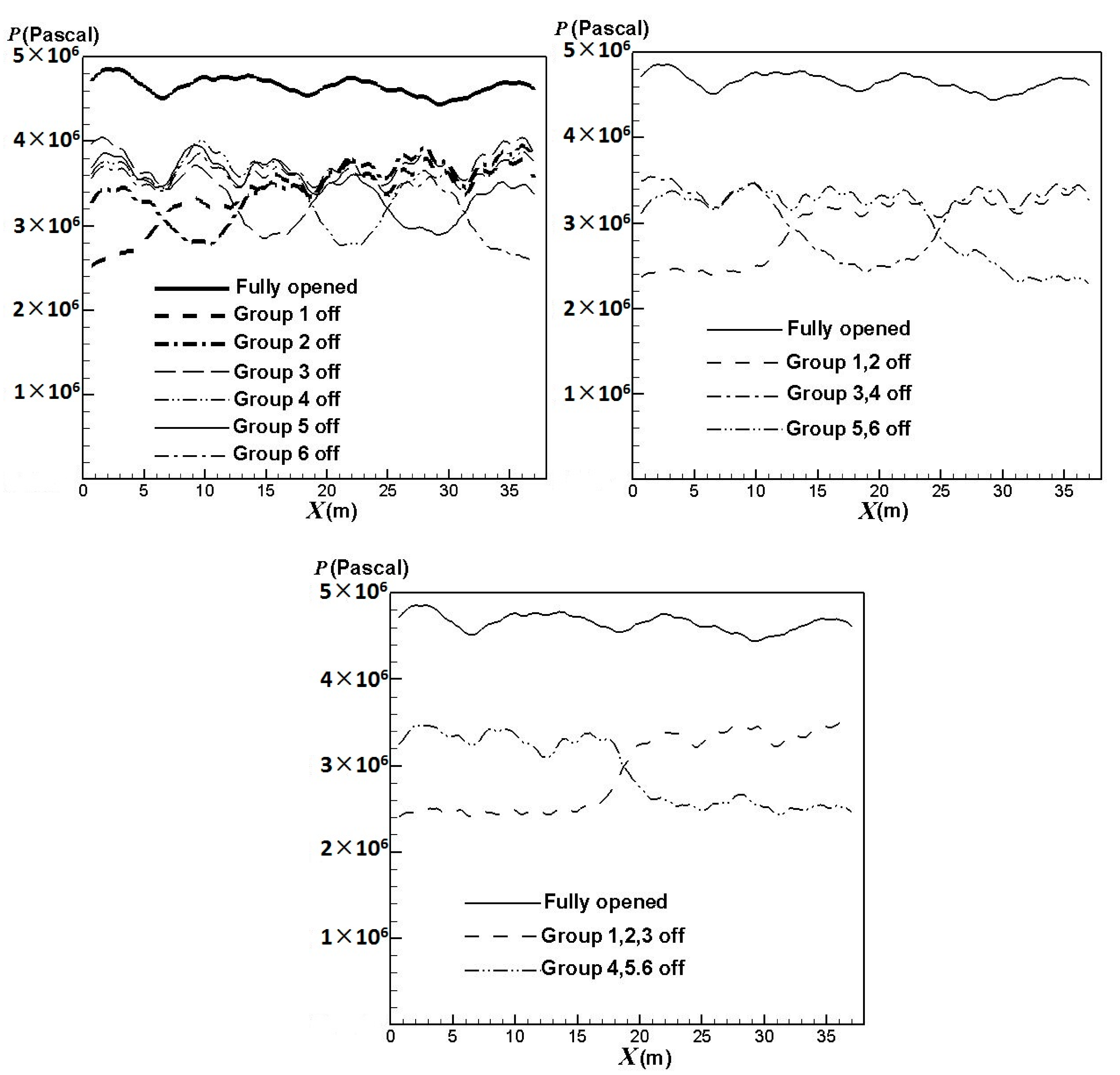
3.3. Influence of the Burners Turned on or off
- (1)
- the first group: x = 0 ~ 6.5 m,
- (2)
- the second group: x = 6.5 ~ 12.67 m,
- (3)
- the third group: x = 12.67 ~ 18.84 m,
- (4)
- the fourth group: x = 18.84 ~ 25.01 m,
- (5)
- the fifth group: x = 25.01 ~ 31.18 m,
- (6)
- the sixth group: x = 31.18 ~ 37.68 m.
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| C | molar concentration |
| Cμ | turbulence model constant (=0.09) |
| D | diffusion coefficient |
| k | turbulence kinetic energy (m2/s2); also reaction rate constant |
| L | hydraulic diameter (m) |
| l | characteristic length (m) |
| M | molecular weight |
| P | pressure (N/m2) |
| R | net generation rate |
| Sct | turbulent Schmidt number |
| T | temperature (K) |
| V | velocity (m/s) |
| Y | mole fraction |
| Greek symbols | |
| ε | turbulence dissipation rate (m2/s3) |
References
- Leta, J.V.; Dirham, T.R.; Dobis, J.; Guo, R.; Roberts, L. A Probabilistic Approach to Fired Heater Tube Remaining Life Assessments. In Proceedings of the ASME 2015 Pressure Vessels and Piping Conference (PVP2015), Boston, MA, USA, 19–23 July 2015; p. PVP2015-45427. [Google Scholar] [CrossRef]
- Tawancy, H.M. Damage analysis of catalyst tube of a reformer furnace used in hydrogen production. Metallogr. Microstruct. Anal. 2012, 1, 199–207. [Google Scholar] [CrossRef]
- Garbiak, M.; Jasiński, W.; Piekarski, B. Materials for reformer furnace tubes: History of evolution. Arch. Foundry Eng. 2011, 11, 47–52. [Google Scholar]
- Liu, C.J.; Chen, Y. Variations of the microstructure and mechanical properties of HP40Nb hydrogen reformer tube with time at elevated temperature. Mater. Des. 2011, 32, 2507–2512. [Google Scholar] [CrossRef]
- Ray, A.K.; Kumar, S.; Krishna, G.; Gunjan, M.; Goswami, B.; Bose, S.C. Microstructural studies and remnant life assessment of eleven years service exposed reformer tube. Mater. Sci. Eng. 2011, A529, 102–112. [Google Scholar] [CrossRef]
- Alvino, A.; Lega, D.; Giacobbe, F.; Mazzocchi, V.; Rinaldi, A. Damage characterization in two reformer heater tubes after nearly 10 years of service at different operative and maintenance conditions. Eng. Fail. Anal. 2010, 17, 1526–1541. [Google Scholar] [CrossRef]
- Swaminathan, J.; Guguloth, K.; Gunjan, M.; Roy, P.; Ghosh, R. Failure analysis and remaining life assessment of service exposed primary reformer heater tubes. Eng. Fail. Anal. 2008, 15, 311–331. [Google Scholar] [CrossRef]
- Maharaj, C.; Imbert, C.A.C.; Dear, J. Failure analysis and creep remaining life of hydrogen reformer outlet pigtail tubes. Eng. Fail. Anal. 2008, 15, 1076–1087. [Google Scholar] [CrossRef]
- Ray, A.K.; Sinha, S.K.; Tiwari, Y.N.; Swaminathan, J.; Das, G.; Chaudhuri, S.; Singh, R. Analysis of failed reformer tubes. Eng. Fail. Anal. 2003, 10, 351–362. [Google Scholar] [CrossRef]
- Gong, J.M.; Tu, S.T.; Yoon, K.B. Damage assessment and maintenance strategy of hydrogen reformer furnace tubes. Eng. Fail. Anal. 1999, 6, 143–153. [Google Scholar] [CrossRef]
- Le May, I.; da Silveira, T.L.; Vianna, C.H. Criteria for the evaluation of damage and remaining life in reformer furnace tubes. Int. J. Press. Vessel. Pip. 1996, 66, 233–241. [Google Scholar] [CrossRef]
- Pashchenko, D. Numerical study of steam methane reforming over a pre-heated Ni-based catalyst with detailed fluid dynamics. Fuel 2019, 236, 686–694. [Google Scholar] [CrossRef]
- Pajak, M.; Mozdzierz, M.; Chalusiak, M.; Kimijima, S.; Szmyd, J.S.; Brus, G. A numerical analysis of heat and mass transfer processes in a macro-patterned methane/steam reforming reactor. Int. J. Hydrogen Energy 2018, 43, 20474–20487. [Google Scholar] [CrossRef]
- Chen, J.; Gao, X.; Yan, L.; Xu, D. Computational fluid dynamics modeling of the millisecond methane steam reforming in microchannel reactors for hydrogen production. RSC Adv. 2018, 8, 25183–25200. [Google Scholar] [CrossRef] [Green Version]
- Tran, A.; Pont, M.; Aguirre, A.; Durand, H.; Crose, M.; Christofides, P.D. Bayesian model averaging for estimating the spatial temperature distribution in a steam methane reforming furnace. Chem. Eng. Res. Des. 2018, 131, 465–487. [Google Scholar] [CrossRef] [Green Version]
- Tran, A.; Pont, M.; Crose, M.; Christofides, P.D. Real-time furnace balancing of steam methane reforming furnaces. Chem. Eng. Res. Des. 2018, 134, 238–256. [Google Scholar] [CrossRef]
- Tran, A.; Aguirre, A.; Crose, M.; Durand, H.; Christofides, P.D. Temperature balancing in steam methane reforming furnace via an integrated CFD/data-based optimization approach. Comput. Chem. Eng. 2017, 104, 185–200. [Google Scholar] [CrossRef]
- Tran, A.; Aguirre, A.; Durand, H.; Crose, M.; Christofides, P.D. CFD modeling of an industrial-scale steam methane reforming furnace. Chem. Eng. Sci. 2017, 171, 576–598. [Google Scholar] [CrossRef]
- Lao, L.; Aguirre, A.; Tran, A.; Wu, Z.; Durand, H.; Christofides, P.D. CFD modeling and control of a steam methane reforming reactor. Chem. Eng. Sci. 2016, 148, 78–92. [Google Scholar] [CrossRef] [Green Version]
- Mokheimer, E.M.A.; Hussain, M.I.; Ahmed, S.; Habib, M.A.; Al-Qutub, A.A. On the modeling of steam methane reforming. J. Energy Resour. Technol. 2015, 137, 012001. [Google Scholar] [CrossRef]
- Ni, M. 2D heat and mass transfer modeling of methane steam reforming for hydrogen production in a compact reformer. Energy Convers. Manag. 2013, 65, 155–163. [Google Scholar] [CrossRef] [Green Version]
- Yeh, C.L. Numerical analysis of an industrial-scale steam methane reformer. Adv. Technol. Innov. 2019, 4, 140–151. [Google Scholar]
- Fluent Inc. ANSYS FLUENT 17 User’s Guide; Fluent Inc.: New York, NY, USA, 2017. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flows; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Siegel, R.; Howell, J.R. Thermal Radiation Heat Transfer, 3rd ed.; Hemisphere Publishing Corporation: Washington, DC, USA, 1992. [Google Scholar]
- Sivathanu, Y.R.; Faeth, G.M. Generalized state relationships for scalar properties in non-premixed hydrocarbon/air flames. Combust. Flame 1990, 82, 211–230. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Yeh, C.L. The effect of fuel mass fraction on the combustion and fluid flow in a sulfur recovery unit thermal reactor. Appl. Sci. 2016, 6, 331. [Google Scholar] [CrossRef] [Green Version]
- Sugihara, S.; Kawamura, Y.; Iwai, H. Rate equation of steam-methane reforming reaction on Ni-YSZ cermet considering its porous microstructure. J. Phys. Conf. Ser. 2016, 745, 032147. [Google Scholar] [CrossRef] [Green Version]
- Ødegård, R.; Johnsen, E.; Karoliussen, H. Methane Reforming on Ni/Zirconia SOFC Anodes. ECS Proc. 1995, 810–819. [Google Scholar] [CrossRef]
- Magnussen, B.F.; Hjertager, B.H. On mathematical models of turbulent combustion. In Symposium (International) on Combustion; The Combustion Institute: Pittsburgh, PA, USA, 1976. [Google Scholar]
- Larson, F.R.; Miller, J. A time-temperature relationship for rupture and creep stresses. Trans. ASME 1952, 74, 765–775. [Google Scholar]
- Manoir Industries: Paris, France, 2012. Available online: https://www.rmg.co.id/MANAURITEXM.pdf (accessed on 9 December 2018).
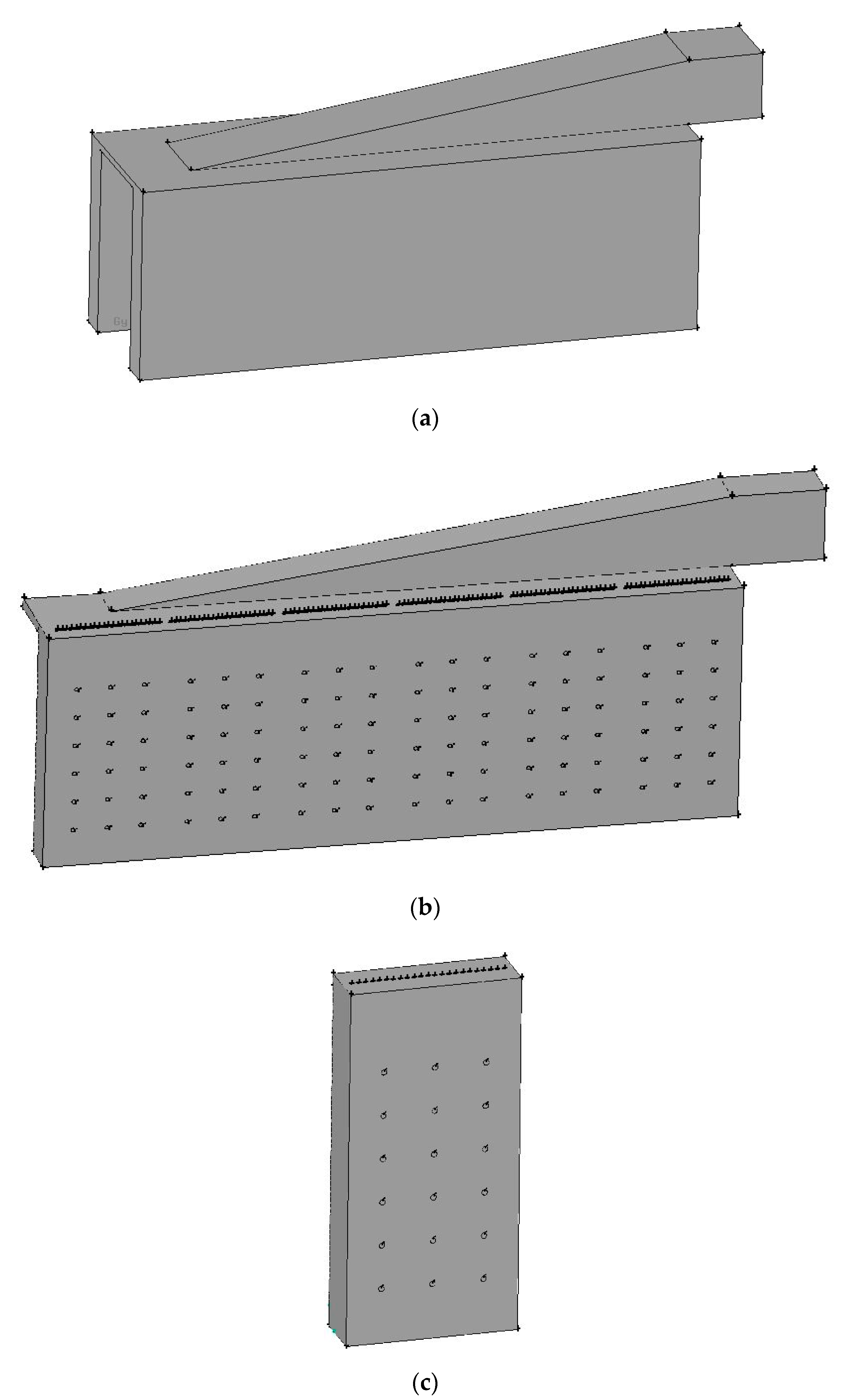
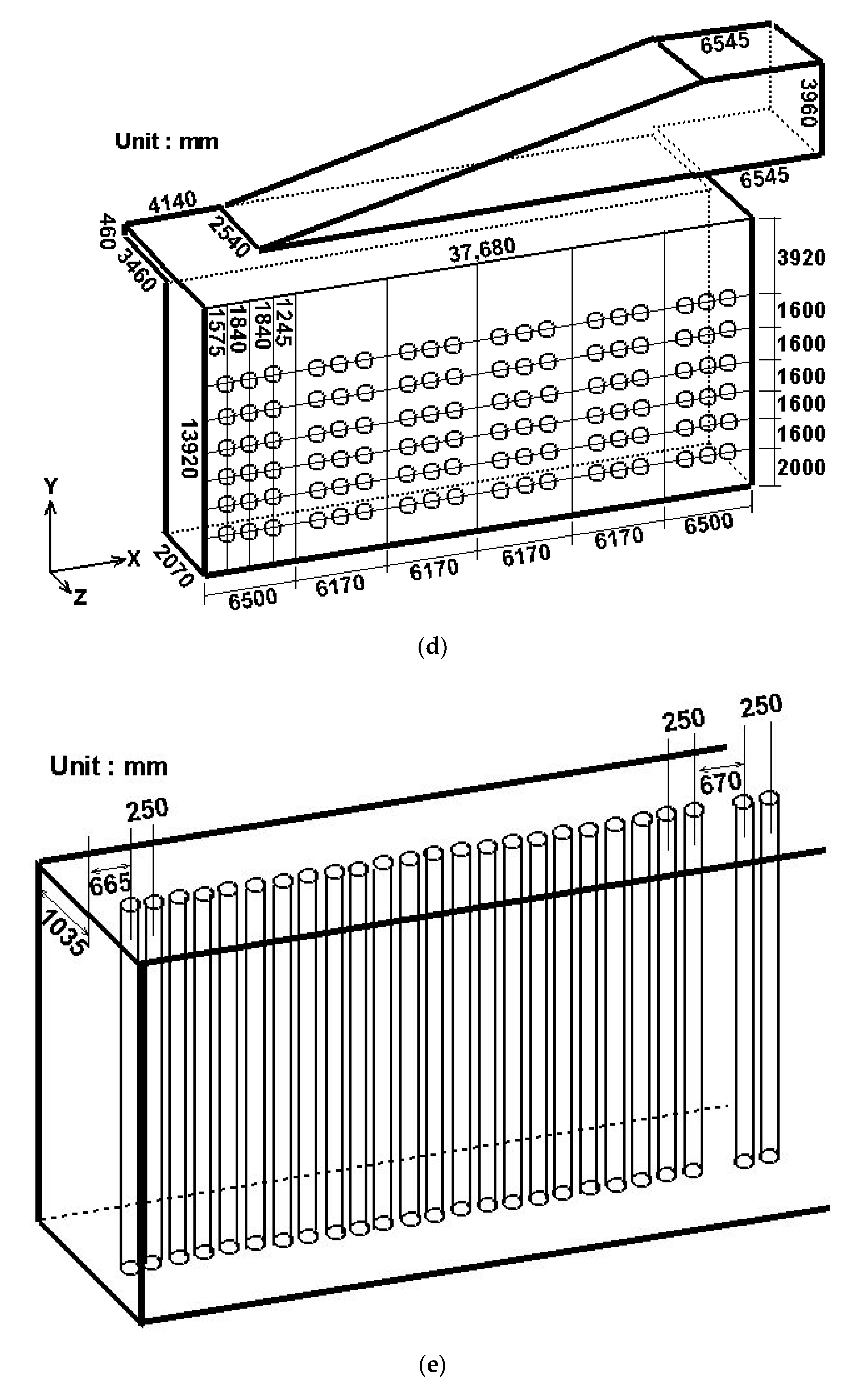
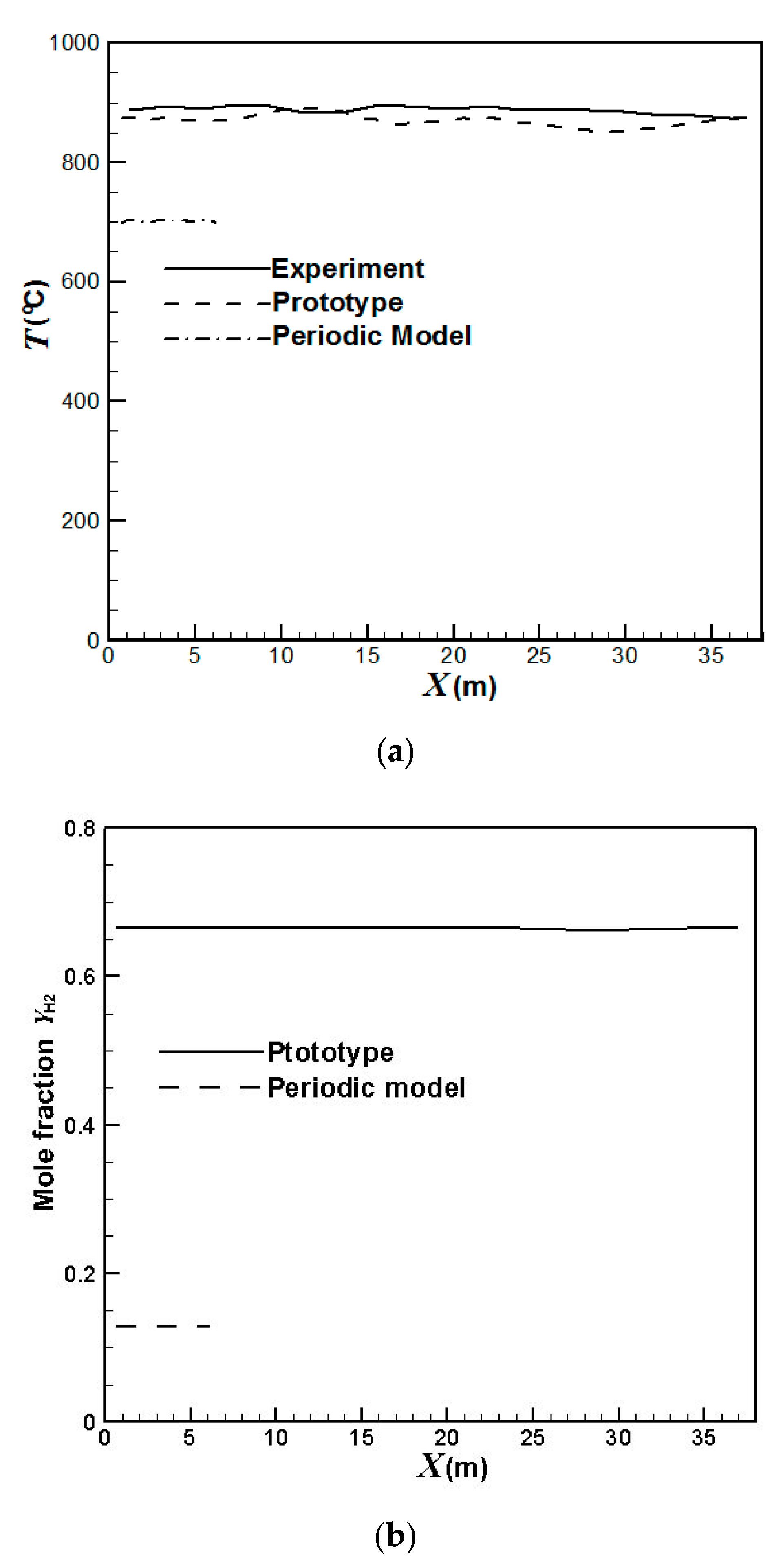

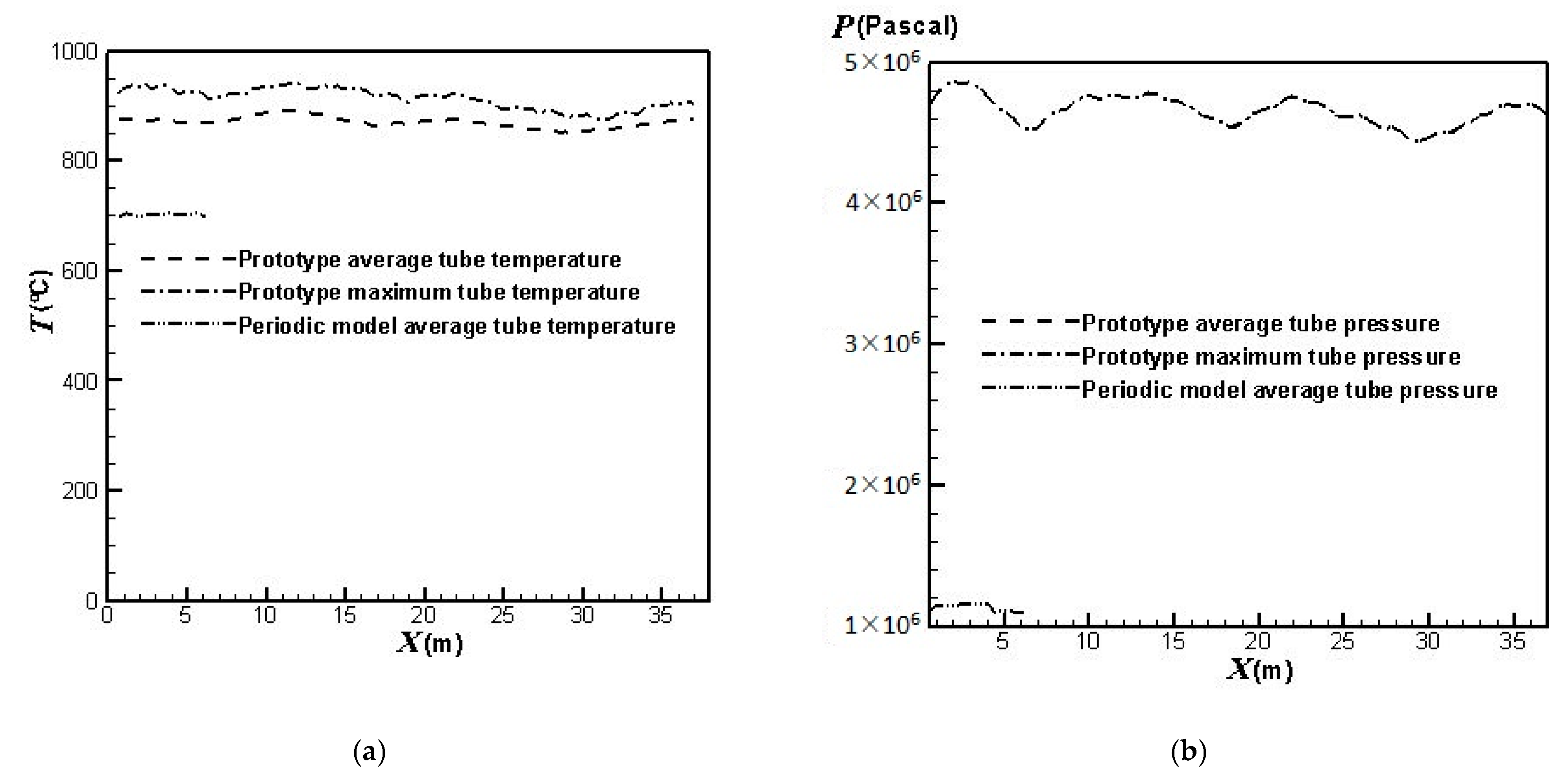

| Front Wall (°C) | Back Wall (°C) | |
|---|---|---|
| Experiment | 923 | 934 |
| Prototype Simulation | 891 | 892 |
| Periodic Model Simulation | 712 | 714 |
| Operating Mode | Hydrogen Yield |
|---|---|
| Fully opened | 0.670 |
| Group 1 off | 0.641 |
| Group 2 off | 0.647 |
| Group 3 off | 0.655 |
| Group 4 off | 0.654 |
| Group 5 off | 0.652 |
| Group 6 off | 0.644 |
| Group 1 & 2 off | 0.616 |
| Group 3 & 4 off | 0.637 |
| Group 5 & 6 off | 0.629 |
| Group 1, 2 & 3 off | 0.602 |
| Group 4, 5 & 6 off | 0.604 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yeh, C.-L. Effect of Burner Operation on the Catalyst Tube Lifetime of a Steam Methane Reformer: A Numerical Study. Appl. Sci. 2021, 11, 231. https://doi.org/10.3390/app11010231
Yeh C-L. Effect of Burner Operation on the Catalyst Tube Lifetime of a Steam Methane Reformer: A Numerical Study. Applied Sciences. 2021; 11(1):231. https://doi.org/10.3390/app11010231
Chicago/Turabian StyleYeh, Chun-Lang. 2021. "Effect of Burner Operation on the Catalyst Tube Lifetime of a Steam Methane Reformer: A Numerical Study" Applied Sciences 11, no. 1: 231. https://doi.org/10.3390/app11010231
APA StyleYeh, C.-L. (2021). Effect of Burner Operation on the Catalyst Tube Lifetime of a Steam Methane Reformer: A Numerical Study. Applied Sciences, 11(1), 231. https://doi.org/10.3390/app11010231




