Effect of Fuel Mass Flow at the End of Injection on Cavitation and Gas Ingestion in the Nozzle

Featured Application

Diesel engine injector.

Abstract

The fuel flow in the diesel engine nozzle has a vital impact on the fuel atomization and spray, and the fuel mass flux affects the internal flow of the nozzle. The visual experimental platform for a transparent nozzle was built to obtain the image of fuel flow in a nozzle with a small sac combining the back-light imaging technology and a high-speed framing camera. A two-phase three-component numerical model, based on the OpenFOAM solver, was calculated to quantitatively analyze gas ingestion and cavitation in the nozzle. The results indicate that at the end of injection (EOI), fuel cavitation and external air backflow (gas ingestion) occur successively in the nozzle, and both phenomena first appear in the orifice and then transition to the sac. Cavitation collapse is the major factor of gas ingestion, and the total amount of gas ingestion and cavitation mainly depends on the sac. The outflow of fuel largely depends on the total amount of cavitation and the inertial outflow of fuel at the EOI. The type of cavitation in the nozzle mainly presents annular and bulk cavitation, the former primarily exists in the sac, while the latter is established within the orifice. Therefore, larger mass flows will contribute to stronger cavitation and gas ingestion.

1. Introduction

With the increasing global energy demand, the research on fuel injection technology, sprays, and combustion, especially in the transportation sector, has been steadily increasing. The effect of fuel injection and spray is inseparable from the combustion and emission performance of internal combustion engines. To produce a suitable and uniform air-fuel mixture, small orifice diameter and higher injection pressure are used in mainstream compression ignition engines. During the fuel injection, sudden changes in fuel pressure and velocity will cause fuel cavitation, then the cavitation collapses as the pressure increases [1,2,3,4,5]. The fuel flow characteristic for the fuel injector has an obvious impact on the fuel atomization and spraying [6,7,8,9], thus it is of certain significance to research the internal flow of the fuel injector.

Due to the extremely high fuel flow rate and small diameter of the actual fuel orifice, it is difficult to carry out actual tests. Therefore, some scholars [10,11,12,13] conducted experimental studies on scaled-up transparent nozzles, which were based on the principle of similarity under the premise of ensuring the geometric similarities between the experimental and real-size nozzles. However, there were many scholars who still performed research on fuel flow on a real-sized nozzle and the effects of X-rays on a transparent real-sized nozzle [14,15,16].

Interestingly, Mitroglou [17] observed that there were stagnant bubbles in the nozzle before fuel injection, and this phenomenon was later confirmed to have an impact on fuel atomization [18,19,20] because different positions of the stagnant bubbles would cause different shapes of the fuel spray. One of the latest experimental studies on these stagnant bubbles was conducted by Guo [21], who pointed out that there were three sources of these initial bubbles: in the start of fuel injection (ingestion gas from the start of injection (SOI)), ingestion gas from the end of injection (EOI) of the last injection, and fuel vapor not discharged from the EOI of the last injection (gas ingestion bubbles from the EOI of the last injection played a major role). However, due to the lack of numerical simulation, he did not explain its mechanism clearly.

The fuel flow in the fuel injector is a highly transient process, limited by the current experimental technology, thus many scholars chose to utilize numerical simulation to obtain the transient information of the complex and variable flow field in the nozzle [22,23,24]. The numerical methods of solving fuel flow in the nozzle can be simply divided into the homogeneous equilibrium model and multi-phase flow model. Because the homogeneous equilibrium model needs less memory and has a faster calculation speed, some researchers chose the homogeneous equilibrium model to study cavitation and therefore achieved good results [25,26]. However, compared with the multi-phase flow model, less flow field information is obtained. Thus, Marcer [27] used the improved volume of fluid (VOF) method to study the vapor-liquid two-phase flow, and he found that the simulation result provided a good fit to that of the experimental. Then, Alajbegovic [28] verified that cavitation was caused by the decrease of fuel pressure via the two-fluid model and believed that the two-fluid model was an engineering tool suitable for large-scale processes. Luis [29] established a VOF model based on Eulerian multi-phase flow to capture the two-phase interface motion, and the effect of fluid parameter on the fuel flow in the nozzle was analyzed. Battistoni [30] proposed a large eddy simulation turbulence model by coupling multi-phase flow to investigate the fuel flow in the nozzle at the SOI and EOI, but he did not study gas ingestion at the EOI. Ghiji [20] studied the phenomenon of fuel cavitation and atomization using an Euler/VOF/LES (large eddy simulation) model and obtained results that were consistent with their experiments.

At present, there is not much research on gas ingestion and cavitation at the EOI. The current research on cavitation mainly focuses on nozzle structure and shape [31,32], injection pressure [33], back pressure [34], wall roughness [35], aspect ratio of orifice [36], and fuel type [22,37,38]. Interestingly, one of the findings is that cavitation possesses a significant cycle-to-cycle variation under the conditions of multiple injections [17,39], which will affect fuel atomization. However, the mechanism of gas ingestion is not clear enough. In this paper, a two-phase three-component numerical method for nozzle studies is presented, combined with a visualization experiment to further study the cavitation and gas ingestion at the EOI and at different fuel mass fluxes. These results are helpful for future researchers to further study cavitation in the nozzle to improve the quality of fuel atomization.

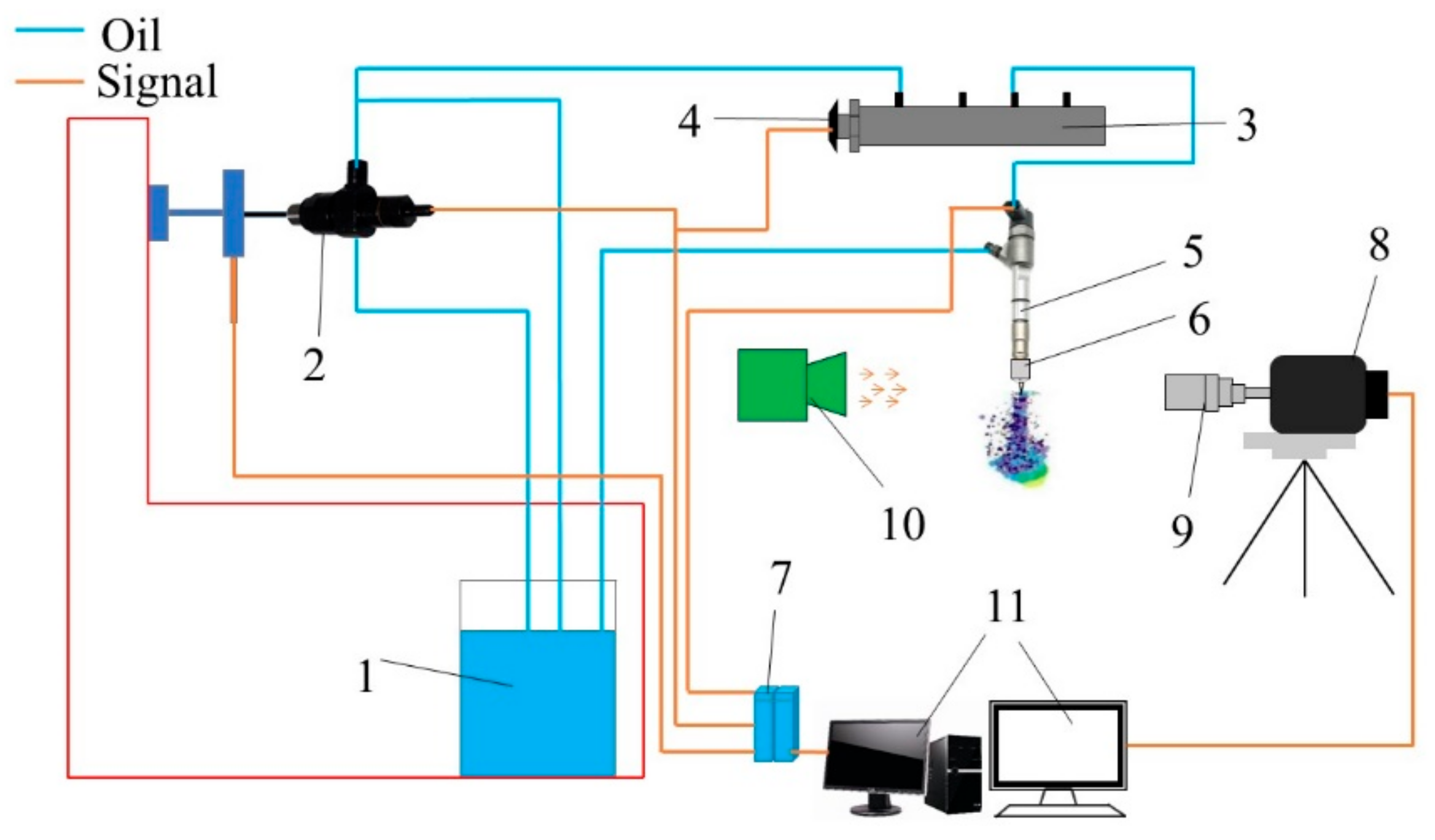
2. Experiment

The visualization experimental platform built for this measurement consisted of three parts—fuel delivery, signal control, and optical imaging system—and it is shown in Figure 1.

The fuel delivery system (Taian) included two parts: a DB2000-75 high-pressure oil pump bench and a Delphi Multec DCR 1400 high-pressure common-rail fuel pipe. The stable injection conditions were maintained by the fuel delivery system under various working conditions and provided an appropriate fuel flux for the injector. This ensured the diesel engine to operate stably and enabled the injector reliable work.

Visu98 signal control system was used to control fuel mass flux and injection pressure. It included a pressure sensor which was mounted on the injection system. The revolution speed should not be too high to avoid excessive injection pressure. Considering the bearing capacity of acrylic material, the excessive injection pressure would cause the transparent nozzle, therefore the revolution speed was set to 250 rpm. For the same reason, 30 MPa was selected as the injection pressure in this experiment.

High-magnification cavitation images were captured by the optical image imaging system, and it consisted of an image acquisition system and a lighting system. The image acquisition system was mainly composed of a long focal distance microscope (QM-100, QUESTAR), a high-speed framing camera (VRI-VEO-710L), and a Phantom camera controller. The lighting system was a prerequisite for the success of the experiment; it consisted of a LED cold-light source and was used for back-lighting technology in this paper. To freeze the flow field and obtain the highest-resolution image possible, the exposure time was set to 1 $\mathsf{\mu }\mathrm{s}$, and the pixel resolution was 720 × 480. Under this shooting condition, the frame rate could be as high as 20,000 frames per second, i.e., the time interval between each image is 50 $\mathsf{\mu }\mathrm{s}$.

Due to the refractive index of 0# diesel (n = 1.46–1.51) being close to that of the polymethyl methacrylate (PMMA) (n = 1.49) [40], the light can pass directly through the fuel and the nozzle without being refracted and appears as a transparent area in the images. Meanwhile, when the light illuminates the interface between the fuel and the cavitation, scattering occurs due to the difference in the refractive index between the two, thereby forming a black area in the images. Based on the above reasons, the spherical part of a real injector was removed, and an optically transparent nozzle made of PMMA (including a small pressure chamber and a straight hole) was used instead of the original nozzle; the diameter of the orifice was 0.3 mm, and the aspect ratio was 5. The experimental nozzle is shown in Figure 2.

The Phantom camera controller (PCC) was adopted to obtain the fuel cavitation images efficiently. All the experimental equipment was controlled synchronously by the corresponding electronic equipment. In addition, the long focal distance microscope, the high-speed framing camera, and the LED light keep the same line. Because the transparent nozzle is deformed when overheated, the temperature was kept at a low level in all experiments, and the nozzle was allowed to take a break every three fuel injection cycles. The optimal injection event was obtained after using five transparent nozzles.

3. Mathematical Model

3.1. Governing Equations

In this paper, based on the finite volume method (FVM), a cavitation numerical model was proposed. This model contained two phases and three components, namely fuel, fuel vapor, and air. Then, coupled with the large eddy simulation [37] (LES), a set of governing equations was shared between the liquid and vapor in the control unit. The continuity equation and momentum equation were as follows:

$$\frac{\partial \rho }{\partial t}+\nabla ·(\rho u)=0$$

(1)

$$\frac{\partial \rho u}{\partial t}+\nabla ·(\rho uu)=-\nabla p+\nabla ·\tau +{\displaystyle \underset{S(t)}{\int }\sigma kn·\delta (x-x\prime )}ds$$

(2)

In Equations (1) and (2), $p$ is pressure, $\rho$ is density, $u$ is velocity, $t$ presents time, and $\tau$ is the viscous shear stress; ${\displaystyle \underset{S(t)}{\int }\sigma kn·\delta (x-x\prime )}ds$ represents the momentum source term of momentum Equation; $\sigma$, $k$, and $n$ represent the surface tension coefficient, interface curvature, and normal unit vector pointing to surface $S$.

Fuel flowed through the nozzle, there were two different flows of liquid-vapor. Cavitation was a dynamic equilibrium process in which the liquid was converted into vapor. Therefore, to establish the cavitation model, it is necessary to take the phase change-transition source term into the corresponding FVM transport equation:

$$\frac{\partial ({\alpha }_l{\rho }_l)}{\partial t}+\nabla ·({\alpha }_l{\rho }_{l}u)=\dot{m}$$

(3)

$$\frac{\partial ({\alpha }_v{\rho }_v)}{\partial t}+\nabla ·({\alpha }_v{\rho }_{v}u)=-\dot{m}$$

(4)

$$\frac{\partial ({\alpha }_g{\rho }_g)}{\partial t}+\nabla ·({\alpha }_g{\rho }_{g}u)=0$$

(5)

$${\alpha }_l+{\alpha }_v+{\alpha }_g=1$$

(6)

In the above equations, the subscripts $l$, $v$, and $g$ are diesel, diesel vapor, and air, respectively; $\alpha$ is the volume fraction of each component; $\dot{m}$ is the mass exchange rate between the liquid-vapor phase. The convection term in Equation (4) is as follows:

$$\nabla ·({\alpha }_v{\rho }_{v}u)={\rho }_v(\nabla ·({\alpha }_{v}u))+{\alpha }_v(u·\nabla {\rho }_v)$$

(7)

In this paper, the fluid assumed incompressible, the convection term in Equations (3)–(5) is expanded as follows:

$$\frac{\partial {\alpha }_l}{\partial t}+\nabla ·({\alpha }_{l}u)=-\frac{{\alpha }_l}{{\rho }_l}(\frac{\partial {\rho }_l}{\partial t}+u·\nabla {\rho }_l)+\frac{\dot{m}}{{\rho }_l}$$

(8)

$$\frac{\partial {\alpha }_v}{\partial t}+\nabla ·({\alpha }_{v}u)=-\frac{{\alpha }_v}{{\rho }_v}(\frac{\partial {\rho }_v}{\partial t}+u·\nabla {\rho }_v)-\frac{\dot{m}}{{\rho }_v}$$

(9)

$$\frac{\partial {\alpha }_g}{\partial t}+\nabla ·({\alpha }_{g}u)=-\frac{{\alpha }_g}{{\rho }_g}(\frac{\partial {\rho }_g}{\partial t}+u·\nabla {\rho }_g)$$

(10)

The mass conservation equation for each component is as follows:

$$\frac{\partial {\rho }_i}{\partial t}+\nabla ·({\rho }_{i}u)=0$$

(11)

Substituting Equation (11) into Equations (8)–(10) to simplify and add:

$$\nabla ·u=\dot{m}(\frac{1}{{\rho }_l}-\frac{1}{{\rho }_v})$$

(12)

Thus, the vapor-liquid phase transport equation is as follows:

$$\frac{\partial {\alpha }_l}{\partial t}+\nabla ·({\alpha }_{l}u)={\alpha }_l(\nabla ·u)+\dot{m}(\frac{1}{{\rho }_l}-{\alpha }_l(\frac{1}{{\rho }_l}-\frac{1}{{\rho }_v}))$$

(13)

$$\frac{\partial {\alpha }_g}{\partial t}+\nabla ·({\alpha }_{g}u)={\alpha }_g\dot{m}(\frac{1}{{\rho }_l}-\frac{1}{{\rho }_v})$$

(14)

3.2. Cavitation Model

Due to its good convergence and numerical stability and the effectiveness of bubble solving, the Schnerr–Saucer cavitation model was added [41,42,43]. Assuming no slip at the interface of liquid and cavitation, the bubble dynamic equation is as follows:

$$R\frac{d^{2}R}{d{t}^2}+\frac{3}{2}{(\frac{dR}{dt})}^2=\frac{p_b-p}{{\rho }_l}-\frac{4{\nu }_l}{R}\frac{dR}{dt}-\frac{2\sigma }{{\rho }_{l}R}$$

(15)

In Equation (15), $R$ is the cavitation bubble radius; $p_b$ is the pressure of cavitation bubble surface; $\sigma$ denotes the surface tension of the cavitation bubble; $v_l$ denotes the kinematic viscosity of the liquid.

In this model, it was assumed that the central pressure of the control unit was the same as the local far-field pressure, and the saturated vapor pressure $p_{sat}$ of the liquid without gas dissolved was regarded as the surface pressure of the cavitation bubble. Here, ignoring the second derivative, viscosity effect, and surface tension term, Equation (15) was simplified as follows:

$$\frac{dR}{dt}=\sqrt{\frac{2}{3}\frac{p_{sat}-p}{{\rho }_l}}$$

(16)

Combining Equations (1) and (12):

$$\dot{m}=-\frac{{\rho }_l{\rho }_v}{\rho }\frac{d{\alpha }_v}{dt}$$

(17)

The equation of the number of bubbles per unit volume of liquid $n_0$, the average bubble radius, and the vapor volume fraction is:

$${\alpha }_v=\frac{n_0·4\pi R^3}{3+n_0·4\pi R^3}$$

(18)

Substituting Equation (18) into (17):

$$\dot{m}=-\frac{3{\alpha }_l{\alpha }_v}{R}\frac{{\rho }_l{\rho }_v}{\rho }\frac{dR}{dt}$$

(19)

Substituting Equation (16) into (19):

$${\dot{m}}^{+}=\frac{3{\alpha }_l{\alpha }_v}{R}\frac{{\rho }_l{\rho }_v}{\rho }\sqrt{\frac{2}{3}\frac{p_{sat}-p}{p_l}}\left(p_{sat}>p\right)$$

(20)

$${\dot{m}}^{-}=\frac{3{\alpha }_l{\alpha }_v}{R}\frac{{\rho }_l{\rho }_v}{\rho }\sqrt{\frac{2}{3}\frac{p-p_{sat}}{p_l}}\left(p_{sat}<p\right)$$

(21)

The average bubble radius was as follows:

$$R={(\frac{{\alpha }_v}{{\alpha }_l}\frac{3}{4\pi }\frac{1}{n_0})}^{\frac{1}{3}}$$

(22)

According to the study of Yuan [41], $n_0=1.5\times {10}^{14}$.

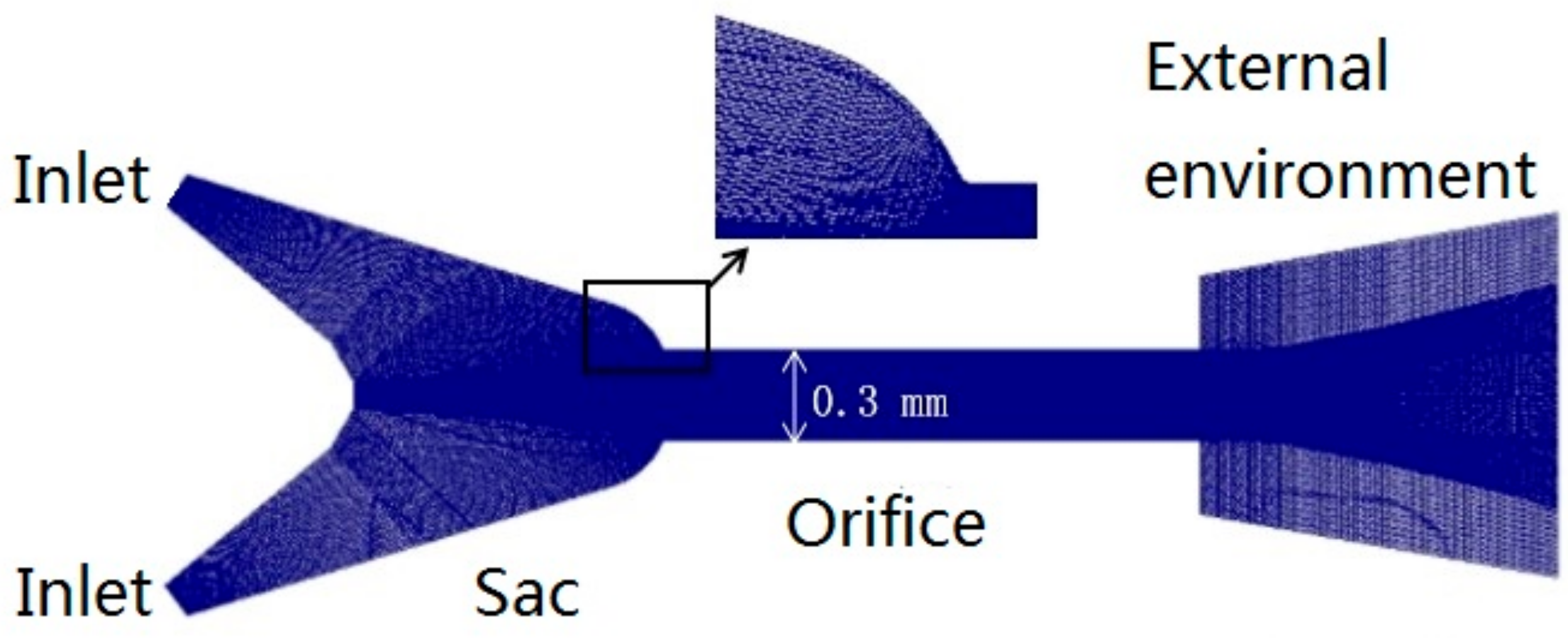
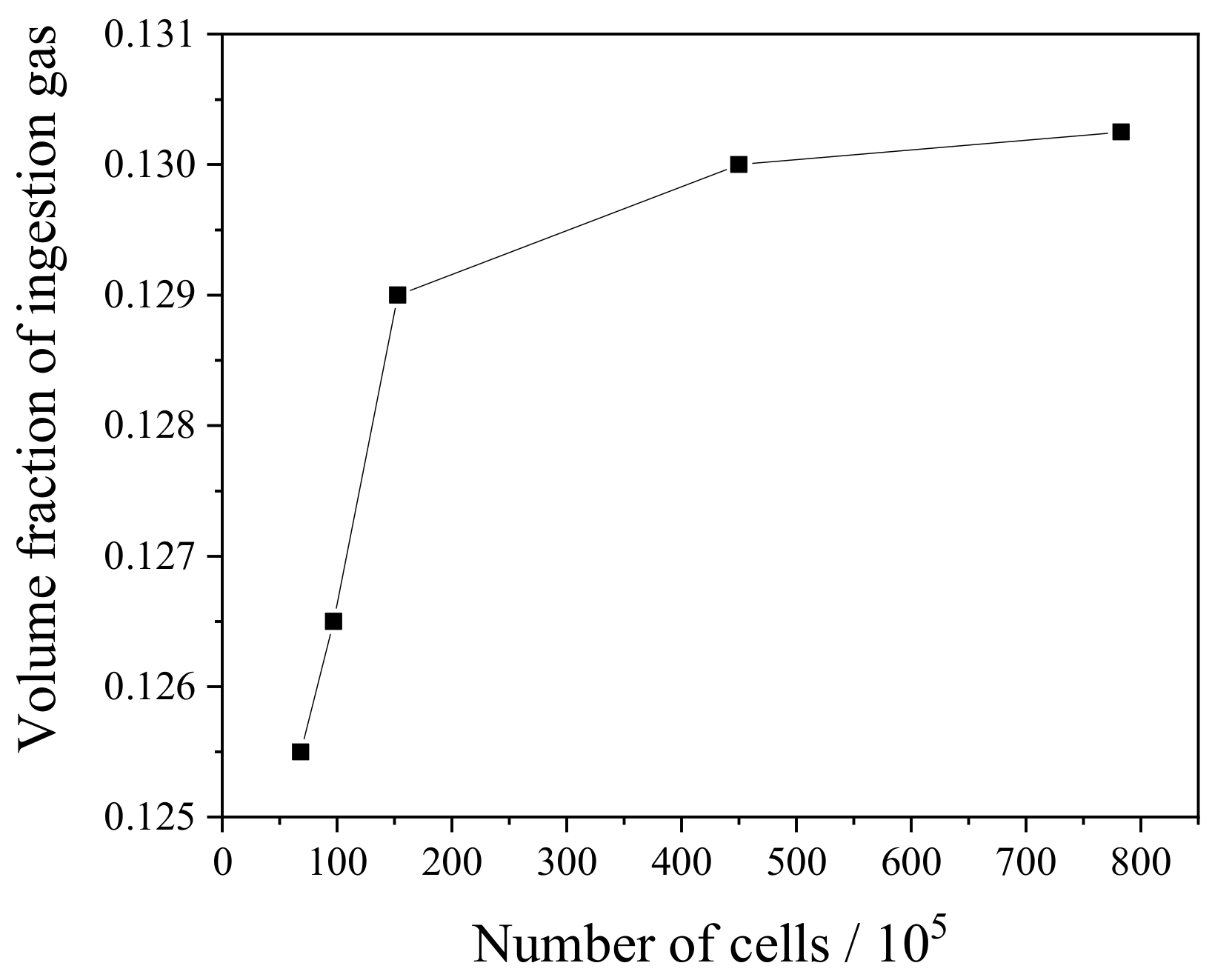
3.3. Computational Domain and Boundary Condition

According to the geometry shape of the experiment nozzle, a geometric model of the nozzle was gotten to guarantee the simulation results, as shown in Figure 3. The experimental conditions and geometry dimensions of the experimental nozzle were the same as those of the nozzle physical model, including sac shape, orifice shape, injection condition, back pressure, and fuel physical parameters. In this model, the inlet boundary extends to the middle of the sealing surface because the needle valve was stationary. The fuel velocity and direction changed sharply when it passed through the orifice entrance during the injection process, resulting in wear of the orifice inlet. Therefore, a small rounded corner was considered at the entrance of the orifice, and its radius was set as 0.04 mm. Considering the existence of gas ingestion and super-cavitation (super-cavitation occurs at very low pressures and/or high velocities where a large and stable vapor cavity develops; when system pressure is decreased or when flow velocity is increased a small cavity will grow, and a large single steady vapor-filled supercavity will develop [44,45]) at the outlet of the orifice during the EOI, the iterative error of the numerical calculation was reduced, and the accuracy of the calculation results was improved. A part of the external environment was considered during the modeling process, whose boundary was set as a pressure boundary.

To ensure the correctness and rationality of the results, it was necessary to verify the independence of the nozzle physical model. According to the previous report [46], the size of the local encrypted mesh of the sac and sac entrance was set to 0.35 mm, the grid size of the spray area at the external boundary was set from 2 μm to 20 μm, and the other grid size was set to 2 μm. The boundary layer, cavitation region, and non-slip condition considered, the block structure method was adopted to generate hexahedral mesh by ICEM software, and the number of meshes was about 4.53 million. Based on the above grid size and the changed basic size of the grid to verify the independence of the grid, we got the following result, as shown in Figure 4.

When the number of cells is 4.53 million and 7.9 million, the relative difference in air volume is 0.192%. Therefore, using the above grid size is acceptable. Other thermophysical parameters of fluids are shown in

Table 1. Thermophysical parameters of fluids.

Parameters	Value	Unit
Density of diesel/ρ	840	kg·m−3
Dynamic viscosity of diesel/μ	0.0065	Pa·s
Density of air/ρ	1.21	kg·m−3
Dynamic viscosity of air/μ	1.85 × 10−5	Pa·s
Density of diesel vapor/ρ	0.14	kg·m−3
Dynamic viscosity of diesel vapor/μ	4.25 × 10−5	Pa·s
Saturated vapor pressure of diesel/pv	2000	Pa
Surface tension/σ	0.03	kg·s−2

.

Since the fact that the needle valve opening and closing were operated periodically in the working process of the actual nozzle, it was relatively difficult to realize the motion of the needle valve with OpenFOAM. Therefore, the needle valve movement model was not considered in the numerical model of the nozzle. To control the change of the mass flux at the nozzle inlet, the corresponding fuel mass flux was calculated according to the movement law of the needle valve, and the dynamic mass flow inlet boundary was used instead of the needle valve movement. According to the experimental statistical results, the sac and 3/4 orifice were filled with liquid fuel when the model was initialized. While the mass flux at the inlet of the nozzle changed according to the change law at the EOI, the fuel cavitation flow in the nozzle was calculated. The dynamic mass flow rate is calculated as Equation (23):

$$q=\sqrt{2}\phi ·A(x)·{(\Delta p·\rho )}^{0.5}$$

(23)

where $A(x)$ is the minimum flow area; $\phi$ is mass flow coefficient, equal to 0.5 [47]; $\Delta p$ is the pressure difference between the nozzle inlet and outlet, and it was equal to 30 MPa, while the environment pressure was atmospheric pressure equal to 0.1 MPa. According to experimental measurement, $x$ denotes the needle valve lift, its value was 0.1 mm, and the movement speed of the needle valve was 0.33 m/s.

In this model, an obvious interface between the diesel and diesel vapor occurred in each grid cell. Based on the discrete points in the finite volume, the VOF phase interface was compressed by using the spatial discretization method and the compression velocity term of the phase transport equation, thus a sharp interface was obtained. The pressure-velocity equation was solved by the Pressure-Implicit with Splitting of Operators (PISO) algorithm [48]. The discrete schemes of each term in the momentum equation were as follows: the time was in Euler Implicit format, the pressure gradient term used the least square discrete scheme, and the convection term and the diffusion term were respectively the Normalized Variable Gamma scheme and the Second-order Gaussian linear discrete scheme. The Courant number adaptive time step was adopted, the average time step was set to 2 × 10⁻⁸ s, the maximum time step was 1 × 10⁻⁶ s, the maximum Courant number (the ratio of time step to space step) was 0.3, and the maximum maxAlphaCo was also 0.3.

4. Results and Discussion

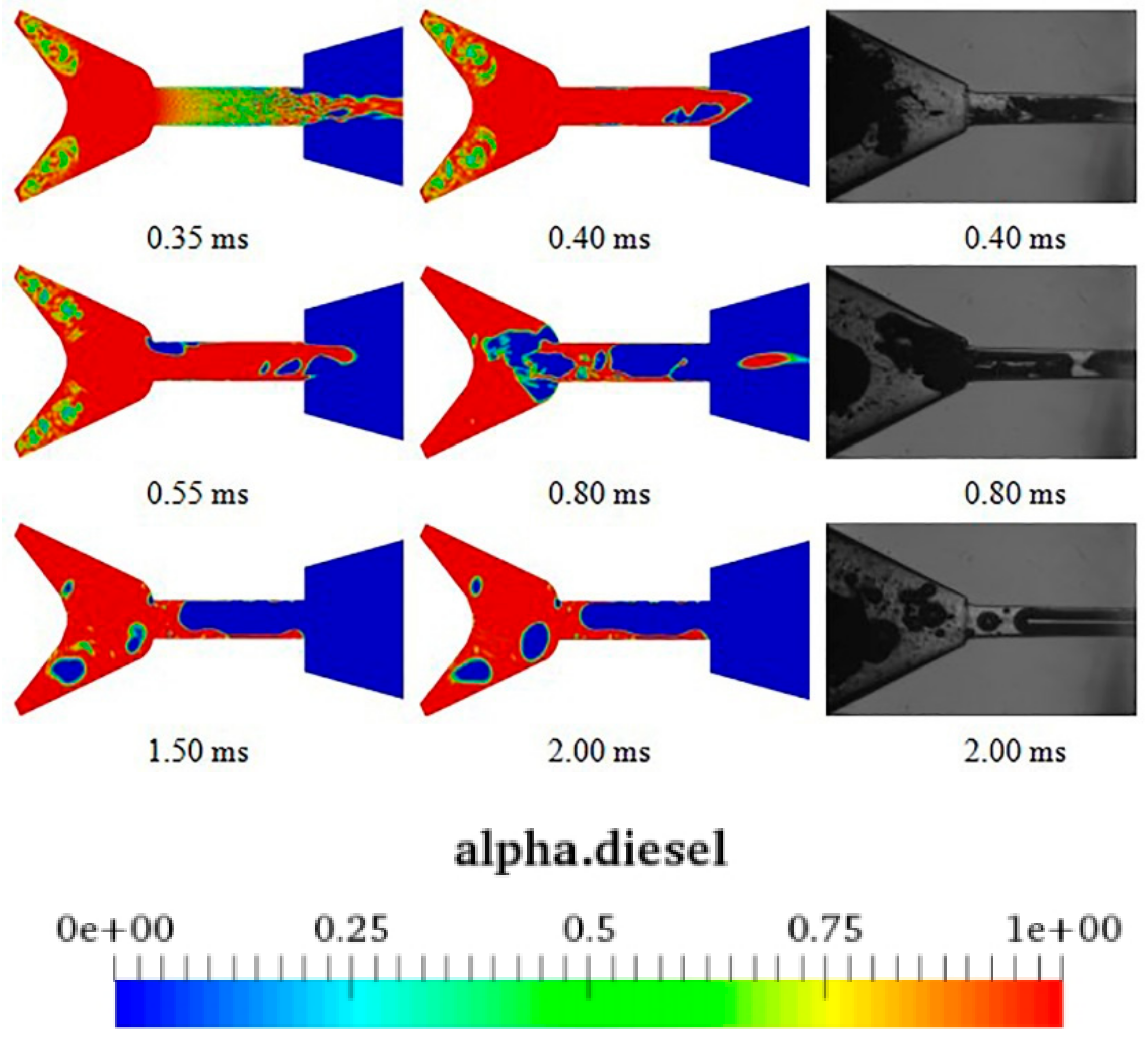
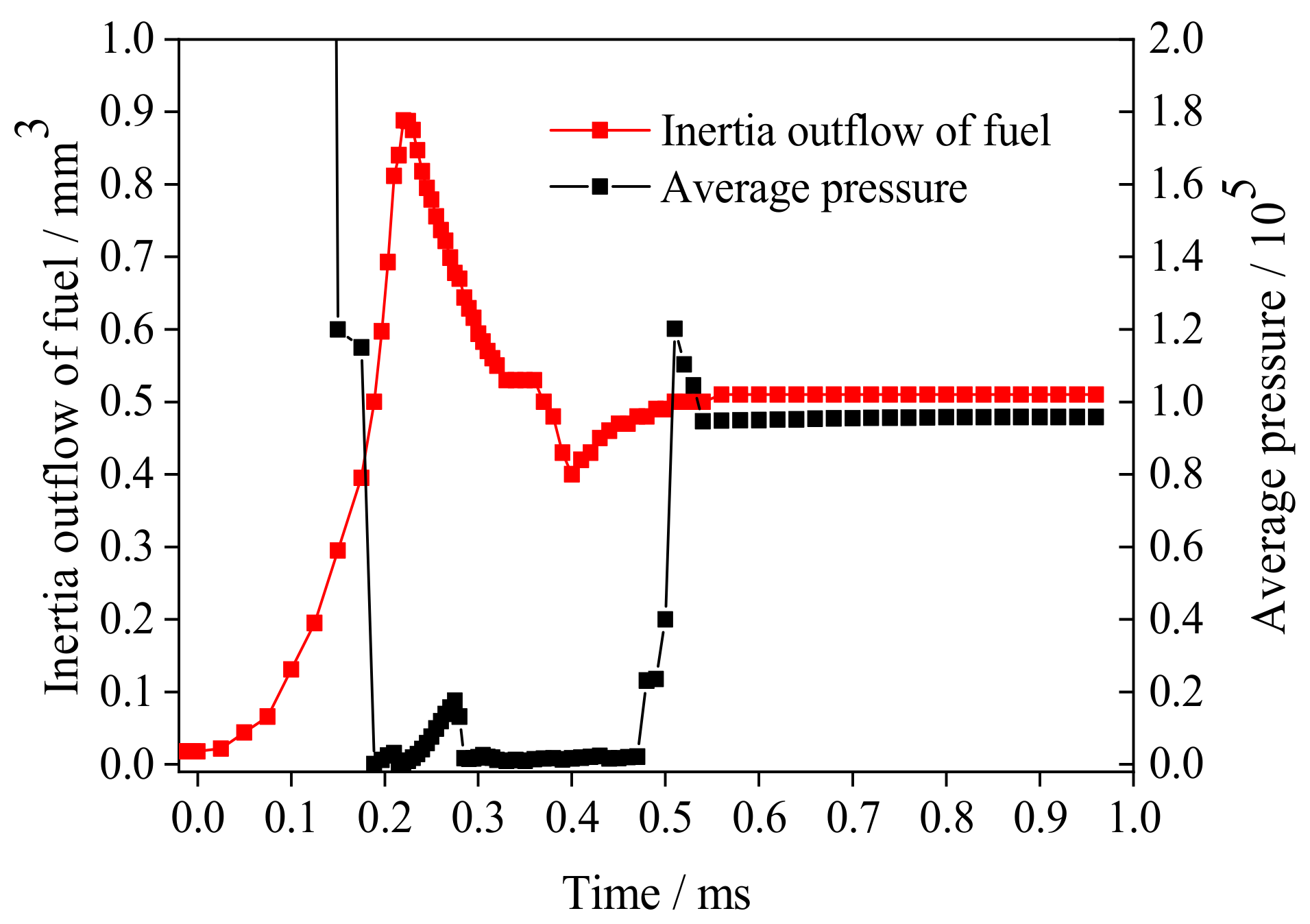
4.1. End of Injection (EOI)

Figure 5 represents the diesel volume fraction (the volume of diesel as a percentage of the fluid volume in the nozzle) in the nozzle at different measurement times at the EOI, and the value is shown in the color bar below. From this figure, it can be clearly observed that the experimental images are very similar to the proposed simulation. Before the needle valve was seated (i.e., 0.2 ms), corresponding to the cavitation occurs only in the orifice. The cavitation occurred in the sac later than in the orifice, and the super-cavitation appeared in the orifice from 0.25 ms.

At the beginning of the EOI, cavitation occurred at the orifice inlet, as shown by 0.02 ms. When the needle valve was seated, cavitation gradually developed along the orifice wall toward the outlet. This is because when the fuel entered the orifice from the sac, the flow direction and flow area of the fuel changed. As the cross-sectional area for the fuel flow was reduced, it caused the increase of flow velocity, which is called the throttling effect. When cavitation began to appear in the nozzle, it also meant that the pressure was already less than 2 kPa, which is the saturated vapor pressure of diesel. Analyzing the experiment and simulation results, from 0.15 ms to 0.25 ms, cavitation mainly extends along the orifice wall to the exit. This is because that the low-pressure zone was easily formed between the fluid boundary layer and wall boundary layer. However, the wall-attached flow was not obvious in the experimental nozzle until the middle of the needle valve was seated. Cavitation also appeared in the sac after 0.25 ms. This phenomenon meant that as the needle valve was seated, the cross-sectional area of the effective fuel flow near the sealing surface decreased, resulting in a decrease in pressure and an increase in velocity. Considering the viscous effect for the diesel, the speed of the real needle valve was different from that of the fuel. The result of this phenomenon was the same as the throttling effect, which led to cavitation. Assuming that the fluid in the nozzle was a continuous model, the central pressure of the vortex core gradually spread to the orifice, which led to a further decrease in orifice pressure and also meant an increase in cavitation.

With the development of cavitation, cavitation bubbles eventually penetrate the entire orifice, as is shown at 0.3 ms. This phenomenon is called super-cavitation. However, the cavitation in the sac was still not at its maximum. The stretching velocity of fuel in the sac was smaller than that in the orifice, while the stretching degree was larger, which caused more cavitation in the sac, and this meant the total amount of cavitation in the nozzle was mainly up to the sac. In addition, due to the influence of the aerodynamic force and the pressure wave in the nozzle, the cavitation at the nozzle outlet was extremely unstable, which made the cavitation bubble burst and caused gas ingestion. This phenomenon has also been reported by Guo [21].

4.2. After Injection (AI)

The diesel volume fraction AI is presented in Figure 6. From 0.40 ms onward, it can be seen that the external air enters the nozzle through the orifice outlet and finally extends into the sac. In this process, cavitation gradually decreased, and the gas ingestion bubbles increased. As can be seen from Figure 6, the zone colored in blue shows that gas ingestion gradually increased, and the area occupied by bright black also increased at the corresponding moment, i.e., the gas ingestion bubbles increased in the nozzle. This phenomenon can be further explained like this: as the cavitation extended to the outlet of the nozzle, under the action of the pressure wave and aerodynamic force, a dynamic pressure imbalance occurred between the external environment and the cavitation. The environmental pressure was greater than the internal pressure of the cavitation bubble, this differential pressure imbalance led to cavitation rupture, and then a new pressure imbalance was created, which resulted in the cavitation collapse [4]. From the simulation result, cavitation reached its maximum at 0.35 ms.

At 0.55 ms, the external air flowed back into the orifice inlet, and the cavitation in the orifice disappeared completely. At 0.8 ms, with the collapse of the cavitation in the sac, the external air also back-flowed into the sac. At 1.5 ms, the cavitation in the nozzle disappeared completely, the gas part in the nozzle was all ingestion gas. Due to surface tension, the gas ingestion bubbles began to fuse and became brighter, more transparent, and regular. When the nozzle was in the static state (2.0 ms), the gas ingestion bubbles were fully fused and occupied 3/4 of the length of the orifice.

In Figure 7, time-dependent changes in ingestion gas and cavitation in the nozzle are presented. Before 0.25 ms, the volume fraction of cavitation in the nozzle was mainly up to the orifice. After 0.25 ms, the total amount of cavitation in the nozzle depended on the sac, and the cavitation in the orifice began to collapse. However, at the initial stage of the EOI (0.2 ms), there was almost no cavitation in the sac. This indicated that cavitation more likely occurred in the orifice, instead of the sac, which further validated the analysis in Figure 6 and Figure 7. The cavitation in the nozzle was almost zero in the later stage of the EOI, and the maximum volume fraction of cavitation in the sac was close to that of ingestion gas. It is noteworthy that the growth rate of the volume fraction of the ingestion gas is $1.06·\times ·{10}^{-5}·/\mathrm{m}\mathrm{s}$, and the volume fraction reduction rate of cavitation is $-1.05·\times ·{10}^{-5}·/\mathrm{m}\mathrm{s}$; it was concluded that gas ingestion was mainly caused by cavitation collapse.

Figure 8 represents the time-dependent variations in fuel inertial outflow and in average pressure within the nozzle. At the beginning of the EOI, the pressure in the nozzle was high. As the fuel injection process progressed, the average pressure in the nozzle dropped rapidly and maintained a certain low pressure for a duration. Then the average pressure increased rapidly, which finally decreased slightly and remained constant. As seen from Figure 7, the duration in a lower pressure was the stage of cavitation development. The fuel inertia outflow increased in the cavitation development stage because there was a lower pressure in the nozzle and a strong pressure difference between the nozzle entrance and exit, thus increasing the fuel kinetic energy. It can be seen from Figure 7 and Figure 8, although the fuel inertial outflow increased at the beginning of the EOI, as the pressure difference decreased, impelling a decrease in the kinetic energy and inertial outflow of fuel, the cavitation amount decreased.

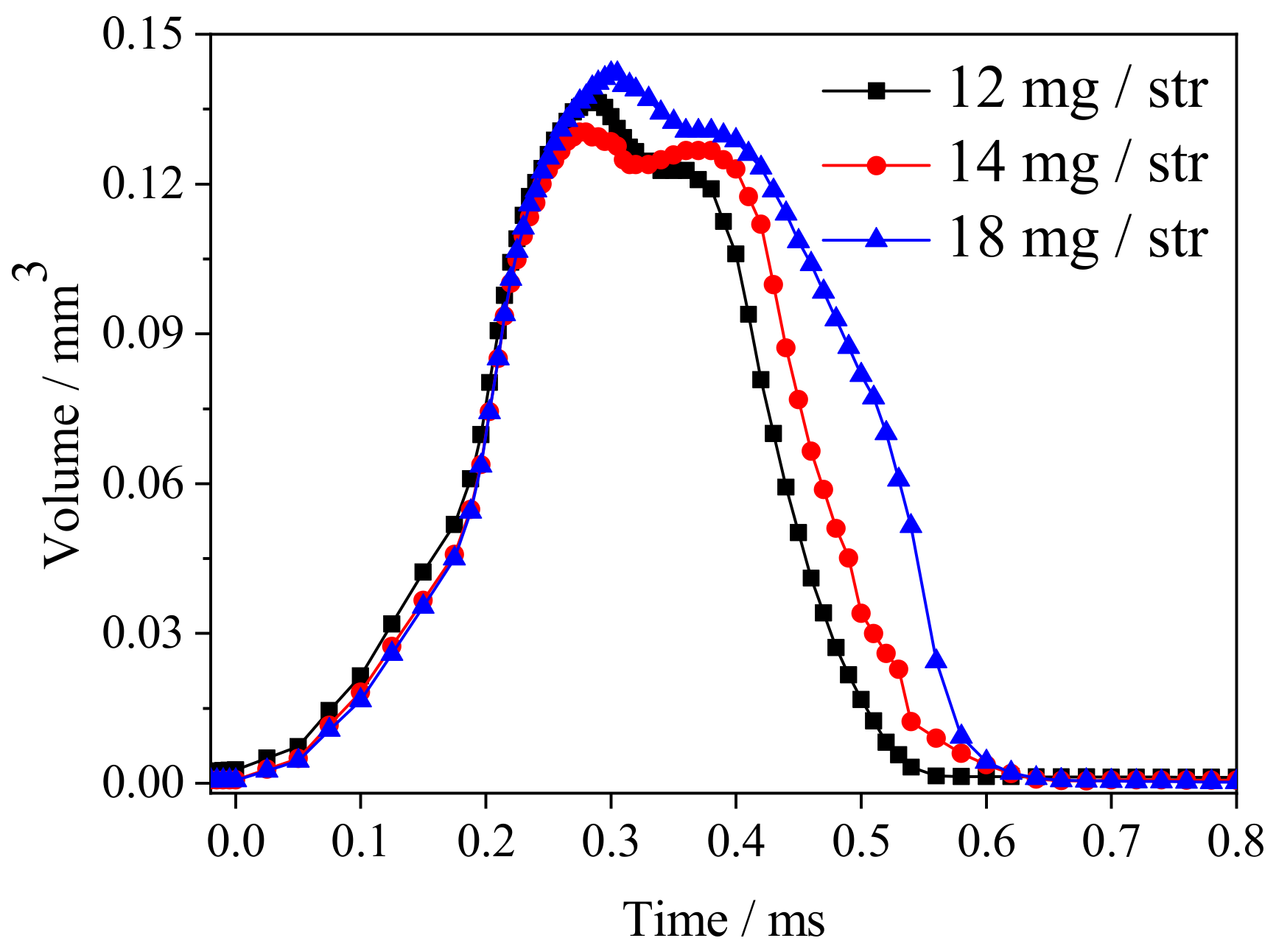
4.3. Influence of Mass Flux

In each complete working cycle, the amount of fuel injected into the internal combustion engine depended on the width of the fuel injection pulse. Nevertheless, during the experiment, the electronic control unit (ECU) could not control the width of the fuel injection pulse. It was controlled by fuel injection feedback, thus not only influencing fuel atomization but also affecting the engine power, economy, and emission performance.

Figure 9 and Figure 10 show the changes in gas volume fraction with time for various fuel mass fluxes (12 mg/str, 14 mg/str, 18 mg/str). As can be seen, the effect of mass flux on cavitation was not obvious at the beginning of the EOI, but it became obvious as the EOI progressed. The sac with a larger fuel mass flow had larger cavitation and lagged at the corresponding time. The reason for this was that because of the larger mass flux fuel with a greater inertia force, the kinetic energy of fuel increased sharply near the sealing surface of the needle valve and inlet of the orifice, resulting in the increased kinetic energy at the nozzle inlet, the rapidly decreased mass flow rate, and the fast velocity of the needle valve, thus making the cross-sectional area of fuel flow near the sealing surface reduce quickly. Therefore, considering the throttle effect and the fuel inertia outflow, a larger velocity and a lower pressure appeared, i.e., the higher fuel mass flux was, the greater cavitation was.

In Figure 9, cavitation in the nozzle reaches its maximum volume at 0.3 ms. The total cavitation had two peaks—the first time at 0.3 ms and the second time at 0.4 ms—which was caused by pressure waves in the nozzle. Analyzing Figure 9 and Figure 10, total cavitation in the nozzle was closed to that in the sac at three different mass fluxes, and the cavitation in the nozzle corresponding to three different mass fluxes was up to the sac after 0.4 ms. After 0.4 ms and until 0.6 ms, the larger the mass flux in the nozzle, the less cavitation reduction there was, which also meant more cavitation. This is because the higher the mass flux near the nozzle inlet was, the more obvious the stretching effect was, and the less viscous dissipation in the wall-attached layer flow was reduced, the more likely it was that the kinetic energy in the nozzle would produce a lower pressure zone. The higher the mass flux, the longer the low-pressure duration was.

Figure 11 shows the effect of different mass fluxes on gas ingestion. As can be seen, the bigger the mass flux, the longer the gas ingestion duration, and the greater the gas ingestion volume. This indicates that the larger mass flux could compensate for the viscous dissipation and stretching effect of fuel in the sac, resulting in lagged gas ingestion. Compared with Figure 10 and Figure 11, the time of cavitation collapse was synchronized with the time of gas ingestion increase, which proves that gas ingestion was mainly caused by cavitation collapse in the nozzle.

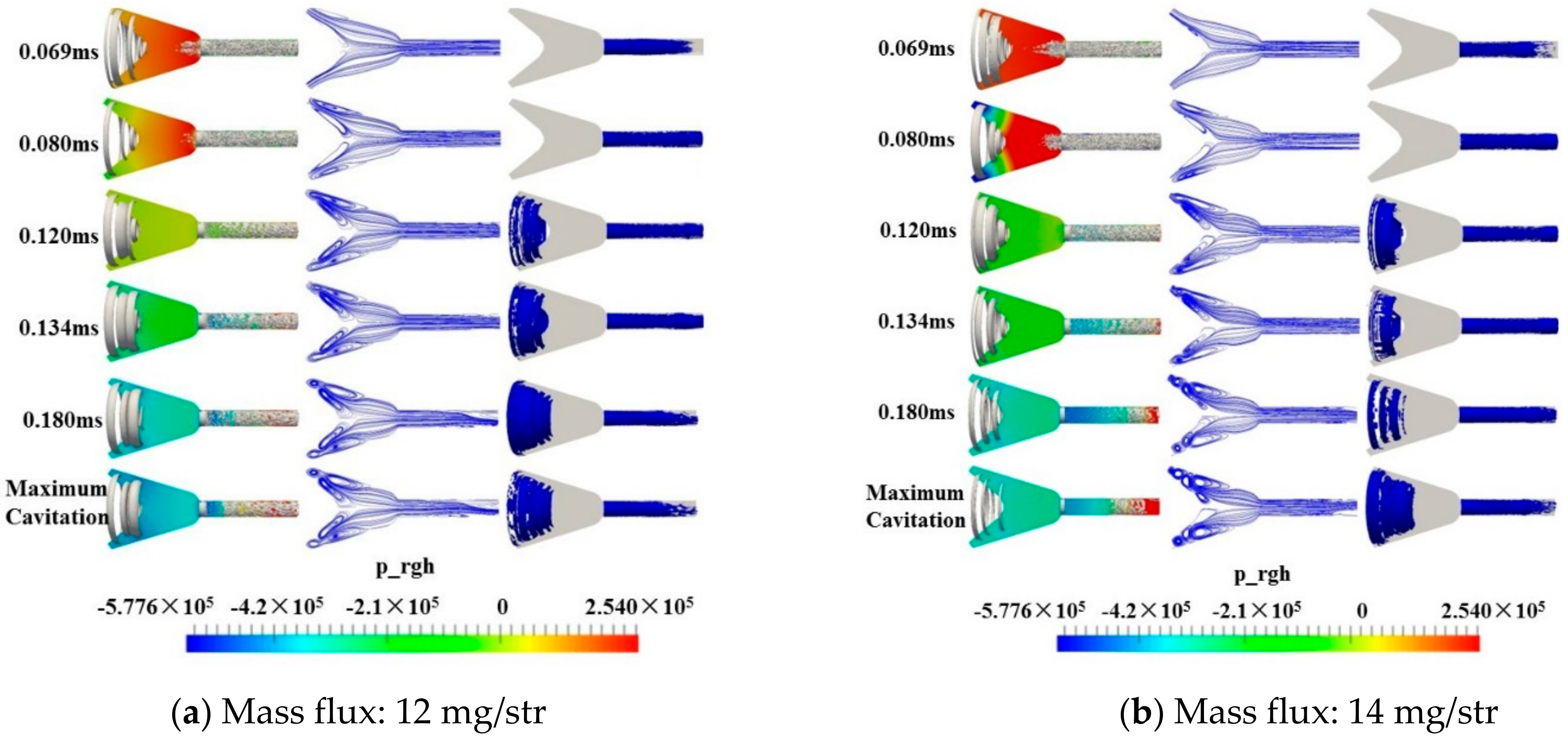
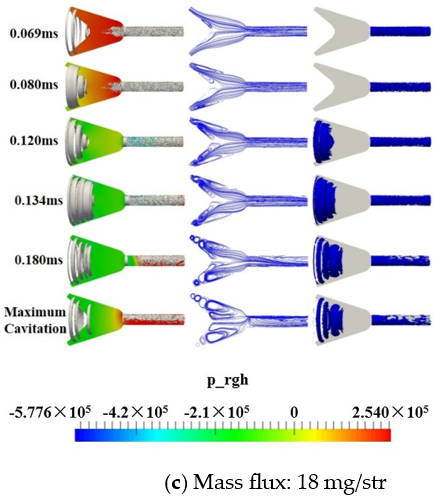
4.4. Analyzing the Cavitation Mechanism of Different Mass Fluxes

Figure 12 shows the distribution of Q = 2 × 10⁹ iso-surface, streamline, and α = 0.25 vapor iso-surface in the nozzle at different mass fluxes. From left to right are cloud pictures of Q = 2 × 10⁹ iso-surface, streamlines, and α = 0.25 vapor iso-surface, respectively. As can be seen, regardless of whether the mass flux was 12 mg/str, 14 mg/str, or 18 mg/str, the orifice always occurred cavitation first, the cavitation in the nozzle had similar morphology, and the sac was dominated by annular cavitation, while the orifice was bulk. In addition, the annular cavitation in the sac was mainly concentrated at the fuel inlet, then developed from the inlet toward the sac downstream but never reached the bottom of the sac.

At 0.069 ms, the streamline in the whole nozzle was relatively smooth, and cavitation occurred only in the orifice. Although there was a strong vortex movement in the sac at 0.08 ms, the vortex did not separate, and its structure was compact, i.e., at this temperature, the pressure in the sac did not drop to the saturated vapor pressure, therefore the sac was still turbulent. As the fuel continued to be injected, the strong vortex motion of the sac could be found in the streamline at three different mass flow rates. As previously shown, the core of the vortex had a higher velocity and was prone to form lower pressure zones, thus enhancing cavitation. The streamline separation in the nozzle corresponding to a mass flux of 18 mg/str was more obvious than the mass flow rates of 12 mg/str and 14 mg/str, and the vortex core morphology was larger. The vortex core morphology of the nozzle with a mass flow rate of 18 mg/str was more distorted than that of the other two. This is because the high mass flow nozzle sac corresponding velocity was higher, considering the viscous force between the fuel, therefore, the stretching effect was more obvious in the sac.

As the fuel injection further continued, the area occupied by the vapor iso-surface in the sac and the orifice increased gradually, i.e., the cavitation increased. The number of vortex cores in the sac increased, which was reflected by the enlargement of the iso-surface area in the nozzle on the Q iso-surface, and the iso-surface passed through the vortex core. This indicated that the surrounding pressure was higher than the central pressure of the vortex core, and the existence of the Q iso-surface was attributed to the internal and external pressure difference of the vortex core. At three different mass fluxes, the bulk cavitation was dominated in the orifice, and the annular cavitation caused by the end stretching was the major one in the conical nozzle sac.

To sum up, annular cavitation was dominant in the conical nozzle sac, and the orifice was dominated by bulk cavitation at different mass flow fluxes. Under a certain Q iso-surface, higher mass flow rates increased the stretching in the nozzle and subsequently the flow velocity, fuel inertial outflow, and cavitation.

5. Conclusions

In this paper, a high-speed framing camera was applied to capture fuel flow images in the nozzle consisting of a single straight orifice and a cone-shaped sac. In addition, a two-phase three-component numerical model was proposed, and the geometric size, initial conditions, and boundary conditions of the experimental nozzle were completely copied into the numerical model. The flow field of the EOI and AI inside the nozzle was calculated by OpenFOAM. Furthermore, because it is difficult to calculate the movement of the needle valve in OpenFOAM, the method of dynamic mass flux was used to replace needle valve movement to guarantee the rationality of the calculation result, which was consistent with the experimental results. Furthermore, the effects of different mass fluxes on gas ingestion and cavitation at the EOI and AI were analyzed. Some conclusions were as follows:

(1)

Cavitation and gas ingestion occurred sequentially in the nozzle, starting with the orifice and finishing in the sac. The sac played a major role in affecting the total amount of ingestion gas and cavitation. The maximum fuel inertial outflow and cavitation in the nozzle were crucial in determining the total fuel outflow.

(2)

The pressure difference between the pressure of the cavitation bubble and that of atmospheric pressure caused the cavitation collapse after the EOI, further generating external air to flow back into the nozzle. In addition, the gas ingestion bubbles in the nozzle began to fuse under the action of the surface tension after the EOI, and finally, its shape became regular.

(3)

The cavitation in the sac was mainly annular, and the orifice was mainly bulk cavitation. The cavitation in the sac concentrated on the nozzle inlet and developed downward. This was attributed to the fact that larger fuel mass increased the amount of gas ingestion and cavitation, and resulted in a longer deformation and fusion time for ingestion bubbles.