Robust Control of Electric Tail Reduction System: Uncertainty and Performance Index
Abstract
:1. Introduction
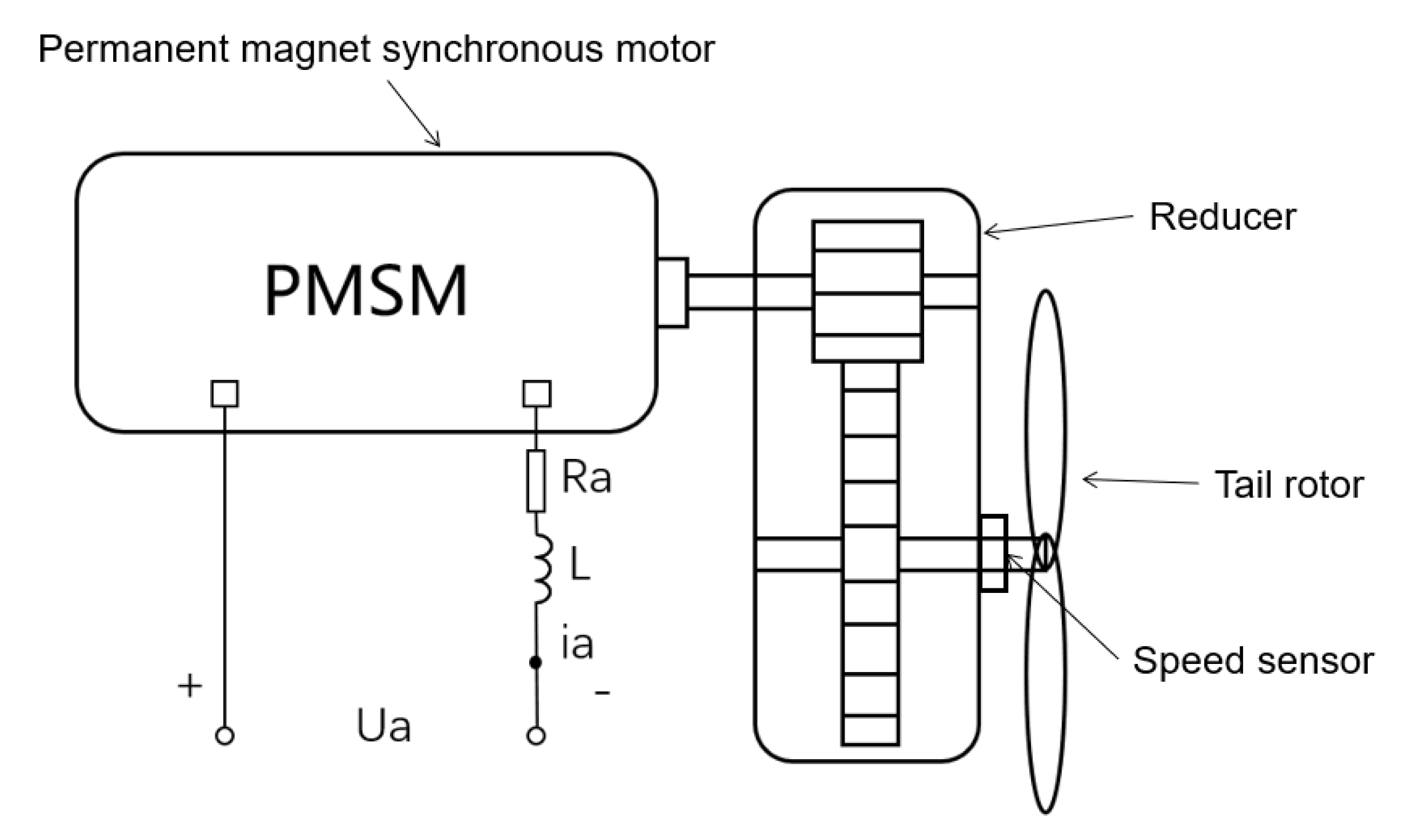
2. Dynamic Modeling of Electric Tail Reduction System
3. Robust Constraint Following Control
3.1. Uncertain Mechanical System
3.2. Robust Constraint Following Control Design
4. Performance Index and Optimization
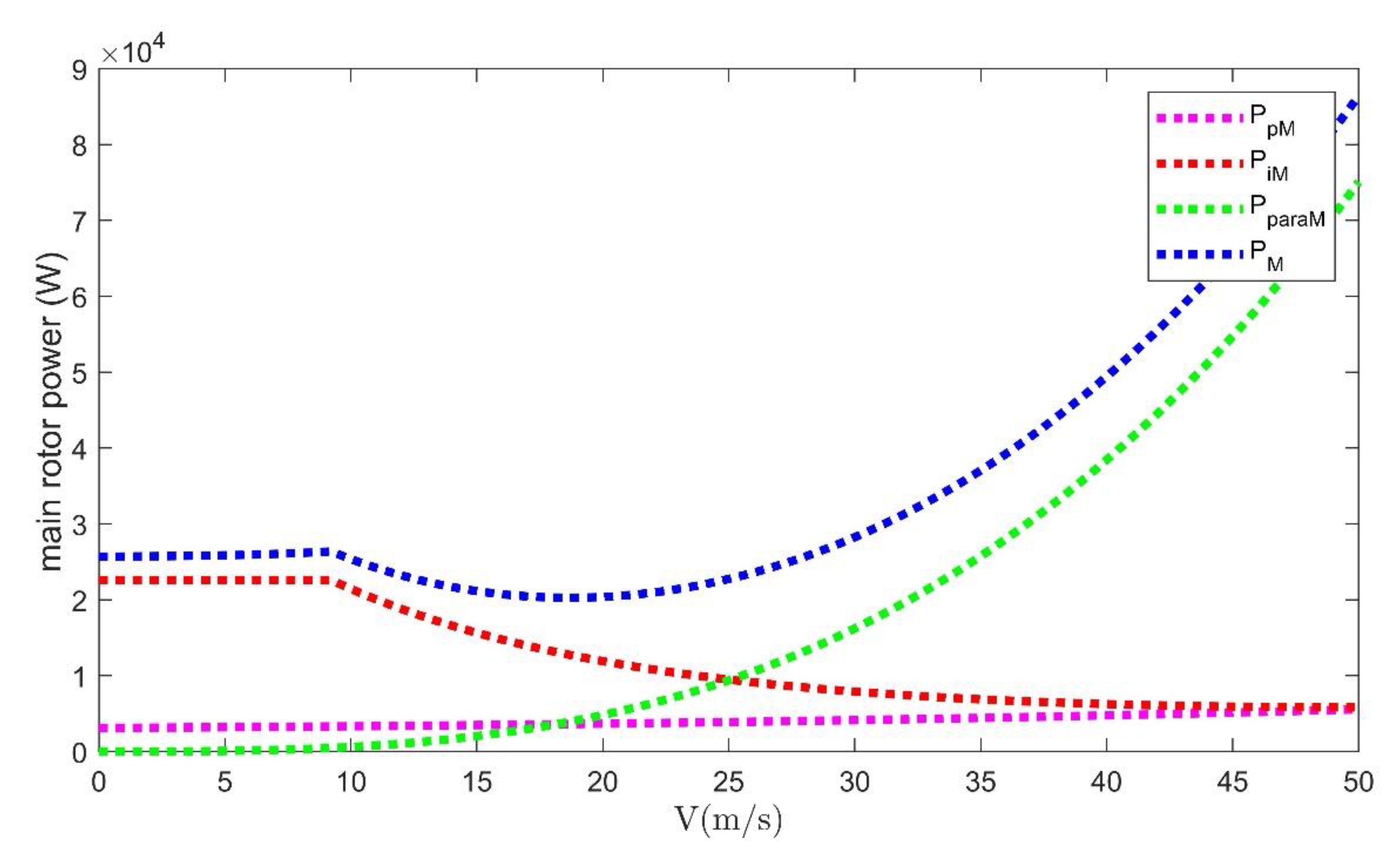
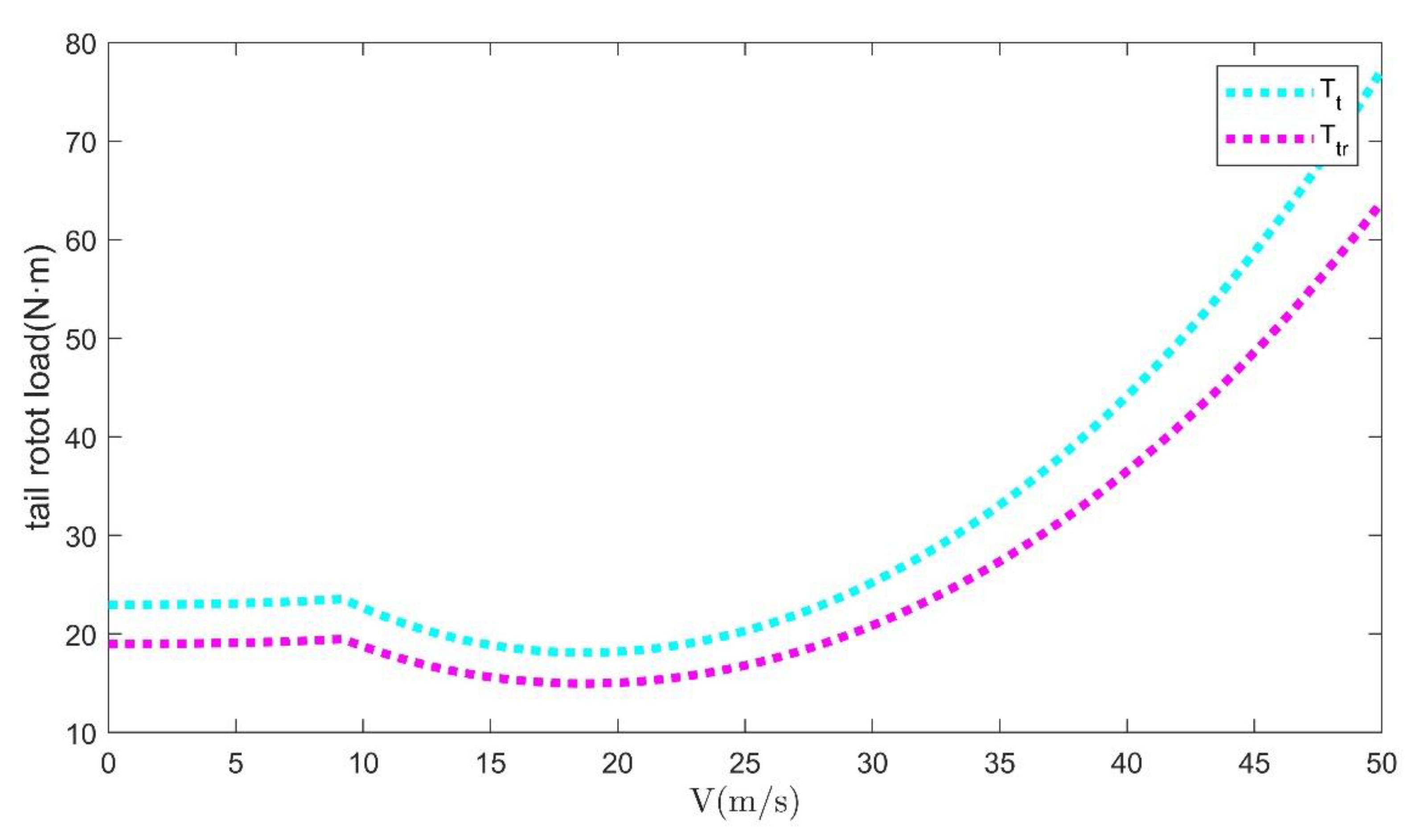
5. Numerical Simulation
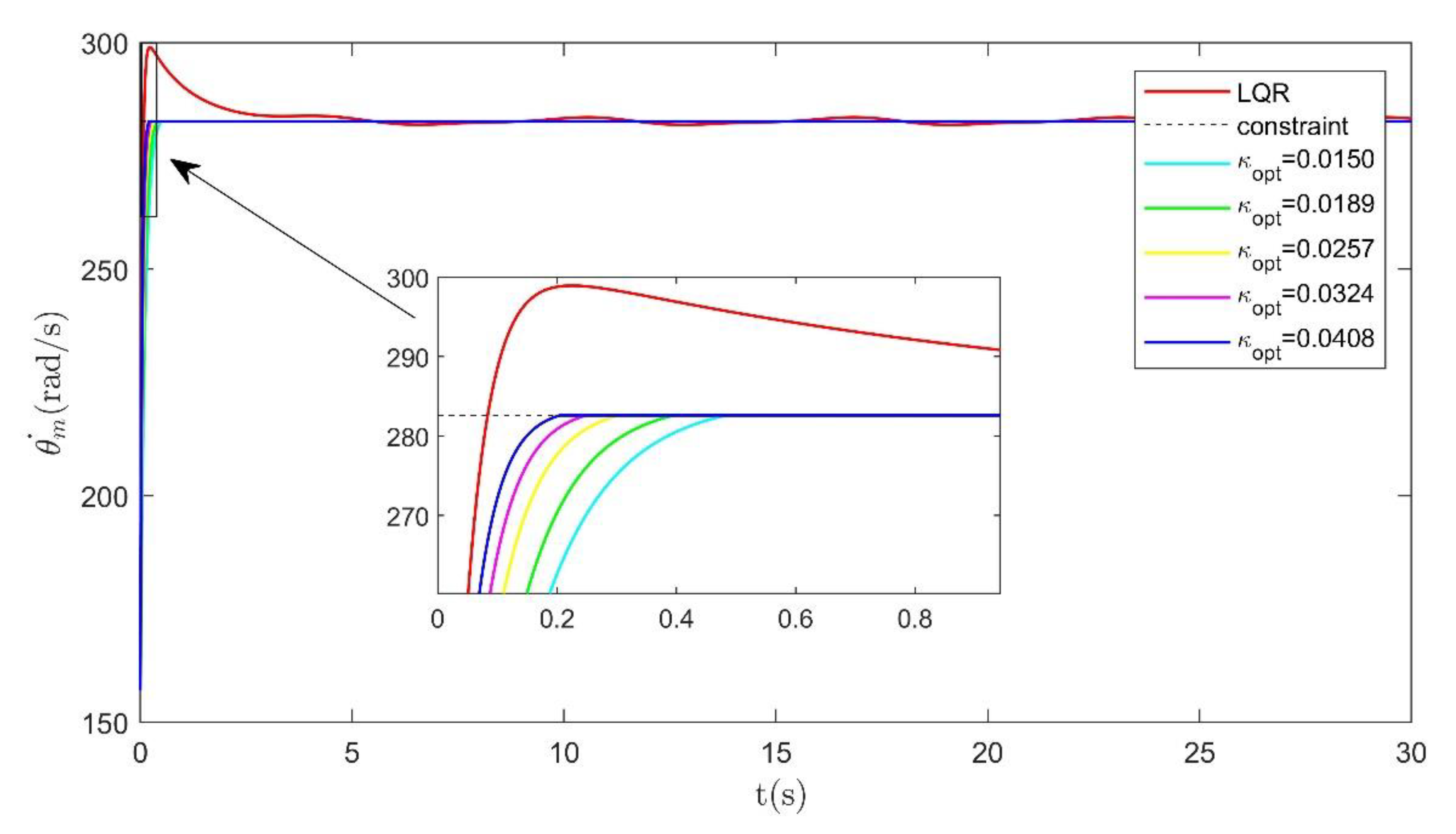
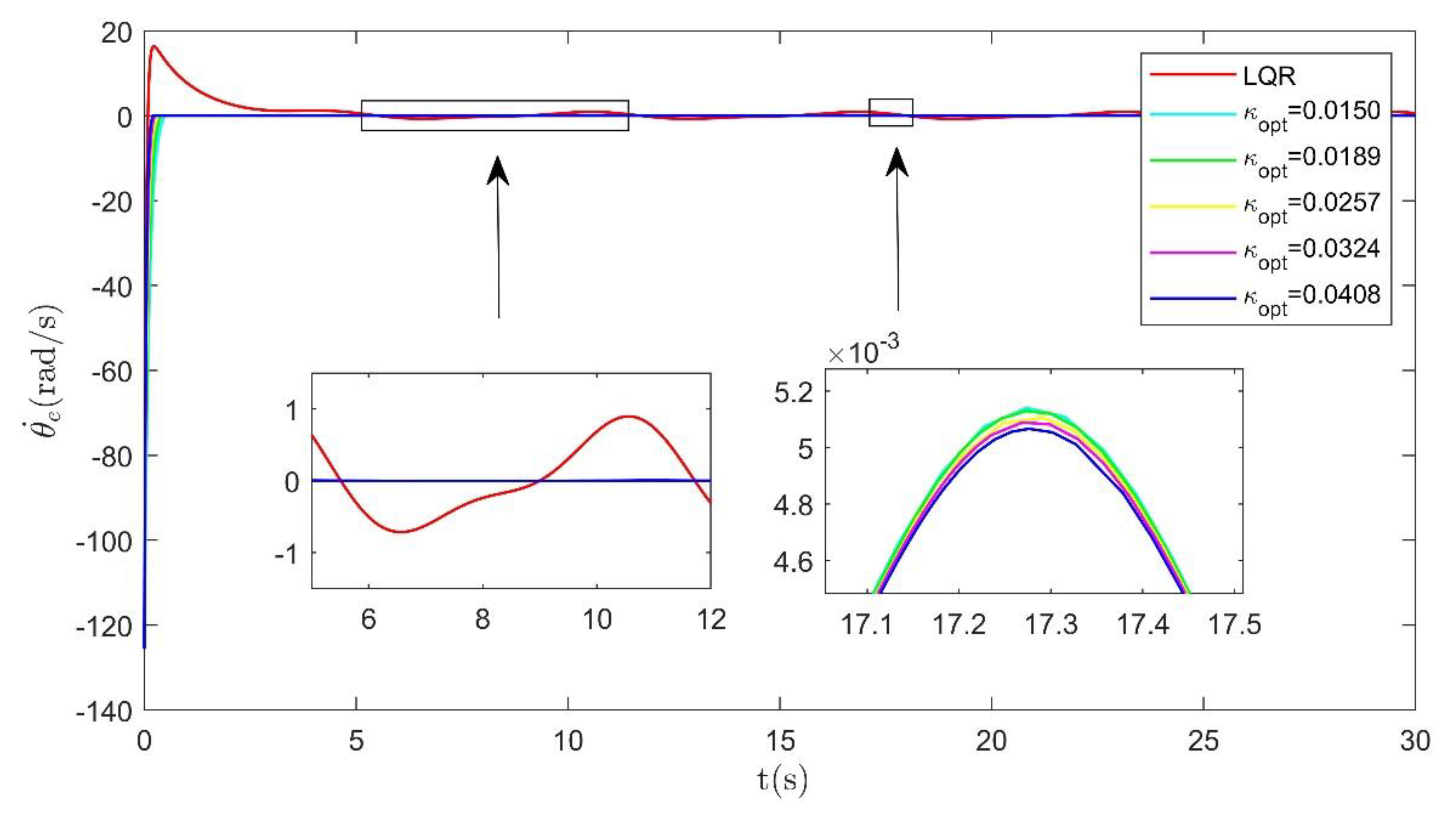
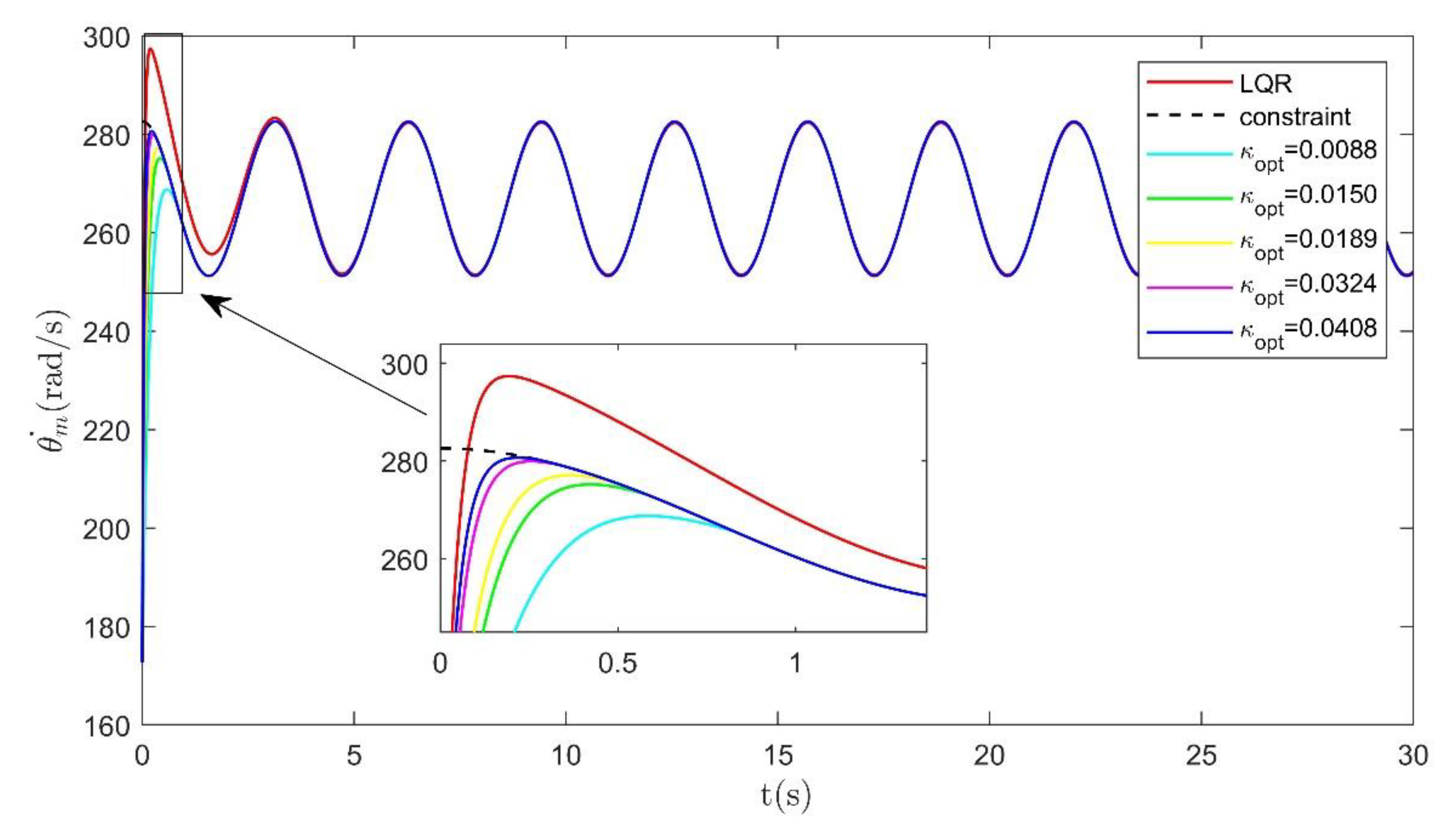
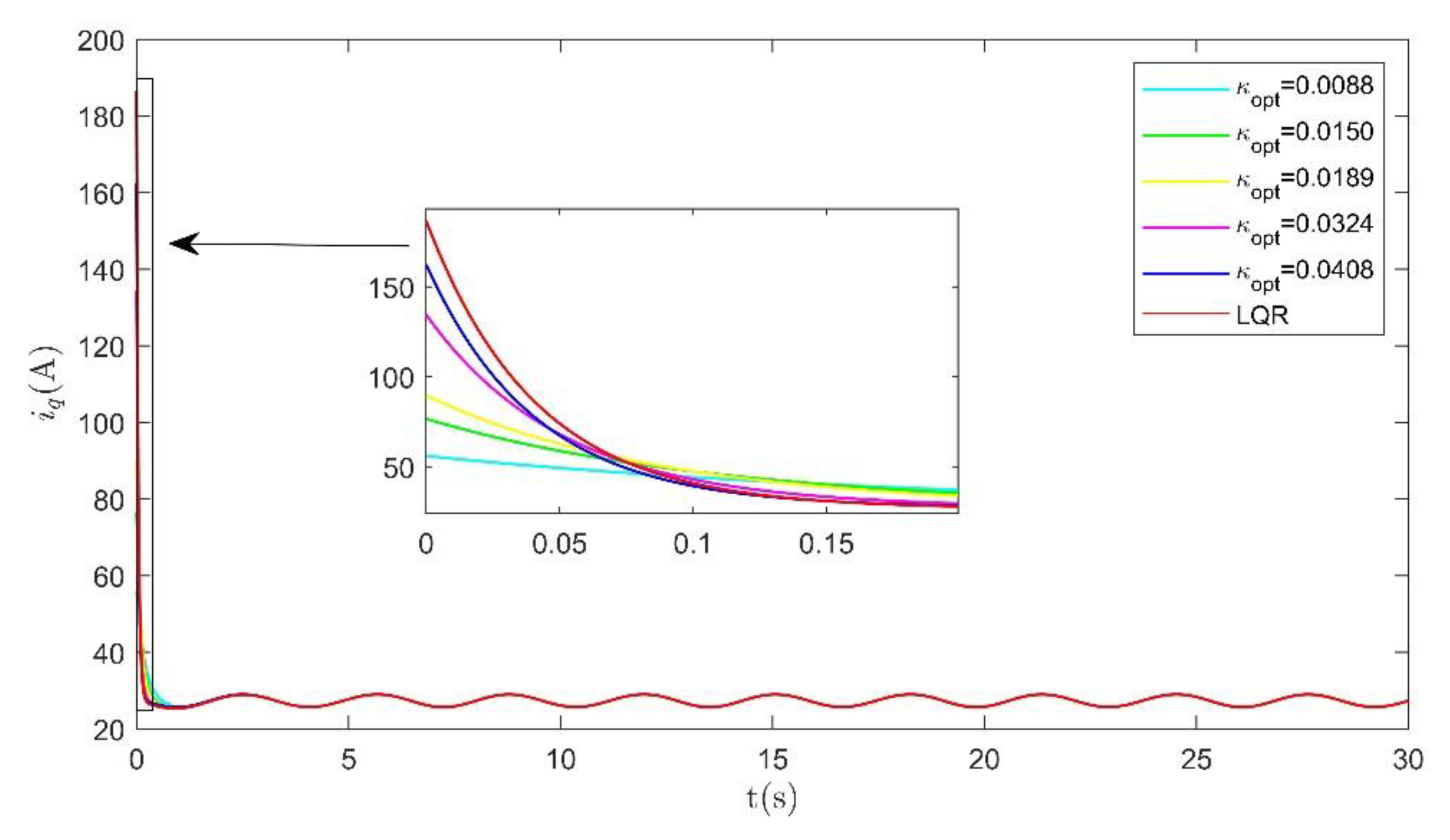
5.1. Step Response under Variable Load Condition
5.2. Sinusoidal Response under Constant Load Condition
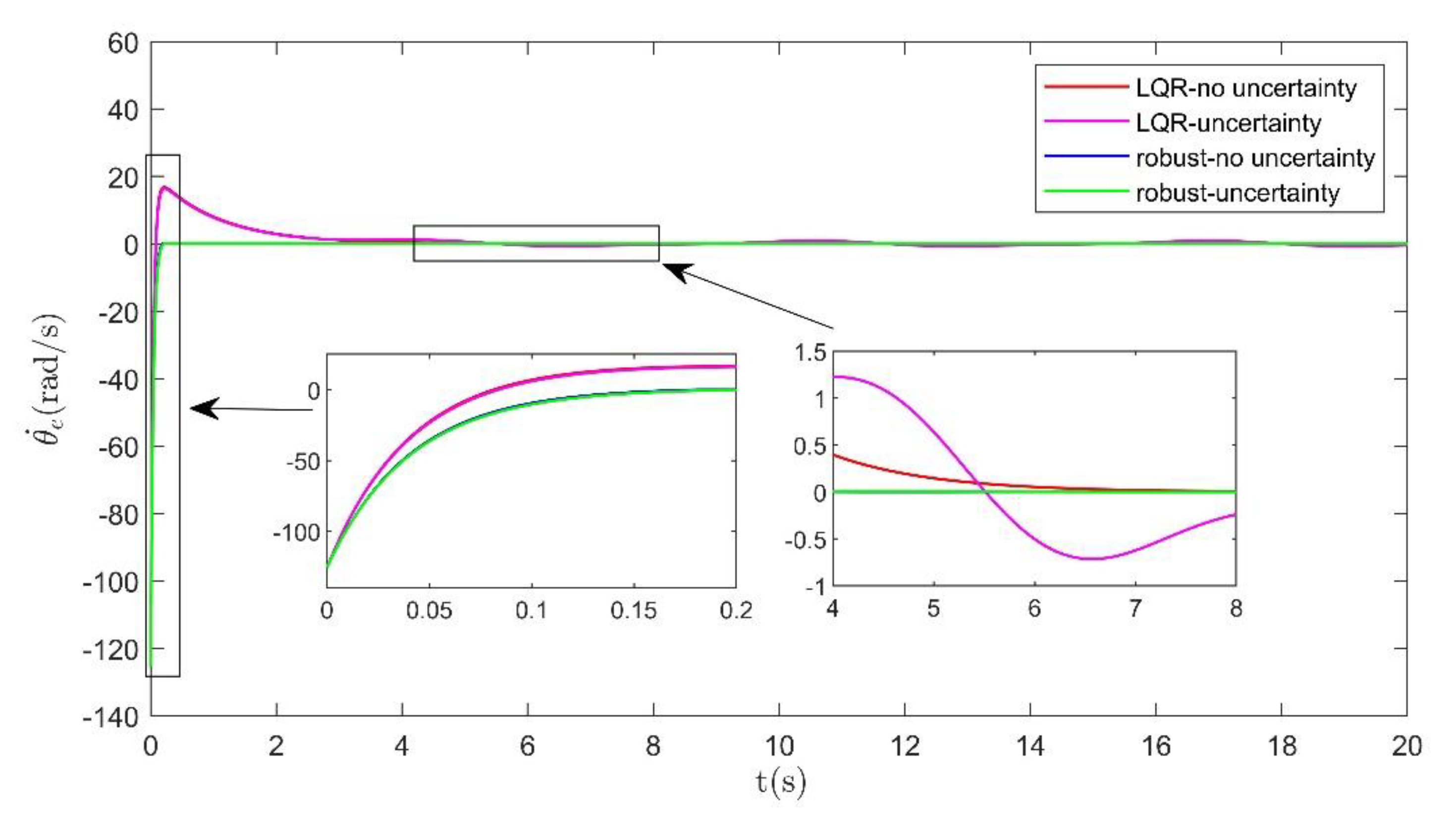
5.3. Tracking Response with Uncertainty or Not
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Alvarenga, J.; Vitzilaios, N.I.; Valavanis, K.P.; Rutherford, M.J. Survey of unmanned helicopter model-based navigation and control techniques. J. Intell. Robot. Syst. 2015, 80, 87–138. [Google Scholar] [CrossRef]
- Kendoul, F. Survey of advances in guidance, navigation, and control of unmanned rotorcraft systems. J. Field Robot. 2012, 29, 315–378. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, C.; Yunjie, W.A.; Fan, S.U.; Haowen, W.A. Design and application of an electric tail rotor drive control (ETRDC) for helicopters with performance tests. Chin. J. Aeronaut. 2018, 31, 1894–1901. [Google Scholar] [CrossRef]
- Zhou, J.; Khot, L.R.; Peters, T.; Whiting, M.D.; Zhang, Q.; Granatstein, D. Efficacy of unmanned helicopter in rainwater removal from cherry canopies. Comput. Electron. Agric. 2016, 2016, 161–167. [Google Scholar] [CrossRef] [Green Version]
- Ma, R.; Ding, L.; Wu, H. Dynamic decoupling control optimization for a small-scale unmanned helicopter. J. Robot. 2018, 2018, 9897684. [Google Scholar] [CrossRef] [Green Version]
- Sheng, Z.; Li, Y. Hybrid Robust Control Law with Disturbance Observer for High-Frequency Response Electro-Hydraulic Servo Loading System. Appl. Sci. 2016, 6, 98. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Chen, M.; Wu, Q. Robust control for an unmanned helicopter with constrained flapping dynamics. Chin. J. Aeronaut. 2018, 31, 2136–2148. [Google Scholar] [CrossRef]
- Sheng, S.; Sun, C. Design of a Stability Augmentation System for an Unmanned Helicopter Based on Adaptive Control Techniques. Appl. Sci. 2015, 5, 575–586. [Google Scholar] [CrossRef] [Green Version]
- Yan, K.; Chen, M.; Wu, Q.; Wang, Y. Adaptive flight control for unmanned autonomous helicopter with external disturbance and actuator fault. J. Eng. 2019, 2019, 8359–8364. [Google Scholar] [CrossRef]
- Yan, K.; Wu, Q.X.; Chen, M. Robust adaptive backstepping control for unmanned autonomous helicopter with flapping dynamics. In Proceedings of the 2017 13th IEEE International Conference on Control & Automation (ICCA), Ohrid, Macedonia, 3–6 July 2017; pp. 1027–1032. [Google Scholar]
- Chen, N.; Huang, J.; Zhou, Y. Adaptive sliding mode for path following control of the unmanned helicopter based on disturbance compensation techniques. In Proceedings of the 2017 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 2670–2677. [Google Scholar]
- Suzuki, S.; Nakazawa, D.; Nonami, K.; Tawara, M. Attitude control of small electric helicopter by using quaternion feedback. J. Syst. Des. Dyn. 2011, 5, 231–247. [Google Scholar] [CrossRef] [Green Version]
- Jiang, T.; Lin, D.; Song, T. Finite-time control for small-scale unmanned helicopter with disturbances. Nonlinear Dyn. 2019, 96, 1–17. [Google Scholar] [CrossRef]
- Mu, D.; Wang, G.; Fan, Y.; Bai, Y.; Zhao, Y. Fuzzy-based optimal adaptive line-of-sight path following for underactuated unmanned surface vehicle with uncertainties and time-varying disturbances. Math. Probl. Eng. 2018, 2018, 7512606. [Google Scholar] [CrossRef] [Green Version]
- Wang, K.; Rong, H.; Shi, M.; Meng, Z.; Zhou, Y. Reactive obstacle avoidance for unmanned helicopter using fuzzy control. In Proceedings of the 37th Chinese Control Conference, Wuhan, China, 25 July 2018; pp. 10026–10031. [Google Scholar]
- Yuan, Y.; Thomson, D.; Chen, R.L.; Dunlop, R. Heading control strategy assessment for coaxial compound helicopters. Chin. J. Aeronaut. 2019, 32, 2037–2046. [Google Scholar] [CrossRef]
- Han, D.; Barakos, G.N. Variable-speed tail rotors for helicopters with variable-speed main rotors. Aeronaut. J. 2017, 121, 433–448. [Google Scholar] [CrossRef] [Green Version]
- Rajendran, S.; Gu, D.W. Fault tolerant control of a small helicopter with tail rotor failures in forward flight. IFAC Proc. Vol. 2014, 47, 8843–8848. [Google Scholar] [CrossRef]
- Fletcher, T.M.; Brown, R.E. Main rotor-tail rotor interaction and its implications for helicopter directional control. J. Am. Helicopter Soc. 2008, 53, 125–138. [Google Scholar] [CrossRef] [Green Version]
- Truong, H.V.A.; Tran, D.T.; To, X.D.; Ahn, K.K.; Jin, M. Adaptive Fuzzy Backstepping Sliding Mode Control for a 3-DOF Hydraulic Manipulator with Nonlinear Disturbance Observer for Large Payload Variation. Appl. Sci. 2019, 9, 3290. [Google Scholar] [CrossRef] [Green Version]
- Iqbal, J.; Zuhaib, K.M.; Han, C.; Khan, A.M.; Ali, M.A. Adaptive Global Fast Sliding Mode Control for Steer-by-Wire System Road Vehicles. Appl. Sci. 2017, 7, 738. [Google Scholar] [CrossRef]
- Udwadia, F.E.; Kalaba, R.E. A new perspective on constrained motion. Proceedings of the Royal Society. Math. Phys. Sci. 1992, 439, 407–410. [Google Scholar]
- Kalaba, R.E.; Udwadia, F.E. Lagrangian mechanics, Gauss’s principle, quadratic programming, and generalized inverses: New equations for nonholonomically constrained discrete mechanical systems. Q. Appl. Math. 1994, 52, 229–241. [Google Scholar] [CrossRef] [Green Version]
- Udwadia, F.E.; Kalaba, R.E. Analytical Dynamics: A New Approach; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Udwadia, F.E.; Kalaba, R.E. Explicit equations of motion for mechanical systems with nonideal constraints. J. Appl. Mech. 2001, 68, 462–467. [Google Scholar] [CrossRef] [Green Version]
- Udwadia, F.E. A new perspective on the tracking control of nonlinear structural and mechanical systems. Math. Phys. Eng. Sci. 2003, 459, 1783–1800. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y. Equations of motion of mechanical systems under servo constraints: The Maggi approach. Mechatronics 2008, 18, 208–217. [Google Scholar] [CrossRef]
- Zhao, H.; Zhen, S.; Chen, Y. Dynamic modeling and simulation of multi-body systems using the Udwadia-Kalaba theory. Chin. J. Mech. Eng. 2013, 26, 839–850. [Google Scholar] [CrossRef]
- Sun, H.; Zhao, H.; Zhen, S.; Huang, K.; Zhao, F.; Chen, X.; Chen, Y.H. Application of the Udwadia-Kalaba approach to tracking control of mobile robots. Nonlinear Dyn. 2016, 2016, 389–400. [Google Scholar] [CrossRef]
- Sun, H.; Zhao, H.; Huang, K.; Qiu, M.; Zhen, S.; Chen, Y.H. A fuzzy approach for optimal robust control design of automotive electronic throttle system. IEEE. Trans. Fuzzy Syst. 2018, 26, 694–704. [Google Scholar] [CrossRef]
- Li, C.; Chen, Y.H.; Sun, H.; Zhao, H. Optimal design of high-order control for fuzzy dynamical systems based on the cooperative game theory. IEEE. Trans. Cybern. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Li, C.; Zhao, H.; Sun, H.; Chen, Y. Robust bounded control for nonlinear uncertain systems with inequality constraints. Mech. Syst. Signal Process. 2020, 140, 106665. [Google Scholar] [CrossRef]
- Dong, F.; Chen, Y.; Zhao, X. Optimal design of adaptive robust control for fuzzy swarm robot systems. Int. J. Fuzzy Syst. 2019, 21, 1059–1072. [Google Scholar] [CrossRef]
- Sun, H.; Yu, R.; Chen, Y.; Zhao, H. Optimal design of robust control for fuzzy mechanical systems: Performance-based leakage and confidence-index measure. IEEE. Trans. Fuzzy Syst. 2019, 27, 1441–1455. [Google Scholar] [CrossRef]
- Chen, Y. Second-order constraints for equations of motion of constrained systems. IEEE/ASME Trans. Mechatron. 1998, 3, 240–248. [Google Scholar] [CrossRef]
- Maxwell, J.C. A treatise on electricity and magnetism 2. Nature 2010, 7, 478–480. [Google Scholar]
- Newman, S.J. Methods of Calculating Helicopter Power, Fuel Consumption and Mission Performance; Technical Report; University of Southampton: Southampton, UK, 2011. [Google Scholar]
- Chen, Y.; Zhang, X. Adaptive robust approximate constraint-following control for mechanical systems. J. Frankl. Inst. 2010, 347, 69–86. [Google Scholar] [CrossRef]
- Zhao, X.; Chen, Y.; Zhao, H.; Dong, F. Udwadia-Kalaba Equation for Constrained Mechanical Systems: Formulation and Applications. Chin. J. Mech. Eng. 2018, 31, 106. [Google Scholar] [CrossRef] [Green Version]
- Zhen, S.; Huang, K.; Sun, H.; Zhao, H.; Chen, Y. Dynamic modeling and optimal robust approximate constraint following control of constrained mechanical systems under uncertainty: A fuzzy approach. J. Intell. Fuzzy Syst 2015, 2015, 777–789. [Google Scholar] [CrossRef]
- Chen, Y. On the deterministic performance of uncertain dynamical systems. Int. J. Control 1986, 43, 1557–1579. [Google Scholar] [CrossRef]


| Parameter | Value | Unit |
|---|---|---|
| 6 | / | |
| 0.09 | Wb | |
| 0.0408 | kg·m2 | |
| 0.01 | N·m·s/rad | |
| 1.3 | / | |
| 0.93 | / | |
| 0.05 | / | |
| 1.6 | / | |
| 89.6 | rad/s | |
| 1.2319 | kg·m3 | |
| 1.93 | m | |
| 1 | / | |
| 0.04758 | / | |
| 0.65 | / | |
| 1.5 | m2 | |
| 1 | / | |
| 250 | kg |
| 100/10 | 0.0150 | 0.0068 |
| 50/10 | 0.0189 | 0.0054 |
| 20/10 | 0.0257 | 0.0040 |
| 10/10 | 0.0324 | 0.0031 |
| 5/10 | 0.0408 | 0.0025 |
| 500/10 | 0.0088 | 0.0116 |
| 100/10 | 0.0150 | 0.0068 |
| 50/10 | 0.0189 | 0.0054 |
| 10/10 | 0.0324 | 0.0031 |
| 5/10 | 0.0408 | 0.0025 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, K.; Ma, C.; Zhao, H.; Zhu, Z. Robust Control of Electric Tail Reduction System: Uncertainty and Performance Index. Appl. Sci. 2021, 11, 260. https://doi.org/10.3390/app11010260
Huang K, Ma C, Zhao H, Zhu Z. Robust Control of Electric Tail Reduction System: Uncertainty and Performance Index. Applied Sciences. 2021; 11(1):260. https://doi.org/10.3390/app11010260
Chicago/Turabian StyleHuang, Kang, Chao Ma, Han Zhao, and Zicheng Zhu. 2021. "Robust Control of Electric Tail Reduction System: Uncertainty and Performance Index" Applied Sciences 11, no. 1: 260. https://doi.org/10.3390/app11010260
APA StyleHuang, K., Ma, C., Zhao, H., & Zhu, Z. (2021). Robust Control of Electric Tail Reduction System: Uncertainty and Performance Index. Applied Sciences, 11(1), 260. https://doi.org/10.3390/app11010260





