1. Introduction
Since the development of helicopter technology, it is increasingly difficult to balance the aerodynamic performance of hovering and high-speed flight with fixed speeds. Variable-speed transmissions will be an effective way to promote the performance of high-speed helicopters. As the core component of the variable-speed helicopter transmission system, the aviation friction clutch plays an important role in the helicopter take-off and variable-speed shifting process, and the wear of the clutch directly affects the service life of the clutch. Therefore, the mechanism and the change law of the friction pair and the calculation method of the relative slip distance of the disks in the clutch engagement process were studied, and some of the existing problems in the current aviation clutch were solved, which are the basis for improving the life of the aviation wet clutch and also for guaranteeing the safety of the aviation wet clutch.
Greenwood and Williamson [
1] assumed that the rough surface is composed of a large number of asperities with equal radius of curvature, highly randomly distributed, spherical peaks, and isotropic. Based on statistical analysis, they proposed an elastic contact model between rough and smooth surfaces. Menga and Ciavarella [
2] optimized the Archard model by assuming the Winkler constant to adapt to changes in contact size. David G. Lewicki and Hans DeSmidt [
3] conducted dynamic simulation analysis and experimental verification on the two-stage gearbox and established a dynamic model of the transmission system and a model of clutch stick–slip friction and wear. They found that the dynamic model of the transmission system was very consistent with the experimental results, especially in terms of speed, torque, and current, which were within 10% of the experimental data. Markus Kneissler [
4] established a wear model of automobile friction disks and determined the difference by comparing the initial clutch engagement process and the clutch engagement process after running-in, respectively. Then, he used the difference to determine the friction disks’ wear in order to reliably determine the wear of the friction disk within a short interval, so as to prevent the function of the friction disks from decreasing due to the fact of wear and affecting the wear calculation. Zhang Zhigang [
5] analyzed the wear of the wet clutch during the engagement process based on the Reynolds equation and the rough surface contact model. The influence of the plastic wear coefficient and the elastic wear coefficient on the overall friction disk wear was considered, but the influence of the running-in number was not considered. Based on the total sliding distance of the friction pair and Archard wear theory, AV Dimaki [
6] simulates the specific engagement time during the engagement process of the friction pair. Wang Liyong [
7] calculated the friction disk wear by regarding the sliding distance as the product of speed and time directly and carried out the test on the clutch bench in accordance with the wet clutch friction element test method. Li Le [
8] studied the influence of the friction disk contact ratio on the wear by regarding the sliding distance and time as a proportional relationship and analyzed the quantitative relationship between the friction disk and wear with different contact ratios.
In conclusion, most of the calculations of the surface wear of friction disks were measured by theoretical calculations or directly through experiments, especially the pin experiment, that is, the fixed pin cannot move, and the friction disk rotates. As for the Archard model, the sliding distance is regarded as the product of rotational speed and time. In the actual work of the friction clutch, the active disk engages with the driven piece with the initial speed difference. The speed of the active disk is reduced, and the speed of the driven disk is increased; then, the speed is completely consistent and the engagement process is completed. The sliding distance in the engagement process is nonlinear and time-varying, and the linearly changing sliding distance in the pin–disk experiment cannot accurately reflect the actual situation. Therefore, this paper proposes a method to calculate the actual sliding distance of friction pairs and which can calculate the nonlinear time-varying sliding distance in the process of friction pair jointing, solving the actual wear of friction pairs. For different groove-shaped friction disks, this paper calculates the amount of wear on friction disks during a single engagement, determines which groove shapes produce less wear during actual working conditions, and uses friction disks with different groove shapes to carry out wear tests on the test machine, demonstrating the accuracy of the theoretical calculations and providing references for the design and analysis of friction clutches.
2. Bearing Capacity Analysis of a Friction Pair Engaging Process
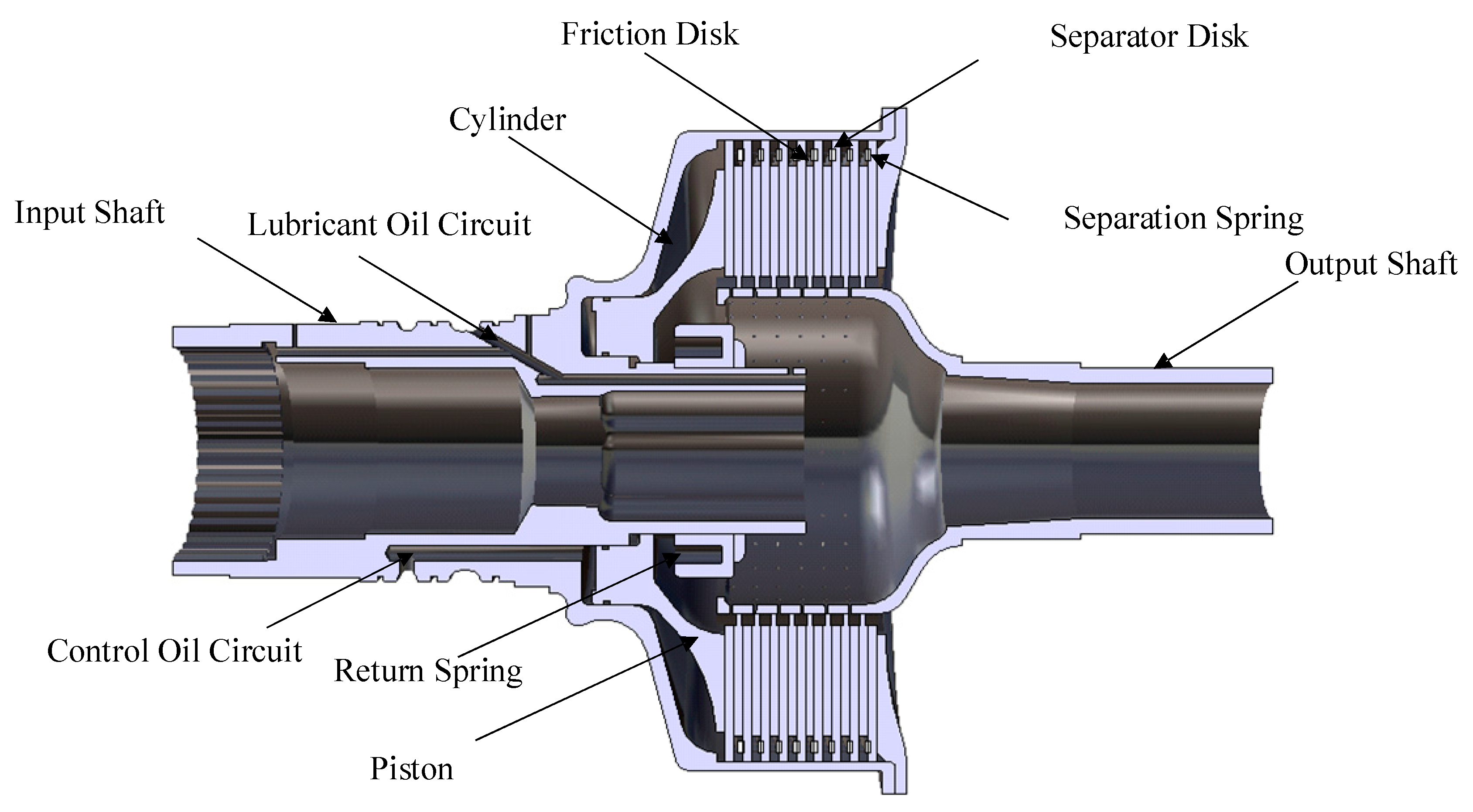
Taking the aviation wet multi-chip clutch as the research object, the friction and wear of friction pairs in the relative sliding grinding process was studied. The wet multi-chip friction clutch mainly includes friction disks, dual steel disks, oil cylinders, separation springs, pistons, back-position springs, control channels, input shafts, output shafts, and other structures, as shown in
Figure 1.
Due to the high-safety and lightweight requirements of helicopter components, the wet friction clutch is mostly thin-walled, and the shaft lubrication is carried out with a multi-channel shaft. Hydraulic oil and lubricant oil enter the input shaft from different channels that apply pressure to the piston and lubricate the bearing. When the hydraulic oil is pressed, the back spring is compressed and the extrusion steel disk is close to the right, that is, the clutch is in an engagement state. At this time, the relative displacement between the disks causes wear due to the different rotation speed differences. When the hydraulic oil is decompressed from the control channel, the back spring causes the piston to reset, and the separation spring between the steel disk and the friction disk promotes its separation.
When the friction disk comes into contact with the dual steel disk, due to the rough surface, the actual contact is only on a very small part of the apparent area. The shape of the rough peak on the actual surface is usually an elliptical body. Because the size of the contact area of the elliptical body is much smaller than its own curvature radius, the rough peak can be approximated to a sphere, and the contact between the two planes can be approximated to a series of uneven spheres. The contact between the two elastomers can be converted into the contact between a rigid smooth plane with an equivalent curvature radius, R, and an equivalent elastic modulus, E’.
As shown in
Figure 2, in the interface contact lubrication of friction disks, the nominal contact area includes two different types of contact: the fluid lubrication area because of the lubricant oil film and the real contact area of the micro-convex body. The total load is borne by the lubricating oil film and micro-convex body contact.
2.1. Bearing Capacity Model of the Clutch Friction Pair
2.1.1. Unimodal Contact Area Model
As shown in
Figure 3, when the two rough peaks are in full elastic contact, the normal deformation
δ will be generated under the action of the load
W, which makes the shape of the elastic sphere change from a dotted line to a solid line. The actual contact area is a circle with radius
a, not a circle with radius
e [
9].
According to Hertz contact theory,
From the above relationship, we can get:
. Thus, the actual contact area
A is
According to the geometric relationship:
Therefore, the geometric contact area
A0 is:
According to the principle of tribology, the profile height of the asperities on the surface of the friction lining is close to the Gauss distribution law. The Gauss probability distribution density function is .
Figure 4a shows the contact between the two rough surfaces of the friction lining and the mating steel sheet. The root mean square values of the two surface roughnesses are
and
, respectively, and
h is the distance between the center lines. Their contact can be converted into a smooth rigid surface and a rough elastic surface with a root mean square value of
, as shown in
Figure 2,
Figure 3, and
Figure 4b.
In
Figure 4b, when the distance between the center lines is
h, only the part of the profile height will be in contact. In the probability density distribution curve, the part area is the probability of surface contact, namely
2.1.2. Elastic Contact Stage
Due to the normal deformation,
is small enough that the micro-convex bodies on the friction disk undergo elastic deformation. The contact load,
W, the actual contact area,
A, and the average contact pressure,
pc, at this stage can be expressed as follows [
9]:
where
,
and
are Poisson’s ratios of the materials,
E1 and
E2 are the elastic modulus, and rigid plane
E2→+∞.
Based on the calculation of plastic deformation, it is shown that, when the average pressure reaches
H/3 (
H is the Boolean hardness value of the material), the micro-convex bodies begin to enter the plastic deformation stage. According to Formula (3), the critical value of the normal deformation of the micro-convex bodies from elastic deformation to elastic–plastic deformation is as follows:
when
, elastic deformation of the micro-convex bodies occurs; when
, the micro-convex bodies undergo elastic–plastic deformation or complete plastic deformation.
2.1.3. Complete Plastic Contact Stage
When the average pressure increases to
H, all micro-convex bodies enter the stage of complete plastic deformation, at which time the contact pressure is uniform on the whole contact surface. The contact load,
Ws, the actual contact area,
As, and the average contact pressure,
ps, at this stage are
2.1.4. Elastic–Plastic Contact Stage
According to the TABOR.D experimental results [
10,
11], plastic load,
Ws, is defined as the complete plastic contact stage when it is 400 times the critical elastic load,
Wc, at this time:
The relationship between complete plastic yield deformation
and elastic critical deformation
is
When
δc ≤
δ ≤
δs, there are both elastic and plastic deformations of the micro-convex body on the friction disks. At this stage, the relationship between the contact area and the average stress of the micro-convex bodies and the normal deformation becomes very complicated. When entering the elastic critical deformation stage, the plastic deformation occurs in a very small volume of the contact area, and the plastic deformation area is surrounded by a large number of elastic deformation areas. When entering the plastic critical deformation stage, there are very few elastic deformation areas in the contact area, and most of the contact areas are plastic deformation. Thus, it can be assumed that, at the elastic critical point and the plastic critical point, the contact area and the average contact stress are continuous, and the relationship when elastic–plastic contact can be established is
where
K is the maximum contact pressure coefficient,
, and
is Poisson’s ratio of softer materials,
.
2.1.5. Bearing Capacity Calculation
The total contact load
Wt can be expressed as [
5]
where
Wt is the total elastic contact load of the friction disk and the surface of the dual steel disk, N;
Wel is the total elastic–plastic contact load of the friction disk and the dual steel disk, N;
Ws is the total plastic load of the surface of the friction disk and the dual steel disk, N;
c is the contact area factor;
η is the rough micro-convex peak density;
An is the actual contact area, mm
2;
E’ is the equivalent elastic modulus, Pa;
R is the radius of the micro-convex peak curvature;
h is the initial clearance between the active and driven disk, m;
δc is the elastic–plastic normal deformation of the micro-convex body, m;
δ is fine-convex normal deformation, m;
φ(
z) is the Gaussian distribution law function;
δs is the plastic normal deformation, m;
K is the maximum contact pressure coefficient;
H is the hardness of the friction plate material, Pa; and
.
2.2. The Load Torque Model of Clutch Friction Pairs
Assuming that the pressure distribution between the active disk and the follower disk is uniform when the wet clutch is engaged, the pressure of the unit area of the friction disk is
where
F is the engagement pressure of the clutch, N;
c is the contact area coefficient of the active and driven disk; and
r2 and
r1 are the inner and outer radius of the friction disk m, respectively.
Taking a micro-circle
dr on the surface of the wet clutch friction plate, we can obtain the friction torque on the micro-circle. Then, we can integrate the friction torque on the micro-circle in the inner and outer diameters of the friction disk, and the friction torque transmitted during the wet clutch is obtained [
12].
Here, N is the number of friction pairs and μ is the friction coefficient, usually taking a value between 0.10 and 0.12.
Making the load torque of the clutch equivalent to the clutch load end, it can be represented as the following equation:
where
T1 is the load torque, N·m;
ω is the real-time angle velocity of the driven disk, rad/s;
TLmax is the load torque when the engagement is completed, N·m; and
ωLmax is the ultimate angular velocity of the driving end.
Here, mK is the torque coefficient; TLmax is the rotor load torque, N/m; R is the radius of the load propeller, m; ρ is the air density, kg/m3; and ω is the angular velocity, rad/s.
2.3. The Motion Differential Equation of the Clutch Active and Driven Disk
Figure 5 is a mechanical model of the torsional motion of the active and driven disk of the friction clutch [
13]. Based on
Figure 5 and the above torque analysis, the torque balance equations of the active and driven disk can be established [
13]:
where
Ie is the equivalent rotation inertia of the driving end, kg·m
2;
I1 is the equivalent rotation inertia of the load end, kg·m
2;
θ1 and
θ2 are the rotational degrees of freedom of the driving end and the load end, respectively;
ce and
c1 are equivalent rotational viscous damping coefficients, respectively, N·m·s/rad;
Te is the input torque, N·m;
Tf is the friction torque in the clutch connection process, N·m; and
Tl is the load torque, N·m.
Here, n1(t) is the active disk speed with time, r/min; and n2(t) is the driven disk speed with time, r/min.
Solving Formula (23) provides values of and with time, and then the values of n1(t) and n2(t) varying with time can be obtained from Formulas (24) and (25).
2.4. Nonlinear Time-Varying Sliding Distance Model
Figure 6 shows a schematic diagram of the actual sliding distance during the friction pair engaging of the friction clutch. As is shown, points A and B are the corresponding position points where the active and driven disks start to contact. A
1 and B
1 are the corresponding positions when the active and driven disks are completed to move together. The actual sliding distance varies nonlinearly with speed and power.
During the friction clutch engagement process, the sliding distance L(t) is the actual sliding distance from the beginning to the same final speed in one engagement time of the friction disk and the dual steel disk. That is, the relative sliding distance from the active disk slows down and the driven disk rising to the same speed is nonlinear and time-varying.
Fitting the equations of speed and time, the expression of the actual nonlinear time-varying sliding distance
L is
2.5. Friction Disk Wear Model
As known from the Archard wear model [
14], for two surfaces of relative sliding contact under load, because the two surfaces are not absolutely smooth, the actual contact area is a discrete micro-convex unit contact between the two surfaces. Assuming [
14] that the radius of the micro-convex body is
a, if the micro-convex body is loaded and the sliding distance is 2a, the surface can completely slip through each micro-convex body. The micro-convex body on the friction disk can be approximated to the hemispheric shape, with the same radius and radius of curvature, and the wear volume is
where
k is the wear coefficient, usually in the range of
and takes
k as
;
H is the hardness of the friction disk material, Pa;
L is the sliding distance, m;
W [
9,
10,
14] is the normal load acting on the friction pair,
N; and
[
15] is the surface film failure coefficient of the two rough surface contact models, usually taken as 0.5.
According to the above analysis, the nonlinear variety relationship of the rotational speed at any time during the dynamic engagement of the friction pair is solved by substituting the rotational speed into Formula (26) and calculating. Finally, the wear amount of a nonlinear variety is determined according to the normal load and surface film failure coefficient acting on the friction pair (27). The formula of wear is
where for the active disk speed
and the driven disk speed
, a series of discrete values can be obtained through the numerical solution from Formula (23). Then, fitting a formula based on the obtained discrete value and substituting the fitted formula into Formula (28), the wear amount is obtained.
Then, the calculation of the wear depth of the friction disk is
3. Analysis of the Simulation Results
Based on the actual operating speed and power parameters of the SAE#2 test machine and according to the wear theory in
Section 2, a single engagement wear of friction pairs under different operating conditions was calculated and analyzed. The parameters are shown in
Table 1.
Comparison and Calculation of Friction Disks’ Wear with Different Groove Shapes
During the engaging process of the friction pair, we used paper-based friction disks, and the changes in the rotational speed of the active disk and the driven disk were analyzed.
Figure 7 shows the relationship between rotation speed and time of the paper-based friction material.
Using the MATLAB toolbox, the expressions of time–rotation speed of the active and driven disks are fitted as shown below:
where the engagement time was 1.3286 s, and the actual nonlinear time-varying sliding distance was calculated based on Formulas (26), (30), and (31) as 11.693 m.
The paper-based friction disks with three-way parallel grooves, waffle grooves, and two-way parallel grooves were modeled by UG. The surface area of the friction area,
An, was calculated, as shown in
Table 2.
Substituting the actual contact area into Formula (31), the wear depth variety of a single engagement can be obtained, as shown in
Figure 8.
As seen from the calculation results, the surface area was different with the different grooves on the friction disk, which affected the actual wear.
Figure 6 shows that, for a single engagement, the actual contact area of the waffle groove friction disk was the smallest, so the wear depth was the largest. However, the actual contact area of the two-way parallel groove was the largest, so the wear depth was the smallest. The reason is that, in the clutch engagement process, the bearing capacity and shear force are mainly borne by the micro-convex bodies. When the actual contact area is small, the bearing capacity and shear force for a single micro-convex body are greater, and it is more likely to wear and peel, causing the wear depth to become larger.
In addition, when the nonlinear time-varying sliding distance is used to calculate the wear depth of the friction pair, although the depth of wear continues to increase, the magnitude of the increase continues to decrease. During the engagement process, the rotational speed of the active disk decreased under the hinderance of the driven disk, and the rotational speed of the driven disk increased under the driving of the active disk. The rotational speed difference between the active disk and the driven disk decreased, so the increment of wear also decreased, which is in line with the actual working conditions.
4. Design of Wear Test Scheme
4.1. Working Principle and Working Condition Design of the Test Bed
The SAE#2 test machine is mainly a test device for evaluating and analyzing the wet clutch and related friction factors. It realizes the automation of program operation and data processing through computers, which is convenient and easy from the setting of test conditions to the operation of data processing. The test machine is shown in
Figure 9.
The schematic diagram of the test machine equipment can be simplified according to the original figure, as shown in
Figure 10.
As shown in
Figure 8, four friction disks and five dual steel disks were used in the clutch test module. At the beginning of the engagement, the motor drove the inertia disk to rotate, and the inertia disk drove the active end of the clutch to rotate. The gas pump directly loaded the clutch on the piston at the active end through the pressure generated by compressed air and caused the clutch to engage. When the engagement was completed, the cooling switch controlled the initial temperature of the lubricant oil, reducing it to 60 °C, and then the next experiment was conducted; this was repeated until the number of engagements was completed. The thermocouple measures the real-time engagement temperature of the clutch steel disks, collecting all sensor signals in the data acquisition system, controlling all equipment, and importing the data into the computer.
The paper-based three-way parallel groove friction disk, the waffle groove friction disk and the two-way parallel groove friction disk are shown in
Figure 11. The thickness of the friction disk, consisting of a 1.8 mm intermediate chip and 0.6 mm friction material on both sides, was 3 mm, and the depth of the groove was 0.3 mm.
4.2. Experimental Test Method and Analysis of the Experimental Results
The surface pressure was set at 1.2 MPa, the initial temperature of the oil was at 60 °C, the rotation speed at 6000 r/min, and the lubricating oil flow rate at 3.4 L/min. It was engaged twice a minute, and the accumulative number of engagements was 2000. The friction disk was removed after a certain number of engagements. The thickness of the three equal division points of the friction disk was measured by a micrometer and taken as the average. A three-dimensional morphology instrument was used to collect the wear morphology and to watch the wear. The wear depths of three kinds grooves of friction disk as shown in the
Table 3,
Table 4 and
Table 5.
We took the three-way parallel groove as an example and used a three-dimensional morphology instrument to measure the height from the bottom of the oil groove to the surface of the friction material of the three-way parallel grooves that engaged 0, 1000, and 2000 times, and then compared that to the measured values using a high-precision micrometer, as shown in
Figure 12:
The data measured by the micrometer are basically consistent with those measured by the three-dimensional morphology meter. We used MATLAB to fit the relationship between the engagement number,
N, and the actual wear depth obtained, as shown in
Figure 13.
Using the CFtool toolbox in MATLAB, the relationships between the depth and engagements of three grooves were fitted as follows:
The fitted degree
, which was close to 1, indicated that the fitted result was fairly accurate. Then, when
N = 1, that is, the wear depth of the three-way parallel groove friction disk was
mm, the wear depth of the waffle friction sheet was
mm, and the wear depth of the two-way parallel groove friction sheet was
mm. A comparison of the experimental value of the wear depth with the simulation value is shown in
Table 6.
As shown in
Table 6, for a single engagement, the wear of the waffle friction disk was the largest, the three-way parallel groove friction disk came second, and the two-way parallel groove friction had the smallest wear, which is consistent with the simulation results in
Section 2, and the difference between the simulation data and the experimental calculation data was small. It can be considered that the friction disk wear analysis method of the clutch is very accurate.
5. Conclusions
In this paper, a calculation method for the actual nonlinear time-varying sliding distance in the process of friction clutch engagement is proposed, a calculation model of friction pair wear is given, and the influence of engaging pressure and lubricant oil temperature on the wear of friction disks of different materials is analyzed. The following conclusions are drawn.
Through the study of the dynamic engaging process characteristics of the active and driven disk, the relationship of the rotational speed variety of the active and driven disk is analyzed, a calculation method of the actual nonlinear time-varying sliding distance is proposed, the wear of the friction pair is calculated and analyzed, and the dynamic variety rule of the wear of the friction pair in a single engagement process is obtained. With the continuous progress of the engaging process, although the wear of the friction pair has an ascending trend, it is not proportional to the engagement time, but, with the increase in time, the surface micro-convex bodies continues to be regular, and the increase in the wear is constantly flat.
Through the SAE#2 machine, three kinds of groove-shaped friction disks of paper-based friction materials were tested, and the wear depths of different engagement times were measured separately. The relationship between the number of engagement times and the wear depth was explored. The wear from a single engagement in the experiment and simulation was compared, where it was found that the experimental results were consistent with the simulation, that is, the waffle groove friction disk wear was the largest, the three-way parallel groove friction disk wear came in second, and the two-way parallel groove friction disk had the smallest wear; the difference between the simulation data and the experimental calculation data was small. Therefore, the theoretical model for calculating the wear of the friction pair was relatively accurate and has certain reference significance.
Author Contributions
Conceptualization, H.B. and C.Z.; methodology, C.Z.; validation, C.Z., H.B. and X.H.; formal analysis, C.Z.; investigation, C.Z.; resources, H.B.; data curation, C.Z.; writing—original draft preparation, C.Z.; writing—review and editing, H.B.; visualization, F.L.; supervision, H.B.; project administration, H.B.; funding acquisition, C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China(Grant No. 51975274) and National Key Laboratory of Science and Technology on Helicopter Transmission(Nanjing University of Aeronautics and Astronautics)(Grant No. HTL-O-19G05).
Data Availability Statement
Data and methods used in the research need to be presented in sufficient detail in the paper so that other researchers can replicate the work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Greenwood, J.A.; Williamson, J.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. Series A Math. Phys. Eng. Sci. 1966, 295, 300–319. [Google Scholar]
- Menga, N.; Ciavarella, M. A Winkler solution for the axisymmetric Hertzian contact problem with wear and finite element method comparison. J. Strain Anal. Eng. Des. 2015, 50, 156–162. [Google Scholar] [CrossRef]
- Lewicki, D.G.; DeSmidt, H.; Smith, E.C.; Bauman, S.W. Dynamics of a dual-clutch gearbox system: Analysis and experimental validation. J. Am. Helicopter Soc. 2013, 58, 17–28. [Google Scholar] [CrossRef]
- Kneissler, M.; Schieferdecker, P. Method for Determining Wear of a Friction Plate. U.S. Patent 8,600,612, 3 December 2013. [Google Scholar]
- Zhang, Z.G. Study on Several Working Characteristics of Wet Clutch. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2010. [Google Scholar]
- Dimaki, A.V.; Dmitriev, A.I.; Menga, N.; Papangelo, A.; Ciavarella, M.; Popov, V.L. Fast high-resolution simulation of the gross slip wear of axially symmetric contacts. In Tribology Transactions; Taylor & Francis: Abingdon, UK, 2016; pp. 189–194. [Google Scholar]
- Wang, L.; Xi, C.; Le, L. Research on wear calculation method and experiment for friction disc of wet clutch. J. Guangxi Univ. Nat. Sci. Ed. 2017, 42, 826–833. [Google Scholar]
- Le, L.; Xi, C.; Liyong, W.; Li, H. Effect of contact area on wear performance of wet clutch friction disc. J. Beijing Univ. Inf. Technol. Nat. Sci. Ed. 2017, 32, 5–9. [Google Scholar]
- Wen, S.; Ping, H. Tribology Principle; Tsinghua University Press: Beijing, China, 2012; pp. 284–313. (In Chinese) [Google Scholar]
- Dong, W.; Chao, X.; Qiang, W. A Normal Mechanical Model for Elastic-Plastic Contact of Rough Surface. J. Shanghai Jiao Tong Univ. 2016, 50, 1264–1269. [Google Scholar]
- Tabor, D. The Hardness of Metals; Oxford University Press: Oxford, UK, 2000; pp. 141–150. [Google Scholar]
- Chen, R.; Zheng, G. Helicopter Flight Dynamics; Science Press: Beijing, China, 2019; pp. 10–25. [Google Scholar]
- Zhiguo, Z.; Jiading, G.; Lu, H. Estimation of Torques Transited by Twin-clutch during Shifting Process for Dry Dual Clutch Transmission. J. Mech. Eng. 2017, 53, 77–87. [Google Scholar]
- Zhao, Z. Study on Wear of Cam in Mixed Lubrication. Ph.D. Thesis, Beijing Institute Technology, Beijing, China, 2015. [Google Scholar]
- Stolarski, T.A. A system for wear prediction in lubricated sliding contact. Lubr. Sci. 1996, 8, 315–351. [Google Scholar] [CrossRef]
Figure 1.
Schematic diagram of a wet multi-disk clutch.
Figure 1.
Schematic diagram of a wet multi-disk clutch.
Figure 2.
Friction contact mixed-lubrication area.
Figure 2.
Friction contact mixed-lubrication area.
Figure 3.
Unimodal elastic contact.
Figure 3.
Unimodal elastic contact.
Figure 4.
Actual contact between friction plate and mating steel plate.
Figure 4.
Actual contact between friction plate and mating steel plate.
Figure 5.
Model of the friction disk rotation of the clutch.
Figure 5.
Model of the friction disk rotation of the clutch.
Figure 6.
Sliding distance L in the course of friction clutch engagement.
Figure 6.
Sliding distance L in the course of friction clutch engagement.
Figure 7.
The relationship between rotation speed and time during paper-based friction disk engagement.
Figure 7.
The relationship between rotation speed and time during paper-based friction disk engagement.
Figure 8.
The wear depth with three different groove shapes.
Figure 8.
The wear depth with three different groove shapes.
Figure 9.
SAE#2 test machine equipment diagram.
Figure 9.
SAE#2 test machine equipment diagram.
Figure 10.
SAE# 2 test machine schematic diagram.
Figure 10.
SAE# 2 test machine schematic diagram.
Figure 11.
Three kinds of friction disk: (a) three-way parallel groove friction disk; (b) waffle groove friction disk; and (c) two-way parallel groove friction disk.
Figure 11.
Three kinds of friction disk: (a) three-way parallel groove friction disk; (b) waffle groove friction disk; and (c) two-way parallel groove friction disk.
Figure 12.
3D Profiler measurement.
Figure 12.
3D Profiler measurement.
Figure 13.
The relationship between the wear depth of the three shapes of grooves and the engagement.
Figure 13.
The relationship between the wear depth of the three shapes of grooves and the engagement.
Table 1.
Simulation parameters of the paper-based three-way parallel groove friction disks.
Table 1.
Simulation parameters of the paper-based three-way parallel groove friction disks.
| Parameters | Value | Parameters | Value |
|---|
| Inner diameter of friction pair, r1/(m) | 0.060 | Initial oil film thickness, h0/(m) | 5 × 10−4 |
| Outer diameter of friction pair, r2/(m) | 0.073 | Lubricant oil viscosity, η/(Pa·s) | 0.0288 |
| Roughness Root Mean Square, σ/(m) | 8.4 × 10–6 | Oil density, ρ/(kg·m–3) | 993 |
| Permeability of friction linings, Φ/(m2) | 4 × 10–13 | Engaging pressure, P0/(Pa) | 1.2 × 106 |
| Friction material thickness, d/(m) | 0.0006 | Initial speed of active disk, n1/(r/min) | 6000 |
| Convex peak density in rough dimension, /(m2) | 7 × 107 | Initial speed of driven disk, n2/(r/min) | 3000 |
| Radius of curvature, R/(m) | 8.0 × 10−4 | Active disk equivalent moment of inertia, Ie/(kg·m2) | 0.1097 |
| Elastic Modulus, E’/(Pa) | 5.47 × 108 | Driven disk moment of inertia, Il/(kg·m2) | 0.3439 |
| Poisson’s ratio of separator disk | 0.29 | Poisson’s ratio of friction disk | 0.12 |
| Engine power, P (kW) | 30 | Area factor, c | 0.75 |
| Brinell hardness, H (N/mm2) | 24 | Centerline distance, h (mm) | 0.005 |
Table 2.
Actual contact area of the friction disks with different grooves.
Table 3.
Measurement results of the friction disk wear with three-way parallel grooves (unit: mm).
Table 3.
Measurement results of the friction disk wear with three-way parallel grooves (unit: mm).
| | Number of Engagements | 500 | 1000 | 2000 |
|---|
| Number of Measurements | |
|---|
| 1 | 0.027 | 0.036 | 0.044 |
| 2 | 0.026 | 0.038 | 0.052 |
| 3 | 0.023 | 0.037 | 0.048 |
| Average value | 0.025 | 0.037 | 0.048 |
Table 4.
Measurement results of the friction disk wear with waffle grooves (unit: mm).
Table 4.
Measurement results of the friction disk wear with waffle grooves (unit: mm).
| | Number of Engagements | 500 | 1000 | 2000 |
|---|
| Number of Measurements | |
|---|
| 1 | 0.037 | 0.046 | 0.067 |
| 2 | 0.030 | 0.044 | 0.048 |
| 3 | 0.030 | 0.049 | 0.053 |
| Average value | 0.032 | 0.046 | 0.056 |
Table 5.
Measurement result of friction disk wear with two-way parallel groove (unit: mm).
Table 5.
Measurement result of friction disk wear with two-way parallel groove (unit: mm).
| | Number of Engagements | 500 | 1000 | 2000 |
|---|
| Number of Measurements | |
|---|
| 1 | 0.025 | 0.032 | 0.047 |
| 2 | 0.023 | 0.034 | 0.044 |
| 3 | 0.020 | 0.036 | 0.045 |
| Average value | 0.023 | 0.034 | 0.045 |
Table 6.
Comparison of the theoretical wear depth and experimental wear depth (unit: mm).
Table 6.
Comparison of the theoretical wear depth and experimental wear depth (unit: mm).
| | Groove | Three-Way Parallel | Waffle | Two-Way Parallel |
|---|
| Analysis Value | |
|---|
| Experimental value | | | |
| Theoretical value | | | |
| Difference value | | | |
| Error rate | 8.04% | 3.41% | 9.09% |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).