Modified Filtered-X Hierarchical LMS Algorithm with Sequential Partial Updates for Active Noise Control
Abstract
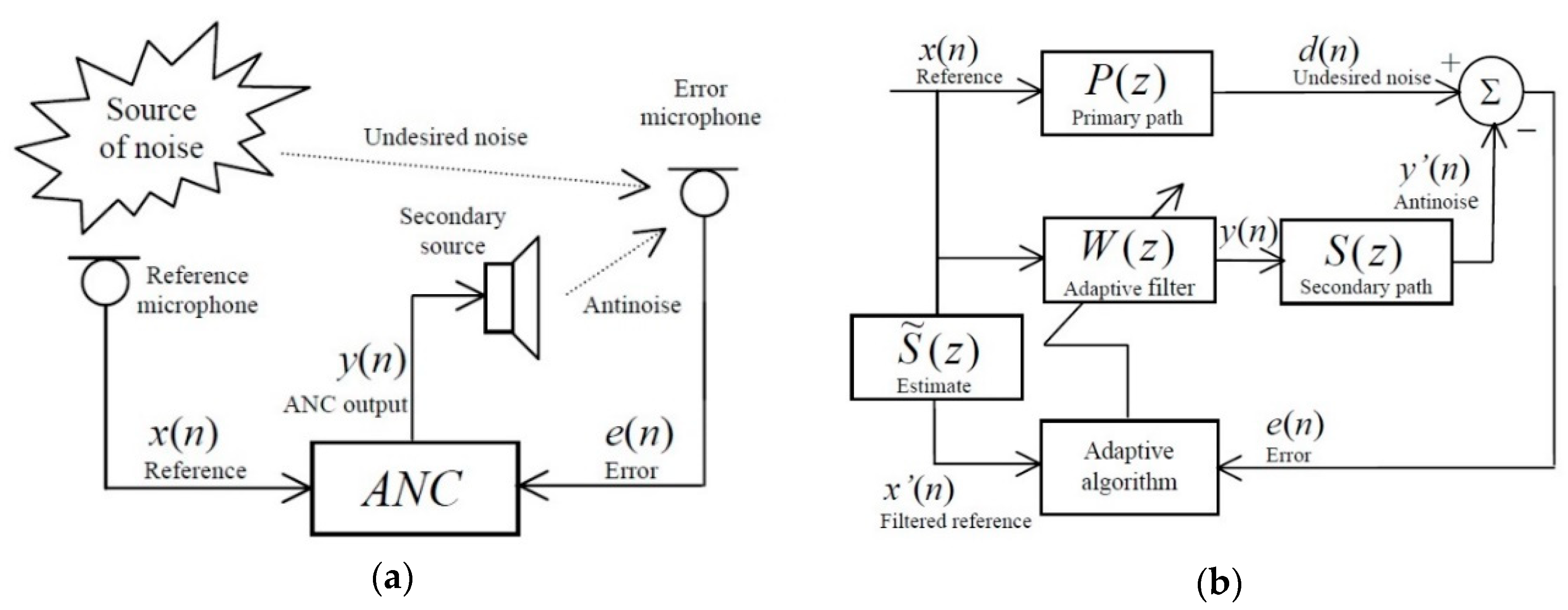
1. Introduction
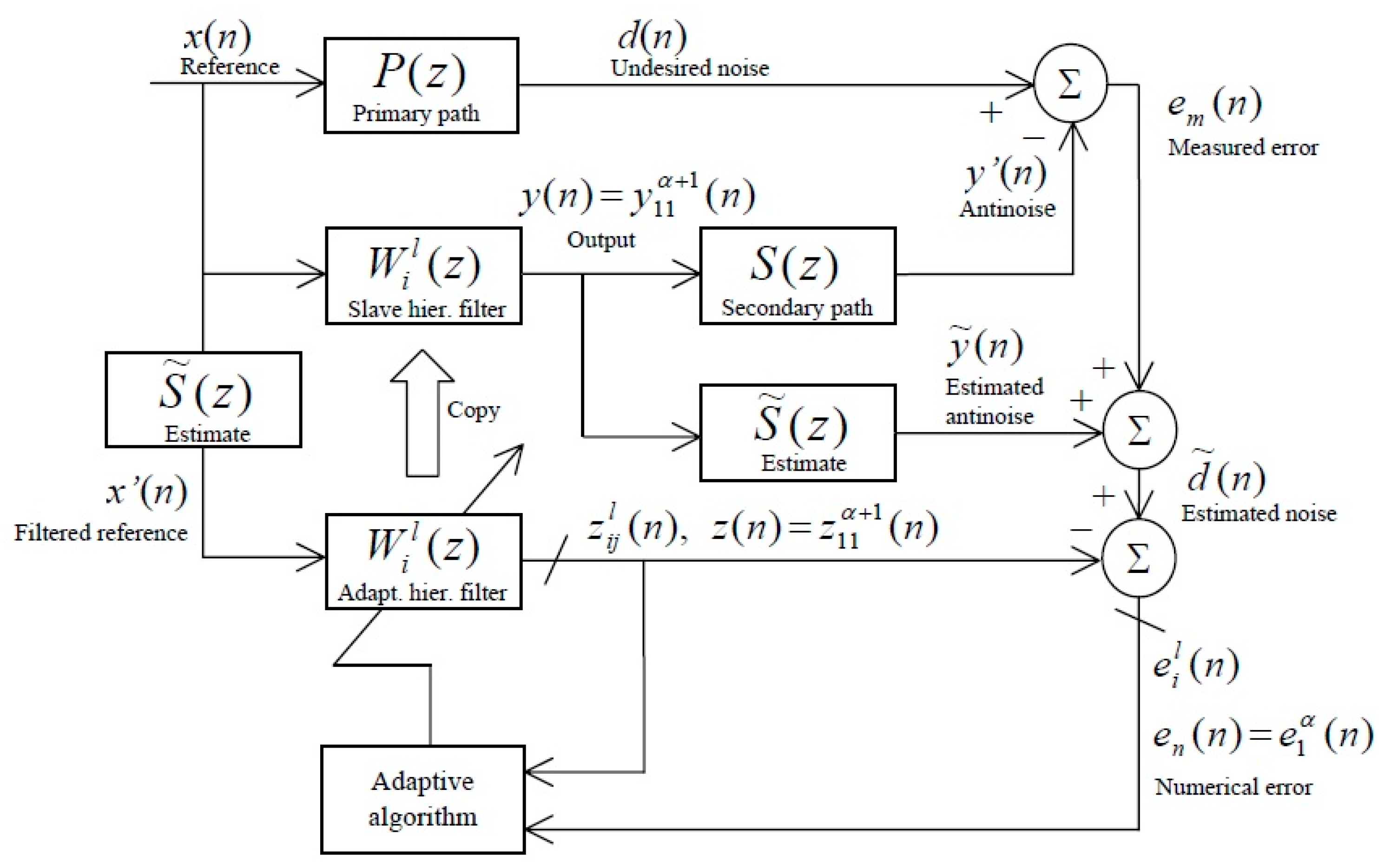
2. Modified FX Hierarchical Sequential PU LMS Algorithm with Gain in Step-Size
| Algorithm 1 Gμ—Mod Fx H Seq LMS algorithm | |
| for i = 1 to # iterations | /* MAIN LOOP*/ |
| /*First level of slave hierarchical filter is filled with*/ | |
| /* SLAVE HIERARCHICAL FILTER */ | |
| for l = 1 to α | /* From first to top (α) level of the hierarchy fo*/ |
| for i = 1 to | /* From first to last subfilter at each level */ |
| /* Computing the output of every subfilter */ | |
| end of for (i) | |
| end of for (l) → | /* END OF SLAVE HIERARCHICAL FILTER */ |
| /* Computing the antinoise signal where */ /*and */ /**/ /* Measured error*/ | |
| /* Computing the estimated noise */ | |
| /* Filtering the reference*/ | |
| /* First level of adaptive hierarchical filter is filled with | |
| *//* ADAPTIVE HIERARCHICAL FILTER */ | |
| for l = 1 to α | /* From first to top level of the hierarchy */ |
| for i = 1 to | /* From first to last subfilter at each level */ |
| /* Computing the output of every subfilter */ | |
| /* Computing the error of every subfilter */ | |
| for j = 1 to | /* For every tap, Sequential partial updates */ |
| if | |
| else | |
| end of if | |
| end of for (j) | |
| end of for (i) | |
| end of for (l) → | /* END OF ADAPTIVE HIERARCHICAL FILTER */ |
| end of for (n) | /* END OF MAIN LOOP */ |
3. Convergence Analysis
3.1. Assumptions in the Convergence Analysis
3.2. Gain in Step-Size of the Gμ—Mod Fx H Seq LMS Algorithm
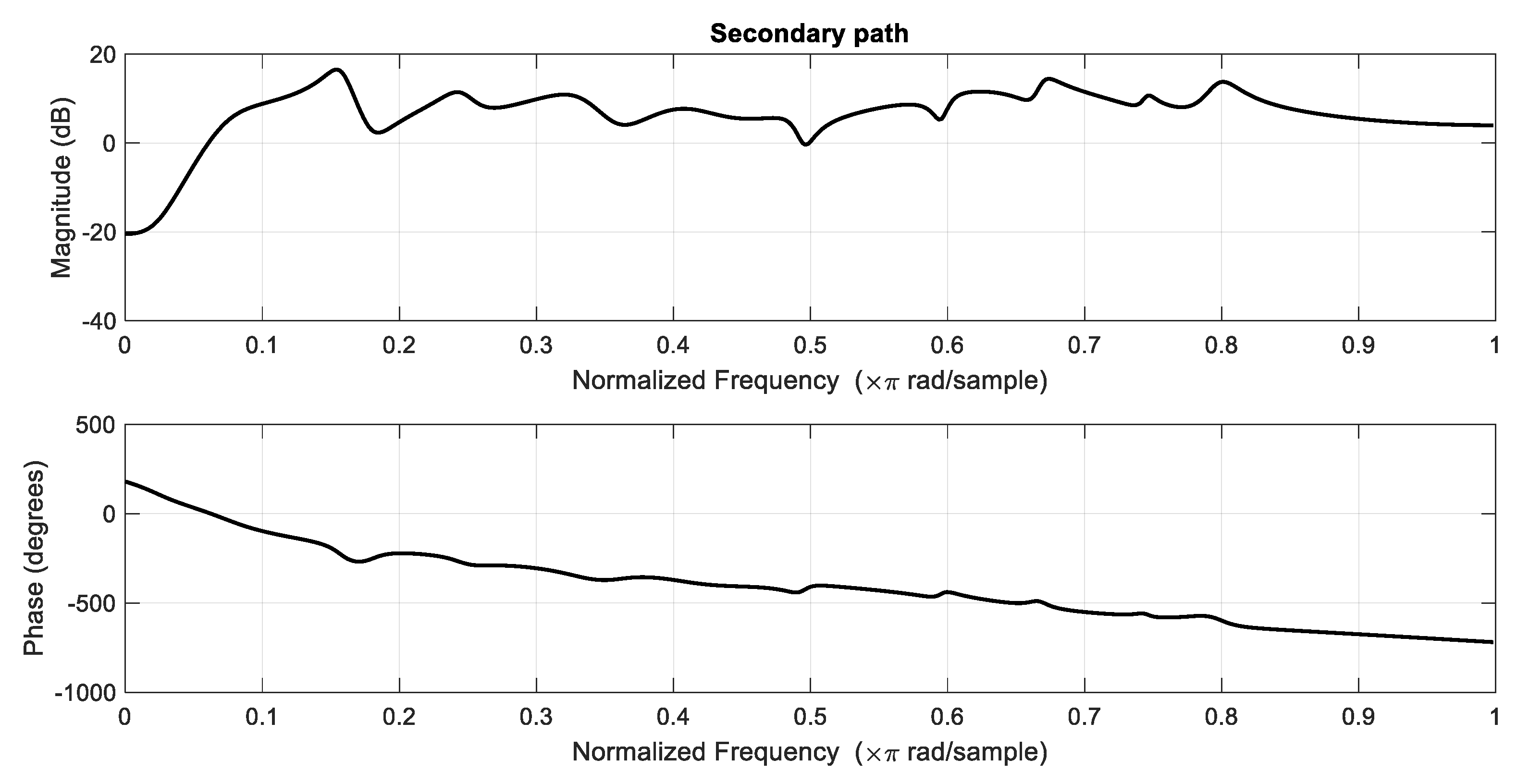
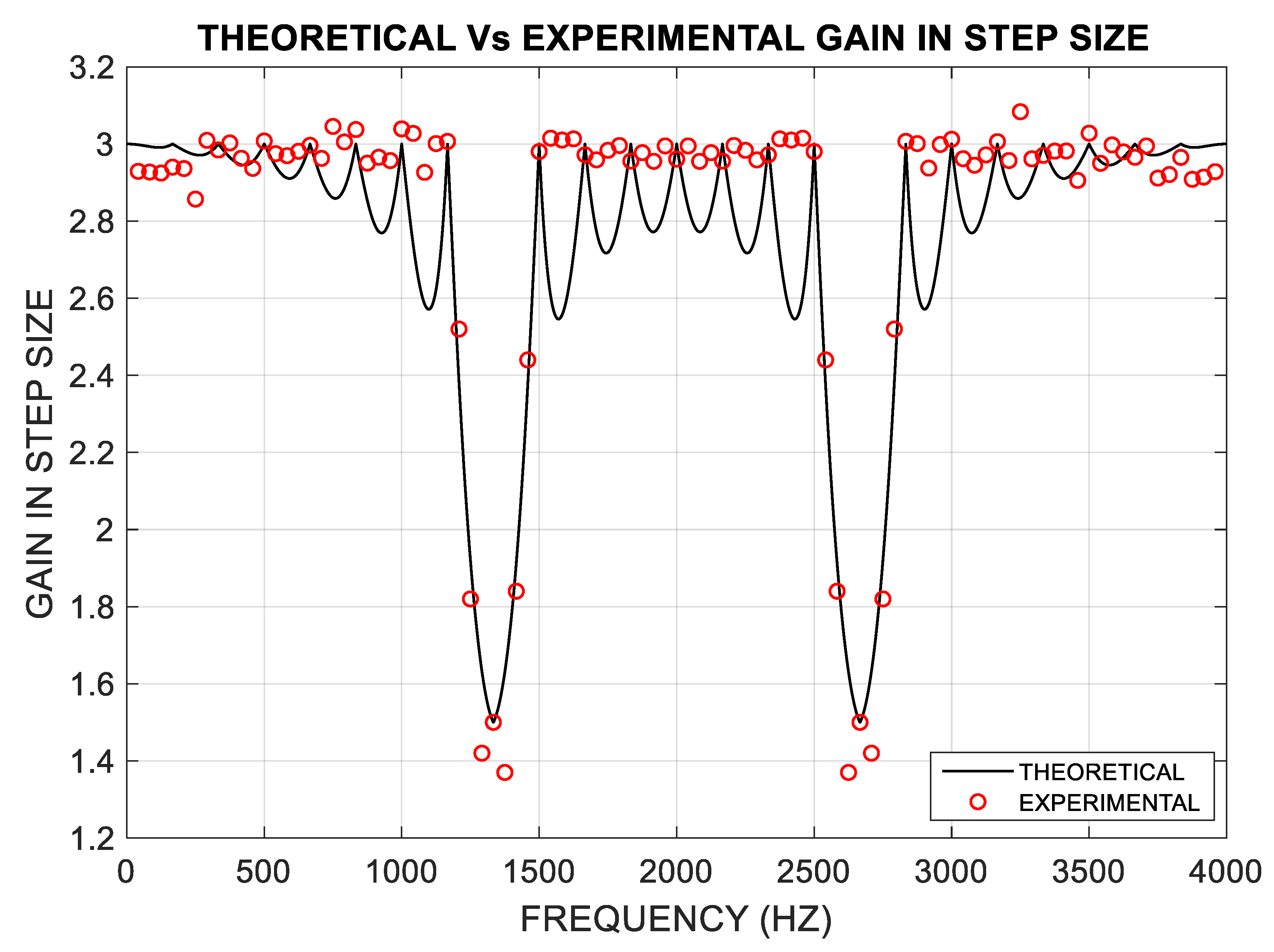
4. Simulation Results
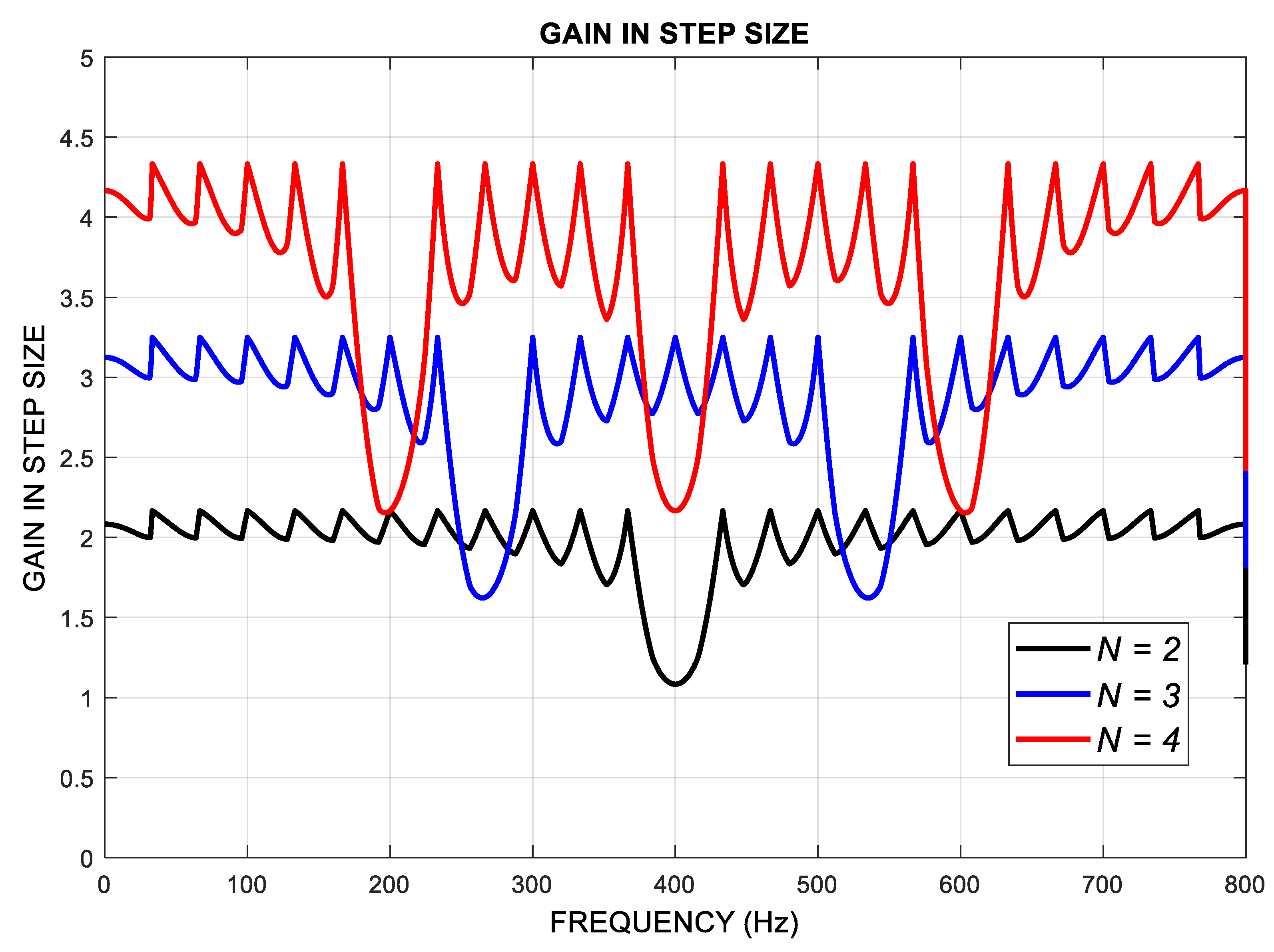
4.1. Gain in Step-Size: Simulation vs. Theory
4.2. Comparative Study between Different ANC Algorithms
- (a)
- Standard FxLMS, with a L-length FIR adaptive filter [4];
- (b)
- (c)
- Mod H FxLMS with L coefficients at the first level of the hierarchical filter.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Autocorrelation Matrix of the Decimated Input Vector of the Sequential PU LMS Algorithm
| # Iteration | Coefficients That Form the Logical Subfilter Updated at the Current Iteration | Samples of the Input Vector Used to Update the Logical Subfilter |
|---|---|---|
| 1 | ||
| N | ||
| N + 1 |
Appendix A.2. Eigenvalues of the Autocorrelation Matrix of a Periodic Signal Consisting of K Harmonics
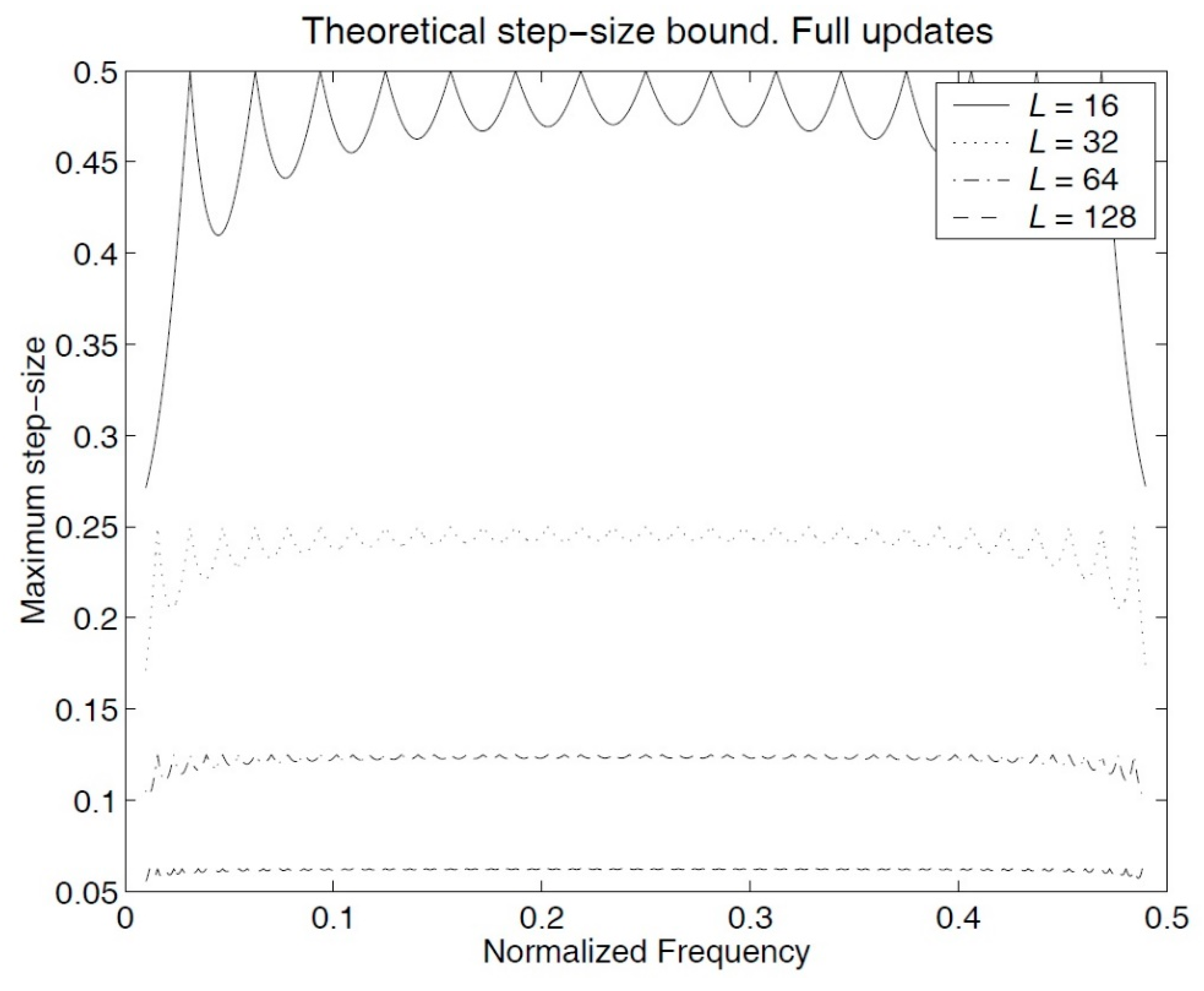
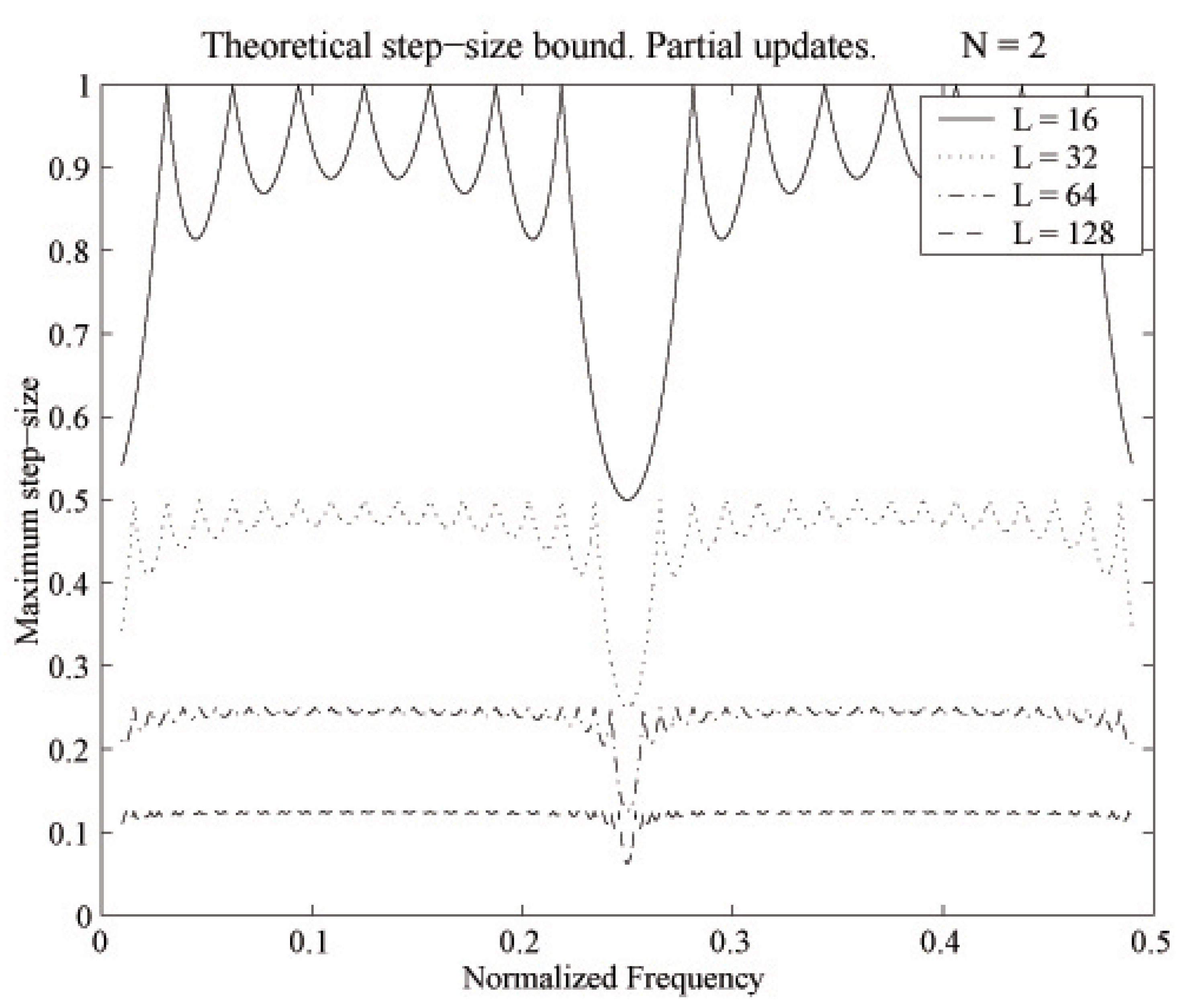
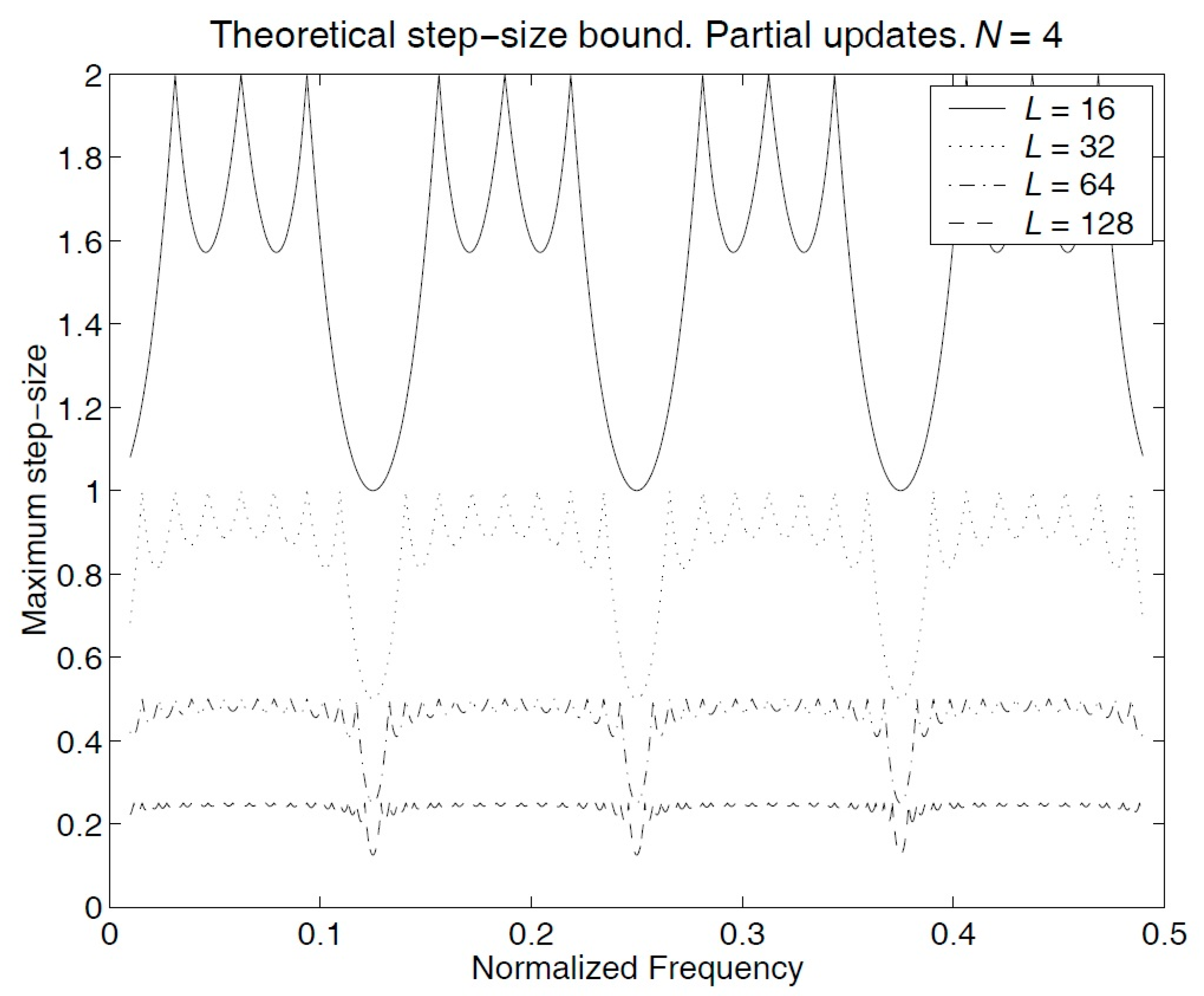
Appendix A.3. Effect of the Length of the Filter on the Step-Size Bound
- (a)
- Full updates LMS algorithm
- (b)
- Sequential PU LMS algorithm.
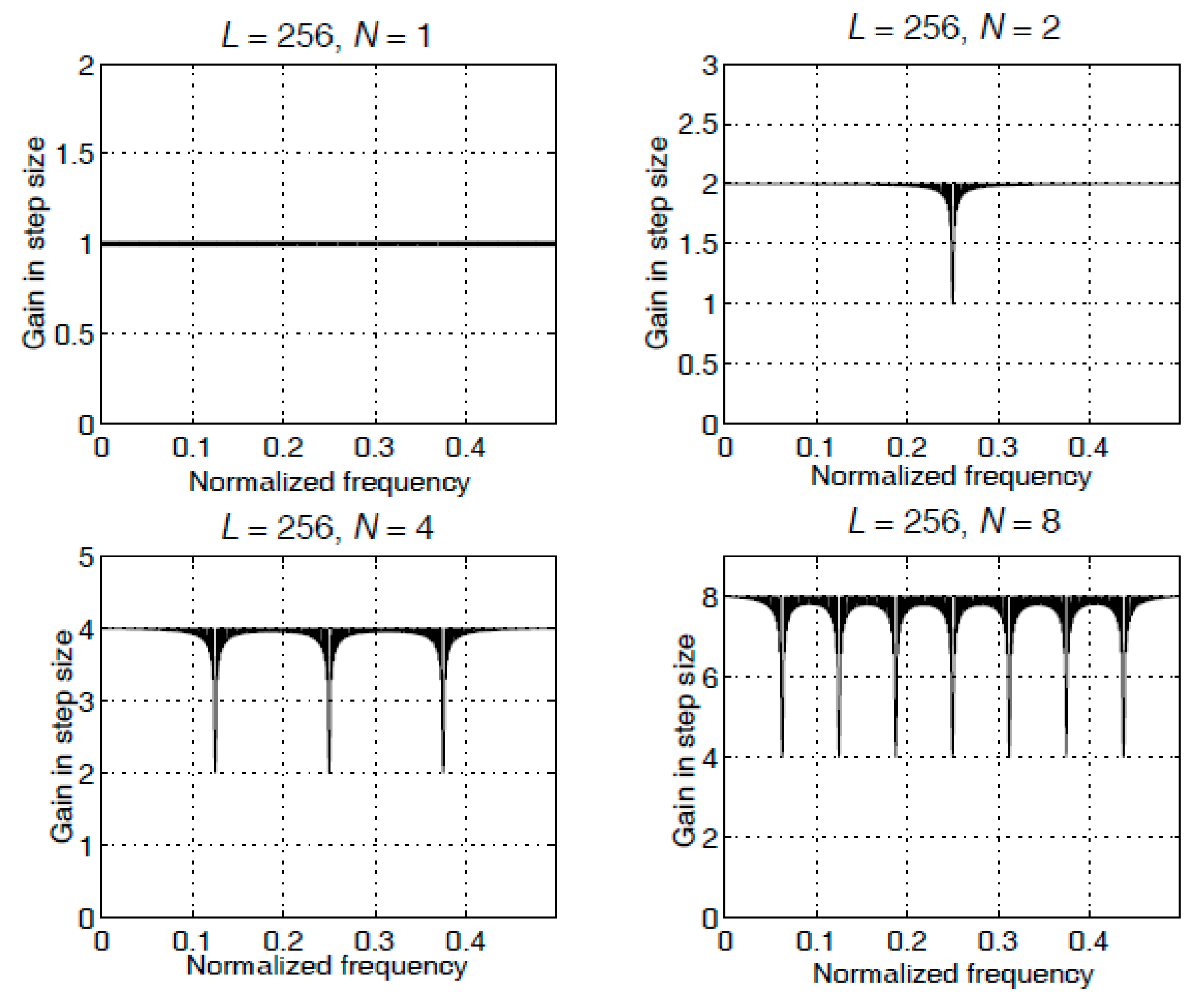
Appendix A.4. The Gain in Step-Size

References
- Stansfeld, S.; Haines, M.; Brown, B. Noise and Health in the Urban Environment. Rev. Environ. Health 2000, 15, 43–82. [Google Scholar] [CrossRef] [PubMed]
- Basner, M.; Babisch, W.; Davis, A.; Brink, M.; Clark, C.; Janssen, S.; Stansfeld, S. Auditory and non-auditory effects of noise on health. Lancet 2014, 383, 1325–1332. [Google Scholar] [CrossRef]
- Minichilli, F.; Gorini, F.; Ascari, E.; Bianchi, F.; Coi, A.; Fredianelli, L.; Licitra, G.; Manzoli, F.; Mezzasalma, L.; Cori, L. Annoyance Judgment and Measurements of Environmental Noise: A Focus on Italian Secondary Schools. Int. J. Environ. Res. Public Health 2018, 15, 208. [Google Scholar] [CrossRef] [PubMed]
- Attenborough, K.; Vér, I.L. Sound-absorbing materials and sound absorbers. In Noise and Vibration Control Engineering; Principles and Applications; John Wiley & Sons, Inc.: New York, NY, USA, 2005. [Google Scholar]
- Munjal, M.; Galaitsis, A.G.; Vér, I.L. Passive silencers. In Noise and Vibration Control Engineering: Principles and Applications Noise; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 279–343. [Google Scholar]
- Kuo, S.; Morgan, D. Active Noise Control Systems: Algorithms and DSP Implementations; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Samarasinghe, P.N.; Zhang, W.; Abhayapala, T.D. Recent Advances in Active Noise Control Inside Automobile Cabins: Toward quieter cars. IEEE Signal Process. Mag. 2016, 33, 61–73. [Google Scholar] [CrossRef]
- Morgan, D. An analysis of multiple correlation cancellation loops with a filter in the auxiliary path. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 454–467. [Google Scholar] [CrossRef]
- Bjarnason, E. Analysis of the filtered-X LMS algorithm. IEEE Trans. Speech Audio Process. 1995, 3, 504–514. [Google Scholar] [CrossRef]
- Vicente, L. Novel FxLMS convergence condition with deterministic reference. IEEE Trans. Signal Process. 2006, 54, 3768–3774. [Google Scholar] [CrossRef]
- Yang, F.; Guo, J.; Yang, J. Stochastic Analysis of the Filtered-x LMS Algorithm for Active Noise Control. IEEE ACM Trans. Audio Speech Lang. Process. 2020, 28, 2252–2266. [Google Scholar] [CrossRef]
- Boucher, C.C. The effects of modeling error on the performance and stability of active noise control systems. In Recent Advances in Active Control of Sound Vibration; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Snyder, S.D.; Hansen, C.H. The effect of transfer function estimation errors on the filtered-x LMS algorithm. IEEE Trans. Signal Process. 1994, 42, 950–953. [Google Scholar] [CrossRef]
- Tobias, O.J.; Seara, R. Leaky-FXLMS algorithm: Stochastic analysis for Gaussian data and secondary path modeling error. IEEE Trans. Speech Audio Process. 2005, 13, 1217–1230. [Google Scholar] [CrossRef]
- Kim, H.-S.; Park, Y. Delayed-X LMS algorithm: An efficient ANC algorithm utilizing robustness of cancellation path model. J. Sound Vib. 1998, 212, 875–887. [Google Scholar] [CrossRef]
- Chen, G.; Sone, T.; Saito, N.; Abe, M.; Makino, S. The stability and convergence characteristics of the delayed-x LMS algorithm in ANC systems. J. Sound Vib. 1998, 216, 637–648. [Google Scholar] [CrossRef]
- Bjarnason, E. Active noise cancellation using a modified form of the filtered-x LMS algorithm. In Proceedings of the EUSIPCO-92, Sixth European Signal Processing Conference, Brussels, Belgium, 24–27 August 1992. [Google Scholar]
- Kim, I.-S.; Na, H.-S.; Kim, K.-J.; Park, Y. Constraint filtered-x and filtered-u least-mean-square algorithms for the active control of noise in ducts. J. Acoust. Soc. Am. 1994, 95, 3379–3389. [Google Scholar] [CrossRef]
- Lopes, P.A.C.; Piedade, M.S. The behavior of the modified FX-LMS algorithm with secondary path modeling errors. IEEE Signal Process. Lett. 2004, 11, 148–151. [Google Scholar] [CrossRef]
- Ramos, P.; Vicente, L.; Torrubia, R.; López, A.; Salinas, A.; Masgrau, E. On the complexity-performance tradeoff of two active noise control systems for vehicles. In Advances for In-Vehicle and Mobile Systems; Springer: Berlin/Heidelberg, Germany, 2007; pp. 85–96. [Google Scholar]
- Rupp, M. Saving complexity of modified filtered-X-LMS and delayed update LMS algorithms. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1997, 44, 57–60. [Google Scholar] [CrossRef]
- Douglas, S.C. An efficient implementation of the modified filtered-X LMS algorithm. IEEE Signal Process. Lett. 1997, 4, 286–288. [Google Scholar] [CrossRef]
- Yang, F.; Cao, Y.; Wu, M.; Albu, F.; Yang, J. Frequency-Domain Filtered-x LMS Algorithms for Active Noise Control: A Review and New Insights. Appl. Sci. 2018, 8, 2313. [Google Scholar] [CrossRef]
- Gaiotto, S.; Laudani, A.; Lozito, G.M.; Riganti Fulginei, F. A Computationally Efficient Algorithm for Feedforward Active Noise Control Systems. Electronics 2020, 9, 1504. [Google Scholar] [CrossRef]
- Woo, T.-K. Fast hierarchical least mean square algorithm. IEEE Signal Process. Lett. 2001, 8, 289–291. [Google Scholar]
- Macleod, M.D. Performance of the hierarchical LMS algorithm. IEEE Signal Process. Lett. 2002, 9, 436–437. [Google Scholar] [CrossRef]
- Tan, L.; Wu, M. Data Reduction in Wireless Sensor Networks: A Hierarchical LMS Prediction Approach. IEEE Sens. J. 2016, 16, 1708–1715. [Google Scholar] [CrossRef]
- Douglas, S.C. Adaptive filters employing partial updates. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1997, 44, 209–216. [Google Scholar] [CrossRef]
- Ramos, P.; Torrubia, R.; López, A.; Salinas, A.; Masgrau, E. Step Size Bound of the Sequential Partial Update LMS Algorithm with Periodic Input Signals. Eurasip J. Audio Speech Music Process. 2007, 2007, 1–15. [Google Scholar] [CrossRef][Green Version]
- Figwer, J.; Michalczyk, M.I. Notes on a New Structure of Active Noise Control Systems. Appl. Sci. 2020, 10, 4705. [Google Scholar] [CrossRef]
- Kuo, S.M.; Tahernehadi, M.; Hao, W. Convergence analysis of narrow-band active noise control system. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 1999, 46, 220–223. [Google Scholar] [CrossRef]
- Haykin, S. Adaptive Filter Theory; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Widrow, B.; Stearns, S.D. Adaptive Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985; ISBN 978-0-13-004029-9. [Google Scholar]



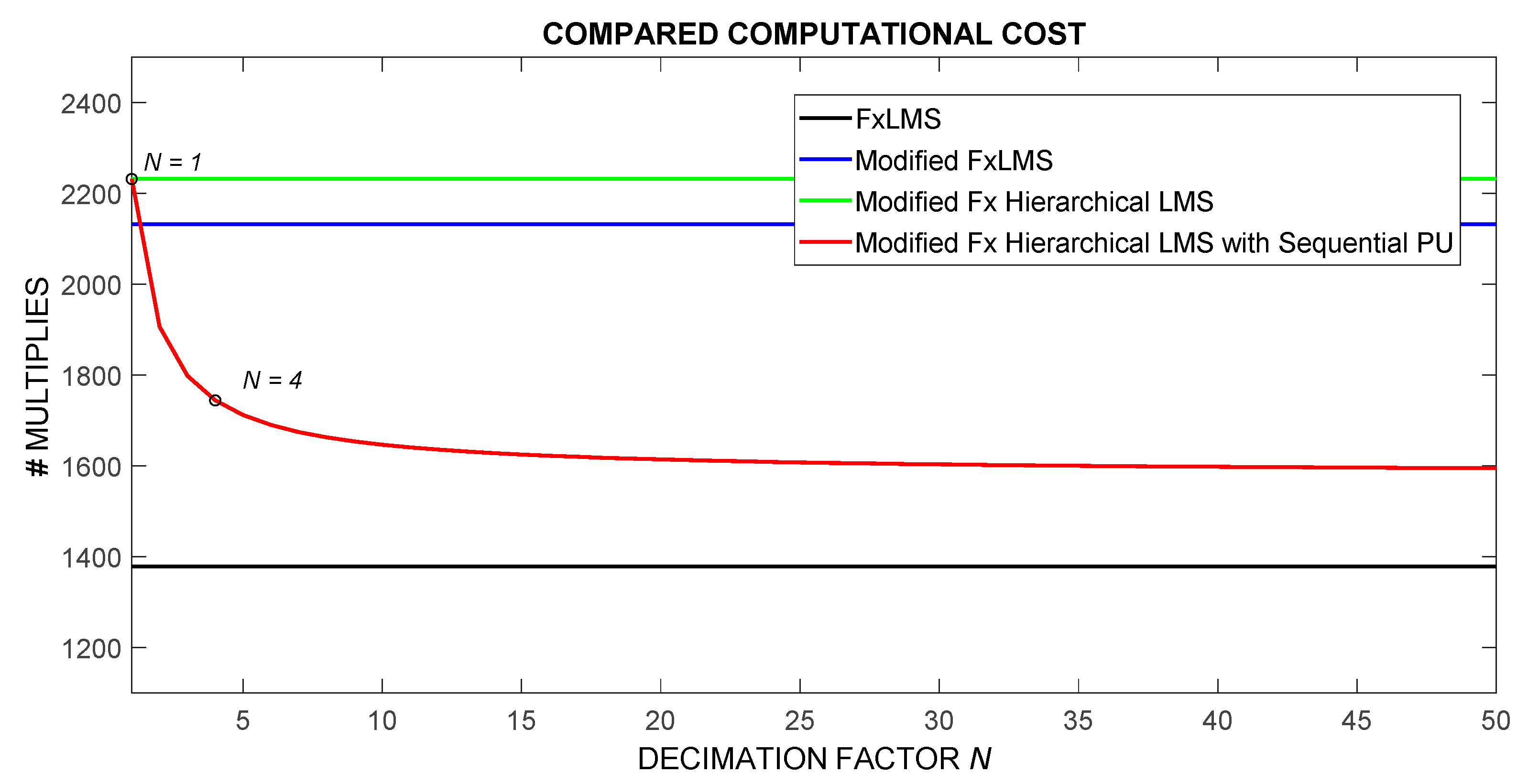
| Task\Algorithm | FxLMS | Mod FxLMS | Mod Fx H LMS | Gµ-Mod Fx H Seq LMS |
|---|---|---|---|---|
| Computing output of the slave filter | - | |||
| Filtering reference with | ||||
| Filtering output of the slave filter with | - | |||
| Computing output of the adaptive filter | ||||
| Updates of the coefficients | ||||
| # Total Mutiplications |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramos Lorente, P.; Martín Ferrer, R.; Arranz Martínez, F.; Palacios-Navarro, G. Modified Filtered-X Hierarchical LMS Algorithm with Sequential Partial Updates for Active Noise Control. Appl. Sci. 2021, 11, 344. https://doi.org/10.3390/app11010344
Ramos Lorente P, Martín Ferrer R, Arranz Martínez F, Palacios-Navarro G. Modified Filtered-X Hierarchical LMS Algorithm with Sequential Partial Updates for Active Noise Control. Applied Sciences. 2021; 11(1):344. https://doi.org/10.3390/app11010344
Chicago/Turabian StyleRamos Lorente, Pedro, Raúl Martín Ferrer, Fernando Arranz Martínez, and Guillermo Palacios-Navarro. 2021. "Modified Filtered-X Hierarchical LMS Algorithm with Sequential Partial Updates for Active Noise Control" Applied Sciences 11, no. 1: 344. https://doi.org/10.3390/app11010344
APA StyleRamos Lorente, P., Martín Ferrer, R., Arranz Martínez, F., & Palacios-Navarro, G. (2021). Modified Filtered-X Hierarchical LMS Algorithm with Sequential Partial Updates for Active Noise Control. Applied Sciences, 11(1), 344. https://doi.org/10.3390/app11010344







