6. Results
This section presents simulation results to compare the different approaches discussed in the paper:
TSID-Rigid: a state-of-the-art approach, see
Section 3.1.
Adm-Ctrl: a state-of-the-art approach, see
Section 3.2.
TSID-Flex-K: a novel approach, see
Section 5.
6.1. Simulation Environment
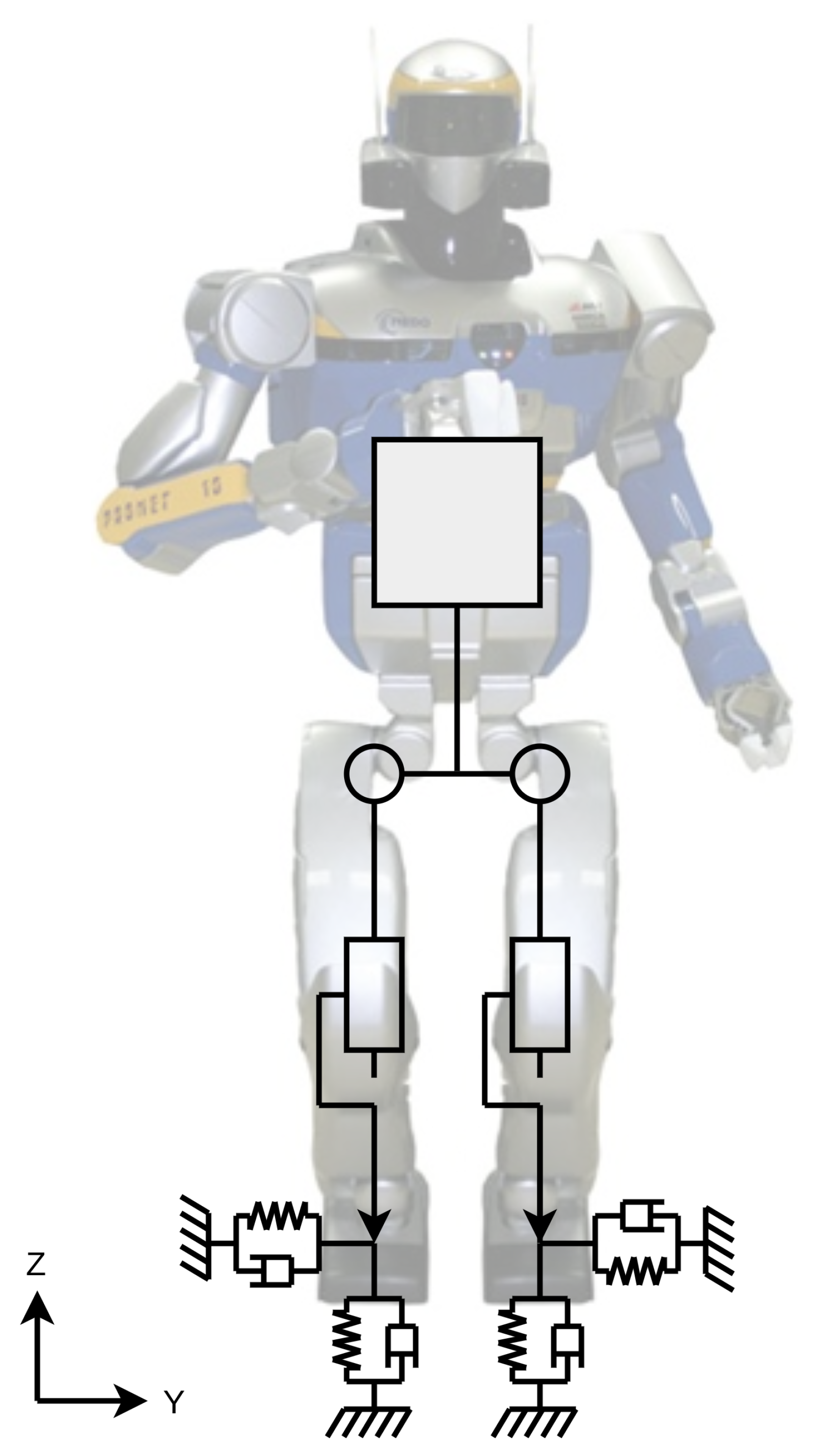
We have carried out all our simulations using a simple 2D biped robot (see
Figure 1), which moves in the YZ plane. The robot is composed by two legs and a torso, and it has 4 actuated joints: two rotatory hip roll joints and two prismatic knee joints. The geometric and inertial parameters of the links have been taken from HRP-2’s model. The simulation is based on a simple explicit Euler integration scheme, and all simulation parameters are listed in
Table 1. The robot has two point feet in contact with a visco-elastic ground. We have investigated different values for the contact stiffness
N/m, ranging from
(i.e., soft) to
(i.e., stiff), while keeping the same contact damping ratio.
We chose to limit our tests to this simple 2D model with point contacts for several reasons. First, this simple model already captures the main features of a biped robot, and it was able to reproduce behaviors that we had previously observed on the real HRP-2 robot [
20]. Second, results obtained with a simple model are easier to analyze and can give us more insights into the behavior of the controllers. Finally, simulations are faster with a simple model, which has allowed us to run more of them, making our statistics more significant.
6.2. Gain Tuning
For tuning the momentum gains we have used the gain-tuning procedure described in
Appendix A for all controllers (except Adm-Ctrl) and for 7 values of a user-specified parameter (
) that defines the trade-off between tracking and control effort. The other task gains and weights have been tuned by hand and are reported in
Table 2. We have set the weight of the postural task so that it would not significantly affect the primary momentum task.
6.3. Test Description
Our tests aim to evaluate the ability of each controller to balance the robot on visco-elastic contacts. To do so, we start the simulation with a non-zero CoM velocity, and we observe whether and how each controller can decelerate the CoM and bring it back to its initial position.
We start by performing three tests, each of which focuses on one specific controller. In our first test (Test A) we show how TSID-Rigid struggles with soft contacts. Then, in Test B, we examine TSID-Flex-K and TSID-Adm, which work well with soft contacts, but get unstable for stiff contacts. Test C shows that Adm-Ctrl remains stable in both cases. Finally, in Test D, we show a comprehensive comparison of all controllers in different situations.
We have tested the controllers both in an ideal simulation (no noise, modeling errors, and perfect state estimation) and in more realistic conditions by introducing:
In the following we will refer to the first kind of simulations as noiseless, and to the second kind as noisy.
6.4. Test A: TSID-Rigid
We have tested TSID-Rigid on both rigid and soft contacts.
Figure 2 shows the CoM trajectories obtained with noiseless simulation. With rigid contacts the controller regulates well the CoM position. Even the CoM velocity is smooth, but looking at the CoM jerk/snap we can see high-frequency oscillations at the beginning of the motion. For soft contacts, even though the system is still stable, performance has deteriorated. We can still see high CoM jerk/snap, which is undesirable, but since this time the oscillations last longer, they are also visible in the CoM velocity. Moreover, with rigid contacts the system remained stable for all gains, but this was not the case with soft contacts, where most gains led to instability (more details in Test D). This clearly highlights the need for a different control strategy to deal with soft contacts.
6.5. Test B: TSID-Flex-K and TSID-Adm
TSID-Flex-K and TSID-Adm have performed extremely well with soft contacts.
Figure 3 shows that TSID-Flex-K gives smoother CoM trajectories than TSID-Rigid, e.g., for the noiseless case, peak CoM jerk is ≈7 ms
rather than ≈26 ms
, while settling time is smaller. TSID-Adm has shown comparable performance on soft contacts, and
Figure 4 shows that it has performed well also on medium contacts. TSID-Flex-K instead performed well on medium contacts only in the noiseless case, whereas it became unstable when noise was introduced. For hard contacts, TSID-Flex-K and TSID-Adm still performed well in noiseless simulations, but got unstable in the noisy case, as we will show in detail in Test D.
6.6. Test C: Adm-Ctrl
Adm-Ctrl has performed well across a large range of contact stiffnesses, as shown in
Figure 5. Moreover, this controller has proven a remarkable robustness to noise, giving similar performance in the noiseless and noisy cases. The price to pay for this robustness seems to be a loss in performance, as measured by the cost function used in our gain-tuning procedure (more details in the following).
6.7. Test D: All Controllers
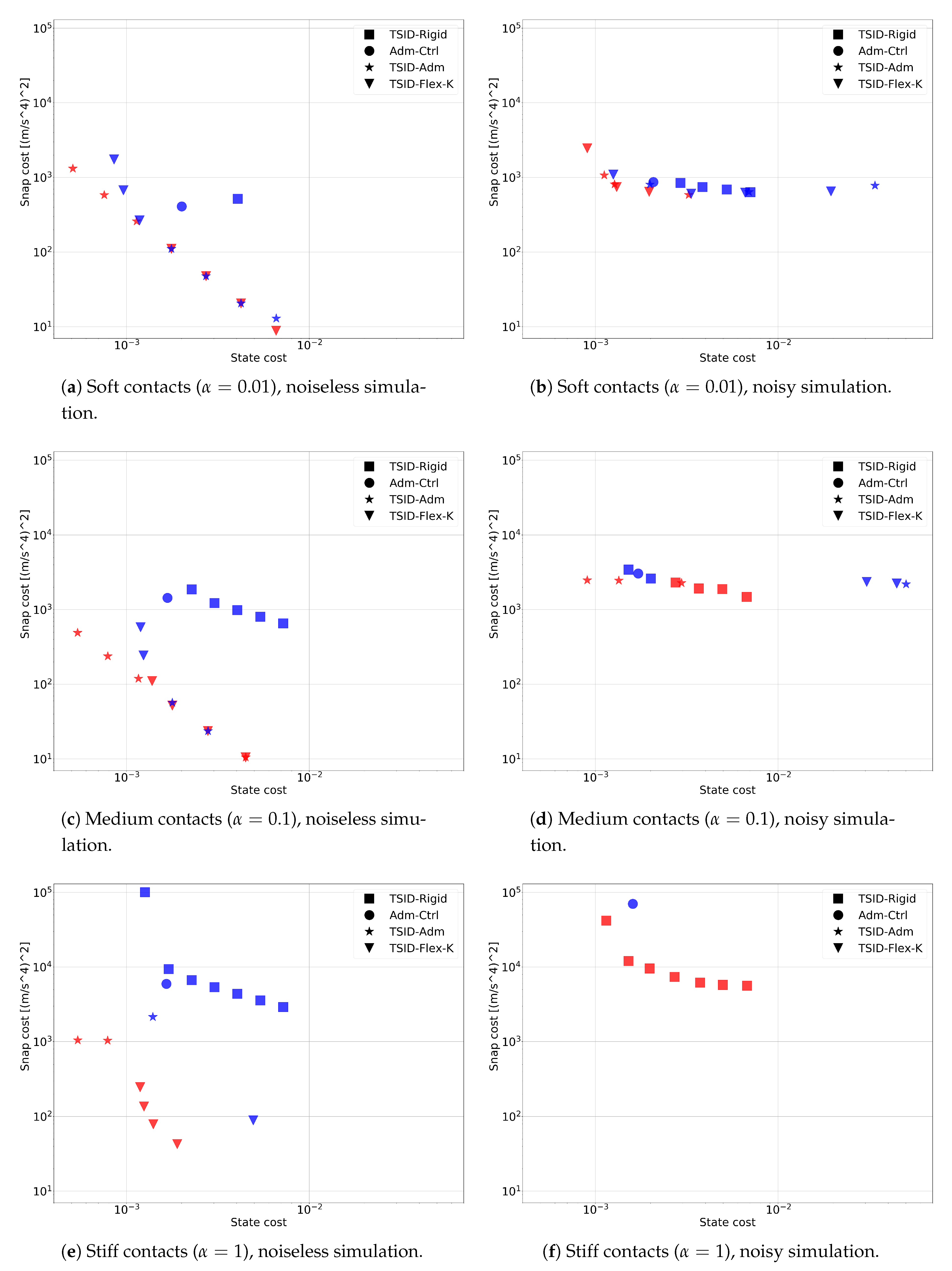
We now compare all four controllers, with different gains and contact stiffnesses. The results are summarized by
Figure 6. Each plot shows the results of the four controllers for all the gain sets (1 for Adm-Ctrl and 7 for the other controllers), but for a specific contact stiffness (either soft, medium, or stiff) and a specific simulation type (either noiseless or noisy). The points missing in the plots are the ones that resulted in unstable simulations (i.e.,
NaN values). The plots highlight the trade-off between average CoM tracking error (
x axis) and average CoM snap (
y axis). The average CoM tracking error (“State cost”) measures how fast balance is recovered after an external perturbation, and it is defined as a weighted sum of CoM position and its first three derivatives along the simulation time:
The average CoM snap (“Snap cost”) quantifies both the CoM oscillations and the control effort, and it is defined as:
6.7.1. Soft Contacts
In the noiseless simulations both TSID-Flex-K and TSID-Adm perform well, meaning that they achieve a good trade-off between state tracking and control effort. For lower feedback gains (i.e., higher position tracking errors) TSID-Flex-K and TSID-Adm achieve very similar performance, whereas for higher feedback gains they differ because of the ways in which they handle friction cones.
The unavoidable force tracking delay of admittance-control strategies is typically seen as an issue in the literature [
3,
8], because it clashes with the assumption of second-order dynamics. However, if we accept a fourth-order dynamics for our system, we can see that this delay is not at all incompatible with good CoM tracking (as long as gains are properly tuned), as shown for instance in
Figure 7. The only downside of this delay is that it may lead TSID-Adm to violate friction cone constraints. Indeed, even though TSID-Adm constrains the desired forces inside friction cones, real forces may violate these constraints because of the tracking delay.
Adm-Ctrl performs reasonably well too, but less than TSID-Flex-K and TSID-Adm. On the contrary, TSID-Rigid is unstable for all the tested gain sets, except one, and even in this one case its performance is inferior to the other controllers (see
Figure 2).
In the noisy simulations, things change remarkably. First, the performance of TSID-Flex-K and TSID-Adm gets worse, especially in terms of CoM snap, and in particular for lower feedback gains. Nonetheless, they remain the best controllers overall. Adm-Ctrl is only slightly affected by the introduction of noise, showing a remarkable robustness. Surprisingly, TSID-Rigid performs much better than in the noiseless case, showing a stable behavior with 3 gain sets, and getting a performance that is much closer to the Pareto front. To understand why, we have performed another test removing Coulomb friction (see
Figure 8). This test shows that Coulomb friction was the cause of the improved stability of TSID-Rigid, and of much of the performance deterioration of the other controllers.
6.7.2. Medium Contacts
In the noiseless case TSID-Flex-K and TSID-Adm perform well, similarly to the soft-contact case. Adm-Ctrl also performs well, resulting in just a slightly higher CoM snap than for soft contacts. The main difference regarding the soft-contact case is that TSID-Rigid is stable for most gain sets (5 out of 7), even though it performs worse than the other controllers.
In the noisy simulations TSID-Flex-K becomes unstable for all feedback gains. TSID-Adm becomes unstable only for low feedback gains, but results in an increased CoM snap for higher gains. The performance of Adm-Ctrl and TSID-Rigid instead gets only slightly worse, showing a significant robustness. Out of the 7 Pareto-optimal points, 4 are associated with TSID-Rigid, and 3 to TSID-Adm.
Despite the performance of TSID-Rigid and TSID-Adm may seem comparable according to this plot, they are qualitatively different.
Figure 9 shows one example of contact forces generated by the two approaches. TSID-Rigid generates fast-changing forces because it immediately applies the joint torques needed to generate the desired contact forces, and given the relatively high contact stiffness, these joint torques quickly result in the desired force change. TSID-Adm instead generates forces with larger oscillations, but with lower frequencies, which may be preferable on real hardware.
6.7.3. Stiff Contacts
In the noiseless case we can already observe a significant performance deterioration for TSID-Flex-K and TSID-Adm, which are unstable for many more gain sets (2 and 4 out of 7, respectively). Nonetheless, they remain the best controllers in this scenario. This deterioration is due to the control frequency, which is insufficient for this contact stiffness, so the sampling starts affecting stability and performance. For high contact stiffnesses, performance could be improved by designing and tuning controllers in the discrete-time domain.
TSID-Rigid and Adm-Ctrl perform similarly to the medium-contact case: stable, but with high CoM snap. In particular TSID-Rigid results in high-frequency oscillations of the contact forces (see
Figure 10), which may excite unmodelled dynamics (e.g., link flexibility) in real systems.
In the noisy case TSID-Flex-K and TSID-Adm became unstable for all gains. We believe that this is due to the delay in the compensation of the estimated contact forces, which triggers instability. This delay is caused by the limited joint torque bandwidth and the joint Coulomb friction.
TSID-Rigid and Adm-Ctrl remained stable, but their performance is far from satisfactory.
Figure 5 and
Figure 11 show the obtained CoM and force trajectories, which are extremely oscillatory (especially for Adm-Ctrl) and are thus unlikely to work on real hardware.
The interested reader is invited to watch the accompanying video for more details about the simulation results.
7. Conclusions
This paper presented two novel control methods for balancing a legged robot on visco-elastic contacts: TSID-Flex-K and TSID-Adm. To ensure a fair comparison between novel and state-of-the-art methods we have used a unified gain-tuning procedure (except for Adm-Ctrl, which we have tuned by hand). We have performed several tests in simulation using a simple 4-DoF robot.
The presented results depict a broad picture of performance for 4 controllers, across 3 contact stiffnesses and 7 gain sets each (except for Adm-Ctrl, for which we have tested only one gain set). We highlight here the main pros and cons of each controller, which are also summarized in
Table 5.
The novel controllers presented in this paper (TSID-Flex-K and TSID-Adm) perform well for soft contacts, reasonably well for medium contacts, but they have showed instability for stiff contacts and noisy simulations.
TSID-Rigid has unsurprisingly shown the opposite trend, getting unstable for soft contacts (even though it was able to regain stability when introducing joint Coulomb friction), but then becoming more and more competitive as the contact stiffness increased. This is actually reasonable because the higher the contact stiffness, the more the system behaves as if contacts were rigid, which is a key assumption in TSID-Rigid.
One of the main advantages of the novel controllers is their ease of gain tuning, which allows for a unified tuning of force and position feedback gains (as acceleration/jerk gains can be seen as force gains). However, the novel controllers have demonstrated a remarkable sensitivity to uncertainties. We believe that this is due to the attempt to compensate for the contact forces, which are rapidly changing (especially for stiff contacts), thus easily leading to destabilizing compensation errors. This makes these methods sensitive to low control frequencies and actuation delays, such as the ones introduced by limited joint torques bandwidth and joint Coulomb friction.
Adm-Ctrl has been the only controller that was always stable, making it the most robust of them all. Despite its superior robustness, in no condition Adm-Ctrl has outperformed all the other controllers. Moreover, its gain tuning remains a heuristic procedure, and its convergence properties are not yet clearly understood. All of this makes this controller hard to use in practice, highlighting the need for more work on this subject.
Overall, the case of stiff contacts was the hardest for the tested controllers: only TSID-Rigid and Adm-Ctrl remained stable, but they resulted in oscillatory trajectories, which are (at best) unpleasant on real hardware. These oscillations are due to the small contact damping, which combined with the high contact stiffness makes it hard for the controller to damp the high-frequency force oscillations.
Finally, these results show that controllers that are well supported by theoretical results and perform exquisitely in ideal conditions, can then fail miserably in realistic simulations. Thus, working on robustness issues seems paramount for future work.
We believe that the subject of balance control on visco-elastic contacts still requires investigation. We are especially interested in improving the robustness of the proposed controllers, in the hope to find a better trade-off between performance and robustness. Another interesting direction could be to understand better the theoretical properties of Adm-Ctrl, which has clearly showed great robustness in our tests, but it remains unclear whether these capabilities can somehow be guaranteed in general.