Method of Calculating the Compensation for Rectifying the Horizontal Displacement of Existing Tunnels by Grouting
Abstract
:1. Introduction
2. Proposed Calculation Method
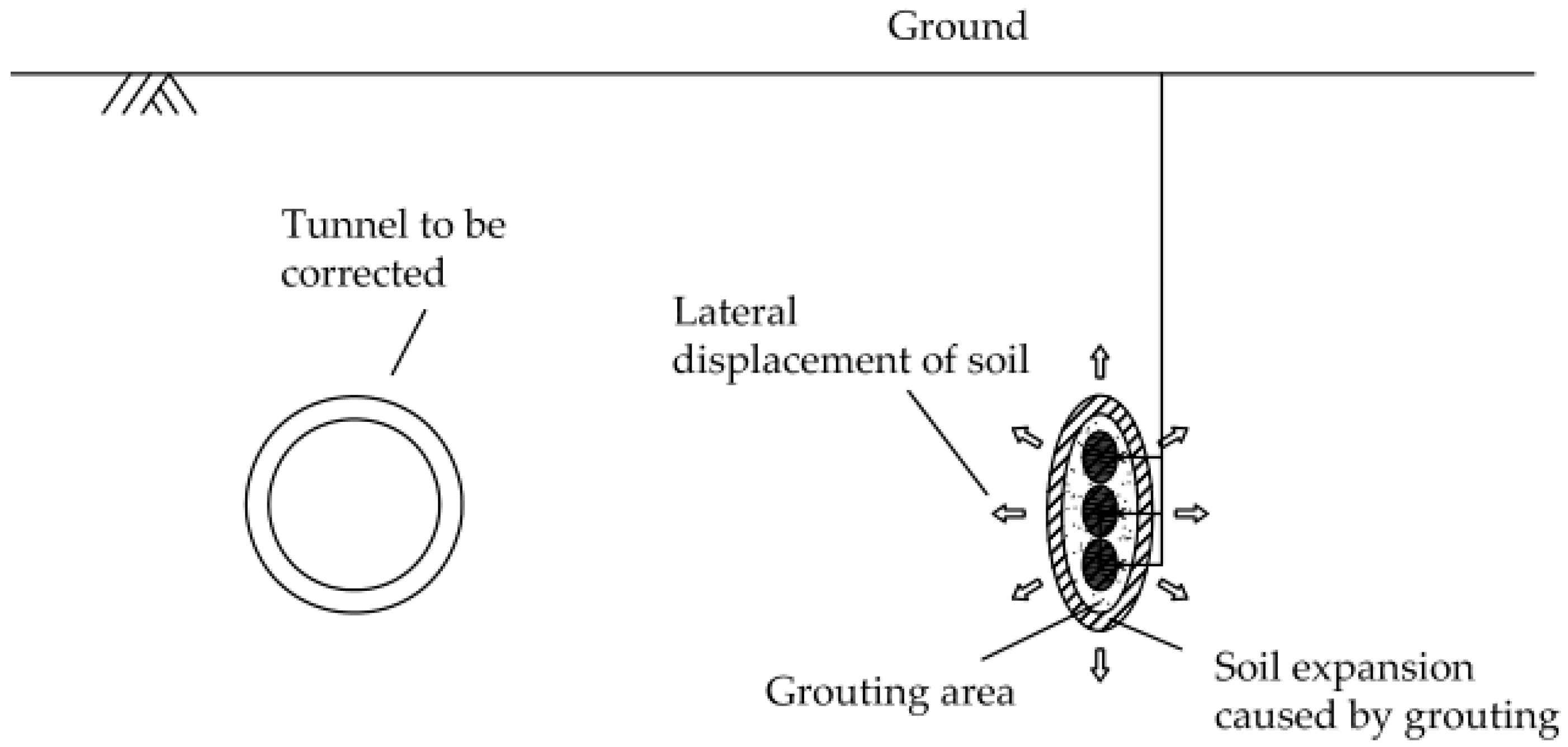
2.1. Principle of Compensated Level of Deflection
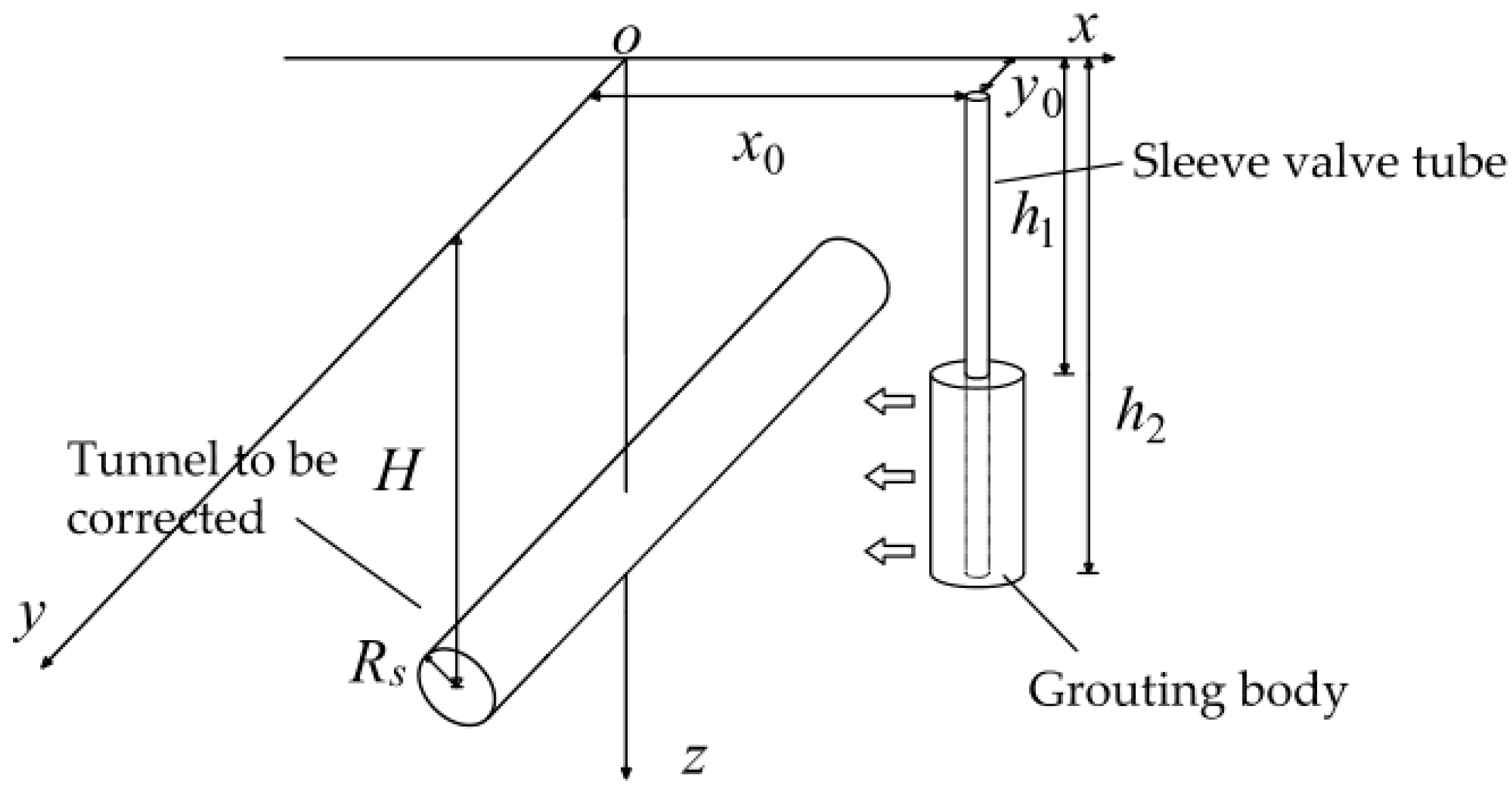
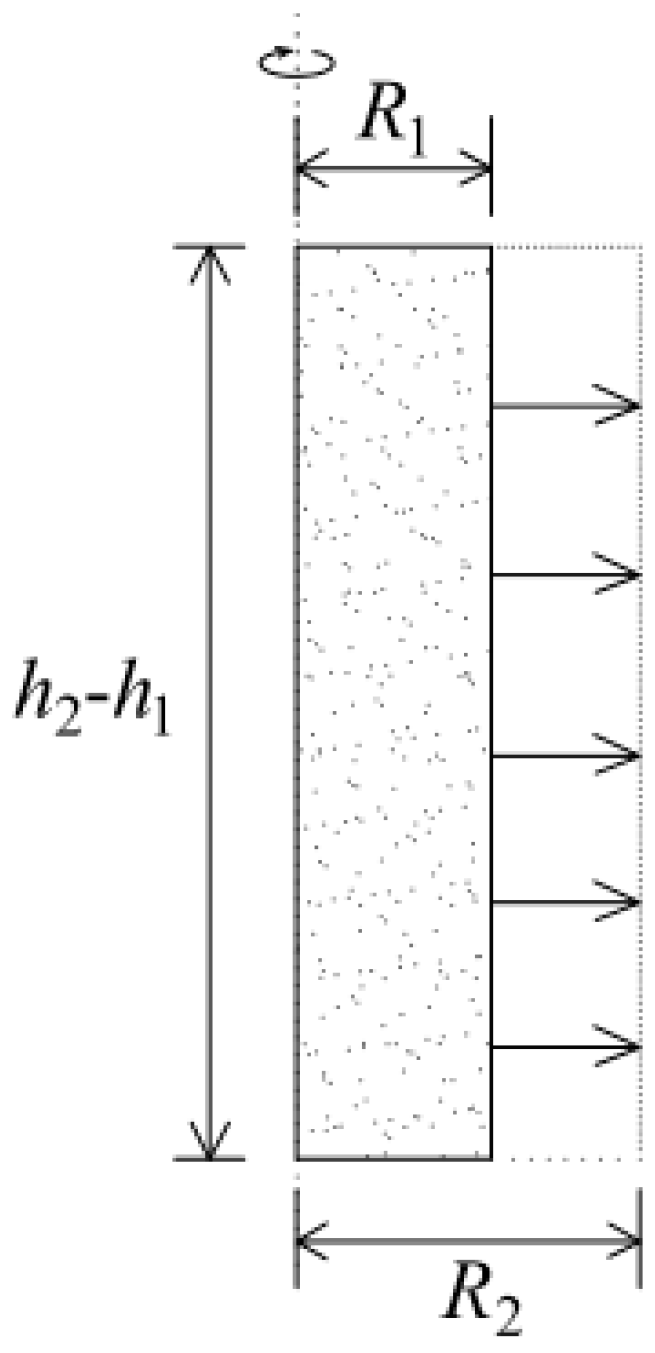
2.2. Calculation of the Additional Stress Caused by Grouting
2.3. Calculation of the Horizontal Displacement in an Existing Tunnel
2.3.1. Energy Conversion of Deformation Process of Existing Tunnel
2.3.2. Derivation of Displacement Function of Existing Tunnel
3. Analysis and Reliability Verification of an Engineering Case
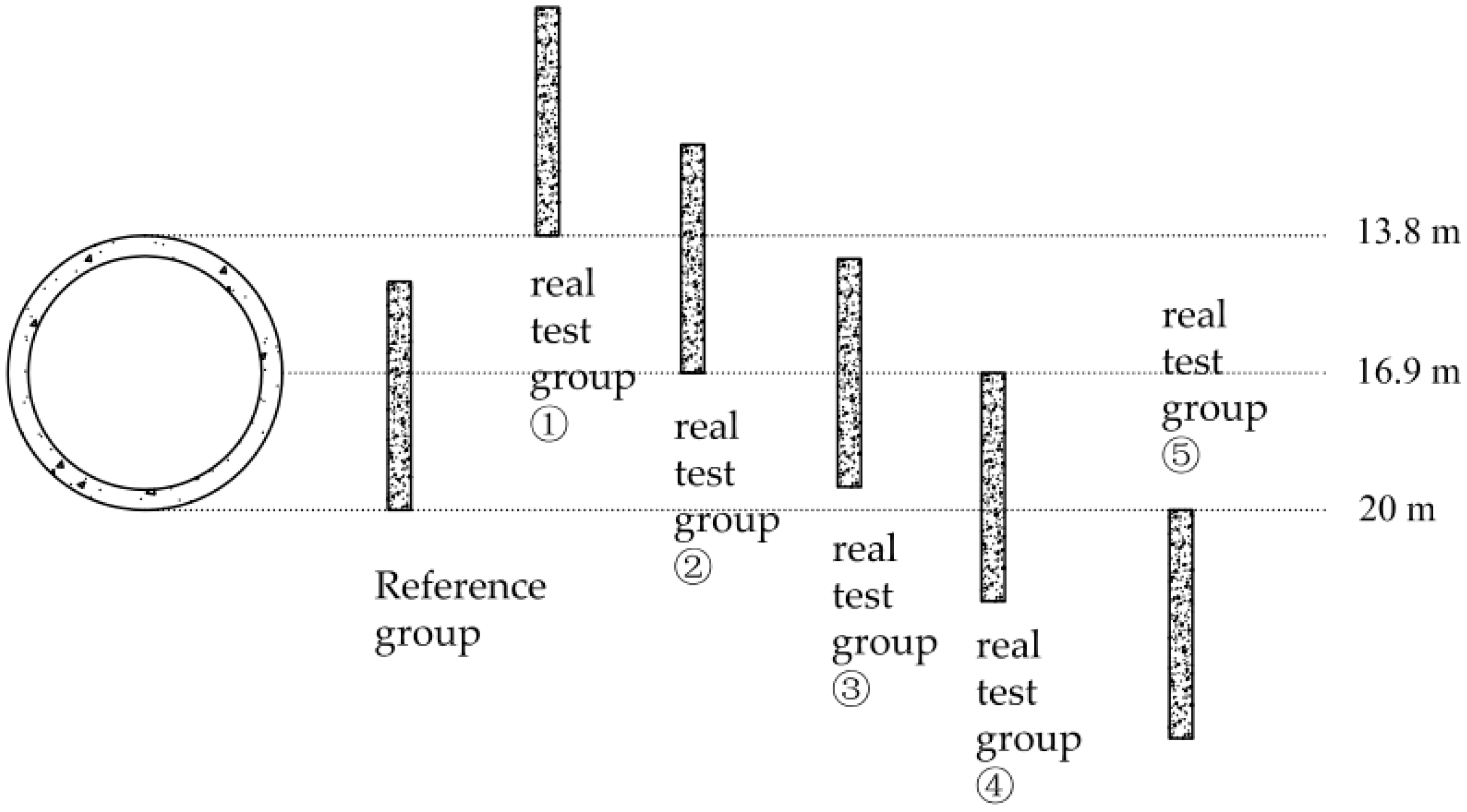
3.1. Operating Conditions
3.2. Analysis of Theoretical Calculation Results
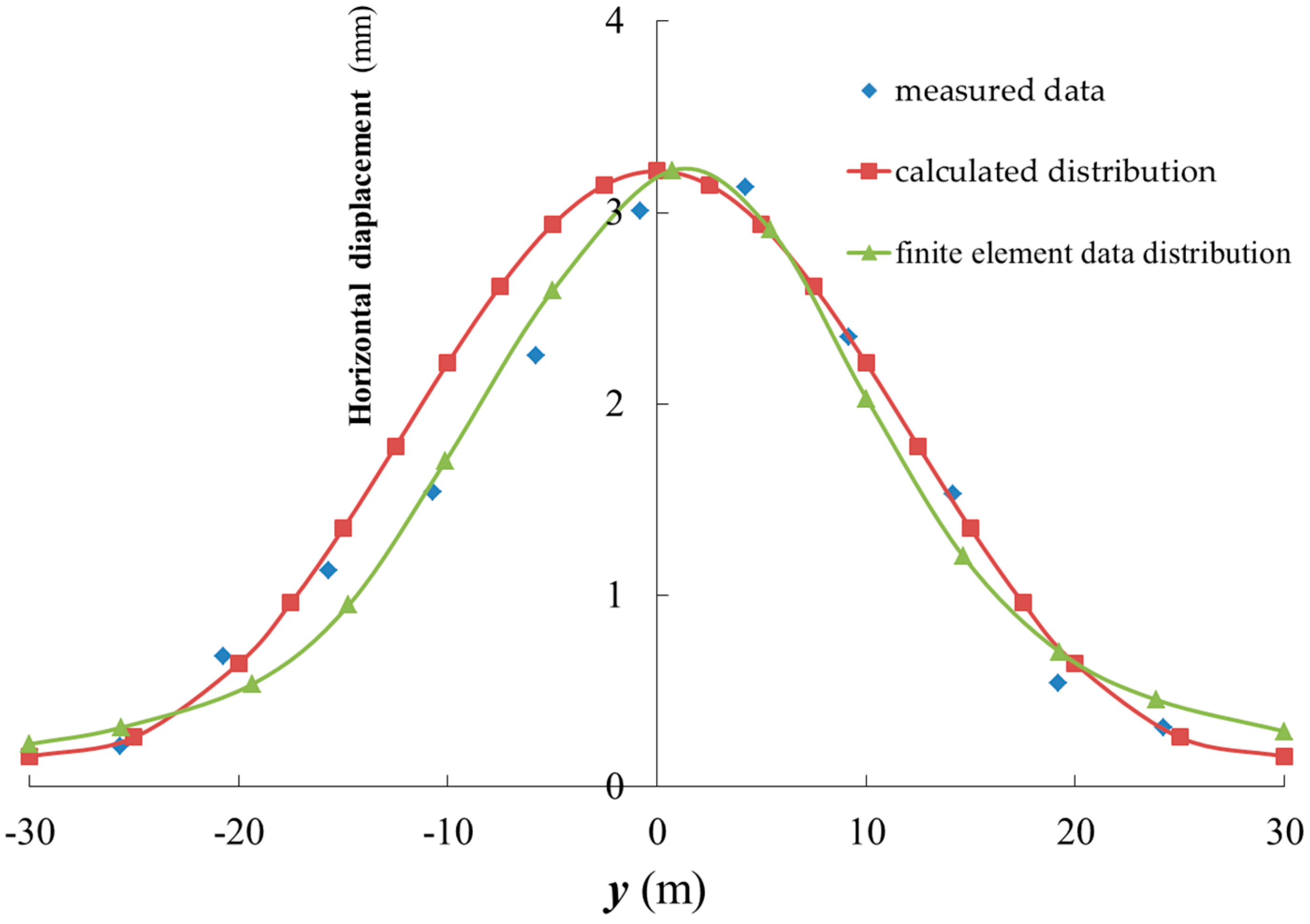
3.2.1. Reliability Verification of the Proposed Method
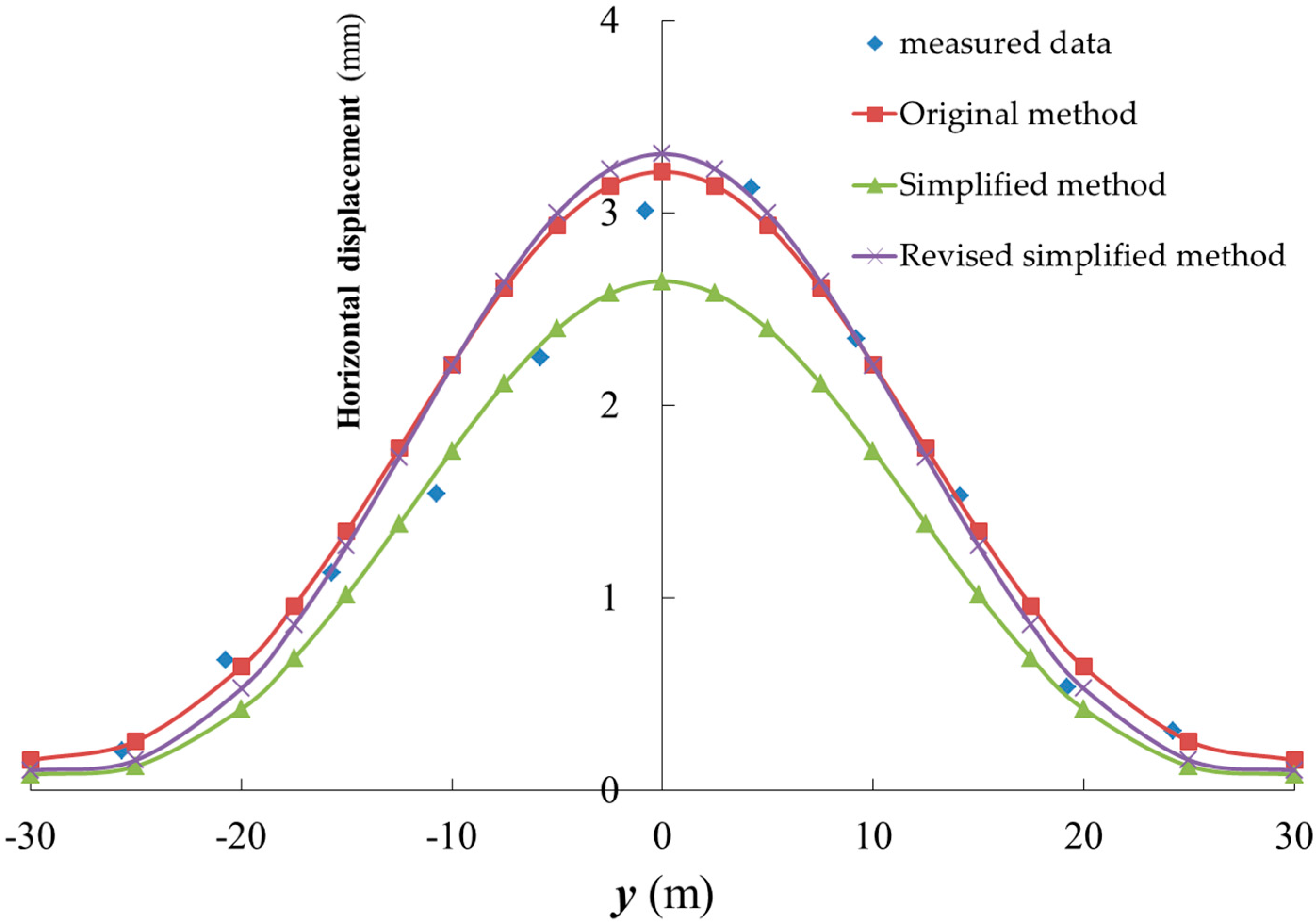
3.2.2. Accuracy Analysis of the Simplified Method
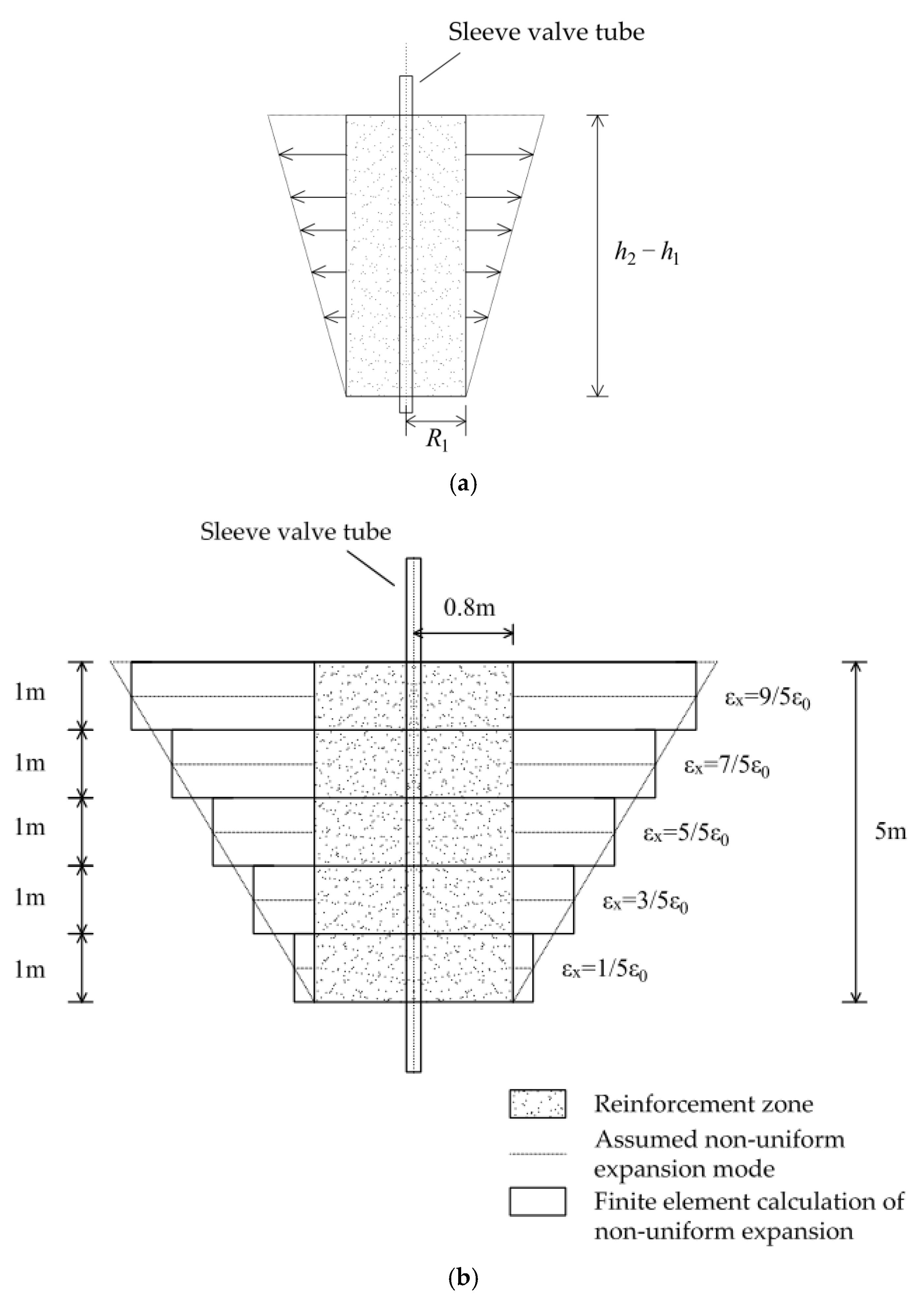
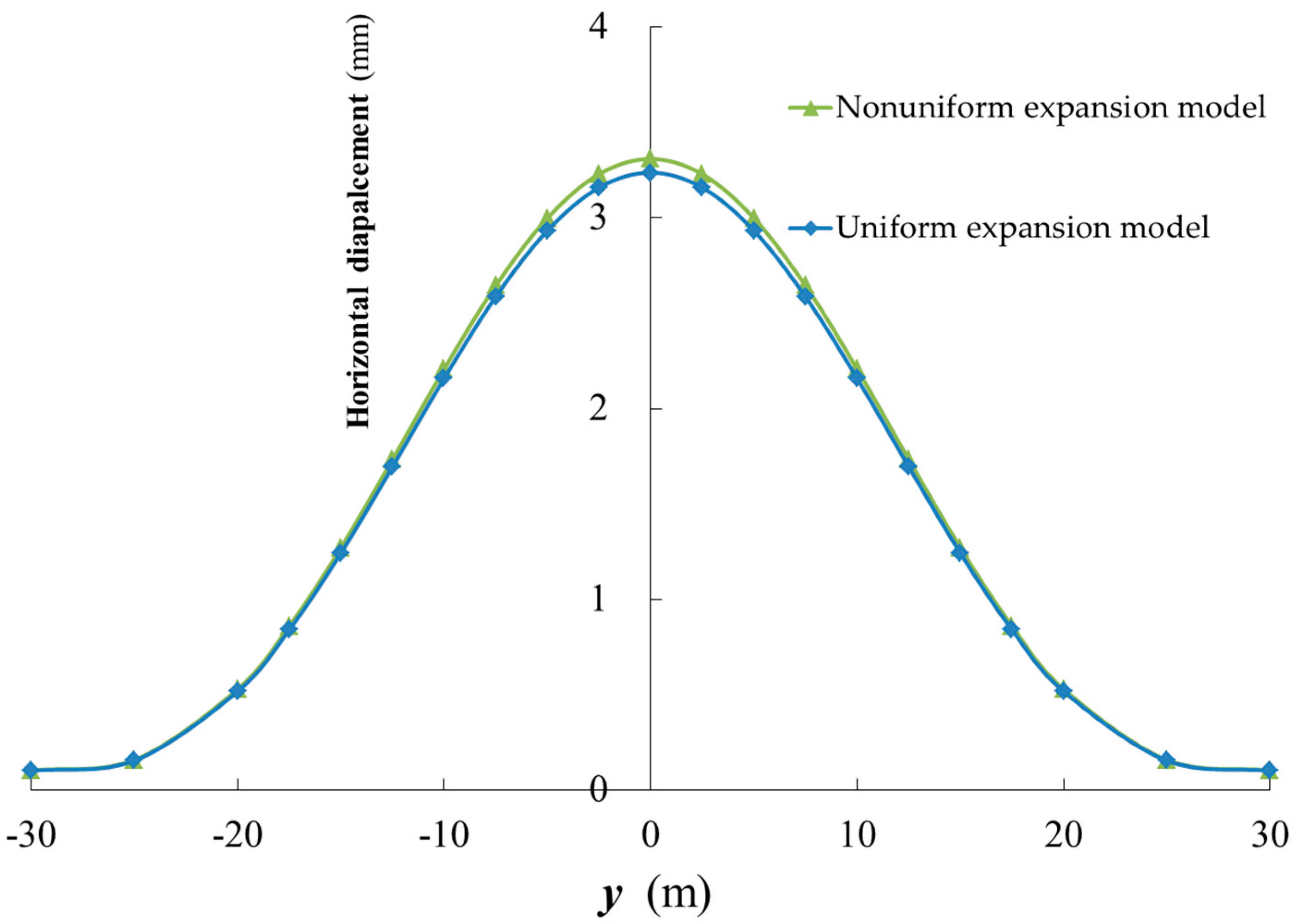
3.2.3. Comparison between Uniform Expansion Model and Nonuniform Expansion Model
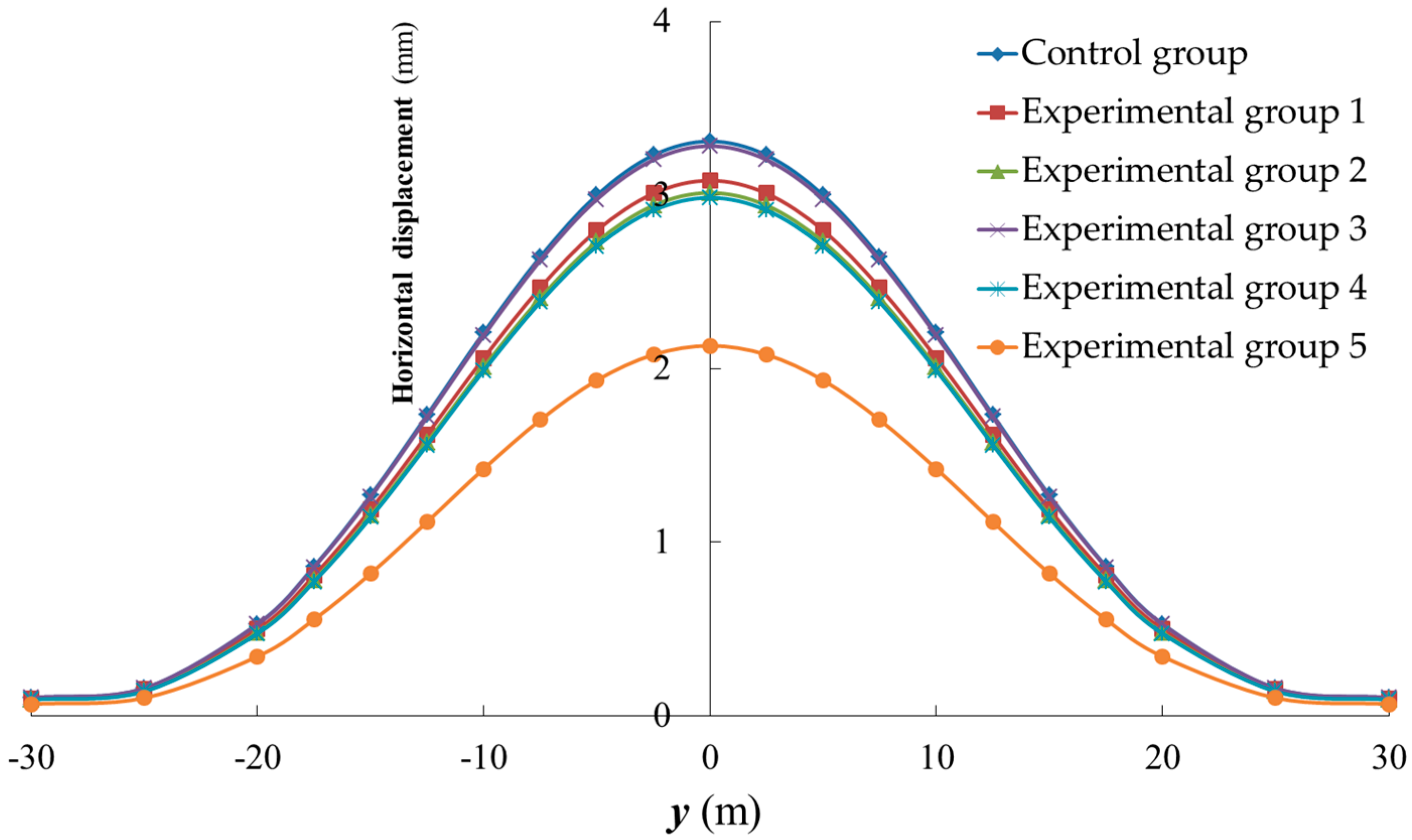
4. Analysis of Single-Factor Influence Law
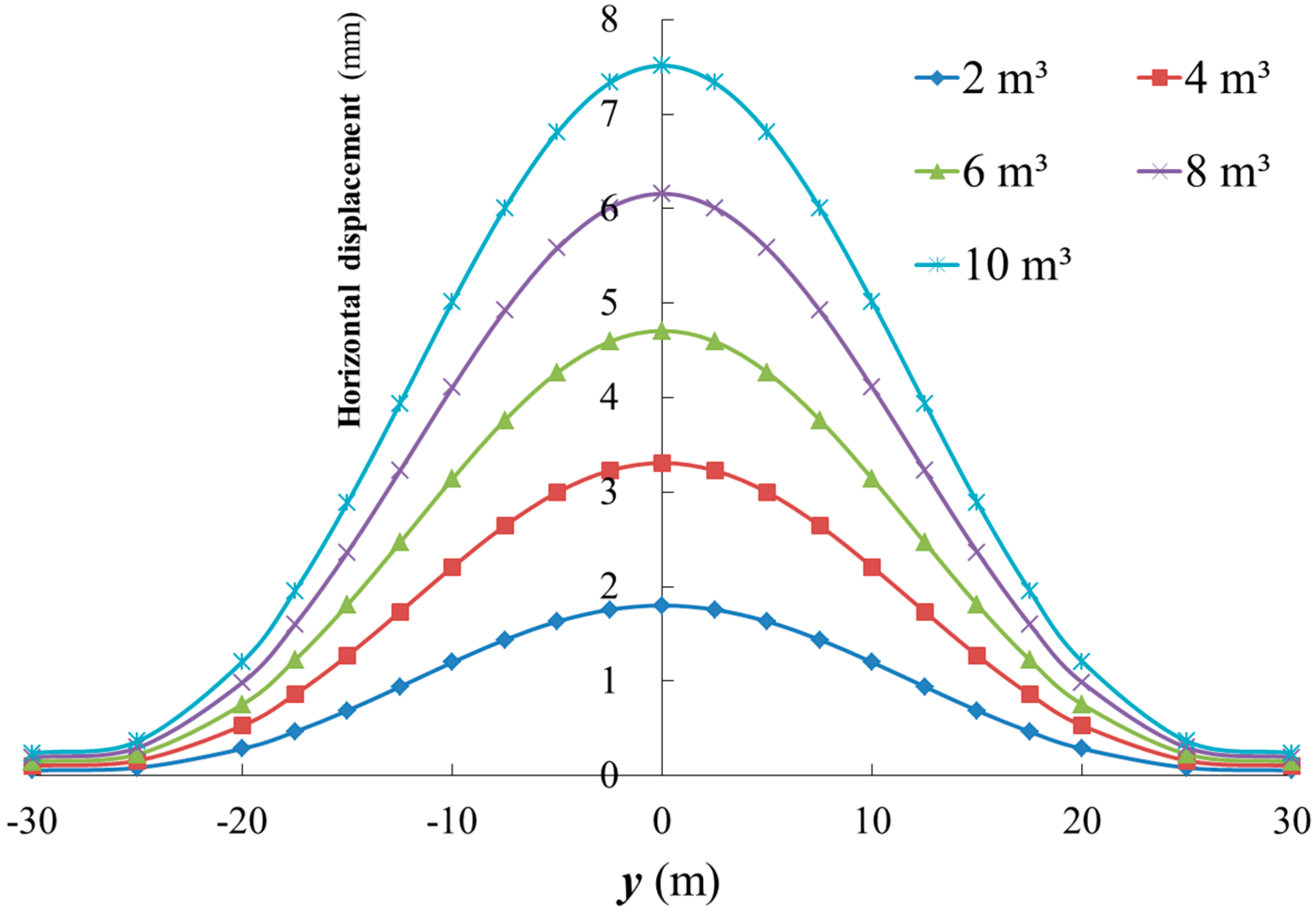
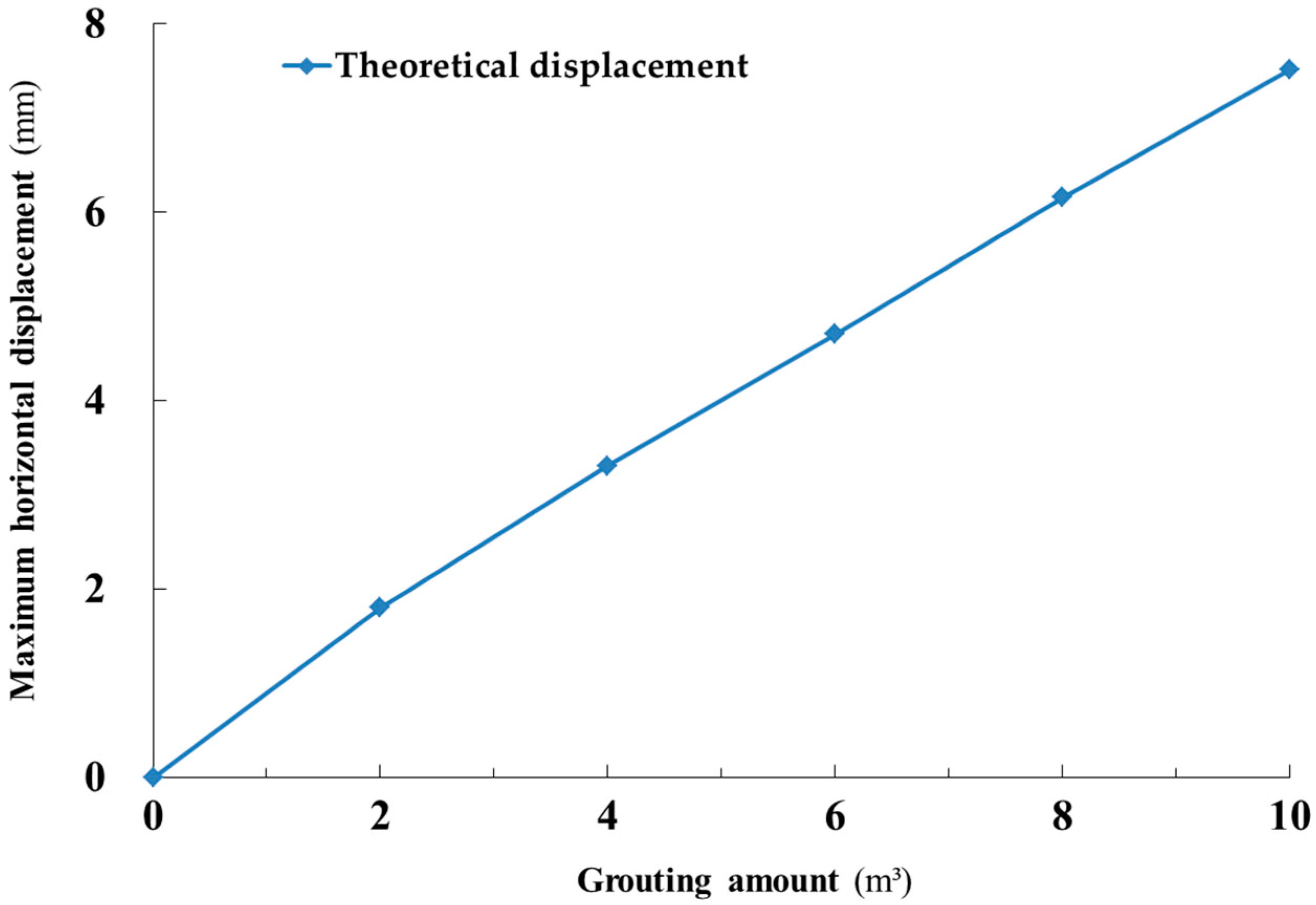
4.1. Influence of Grouting Volume on Compensated Level of Horizontal Displacement of the Tunnel
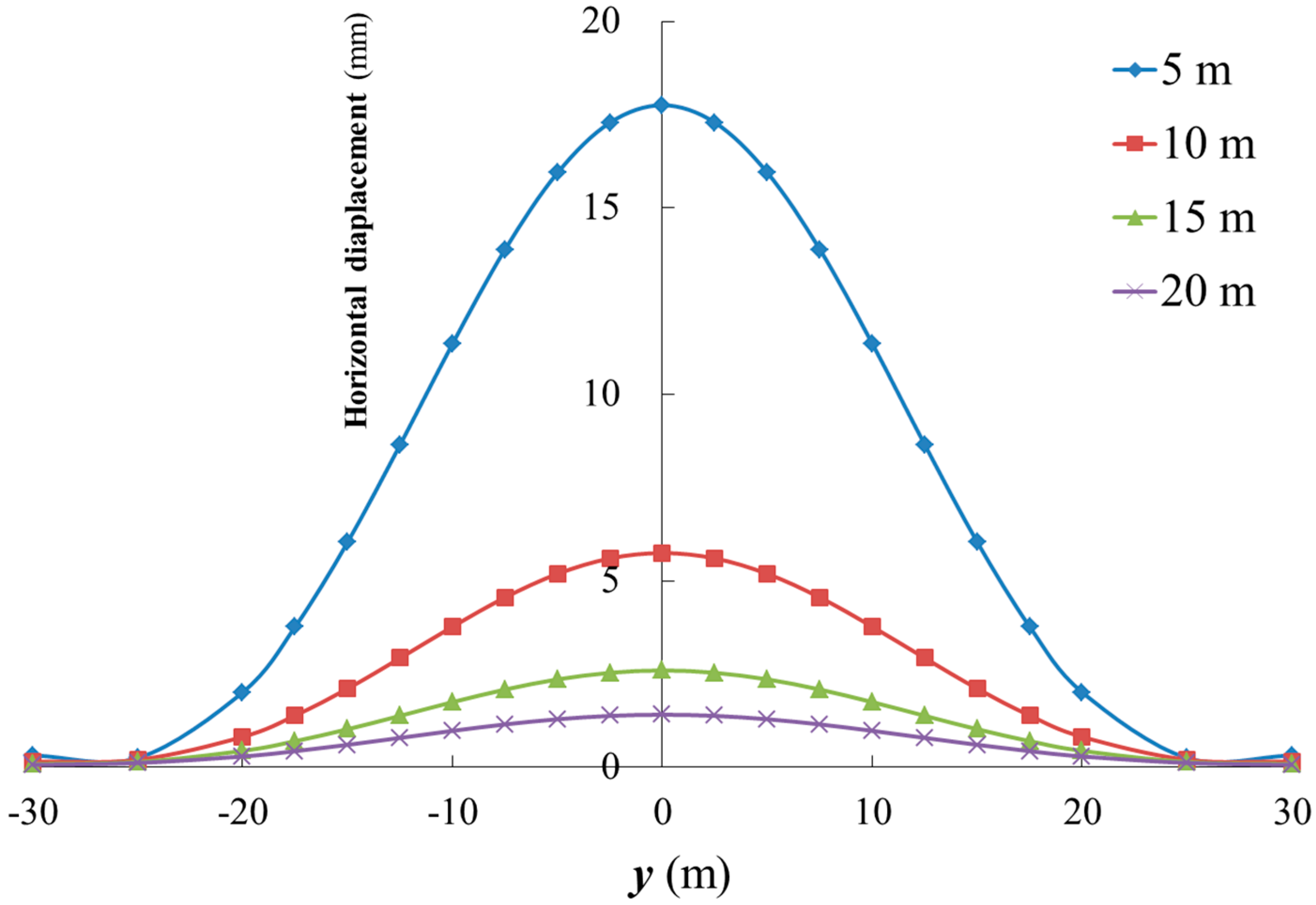
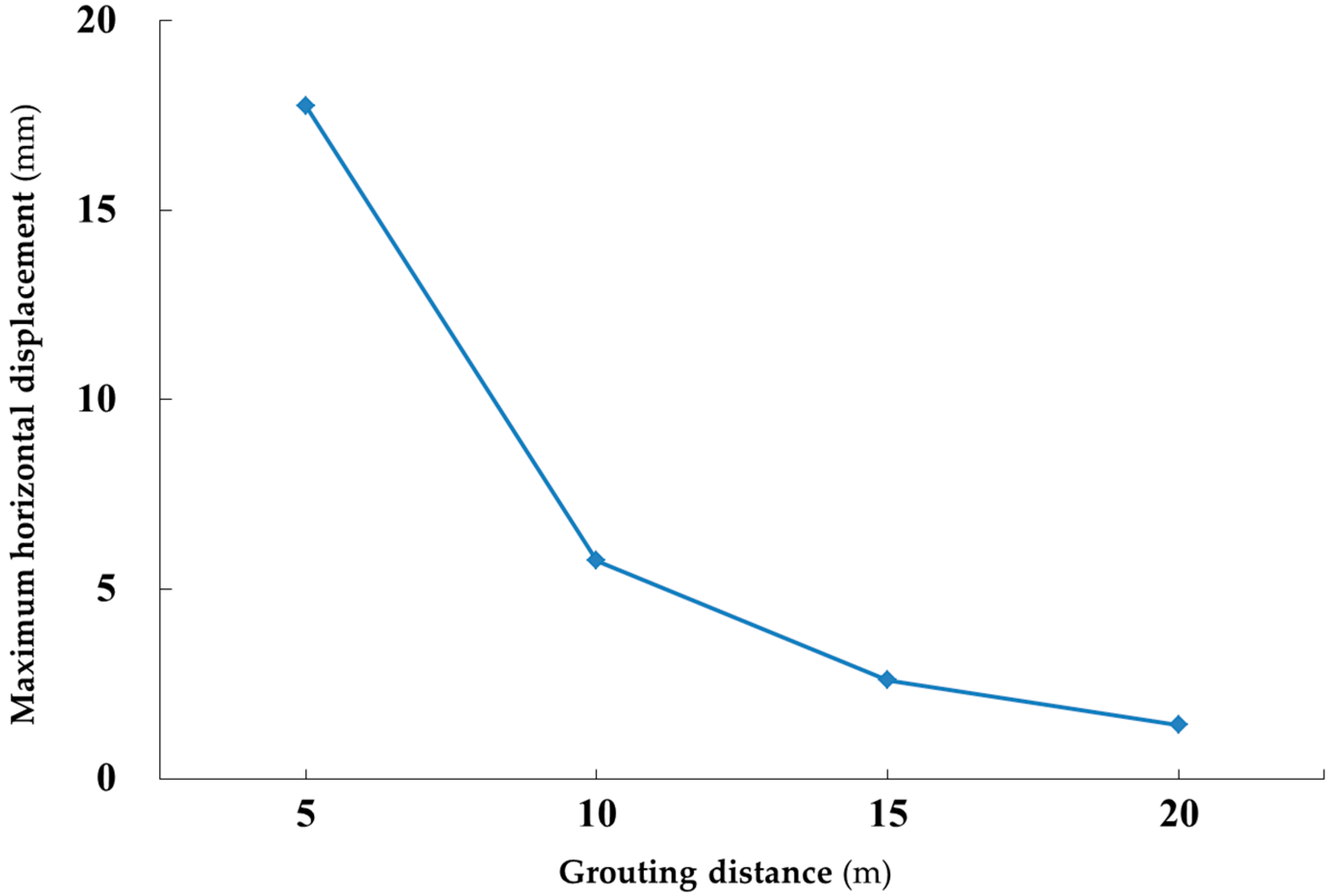
4.2. Influence of Grouting Distance on Compensated Level of Horizontal Displacement of the Tunnel
4.3. Influence of Grouting Depth on Compensated Level of Horizontal Displacement of the Tunnel
5. Conclusions
- The theoretical method developed in this work can calculate the compensation for rectifying the horizontal displacement of existing tunnels by grouting. It can also be used to determine the amount of horizontal displacement of tunnels corrected by grouting. The reliability of the method was verified by comparing the calculated results with actual engineering data. The nonuniform expansion model and the uniform expansion model function similarly in simulating the compensation for rectifying the horizontal displacement of tunnels by grouting. Moreover, both the original method and the revised simplified method proposed herein can properly calculate the horizontal displacement of existing tunnels caused by grouting. The revised simplified method has higher computational efficiency and thus is more suitable for promotion and application.
- The variation of the grouting volume and the grouting distance in a small range has a more significant impact on rectification of the horizontal displacement of existing tunnels; beyond a certain range, the impact of the grouting volume and the grouting distance lessens. At a constant length of grouting section, setting the bottom of the grouting section at the same depth as the lower end of the tunnel maximizes the effect of grouting correction.
- The method proposed herein can help guide actual construction in two ways. First, by substituting the relevant parameters of grouting into this model, the maximum horizontal displacement of the tunnel and the influence range of grouting can be calculated; thus, the results can determine whether the grouting scheme is appropriate. Second, the impact of grouting on rectification of the horizontal displacement of the tunnel can be adjusted by tuning the grouting parameters.
- Finally, a single-factor analysis of the grouting volume, the grouting distance, and the grouting depth was conducted, which resulted in an understanding of the influence law of these parameters and some conclusive suggestions that are of great significance in guiding actual construction projects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, G.; Jian-bo, L.; Xiong-wu, C. Research on the rectifying technology and automatic monitoring of shield tunnel operation in metro. Highw. Automot. Appl. 2018, 4, 150–154, 158. [Google Scholar]
- Ru-bing, B.; Gang, Z.; Yu, D.; Yi-ming, D.; Xue-song, C. Experimental study and numerical analysis of tunnel deformation control by compensation grouting. China Harb. Eng. 2018, 38, 24–28, 55. [Google Scholar]
- Wang, R.L.; Chen, Y.; Ren, J. Application of compensation grouting in the existing tunnels’repair. Under Ground Eng. Tunn. 2013, 51–57. [Google Scholar]
- Min, Z.; Xiao-Nan, G.; Xiang, G.; Shi-Ming, L.; Jia-Jia, Y. Model tests of correction of displaced shield tunnel using grouting technique. J. Railw. Sci. Eng. 2020, 17, 660–667. [Google Scholar]
- Zhang, D.M.; Zou, W.B.; Yan, J.Y. Effective control of large transverse deformation of shield tunnels using grouting in soft deposits. Chin. J. Geotech. Eng. 2014, 36, 2203–2212. [Google Scholar]
- Au, S.K.A.; Soga, K.; Jafari, M.R.; Bolton, M.D.; Komiya, K. Factors affecting long-term efficiency of compensation grouting in clays. J. Geotech. Geoenviron. Eng. 2003, 129, 254–262. [Google Scholar] [CrossRef]
- Min, Z.; Jun-Jun, L.; Wen-Quan, Q. Prediction and simplified model of uplift displacement by grouting. J. Taiyuan Univ. Technol. 2015, 46, 298–302. [Google Scholar]
- Li-Xin, L.; Wu-Li, T.; Jin-Feng, Z. Study on grouting uplift displacement prediction using stochastic medium theory. J. Railw. Sci. Eng. 2013, 10, 47–51. [Google Scholar]
- Sagaseta, C. Analysis of undrained soil deformation due to ground loss. Geotechnique 1987, 37, 301–320. [Google Scholar] [CrossRef]
- Tao, W.; Ri-Qing, X.; Jing-Jing, Q.; Hao, L. Additional stress field of surrounding soil due to shield tunneling. J. Zhejiang Univ. (Eng. Sci.) 2008, 42, 2009–2014. [Google Scholar]
- Ru-Bing, B. Study on Grouting Control of Influence of Foundation Pit Construction on Deformation of Adjacent Tunnels. Ph.D. Thesis, Tianjin University, Tianjin, China, 2018. [Google Scholar]
- Schweiger, H.F.; Kummerer, C.; Otterbein, R.; Falk, E. Numerical modelling of settlement COMPENSATION by means of fracture grouting. J. Jpn. Geotech. Soc. Soils Found. 2004, 44, 71–86. [Google Scholar] [CrossRef] [Green Version]
- Komiya, K.; Soga, K.; Akagi, H.; Jafari, M.R.; Bolton, M.D. Soil consolidation associated with grouting during shield tunneling in soft clayed ground. Geotechnique 2001, 51, 835–846. [Google Scholar] [CrossRef]
- Gollegger, J. Numerical and Analytical Studies of the Effects of Compensation Grouting. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2001. [Google Scholar]
- Xin-Liang, J.; Zhi-Min, Z. Application of image method in calculating tunneling-induced soil displacement. J. Harbin Inst. Technol. 2005, 37, 801–803. [Google Scholar]
- Gang, W.; Yong-Jie, Q.; Hua-Jun, W. Calculation of rotation and segment ring dislocation deformation caused by surcharge in shield tunnels. Tunn. Constr. 2019, 39, 1781–1789. [Google Scholar]
- Gang, W.; Xin-Hai, Z. Calculation of rotation and shearing dislocation deformation of underlying shield tunnels due to foundation pit excavation. J. Cent. South Univ. (Sci. Technol.) 2019, 50, 2273–2284. [Google Scholar]
- Qi, Y.; Wei, G.; Xie, Y. Method of Calculating the Vertical Displacement and Additional Stress of Existing Tunnels under the Influence of Grouting Rings of New Tunnels. Symmetry 2020, 12, 1623. [Google Scholar] [CrossRef]
- Shen, S.L.; Wu, H.N.; Cui, Y.J.; Yin, Z.Y. Long-term settlement behavior of metro tunnels in the soft deposits of Shanghai. Tunn. Undergr. Space Technol. 2014, 40, 309–323. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, Y.; Wei, G.; Feng, F.; Zhu, J. Method of Calculating the Compensation for Rectifying the Horizontal Displacement of Existing Tunnels by Grouting. Appl. Sci. 2021, 11, 40. https://doi.org/10.3390/app11010040
Qi Y, Wei G, Feng F, Zhu J. Method of Calculating the Compensation for Rectifying the Horizontal Displacement of Existing Tunnels by Grouting. Applied Sciences. 2021; 11(1):40. https://doi.org/10.3390/app11010040
Chicago/Turabian StyleQi, Yongjie, Gang Wei, Feifan Feng, and Jiaxuan Zhu. 2021. "Method of Calculating the Compensation for Rectifying the Horizontal Displacement of Existing Tunnels by Grouting" Applied Sciences 11, no. 1: 40. https://doi.org/10.3390/app11010040
APA StyleQi, Y., Wei, G., Feng, F., & Zhu, J. (2021). Method of Calculating the Compensation for Rectifying the Horizontal Displacement of Existing Tunnels by Grouting. Applied Sciences, 11(1), 40. https://doi.org/10.3390/app11010040




