Computationally Efficient Models of High Pressure Rolling for Wire Arc Additively Manufactured Components

Abstract

High pressure multi-layer rolling is an effective method to reduce residual stress and distortion in metallic components built by wire arc additive manufacturing (WAAM). However, the mechanisms of the reduction in residual stress and distortion during multi-layer rolling are not well understood. Conventional finite element models for rolling are highly inefficient, hindering the simulation of multi-layer rolling for large WAAM components. This study aims to identify the most suitable modelling technique for finite element analysis of large WAAM component rolling. Four efficient rolling models were developed, and their efficiency and accuracy were compared with reference to a conventional large-scale rolling model (i.e., control model) for a WAAM built wall. A short-length transient model with fewer elements than the control model was developed to reduce computational time. Accurate predictions of stress and strain and a reduction in computational time by 96.5% were achieved using the short-length model when an implicit method for numerical solution was employed, while similar efficiency but less accurate prediction was obtained when an explicit solution method was adopted. A Eulerian steady-state model was also developed, which was slightly less efficient (95.91% reduction in computational time) but was much less accurate due to unrealistic representation of rolling process. The applicability of a 2D rolling model was also examined and it was found that the 2D model is highly efficient (99.52% time reduction) but less predictive due to the 2D simplification. This study also shows that the rigid roller adopted in the models is beneficial for improving efficiency without sacrificing accuracy.

1. Introduction

Wire arc additive manufacturing (WAAM) is an emerging technology that is particularly suited to building large components through adding multiple layers of materials with the aid of an arc heat source, robotic manipulator and computer control. WAAM allows production of large components with medium resolution and surface quality [1], using a wide range of materials, such as steel [2,3], titanium alloy [4], nickel superalloy [5], aluminium [6], tantalum [7,8] and tungsten [9,10]. It was used for building a variety of components, from relatively simple walls [3] and cylindrical structures [11] to complex components with variable wall thicknesses, e.g., demo parts of turbine blades, wing spar and landing gear structures [11]. WAAM utilises off-the-shelf industrial robots, conventional welding power sources and cheap welding wire consumables that are readily available in the market, thereby reducing initial investments, build-up and operational costs [12,13,14,15]. WAAM is also more environmentally friendly compared to powder based additive manufacturing processes [16]. In comparison with traditional manufacturing techniques, WAAM can substantially reduce material usage, manufacturing costs and lead time, and hence it has attracted great interest for applications in aerospace, transport and energy industries.

During WAAM deposition the concentrated heating by the electric arc causes local material expansion. The material with low yield strength at elevated temperature deforms in compression during heating due to the constraint imposed by the surrounding material. After the arc heat source passes, the deformed material cools down and tends to shrink [17]. The heating-cooling cycle results in thermal stresses and plastic strains (PSs) in the deposited layers and the substrate (usually restrained by clamps, fixtures, etc.). After the deposition, residual stress (RS) arises in the built part, which can lead to distortion after removal of the external restraint [3,18,19]. RS is usually detrimental to performance, since it can adversely affect fatigue life, increase probability of brittle fracture and reduce corrosion resistance [20,21,22,23].

High pressure rolling was found effective in reducing RS and distortion in WAAM built components [3,4,24], since it induces tensile PS in the built part and substrate, which compensates for the compressive PS caused by the thermal deposition cycle. The rolling can be implemented in different ways. For instance, inter-pass rolling after WAAM deposition of each layer was demonstrated as effective in reducing RS and distortion [3,4]; rolling every four deposited layers and rolling solely on the last layer of a WAAM built component were found effective as well [3]. Effective rolling should commence when the WAAM component is cooled to ambient temperature (below 50 °C), because in situ rolling (i.e., roller follows welding torch) has a negligible effect on distortion [3]. Experiments showed that an increase in rolling load is beneficial for the mitigation of RS and distortion [3,4]. Regarding the effect of roller geometry, the use of a slotted roller instead of a flat or profiled roller (i.e., roller with a groove) can significantly improve the efficacy of rolling, since the lateral restraint of the slotted roller promotes larger longitudinal deformation in the rolled material [3]. High pressure rolling has been successfully applied to WAAM deposited walls [3,4] and intersections [25,26], using materials such as mild steel [3] and titanium alloy [4,24,25]. The rolling also can improve fatigue life and mechanical properties [27,28], refine microstructure [3,24,25,26,29] and reduce porosity [6,30]. However, detailed mechanisms of the reduction in RS and distortion during high pressure rolling of WAAM built components are not well understood.

The finite element method (FEM) is widely used in simulations of rolling [31,32], which can reduce experimental effort, time and cost. However, current FEM simulations of rolling in WAAM are highly inefficient, especially for large components. For instance, high performance computing (HPC) facility was required to simulate rolling in a 456 mm long part, and the computational time was up to 92 h [33]. When multi-layer rolling is used in WAAM [3,4,24], the computational demands are further exacerbated, and the simulation of rolling for a typical 20-layer WAAM part could take weeks. This makes multi-layer rolling simulation impractical. Therefore, efficient modelling techniques are needed to reduce computational time while still ensuring accuracy.

In current literature only two publications were found to address rolling simulation for WAAM built components [34,35]. For similar problems, the modelling research relevant to WAAM rolling includes the simulations of burnishing [36,37,38,39], deep rolling processes [40,41,42,43], hot and cold manufacture rolling processes [44,45], and rolling for reducing RS in quenched block [46] and weld seams [33,47]. All of these aforementioned rolling processes are technically similar to high pressure rolling in WAAM, i.e., additional plastic deformation is introduced in the component to impose a desired effect. Thus, the development of efficient rolling models for WAAM will be mainly based on a literature survey of the allied fields. The available efficient modelling techniques are summarised as follows.

1.1. Non-Uniform Mesh Density

The time required to solve an FEM model largely depends on the number of elements involved in analysis. Rolling is a highly nonlinear contact problem, which usually involves large deformation and requires fine mesh for numerical convergence [33,40,41] and accurate prediction [48]. Non-uniform mesh density, actively used in most of the FEM simulations of rolling, keeps the dense mesh in the contact region and the coarse mesh in other regions far from the roller, thereby reducing the total number of elements with minimum impact on accuracy. The creation of non-uniform mesh density does not require special techniques or algorithms and can be done using standard finite element analysis (FEA) software tools. Such a strategy to generate efficient models has been widely adopted in 2D [40,49,50] and 3D [33,34,38,41,42,43,45,46,47] simulations of rolling and burnishing.

1.2. Reduced Length of Modelled Component

Reducing the length of the modelled component is also effective for improving efficiency, since it can reduce the number of elements in the FEM model. However, it is questioned whether a short model can represent the behaviour of a large full-scale model. An early study by Bijak-Żochovski et al. [49] examined rolling contact with friction, and it was found that short models are sufficient to “stabilize analyzed quantities” [49] and “further wheel travel does not effectively change the pictures of stresses and strain in tested area” [49]; in other words, the reduced length is sufficient for the model to reach a steady state of rolling.

Cozzolino et al. [33] used an FEM model with significantly shorter length (465 mm) compared to the actual workpiece (750 mm) that was rolled during experiments, so as to reduce computational time, and the short model predicted similar results to the full scale model. For rolling in a WAAM component, Abbaszadeh et al. [34] developed a model with a length of 100 mm for a deformable component, which was rolled along the minimal length under steady state, and they found that a further increase of the rolling distance in analysis did not make any marked difference in the result. Short models have also been used in other rolling scenarios. For instance, Trauth et al. [42] and Perenda et al. [43] used short segments for simulations of deep rolling of a circular component. Pan et al. [46] developed a 62 mm long model for rolling simulation of quenched aluminium blocks. Hassani-Gangaraj et al. [41] and Balland et al. [51] employed short models for deep rolling and burnishing.

The main criterion to determine the shortest length for the rolled component is that the shortened component should be able to reach a steady state of rolling. The manual of the FEM analysis software, Abaqus, suggests that the equivalent plastic strain, rolling force and torque should be used as the norms for steady-state detection. Steady-state rolling is reached when the reaction force and moment are stabilised, while the equivalent plastic strain in the rolled material becomes constant or fluctuates around a certain value [52].

1.3. Rigid Roller

Normally, roller material (e.g., tungsten carbide [40] and H13 steel [46]) is much harder than rolled material. The elastic deformation of the roller is insignificant and barely affects the solution accuracy [41]. Therefore, rollers in most of the rolling models are assumed to be rigid and are defined as analytic surfaces, preventing discretisation of the roller and hence reducing the total number of elements. In addition, compared to the discretised elastic or rigid surface that is represented by element faces, a smooth analytic surface allows lower contact noise and better approximation in contact formulation to improve computational efficiency [48,53]. A rigid roller or tool was adopted in the deep rolling and burnishing models by Perenda et al. [43] and Manouchehrifar et al. [39] and the weld rolling model by Cozzolino et al. [33], among many other models [40,41,42,44,45,46,47,51]. However, Hassani-Gangaraj et al. [41] found that their deep rolling model underestimated compressive RS in a depth of 0.2 mm below the rolled surface, and they attributed the error to the use of a rigid roller in their model. To eliminate potential errors, Abbaszadeh et al. [34] considered elastic deformation of the roller in their rolling model.

1.4. 2D Rolling Model

Rolling simulation for a simple component (e.g., single wall) can be simplified as a 2D problem, particularly when the material response to rolling is similar in the out-of-plane direction. Compared to 3D models, a 2D model can dramatically reduce the number of elements and hence significantly improve the computational efficiency. 2D models in structural analysis are usually based on plane stress and plane strain theories. Rodríguez et al. [50] demonstrated that the predictions of a 2D burnishing model are close to those of a 3D model, and the modelling results are correlated well with experimental results. Röttger [36] created a 2D plane strain model of burnishing, which underestimated the penetration depth of the spherical rolling tool as a result of the overestimated contact surface area due to plane strain assumption. Similar research was conducted by Yen et al. [37], who used a 3D model to accurately predict tool penetration.

1.5. Explicit Analysis for Contact Problems in Rolling

Numerical methods used by FEM software to solve contact problems can influence the computational time and simulation accuracy. As suggested by the Abaqus manual, explicit dynamics solution techniques can be more computationally efficient and reliable than implicit methods for 3D rolling models with complex geometries, nonlinear material properties and discontinuous effects such as contact and friction [52]. However, Harewood et al. [54] found that for simple loading conditions with rigid bodies involved in contact simulation, implicit analysis solver requires less computational time than explicit analysis solver. The explicit method was found preferable for complex contact interactions, for example, between deformable bodies or where large deformation is involved. The explicit method demonstrates increased robustness/convergence and greater suitability for parallel calculations using multiple processors [54]. In contrast, Oliver et al. [55] suggested that the implicit method is more accurate and efficient, although less robust than the explicit method.

To accelerate explicit analysis for quasi-static problems, material density can be artificially increased (i.e., using mass scaling method) [52]. However, with aggressive mass scaling, inertia starts to play a significant role in the solution and will affect the result [48]. To restrict the artificial inertia effect, it is recommended by Chin et al. [56] and Abaqus Analysis User’s Guide [48] that the ratio between kinetic and internal energies of the model should be maintained at no larger than 5%.

Specifically for rolling, the problem can be treated as quasi-static and solved by the explicit method for FEM analysis. For instance, Hassani-Gangaraj et al. [41] investigated RS in railway axles that experienced multi-run parallel deep rolling. Trauth et al. [42] created a model to optimise the deep rolling process for IN718 turbine blades and 42CrMo4 crankshafts, in which a mass scaling factor of 250 was used and a reduction in CPU time by two-thirds was achieved without impairing the accuracy. Lan et al. [45] developed a rolling model to predict the RS in a rolled bearing race, and a mass scaling factor of 400 was adopted to reduce computational time.

1.6. Eulerian Analysis for Contact Problems in Rolling

Eulerian analysis is a computationally efficient way to model large deformation [48]. Based on the Eulerian method, the rolling is simulated via material flow through the mesh in the space instead of moving the roller, such that mesh refinement is needed only near a “stationary” roller and the number of elements can be greatly reduced [48]. The “mass scaling” option is also available for Eulerian explicit analysis to increase the stable time increment and reduce computational time for quasi-static analysis. The steady state detection option of Eulerian explicit analysis halts simulation as soon as steady state is detected [52]. The Eulerian method was used by Maniatty et al. [57] to simulate steady-state rolling and extrusion processes. The mixed Eulerian–Lagrangian method for steady-state modelling of a hot rolling process was developed by Synka et al. [58] and refined by Vetyukov et al. [59].

The literature survey summarised above shows that efficient models for simulation of high pressure rolling for WAAM components have not been reported. The conventional WAAM rolling model is computationally inefficient. The research pertinent to rolling simulations was conducted mainly in the allied fields of high pressure weld seam rolling, deep rolling and burnishing. This limits the development of a multi-layer WAAM rolling model, which still faces practical challenges of high computational cost.

In general, a WAAM rolling model differs from the aforementioned relevant rolling models in a number of aspects, such as the unique WAAM process, component geometry, constraints and cyclic deformations involved in multi-layer rolling. In this paper, the potential efficient modelling techniques for rolling processes are investigated for application specifically in the rolling of a WAAM component. Four efficient rolling models for a WAAM deposited wall are proposed, and their computational efficiency and solution accuracy are examined relative to a large scale rolling model [35]. The large scale model is considered as a control model, as it most accurately represents the dimensions and the rolling process of the WAAM component built in the experiment [35]. The most efficient WAAM rolling model will be employed for future analysis of multi-layer WAAM rolling.

2. Material and Methods

S355 steel was used to build a wall in a previous WAAM experiment [35]. Twenty layers were deposited on a S355 steel base plate with chemical composition in accordance with BS EN 10225:2009. The height, width and length of each layer were approximately 2 mm, 5 mm and 500 mm, respectively. The wire feeding speed, deposition rate and weld torch travelling speed were 10 m/min, 2.352 kg/h and 0.5 m/min, respectively.

The WAAM built wall was selected for modelling in this study. The material model for the wall and substrate was based on the continuum elasticity and Mises plasticity theories, and isotropic strain hardening was assumed after initial yielding. The elastic–plastic material properties reported by Michaleris and DeBiccari [60] were adopted in this study. For the roller, rigid body assumption was adopted unless otherwise stated. General purpose FEM analysis software, Abaqus, was used for the modelling.

For simplicity and focusing on computational efficiency, the RS in the WAAM component was not considered in the rolling simulation. The rolling models developed here were used mainly to identify the most suitable modelling technique for large WAAM components. Nevertheless, a technique for including WAAM deposition RS in the rolling model has also been developed by the authors. An example of the final RS distribution predicted by a rolling model with initial RS after WAAM deposition will be presented in the discussion section. More analysis of the coupled modelling of WAAM deposition and rolling will be reported separately in another study, wherein the efficient modelling technique developed in this study will be employed for the rolling simulation.

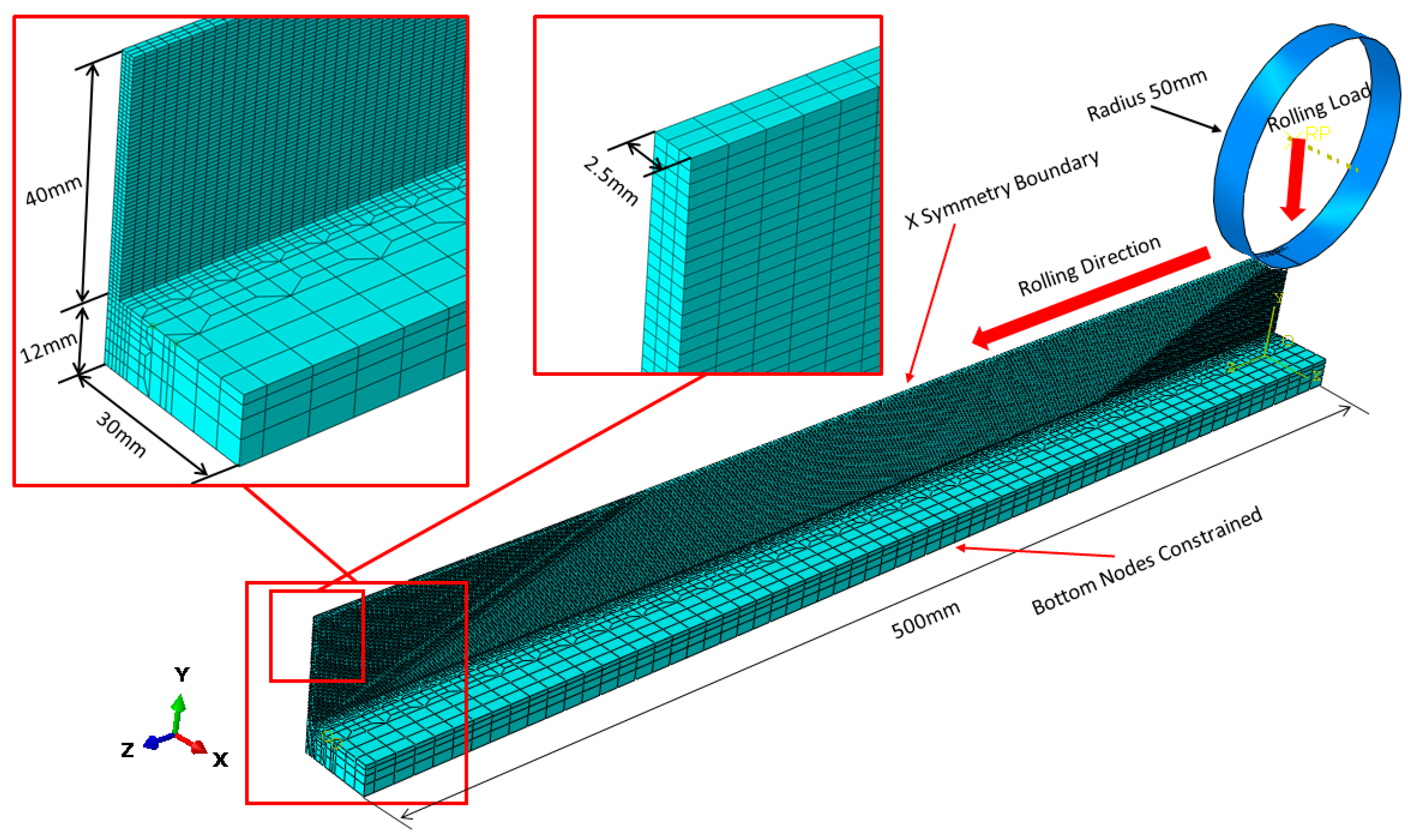
2.1. Large Scale Implicit Transient Load-Controlled Model

A large scale transient load-controlled rolling model was developed, following the work by Kashoob [35]. The term of transient model for mechanical analysis in the context of this research means that the solution of the model is time dependent (i.e., equilibrium at different moments), but does not involve any inertial effects. The large scale model simulated the rolling on the last layer of a full-size (500 mm in length) wall built using the WAAM process [35]. In the 3D model, the wall and substrate were modelled as a deformable body, while the roller was idealised as an analytical rigid shell. The model was solved using Abaqus/Standard (Static, General), based on an implicit numerical algorithm. The dimensions of the model are depicted in Figure 1.

Simulating the actual rolling process, the model comprised the steps of placement, loading, rolling, unloading and removal of the roller. During rolling, a 50 kN vertical load was maintained (load-controlled mode), while no torque was applied. The roller was moved via imposing a horizontal displacement, and it also rotated due to friction between the roller and the wall. Only half of the wall and substrate was considered due to symmetry, and the out-of-plane displacement was constrained on the symmetry plane. To take account of the clamping of the substrate to the work table during the rolling process, the displacements of all nodes on the bottom surface were constrained in vertical direction. The model consisted of 63008 C3D8R (8-node, linear brick, reduced integration, hourglass control) elements. Graded mesh was employed for the model discretisation (Figure 1). The element sizes were 8 × 5 × 4.521 mm and 2 × 0.833 × 0.667 mm for the regions far from and near to the roller, respectively. Surface-to-surface contact interaction was used in the model. The outer surface of the roller and the top surface of the wall were treated as master and slave surfaces, respectively. Finite sliding was allowed between the contact surfaces. Isotropic friction (µ = 0.3) was specified for the contact interaction. Coules et al. [47] and Abbaszadeh et al. [34] suggested that a friction coefficient of 0.3 is representative for non-lubricated contact between the metallic roller and components. It was also found that the predicted RS distribution was not sensitive to the friction coefficient between the roller and component [33,34,47]. As per Cozzolino et al. [33] the difference became considerable only at high rolling loads (150 kN and higher).

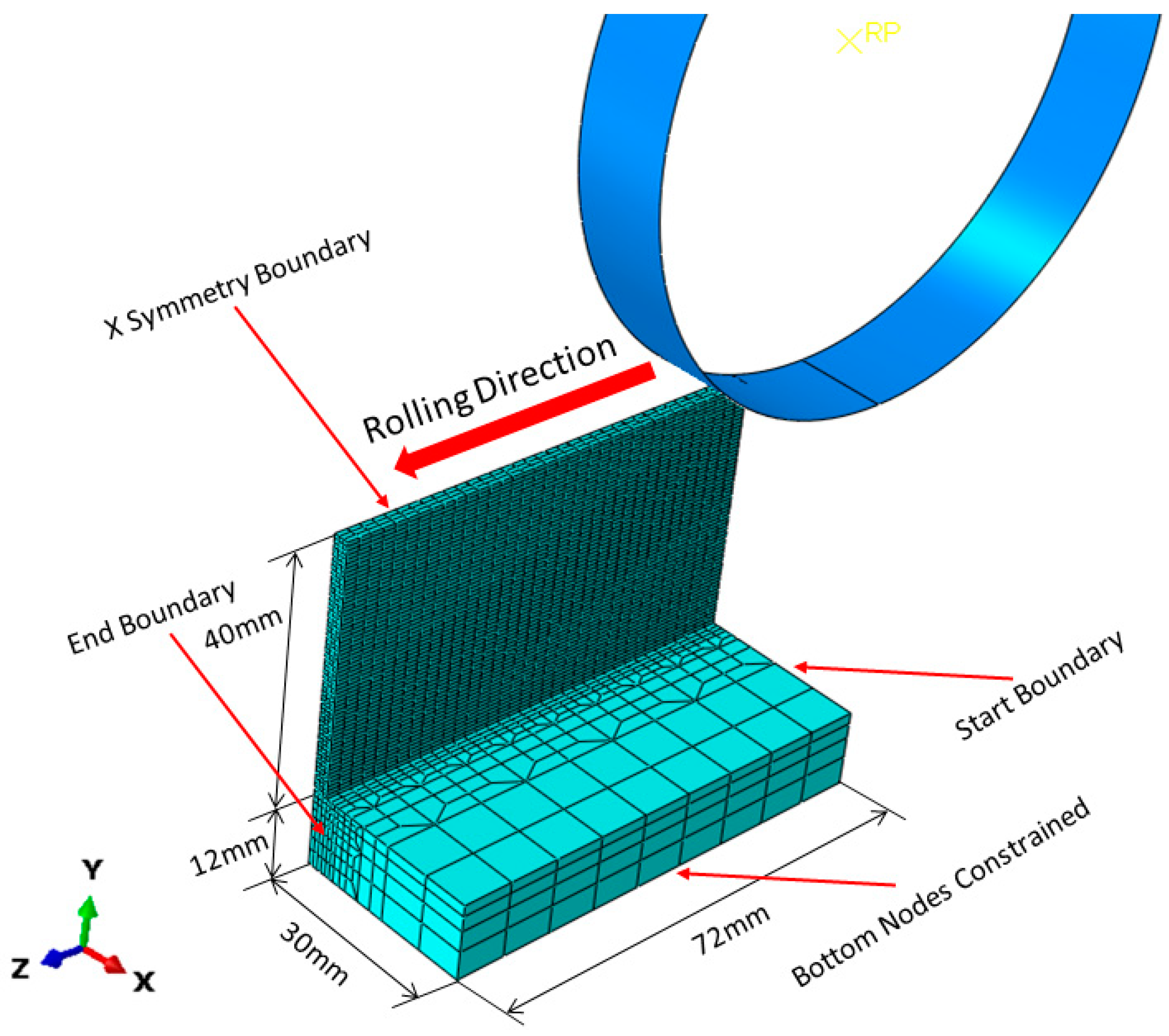
2.2. Short Implicit Transient Displacement-Controlled Model

A short implicit transient displacement-controlled model was developed (Figure 2) as a simplified counterpart to the large scale transient model (Figure 1).

To increase computational efficiency, the length of the deformable component was reduced from 500 mm to 72 mm. The 72 mm length was selected after a preliminary parametric study, and this length ensured that steady state could be reached in the rolling simulation. This meant that the short model was sufficient to obtain a stable and consistent solution, which was not affected by the transient states at the beginning and termination of the rolling simulation.

Due to the short length of the model, there was no place for the precise simulation of the rolling process sequence. To overcome this limitation, displacement-controlled penetration of the roller was used, which allowed for the simplification of analysis steps while using the same rolling load as applied in the large scale load-controlled model. The displacement-controlled penetration enhanced computational efficiency and avoided numerical problems related to establishment of initial contact. In all the efficient models developed here, the roller penetration was controlled by displacement, which was obtained from the results of the large scale transient model and was equivalent to a 50 kN rolling load. The displacement-controlled roller penetration modelling technique was also used in the WAAM rolling simulation by Abbaszadeh et al. [34].

Another problem associated with the short length of the efficient model is the lack of stiffness in the rolling direction. In order to prevent unrealistic deformation in the rolling direction, a boundary condition of zero displacement was applied in the longitudinal direction at the Start and End boundaries of the short model.

To simulate clamping, nodes at the bottom of the model were constrained from movement in all directions. Element type and mesh topology were the same as those for the large scale transient model. Smooth step amplitude was used in order to prevent instantaneous movement of the roller at the beginning of analysis. The model was solved using Abaqus/Standard (Static, General).

2.3. Short Explicit Trasient Displacement-Controlled Model

A short explicit transient model was also developed, which was identical to the short implicit transient model (Figure 2), except that a different solver was used. Mass scaling was used to improve the computational efficiency of the explicit analysis model, and a scaling factor of 6000 was selected after a parametric study. It should be mentioned that this scaling factor restricted the kinetic energy to less than 5% total energy, although it was significantly larger than the values (250 to 400) reported in the literature [42,43,53].

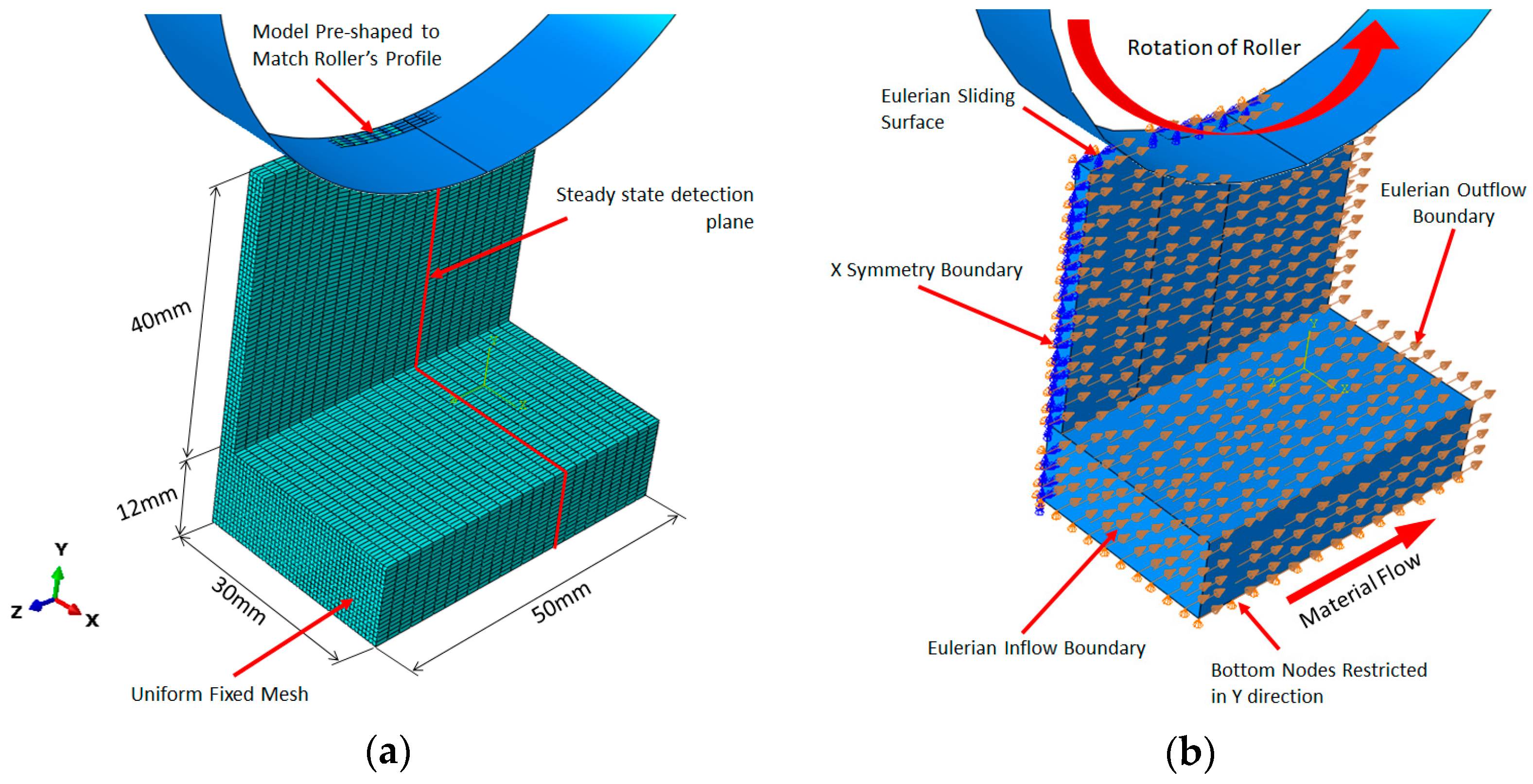
2.4. Eulerian Steady-State Model

A 3D Eulerian steady-state model was also developed based on the short length simplification, as shown in Figure 3. In the Eulerian short model, the material was drawn into the inflow border, underwent deformation, passed through the fixed mesh, and finally was pushed away through the outflow border. The Eulerian model comprised a 50 mm long fixed mesh (Figure 3a), through which material flowed over a 500 mm distance during the rolling analysis. The Eulerian boundary conditions regulated the material flow at the inflow and outflow borders, where adaptive mesh constraints were applied to specify the material velocity perpendicular to the borders, as shown in Figure 3b. The model consisted of 27600 C3D8R elements (8-node linear brick, reduced integration, hourglass control) and the element dimensions were 1.881 × 0.625 × 0.667 mm. An adaptive mesh domain was specified near the roller to improve mesh quality for large deformation.

The interface between the roller and the wall was specified as the Eulerian sliding surface. On the bottom surface, the nodal displacement was constrained in the vertical direction to represent the clamping, while on the inflow and outflow borders, all the nodal displacements were fixed. The rolling load of 50 kN was imposed by prescribing a vertical displacement of the roller. Translation of the roller was constrained in all directions, while rotation was allowed only around the X axis. An angular velocity boundary condition was applied to the roller around of the spinning axis in order to provide the rolling torque. A predefined field of translational velocity was applied to the wall and substrate, as required to initiate contact and minimise the transient effect of instantaneous movement at the beginning of analysis. The model was solved using Abaqus/Explicit, and the steady-state detection option was used in the model. The steady-state detection plane was positioned perpendicular to the rolling direction and behind the last point of contact (Figure 3a). As soon as a constant deformed shape was achieved on the steady-state detection plane, it was considered that the rolling had reached the steady state and the analysis was terminated.

To improve computational efficiency, rolling speed was artificially increased, i.e., the analysis step time was approximately 1% of the actual rolling time, which did not affect the result under the steady state. In addition, a fixed mass scaling factor of 2750 was used in the analysis, close to the maximum value recommended by Abaqus Example Problems Guide [52] for similar problems. This scaling factor was deemed optimal as a result of iterative trials to minimise the computational time and the potential adverse effect of mass scaling on the accuracy.

2.5. 2D Short Implicit Transient Displacement-Controlled Model

The plane stress theory was utilised for the creation of a 2D model. The symmetry plane in the 3D model (Figure 2) was used to define the 2D model geometry, as shown in Figure 4a, since the WAAM deposited wall is thin and flat and the RS and PS distributions in the rolling direction are of major interest in this study. The 2D model consisted of 2516 CPS4R elements (4-node, bilinear, plane stress, quadrilateral, reduced integration) and its mesh topology was similar to that for the symmetry plane of the 3D short implicit transient model. The 2D and 3D short models also had similar boundary conditions and loading process, and they were both solved using Abaqus/Standard (Static, General).

To assess the potential influence of the deformable elastic roller on simulation results, an additional model with a roller made of H13 steel (Young’s modulus of 230 GPa and Poisson’s ratio of 0.3 [34]) was generated, as shown in Figure 4b. The mesh density of the elastic roller was selected to be the same as that of the WAAM wall. As a result, the roller was discretised using 3611 linear quadrilateral CPS4R elements and 157 linear triangular CPS3 elements.

2.6. Inspection Planes for Comparison between Different Models

The accuracy of different efficient models was evaluated by comparison with the control model. The results for the comparison were extracted from an inspection plane corresponding to the steady-state rolling. In the control model (3D large scale transient model), the inspection was performed in the mid-length plane. In the 3D short implicit transient, 3D short explicit transient and 2D short implicit transient models, the inspection plane was located in the x-y plane, 48 mm away from the start position of the rolling. In the Eulerian steady-state model, the inspection plane coincided with the steady-state detection plane, which was 20 mm away from the material outflow border.

3. Results

3.1. Computational Efficiency

The computational efficiency was compared between different rolling models, and the total time saving for each model with reference to the control model was calculated, as shown in

Table 1. Comparison of computational efficiency between different models.

Model	Number of Elements	Wall Clock Time with 4 CPUs Used (Seconds)	Total Time Saving, %
3D large scale implicit transient model (control model)	63,011	64,002	N/A
3D short implicit transient model	9036	2238	96.50%
3D short explicit transient model	9036	2355	96.32%
3D Eulerian steady-state model	27,600	2613 #	95.91%
2D short implicit transient model with analytic rigid roller	2516	302	99.52%
2D short implicit transient model with elastic roller	6284	588	99.08%

^# Single CPU was used, since the Eulerian model using Abaqus/Explicit is restricted to serial computation.

.

The wall clock time, i.e., the actual time required to obtain a solution, was used for the evaluation of the computational efficiency. All the models were solved using 4 CPUs, except the Eulerian model, which was solved using a single CPU since multiple CPUs are not supported for analysis with steady-state detection in Abaqus. It was found that the 2D short implicit transient model with analytic rigid roller was most efficient, which saved 99.52% time relative to the control model, while the Eulerian steady-state model was least efficient, despite 95.91% time saved.

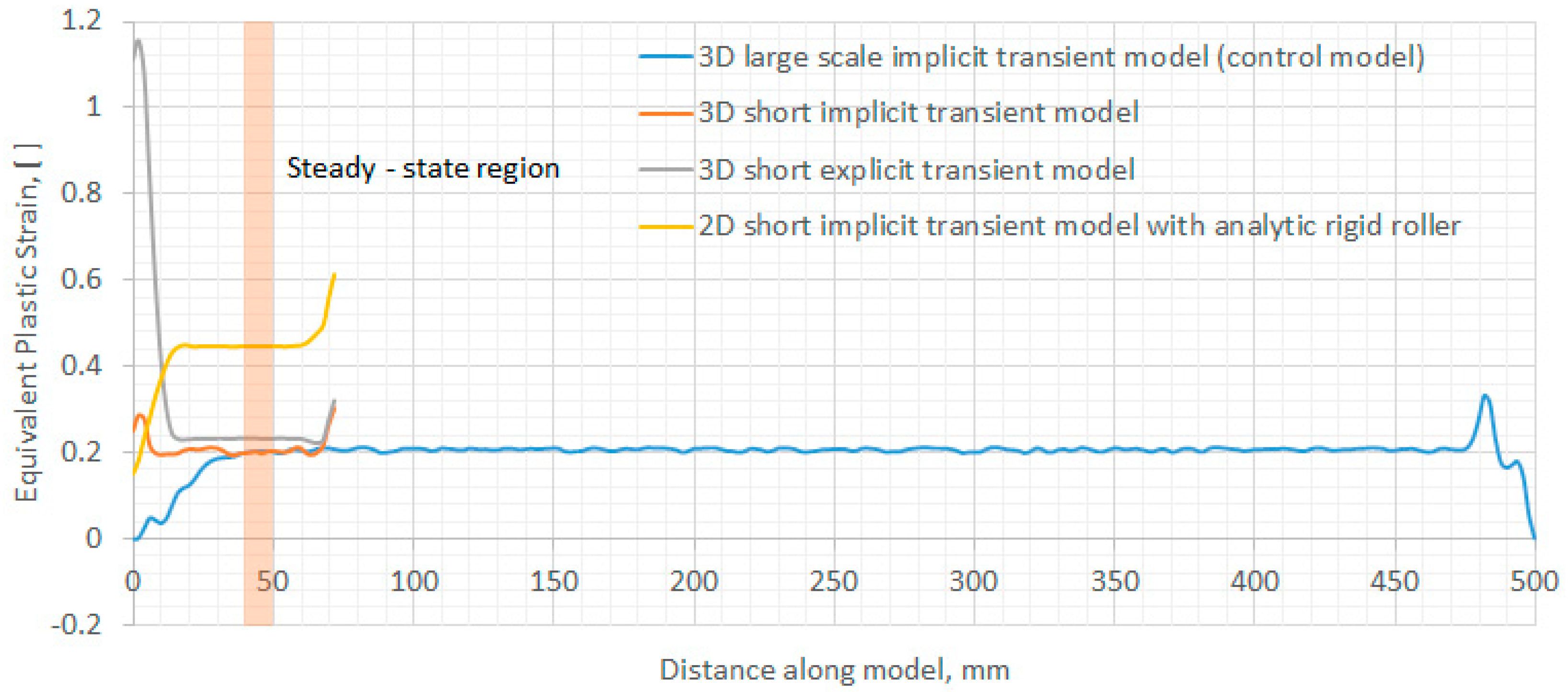
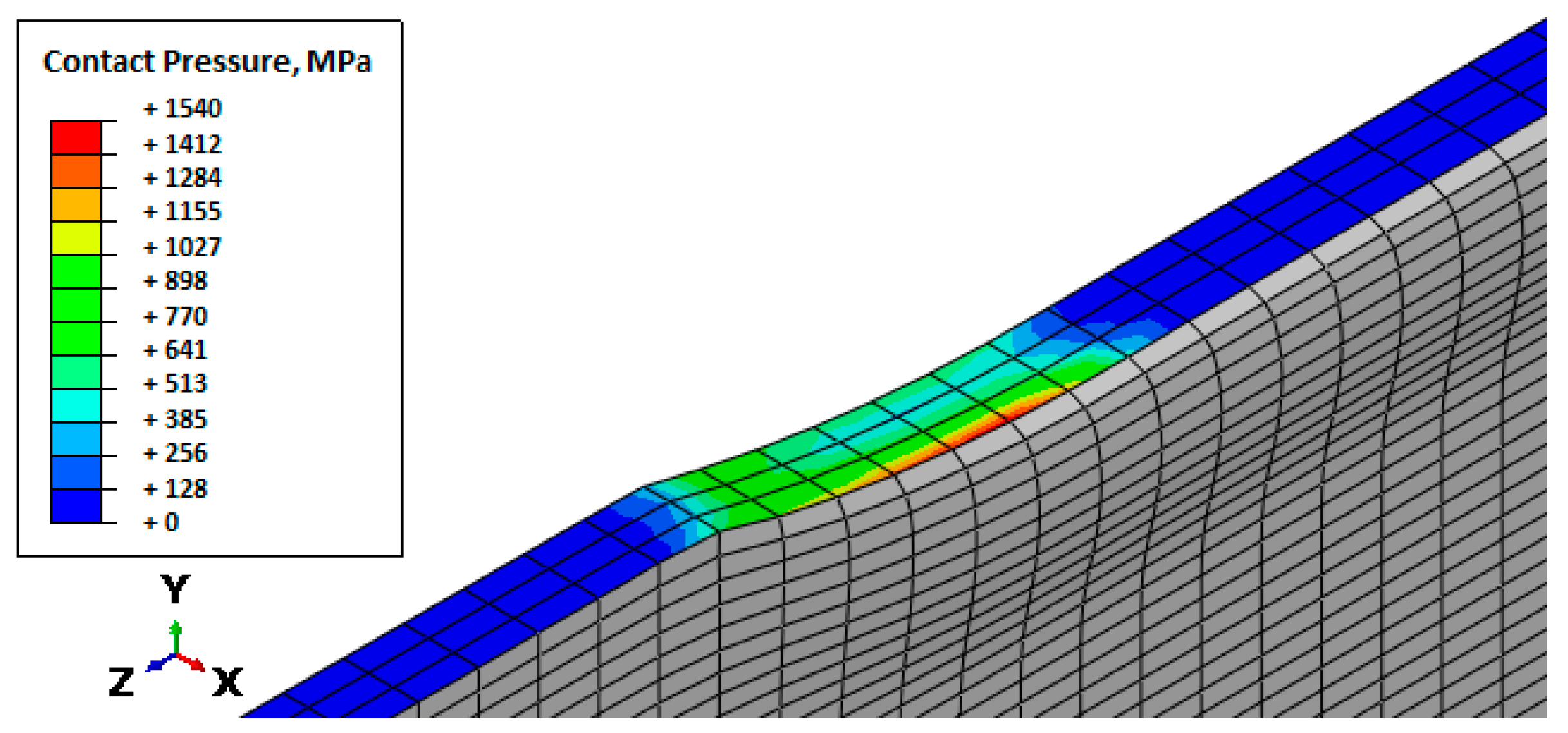
3.2. Steady-State Rolling

Equivalent plastic strain (EPS) was used to detect the steady-state rolling. The rolling in the large scale implicit transient model (i.e., control model) reached steady state in a range of distance between 40 mm and 470 mm along the rolling direction, while this range was between 20 mm and 60 mm for the short transient models. In the steady-state rolling range, the EPS remained constant or fluctuated around a constant value, as shown in Figure 5.

The EPS predicted by the short implicit transient model demonstrated slightly larger fluctuation than other short models, and the fluctuation became negligible in the distance range from 40 mm to 50 mm. Based on the EPS distributions, the inspection plane of the short models was selected with a location at 48 mm from the rolling start position. The Eulerian model reached steady state after 7 s rolling, and then the analysis halted, which was equivalent to a rolling distance of 58 mm.

In the developed efficient models, the rolling load was maintained by applying a constant roller displacement (1.674 mm) in the vertical direction. The applied displacement was equivalent to a rolling load of 50 kN (25 kN for the half model due to symmetry). The rolling load was verified by examining the reaction force on the pivot of the roller (Figure 6) and by comparing contact pressure during rolling on the surface of the WAAM wall (Figure 7). Similar distribution and magnitude of contact pressure was obtained in all the models.

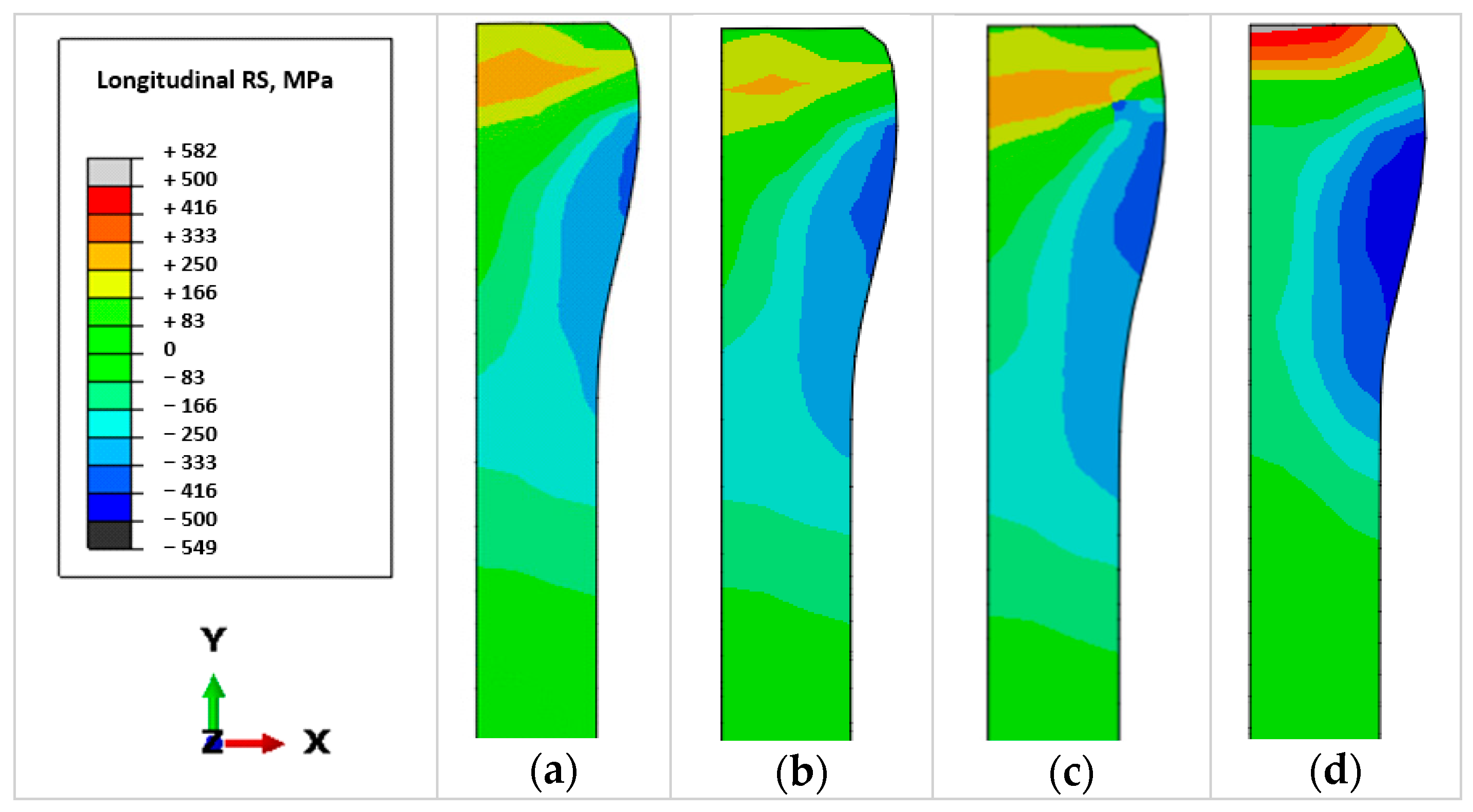
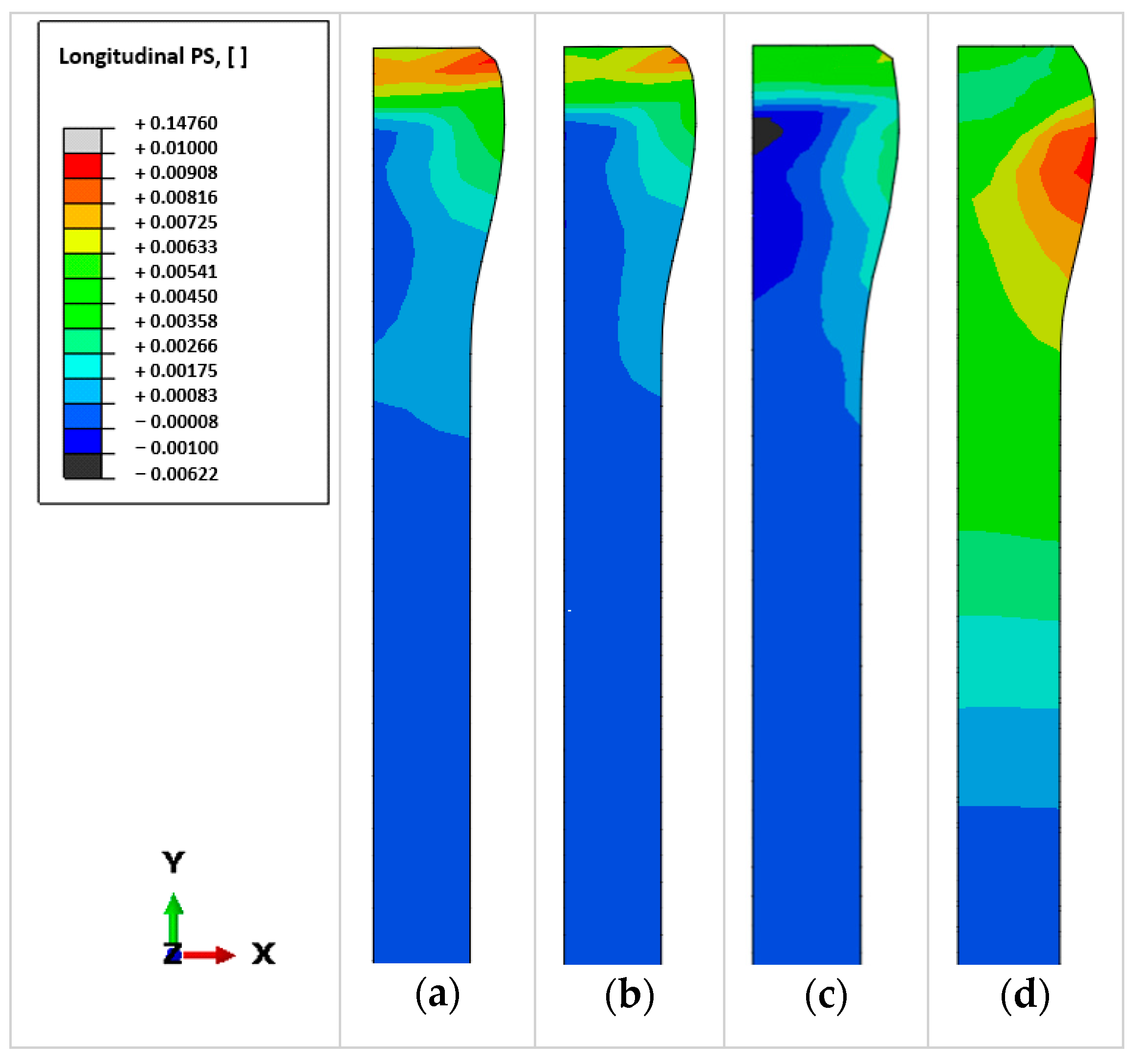
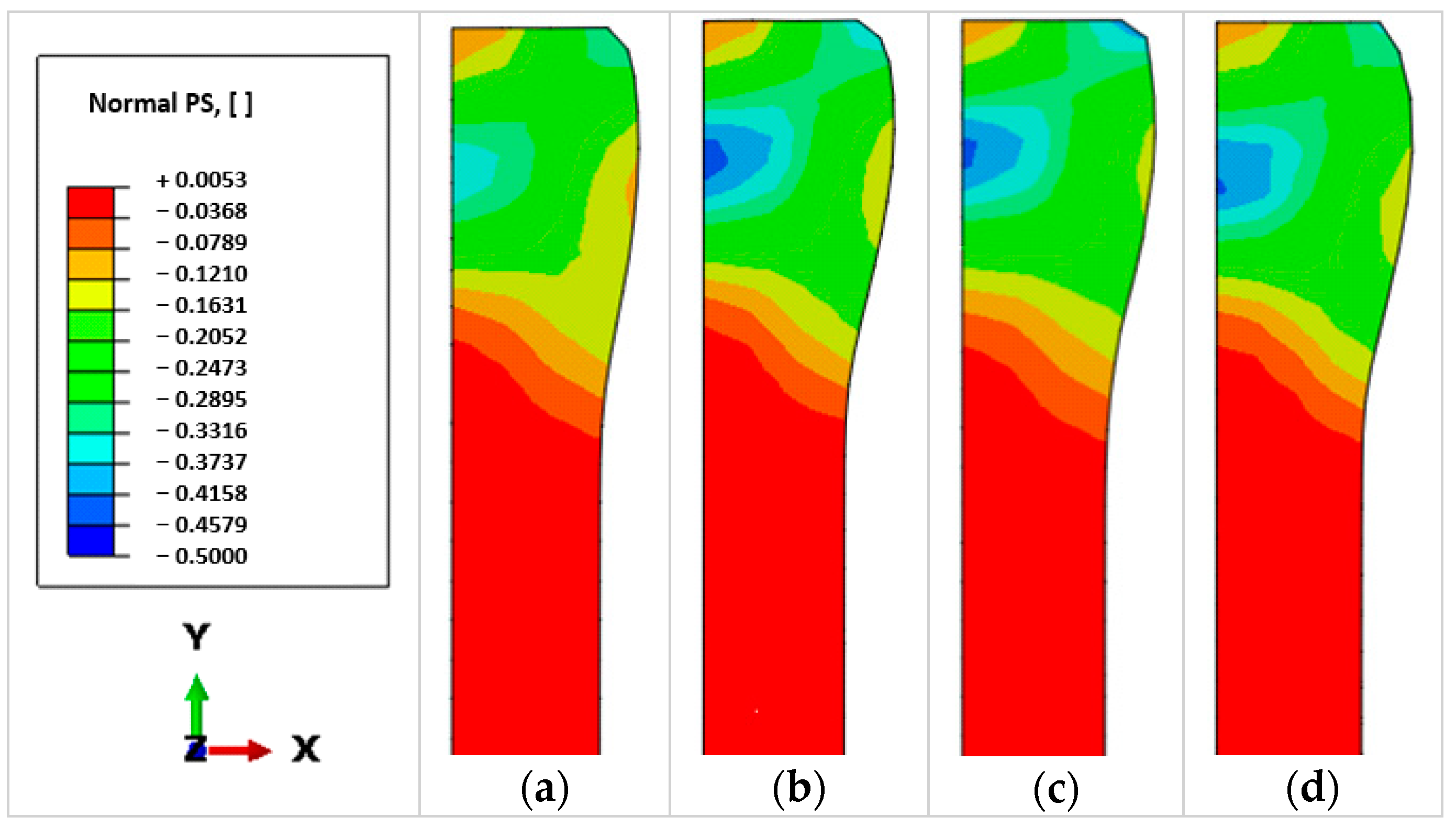
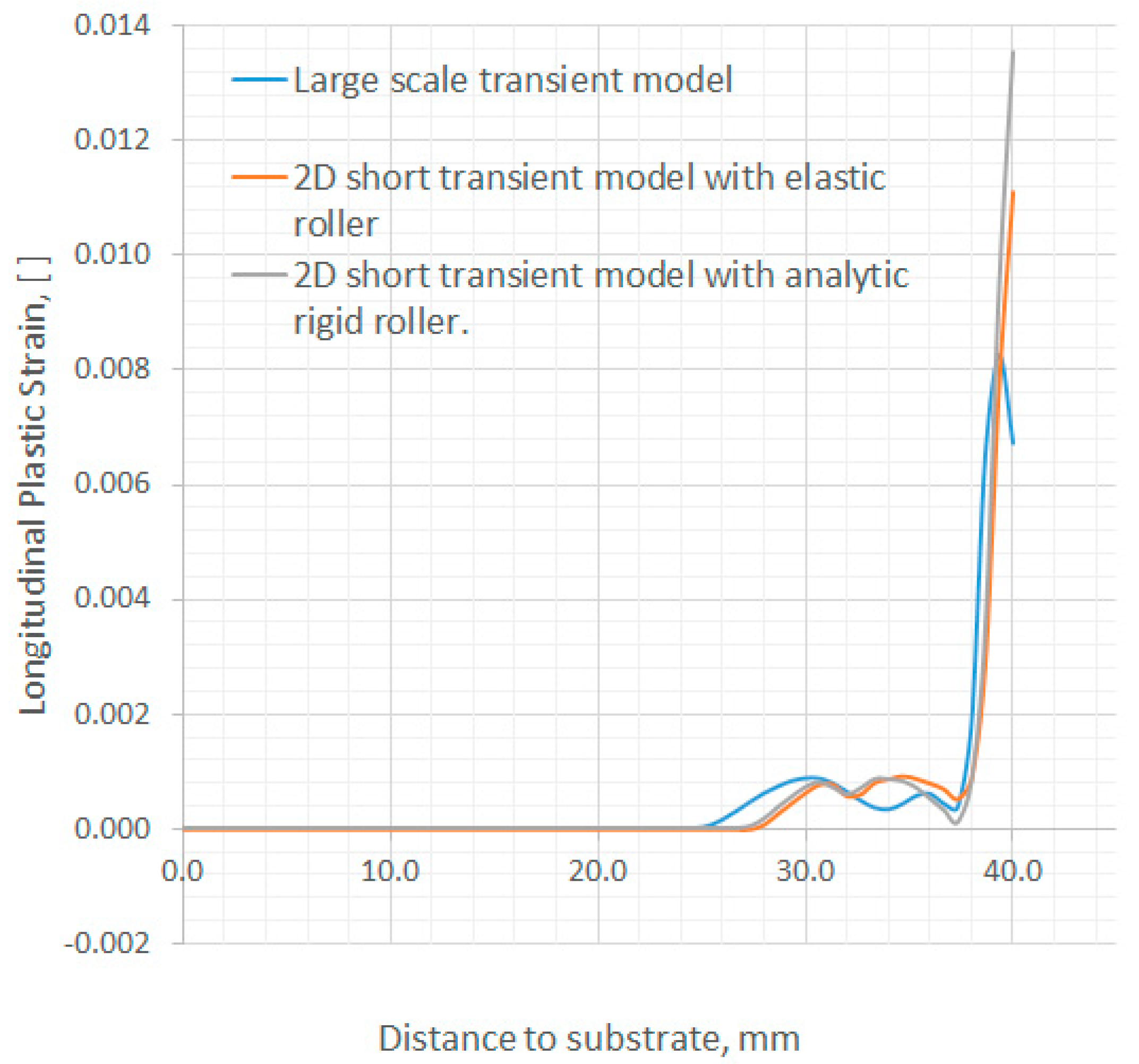
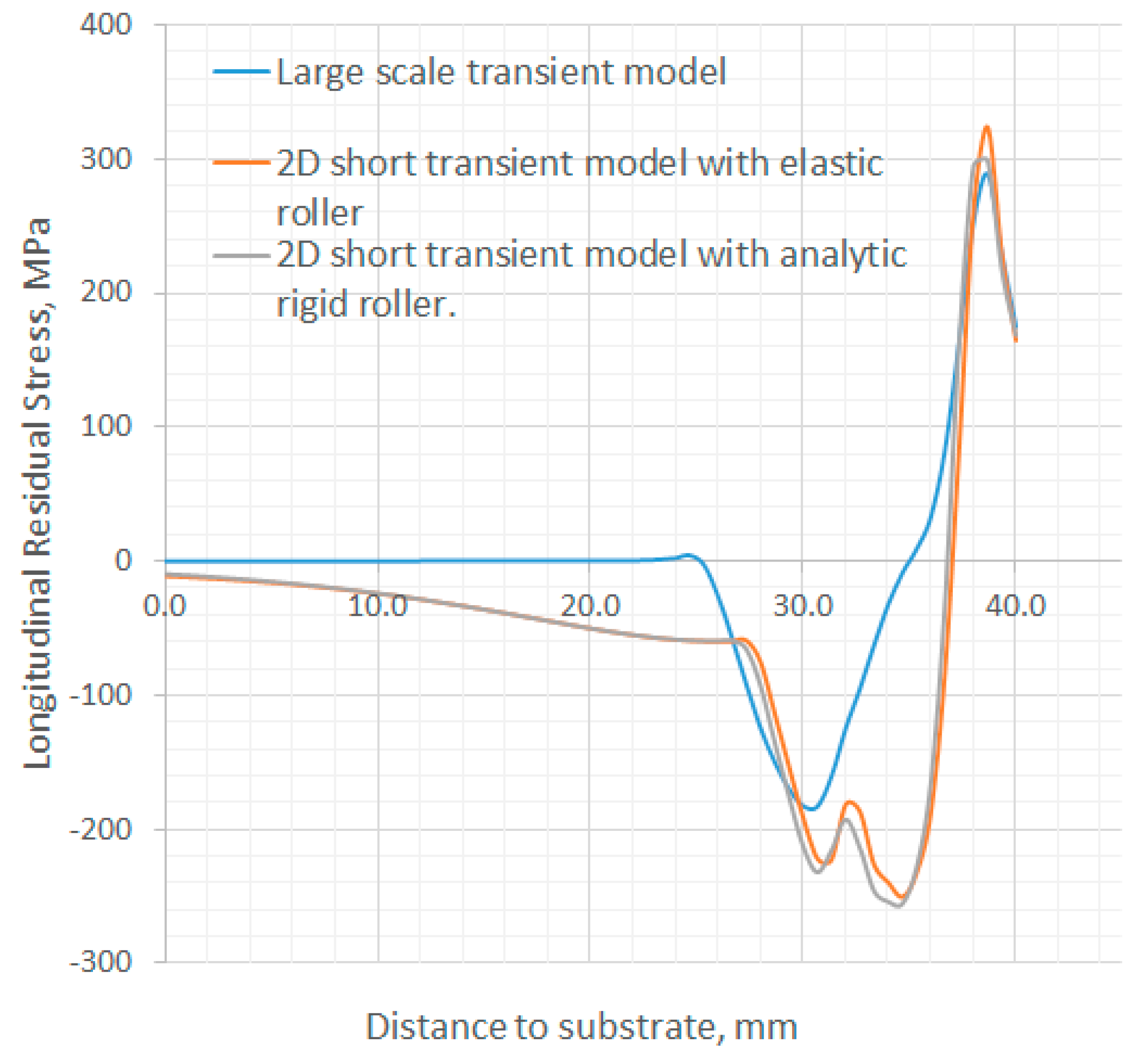
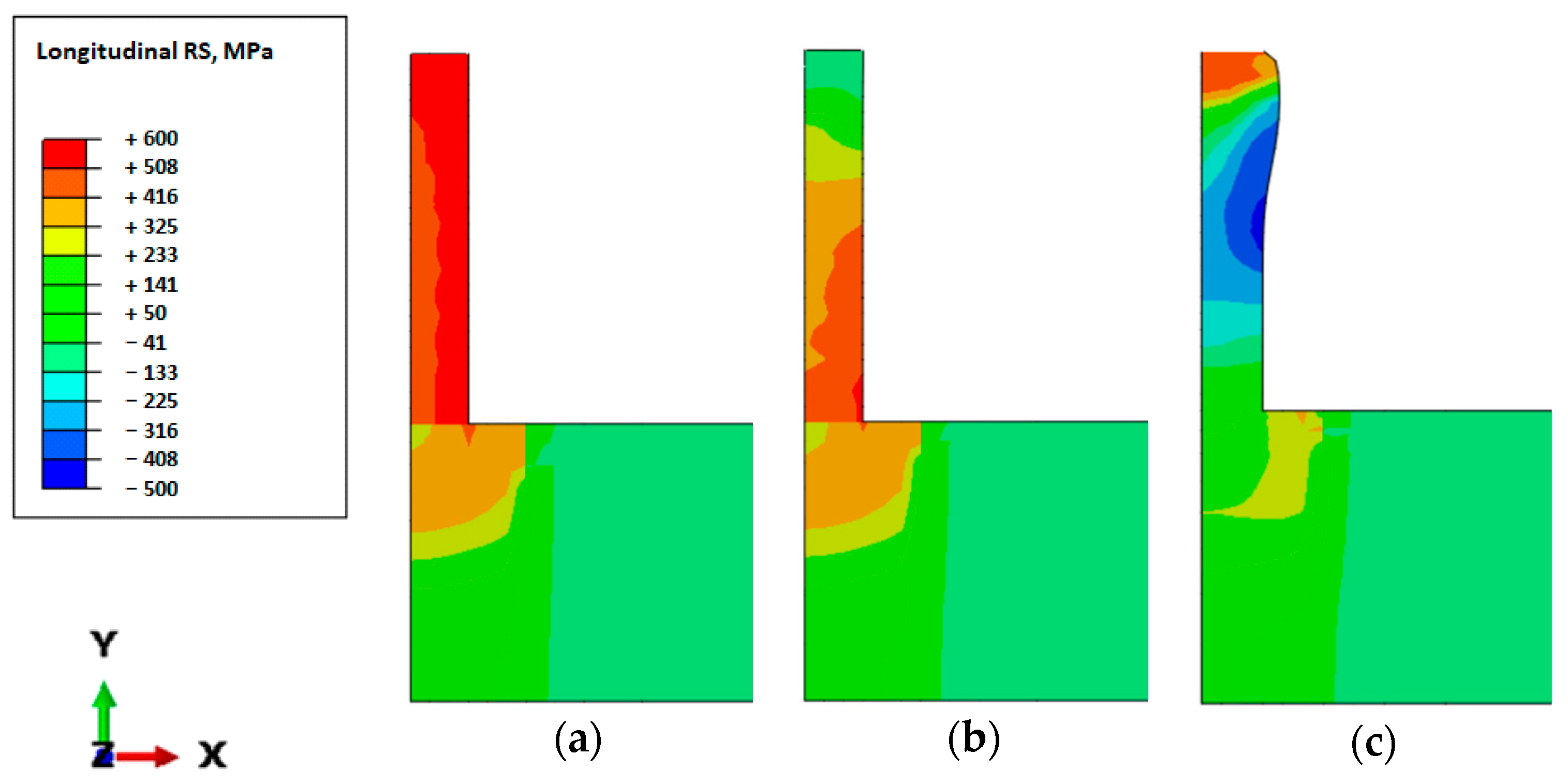
3.3. Solution Accuracy

The accuracy of the efficient models was examined through comparison with the large scale implicit transient model, which was based on the actual dimensions and rolling process of the WAAM component built in the previous experiment [35] and hence used here as the control model. Figure 8 presents longitudinal RS distributions on the inspection planes for different rolling models. All models predicted tensile RS with a magnitude up to 582 MPa underneath the rolled surface and compressive RS with a magnitude up to 545 MPa underneath the tension zone. The peak of the compressive RS shifted towards the outer surface of the wall (opposite to the symmetry plane). The short implicit transient model predicted the most accurate RS distribution compared to the control model. The short explicit transient model and the Eulerian steady-state model predicted larger regions under tensile RS, and the Eulerian model predicted larger magnitudes of both tensile and compressive RS.

Figure 9 shows the longitudinal PS distributions on the inspection planes for different rolling models. All models, except the Eulerian model, predicted concentrated tensile PS immediately under the rolled surface, while the Eulerian model predicted the highest tensile PS further underneath the rolled surface, which was concentrated on the side surface of the wall. The models predicted compressive PS in regions relatively far from the rolled surface. The longitudinal PS distribution predicted by the short implicit transient model was in best agreement with that predicted by the control model.

Figure 10 shows the normal PS distributions on the inspection planes for different rolling models. Compressive PS was dominant in the deformed region, and the peak PS was located approximately 2.2 mm below the rolled surface and close to the symmetry plane. No considerable tensile PS was found in the wall. The predictions of normal PS by all the efficient models achieved similar agreement with that obtained by the control model.

Figure 11 compares the transverse PS distributions predicted by different models. The predicted results were similar between all the models. In contrast to the normal PS, the transverse PS was overwhelmingly tensile. The peak PS was located in the central portion of the deformed region.

Figure 12 compares the transverse displacement distributions predicted by different rolling models. There was an overall similarity between the results, while the displacement contour obtained by the Eulerian model was somewhat elongated in the vertical direction.

2D vs. 3D Rolling Models

Figure 13 and Figure 14 compare the longitudinal PS and RS distributions, respectively, as obtained from the 3D large scale model (control model) and the 2D short transient models with elastic roller and analytic rigid roller. The 2D models captured the longitudinal tensile PS distribution in the region near the substrate, but they overestimated the tensile PS magnitude in the region close to the rolled surface. Nevertheless, the 2D modelling results for the longitudinal tensile RS distribution near the rolled surface were consistent with the prediction by the 3D control model. However, there was marked discrepancy in the compressive RS distribution near the substrate between the predictions by the 2D and 3D models.

Figure 13 and Figure 14 also demonstrate a minor effect of elastic deformation of the roller on the predicted longitudinal PS and RS distributions under steady-state rolling. Figure 15 confirms such a minor effect on the longitudinal RS when the full-field stress distributions are compared. The minor effect of the elastic deformation of the roller found here was consistent with the findings of Abbaszadeh et al. [34] using a 3D rolling model. However, it should be noted that a typical rolling load of 50 kN for WAAM was used in this study; the difference in results between elastic and rigid roller models could be considerable at significantly larger rolling loads.

The use of an elastic roller in the 2D model doubled the number of elements involved in the analysis and increased the wall clock time by 48% (Table 1). Given the minor difference in results between the elastic and rigid roller models, it can be confirmed that the analytic rigid roller in the rolling model allowed significant computational savings with almost equivalent accuracy of predicted results.

4. Discussion

4.1. Computational Efficiency

The highest computational efficiency was achieved by the 2D short implicit transient model with an analytic rigid roller, thanks to the dramatic computational saving by using fewer 2D elements (2516 elements) with reduced degrees of freedom. The 2D model with an elastic roller led to twice the number of elements (6284) and demonstrated 48.6% lower efficiency compared to the 2D model with an analytic rigid roller. Besides the number of elements, the solution method also affects the computational efficiency. The short explicit and implicit transient models comprised an identical number of elements, but the explicit analysis model demonstrated slightly lower efficiency than the implicit analysis model. This was mainly because the explicit solver was more computationally expensive than the implicit solver for problems involving contact with rigid bodies [54]. The uncertainty in efficacy of mass scaling techniques for explicit analysis also affected the computational efficiency. It was interesting to see that although the Eulerian steady-state model used a large number of elements (27,600), it still demonstrated high computational efficiency, similar to the short explicit transient model, with three times fewer elements used (9036). Such a computational saving can be attributed to the steady-state detection option in the Eulerian model, which halted the analysis after rolling along a distance equivalent to 11.6% the modelled wall length. However, the steady-state detection option in Abaqus requires consistent mesh topology in the rolling direction [48], and it does not support the use of multiple CPUs. For all the developed efficient models, the benefits brought by the attempt to further reduce the elements through progressive meshing techniques were deemed to be limited.

4.2. Steady-State Rolling and Its Implicaiton in Computational Efficiency

The steady-state rolling is of major interest for analysis since it dominates the mechanical response of the WAAM component to the rolling. The efficient model is effective and acceptable if it can capture the steady-state rolling. It was demonstrated that all the efficient models developed here had sufficient wall length to obtain a stable and consistent solution for the steady-state rolling (Figure 5).

The computational efficiency of the 3D short explicit transient model could be increased further by reducing the wall length in the model, since the whole length was still considerably larger than the length of the region where steady-state rolling was established (Figure 5). Similarly, to further increase efficiency, the wall length in the 2D short implicit transient model could be reduced. For the Eulerian model, the application of less strict steady-state detection norms could reduce the time required to reach steady state and hence increase the efficiency of the model. As the solution to the 3D short implicit transient model experienced appreciable fluctuation in the region under steady-state rolling, further reduction in wall length is not suggested due to concern about solution accuracy.

4.3. Solution Accuracy

To assess the solution accuracy of the efficient models, the distributions of longitudinal RS and PS in three directions were compared to the solution of the large scale implicit transient model (control model).

The solution of the short implicit transient model was in best agreement with the solution of the control model (Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12). The short explicit transient model, Eulerian steady-state model and 2D plane stress model demonstrated different levels of discrepancy of the predicted results compared to the control model.

The overall consistent results of the rolling simulations by the short implicit transient model and the control model could be explained by the fact that the largely reduced length of the WAAM component considered in the rolling model did not significantly impair the accuracy of the model solution, as long as the steady state was reached. Moreover, the same mesh topology and Abaqus Standard solver (implicit method) were used in both models. The slight discrepancy in the results could be attributed to the applied constraints on the Start and End boundaries in the short model, which could lead to enhanced stiffness in the rolling direction.

The solution accuracy of the short explicit transient model (Figure 8 and Figure 9) was impaired by the artificially increased density of the material, as a result of the mass scaling which was used to accelerate computation. The increased density could exacerbate the effect of inertial force which could violate the equilibrium state assumed in the rolling process. As found in a parametric study conducted in this research, using lower values of mass scaling factor made the short transient explicit model more accurate, but led to significantly lower efficiency compared to the short implicit transient model. This confirmed the findings of Harewood et al. [54] and Oliver et al. [55] that the implicit solver is more accurate and less computationally expensive than the explicit solver for relatively simple contact problems with rigid bodies involved.

Nevertheless, an explicit analysis still has the potential to better handle complex contact problems and large deformations than an implicit analysis. Furthermore, the short explicit transient model reached steady state earlier than the short implicit transient model (Figure 5). This allowed further reduction of the wall length, and as a result, a considerable reduction of elements used in the analysis could be achieved. From a numerical algorithm point of view, the explicit solution method was better suited to parallel computation than the implicit method.

The Eulerian model was less accurate than the short implicit and explicit models due to the unrealistic rolling process simulated in the Eulerian model. The control model simulated the actual rolling process in reality [3], in which the deformable wall remained steady and the roller moved along the wall, causing the free rotation of the roller due to friction between the roller and the wall. In contrast, in the Eulerian model, the torque was applied to the steady roller, and the wall material movement was caused by the rotation of the roller and the friction between the roller and the wall. The friction caused material to “stick” to the roller, and the applied torque drew the material underneath, which increased longitudinal tensile PS under the roller (3 mm below the rolled surface) as compared to the control model (Figure 9). As a result, larger tensile deformation and higher compressive longitudinal RS were generated in this region (Figure 8). More extensive stretching of material due to the applied torque occurred as well on the rolled surface, which caused longitudinal tensile RS (Figure 8). As the Eulerian model also employed an explicit solver, similar issues to the short explicit transient model could affect the solution accuracy of the Eulerian model.

The 2D plane stress model did not accurately represent a rolling process for the WAAM component in which the RS and PS were non-uniformly distributed in the through-thickness direction of the wall (Figure 13 and Figure 14). During the rolling, the normal and longitudinal strains were accommodated by the transverse strain [4]. Meanwhile, the isotropic friction restricted the longitudinal and transverse deformation under the roller. The 2D model could not capture these complex 3D phenomena due to its plane-stress assumption. In fact, the out-of-plane stress played a considerable role in the final state of the longitudinal residual stress and strain. As the wall and substrate were not actually aligned within the same plane, the substrate effect could not be realistically represented in a 2D model. For a similar reason, a 2D plane strain model defined on the transverse section (e.g., y-z plane of the 3D model in Figure 2) is not suitable for accurate simulation of the rolling process. It assumes zero strain in the longitudinal/rolling direction, where large deformation was observed in the 3D models. Nevertheless, the 2D plane stress model was 86.5% more efficient than the short 3D models (Table 1). Considering the computational efficiency, the 2D model could be used for rough and fast estimation of major rolling parameters for analysis later refined using 3D models.

4.4. Rolling Model with WAAM Deposition RS

Although the rolling models used for efficiency evaluation did not consider the WAAM deposition RS, the modelling technique developed here can be applied when the modelling of WAAM and rolling processes is sequentially coupled. Figure 16 shows the longitudinal RS distributions predicted by a rolling model with WAAM RS as an initial condition. It should be noted that this model considered only eight deposited layers of the WAAM wall, which was rolled with a flat roller at rolling loads of 10 kN and 50 kN. Before rolling, the WAAM RS was tensile in the wall and the substrate region under the wall. After the rolling at a load of 10 kN, the RS converted to low-level compressive stress under the rolled surface, and the magnitude of tensile RS was reduced in the regions 3 mm below the rolled surface. After the rolling at a load of 50 kN, the model predicted tensile RS immediately under the rolled surface, but compressive RS in the regions 5 mm and further below the rolled surface. In the substrate underneath the wall, the magnitude of the original tensile RS was lowered after the rolling. The compressive RS in the regions of the substrate far away from the wall remained unchanged. More analysis of the effect of rolling on WAAM deposition RS will be presented separately in another paper.

5. Conclusions

In the present study, the efficiency and prediction of four models of high pressure rolling for a WAAM deposited wall, including the 3D short implicit transient model, 3D short explicit transient model, 3D Eulerian steady-state model and 2D short implicit transient model, were evaluated. The computational efficiency and solution accuracy of these models were compared with a conventional large-scale transient model (control model). It was demonstrated that the developed efficient models allowed for the simulation of rolling on the top layer of the built wall, with a computational time of less than one hour, using a desktop computer. This will enable development of efficient models to simulate multi-layer rolling for WAAM components; such simulation is currently unpractical. Based on the results and analyses, following conclusions are made:

• The efficiency of a rolling model depends largely on the number of elements (or degrees of freedom) involved in the FEM analysis. Reduction of component length in the model can dramatically improve the computational efficiency without impairing solution accuracy, since steady-state rolling can be established within a region of short length.
• The implicit analysis method is more accurate and efficient than the explicit analysis method for the short rolling models with analytic rigid rollers and relatively low rolling loads.
• The solution of the 3D short implicit transient model is most accurate among the developed efficient models, as compared to the control model. The accuracy of the 3D short explicit transient model was impaired by the artificially assigned high density of material (mass scaling for acceleration of computation). Reduction of the mass scaling factor improved accuracy, but increased computational cost significantly. The 3D Eulerian steady-state model is less accurate due to unrealistic representation of the rolling process, and its efficiency is limited by the restriction that parallel computation is not supported when the steady-state detection feature is enabled using the employed version of Abaqus software.
• The 2D implicit transient model cannot capture the 3D deformation mechanism during rolling, and hence it is least accurate in predicting the distributions of longitudinal residual stress and plastic strain. Nevertheless, the 2D transient model is much more efficient than the 3D models, and it could be used for a quick qualitative estimate of the mechanical response of the WAAM component to rolling.
• Application of an elastic deformable roller instead of an analytic rigid roller in the 2D rolling model barely affected the solution, but significantly reduced computational efficiency.