Influence of Microcracks on Silver/Polydimethylsiloxane-Based Flexible Microstrip Transmission Lines
Abstract
1. Introduction
2. Design, Fabrication and Characterization
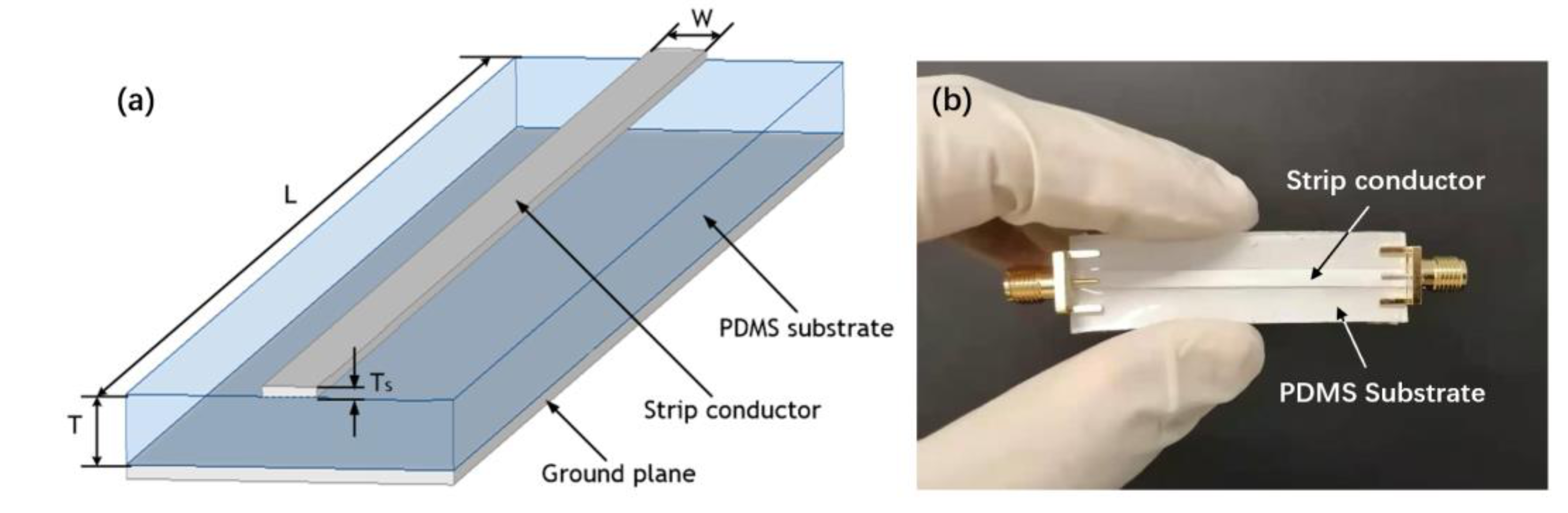
2.1. Microstrip Design
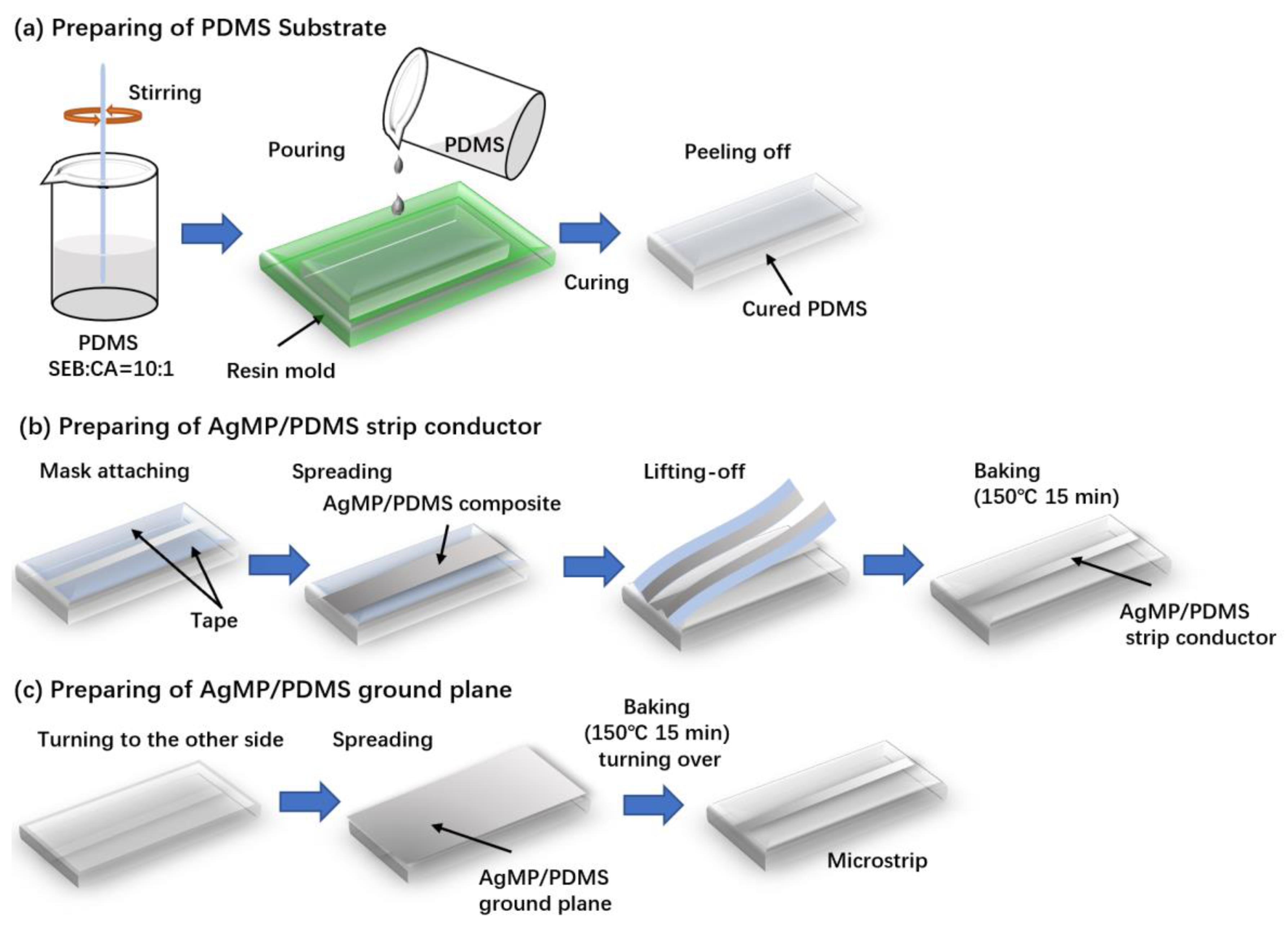
2.2. Fabrication Process
2.3. Characterization
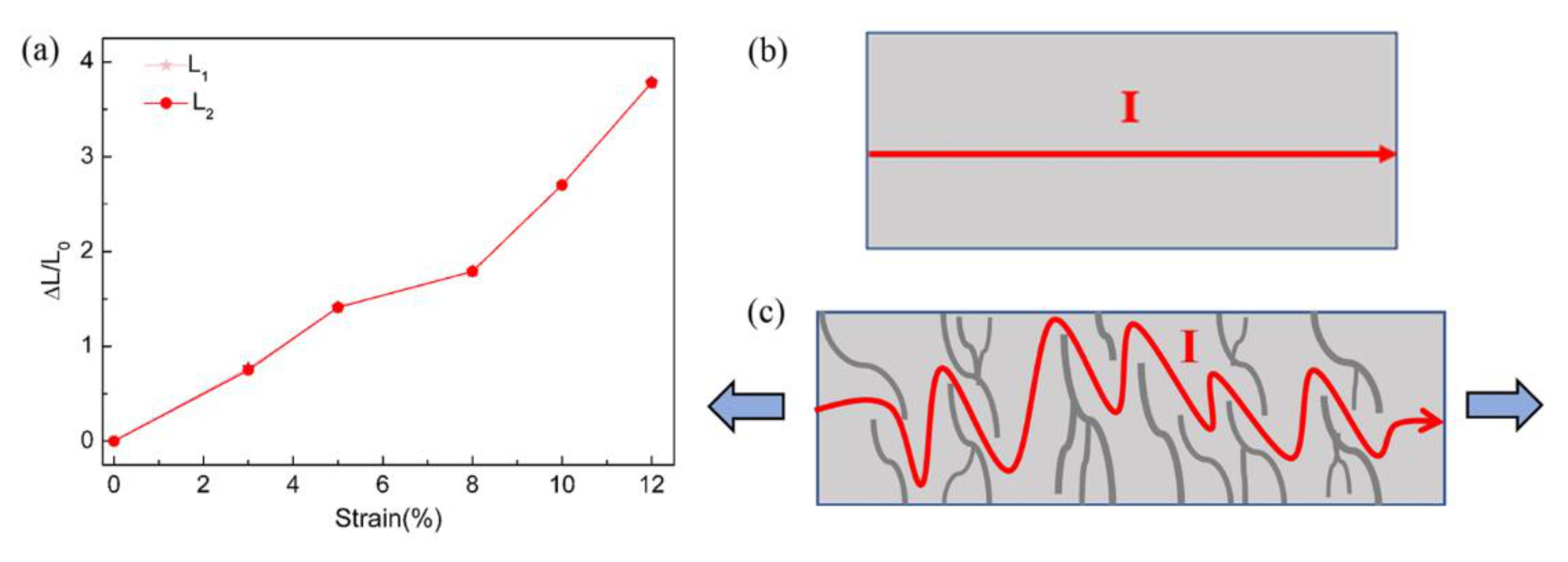
3. Results and Discussions
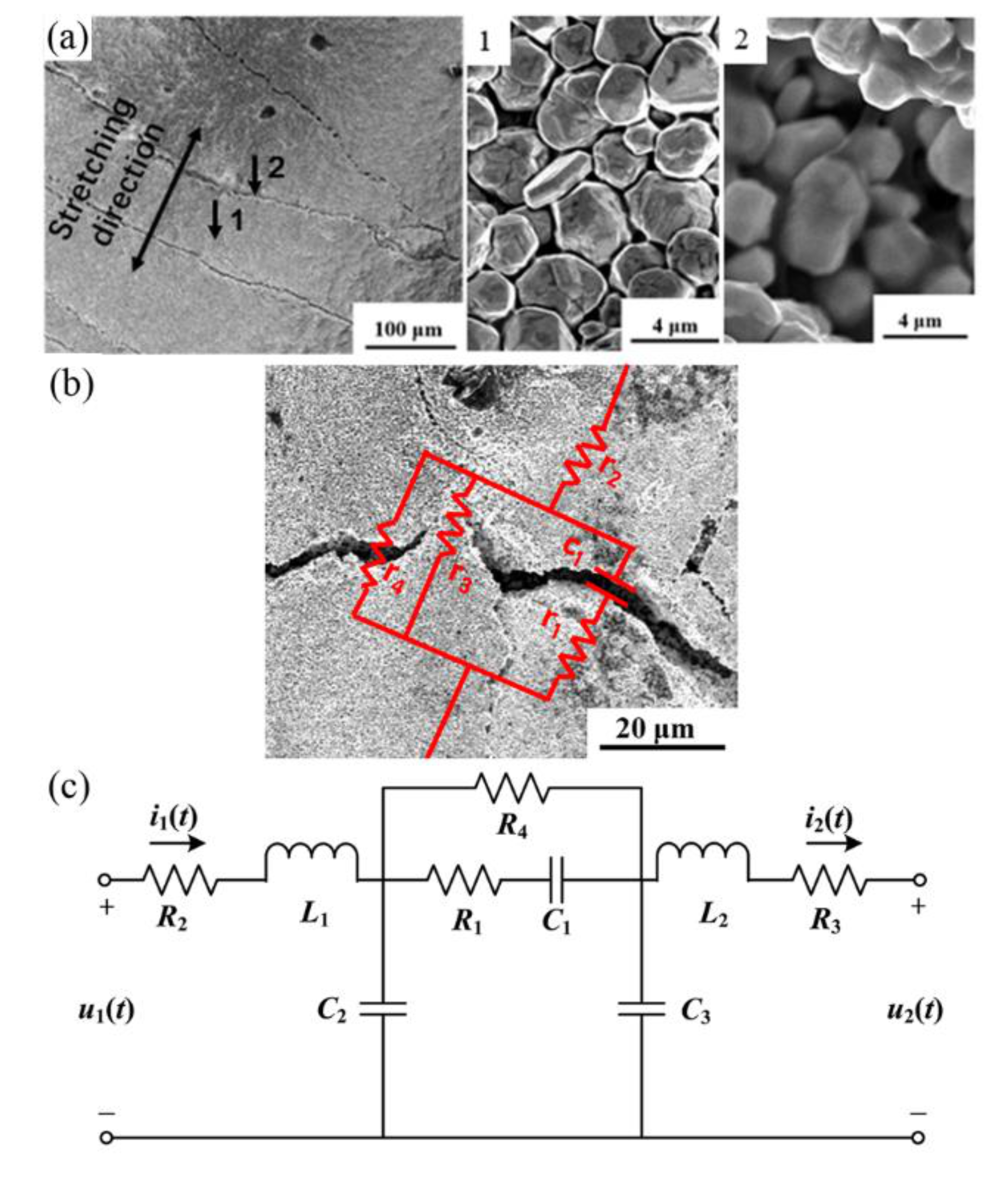
3.1. The Equivalent Circuit Model of the Microstrip with Microcracks
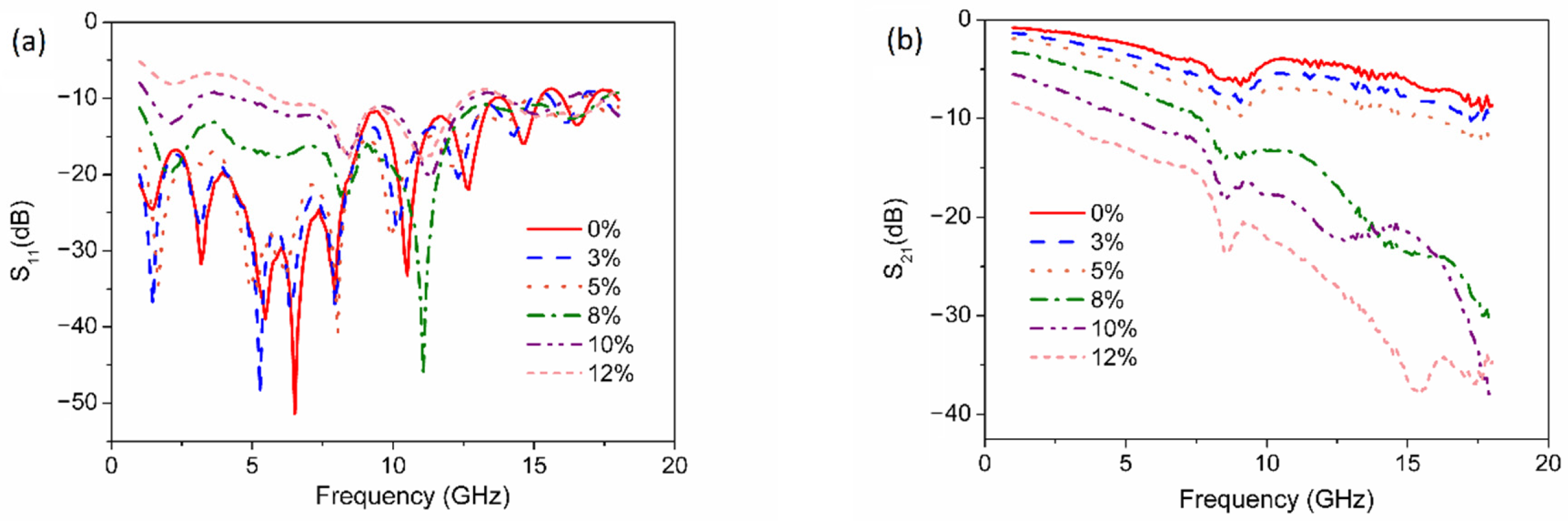
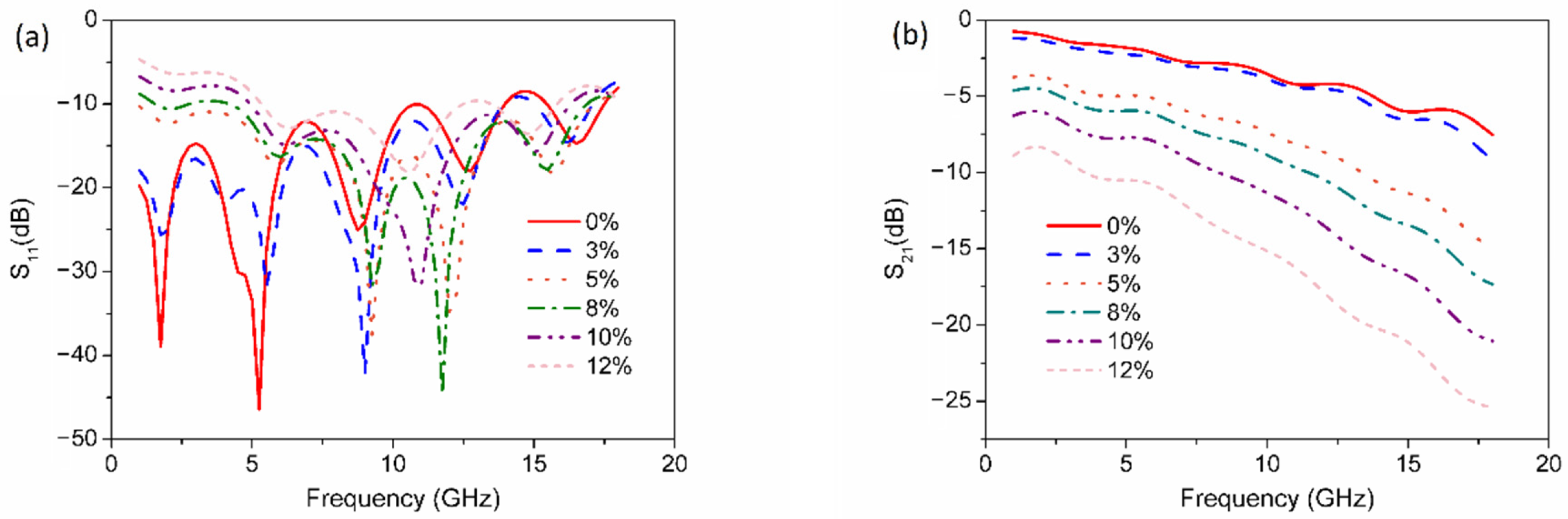
3.2. RF Characteristics of the Microstrips under Strain
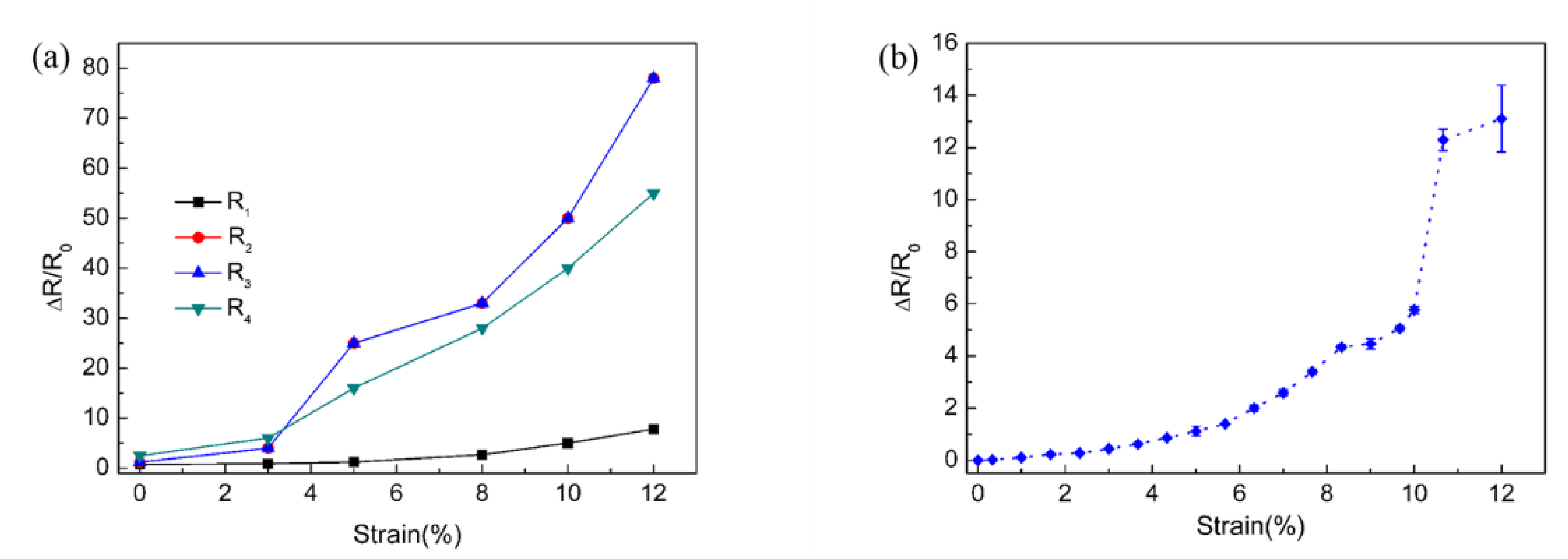
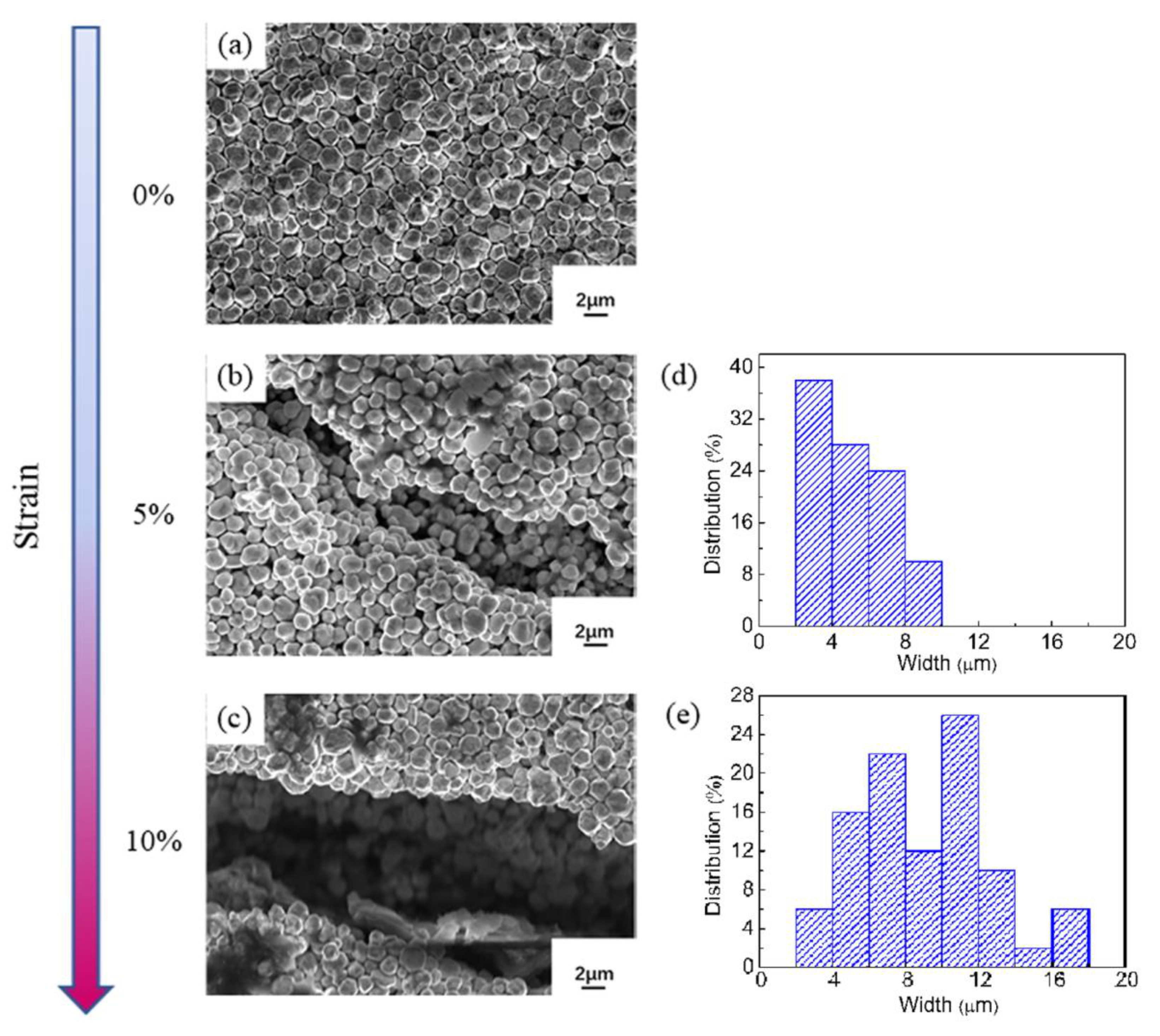
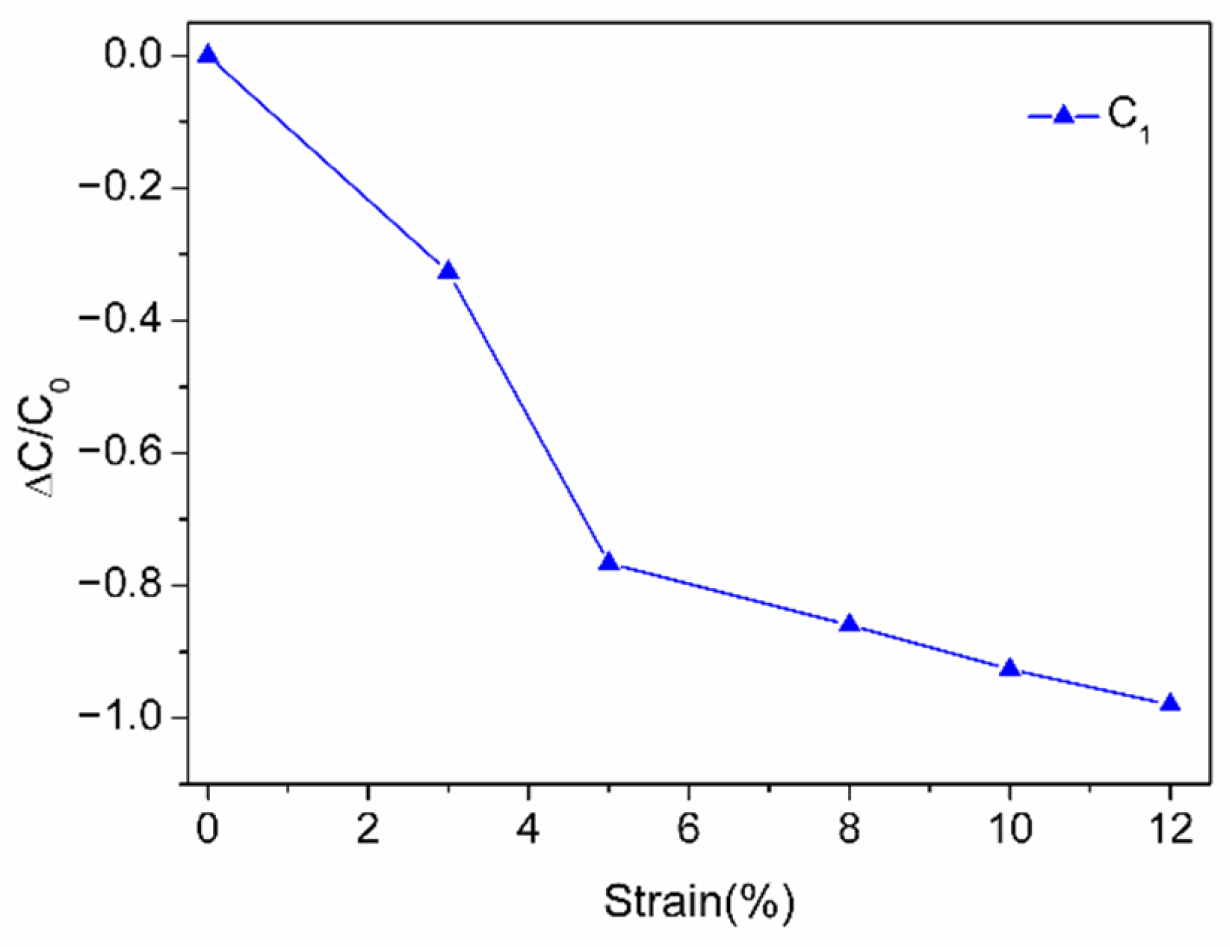
3.3. Analysis and Discussions of the Element Parameters
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yun, Y.; Kim, H.S.; Jang, N. Study on Characteristics of Various RF Transmission Line Structures on PES Substrate for Application to Flexible MMIC. ETRI J. 2014, 36, 106–115. [Google Scholar] [CrossRef]
- Qin, G.-X.; Yuan, H.-C.; Celler, G.K.; Ma, J.G.; Ma, Z.Q. RF model of flexible microwave switches employing single-crystal silicon nanomembranes on a plastic substrate. Microelectron. Eng. 2012, 95, 21–25. [Google Scholar] [CrossRef]
- Huang, C.-U.; Chen, I.-Y.; Henry, J.H.; Christina, F.J.; Huang, R.-S. 2.4 and 5.2 GHz Dual-Band Antenna Fabricated on Flexible Parylene Membrane. Jpn. J. Appl. Phys. 2005, 44, 8356–8361. [Google Scholar] [CrossRef]
- Li, Y.; Torah, R.; Steve, B.; Turdor, J. Inkjet printed flexible antenna on textile for wearable applications. In Proceedings of the 2012 Textile Institute World Conference, Shah Alam Selangor, Malaysia, 15–17 May 2012. [Google Scholar]
- Inui, T.; Koga, H.; Nogi, M.; Komoda, N.; Suganuma, K. A Miniaturized Flexible Antenna Printed on a High Dielectric Constant Nanopaper Composite. Adv. Mater. 2014, 27, 1112–1116. [Google Scholar] [CrossRef] [PubMed]
- Glavin, N.R.; Chabak, K.D.; Heller, E.R.; Moore, E.A.; Prusnick, T.A.; Maruyama, B.; Walker, D.E.; Dorsey, D.L.; Paduano, Q.; Snure, M. Flexible gallium nitride: Flexible gallium nitride for high-performance, strainable radio-frequency devices. Adv. Mater. 2017, 47, 1701838. [Google Scholar] [CrossRef] [PubMed]
- Fan, C.-Y.; Wei, M.-D.; Gjurovski, P.; Saeed, M.; Hamed, A.; Negra, R. Concept for a 16-QAM RF Transmitter on Flexible Substrate using a Graphene Technology. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019. [Google Scholar]
- Scarpello, M.L.; Kurup, D.; Rogier, H.; Ginste, D.V.; Axisa, F.; Vanfleteren, J.; Joseph, W.; Martens, L.; Vermeeren, G. Design of an implantable slot dipole conformal flexible antenna for biomedical applications. IEEE Trans. Antennas Propag. 2011, 59, 3556–3564. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, S.; Pratap, R.; Galstyan, E.; Wosik, J.; Selvamanickam, V. Development of rebco tapes on nonmetallic flexible substrates for rf applications. IEEE Trans. Appl. Supercond. 2019, 335, 3500405. [Google Scholar] [CrossRef]
- Tiwari, N.K.; Singh, S.P.; Mondal, D.; Jaleel Akhtar, M. Flexible biomedical RF sensors to quantify the purity of medical grade glycerol and glucose concentrations. Int. J. Microw. Wirel. Technol. 2019, 12, 120–130. [Google Scholar] [CrossRef]
- Alipour, A.; Gokyar, S.; Algin, O.; Atalar, E.; Demir, H.V. An Inductively Coupled Ultra-Thin, Flexible, and Passive RF Resonator for MRI Marking and Guiding Purposes:Clinical Feasibility. Magn. Reson. Med. 2018, 80, 3613–3670. [Google Scholar] [CrossRef]
- Rai, T.; Dantes, P.; Bahrevni, B.; Kim, W.S. A Stretchable RF Antenna with Silver Nanowires. IEEE Electron Device Lett. 2013, 34, 544–546. [Google Scholar] [CrossRef]
- Eom, S.-H.; Lim, S. RF Stretchable Sensor Using Flexible Substrate and Eutectic Gallium-Indium. In Proceedings of the ISAP2016, International Symposium on Antennas & Propagation, Okinawa, Japan, 24–28 October 2016. [Google Scholar]
- Sivasamy, R.; Kanagasabai, M. Design and fabrication of flexible FSS polarizer. Int. J. RF Microw. Comput. Aided Eng. 2020, 30, 22002. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Obata, M. A microcrack model of dilatancy in brittle materials. J. Appl. Mech. 1988, 55, 24–35. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, Z.-Y.; Zhong, M.-J.; Wan, P.-B.; Zhang, W.-X.; Zhang, L.-Q. A Flexible Wearable Pressure Sensor with Bioinspired Microcrack and Interlocking for Full-Range Human–Machine Interfacing. Small 2018, 14, 1803018. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Lou, H.-Y.; Meng, J.-J.; Peng, Z.-Q.; Wang, B.; Wan, J.-M. Stretchable Energy Storage E-skin Supercapacitors and Body Movement Sensors. Sens. Actuators B Chem. 2019, 305, 127529. [Google Scholar] [CrossRef]
- Lee, J.K.; Kim, S.S.; Park, Y.I.; Kim, C.D.; Hwang, Y.K. In-cell adaptive touch technology for a flexible e-paper display. Solid State Electron. 2011, 56, 159–162. [Google Scholar] [CrossRef]
- Gibney, E. The inside story on wearable electronics. Nature 2015, 56, 26–28. [Google Scholar] [CrossRef]
- Lei, K.F.; Lee, K.F.; Lee, M.Y. Development of a flexible PDMS capacitive pressure sensor for plantar pressure measurement. Microelectron. Eng. 2012, 99, 1–5. [Google Scholar] [CrossRef]
- Zou, S.-M.; Yelamanchili, B.; Gupta, V.; Sellers, J.A.; Isaacs-smith, T.; Tuckerman, D.B.; Hamilton, M.C. Low-loss cable-to-cable parallel connection method for thin-film superconducting flexible microwave transmission lines. Supercond. Sci. Technol. 2019, 32, 1361–1373. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Y.; Wei, S.-M.; Lin, Y.; Liu, L. Ultrasensitive Cracking-assisted Strain Sensors Based on Silver Nanowires/Graphene Hybrid Particles. ACS Appl. Mater. Int. 2016, 8, 25563–25570. [Google Scholar] [CrossRef]
- Li, R.-Z.; Yan, J.; Fang, Y.-M.; Fan, X.-Y.; Sheng, L.-K.; Ding, D.-Y.; Yin, X.-X.; Yu, Y. Laser-Scribed Lossy Microstrip Lines for Radio Frequency Applications. Appl. Sci. 2019, 9, 415. [Google Scholar] [CrossRef]
- Xu, C.-C.; Hu, S.-F.; Zhang, R.; Hu, H.-L.; Ying, C.; Zhang, F.; Liu, Q.-T.; Fu, X.-D. Preparation and properties of fexible conductive polydimethylsiloxane composites containing hybrid fllers. Polym. Bull. 2019, 76, 6487–6501. [Google Scholar] [CrossRef]
- Li, R.-Z.; Hu, A.-M.; Zhang, T.; Oakes., K.-D. Direct Writing on Paper of Foldable Capacitive Touch Pads with Silver Nanowire Inks. ACS Appl. Mater. Inter. 2014, 6, 21721–21729. [Google Scholar] [CrossRef] [PubMed]
- Pozar, D.M. Microwave Engineering, 3rd ed.; John Wiley& Sons: New York, NY, USA, 2010; pp. 446–448. [Google Scholar]
| Parameters | Value |
|---|---|
| Length of microstrip, L | 50 mm |
| Width of strip conductor, W | 2.7 mm |
| Thickness of the strip conductor, Ts | 0.14 mm |
| Thickness of the PDMS substrate, T | 1 mm |
| Dielectric constant of the PDMS substrate | 2.68 |
| Loss tangent of the PDMS substrate | 0.0375 |
| Δε | R1 | R2 | R3 | R4 | L1 | L2 | C1 |
|---|---|---|---|---|---|---|---|
| 0% | 0.77 Ω | 1.2 Ω | 1.2 Ω | 2.5 Ω | 251 pH | 251 pH | 150 pF |
| 3% | 0.89 Ω | 4 Ω | 4 Ω | 6 Ω | 445 pH | 439 pH | 101 pF |
| 5% | 1.2 Ω | 25 Ω | 25 Ω | 16 Ω | 605 pH | 605 pH | 35 pF |
| 8% | 2.7 Ω | 33 Ω | 33 Ω | 28 Ω | 700 pH | 700 pH | 21 pF |
| 10% | 5 Ω | 50 Ω | 50 Ω | 40 Ω | 929 pH | 929 pH | 11 pF |
| 12% | 7.8 Ω | 78 Ω | 78 Ω | 55 Ω | 1.2 nH | 1.2 nH | 3 pF |
| Δε | ΔR1 | ΔR2 | ΔR3 | ΔR4 | ΔL1 | ΔL2 | ΔC1 |
| 0% | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3% | 0.12 Ω | 2.8 Ω | 2.8 Ω | 3.5 Ω | 194 pH | 188 pH | −49 pF |
| 5% | 0.43 Ω | 23.8 Ω | 23.8 Ω | 13.5 Ω | 354 pH | 354 pH | −115 pF |
| 8% | 1.93 Ω | 31.8 Ω | 31.8 Ω | 25.5 Ω | 449 pH | 449 pH | −129 pF |
| 10% | 4.23 Ω | 48.8 Ω | 48.8 Ω | 37.5 Ω | 678 pH | 678 pH | −139 pF |
| 12% | 7.03 Ω | 76.8 Ω | 76.8 Ω | 52.5 Ω | 949 pH | 949 pH | −147 pF |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, D.; Li, R.; Yan, J.; Liu, J.; Fang, Y.; Yu, Y. Influence of Microcracks on Silver/Polydimethylsiloxane-Based Flexible Microstrip Transmission Lines. Appl. Sci. 2021, 11, 5. https://doi.org/10.3390/app11010005
Ding D, Li R, Yan J, Liu J, Fang Y, Yu Y. Influence of Microcracks on Silver/Polydimethylsiloxane-Based Flexible Microstrip Transmission Lines. Applied Sciences. 2021; 11(1):5. https://doi.org/10.3390/app11010005
Chicago/Turabian StyleDing, Daye, Ruozhou Li, Jing Yan, Jiang Liu, Yuming Fang, and Ying Yu. 2021. "Influence of Microcracks on Silver/Polydimethylsiloxane-Based Flexible Microstrip Transmission Lines" Applied Sciences 11, no. 1: 5. https://doi.org/10.3390/app11010005
APA StyleDing, D., Li, R., Yan, J., Liu, J., Fang, Y., & Yu, Y. (2021). Influence of Microcracks on Silver/Polydimethylsiloxane-Based Flexible Microstrip Transmission Lines. Applied Sciences, 11(1), 5. https://doi.org/10.3390/app11010005






