Forecasting Irregular Seasonal Power Consumption. An Application to a Hot-Dip Galvanizing Process

Featured Application

The method described in this document makes it possible to use the techniques usually applied to load prediction efficiently in those situations in which the series clearly presents seasonality but does not maintain a regular pattern.

Abstract

Distribution companies use time series to predict electricity consumption. Forecasting techniques based on statistical models or artificial intelligence are used. Reliable forecasts are required for efficient grid management in terms of both supply and capacity. One common underlying feature of most demand–related time series is a strong seasonality component. However, in some cases, the electricity demanded by a process presents an irregular seasonal component, which prevents any type of forecast. In this article, we evaluated forecasting methods based on the use of multiple seasonal models: ARIMA, Holt-Winters models with discrete interval moving seasonality, and neural networks. The models are explained and applied to a real situation, for a node that feeds a galvanizing factory. The zinc hot-dip galvanizing process is widely used in the automotive sector for the protection of steel against corrosion. It requires enormous energy consumption, and this has a direct impact on companies’ income statements. In addition, it significantly affects energy distribution companies, as these companies must provide for instant consumption in their supply lines to ensure sufficient energy is distributed both for the process and for all the other consumers. The results show a substantial increase in the accuracy of predictions, which contributes to a better management of the electrical distribution.

1. Introduction

Demand management is a primary process in the development of industrial activity. Distribution companies must ensure a supply is provided at a reasonable cost, and for this reason, they need to manage resources efficiently. The use of electrical prediction models contributes to their management of the distribution lines by offering tools to estimate future demand with great precision. The techniques allow for forecasting based on time series using statistical models or artificial intelligence (AI).

The most widely used univariate forecasting tools for electricity demand can be classified into three broad groups [1]: fundamental models, statistical models, and computational models. There is growing interest in the use of computational models, although the most widely used models are statistical models, both exponential smoothing models and autoregressive integrated moving average (ARIMA) models.

The fundamental models are made up of hybrid models that introduce all the possible physical variables, adopting a complex relationship between them and also using the techniques of statistical models.

Computational models are based on AI and emulate natural behaviors through the use of mathematical models. These are algorithms whose learning is automatic and are part of the science of Machine Learning [2]. At present, deep learning techniques represent an evolution and have found applications in demand forecasting, especially in areas where prediction is difficult, such as renewable energies [3]. The most widely used techniques for electricity demand are artificial neural networks (ANN) [4], particularly non-linear autoregressive neural networks with exogenous variables (NARX) [5,6]. Support vector machines (SVM) [7] and bagged regression trees (BRT) [8] also stand out, and these occasionally apply fuzzy logic [9].

Electricity demand series show stochastic behavior, and they have traditionally been modeled using statistical methods. The ARIMA models are considered to be the econometric models par excellence. The Box–Jenkins methodology [10] is used to determine which ARIMA model to use, although some authors [11] state that simpler methods are better than this methodology at providing forecasts. The application of ARIMA models to demand is usually carried out in a general way in Seasonal Autoregressive Integrated Moving Average Exogenous (SARIMAX) models [12,13,14] in which exogenous variables are included to improve demand. The introduction of two seasonalities allows substantial improvement in the predictions of these models [15].

State-space models (SSM) are a form of exponential smoothing representation. They are commonly applied to demand [16], especially since the introduction of the Kalman filter (see [17]). They also allow the introduction of various seasonalities in a complex way [18] and with covariates [19]. De Livera and Hyndman include modifications that include adjustment of the error using autoregressive moving average (ARMA) models and with Box-Cox transformations (BATS [20]) and trigonometric seasonality (TBATS [18]).

Other very common smoothing techniques are the Holt-Winters models [20]. These models are excellent predictors for time series with marked seasonality [1,21]. The inclusion of more seasonality [22,23,24] improves their forecasts, leading to the development of multiple seasonal Holt-Winters models (nHWT). Trull et al. [25] introduce discrete seasonality that takes into account seasonalities whose occurrences are not regular (nHWT-DIMS models).

The current trend is to create hybrid models in which traditional techniques are combined with machine learning [26,27]. An example can be found in [28], which applies an exponential smoothing method and neural networks to divide the forecasting process between a linear part and a non-linear part.

The use of wavelets for irregular series has been combined with ARIMA models [29], Holt-Winters models [30], or ANN [31].

Regularization techniques have also been applied to prevent over- and under-fitting issues, based on a Least Absolute Shrinkage and Selection Operator (LASSO) [32], and have been applied to short-term load forecasting models based on multiple linear regression [33]. Banded regularization is also used to estimate parameters without overfitting in autoregressive models [34].

Newer methods use an anti-leakage least-squares spectral analysis (ALLSSA) to simultaneously estimate the trend and seasonal components before making a regularization and make forecasts [35]. The ALLSSA method determines the statistically significance of the components preventing under- and over-fitting issues. The least-squares wavelet analysis (LSWA) is a natural extension of the least-squares spectral analysis and allows the forecaster to obtain spectrograms for equally and unequally spaced time series and identify statistically significant peaks in the time series [36].

One common feature of most demand-related time series is their strong seasonality components [37]. In some cases, the electricity demanded by a process could present an irregular seasonal component that seriously distorts the behavior of the series in a way that the models cannot deal with.

The zinc hot-dip galvanizing process is a process that is widely used in the automotive sector to protect steel against corrosion [38,39]. It requires an enormous consumption of energy, and this has a direct impact on companies’ income statements. However, the process also significantly affects energy distribution companies, since they must foresee the instantaneous consumption in their lines in order to ensure the distribution of energy both for the process and for the other consumers. A characteristic of the demand in this process is the presence of seasonal patterns that resemble seasonality but, because of their irregular behavior, are difficult to assimilate to seasonality.

The structure shown by the series in this study means that it is more suitable to work with time series models rather than frequency or signal analysis. We have therefore considered it convenient to preferably use traditional time series models with seasonality.

In this article, we present several solutions to this problem based on the use of ARIMA models, multiple seasonal Holt-Winters models with and without discrete interval moving seasonalities (DIMS), state space models, and neural network models. To verify the effectiveness of the techniques described, they are applied to the industrial process of hot-dip galvanizing.

The article is organized as follows: Section 2 conducts a review of the forecasting methods as well as an explanation of the production process; Section 3 demonstrates the results and their analysis; Section 4 discusses the results; and finally, in Section 5, the conclusions are summarized.

2. Materials and Methods

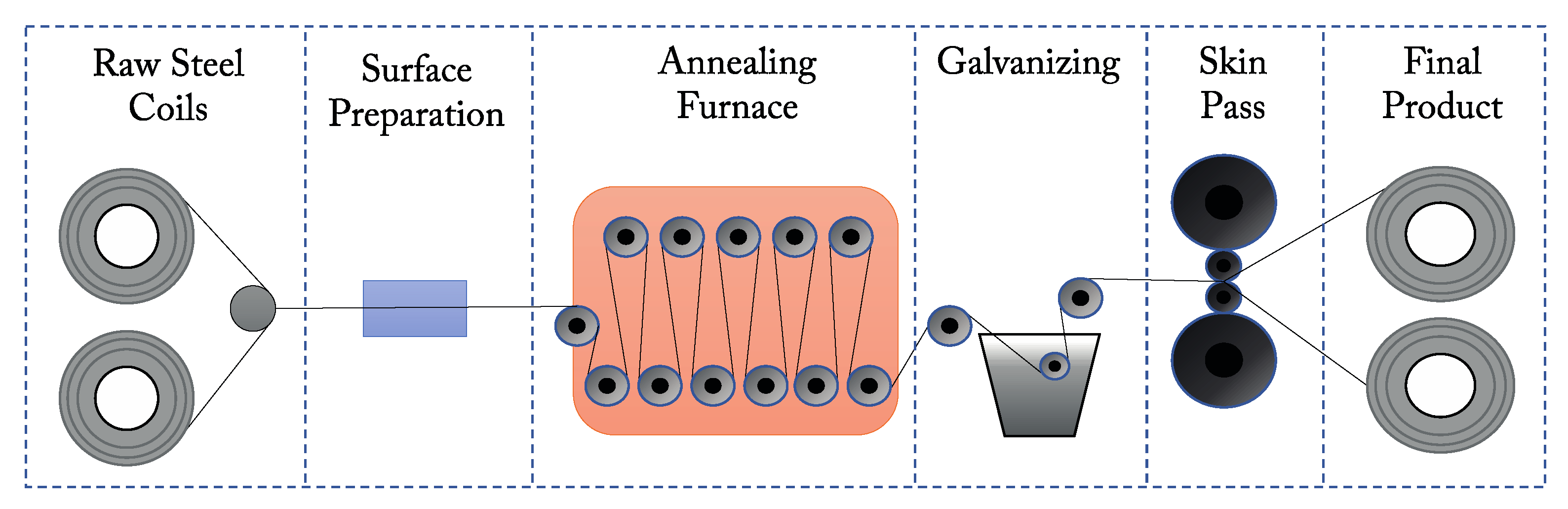
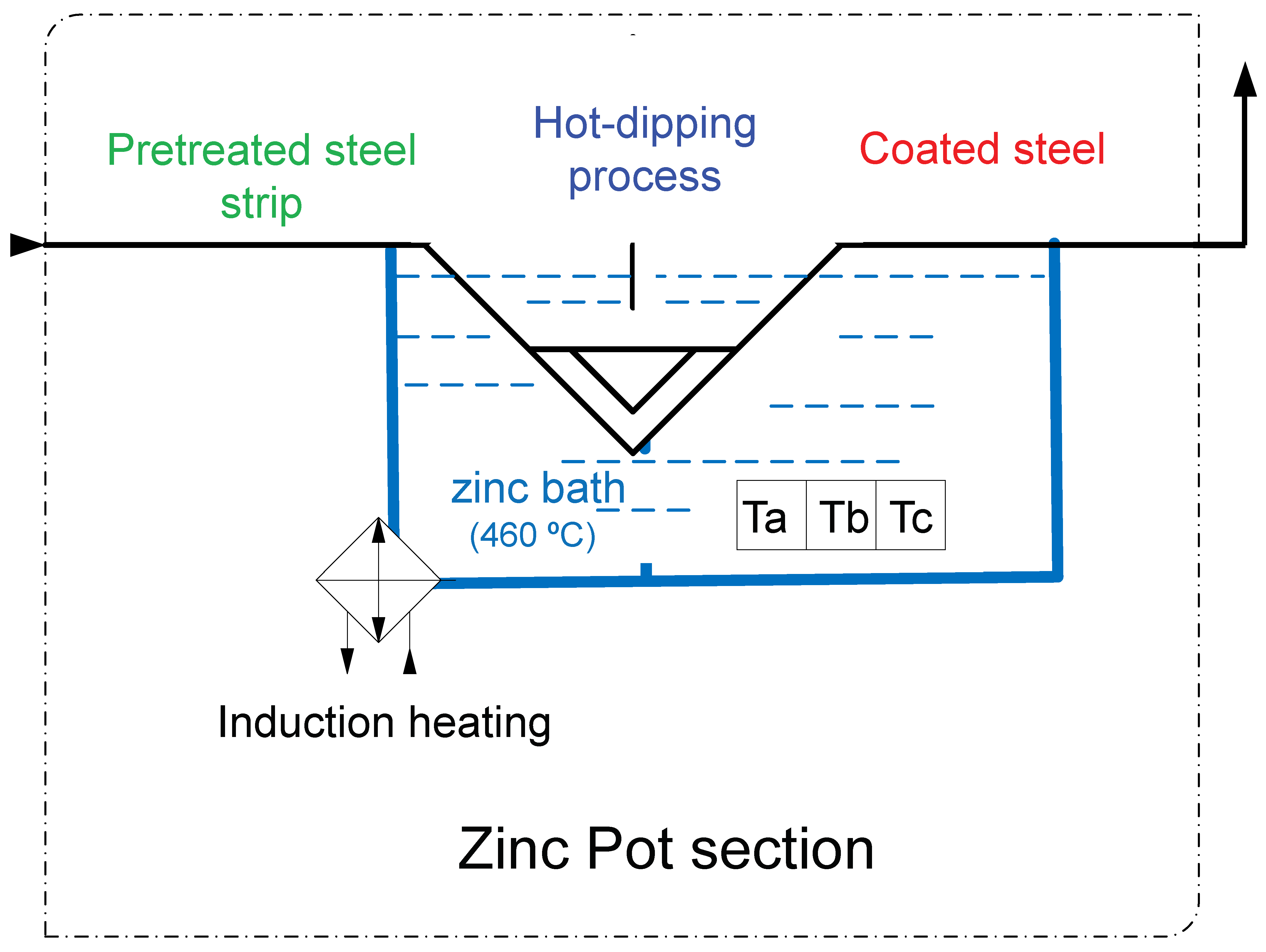
2.1. Study Area

The study has been applied to the consumption node of a hot-dip galvanizing company. The process is carried out by coating extruded steel strips with a zinc foil that forms an alloy with the steel and gives the desired properties. This process is continuous and produces high-quality products [40].

Figure 1 shows a general scheme for the galvanizing process, where the greatest consumption is in the zinc bath. In the annealing furnace, the steel strip is preheated, and then it is immersed in a bath of molten zinc at 460 °C. Subsequently, the galvanized steel strip goes through the skin-pass process [41,42,43] after it has cooled down.

The zinc bath consists of a molten alloy of Zn in a bath, which is kept at 460 °C by the action of two heating inductors located at the bottom of the bath. Figure 2 schematically shows the operation of the zinc bath. The bath temperature is measured as an average of the local temperatures provided by the thermocouples Ta, Tb and Tc. The inductors heat from the bottom of the bath and a natural flow inside the bath is produced so that the bath achieves the targeted temperature.

The electrical consumption associated with the process can be seen in Figure 3. This graph shows the consumption for eight working days, measured every six minutes. It begins on 14 November, 2009 at 00:00 am and ends on 22 November, 2009 at 08:00 am. There are in total 2000 measurements. The oscillations shown in the time series are produced by the action of induction heaters that keep the bath at the targeted temperature. The big peaks in consumption are produced when the bath needs to be recharged, and new Zn (dropped in ingots) is added into the bath. At this moment, the heaters must be put into full operation. From this dataset, the first 1800 observed values are used for training purposes, and the last 200 ones are used for validation.

A series of cyclical patterns can be observed (oscillations) that are repeated throughout the series, with a short–length pattern that is repeated continuously throughout the series clearly standing out. There are other patterns that are repeated irregularly, with differentiated behaviors. A closer view of the series is shown in Figure 4. In graph (a) and graph (b), a common underlying pattern can be identified, with a length of around ten time units (which means an hour, as the temperature is measured every six minutes). This first pattern is repeated regularly over the whole time period, and it is considered as a seasonality.

Figure 4, graph (c) and (d) show the time series after removing the first seasonal pattern. It can also be seen that other patterns develop throughout the series in such a way that the time of their appearance or their length are not constant. Technically, this non-regular behavior cannot be considered as a seasonality, since it is not possible to predict the fluctuation pattern that will develop in the future. To make consumption predictions, it is necessary to take into account this seasonal behavior, even though it is not regular.

2.2. Forecasting Methods

In this section, we describe the forecasting methods applied to the time series under study. The most common methods applied to short-term electricity demand forecasting, using both AI and statistical methods, have been chosen. First, the methods used with regular seasonal behavior are described, and then we describe the models with discrete seasonality.

2.2.1. Artificial Neural Networks

Neural networks are computational models structured in the form of layers with nodes interconnected as a network. They are named because of their resemblance to the human brain structure. The nodes, called neurons, perform simple operations in parallel and are located in each of the layers of the network. The layers are of three different types: the input layer, where neurons receive direct information from the inputs; hidden layer (s), whose neurons use the information from the neurons of previous layers and feed the next layers; and the output layer, where neurons use the information from the hidden layers to produce an output. Thus, there is an input layer, one or more hidden layers, and an output layer. The connections between the different layers are made through the connection of their neurons, which are called synapses. The strength of the connection between neurons is determined by a weighting established at the synapse.

The most suitable structure for forecasting time series is the NARX type structure [44,45]. It is a recurrent dynamic neural network, with feedback connections. Figure 5 shows a close-loop representation of the NARX structure [46]. Neurons receive information from exogenous input variables in addition to the target series itself and the feedbacks. In order to improve forecasts, it can be used the past predicted and observed values delayed through a tapped delay line (TDL) memory. The circles after the input layers denote the TPL delay (e.g., one to two delays in the figure).

The input variables $x_t$ are exogenous variables used in the model. Both $x_i$ and $y_t$ are connected by axioms to which weights $w_i$ are assigned, and with an activation function f that is integrated with an aggregation function Σ. The output ${\widehat{y}}_{t+1}$ provides future forecasts after the network has been trained. $b$ stands for the bias whose presence increases or decreases the neuron’s processing capacity.

The mathematical and non-linear representation that governs the network is shown in (1), where $x_t$ represents the inputs and $y_t$ the objective function, while ${\widehat{y}}_{t+1}$ represents the prediction. $D_x$ and $D_y$ are the time delays applied in the network.

$${\widehat{y}}_{t+1 }=f\left[x_t,x_{t-1},\dots ,x_{t-D_x+1},y_t,y_{t-1},\dots ,y_{t-D_y+1}\right].$$

(1)

The NARX neural network maps the function through the multilayer perceptron, using the time delays for both the input variables and the output feedback [47].

An alternative to this neural network is a function fitting neural network. This is a type of shallow neural network based on multilayer perceptron (MLP) with which we can make adjustments to non-linear functions (non-linear regression, NLR). The use and application of such a network for the prediction of electricity demand has been discussed previously [48]. The mathematical representation that governs this network is shown in (2).

$${\widehat{y}}_{t+1 }=f\left[x_t,x_{t-1},\dots ,x_{t-D_x+1}\right].$$

(2)

Here $x_t$ are the predictors, which are several variables (including the observed values of the time series) used to feed the model. A representative schema for this neural network is shown in Figure 6.

By training the network, weights are assigned to the synaptic connections, minimizing an error criterion. The ANNs used in this work are trained using the Levenberg-Marquardt algorithm [49], and minimizing the mean squared error (MSE). After the training process, to give the predictions, a closed loop network is performed, and forecasts are provided.

2.2.2. ARIMA Models

ARIMA models were introduced by Box and Jenkins [50] to model non–stationary series and allow predictions to be made. A description and in-depth analysis can be found in [51] and in the book by Brockwell and Davis [52]. Seasonal ARIMA models are usually denoted by ARIMA$\left(p,d,q\right)x{\left(P,D,Q\right)}_S$. S indicates the length of the seasonal pattern under consideration. The compact representation of the ARIMA model is usually, as shown in (3), a function of autoregressive polynomials and polynomials of moving means, and of the difference operators.

$$\begin{gathered} {\varphi }_p\left(B\right){\Phi }_P\left(B^S\right){\nabla }^d{\nabla }_S^D\left(y_t^{\left(\lambda \right)}-c\right)={\theta }_q\left(B\right){\Theta }_Q\left(B^S\right){\epsilon }_t, \\ \left\{{\epsilon }_{\mathrm{t}}\right\}~\mathrm{N}\left(0,{\sigma }^2\right). \end{gathered}$$

(3)

$\{y_t, t=0,\pm 1,\pm 2,\dots \}$ are the observed data of the univariate series. If the variability in the data grows with time, it is necessary to transform the data to stabilize the variance. The Box-Cox power transformation family is a general class of variance-stabilizing transformations. The Box-Cox transformation of $y_t$ with power parameter $\lambda$ to the transformed data $y_t^{\left(\lambda \right)}$ is defined by (4).

$$y_t^{\left(\lambda \right)}=\{\begin{array}{c}\begin{array}{cc}\frac{y_t^{\lambda }-1}{\lambda };& if \lambda \ne 0,\end{array}\\ \begin{array}{cc}ln y_t;& if \lambda =0\end{array}.\end{array}$$

(4)

The power parameter $\lambda$ is estimated by the maximum–likelihood method. The polynomials ${\varphi }_p\left(B\right)=1- {\varphi }_{1}B-{\varphi }_2{B}^2-\cdots -{\varphi }_p{B}^p$ and ${\theta }_q\left(B\right)=1- {\theta }_{1}B-{\theta }_2{B}^2-\cdots -{\theta }_q{B}^q$ represent the regular or non–seasonal autoregressive and the moving averages components, respectively, and the polynomials ${\mathsf{\Phi }}_{\mathrm{P}}\left(B^S\right)=1- {\mathsf{\Phi }}_1{B}^S-{\mathsf{\Phi }}_2{B}^{2S}-\cdots -{\mathsf{\Phi }}_{\mathrm{P}}{B}^{PS}$ and ${\mathsf{\Theta }}_{\mathrm{Q}}\left(B^S\right)=1- {\mathsf{\Theta }}_1{B}^S-{\mathsf{\Theta }}_2{B}^{2S}-\cdots -{\mathsf{\Theta }}_{\mathrm{Q}}{B}^{QS}$ represent the seasonal autoregressive and the moving averages components, respectively, with $B$ as the lag operator. ∇ is the is the backward difference operator, [$B{y}_{t }=y_{t-1}; B^S{y}_{t }=y_{t-S};$∇ = $\left(1-B\right); {\nabla }^d={\left(1-B\right)}^d; {\nabla }_{\mathrm{S}}^D={\left(1-B^S\right)}^D$]. d and D are the number of differencings required to make the time series stationary (d, D ≤ 2). $\left\{{\epsilon }_t\right\}$ is a Gaussian white noise process, [$\left\{{\epsilon }_t\right\}$ $~N\left(0,{\sigma }^2\right)]$. c is the model constant.

The orders of the polynomials {p, d; P, Q} are selected using the Akaike’s Information Criterion (AIC, AICc) or Schwarz’s or the Bayesian Information Criterion (SIC or BIC). The model coefficients $\left\{ {\varphi }_1,{\varphi }_2,\dots ,{\varphi }_p; {\theta }_1,{\theta }_2,\dots ,{\theta }_q; {\mathsf{\Phi }}_1,{\mathsf{\Phi }}_2,\dots ,{\mathsf{\Phi }}_{\mathrm{P}};{\mathsf{\Theta }}_1,{\mathsf{\Theta }}_2,\dots ,{\mathsf{\Theta }}_{\mathrm{Q}}\right\}$ and ${\sigma }^2$ are estimated by the maximum likelihood method.

ARIMA models can present more than one seasonality, as indicated in (5). To do this, the models are expressed as ARIMA $\left(p,d,q\right)x{\left(P_1,D_1,Q_1\right)}_{S_1}x{\left(P_2,D_2,Q_2\right)}_{S_2}$ where $S_1 and S_2$ indicate the two seasonalities to which they refer.

$${\varphi }_p\left(B\right){\mathsf{\Phi }}_{{\mathrm{P}}_1}\left(B^{S_1}\right){\mathsf{\Omega }}_{P_2}\left(B^{S_2}\right){\nabla }^d{\nabla }_{{\mathrm{S}}_1}^{D_1}{\nabla }_{{\mathrm{S}}_2}^{D_2}\left(y_t^{\left(\lambda \right)}-\mathrm{c}\right)={\theta }_q \left(B\right){\mathsf{\Theta }}_{{\mathrm{Q}}_1}\left(B^{S_1}\right){\mathsf{\Psi }}_{{\mathrm{Q}}_2}\left(B^{S_2}\right){\epsilon }_t.$$

(5)

The polynomials ${\mathsf{\Omega }}_{P_2}\left(B^{S_2}\right)$ and ${\mathsf{\Psi }}_{{\mathrm{Q}}_2}\left(B^{S_2}\right)$ represent the second seasonal autoregressive and the moving averages components, respectively.

2.2.3. Multiple Seasonal Holt-Winters Models

Exponential smoothing uses information from the past through weighted averages to make predictions. The weight decreases as newer values are entered into the time series, giving more importance to newer data over older. A smoothing parameter determines this weight. The introduction of these models dates back to the 1960s with the work of Holt [53] and Brown [54]. Winters [20] presented the Holt-Winters models, in which exponential smoothing techniques are performed on the three components of the series: level ($l_t)$, trend ($b_t$) and seasonality ($s_t$). The model includes a series of structured equations, called smoothing equations, the information from which is compiled by a forecast equation to provide forecasts. The equations can be combined with additive or multiplicative trends and seasonality.

Gardner and McKenzie [55] introduced a damping factor for the trend, and their model outperforms the previous models when the trend shows high variations [56]. Taylor broke down seasonality into two or three nested components so that the models can capture the series that present more than one seasonality, such as series for short-term demand [22,23]. Taylor also included in the model an adjustment using the one-step-ahead error as proposed by Chatfield [57]. This adjustment adds an AR(1) model for the residuals, obtaining the parameter at the same time as the smoothing parameters are obtained. In the same way, García-Díaz and Trull [24] generalized the model including the way the initial values are obtained, to n seasonalities. The nHWT models are shown in Equations (6)–(9).

$$l_t=\alpha \left(\frac{y_t}{{\displaystyle \prod }{s}_{t-s_i}^{\left(i\right)}}\right)+\left(1-\alpha \right)\left(l_{t-1}+\varrho b_{t-1}\right),$$

(6)

$$b_t=\gamma \left(l_t-l_{t-1}\right)+\left(1-\gamma \right)\varrho b_{t-1},$$

(7)

$$s_t^{\left(i\right)}={\delta }^{\left(i\right)}\left(\frac{y_t}{l_t{{\displaystyle \prod }}_{j\ne i}{s}_{t-s_j}^{\left(j\right)}}\right)+\left(1-{\delta }^{\left(i\right)}\right)s_{t-s_i}^{\left(i\right)},$$

(8)

$${\widehat{y}}_{t+k}=\left(l_t+{\displaystyle \sum }_{j=1}^k{\varrho }^j{b}_t\right){\displaystyle \prod }_i{s}_{t-s_i+k}^{\left(i\right)}+{\phi }_{AR}^k{\epsilon }_t.$$

(9)

The smoothing equations include the smoothing parameters $\alpha$, $\gamma$ and ${\delta }^{\left(i\right)}$ for smoothing the level, the trend and the different seasonal indices $\left(i\right)$ of length $s_i$. The equation ${\widehat{y}}_{t+k}$ provides the k–future prediction values from the observed values of the series $y_t$. Here, ${\epsilon }_t$ is the one–step–ahead error, and the parameter ${\phi }_{AR}$ is the parameter for the AR(1) adjustment. The damping parameter for the trend is denoted by $\varrho$ [58].

The equations of the model are recursive, and therefore they need initial values so that they can fit the model. Several methodologies for initialization have been documented [56,57]. To be able to use the models, it is necessary to estimate the smoothing parameters by minimizing the error using non-linear algorithms [59,60]. The Nelder-Mead [61,62] simplex method has been used, which minimizes the root of mean squared error (RMSE).

2.2.4. State Space Models

The SSM refers to a form of graphical–probabilistic representation [63] to describe the dependence between an observed measurement and a series of latent state variables through equations called state equations that describe its evolution. Taking into account the fact that a time series can be decomposed into components of level, seasonality and trend, this terminology applied to time series would be understood as the model that interprets the evolution of the relationship of the observed variables ($y_t$) with the latent unobservable variables (level, trend, and seasonality).

SSMs have a great variety of formulations. In this paper, the formulation indicated by Durbin and Koopman [64] and Hyndman et al. [16] applied to univariate stochastic time series is used. These models are structured through a formulation of two matrix equations, as shown in (10)–(11):

$$y_t={\mu }_t+\mathit{r}{x}_{t-1}+ {\epsilon }_t,$$

(10)

$$x_t=\mathit{f}{x}_{t-1}+\mathit{g}{\epsilon }_t.$$

(11)

Equation (11) is known as the state transition equation, and Equation (10) is known as the observation equation. Here $x_{t-1}$ is known as the vector of states, $y_t$ is the vector of observations, while ${\epsilon }_t$ is a vector of Gaussian white noise and is known as the innovation process. $\mathit{r}$, $\mathit{f}$ and $\mathit{g}$ are matrices and vectors of coefficients with appropriate dimensions. $\mathit{f}$ explains the evolution of $x_t$ and $\mathit{g}$ provides the innovation correction of ${\epsilon }_t$. The term ${\mu }_t$ is the one step ahead forecast, and $\mathit{r}$ is a term to include the error additively.

De Livera [18] introduced modified models, based on the exponential smoothing methods, in which a Box-Cox transformation is applied to the data, and the residuals are modeled using an ARMA process and include the damping factor for trend and multiple seasonalities. The acronym for this method is BATS (Box-Cox transform ARMA errors Trend and Seasonal Components). This model is described in (12)–(16).

$$y_t^{\left(\lambda \right)}=l_{t-1}+\varrho b_{t-1}+{\displaystyle \sum }_{i=1}^{n_s}{s}_{t-s_i}^{\left(i\right)}+d_t,$$

(12)

$$l_t=l_{t-1}+\varrho b_{t-1}+\alpha d_t,$$

(13)

$$b_t=\left(1-\varrho \right)b+b_{t-1}+\gamma d_t,$$

(14)

$$s_t^{\left(i\right)}=s_{t-s_i}^{\left(i\right)}+{\delta }_i{d}_t,$$

(15)

$$d_t={\displaystyle \sum }_{i=1}^p{\phi }_i{d}_{t-i}+{\displaystyle \sum }_{i=1}^q{\theta }_i{\epsilon }_{t-i}+{\epsilon }_t.$$

(16)

In these equations, $y_t^{\left(\lambda \right)}$ indicates the value of the observed data after the Box-Cox transformation with the value $\lambda$, described in (4). $l_t$, $b_t$ and $s_t^{\left(i\right)}$ are the values of the level, trend and seasonalities with smoothing parameters $\alpha$, $\gamma$ and ${\delta }_i$. The subscript $i$ denotes the seasonality under consideration, of seasonal length $s_i$, and $n_s$ is the number of seasonalities. $d_t$ is an ARMA (p, q) process with residuals whose coefficients are determined by ${\phi }_i$ and ${\theta }_i$. $\varrho$ is the damping factor for trend. The term $b_t$ stands for a long–run trend term. ${\epsilon }_t$ is a Gaussian white noise process $N\left(0,{\sigma }^2\right)$. The nomenclature for BATS includes the following arguments $\left(\lambda ,\varrho ,p,q,s_1,\dots ,s_{n_s}\right)$.

Additionally, De Livera et al. [18] presented the same model but with seasonality based on trigonometric models. The seasonality Equation (16) is replaced by the set of Equations (17)–(20), a seasonal component based on Fourier series. These are known as TBATS (Trigonometric seasonal BATS).

$$s_t^{\left(i\right)}={{\displaystyle \sum }}_{j=1}^{\left(k_i\right)}{s}_{j,t}^{\left(i\right)} ,$$

(17)

$$s_{j,t}^{\left(i\right)}=s_{j,t-1}^{\left(i\right)}\cos \left({\omega }_{j,i}\right)+s_{j,t-1}^{*\left(i\right)}\sin \left({\omega }_{j,i}\right)+{\delta }_1^{\left(i\right)}{d}_t,$$

(18)

$$s_{j,t}^{*\left(i\right)}=-s_{j,t-1}^{\left(i\right)}\sin \left({\omega }_{j,i}\right)+s_{j,t-1}^{*\left(i\right)}\cos \left({\omega }_{j,i}\right)+{\delta }_2^{\left(i\right)}{d}_t,$$

(19)

$${\omega }_{j,i}=2\pi j/s_i.$$

(20)

Every seasonal component of the model $s_t^{\left(i\right)}$ results from the sum of the $k_i$ stochastic levels $s_{j,t}^{\left(i\right)}$ of period i. $s_{j,t}^{*\left(i\right)}$ is the stochastic growth for each period. ${\delta }_1^{\left(i\right)}$ and ${\delta }_2^{\left(i\right)}$ are the smoothing parameters. The nomenclature for TBATS includes the following arguments $\left(\lambda ,\varrho ,p,q,\left\{s_1,k_1\right\},\dots ,\left\{s_i,k_i\right\}\right)$.

Obtaining the values of the previous matrices and vectors requires the application of an algorithm based on the Kalman filter and the maximum likelihood function using the sum of squared errors (SSE) as the minimization criterion. This algorithm carries a high computational load and manages to obtain these parameters iteratively. The reference [18] explains in detail the process to be carried out in order to use the BATS and TBATS methods.

2.2.5. Multiple Seasonal Holt-Winters Models with Discrete Interval Moving Seasonalities

nHWT models are robust to variations in the series, but sometimes special situations occur in which it is interesting to take these anomalies into account. One of the clearest examples is the influence of the calendar effect on electricity demand [65]. These anomalous and specific situations can sometimes be modeled as a discrete seasonality, if they follow a repetitive pattern. Despite being seasonal, since they are discrete, they have the particular quality that they are not located at fixed moments in the time series; therefore, they are not linked to a deterministic appearance, as would be the case for regular seasonality. These seasonalities are called discrete interval moving seasonality (DIMS).

Trull et al. [25] include the use of discrete seasonality in their model, so that the model seen in (6)–(9) now results in (21)–(25), which is named nHWT–DIMS:

$$l_t=\alpha \left(\frac{y_t}{{\displaystyle \prod }{s}_{t-s_i}^{\left(i\right)}{\displaystyle \prod }{D}_{t_h^{*}-s_m^{*}}^{\left(m\right)}}\right)+\left(1-\alpha \right) \left(l_{t-1}+ \varrho b_{t-1}\right),$$

(21)

$$b_t=\gamma \left(l_t-l_{t-1}\right)+\left(1-\gamma \right)\varrho b_{t-1},$$

(22)

$$s_t^{\left(i\right)}={\delta }^{\left(i\right)}( \frac{y_t}{l_t{{\displaystyle \prod }}_{j \ne i}{s}_{t-s_j}^{\left(j\right)}{{\displaystyle \prod }}_m{D}_{t_h^{*}-s_m^{*}}^{\left(m\right)}}) + \left(1- {\delta }^{\left(i\right)}\right) s_{t-s_i}^{\left(i\right)},$$

(23)

$$D_{t_h{}^{*}}^{\left(h\right)}={\delta }_D^{\left(h\right)}( \frac{y_t}{l_t{{\displaystyle \prod }}_{j }{s}_{t-s_j}^{\left(j\right)}{{\displaystyle \prod }}_{m\ne h}{D}_{t_h{}^{*}-s_m^{*}}^{\left(m\right)}})+ \left(1-{\delta }_D^{\left(h\right)}\right)D_{t_h{}^{*}-s_h^{*}}^{\left(h\right)},$$

(24)

$${\widehat{y}}_{t+k}=\left(l_t+{\displaystyle \sum }_{v=1}^k{\varrho }^v{b}_t\right){\displaystyle \prod }_i{s}_{t-s_i+k}^{\left(i\right)}{\displaystyle \prod }_j{D}_{t_h^{*}-s_h^{*}+k}^{\left(h\right)}+{\phi }_{AR}^k{\epsilon }_t.$$

(25)

Here the term $D_{t_h{}^{*}}^{\left(h\right)}$ is included, which represents the discrete seasonal indices, for each DIMS $\left(h\right)$ considered up to $n_{DIMS}$. DIMS are only defined in the time intervals in which the special event takes place. These time intervals are designated using $t_h^{*}$ for each DIMS (h). This nomenclature is chosen in order to distinguish this from the continuous time interval $t$.

The great difference between this model and other methods of modeling special situations is that the effect produced by the anomaly in the series is modeled as an internal part of the model, as one more seasonality, and is smoothed with each new appearance, unlike the use of models with dummy variables and/or modifications of the original series.

In the nHWT models, the seasonality equation shows a fixed recurrence for each seasonal pattern ($s_i$) being considered. With DIMS, this is not possible, since the occurrences of special events are not subjected to a deterministic pattern in the series. Therefore, the use of the variable $s_h^{*}$ indicates, for each DIMS and each occurrence, which is the recurrence to consider.

One possible situation with special events is the simultaneous occurrence of two events. In such a case, the forecaster should consider the option of using only one of the DIMS that occur at that time, or using both, if the effects produced by the two special events add up.

An important aspect to consider is the initialization of the DIMS. A DIMS may have few occurrences in the time series and, therefore, its seasonal indexes must be calculated in such a way that it converges rapidly to the desired effect.

The initialization method consists in first obtaining the initial values of the level, the trend, and the seasonal indices for the regular seasonality. Subsequently, a decomposition of the series is carried out using trend and multiple seasonality. It is common to use the multiple STL method (Seasonal–Trend decomposition procedure using Loess [66], where Loess is a method to estimate linear relationships).

From the decomposition, the series can be reconstructed without including the irregular part, which is where the information necessary to obtain the desired indices is found. The initial values are obtained by weighting the time series against the reconstructed series.

The adjustment of the parameters is carried out following the same procedure as for the nHWT, with the exception that, if necessary, this adjustment can be carried out in two steps—first adjusting the parameters of the regular model and then adjusting the parameters associated with the DIMS. Adjusting all the parameters simultaneously obtains models with more reliable predictions, while the second option is faster. Thus, the first option is chosen for this work.

3. Results

The approach proposed for the work described below has the following scheme. First, a study of the series is carried out to determine the seasonal periods. The study is carried out using continuous seasonality models and discrete seasonality models, all as described in the previous section. Although it is preferable to use an error minimization criterion for each technique when fitting the models, the RMSE—defined in (26)—is used to standardize and compare the fitted results.

$$\mathrm{RMSE}=\sqrt{\frac{1}{N}{\displaystyle \sum }_{t=1}^N{\left(y_t-{\widehat{y}}_t\right)}^2 }.$$

(26)

Here N stands for length of the dataset used for the training. The final comparison will be made according to the forecasts made in the validation set.

3.1. Analysis of the Seasonality of the Series

The series shown in Figure 3 clearly presents a seasonality with periodicity of one hour. However, to study the following seasonal patterns it is necessary to perform an analysis on the frequency domain. To investigate the appreciable frequencies in the time series, a spectral density analysis is carried out, the result of which is shown in Figure 7 in the form of a smoothed periodogram. A smoothed periodogram is the preferred tool here as the periodic cycles do not show a regular periodicity [67].

Analyzing the figure, the presence of a clearly dominant frequency is observed, which corresponds to the periodicity of ten units of time (one hour). Also, the presence of another dominant frequency can be observed. This corresponds to a second seasonality with a period of 106 time-units. However, this is the second seasonality and is associated with a greater variability around its value, which confirms what is seen in Figure 3.

To confirm these hypotheses, an ALLSSA analysis is performed. This method is robust against unequally spaced time series, estimating trend and seasonal components simultaneously, and providing statistically significant components in the time series [35]. The analysis shows three main and significant frequencies at periodicities of 10, 118, and 203 time-units. This disagreement between the two methods suggests that, despite various seasonalities clearly coexisting, non-dominant seasonalities do not occur continuously and may influence the analysis.

In contrast to this result, an analysis based on the use of wavelets is also carried out. The advantage of using wavelets to analyze the spectral content of the series is that we obtain a map in the time-scale plane. The concept of frequency in spectral analysis is now replaced by the scale factor, and therefore, instead of using a periodogram, we use a scalogram. The scale measures the stretching of the wavelets, being directly related to frequency, as the greater the scale is, the higher the frequency of the series, which is related to the inverse of a frequency, that is, to a period [68]. This map allows the non–stationary characteristics of the signal, including changes in periodicity, to be studied, which is the objective.

Figure 8 shows the average wavelet power graph. This graph shows the means of the powers developed over time for each period or frequency. Although the results are similar to those shown in the previous graph, a greater variability is observed in the longer periods. Three main periods are located at 10, 94, and 196 time units. The results are very close to the previous one.

The need for a robust analysis using the time and frequency domain motivates the use of LSWA [35,69]. The software LSWAVE [70] in MATLAB^® is an easy and intuitive tool for performing this analysis. This software computes the least square wavelet spectrum (LSWS) for the series, with no need for preprocessing, transforming, or detrending. LSWA considers the correlations of the sinusoidal functions and constituents and the noise at the same time. We apply LSWA to the training set, with the results shown in Figure 9.

The abscissa axis indicates the time scale used, while the ordinate axis shows the cyclical frequencies (as 1/period). The level of variance explained is reflected by colors, according to the scale to the right of the graph.

The first conclusion is clear from the graph: the one–hour seasonality remains practically throughout the series as the predominant seasonality (with a percentage of variance greater than 90%), but discontinuously. In the sections where this does not occur, a series of sawtooth-shaped formations stand out from the rest, although the percentage of variance that it reflects does not exceed 30%. Some areas are shaded with more than 40% of the variation within high frequencies areas. This graph is shown in closer detail of in Figure 10.

We decided to use a 3D representation because it is then easier to appreciate the lowest cyclic frequencies. Between 14th November and 15th November and later between 19th November and 21st November, two frequencies with a percentage of variance of over 40% appear. This corresponds to a period of 100 time-units. In the middle, between the two intervals, some peaks with 30% of the variance are also located. This corresponds to a periodicity of 200-time units.

The conclusion from this analysis is that there is clearly one seasonality that occurs every hour (ten-time units), and a second pattern with unregular behavior over time and a periodic length that has been established at between 94 and 118 units. Although it is not strictly a seasonality, it can be modeled as a second seasonality. A marginal seasonality can be obtained for long cycles but will not be taken into account as it seems that its influence on the time series is very small compared to the previous one.

3.2. Application of Models with Regular Seasonality

Given this disparity of values for the determination of the length of the seasonal periods, we choose to carry out one analysis with the models using a single seasonality (ten-time units) and another using two seasonalities.

For the models with regular seasonality, the second seasonality to be tested will be for a range of periods of between 90 and 110 time-units.

3.2.1. Application of ANN

One of the most powerful tools for working with neural networks is the MATLAB^® Deep Machine Learning toolbox. This toolbox includes a great variety of possibilities and different neural networks. From this range of possibilities, the NARX network and the NLR network are used. These two networks have been proven to be efficient in predicting future electricity demand values. The method of working with them is described in Figure 11. Here, it can be seen that it is first necessary to use the historical information about demand.

To address the observed seasonality, the series is additionally given a delay, according to the seasonality. In this case, the seasonality of one hour corresponds to ten units of time of six minutes, so a delay of ten units is introduced to the series. Additional variables are added to the information provided by the time series. The exogenous information supplied to the model is:

• Previous hour’s average electricity consumption.
• Consumption of electricity from the previous hour.
• Timestamp (only in NARX model).

The networks used are described in

Table 1. Neural network parameters and RMSE for fitted results.

Neural Network	Parameters	Fit RMSE
NARX	1 input layer 1 hidden layer with 20 neurons 1 output layer TDL = 3	33.95
NLR	1 input layer 1 hidden layer with 20 neurons 1 output layer	33.21

. The NARX model includes a single hidden layer and a TDL of three time units. It was checked that greater TDL did not improve the results. NLR model also include a single hidden layer.

The training process is performed by minimizing the MSE and using the Levenberg-Marquardt algorithm. The training result is displayed as the RMSE in Table 1.

In the same way as the first seasonality was introduced, the second seasonality is added, following what we have seen in Section 3.2. The result of adding a new seasonality does not improve the result. The chosen model has only one seasonality.

3.2.2. Application of ARIMA Models

To apply the ARIMA models, MATLAB^® is the chosen platform, using Econometrics Toolbox and SSMMATLAB [71] for double seasonal ARIMA. R is also tested with the ‘forecast’ package, but the MATLAB^® results outperformed the R results. Like the previous models, models with one and two seasonalities according to Section 3.2 are tested. The best results are found using a single seasonality of one hour (ten-time units). The best model is ARIMA (4,2,4) × (4,1,4)₁₀, for which the parameters are shown in

Table 2. ARIMA parameters and RMSE for fitted results.

Parameters		Fit RMSE
AR	${\varphi }_1=$$-0.145; {\varphi }_2=$$-0.472; {\varphi }_3$$= -0.190; {\varphi }_p=$0.170	50.42
MA	${\theta }_1=$$0.861; {\theta }_2=$$-0.601; {\theta }_3=$$0.443; {\theta }_4$= 0.174
SAR	${\mathsf{\Phi }}_1=$$-0.487; {\mathsf{\Phi }}_2=$$0.067; {\mathsf{\Phi }}_3=$$-0.260; {\mathsf{\Phi }}_4=$−0.067
SMA	${\mathsf{\Theta }}_1=$$0.142; {\mathsf{\Theta }}_2=$$0.069; {\mathsf{\Theta }}_3=$$-0.292; {\mathsf{\Theta }}_4=$−0.065

.

3.2.3. Application of nHWT Models

To perform the analysis using the nHWT models, a proprietary tool developed in MATLAB ^® is used. This tool comes in the form of a toolbox, but it has not been published yet. Models with one and two seasonalities are tested.

The results show that the model that best adapts to this series presents a single seasonality, with the parameters $\alpha = 0.0001$, $\gamma = 0.0001$, ${\delta }_{10}= 0.4856$ and ${\phi }_{AR}=0.9286$. The damping factor $\varrho$ is set to 0. Models including this parameter were tested, but results were not improved, thus it was removed from the model. The RMSE of the fit process is 54.93.

The result is not surprising since the nHWT models are structural and do not allow for a relaxation of seasonality. Once seasonality is established, the model will continue to develop the same pattern, even though this is not really reflected in the series. When using a single seasonality, the information provided by the second seasonal pattern is lost, but it has less influence than the error caused by a second seasonality that does not coincide with the real seasonality of the series.

3.2.4. Application of SSM Models

To work with the state spaces, the ‘forecast’ library is used in R [72]. Models with a single seasonality are tested, as well as models that include several seasonalities as indicated in Section 3.1. Here again, the use of the trend damping parameter did not provide better results and was removed from the model.

As in the previous cases, the models with several seasonalities do not show better results than the models with a single seasonality.

Table 3. SSM models, their parameters, and fit RMSE for fitted results.

Model Arguments	Parameters	Fit RMSE
BATS (0.717,0, 5,2, 10)	$\lambda =$0.717, $\alpha =$0.120,$\gamma =$0.206, $\delta =$− 0.004, ${\varphi }_1$= 0.945, ${\varphi }_2 =$− 0.625, ${\varphi }_3 =$0.022, ${\varphi }_4 =$0.104, ${\varphi }_5 =$− 0.500, ${\theta }_1 =$− 0.153, ${\theta }_2=$0.515.	46.77
TBATS (0.756,0, 5,2, {10,1})	$\lambda =$0.756, $\alpha =$0.862, $\gamma =$0.105, ${\delta }_1=$− 0.0004, ${\delta }_2=$0.0001, ${\varphi }_1$= 1.293, ${\varphi }_2 =$– 0.552, ${\varphi }_3 =$− 0.359, ${\varphi }_4 =$0.227, ${\varphi }_5 =$– 0.1968, ${\theta }_1$= −1.358, ${\theta }_2 =$0.783.	45.44

shows the models used—including their arguments—in the first column, the parameters obtained after the adjustment process in the second column, and the RMSE value of the adjustment in the third column.

3.3. Application of Discrete Seasonality Models (nHWT-DIMS)

The application of discrete seasonality carries with it a differentiated strategy. The use of nHWT-DIMS models makes it possible to model localized seasonality at specific instants of time, independently of other seasonality. In Figure 12, we show two different periods for the series. In addition to the seasonal pattern described at the beginning (of one hour), a new pattern can also be observed in Figure 12a, whose length is established at 27 time units (2 h and 42 min). This pattern is framed between two dashed lines including the demand peaks. Figure 12b shows another seasonal pattern that has the same length, but a different behavior. These two patterns will be called DIMS a and DIMS b.

The appearance of each discrete seasonality does not occur on a regular basis. This situation causes the recursion required in the Holt-Winters models to be variable. This is indicated in Figure 12 by the lines with arrows. The solid lines indicate the recursion for the DIMS a, and the dashed lines indicate it for the DIMS b. The information regarding the DIMS is organized in

Table 4. Location in the time series of the discrete seasonalities (DIMS) and their recursivity. The column Nr. indicates the order of appearance of the corresponding DIMS. ‘Time starts’ and ‘Time ends’ reflect the moving interval in which DIMS is defined, and ‘Recursivity’ shows the length of time since the previous appearance.

DIMS	Nr.	Time Starts	Time Ends	Recursivity
DIMS a	1	14th November at 05:42 am	14th November at 08:24 am	––––––––
	2	14th at 04:00 pm	14th at 06:42 pm	618 min.
	3	15th at 00:18 am	15th at 03:00 am	498 min
	4	15th at 07:30 am	15th at 10:12 am	432 min
	5	15th at 06:42 pm	15th at 09:24 pm	672 min
	6	16th at 07:24 pm	16th at 10:06 pm	1482 min
	7	17th at 10:42 am	17th at 01:24 pm	918 min
	8	18th at 06:06 am	18th at 08:48 am	1164 min
	9	19th at 02:30 am	19th at 05:12 am	1224 min
	10	19th at 08:48 pm	19th at 23:30 pm	1098 min
	11	21th at 06:06 pm	21th at 20:48 pm	2718 min
DIMS b	1	16th November at 07:06 am	16th November at 09:48 am	––––––––
	2	20th at 05:06 am	20th at 07:48 am	5640 min
	3	20th at 05:24 pm	20th at 08:06 pm	738 min
	4	21th at 02:36 am	21th at 05:18 am	552 min
	5	22th at 02:24 am	22th at 05:06 am	1428 min

. This table includes the locations of the discrete seasonalities on every appearance (starting and ending time when the DIMS is defined, used in the variable $t_h^{*}$) and the associated recursivity in minutes, which corresponds to $s_h^{*}$. As an example, the time interval when the second appearance of DIMS a is defined starts at 04:00 pm on the 14th and ends at 06:42 pm on the 14th. The recursivity $s_h^{*}$ during this interval is 618 min.

The general model described by Equations (21)–(25) now results in the Equations shown in (27)–(32), with one seasonality of length ten time units and two DIMS as described in Table 4.

$$l_t=\alpha \left(\frac{y_t}{I_{t-s_{10}}^{\left(10\right)}{D}_{t_a^{*}-s_a^{*}}^{\left(a\right)}{D}_{t_b^{*}-s_b^{*}}^{\left(b\right)}}\right)+\left(1-\alpha \right) \left(l_{t-1}+ b_{t-1}\right),$$

(27)

$$b_t=\gamma \left(l_t-l_{t-1}\right)+\left(1-\gamma \right)b_{t-1},$$

(28)

$$s_t^{\left(10\right)}={\delta }^{\left(10\right)}( \frac{y_t}{l_t{D}_{t_a^{*}-s_a^{*}}^{\left(a\right)}{D}_{t_b^{*}-s_b^{*}}^{\left(b\right)}})+\left(1- {\delta }^{\left(10\right)}\right) s_{t-10}^{\left(10\right)},$$

(29)

$$D_{t_a{}^{*}}^{\left(a\right)}={\delta }_D^{\left(a\right)}( \frac{y_t}{l_t{s}_{t-s_{10}}^{\left(10\right)}{D}_{t_b^{*}-s_b^{*}}^{\left(b\right)}})+ \left(1-{\delta }_D^{\left(a\right)}\right)D_{t_a{}^{*}-s_a^{*}}^{\left(a\right)},$$

(30)

$$D_{t_b{}^{*}}^{\left(b\right)}={\delta }_D^{\left(b\right)}( \frac{y_t}{l_t{s}_{t-s_{10}}^{\left(10\right)}{D}_{t_a^{*}-s_a^{*}}^{\left(a\right)}})+ \left(1-{\delta }_D^{\left(b\right)}\right)D_{t_b{}^{*}-s_b^{*}}^{\left(b\right)},$$

(31)

$${\widehat{y}}_t\left(k\right)=\left(l_t+k{b}_t\right)s_{t-s_{10}+k}^{\left(10\right)}{D}_{t_a^{*}-s_a^{*}+k}^{\left(a\right)}{D}_{t_b^{*}-s_b^{*}+k}^{\left(b\right)}+{\phi }_{AR}^k{\epsilon }_t.$$

(32)

Here, $s_t^{\left(10\right)}$ is the seasonal equation for the regular seasonality of ten-time units with smoothing parameter ${\delta }^{\left(10\right)}$. $D_{t_a{}^{*}}^{\left(a\right)}$ and $D_{t_b{}^{*}}^{\left(b\right)}$ are the DIMS as described in Table 4 with smoothing parameters ${\delta }_D^{\left(a\right)}$ and ${\delta }_D^{\left(b\right)}$ defined only in time $t_a^{*}$ and $t_b^{*}$. The recursivity $s_a^{*}$ and $s_b^{*}$ is defined in Table 4.

To use the model, the procedure described in [25] is carried out. Initially, the initial values for the level are obtained as the moving average of the first period of one hour; for the trend as the slope between the first and second cycle of one hour; and for the seasonal indices, the weighting of the series in the first cycle on the moving average. Subsequently, the seasonal indices of the DIMS are obtained. The time series is decomposed into its trend, seasonality, and irregular components using STL decomposition with the period length of one hour. From these components, the series is rebuilt, but without the irregular component being included. The seasonal indices are obtained by weighting the original series over the reconstructed one.

Once the initial values of the model have been determined, the model is fitted by minimizing the RMSE, and the smoothing parameters are obtained. The tool for this analysis is software developed in MATLAB (R) for this purpose. The obtained RMSE is 58.65. The smoothing parameters of the model obtained are $\alpha =$0.0001, $\gamma =$0.0001, ${\delta }^{\left(10\right)}=$ 0.4853 for the first regular seasonality, ${\delta }^{\left(a\right)}=$0.0005 for DIMS type a (see Figure 12a), ${\delta }^{\left(b\right)}=$0.0652 for DIMS type b (see Figure 12b) and ${\phi }_{AR}=$0.9056. Here again, it has is decided not to use the damping parameter for trend. The RMSE of the fitted model is 58.65.

3.4. Model Fit Comparison

A benchmark summary is reported in

Table 5. Main benchmarking results. RMSE used to compare fitted results. MAPE used to compare forecasts accuracy.

	RMSE on Fit	Average MAPE for Forecasts
NARX	33.95	26.63%
NN-NLR	33.21	13.94%
ARIMA	50.42	24.03%
nHWT	54.93	18.55%
TBATS	46.77	37.60%
BATS	45.44	37.61%
nHWT-DIMS	58.65	16.00%

, where the RMSE in the fit process is summarized. The RMSE used to compare the models while fitting shows that the ANN fits better than the other models to the time series. The worst case seems to be nHWT-DIMS. The comparison shows that the state space models and the ARIMA models fit the observed data better than the nHWT and nHWT–DIMS models. Similar behavior is expected in the forecasts.

3.5. Forecasts Comparison

The greatest interest is in forecast reliability. To compare the results of the forecasts given by the different methods, the mean absolute percentage error (MAPE) as a percentage is used, as indicated in (33). This is a common indicator used to compare forecasts of demand [73].

$$\mathrm{MAPE}\left(h\right)=\frac{1}{h}{\displaystyle \sum }_{t=1}^h\left|\frac{y_t-{\widehat{y}}_t}{y_t}\right|.$$

(33)

Here, h is the forecast horizon to evaluate. As the forecasts are made one hour ahead (ten units) throughout the validation subset, h can take values from one to ten time units. From the forecasts of one hour ahead, the MAPE is obtained by comparing these with the real values of the validation set, using the procedure described in [74]. The benchmark summary in Table 5 includes the average of the MAPE. The average is obtained as the mean of the MAPE(h) with h = 1,2,…,10. The best forecasts, on average, are produced by the NLR. The nHWT-DIMS models are revealed as a competitive method against the regular seasonal models, outperforming the other models.

Figure 13 shows the MAPE of these forecasts as a function of the forecasting horizon. It is clear from the results obtained that traditional models with one seasonality are not capable of working with this type of series. The BATS and TBATS models of state spaces do not drop below 30% MAPE. The ARIMA model starts by making very short-term forecasts that have MAPE of below 15%, but beyond three time units it is not capable of making good predictions. The nHWT models improve the forecasts with respect to the previous ones, although the use of the DIMS allows the level of the predictions to be always kept below 20%. However, the method that produces the best results is NN–NLR. These models give forecasts that remain almost constant with an accuracy of about 14% of MAPE.

4. Discussion

The results obtained in the previous exercise show that the fact that having irregularities in the series has an enormous influence on the result in statistical models used in this article. The models that use regular seasonalities require that they appear with a regular length, regardless of whether the pattern varies. When dealing with series whose seasonality is not completely defined, the models cannot overcome these variations. The use of models with discrete seasonality allows for progress in this problem, since it is capable of introducing seasonality only where it occurs.

Though the periodicity of 200-time units did not show a consistent pattern over time in this data set, having a longer time series more than seven days (e.g., two-month record or more) may reveal discontinuous patterns repeating themselves at that low frequency, which may help to better train the model for forecasting such signals. This requires further investigation and research.

However, the best tool for this series is the use of AI to address these irregularities. Curiously, the NARX neural network does not offer good results, but the NLR neural network manages to improve the results. This situation responds to the fact that the previously described models require seasonal stability if they are to make predictions, since they are based on linear or structural models. The neural network model is not subject to these restrictions and uses these irregularities to make forecasts.

Future studies in this area should aim to ensure that the structural models are capable of introducing an ambiguity between their seasonal processes produced by the inconsistency of the series in terms of seasonality.

5. Conclusions

In this article, we have analyzed time series forecasting methods applied to a pattern of electricity demand that has an irregular periodicity, so that the seasonality is not well defined. We have analyzed models of neural networks, ARIMA, multiple seasonal Holt-Winters models and state spaces using regular seasonalities, and multiple seasonal Holt-Winters models with discrete interval moving seasonalities.

To compare the behavior of all the models discussed, they were applied to the situation of a connection node with a hot-dip galvanizing company, where the time series of electricity consumption due to the heating of the bath causes seasonalities. A frequency analysis using spectral density and least square wavelets with the series showed that a first seasonality of one hour could be easily located; some other seasonalities could be considered, but their period was not clear. The problem with irregular seasonality is that the models need to use patterns that constantly repeat themselves, so the pattern must be defined for the entire time series. Nevertheless, the use of Holt-Winters models with discrete seasonality (nHWT-DIMS) allows these seasonalities to be separated efficiently and reliable predictions to be made.

The results showed that the use of nHWT–DIMS models improves the results compared to the rest of the models. This is an interesting proposal for companies because of the simplicity of its application and good results—the MAPE obtained is around 16%. However, NLR (ANN) showed better predictions, with a MAPE of 14%.

Our study contributes to the improvement of forecasting systems with time series by including discrete seasonality in the model. This allows for an efficient method of prediction to be applied in situations of electrical demand with marked seasonality but non–regular periodic appearances.