1. Introduction
Graphs are prevalent data structures produced with computers and represent and visualize data from various research fields. Drawing graphs or network diagrams is an illustration of their vertices and edges. Vertices are used to symbolize an item or entity, while edges represent the relationship among those items or entities.
Visualizing graph data is important, because good visualizations can represent patterns and insights and support or falsify hypotheses. Much effort has been directed toward making such visually pleasing diagrams. In 1989, Kamada and Kawai [
1] presented an algorithm to solve this problem. They drew general graphs based on a spring model and suggested that the total balanced layout is at least as important as the reduction of edge crossings for human understanding. In their model, the total balance condition is formulated as the square summation of the differences between desirable distances and real ones for all the pairs of vertices.
Another algorithm of force-directed graph drawing was also presented by Fruchterman and Reingold [
2]. They were inspired by a natural system such as springs and macro-cosmic gravity, where the vertices behave as atomic particles or celestial bodies, exerting attractive and repulsive forces on one another; the forces induce movement.
In 1996, Davidson and Harel (DH) [
3] proposed a drawing algorithm using simulated annealing to reduce the energy of a system. The problem of drawing a graph is restated as a problem in minimizing the energy and can be considered one of the optimization problems. Many aesthetic criteria [
4] can be regarded, and the generally accepted ones include:
Uniform spatial distribution of the vertices.
Minimum total edge length on the precondition so that the distance between any two vertices is not less than a given minimum value.
Uniform edge length.
Small angle between edges incident on the same vertex.
Similar angles between edges incident on the same vertex.
Minimum number of edge crossings.
To exhibit any existing symmetric features.
These criteria can be combined to form a multi-criterion weighted sum objective function that measures the quality of a graph, which is then optimized by search-based methods (optimization methods). By applying a metaheuristic algorithm such as simulated annealing, a user can choose a flexible energy function by utilizing its weights to emphasize which aesthetic standard would be prioritized. Following these directions, many drawing algorithms have emerged using different metaheuristic algorithms, such as Stochastic Hill Climbing (HC) [
5], Genetic Algorithm (GA) [
4,
6,
7,
8], Particle Swarm Optimization (PSO) [
9] and Tabu Search (TS) [
10], and all of them have shown promising results.
A graph can be drawn in many forms, where the position of each vertex could be restricted to a layer, circle or a grid point, while the edges can also be drawn not only as a straight line but, also, polygonal lines or curves. The main problem is arranging the vertices and edges; thus, it could affect the aesthetics of a graph and its comprehension and application. The problem gets worse if the graph changes over time by adding and deleting nodes and edges (dynamic graph drawing), and the goal is thus also to preserve a user’s mental map regarding a changing graph.
In 1991, Eades et al. [
11] proposed the mental map concept in graph drawing, in which predictability and traceability are identified so that movement is easy to follow. Preserving a user’s mental map is important in dynamic graph drawing in order to quickly recognize and understand the redrawn layout of a modified graph.
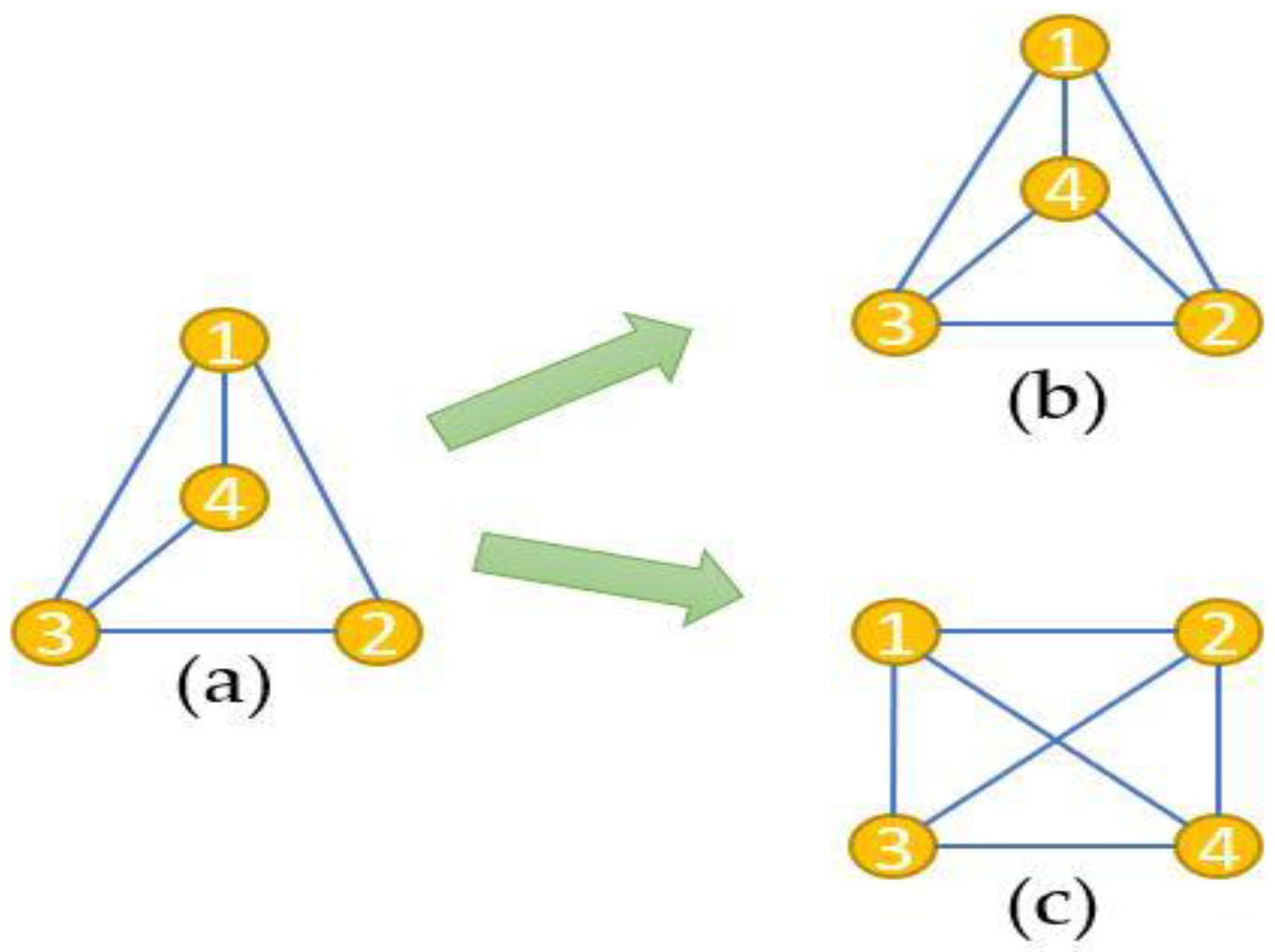
Figure 1 shows a simple example of how important mental map preservation is in a dynamic graph drawing.
Our current research focuses on drawing undirected graphs where each vertex is not restricted, and each edge is a straight line. To draw graphs nicely, and considering dynamic stability, we used a genetic algorithm (GA) with the fitness value based on the aforementioned requirements. This allows our system to adjust the relative weight accordingly, preserve a better mental map or get a better appearance. By creating a smooth animation of a precalculated undirected graph by preserving a user’s mental map, we developed a web-based application that can produce and show the smooth animation of multiple undirected graphs of video game data.
We made the following contributions. First, we proposed a mental map preserving algorithm for an undirected graph using the GA. Second, we developed a web-based application that allows users to create and control the animation of graphs. Third, our proposed system can be generalized and applied in various domains, such as archiving data from the work of Paszkiel et al. [
12] or movie datasets or can be used to visualize word embedding or topic modeling.
The rest of the paper is organized as follows. In
Section 2, we will explain the proposed system, including the system architecture design and methods used in this system. In
Section 3, we will demonstrate the results of the experiment that we conducted. In the last two sections, we will discuss, conclude our research and point out some possibilities for future works.
2. Materials and Methods
2.1. System Overview
Our algorithm can be applied to every dataset, as long as the relationship between two entities can be calculated, and we used a video game dataset as our main dataset. Our graph is a pictorial representation of the vertices and edges of a graph, shown in
Figure 2, where a vertex represents an item or entity, while an edge is used to represent the relationship or similarity between two objects. The main problem is how to arrange these vertices and edges that could affect the understandability, usability and aesthetics of a graph.
2.2. System Architecture
The system architecture is shown in
Figure 3. It is based on basic web application architecture, where it consists of the front end and back end. The front-end part handles a user’s input command and displays the result that was given by our web server.
Through the web application, a user can filter the data he/she wants to be drawn and fully control the animation, including play, pause and choice of the next or previous periods to be shown. Most of the calculation of the node positions is done on the server side, which will then be stored in our database.
Figure 4 shows our front-end interface where a user can filter data, such as the number of displayed nodes; the threshold for similarity link and algorithm simplicity; the year of release; user ratings; difficulty ratings; number of people owning the game; number of people who completed the game, a text-based filter for the title, genre, publisher and developer of the game and, also, the set period window size and its step size on the animation set before performing the animation calculation. Smaller period window sizes mean lesser nodes in each period, while a smaller step size gives minor visual changes during the animation.
The web server will receive an input filter as a request from the front end and retrieve the necessary data from the database during the calculations. The retrieved data will then be calculated using our algorithm to produce the best position for each node period by period and then stored in the database. Using GA, where it is slow to converge and needs much memory space, our experimental results concluded that a higher number of nodes (above 100) takes too much processing time, and the drawing of too many nodes could cause a user to be unable to comprehend any information. Therefore, we implemented a simplification algorithm to reduce the processing time and make the information easier to understand.
Our simplification algorithm works by combining several similar nodes (nodes of the same genre) into one larger node by checking it against a threshold. This threshold is based on a simplification threshold filter that can be adjusted in the filter area. The default threshold setting is auto, where aggregating nodes reduce the number of nodes for every group, starting from the largest group size until the total number of nodes is below 100. As a result, if a user wants to see more details during animation, he/she can pause the animation and click on a merged node to expand into several nodes based on its original filter. D3′s force-directed algorithm handles the movement of the expanded nodes.
Table 1 shows the details of the hardware and software environments of our experiments.
Once the calculation process is done and stored in the database, a user can play the animation. For every period, the front-end part requests the server for the data in that period and displays it accordingly, so each node moves to its previously calculated positions.
2.3. Dataset and Similarity Calculation
The dataset used for this research was collected from GameFAQs.com on 24 April 2019. It consists of 63,952 games with English titles from 1985 to 2019. We performed some preprocessing by removing the games that were not rated at all and were left with 36,696 games. Next, we defined the relationship between each data (node) using similarity calculations. Defining similarity is one of the important key points in graph drawing, as different similarities will provide different results for an undirected graph. The higher the value, the more similar the two nodes are. Equation (1) shows how we define our similarity function.
The similarity function is based on a simple linear equation with a manually determined weight for each attribute. S is our similarity value, and Oi and Oj are our pair of nodes. ωk is our weight for attribute k, and f (Aki and Akj) is a function to determine the difference between attribute k of nodes i and nodes j, and it returns a value between 0 and 1, where 0 means no similarity and 1 means the most similarity.
For the numerical value features (rating and difficulty), we first calculated the difference of their values and then normalized them with the max value, which was five.
Table 2 shows how we defined our similarity weights for each attribute. We decided to give the highest weight to the “Genre” attribute, as we perceived it to be the most effective attribute in the similarities between games.
2.4. Transition Animation
A bad transition technique of visualizing evolving graphs can cause distraction to the user’s mental map. When the movements of graph layout iterations are mixed with the additions and removals of nodes and edges simultaneously, the user may not be able to perceive the changes appropriately. We applied Walter’s work on visualizing evolving graphs [
13], because without that, the changes will be difficult to recognize.
Figure 5 is an example to show our transition animation procedure from the first period to the next period. To avoid changing the layout simultaneously, Walter introduced a way of displaying the layout iteratively, which was modified to fit our system. Firstly, we removed all nodes and edges slowly; we then moved each node to its position and, finally, showed the rest of the nodes and edges. The user can see the removal and insertion changes much better than changing them simultaneously, thus preserving the user’s mental map.
2.5. Genetic Algorithm
2.5.1. Fitness Function
The input of our GA algorithm is a graph G = (V, E), where V is the set of nodes, and E is the set of edges. Each candidate solution is encoded as a vector containing coordinates (, ) and its previous position (’, ’), if it existed, to calculate the mental map preservation. We use several aesthetic criteria that will be minimized, and they are composed by a weighted sum. A user will define these weights to adjust the graph drawing.
Equation (2) is our fitness function f, where
is our weight for each term,
is the distance between node
i and node j using the Euclidean distance,
is the distance between node
i and center c using the Euclidean distance and
size is the number of nodes inside a merged node. Every term will be normalized by dividing it by its first calculated value; hence, a lower value will be below one.
By maximizing the distance among nodes, they can spread evenly. We added into consideration, so the larger a node size, the greater the distance between the node and the other nodes; then, a bigger size node can have enough space when a user wants to expand it to see more detail.
The next term is the uniform edge length, where all edges supposedly have a uniform length to achieve a better aesthetic result. A similarity value is also used between them so that the more similar two nodes are, the shorter the length is. We defined
to be the shortest paths between node
i and
j based on its similarity value. Our third term is basically used to pull every node to the center of a screen instead of letting them stay along the screen’s boundary. The last criteria used is the greadability.js to measure our graph readability, where the input is our graph (V and E), and the output includes four global graph readability metrics [
14]. All of these metrics are between [0, 1], and higher numbers indicate better layouts, so the average of all the metrics is our third term in the fitness function. We consider these three terms sufficient to draw a good layout, as they cover most of the aesthetic criteria.
2.5.2. Genetic Operator
The genetic operator in this paper consists of three methods: Crossover, Mutation and Inversion. Our Inversion and Mutation operators are based on the previous work of Zhang et al. [
4] on a genetic algorithm graph drawing, as it was proven to help draw large cycles with no chords as convex polygons and can reach an optimum solution faster.
Choosing a desirable crossover operator in graph drawing is hard. Here, a desirable crossover should generate an offspring that is similar to its parent. Our crossover operator, called
single-link crossover, will exchange a chain of connected points, thus inheriting characteristics much better than only exchanging a single point. As shown in
Figure 6, both offsprings obtained a much better fitness value as they reduced the edge-crossing while still maintaining some characteristics from their parents.
We have two types of mutation operators that will be sequentially applied. The first one, called a nonuniform mutation [
4], is defined in Equation (3), where S = (
,
, …,
, …,
) is a chromosome (a node
is (
,
), in this case), and element
is selected to be mutated:
In Equation (3),
is a random value between 0 or 1,
is our current generation, [
,
] is the lower and upper bounds for
and function
returns a value in the
range
such that the probability of returning 0 increases when
value increases. The equation for this function is shown with more detail in Equation (4):
where
is our max number of generations, and
is our learning parameter chosen by a user. This property of nonuniformity will search a broad area in the initial generation while moving on to the local one in later stages. It tunes the solutions in later stages of evolution.
The second one is called the single-vertex neighborhood mutation [
4], which chooses a random node and moves it to a random point on a circle of decreasing radii, along with the generation. Suppose vertex
is chosen; then,
is the new coordinate of
, defined in Equation (5):
where
, and
is a random number between
.
is the ideal edge length calculated based on the number of nodes, and our drawing size is shown in Equation (6):
where
is the maximum length of a side of a square area display, and diameter is the diameter of the visible graph. In other words, the diameter is the distance between the farthest pair of nodes, and we set the value to be
, where
is the total number of nodes. This method also has the nonuniformity to make a broad search in the early stages and a more focused search on the later stages.
We also implemented a relinking path algorithm at each generation with a certain percentage. Path relinking is a search intensification strategy [
15]. With this research, we want to verify if a path relinking could work with GA to get a better drawing result, just like Dib and Rodgers [
10], on a graph drawing by combining Tabu search with path relinking.
Figure 7 shows how our relinking path process works. The path relinking algorithm starts with two solutions, a source and a target solution, where the target solution usually has a better fitness value than the source solution. Based on Dib and Rodgers [
10], here, the most distant solution is the one with the maximum summed distance of each node to the node of the best solution. We then start moving each node in source A towards each node position in target B, shown in
Figure 7, with the movement size of a random value between 0 and
PRstepsize, which is defined by the user. This
PRstepsize starts with a large value and decreases at each iteration, so that, at later iterations, a minor movement is made to achieve better precision. At every iteration, after moving every node, we calculated its fitness value and stored the best solution. The best solution found during the moving process of source A to target B will be replaced by the worst solution in the current generation if it has a better value.
2.6. Mental Map Preservation
This subsection describes how we tackle the preservation of a mental map by combining both the aesthetic criteria and mental map preservation criteria to be one energy function to be minimized. We define our mental map cost
between the previous drawing
and current drawing
, defined in Equation (7). Note that
means both drawings are the same; hence, a larger value means a higher degree of difference between two drawings. The position of an overlapped node is based on the previous drawing, so that the preservation is easier to do.
Our mental map cost is based on what Bridgeman and Tamassia [
16] proposed, which is shown in Equations (8)–(10). Although there are many similarity measurements, we only use ranking, nearest neighbor within and nearest neighbor between. Using only these three measurements is good enough to preserve a mental map while not necessarily fixing the overlap node positions between two periods. As our main purpose is to create a smooth transition between two graphs—that is, between our previous graph
and our current graph
—we only measured based on the node that exists in both periods.
We used a similar method as our fitness function, where
was our weight for each term. The first term is called ranking [
16], used to measure the relative horizontal and vertical positions of a point. Equation (8) shows our ranking measurement:
where the upper bound
is to normalize the value to be between 0 and 1; also noted here is that the upper bound is taken as
instead of
, where the actual maximum value occurs when a point moves from one corner of the drawing to the opposite corner. The motivation for this is simply that it scales the measurements more satisfactorily. Right
and above
are the numbers of nodes to the right and above of v (similarly, the
). This measures how many changes have happened on a node’s viewpoint between the previous drawing and the current drawing.
where
is the upper bound for the normalization of the number of nodes that exist in both layouts, while
is the nearest neighbor of node
. Our second term, called nearest neighbor within [
16], shown in Equation (9), is the idea that a node neighborhood in the previous layout should be its neighborhood as well in the current layout. This term calculates the number of nodes that have their nearest neighbor changed.
Our last term, called the nearest neighbor between [
16], shown in Equation (10), is similar to the nearest neighbor within, except this term idea is that a node nearest neighbor in the current layout should be itself from the previous layout. This will make a node bound within its previous position but free to move as long as its nearest neighbor is itself. We used the unweighted version for both nearest-neighbor terms, where we did not count the number of nodes between
and
.
Multiple terms were not included in our mental map cost function. We also removed other terms that Lee et al. [
14] used in their SA to make the computations faster, as, in general, GA needs much more resources than SA.
In the work of Lee et al. [
14], for solving a problem of combining two cost functions with different scales, they considered the energy cost and mental map cost independently in their SA algorithm. Our research faced a similar problem, so instead of considering them independently, we gradually considered the mental map cost across generations.
We started with weight of the mental map cost on the initial generation and started considering a half-weight of the mental map cost when reaching of the generation and, finally, the full weight of the mental map cost after of the generation. In this way, our system prioritizes creating an excellent aesthetic drawing during the early generations and then considers the mental map cost during later generations.
4. Discussion
Through our generated animation, we observed that, throughout the years, adventure and action games have never ceased to be released. They dominate most of the time, even until 2019. We observed that most of the adventure games are Japanese titles, and Japan seems to contribute to most of the video game development and, thus, why adventure games are always released each month. In early 1998, most of the released games were action and fighting games like Street Fighter and Mortal Kombat, as they were popular in arcades. There were also a lot of miscellaneous games released, such as chess or a compilation of games. During the period from 2000 to 2008, adventure and action games dominated where action games were mostly first-person shooter, such as Counter Strike, Doom and the Call of Duty series. From 2007 to 2011, there was a rise in puzzle games, and they were mostly of hidden object games by developers such as PopCap studios, BigFish games or GameHouse, which also led the trend of puzzle games such as Mystery Case File, Zuma, Diner Dash and Bejeweled becoming popular among PC users. During 2010–2012, role playing games also seemed to rise with the hype of famous role playing game titles such as Diablo III, The Witcher 2 and the Assassin Creed series. Lastly, during 2015–2018, action games kept rising and dominated most of the time. Although our dataset did not include neurogaming, it seems as though it may be more popular in the future, because a potential user, a player, may interfere with the world of the game without using traditional peripheral devices such as a keyboard, mouse or a joystick [
20].
Based on the experiment results, we can also conclude that considering the mental map weight since the start of the GA generations gives the best preservation, as our GA is better at preserving the mental map by constraining the nodes to their previous positions. We also proved that combining Path Relinking (PR) with GA is not as good as combining PR with Tabu Search through our experiments. However, using PR indeed gives a considerably faster convergence rate but not a better result. As our implementations are web-based systems using the usual front-end and back-end approaches, most of the calculations are done in Node.js. However, Node.js is not optimized for this kind of processing like C++ or python is, resulting in a slow calculation process and computing time. Another solution is to find a way to process them in parallel through the GPU, similar to the works of Qu et al. [
9], to reduce the calculation time needed. It is also hard to tinker with too many nodes, even with our simplification algorithm, because most of the results are not informative enough. Compared with the cases of lesser nodes, more nodes means more edges, and D3.js cannot handle drawing too many edges. We also observed a slow computing time calculating our proposed fitness value, because the Greadability.js library calculates edge crossing and angular resolution for our system. With more edges, the processing times increase exponentially, and this is a problem that every graph-drawing algorithm encounters. Graph features such as the node’s color and size may also affect a user’s mental map.