Optimal Integration of Photovoltaic Sources in Distribution Networks for Daily Energy Losses Minimization Using the Vortex Search Algorithm
Abstract
1. Introduction
2. MINLP Model
2.1. Objective Function
2.2. Restrictions
3. Materials and Methods
3.1. Vortex Search Algorithm (VSA)
3.2. Hybrid Discrete-Continuous Vortex Search Algorithm (DCVSA) Encoding
- ✓
- ✓
- In its master stage, with hybrid coding, DCVSA will explore and exploit the solution space to identify the optimal location and dimensioning to reduce energy losses. Algorithm 1 represents the computational logic to implement the DCVSA based on the structure proposed in [7].
| Algorithm 1: Implementation of the DCVSA algorithm for the optimal location and dimensioning of PV systems in distribution networks. |
 |
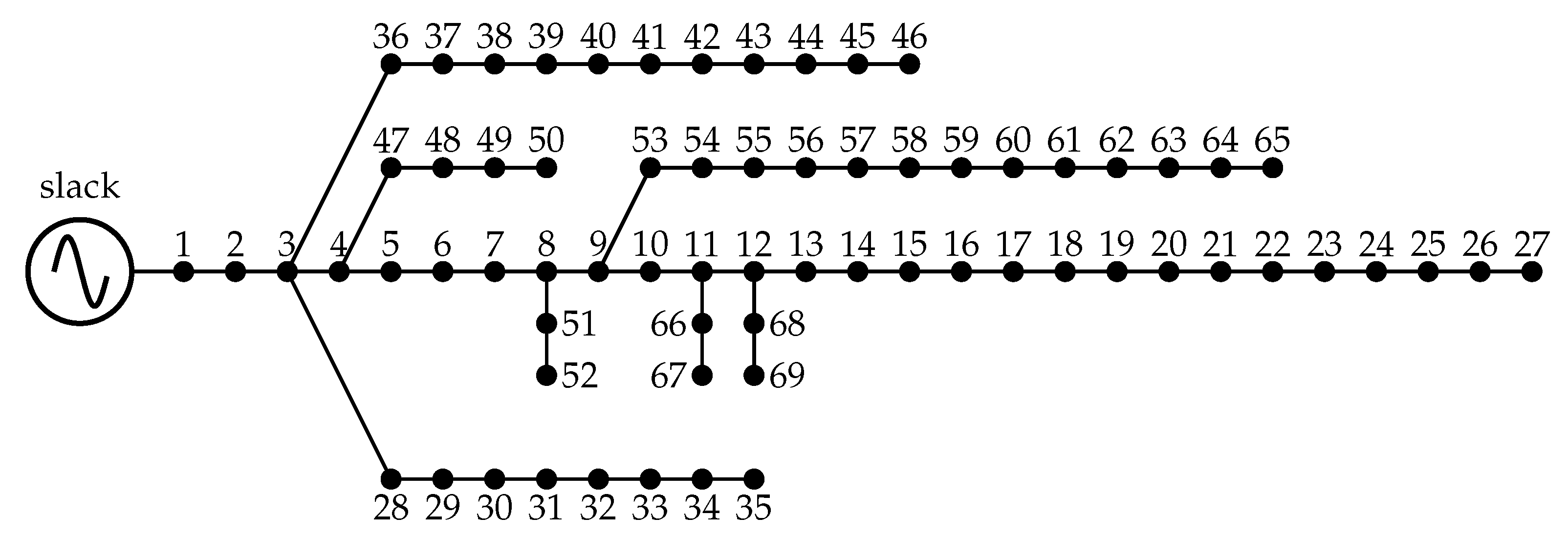
3.3. Case Studies: Distribution Systems
4. Results
4.1. Reduction of Power Losses in Peak Hours
4.1.1. Distribution System of 33 Nodes
- ✓
- The best method for solving the power loss reduction problem through the location and optimal generation size is MOHTLBOGWO, whose solution is the discrete vector of as the location at the node of the generation and MW of installed capacity for a reduction in percentage losses of 65.8226%.
- ✓
- The results obtained by the DCVSA demonstrate the effectiveness of the proposed algorithm since it achieves the reduction of losses of the CBGA-VSA and DSCA-SOCP methods with a solution vector of nodes and installed power of MW to achieve a percentage reduction of 65.5026% in power losses.
- ✓
- The DCVSA method proposed in this document presents a reduction in power losses of 65.5026% for the peak hour, with a total injection of the active power of 2.9476 MW. This result obtains a higher reduction in power losses than 86% of the methods presented in Table 3.
- ✓
- The power loss reduction of the proposed algorithm concerning the lower power loss reduction presented by HSA is higher by 29.8144%. Likewise, it represents that the DCVSA power loss reduction is 0.32% lower than the method with the highest power loss reduction presented by MOHTLBOGWO.
4.1.2. Distribution System of 69 Nodes
- ✓
- Unlike the 33-node system, there are four methods among the most efficient for reducing power losses, with a location vector of , of which one is the method proposed in this article. The reduction percentage of the power, the MSSA, DCVSA, CBGA-VSA, and DSCA-SOCP methods present 69.1455%, with the difference that the first proposes a total of 2.624 MW of installed power for the PV systems, while the three other systems rise to 2.6259 MW.
- ✓
- The DCVSA method proposed in this article presents a reduction in power losses for the peak hour of 69.1455% with a power injection in the nodes of MW. This result presents a higher reduction in power losses than 84% of the methods represented in the comparative Table 4.
- ✓
- It validates the performance of the proposed algorithm concerning the presented lower reduction in power losses, which, unlike the 33-node system, is not HSA but PMC, which implies that the DCVSA is 9.8654% better.
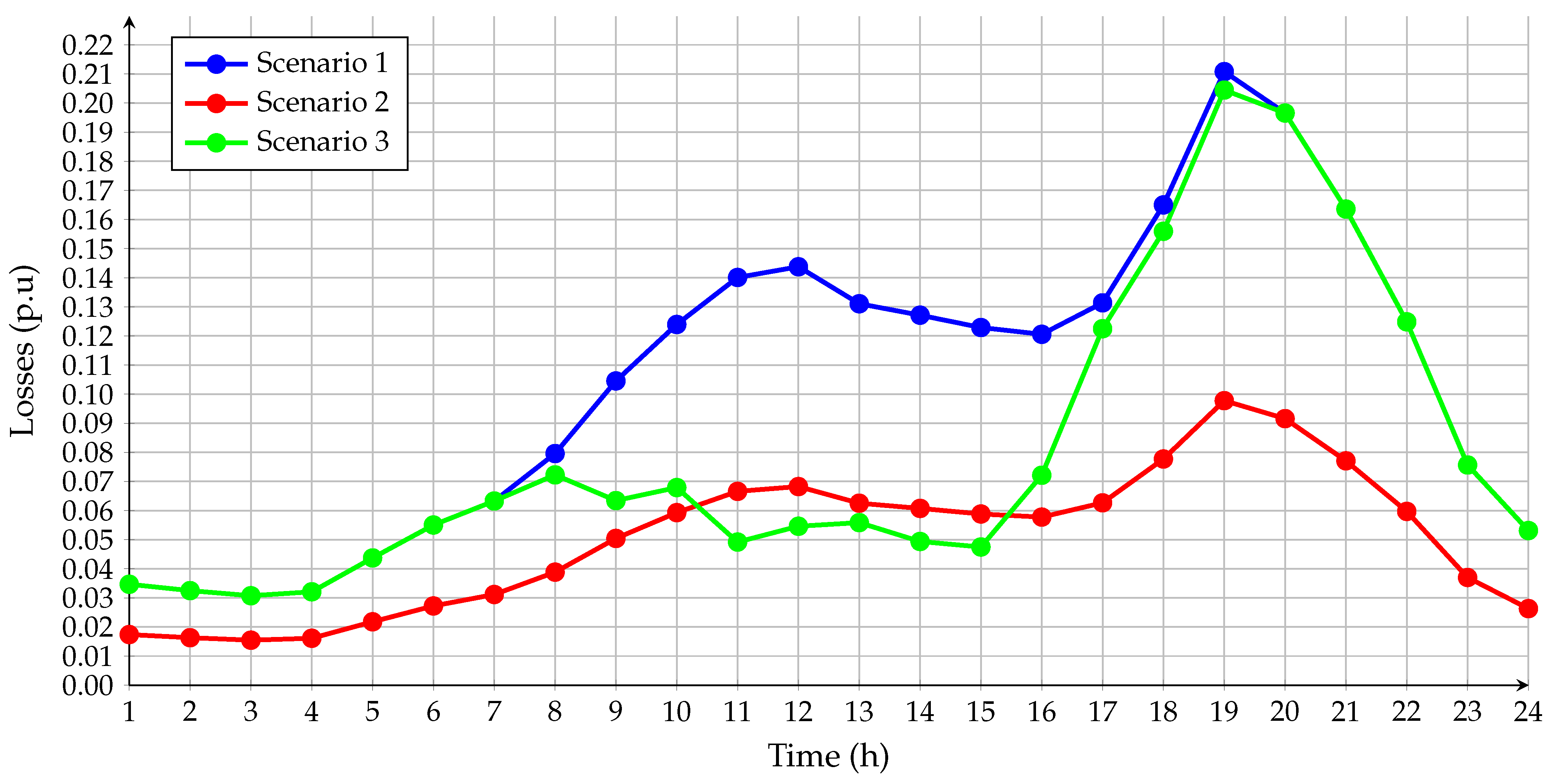
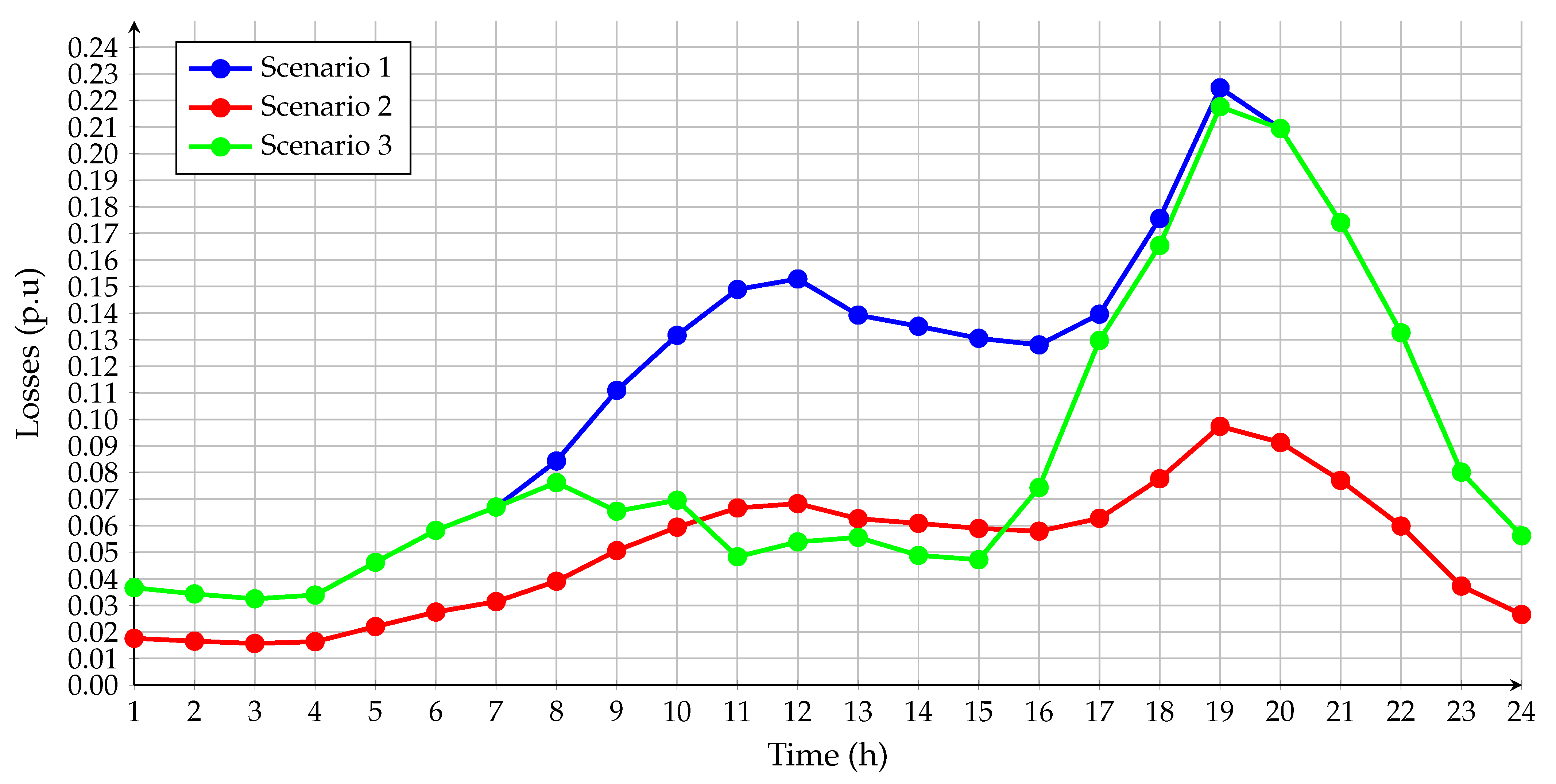
4.2. Reduction of Energy Losses for 24 h
4.2.1. Distribution System of 33 Nodes
4.2.2. Distribution System of 69 Nodes
4.2.3. Comparative Analysis for Reducing Energy Losses with GAMS
4.3. Additional Comments
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Other Symbols | |
| e | Euler number. |
| i,j | Indices of nodes in the system. |
| t | Current iteration of the algorithm. |
| The maximum number of iterations decreasing by one for each iteration t. | |
| Mathematical Operators | |
| Complex conjugate operator. | |
| Transpose matrix operator. | |
| Inverse matrix operator. | |
| Incomplete gamma function. | |
| Diagonal of the conjugate matrix (V). | |
| Inverse incomplete gamma function in MATLAB. | |
| Identity matrix of dimension . | |
| Function for a random number between 1 and 0 with normal distribution. | |
| Parameters | |
| Maximum error of the successive approximations method. | |
| Complex power demanded at the node i in period h (VA). | |
| Complex power of the PV system connected to the bus i in period h (VA). | |
| Complex power of the slack node connected to the bus i in period h (VA). | |
| Initial center of the hyper-ellipsoid. | |
| Initial standard deviation of the Gaussian distribution. | |
| Maximum number of continued iterations with the center of the hyper-ellipsoid constant. | |
| H | Set containing all evaluated periods. |
| N | Set that contains all the nodes of the system. |
| The maximum number of iterations. | |
| d | Dimension of the solution space. |
| The highest PV systems install number. | |
| The PV system maximum active power (W). | |
| The PV system minimal active power (W). | |
| Initial radius of the hyper-ellipse. | |
| Base power for the case studies (VA). | |
| Complex power of the demand nodes (VA). | |
| System nodes maximum voltage value (V). | |
| System nodes minimal voltage value (V). | |
| Base voltage for the case studies (V). | |
| Voltage value of the generation nodes (V). | |
| Variables | |
| Bar voltage i in period h (V). | |
| Bar voltage j in period h (V). | |
| The matrix admittance that relates the nodes of the system (S). | |
| Component of the matrix admittance that relates the demand nodes among them (S). | |
| Component of the matrix admittance that relates the demand nodes with generation nodes (S). | |
| Complex admittance matrix that relates nodes i and j (S). | |
| Component of the matrix impedance that relates the demand nodes among them (). | |
| Vector of dimension of the sample mean. | |
| Covariance matrix. | |
| Variance of the Gaussian distribution. | |
| Number of consecutive iterations. | |
| Value of energy losses in the study period (Wh/day). | |
| k | Number of a random node. |
| m | Counter of the successive approximations method. |
| q | Random power between and (W). |
| Gaussian distribution for solutions with position i and iteration t. | |
| Current value of the demand nodes (A). | |
| Active power injected by a PV system at node i (W). | |
| Radius at iteration t. | |
| Voltage value of the demand nodes (V). | |
| x | Solution vector of dimension of a random value. |
| Maximum amount of the solution vector. | |
| Minimum amount of the solution vector. | |
| Existence of a PV system at node i. | |
References
- UPME. Reference Expansion Planning Generacion Transmision 2004–2018; Resreport, Unidad de Planeación Minero Energética: Bogotá, Colombia, 2004. [Google Scholar]
- Castro-Galeano, J.C.; Cabra-Sarmiento, W.J.; Ortiz-Portilla, J.F. Fault and load flows analysis of electricity transmission and distribution system in Casanare (Colombia). Rev. Fac. Ing. 2017, 26, 7. [Google Scholar] [CrossRef]
- Montoya, O.D.; Serra, F.M.; Angelo, C.H.D. On the Efficiency in Electrical Networks with AC and DC Operation Technologies: A Comparative Study at the Distribution Stage. Electronics 2020, 9, 1352. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.; Montoya, D.G.; Ramos-Paja, C. Optimal Sizing and Location of Distributed Generators Based on PBIL and PSO Techniques. Energies 2018, 11, 1018. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Orozco-Henao, C. Vortex search and Chu-Beasley genetic algorithms for optimal location and sizing of distributed generators in distribution networks: A novel hybrid approach. Eng. Sci. Technol. Int. J. 2020, 23, 1351–1363. [Google Scholar] [CrossRef]
- Montoya, O.D.; Molina-Cabrera, A.; Chamorro, H.R.; Alvarado-Barrios, L.; Rivas-Trujillo, E. A Hybrid Approach Based on SOCP and the Discrete Version of the SCA for Optimal Placement and Sizing DGs in AC Distribution Networks. Electronics 2020, 10, 26. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Hernández, J.C. Efficient Operative Cost Reduction in Distribution Grids Considering the Optimal Placement and Sizing of D-STATCOMs Using a Discrete-Continuous VSA. Appl. Sci. 2021, 11, 2175. [Google Scholar] [CrossRef]
- Esmaeilian, H.; Fadaeinedjad, R.; Attari, S. Distribution network reconfiguration to reduce losses and enhance reliability using binary gravitational search algorithm. In Proceedings of the 22nd International Conference and Exhibition on Electricity Distribution (CIRED 2013), Stockholm, Sweden, 10–13 June 2013. [Google Scholar]
- Krstic, N. Reduction of Energy and Power Losses in Distribution Network Using Energy Storage Systems. In Proceedings of the 2020 55th International Scientific Conference on Information, Communication and Energy Systems and Technologies (ICEST), Niš, Serbia, 10–12 September 2020. [Google Scholar]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar] [CrossRef]
- Reyes-Belmonte, M.A. Quo Vadis Solar Energy Research? Appl. Sci. 2021, 11, 3015. [Google Scholar] [CrossRef]
- Catalbas, M.C.; Gulten, A. Circular structures of puffer fish: A new metaheuristic optimization algorithm. In Proceedings of the 2018 Third International Conference on Electrical and Biomedical Engineering, Clean Energy and Green Computing (EBECEGC), Beirut, Lebanon, 24–26 April 2018. [Google Scholar]
- Samala, R.K.; Kotapuri, M.R. Hybridization of Metaheuristic Algorithms for Optimal Location and Capacity in Radial Distribution System. In Proceedings of the 2019 2nd International Conference on Power and Embedded Drive Control (ICPEDC), Chennai, India, 21–23 August 2019. [Google Scholar]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L. An exact MINLP model for optimal location and sizing of DGs in distribution networks: A general algebraic modeling system approach. Ain Shams Eng. J. 2020, 11, 409–418. [Google Scholar] [CrossRef]
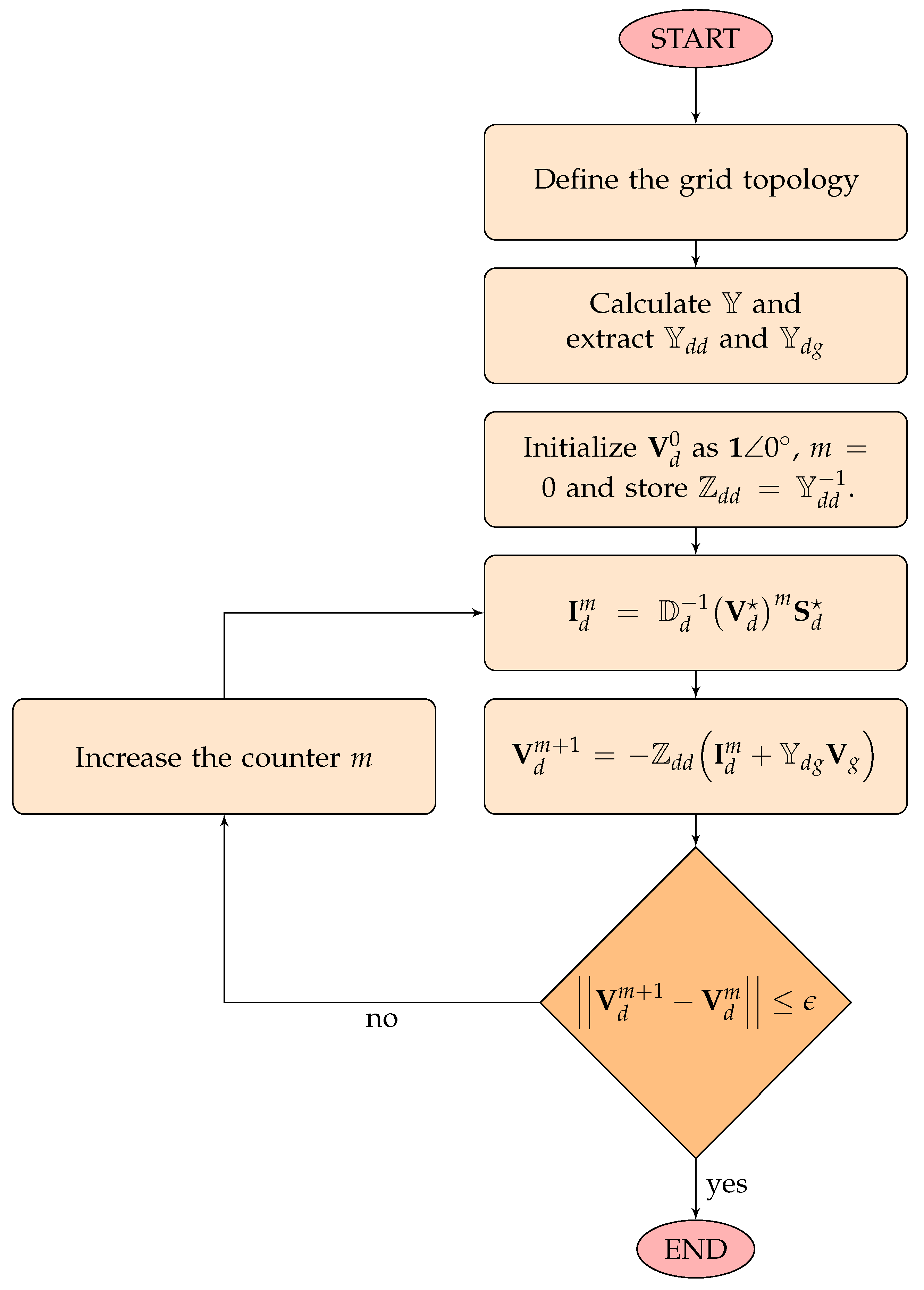
- Montoya, O.D.; Gil-González, W. On the numerical analysis based on successive approximations for power flow problems in AC distribution systems. Electr. Power Syst. Res. 2020, 187, 106454. [Google Scholar] [CrossRef]
- Moradi, M.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Injeti, S.K.; Kumar, N.P. A novel approach to identify optimal access point and capacity of multiple DGs in a small, medium and large scale radial distribution systems. Int. J. Electr. Power Energy Syst. 2013, 45, 142–151. [Google Scholar] [CrossRef]
- Mohanty, B.; Tripathy, S. A teaching learning based optimization technique for optimal location and size of DG in distribution network. J. Electr. Syst. Inf. Technol. 2016, 3, 33–44. [Google Scholar] [CrossRef]
- Kollu, R.; Rayapudi, S.R.; Sadhu, V.L.N. A novel method for optimal placement of distributed generation in distribution systems using HSDO. Int. Trans. Electr. Energy Syst. 2012, 24, 547–561. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Multi-objective quasi-oppositional teaching learning based optimization for optimal location of distributed generator in radial distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 534–545. [Google Scholar] [CrossRef]
- Muthukumar, K.; Jayalalitha, S. Optimal placement and sizing of distributed generators and shunt capacitors for power loss minimization in radial distribution networks using hybrid heuristic search optimization technique. Int. J. Electr. Power Energy Syst. 2016, 78, 299–319. [Google Scholar] [CrossRef]
- Jamian, J.; Mustafa, M.; Mokhlis, H. Optimal multiple distributed generation output through rank evolutionary particle swarm optimization. Neurocomputing 2015, 152, 190–198. [Google Scholar] [CrossRef]
- Gupta, S.; Saxena, A.; Soni, B.P. Optimal Placement Strategy of Distributed Generators based on Radial Basis Function Neural Network in Distribution Networks. Procedia Comput. Sci. 2015, 57, 249–257. [Google Scholar] [CrossRef]
- Bayat, A.; Bagheri, A. Optimal active and reactive power allocation in distribution networks using a novel heuristic approach. Appl. Energy 2019, 233–234, 71–85. [Google Scholar] [CrossRef]
- Moradi, M.; Abedini, M. A novel method for optimal DG units capacity and location in Microgrids. Int. J. Electr. Power Energy Syst. 2016, 75, 236–244. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Krill herd algorithm for optimal location of distributed generator in radial distribution system. Appl. Soft Comput. 2016, 40, 391–404. [Google Scholar] [CrossRef]
- Nguyen, T.P.; Dieu, V.N.; Vasant, P. Symbiotic Organism Search Algorithm for Optimal Size and Siting of Distributed Generators in Distribution Systems. Int. J. Energy Optim. Eng. 2017, 6, 1–28. [Google Scholar] [CrossRef]
- Deshmukh, R.; Kalage, A. Optimal Placement and Sizing of Distributed Generator in Distribution System Using Artificial Bee Colony Algorithm. In Proceedings of the 2018 IEEE Global Conference on Wireless Computing and Networking (GCWCN), Lonavala, India, 23–24 November 2018. [Google Scholar]
- Nowdeh, S.A.; Davoudkhani, I.F.; Moghaddam, M.H.; Najmi, E.S.; Abdelaziz, A.; Ahmadi, A.; Razavi, S.; Gandoman, F. Fuzzy multi-objective placement of renewable energy sources in distribution system with objective of loss reduction and reliability improvement using a novel hybrid method. Appl. Soft Comput. 2019, 77, 761–779. [Google Scholar] [CrossRef]
- Gholami, K.; Parvaneh, M.H. A mutated salp swarm algorithm for optimum allocation of active and reactive power sources in radial distribution systems. Appl. Soft Comput. 2019, 85, 105833. [Google Scholar] [CrossRef]
- Bocanegra, S.Y.; Montoya, O.D. Heuristic approach for optimal location and sizing of distributed generators in AC distribution networks. WSEAS Trans. Power Syst. 2019, 14, 113–121. [Google Scholar]
- HassanzadehFard, H.; Jalilian, A. A novel objective function for optimal DG allocation in distribution systems using meta-heuristic algorithms. Int. J. Green Energy 2016, 13, 1615–1625. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. A new metaheuristic for numerical function optimization: Vortex Search algorithm. Inf. Sci. 2015, 293, 125–145. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Rajagopalan, A.; Grisales-Noreña, L.F.; Hernández, J.C. Optimal Selection and Location of Fixed-Step Capacitor Banks in Distribution Networks Using a Discrete Version of the Vortex Search Algorithm. Energies 2020, 13, 4914. [Google Scholar] [CrossRef]
- Doğan, B.; Ölmez, T. Vortex search algorithm for the analog active filter component selection problem. AEU Int. J. Electron. Commun. 2015, 69, 1243–1253. [Google Scholar] [CrossRef]
- Saka, M.; Tezcan, S.S.; Eke, I.; Taplamacioglu, M.C. Economic load dispatch using vortex search algorithm. In Proceedings of the 2017 4th International Conference on Electrical and Electronic Engineering (ICEEE), Ankara, Turkey, 8–10 April 2017. [Google Scholar]
- Soroudi, A. Power System Optimization Modeling in GAMS; Springer International Publishing: New York, NY, USA, 2017. [Google Scholar]
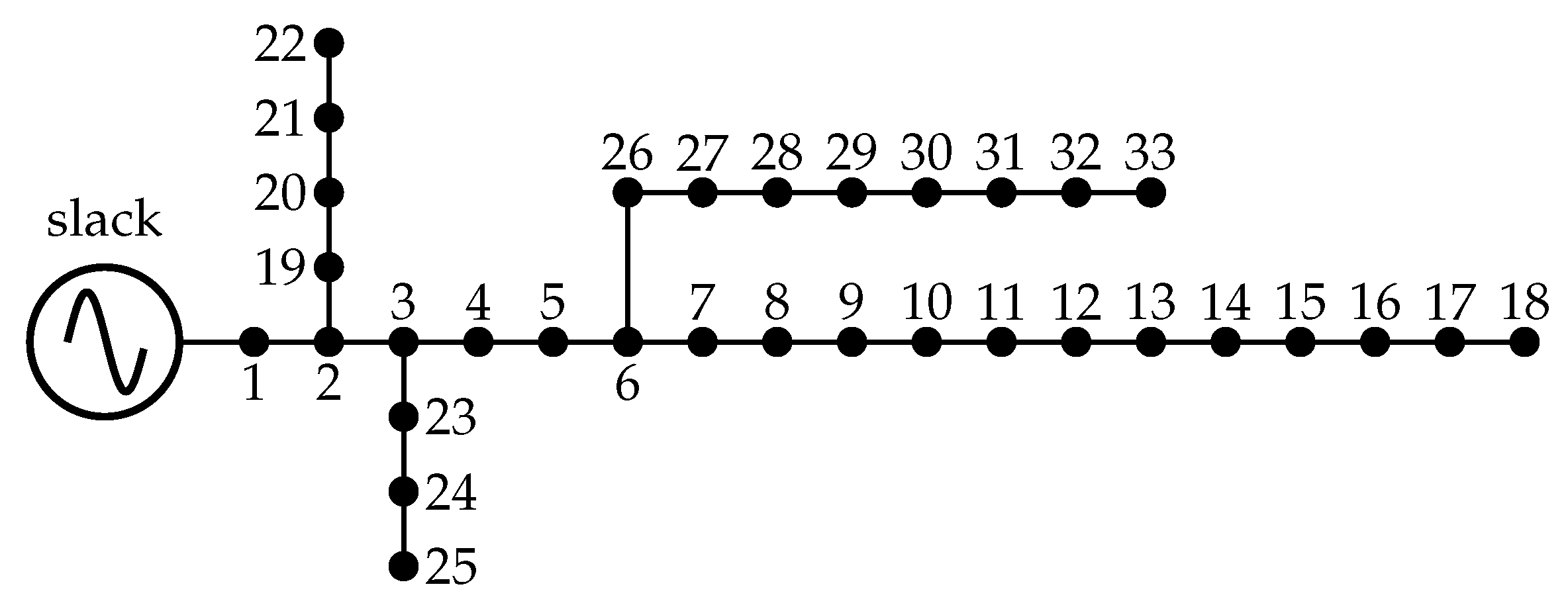
| Acronym | Optimization Method | Ref. | Year |
|---|---|---|---|
| GA | Genetic Algorithm | [16] | 2012 |
| PSO | Particle Swarm Optimization | [16] | 2012 |
| LSFSA | Loss Sensitivity Factor Simulated Annealing | [17] | 2013 |
| TLBO | Teaching Learning Based Optimization | [18] | 2014 |
| PMC | Parallel Monte Carlo | [4] | 2014 |
| HSA | Harmony Search Algorithm | [19] | 2014 |
| QOTLBO | Quasi-Oppositional Teaching Learning Based Optimization | [20] | 2014 |
| HSA-PABC | Harmony Search Algorithm and Particle Artificial Bee Colony Algorithm | [21] | 2014 |
| MINLP | Mixed-Integer Nonlinear Programming Formulation | [10] | 2014 |
| REPSO | Rank Evolutionary Particle Swarm Optimization | [22] | 2015 |
| RBFNN-PSO | Radial Basis Function Neural Network and Particle Swarm Optimization | [23] | 2015 |
| AHA | Algorithmic Heuristic Approach | [24] | 2016 |
| GA-IWD | Genetic Algorithm and Intelligent Water Drops | [25] | 2016 |
| KHA | Krill-Herd Algorithm | [26] | 2016 |
| SOS | Symbiotic Organism Search | [27] | 2017 |
| PBIL-PSO | Population-Based Incremental Learning and Particle Swarm Optimizer | [4] | 2018 |
| ABCA | Artificial Bee Colony Algorithm | [28] | 2018 |
| MOHTLBOGWO | Multi-Objective Hybrid Teaching–Learning Based Optimization-Grey Wolf Optimizer | [29] | 2019 |
| MSSA | Mutated Salp Swarm Algorithm | [30] | 2019 |
| CHVSA | Constructive Heuristic Vortex Search Algorithm | [31] | 2019 |
| GAMS | General Algebraic Modeling System | [14] | 2020 |
| CBGA-VSA | Chu and Beasley Genetic Algorithm and Vortex Search Algorithm | [5] | 2020 |
| DSCA-SOCP | Discrete Sine Cosine Algorithm and Second-Order Cone Programming | [6] | 2021 |
| Hour | Demand (p.u) | PV System Generation (p.u) | Hour | Demand (p.u) | PV System Generation (p.u) |
|---|---|---|---|---|---|
| 1 | 0.4240 | 0 | 13 | 0.8013 | 0.926 |
| 2 | 0.4108 | 0 | 14 | 0.7899 | 0.851 |
| 3 | 0.3999 | 0 | 15 | 0.7774 | 0.521 |
| 4 | 0.4083 | 0 | 16 | 0.7774 | 0.255 |
| 5 | 0.4744 | 0 | 17 | 0.8022 | 0.035 |
| 6 | 0.5301 | 0 | 18 | 0.8926 | 0.028 |
| 7 | 0.5669 | 0 | 19 | 1 | 0.015 |
| 8 | 0.6326 | 0.0490 | 20 | 0.9682 | 0 |
| 9 | 0.7202 | 0.2490 | 21 | 0.8890 | 0 |
| 10 | 0.7805 | 0.300 | 22 | 0.7832 | 0 |
| 11 | 0.8268 | 0.683 | 23 | 0.6175 | 0 |
| 12 | 0.8369 | 0.835 | 24 | 0.5212 | 0 |
| Method | (kW) | Nodes Localization | Sizing (MW) |
|---|---|---|---|
| MOHTLBOGWO | 72.1100 | ||
| CBGA-VSA | 72.7853 | ||
| DSCA-SOCP | 72.7853 | ||
| MSSA | 72.7854 | ||
| MINLP | 72.7862 | ||
| GAMS | 72.7900 | ||
| HSA-PABC | 72.8129 | ||
| AHA | 72.8340 | ||
| QOTLBO | 74.1008 | ||
| KHA | 75.4116 | ||
| REPSO | 76.9100 | ||
| CHVSA | 78.4534 | ||
| LSFSA | 82.0300 | ||
| PBIL-PSO | 91.5000 | ||
| PMC | 91.6000 | ||
| TLBO | 104.000 | ||
| SOS | 104.190 | ||
| PSO | 105.350 | ||
| GA | 106.300 | ||
| GA-IWD | 110.510 | ||
| HSA | 135.690 | ||
| DCVSA | 72.7853 |
| Method | (kW) | Nodes Localization | Sizing (MW) |
|---|---|---|---|
| MSSA | 69.4077 | ||
| CBGA-VSA | 69.4077 | ||
| DSCA-SOCP | 69.4077 | ||
| CHVSA | 69.4088 | ||
| MINLP | 69.4090 | ||
| KHA | 69.5730 | ||
| AHA | 69.6669 | ||
| QOTLBO | 71.6345 | ||
| MOHTLBOGWO | 71.7400 | ||
| GAMS | 72.0900 | ||
| LSFSA | 77.1000 | ||
| GA-IWD | 80.9100 | ||
| TLBO | 81.0000 | ||
| SOS | 82.0800 | ||
| PSO | 83.2000 | ||
| HSA | 86.6600 | ||
| PBIL-PSO | 86.9000 | ||
| GA | 89.0000 | ||
| PMC | 91.6000 | ||
| DCVSA | 69.4077 |
| Scenario | Characteristic |
|---|---|
| (1) | Power losses without PV system |
| (2) | Power losses with constant PV system |
| (3) | Power losses with variable PV system |
| Scenario | (kWh/day) |
|---|---|
| (1) | 2508.6343 |
| (2) | 1199.4596 |
| (3) | 1922.5098 |
| Scenario | (kWh/day) |
|---|---|
| (1) | 2664.7952 |
| (2) | 1202.1918 |
| (3) | 2014.9508 |
| Method | Nodes Localization | Sizing (MW) | (kWh/day) |
|---|---|---|---|
| GAMS-BONMIN | 2034.9850 | ||
| DCVSA | 1922.5098 |
| Method | Nodes Localization | Sizing (MW) | (kWh/day) |
|---|---|---|---|
| GAMS-BONMIN | 2051.4900 | ||
| DCVSA | 2014.9508 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paz-Rodríguez, A.; Castro-Ordoñez, J.F.; Montoya, O.D.; Giral-Ramírez, D.A. Optimal Integration of Photovoltaic Sources in Distribution Networks for Daily Energy Losses Minimization Using the Vortex Search Algorithm. Appl. Sci. 2021, 11, 4418. https://doi.org/10.3390/app11104418
Paz-Rodríguez A, Castro-Ordoñez JF, Montoya OD, Giral-Ramírez DA. Optimal Integration of Photovoltaic Sources in Distribution Networks for Daily Energy Losses Minimization Using the Vortex Search Algorithm. Applied Sciences. 2021; 11(10):4418. https://doi.org/10.3390/app11104418
Chicago/Turabian StylePaz-Rodríguez, Alejandra, Juan Felipe Castro-Ordoñez, Oscar Danilo Montoya, and Diego Armando Giral-Ramírez. 2021. "Optimal Integration of Photovoltaic Sources in Distribution Networks for Daily Energy Losses Minimization Using the Vortex Search Algorithm" Applied Sciences 11, no. 10: 4418. https://doi.org/10.3390/app11104418
APA StylePaz-Rodríguez, A., Castro-Ordoñez, J. F., Montoya, O. D., & Giral-Ramírez, D. A. (2021). Optimal Integration of Photovoltaic Sources in Distribution Networks for Daily Energy Losses Minimization Using the Vortex Search Algorithm. Applied Sciences, 11(10), 4418. https://doi.org/10.3390/app11104418







