Prediction of Post-Yield Performance of Hybrid Precast Beams Based on Strength Degradation
Abstract
1. Introduction
2. Materials and Methods
2.1. Descriptions of Specimens
2.2. Material Properties
3. Analytical Prediction of Post-Yield Deflection
3.1. Stiffness at Yield Limit State
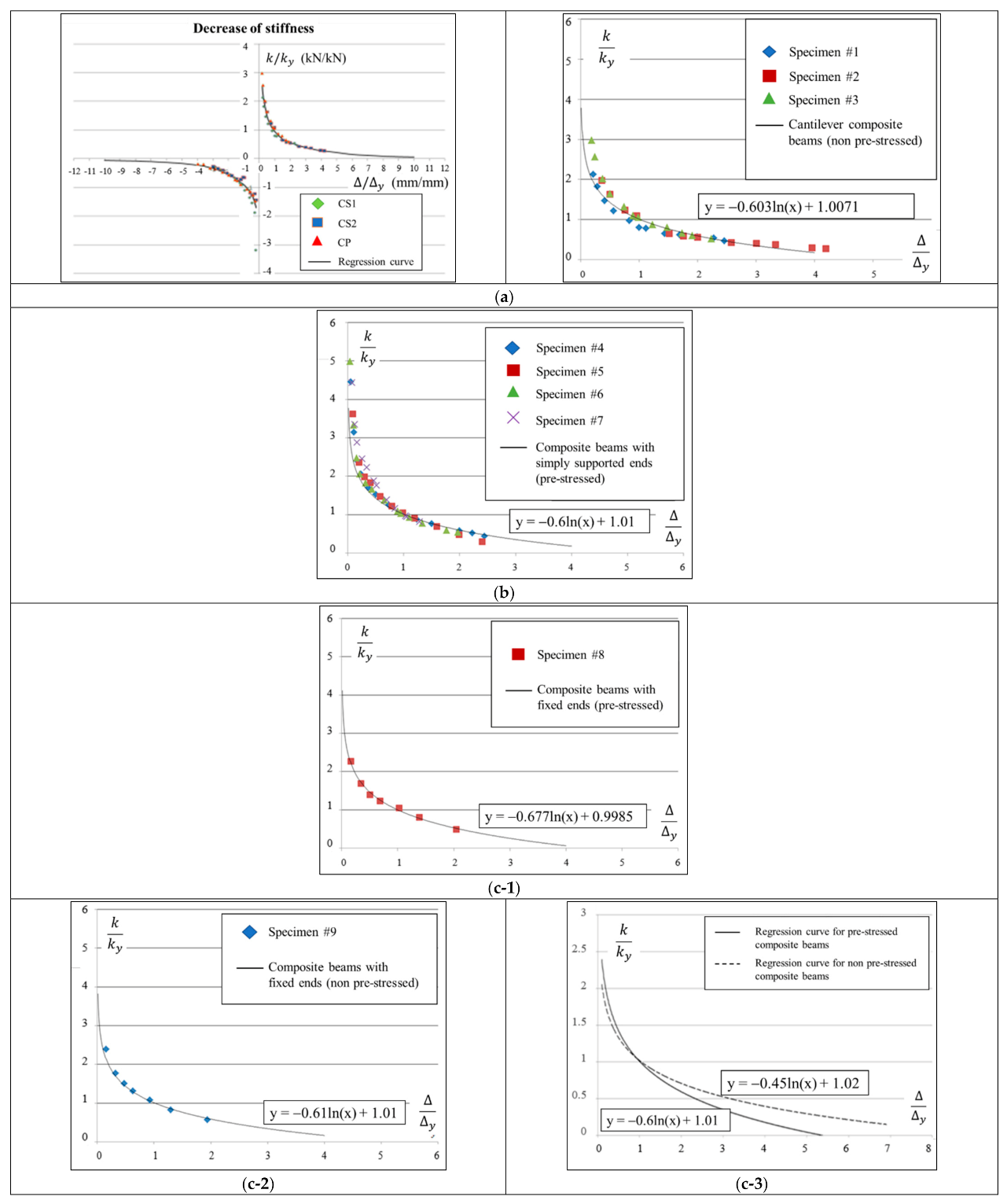
3.2. Stiffness Degradation
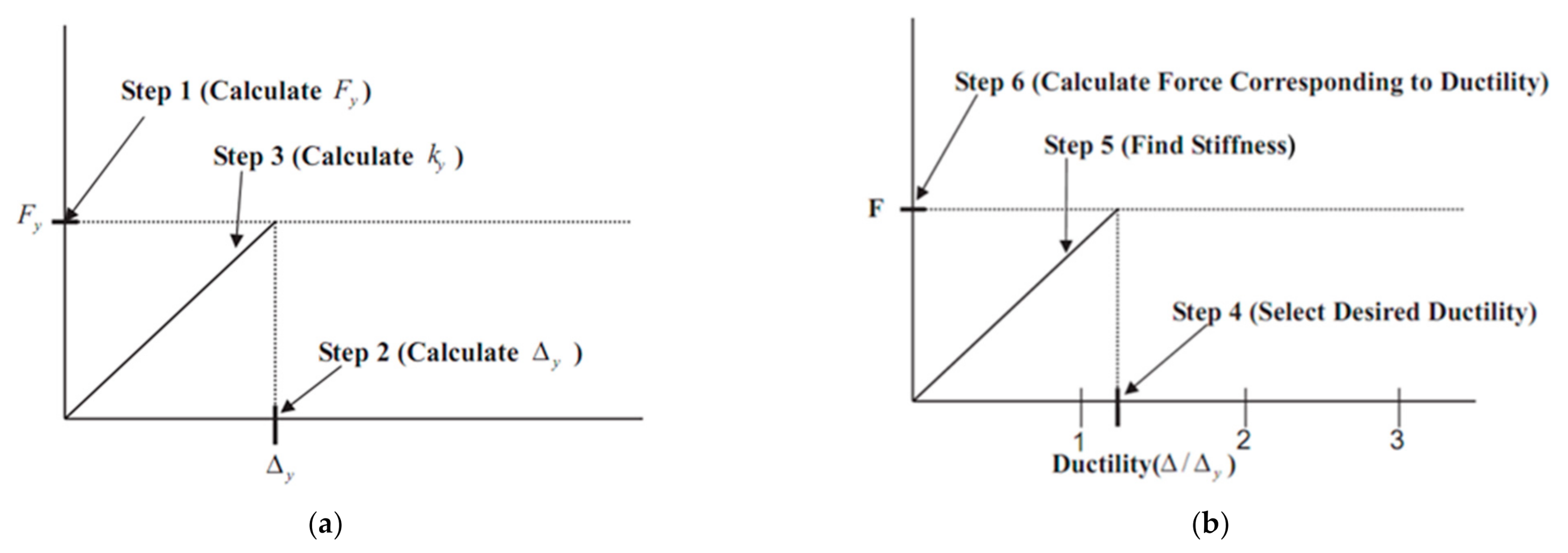
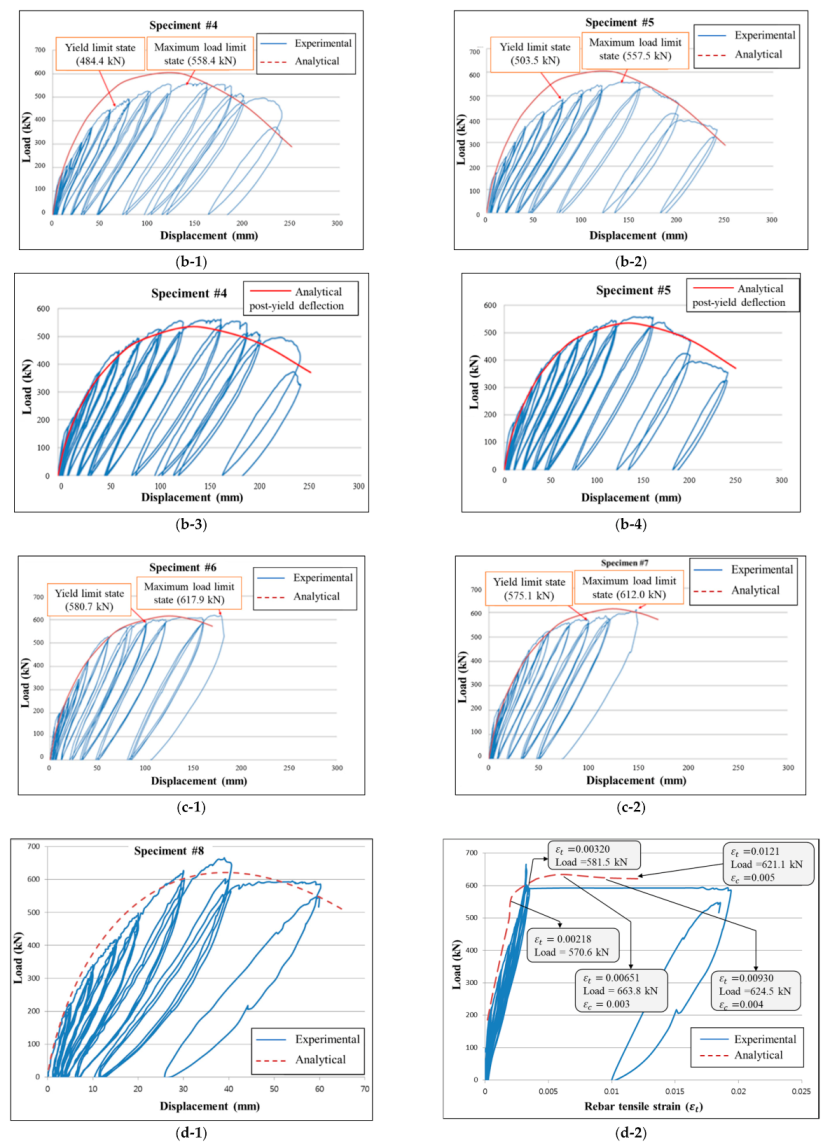
3.3. Prediction of Post-Yield Behavior
- Calculate the displacement () from Equations (4) and (5).
- Calculate the stiffness of the composite beams at the yield limit state from Figure 2a.
- Select the desired ductility from the load-displacement curve ( from Figure 2b.
- Find corresponding to the selected ductility from Figure 2b.
- Calculate and from Figure 2b in order to determine .
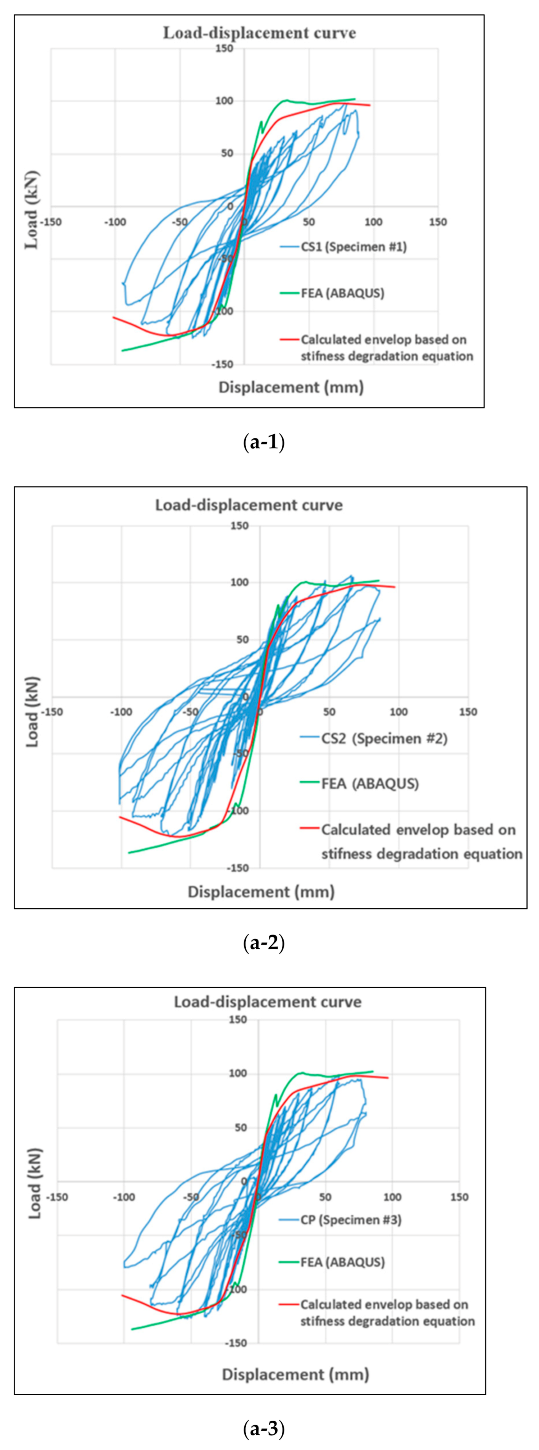
3.4. Verification Based on Finite Element Analysis
3.4.1. Symmetrical Modeling
3.4.2. Choice of Elements
3.4.3. Modeling of Embedded Elements
4. Results, Discussion and Conclusions
4.1. Contribution to the Understanding of the Post-Yield Structural Behavior of Pre-Stressed Precast Composite Beams Based on Proposed Degradation Equations
4.2. Validated by Numerical Investigation
4.3. Further Refinement of the Degradation Model; The Applicability and Limitations of the Proposed Equations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Xue, Y.; Yu, Y.; Ma, N.; Shao, Y. Experimental study on flexural performance of partially precast steel reinforced concrete beams. J. Constr. Steel Res. 2017, 133, 192–201. [Google Scholar] [CrossRef]
- Nie, J.; Fan, J.; Cai, C.S. Stiffness and deflection of steel-concrete composite beams under negative bending. J. Struct. Eng. 2004, 130, 1842–1851. [Google Scholar] [CrossRef]
- Uy, B.; Bradford, M.A. Ductility of profiled composite beams. Part I: Experimental study. J. Struct. Eng. 1995, 121, 876–882. [Google Scholar] [CrossRef]
- Hajjar, J.F. Composite steel and concrete structural systems for seismic engineering. J. Constr. Steel Res. 2002, 58, 703–723. [Google Scholar] [CrossRef]
- Hong, W.K.; Kim, J.M.; Park, S.C.; Kim, S.I.; Lee, S.G.; Lee, H.C.; Yoon, K.J. Composite beam composed of steel and pre-cast concrete (modularized hybrid system, MHS) Part II: Analytical investigation. Struct. Des. Tall Spec. Build. 2009, 18, 891–905. [Google Scholar] [CrossRef]
- Faella, C.; Martinelli, E.; Nigro, E. Shear connection nonlinearity and deflections of steel-concrete composite beams: A simplified method. J. Struct. Eng. 2003, 129, 12–20. [Google Scholar] [CrossRef]
- Lim, G.T. An Investigation of Hybrid Pre-Stressed Composite Beam Flexural Capacity and Tendon Loss. Master’s Thesis, Kyung Hee University, Seoul, Korea, 2013. [Google Scholar]
- Nie, J.; Cai, C.S.; Wang, T. Stiffness and capacity of steel-concrete composite beams with profiled sheeting. Eng. Struct. 2005, 27, 1074–1085. [Google Scholar] [CrossRef]
- Nie, J.G.; Cai, C.S.; Wu, H.; Fan, J.S. Experimental and theoretical study of steel-concrete composite beams with openings in concrete flange. Eng. Struct. 2006, 28, 992–1000. [Google Scholar] [CrossRef]
- Wang, C.; Shen, Y.; Yang, R.; Wen, Z. Ductility and Ultimate Capacity of Prestressed Steel Reinforced Concrete Beams. Math. Probl. Eng. 2017, 2017, 1467940. [Google Scholar] [CrossRef]
- Nie, J.G.; Tian, C.Y.; Cai, C.S. Effective width of steel-concrete composite beam at ultimate strength state. Eng. Struct. 2008, 30, 1396–1407. [Google Scholar] [CrossRef]
- Liu, X.; Bradford, M.A.; Ataei, A. Flexural performance of innovative sustainable composite steel-concrete beams. Eng. Struct. 2017, 130, 282–296. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, L.; Qu, B.; Zhang, S. Experimental investigation on the flexural behavior of steel-concrete composite beams with U-shaped steel girders and angle connectors. Eng. Struct. 2017, 131, 492–502. [Google Scholar] [CrossRef]
- Elamary, A.; Ahmed, M.M.; Mohmoud, A.M. Flexural behaviour and capacity of reinforced concrete-steel composite beams with corrugated web and top steel flange. Eng. Struct. 2017, 135, 136–148. [Google Scholar] [CrossRef]
- Chen, S. Experimental study of prestressed steel-concrete composite beams with external tendons for negative moments. J. Constr. Steel Res. 2005, 61, 1613–1630. [Google Scholar] [CrossRef]
- Saadatmanesh, H.; Albrecht, P.; Ayyub, B.M. Experimental study of prestressed composite beams. J. Struct. Eng. 1989, 115, 2348–2363. [Google Scholar] [CrossRef]
- Chen, S.; Gu, P. Load carrying capacity of composite beams prestressed with external tendons under positive moment. J. Constr. Steel Res. 2005, 61, 515–530. [Google Scholar] [CrossRef]
- Ayyub, B.M.; Sohn, Y.G.; Saadatamanesh, H. Prestressed composite girders I: Experimental study for negative moment. J. Struct. Eng. 1992, 118, 2743–2762. [Google Scholar] [CrossRef]
- Galvez, J.C.; Benitez, J.M.; Tork, B.; Casati, M.J.; Cendon, D.A. Splitting failure of precast prestressed concrete during the release of the prestressing force. Eng. Fail. Anal. 2009, 16, 2618–2634. [Google Scholar] [CrossRef]
- Ghallab, A. Calculating ultimate tendon stress in externally prestressed continuous concrete beams using simplified formulas. Eng. Struct. 2013, 46, 417–430. [Google Scholar] [CrossRef]
- Yoon, T.H. An Analytical and Experimental Investigation of Flexural Capacity for Steel-Pre-Stressed Composite Beam during Construction Phase. Master’s Thesis, Kyung Hee University, Seoul, Korea, 2011. [Google Scholar]
- Jeong, S.Y. Experimental and Analytical Investigation of Pre-Stressed Composite Beam Having Sleeves for Steel Pipes. Master’s Thesis, Kyung Hee University, Seoul, Korea, 2012. [Google Scholar]
- Hong, W.K.; Lee, Y.; Kim, S.; Kim, S.I.; Yun, Y.J. Analytical investigation of hybrid composite precast beams with modified strain compatibility for entire history of nominal flexural capacity. Struct. Des. Tall. Spec. Build. 2015, 24, 835–852. [Google Scholar] [CrossRef]
- Hong, W.K.; Jeong, S.Y.; Park, S.C.; Kim, J.T. Experimental investigation of an energy-efficient hybrid composite beam during the construction phase. Energy Build. 2012, 46, 37–47. [Google Scholar] [CrossRef]
- Yoon, D.Y. An Analytical and Experimental Investigation of Deflection for Steel Pre-Stressed Composite Beam during Construction Phase. Master’s Thesis, Kyung Hee University, Seoul, Korea, 2011. [Google Scholar]
- Park, S.C. Study of Steel-Reinforced Concrete Composite Beam Based on Strain Compatibility. Ph.D. Thesis, Kyung Hee University, Seoul, Korea, 2010. [Google Scholar]
- Kim, J.; Hong, W.K.; Lim, G.T. Losses of prestressed forces of pre-tensioned precast composite beams. Spec. Des. Tall Spec. Build. 2017, 26, e1339. [Google Scholar] [CrossRef]
- Hong, W.K. Development of Analytical Models for Reinforced Concrete Masonry Flexural Walls. Ph.D. Thesis, University of California, Los Angeles, CA, USA, 1989. [Google Scholar]
- Nzabonimpa, J.D.; Hong, W.K.; Kim, J. Strength and post-yield behavior of T section steel encased by structural concrete. Spec. Des. Tall Spec. Build. 2018, 27, e1447. [Google Scholar] [CrossRef]
- Liu, G.R.; Quek, S.S. Finite Element Method: A Practical Course, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2003. [Google Scholar]
- Systemes, D. Abaqus Analysis User’s Guide; Dassault Systemes: Waltham, MA, USA, 2015; Volume 6.14-2. [Google Scholar]

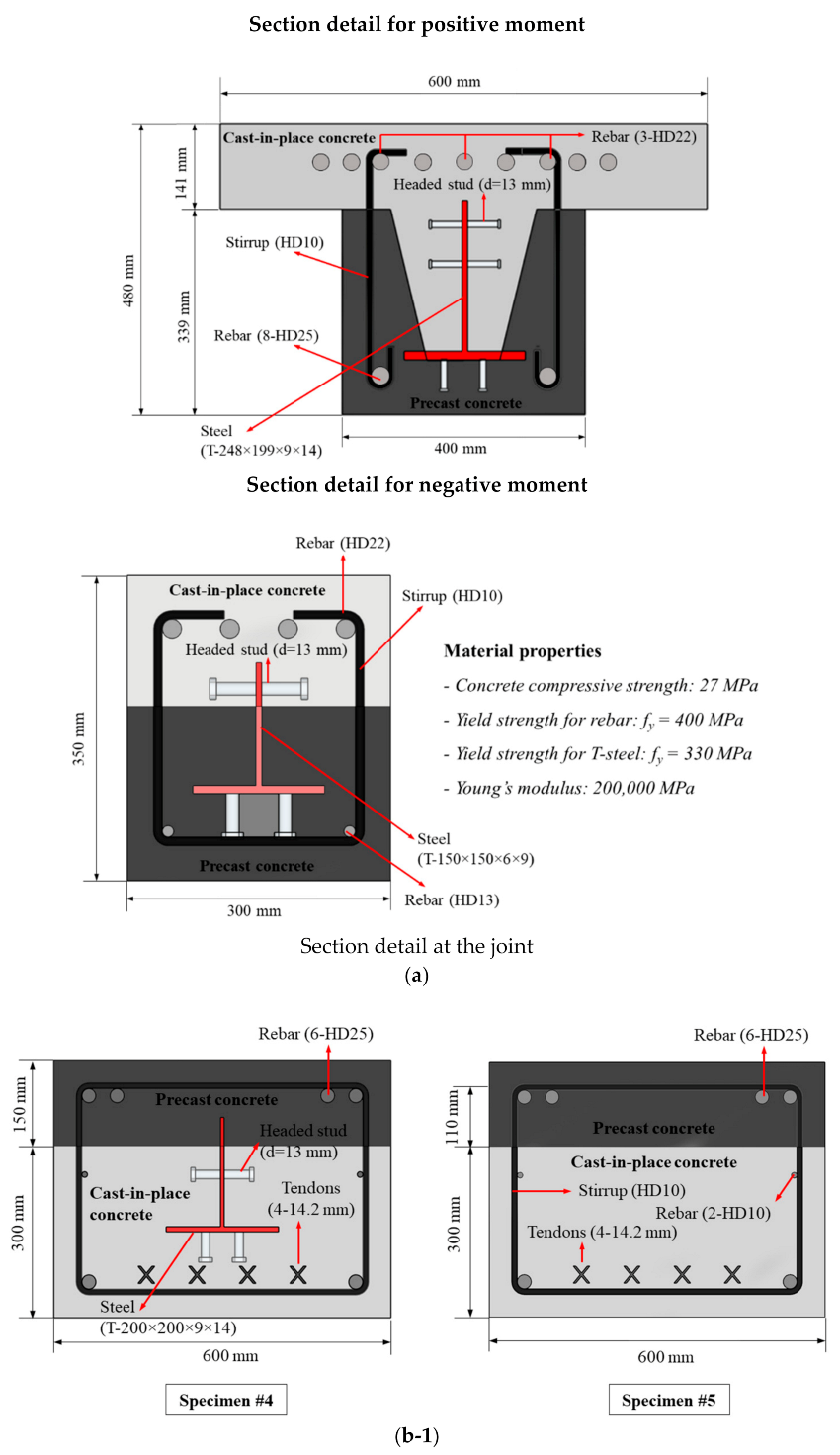
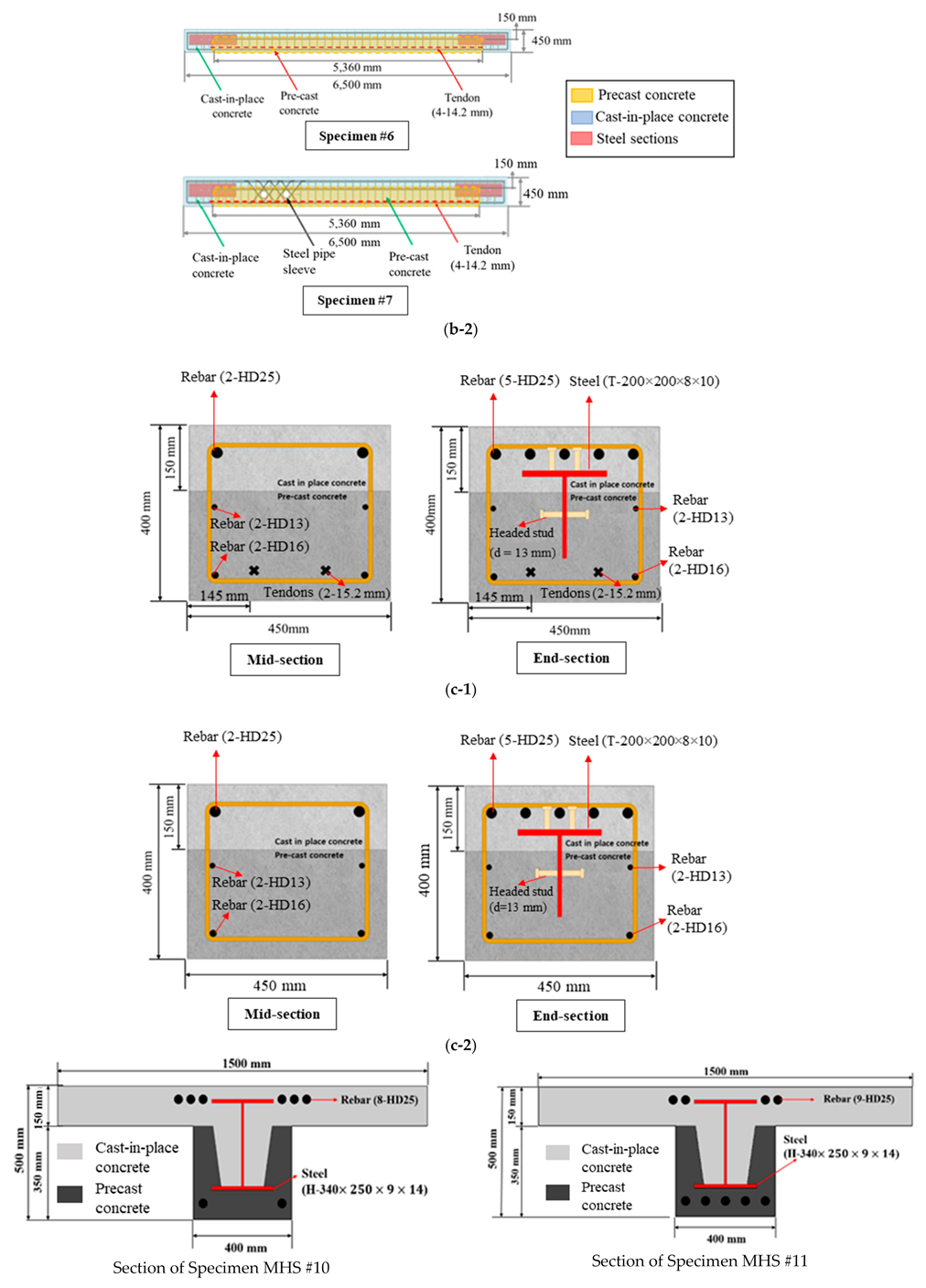
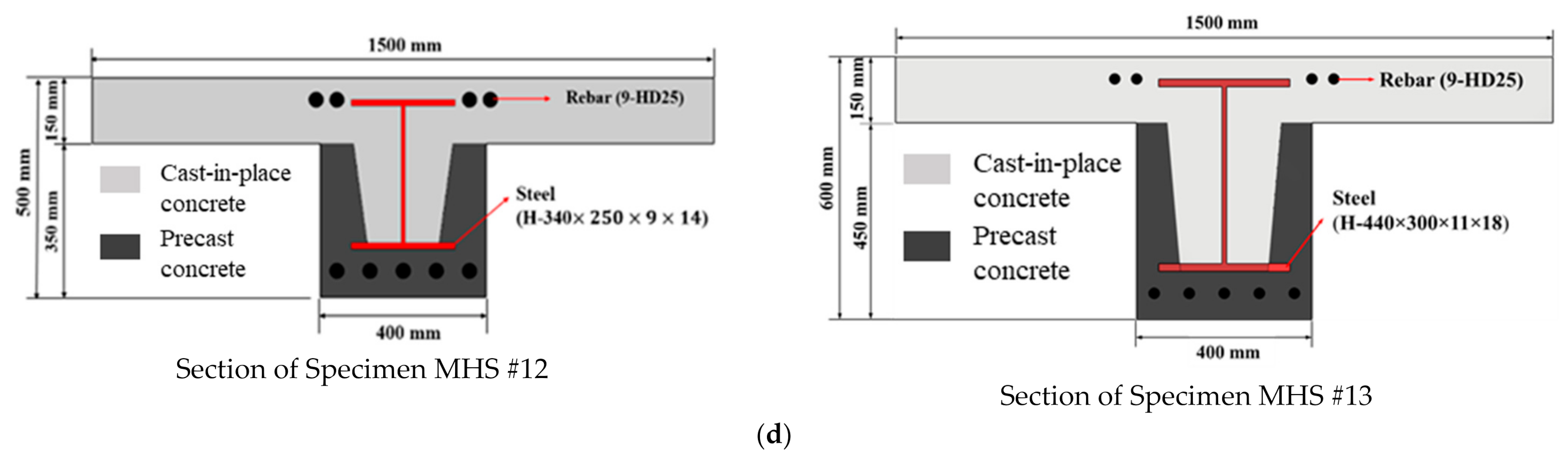




| Specimen | Boundary Condition | Pre-Stressed | Sleeve Openings | End Steel Sections |
|---|---|---|---|---|
| CS1 #1 | Cantilever with Fixed ends | No | No | Reverse T steel section through entire span of the beams [24] |
| CS2 #2 | ||||
| CP #3 | ||||
| S-PS #4 | Pinned ends | Yes | T steel section at both ends of the beams [7,22,25,26] | |
| S-PS #5 | ||||
| S-PS #6 | Yes | |||
| S-PS #7 | ||||
| F-PS #8 | Fixed ends | No | ||
| F-NPS #9 | No | |||
| MHS #10 to #13 | Fixed end | No | No | Wide flange steel section throughout entire span of the beams [5] |
| Specimen | Material Properties | |
|---|---|---|
| CS1 #1 | | |
| CS2 #2 | ||
| CP #3 | ||
| S-PS #4 | ||
| S-PS #5 | ||
| S-PS #6 | ||
| S-PS #7 | ||
| F-PS #8 | ||
| F-SRC #9 | ||
| MHS #10to #13 | ||
| Specimens | Stiffness Degradations | |
|---|---|---|
| Non-pre-stressed composite beams | Cantilever (#1 to #3) Figure 4a For positive, negative dir. | |
| Fixed ends (#9) Figure 4c-2 | [22] | |
| Pre-stressed composite beams | Simply supported ends (#4 to #7) Figure 4b | [21] |
| Fixed ends (#8) Figure 4c-1 | [22] | |
| MHS #10 to #13 [5] | Fixed end Figure 4d | |
| Specimens #1 to #13 (all specimens) | Global stiffness degradation tendency (Figure 4e-2) | |
(kN/mm) | (mm) | F (kN) | |||||
|---|---|---|---|---|---|---|---|
| (A] | (B) | (C] = (A)/(B) | (D) | (E) | (C) × (E) | (B) × (D) | ((C) × (E)) × ((B) × (D)) |
| 570.6 | 24.4 | 23.4 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0.1 | 2.56 | 59.80 | 2.44 | 145.92 | |||
| 0.25 | 1.94 | 45.30 | 6.10 | 276.32 | |||
| 0.5 | 1.47 | 34.32 | 12.20 | 418.75 | |||
| 0.75 | 1.19 | 27.90 | 18.30 | 510.66 | |||
| 1 | 1.00 | 23.35 | 24.40 | 569.74 | |||
| 1.25 | 0.85 | 19.82 | 30.50 | 604.43 | |||
| 1.5 | 0.72 | 16.93 | 36.60 | 619.67 | |||
| 1.75 | 0.62 | 14.49 | 42.70 | 618.74 | |||
| 2 | 0.53 | 12.38 | 48.80 | 603.97 | |||
| 2.25 | 0.45 | 10.51 | 54.90 | 577.09 | |||
| 2.5 | 0.38 | 8.84 | 61.00 | 539.46 | |||
| 2.75 | 0.31 | 7.33 | 67.10 | 492.16 | |||
| 3 | 0.25 | 5.96 | 73.20 | 436.06 | |||
| 3.25 | 0.20 | 4.69 | 79.30 | 371.91 | |||
| 3.5 | 0.15 | 3.52 | 85.40 | 300.32 | |||
| 3.75 | 0.10 | 2.42 | 91.50 | 221.83 | |||
| 4 | 0.06 | 1.40 | 97.60 | 136.90 |
| Size | Material Properties | |
|---|---|---|
| Concrete beam | 300 × 350 (mm2) | = 33.1 MPa |
| Concrete column | 550 × 550 (mm2) | = 33.1 MPa |
| T-Steel (SM490) | 150 × 150 × 6.5 × 9 (mm3) | = 0.00165 |
| Bolt | M22-F10T | = 0.0045 |
| Stud bolt | D13 (height: 53 mm) | = 0.0019 |
| Rebar | D22, D13 | = 0.0019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, W.-K.; Lim, G.-T. Prediction of Post-Yield Performance of Hybrid Precast Beams Based on Strength Degradation. Appl. Sci. 2021, 11, 4482. https://doi.org/10.3390/app11104482
Hong W-K, Lim G-T. Prediction of Post-Yield Performance of Hybrid Precast Beams Based on Strength Degradation. Applied Sciences. 2021; 11(10):4482. https://doi.org/10.3390/app11104482
Chicago/Turabian StyleHong, Won-Kee, and Gyun-Taek Lim. 2021. "Prediction of Post-Yield Performance of Hybrid Precast Beams Based on Strength Degradation" Applied Sciences 11, no. 10: 4482. https://doi.org/10.3390/app11104482
APA StyleHong, W.-K., & Lim, G.-T. (2021). Prediction of Post-Yield Performance of Hybrid Precast Beams Based on Strength Degradation. Applied Sciences, 11(10), 4482. https://doi.org/10.3390/app11104482






