Abstract
Aiming at analyzing the temporal structures in evolutionary networks, we propose a community detection algorithm based on graph representation learning. The proposed algorithm employs a Laplacian matrix to obtain the node relationship information of the directly connected edges of the network structure at the previous time slice, the deep sparse autoencoder learns to represent the network structure under the current time slice, and the K-means clustering algorithm is used to partition the low-dimensional feature matrix of the network structure under the current time slice into communities. Experiments on three real datasets show that the proposed algorithm outperformed the baselines regarding effectiveness and feasibility.
1. Introduction
The evolutionary network refers to a network in which the nodes and edges change over time. As a typical evolutionary network, social networks are very common in modern life, such as Flickr, Facebook, Twitter, and so on. In the above-mentioned social networks, an individual or a group of users may join and exit the network, and the intimacy with friends is increased through obtaining to know friends of friends. Community detection in an evolutionary network is a complex and challenging problem. The development and change of the network structure under the adjacent time slices are slow, however, the statistical characteristics of the network will change significantly over a long period.
Therefore, it is necessary to re-identify the community structure. As the organization of a dynamic community changes constantly, a dynamic community tends to be more complex. Network representation has gradually become the main supporting technology of dynamic community detection, which provides great convenience for dynamic community detection. The application of network representation technology can greatly improve the detection performance [1,2].
Traditional community detection algorithms are mostly based on static networks, and the influence of time on the network structure is ignored. For example, network communication operators hope to reduce the communication costs in the same social circle in different periods, proposing a flexible billing activity for their customers. The static community is uncertain about the actual network connectivity, and this marketing policy is obviously not effective. If considering the change of time for community detection, the real-time community structure can be dynamically represented, which is beneficial to providing individualized services for users.
Thus, it can be seen that the evolution of the network structure has an important impact on community detection, which is likely to bring commercial value [3]. Early research on the division of dynamic network communities [4,5,6,7,8] viewed the dynamic network as a series of snapshot networks in chronological order, and obtained the community structure of each snapshot by using the static network community detection algorithm; however, this kind of thinking does not make full use of the evolution information of the network structure, and a fundamental drawback rooted in such schemes is that most of traditional algorithms are sensitive to tiny changes in the network structure [9].
The DeepWalk [10] algorithm uses a random walk method to obtain the neighbors of nodes in the network to generate a fixed-length node sequence, and the node sequence is fed into the Skip-Gram model for learning representation to apply to other tasks. The SDNE [11] algorithm uses a deep sparse autoencoder [12] to simultaneously optimize the first-order and second-order similarity objective functions, conducting semi-supervised learning representation, and it is applied to visualization, multi-label classification, link prediction, etc. In machine learning research, scholars have proposed learning methods for graph embedding [13,14,15]; however, these methods usually only work well on certain networks.
To overcome these limitations, we propose a novel community detection algorithm based on evolutionary network representation learning (Learning Community Detection Based on Evolutionary Network, LCDEN). The LCDEN algorithm uses a Laplacian matrix to obtain the node relationship information of the directly connected edges in the network structure of the previous time slice, learns the network structure under the current time slice through the deep sparse autoencoder, and uses a K-means clustering algorithm to divide the community of the obtained low-dimensional feature matrix of the network structure under the current time slice. Our contributions can be summarized as follows:
- (1)
- We propose a novel algorithm for community detection in evolutionary networks, which solves the limitation that traditional community detection algorithms were unable to handle the temporal information of a network structure.
- (2)
- The proposed algorithm can effectively use the historical temporal information of a network structure and apply a deep learning model to the research of evolutionary network representation learning.
- (3)
- The proposed algorithm has advantages in different datasets and has higher detection performance and computational efficiency.
2. Related Work
Community detection is one of the most active topics in the field of graph mining and network science. With the continuous expansion of the real-world network scale and the introduction of temporal information, the research on community detection in evolutionary networks can explore community detection algorithms based on the network structure and network information conforming to the real world.
Network representation learning. In the research of network representation learning, one of the foremost requirements of network representation learning is preserving network topology properties in learned low-dimension representations [16]. Researchers often use methods based on matrix decomposition or random walking to learn the graph representation, such as LLE [17], Laplacian Eigenmaps [14], Deepwalk [10], and LINE [18]. However, these methods typically have high computational complexity and poor generalization ability. In addition, they lack the use of temporal information in evolutionary networks.
Evolutionary network. The research on the dynamic evolution of networks has been an ongoing hotspot. The dynamic information in networks has proven to be crucial for understanding networks. Many works have attempted to combine the research of evolutionary network representation learning with the basic research of complex networks. To reveal the dynamic mechanism of information dissemination networks, Rodriguez et al. [19] modeled the information propagation process as several discrete networks with continuous-time slices occurring at different rates.
Fathy et al. [20] realized the joint learning of the graph structure information and time dimension information by combining the graph attention mechanism with the convolution of the time dimension, and processing the dynamic graph structure data by using the self-attention layer as time passes. It is of great significance to learn and fuse a network structure, multi-modal information, and temporal information based on effective methods, which can obtain more accurate representations of evolutionary networks.
Community detection. In recent years, community structure detection has received extensive attention, and communities play an important role in complex systems [21]. However, most of the traditional community detection algorithms for static networks are not suitable for research on evolutionary network structures. Chen et al. [22] proposed a community detection algorithm based on the minimum change granularity for evolutionary networks (DWGD), which can complete dynamic community detection with time slices as the minimum granularity. Wang et al. [23] proposed that Markov chain-based community detection algorithm for evolutionary networks had better computational efficiency and detection performance. In addition, many researchers also studied community detection in evolutionary networks by the Coherent Neighborhood Propinquity of dynamic networks [24], building compressed graphs [25], etc.
3. Preliminaries
3.1. Definitions
Given a network , where is the set of nodes, is the set of edges. The adjacency matrix represents the connection relationship between nodes, the value of the corresponding element in the matrix indicates whether the edge exists, if there is an edge between node vi and node vj, then aij = 1; otherwise aij = 0. In this paper, we take the adjacency matrix A as the closest relation matrix in the network to describe the similarity between nodes in the graph and their proximity relation.
(1) Node proximity
Given a network , , the proximity between node and node is defined as
where is the shortest path length from node to node , , is the degree of attenuation, and the value range is . If the path length l increases, the proximity decreases, and controls the degree of proximity attenuation. The larger the value of , the faster the proximity relationship between the nodes decays.
(2) Proximity matrix
Given a network , is a matrix corresponding to the network , where we use the proximity formula to calculate the proximity between the two corresponding nodes vi and vj in M, , with then, we call the proximity matrix of .
3.2. Data Preprocessing
The data preprocessing mainly converts the adjacency matrix into a proximity matrix. The breadth-first traversal algorithm is employed to obtain the path length, then we calculate the neighbor relationship between nodes that are not directly connected by the attenuation, and the topology of the community can be well exhibited. However, when the path length is greater than a certain threshold, node pairs that are not in the same community may also have a certain proximity value, which will lead to an ambiguous partition of the community. Therefore, we set the threshold Le of the path length. By adjusting the parameters empirically, we only calculate the proximity value between nodes that are mutually reachable within the length of Le.
At the same time slice, we construct a loss function for directly connected nodes in the network, this is formulated as
where represent two adjacent nodes, is the number of nodes, is the adjacency matrix, and are the representations of two adjacent nodes corresponding to the presentation layer, and is the Laplacian matrix of the network, obtained from the corresponding diagonal matrix and adjacency matrix. The Laplacian matrix is calculated as
where is a diagonal matrix, is the adjacency matrix of the network. To ensure that the evolutionary network can smoothly evolve with time, the relational information of the directly connected nodes of the network structure of the last time slice are obtained by using the Laplacian matrix. By employing the Laplacian matrix, the node information loss function of directly connected nodes is constructed as
where is the representation of the network structure of time slice , is the Laplacian matrix of the network structure of time slice .
Under different time slices, the scale of the evolutionary network varies. A zero-filling operation is usually performed for training the data calculations in neural networks. However, there may be such cases where non-zero elements are far less than the zero elements in the data matrix. In this way, the increase of zero elements will affect the sparsity of the matrix, and it is easy to increase the error of zero elements due to the reconstruction of the deep autoencoder. Therefore, a sparsity constraint based on the deep automatic encoder is beneficial to control the reconstruction difference of the deep autoencoder. In the proposed algorithm, the sparsity parameter is added to the depth autoencoder during the encoding process, and we obtain a deep sparse autoencoder, which is helpful to express the information of the original data without loss.
The first layer to the second layer in the deep sparse autoencoder is an encoding process as well as a dimensionality reduction process. According to the size of the data, we set the number of data nodes in each layer, which is also the data dimension. By setting the data dimension size in each layer, the deep sparse autoencoder will obtain the low-dimensional vector corresponding to the input data after encoding. From the second layer to the third layer, this is a decoding process. The deep sparse autoencoder decodes the low-dimensional vector obtained from the input data and then outputs the vector of the same dimension as the input data.
This process employs the backpropagation algorithm to train the data by adjusting the parameters related to the encoder and decoder—for example, weights, deviations, etc., to minimize the reconstruction difference. Consequently, the output expression vector approximates the input data information. Finally, the resulting representation of the coding layer is exactly the low-dimensional Eigenmatrix that needs to be output.
In the proposed algorithm, a deep sparse autoencoder is used to represent and learn the network structure under the current time slice of the evolutionary network. We adopt a similar idea to calculate the reconstruction error of building deep sparse autoencoders [11], and a backpropagation algorithm is employed to obtain the node information expression of the network at the next time slice. The reconstruction error of the deep sparse autoencoder is established, which is formulated as
where and are the input data and reconstructed data, respectively. , is a sparsely constrained parameter, and is a tunable parameter.
To satisfy the temporal smooth transition of the evolutionary network structure, the node information of the directly connected edges in the network of the last time slice is employed to construct the loss function, and the reconstruction error of the deep sparse autoencoder is incorporated to construct the overall loss function.
In the proposed algorithm, to preserve part of the historical node information of the network structure of the last time slice and, simultaneously, effectively present the feature of the network structure of the next time slice, the overall loss functions are jointly optimized to effectively train the data. The loss function on constructing the learning model of the overall graph presentation is defined as
where and are two tunable parameters.
4. Methods
The proposed algorithm employs a Laplacian matrix to map the nodes with directly connected edges in the network structure of the last time slice to the deep sparse autoencoder representation layer. It is beneficial to retain the node information of the network of the last time slice, and it is not easy to lose the historical evolution information of the network. Meanwhile, the temporal smoothness affects the structure of the evolutionary network and, thus, is taken into account in the graph representation learning algorithm.
Furthermore, the deep sparse autoencoder is used to represent the network structure under the current time slice of the evolution network, to obtain a better expression of the characteristics of the network structure, and then the representation vector of the node is achieved. Finally, the K-means clustering algorithm is used to cluster the low-dimensional feature matrix of the network structure under the current time slice to obtain the community structure.
For the network structure of continuous-time slices, we successively utilize the information between the node pairs of the network structure under the last time slice. The network structure of the current time slice is learned and presented through the deep sparse autoencoder, and then the low-dimensional representation matrix of the network structure of the current time slice is obtained.
The following shows the process of the proposed algorithm:
- (1)
- Initialize the relevant parameters and load the dataset.
- (2)
- Based on the breadth-first traversal algorithm to traverse the network structure adjacency matrix of the current time slice.
- (3)
- Calculate the degree by using the path length to obtain the proximity matrix.
- (4)
- Use a Laplacian Matrix to obtain the information of directly connected nodes in the network of a time slice, and the features of the proximity matrix of the network under the current time slice are extracted by employing a deep sparse autoencoder.
- (5)
- Use the K-means algorithm to obtain the network community structure under the current time slice.
The proposed algorithm (Algorithm 1) is based on the TensorFlow framework, and its pseudocode is as follows.
| Algorithm 1. LCDEN algorithm | |
| Input: Evolution graph , adjacency matrix , adjacency matrix , number of communities , path length threshold , degree of attenuation , deep sparse autoencoder with 3 layers, number of nodes in each layer of the deep autoencoder , i = 1, 2, 3. Output: Community results . | |
|
In this pseudocode, the Breadth-first traversal algorithm is used to convert the adjacency matrix into the proximity matrix , and then to input it into the deep sparse autoencoder for encoding. Simultaneously, we use the adjacency matrix to calculate the Laplacian matrix, to map the node information with directly connected edges to the presentation layer of the deep sparse autoencoder, and to obtain the result of the presentation layer—that is, the required low-dimensional matrix representation vector . Finally, the K-means clustering algorithm is used to cluster the low-dimensional matrix representation vector , and the community results are obtained.
5. Experiments
In this section, we evaluate the computational efficiency and detection performance of our proposed algorithm on three different datasets. We use the Silhouette Coefficient [26] and time-consumption as evaluation metrics to evaluate the performance of different models.
5.1. Datasets
The following three network datasets were employed for the experiments.
(1) Superuser temporal network [27]
The stack exchange website super user network dataset is an interactive temporal network on the stack exchange website. The relevant metadata stored are users and the interactions between users. Here, nodes represent users, and edges indicate interactions between users.
(2) Wiki-Talk-Temporal dataset [27]
The Wikipedia network is a temporal network, and Wikipedia users edit each other’s “conversation” pages. The directed edge indicates that a user edited the conversation page of user at time .
(3) Twitter network dataset [28]
The data were purchased by The Numerical Analysis and Scientific Computing research group in the Department of Mathematics and Statistics at the University of Strathclyde, using a grant made available by the University of Strathclyde through their EPSRC-funded “Developing Leaders” program. In the dataset, node and node represent the node numbers.
5.2. Evaluation Metrics
We employed the Silhouette Coefficient and time-consumption to evaluate the experimental results. The Silhouette Coefficient effectively combines the cohesion and separation of the clustering for evaluation. The advantage of employing the Silhouette Coefficient as a cluster result evaluation is that no real data information is needed for comparison. The range of the Silhouette Coefficient is [–1, 1], and the larger the value is, the better the clustering effect.
The calculation formula of the Silhouette Coefficient of each sample point is as follows:
where represents a sample point, represents the average distance between each sample and all other sample points in a cluster. It is used to quantify the cohesion of the cluster. We select cluster , which does not contain sample point , and then calculate the average distance between sample point and all sample points in cluster . Similarly, we traverse all other clusters until the nearest average distance is found. This is represented as , which is used to quantify the degree of separation between clusters.
We calculate the Silhouette Coefficient of the overall sample—that is, we find the average value as the overall Silhouette Coefficient of the data cluster, to denote the closeness of the data cluster.
5.3. Baselines
To verify the effectiveness of the proposed algorithm, we chose the DWGD algorithm [22] for our comparative experiments. The DWGD algorithm can partition communities for dynamic weighted networks. The weight of the edges may increase, decrease, or remain unchanged with the change of time. The DWGD algorithm can well deal with the increase and decrease of the edge weight. Experiments on certain datasets verified the effectiveness of the algorithm. The DWGD algorithm can perform community detection for evolutionary networks and weighted networks. Therefore, the algorithm proposed in this paper was compared with the DWGD algorithm on the problem of community detection in dynamic weighted networks.
5.4. Experimental Analysis
The proposed algorithm (abbreviated as LCDEN) and the DWGD algorithm were used to divide the network structure of the data set containing a time stamp under different time slices, and the obtained Silhouette Coefficient and running time were compared. The experimental results and analysis are as follows.
- (1)
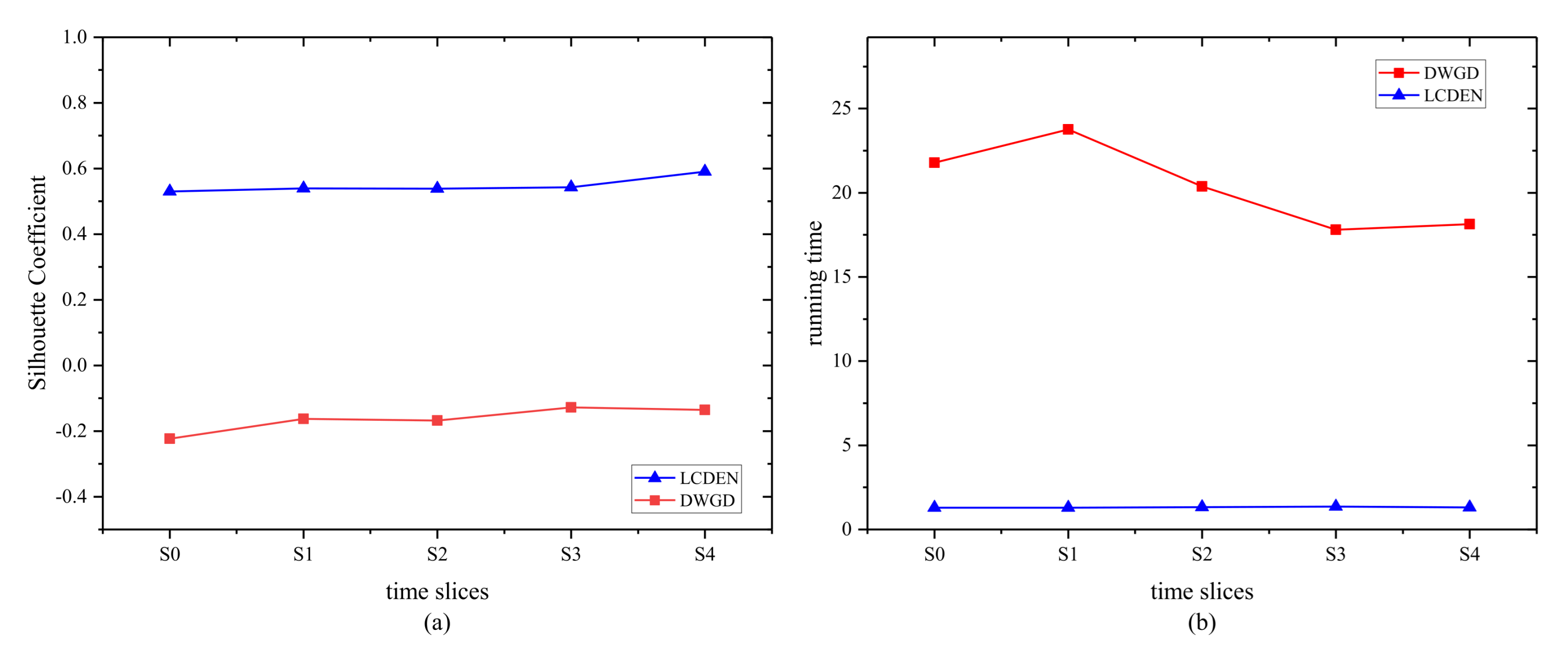
- The comparative experimental results on the Superuser temporal network are shown in Figure 1. As shown in Figure 1a, we can conclude that, in the same time slice, the Silhouette Coefficient of the proposed algorithm is higher than that of the DWGD algorithm, that is, the clustering effect is better. Figure 1b demonstrates that, in the same time slice, the running time of the proposed algorithm is less than the DWGD algorithm.
 Figure 1. Comparison of the Silhouette Coefficient (a) and running time (b) on the Superuser temporal network.
Figure 1. Comparison of the Silhouette Coefficient (a) and running time (b) on the Superuser temporal network. - (2)
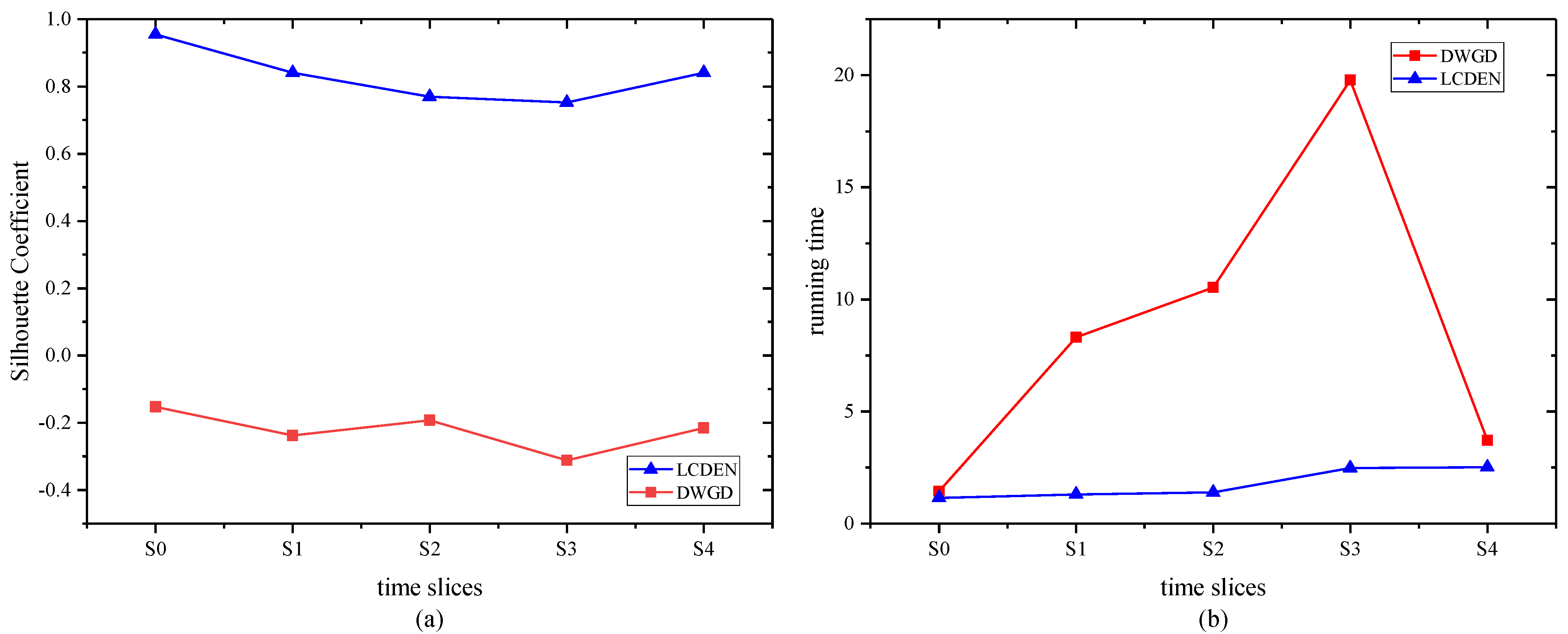
- The comparative experimental results based on the Wiki-Talk-Temporal network (Wikipedia network dataset) are shown in Figure 2.
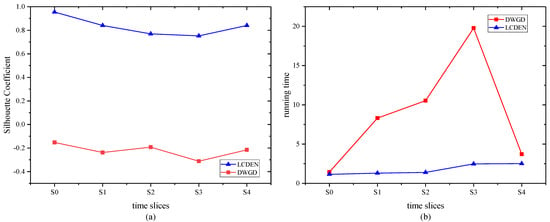 Figure 2. Comparison of the Silhouette Coefficient (a) and running time (b) on the Wiki-Talk-Temporal network.
Figure 2. Comparison of the Silhouette Coefficient (a) and running time (b) on the Wiki-Talk-Temporal network.
Figure 2a also shows that the Silhouette Coefficient of the proposed algorithm is higher than the DWGD algorithm at the same time slice, indicating a better clustering effect of the proposed algorithm. From Figure 2b, we can see that in the time slices of S0 and S4, the running time of the proposed algorithm and the DWGD algorithm are close to each other, and, in other time slices, the running time of the proposed algorithm is less than that of the DWGD algorithm.
- (3)
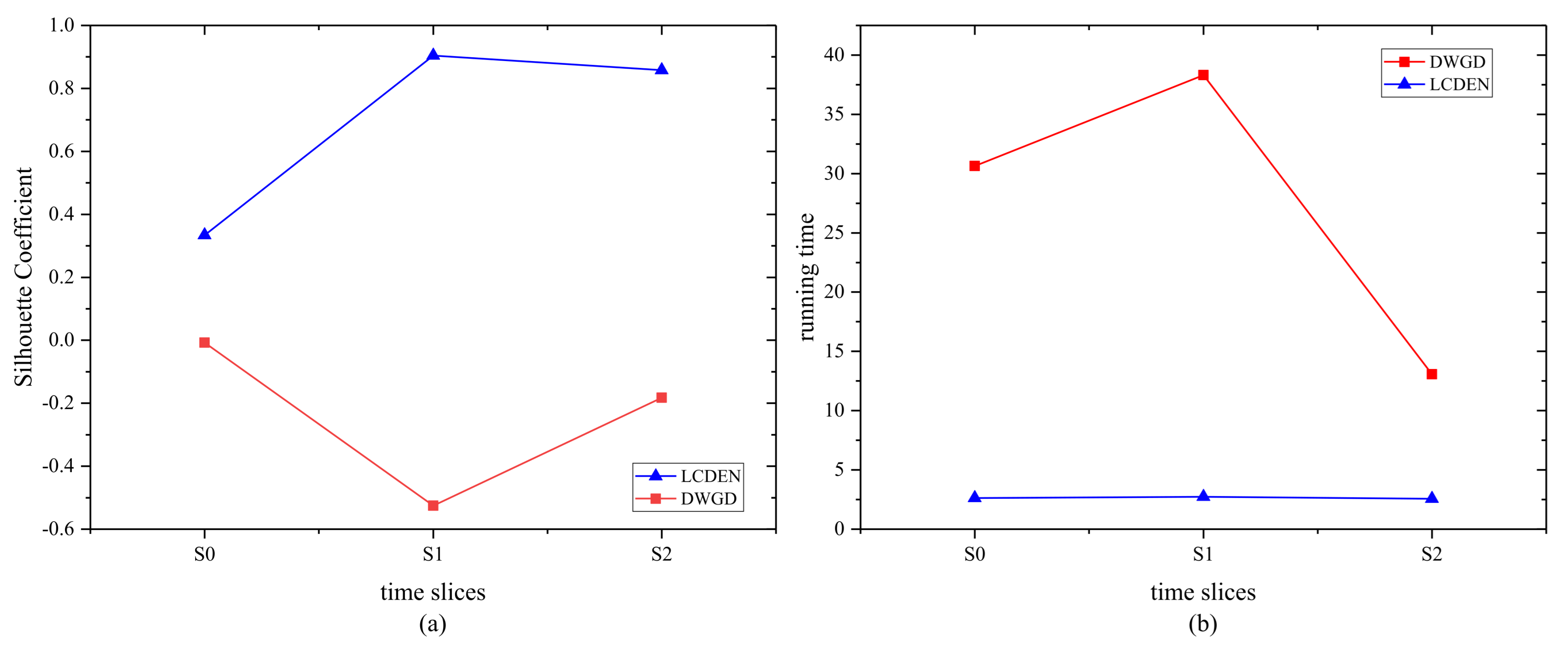
- The comparative experimental results based on the Twitter dataset are shown in Figure 3.
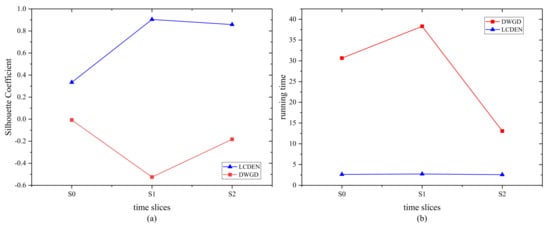 Figure 3. Comparison of the Silhouette Coefficient (a) and running time (b) on the Twitter network.
Figure 3. Comparison of the Silhouette Coefficient (a) and running time (b) on the Twitter network.
Figure 3a illustrates that the Silhouette Coefficient of the proposed algorithm is higher than that of the DWGD algorithm, indicating a better clustering effect of the proposed algorithm. Figure 3b discloses that the running time required for the proposed algorithm is less than that of the DWGD algorithm.
6. Results and Discussion
The community structures are groups of nodes that are more strongly or frequently connected among themselves than with others. Community detection is proposed to find the most reasonable partitions of a network via the observed topological structures [29]. However, traditional community detection methods are usually oriented to static networks and cannot deal with large-scale evolutionary networks, while the most common ones in the real world are complex systems that change with time.
The proposed algorithm makes full use of the historical structure of the network and uses the deep learning model to process the temporal information of the evolutionary network, thus, obtaining the most reasonable communities in different time slices of the given evolutionary network. By comparing with the baselines, the proposed algorithm demonstrated advantages in computational efficiency and detection performance.
This is because the use of the deep learning model uses the historical structure of the network as the prior knowledge of the community detection at the current time, and the deep learning model obtains more input data when compared with the baselines. The research in community detection will further promote the development of the optimization of transportation network structures [30,31], the analysis of social networks [32,33], and research of biological systems [3,34].
7. Conclusions
In this paper, we propose an evolutionary network community detection algorithm that embeds nodes into vectors and uses the K-means algorithm for community member clustering. To process the temporal data, the proposed algorithm employs a Laplacian matrix to represent the historical network structural information and uses a deep sparse autoencoder to encode the prior and the current information. The experimental results on representative datasets showed that the proposed algorithm outperformed the baselines in computational efficiency and detection performance.
Author Contributions
Conceptualization, D.C., Y.K. and D.W.; Formal analysis, M.N., J.W. and X.H.; Funding acquisition, D.C. and D.W.; Methodology, M.N. and Y.K.; Project administration, D.C. and D.W.; Resources, M.N. and X.H.; Software, M.N., J.W. and Y.K.; Supervision, D.C. and D.W.; Validation, D.C. and D.W.; Visualization, M.N. and J.W.; Writing–original draft, M.N., J.W. and Y.K.; Writing–review & editing, D.C., D.W. and X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially supported by the Natural Science Foundation of Liaoning Province under Grant No. 20170540320, the Doctoral Scientific Research Foundation of Liaoning Province under Grant No. 20170520358, and the Fundamental Research Funds for the Central Universities under Grant No. N161702001, No. N172410005-2.
Conflicts of Interest
The authors declare no conflict of interest.
References
- He, T.; Hu, L.; Chan, K.C.C.; Hu, P. Learning Latent Factors for Community Identification and Summarization. IEEE Access 2018, 6, 30137–30148. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Yang, J. Dynamic Community Recognition Algorithm Based on Node Embedding and Linear Clustering. In Innovative Computing; Springer: Singapore, 2020; pp. 829–837. [Google Scholar]
- Martinet, L.-E.; Kramer, M.A.; Viles, W.; Perkins, L.N.; Spencer, E.; Chu, C.J.; Cash, S.S.; Kolaczyk, E.D. Robust dynamic community detection with applications to human brain functional networks. Nat. Commun. 2020, 11, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nat. Cell Biol. 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Asur, S.; Parthasarathy, S.; Ucar, D. An Event-Based Framework for Characterizing the Evolutionary Behavior of Interaction Graphs. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining—KDD ’07, San Jose, CA, USA, 12–15 August 2007; pp. 913–921. [Google Scholar] [CrossRef]
- Kumar, R.; Novak, J.; Raghavan, P.; Tomkins, A. On the Bursty Evolution of Blogspace. World Wide Web 2005, 8, 159–178. [Google Scholar] [CrossRef]
- Kumar, R.; Novak, J.; Tomkins, A. Structure and Evolution of Online Social Networks. In Link Mining: Models, Algorithms, and Applications; Springer: New York, NY, USA, 2010; pp. 337–357. [Google Scholar]
- Lin, Y.-R.; Sundaram, H.; Chi, Y.; Tatemura, J.; Tseng, B.L. Blog Community Discovery and Evolution Based on Mutual Awareness Expansion. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence (WI’07), Fremont, CA, USA, 2–5 November 2007; pp. 2–5. [Google Scholar]
- Yu, L.; Li, P.; Zhang, J.; Kurths, J. Dynamic community discovery via common subspace projection. New J. Phys. 2021, 23, 033029. [Google Scholar] [CrossRef]
- Yang, C.; Liu, Z.; Zhao, D.; Sun, M.; Chang, E.Y. Network Representation Learning with Rich Text Information. In Proceedings of the 24th International Conference on Artificial Intelligence, Buenos Aires, Argentina, 25–31 July 2015; pp. 2111–2117. [Google Scholar]
- Wang, D.; Cui, P.; Zhu, W. Structural Deep Network Embedding. In the Proceedings of 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–16 August 2016; pp. 1225–1234. [Google Scholar]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy Layer-Wise Training of Deep Networks. In Advances in Neural Information Processing Systems 19, Proceedings of the 20th Annual Conference on Neural Information Processing Systems (NIPS 2006), Vancouver, BC, Canada, 4–5 December 2007; MIT Press: Cambridge, MA, USA, 2007; p. 153. [Google Scholar]
- Cox, M.A.; Cox, T.F. Multidimensional Scaling. In Handbook of Data Visualization; Springer: Berlin/Heidelberg, Germany, 2008; pp. 315–347. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering. In Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic, Vancouver, BC, Canada, 3–8 December 2001; pp. 585–591. [Google Scholar]
- Tenenbaum, J.B.; De Silva, V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Sun, H.; Jie, W.; Loo, J.; Chen, L.; Wang, Z.; Ma, S.; Li, G.; Zhang, S. Network Representation Learning Enhanced by Partial Community Information That Is Found Using Game Theory. Information 2021, 12, 186. [Google Scholar] [CrossRef]
- Hou, Y.; Zhang, P.; Xu, X.; Zhang, X.; Li, W. Nonlinear Dimensionality Reduction by Locally Linear Inlaying. IEEE Trans. Neural Netw. 2009, 20, 300–315. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Qu, M.; Wang, M.; Zhang, M.; Yan, J.; Mei, Q. LINE: Large-scale Information Network Embedding. In Proceedings of the 24th International Conference on World Wide Web, Florence, Italy, 18–22 May 2015; pp. 1067–1077. [Google Scholar]
- Rodriguez, M.G.; Balduzzi, D.; Schölkopf, B. Uncovering the temporal dynamics of diffusion networks. arXiv 2011, arXiv:1105.0697 2011. [Google Scholar]
- Fathy, A.; Li, K. TemporalGAT: Attention-Based Dynamic Graph Representation Learning. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Singapore, 11–14 May 2020; pp. 413–423. [Google Scholar]
- Li, M.; Liu, J.; Wu, P.; Teng, X. Evolutionary Network Embedding Preserving both Local Proximity and Community Structure. IEEE Trans. Evol. Comput. 2019, 24, 523–535. [Google Scholar] [CrossRef]
- Chen, D.M.; Wang, Y.K.; Huang, X.Y.; Wang, D.Q. Community Detection Algorithm for Complex Networks Based on Group Density. J. Northeast. Univ. Nat. Sci. Ed. 2019, 40, 186–191. [Google Scholar]
- Wang, Z.; Wang, C.; Li, X.; Gao, C.; Li, X.; Zhu, J. Evolutionary Markov Dynamics for Network Community Detection. IEEE Trans. Knowl. Data Eng. 2020, 1. [Google Scholar] [CrossRef]
- Chen, N.; Hu, B.; Rui, Y. Dynamic Network Community Detection with Coherent Neighborhood Propinquity. IEEE Access 2020, 8, 27915–27926. [Google Scholar] [CrossRef]
- Seifikar, M.; Farzi, S.; Barati, M. C-Blondel: An Efficient Louvain-Based Dynamic Community Detection Algorithm. IEEE Trans. Comput. Soc. Syst. 2020, 7, 308–318. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Paranjape, A.; Benson, A.R.; Leskovec, J. Motifs in Temporal Networks. In Proceedings of the 10th ACM International Conference on Web Search and Data Mining, Cambridge, UK, 6–10 February 2017; pp. 601–610. [Google Scholar]
- Yang, J.; Leskovec, J. Patterns of Temporal Variation in Online Media. In Proceedings of the 4th ACM International Conference on Distributed Event-Based Systems—DEBS ’10, Cambridge, UK, July 12–15 2010; pp. 177–186. [Google Scholar]
- Huang, X.; Chen, D.; Ren, T.; Wang, D. A survey of community detection methods in multilayer networks. Data Min. Knowl. Discov. 2021, 35, 1–45. [Google Scholar] [CrossRef]
- Ding, R.; Ujang, N.; Bin Hamid, H.; Manan, M.S.A.; He, Y.; Li, R.; Wu, J. Detecting the urban traffic network structure dynamics through the growth and analysis of multi-layer networks. Phys. A Stat. Mech. Appl. 2018, 503, 800–817. [Google Scholar] [CrossRef]
- Liu, R.-R.; Jia, C.-X.; Lai, Y.-C. Remote control of cascading dynamics on complex multilayer networks. New J. Phys. 2019, 21, 045002. [Google Scholar] [CrossRef]
- Rozario, V.S.; Chowdhury, A.; Morshed, M.S.J. Community detection in social network using temporal data. arXiv 2009, arXiv:1904.05291. [Google Scholar]
- Al-Garadi, M.A.; Varathan, K.D.; Ravana, S.D.; Ahmed, E.; Mujtaba, G.; Khan, M.U.S.; Khan, S.U. Analysis of online social network connections for identification of influential users: Survey and open research issues. ACM Comput. Surv. 2018, 51, 1–37. [Google Scholar] [CrossRef]
- Sanchez-Rodriguez, L.M.; Iturria-Medina, Y.; Mouches, P.; Sotero, R.C. A method for multiscale community detection in brain networks. bioRxiv 2019, 743732. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).