Partial Energy Transfer Model of Lamb Waves Scattering in Materially Isotropic Waveguides
Abstract
1. Introduction
2. Mode Matching Technique
2.1. General Background
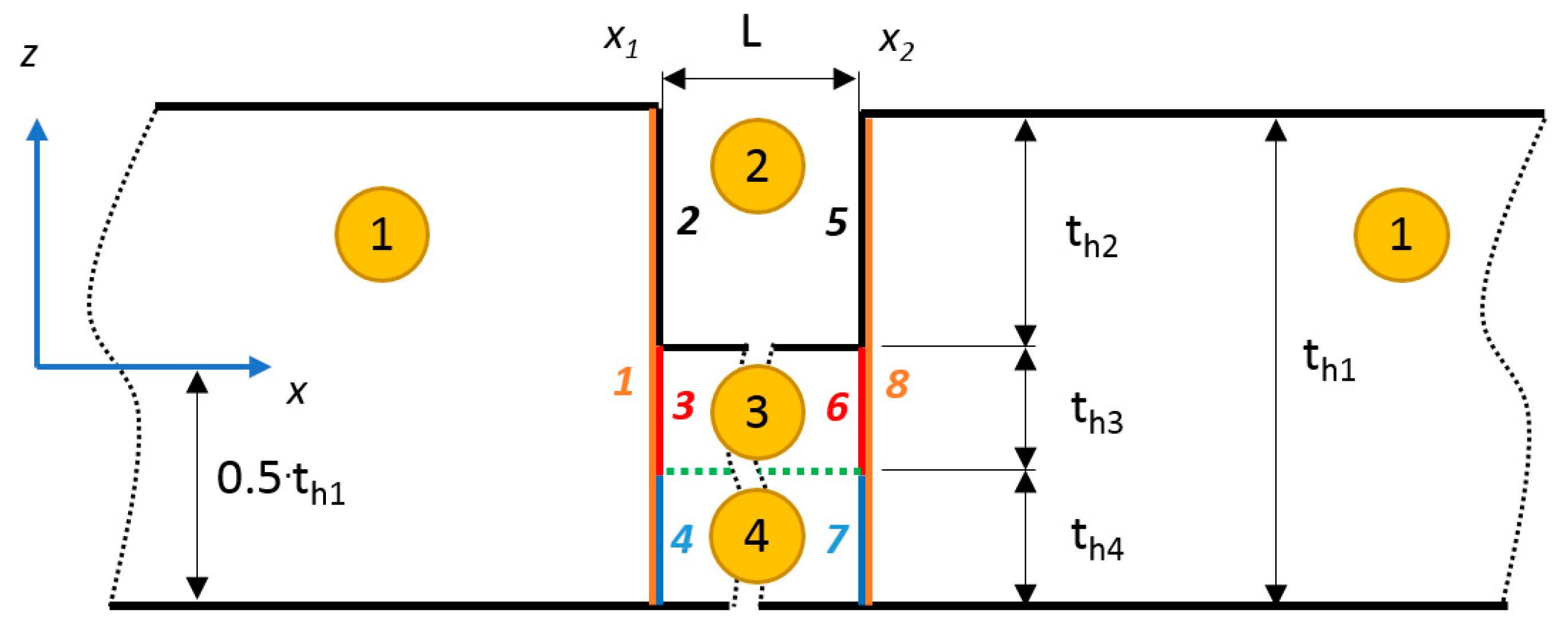
2.2. Scattering of Lamb Waves at Vertical Notch
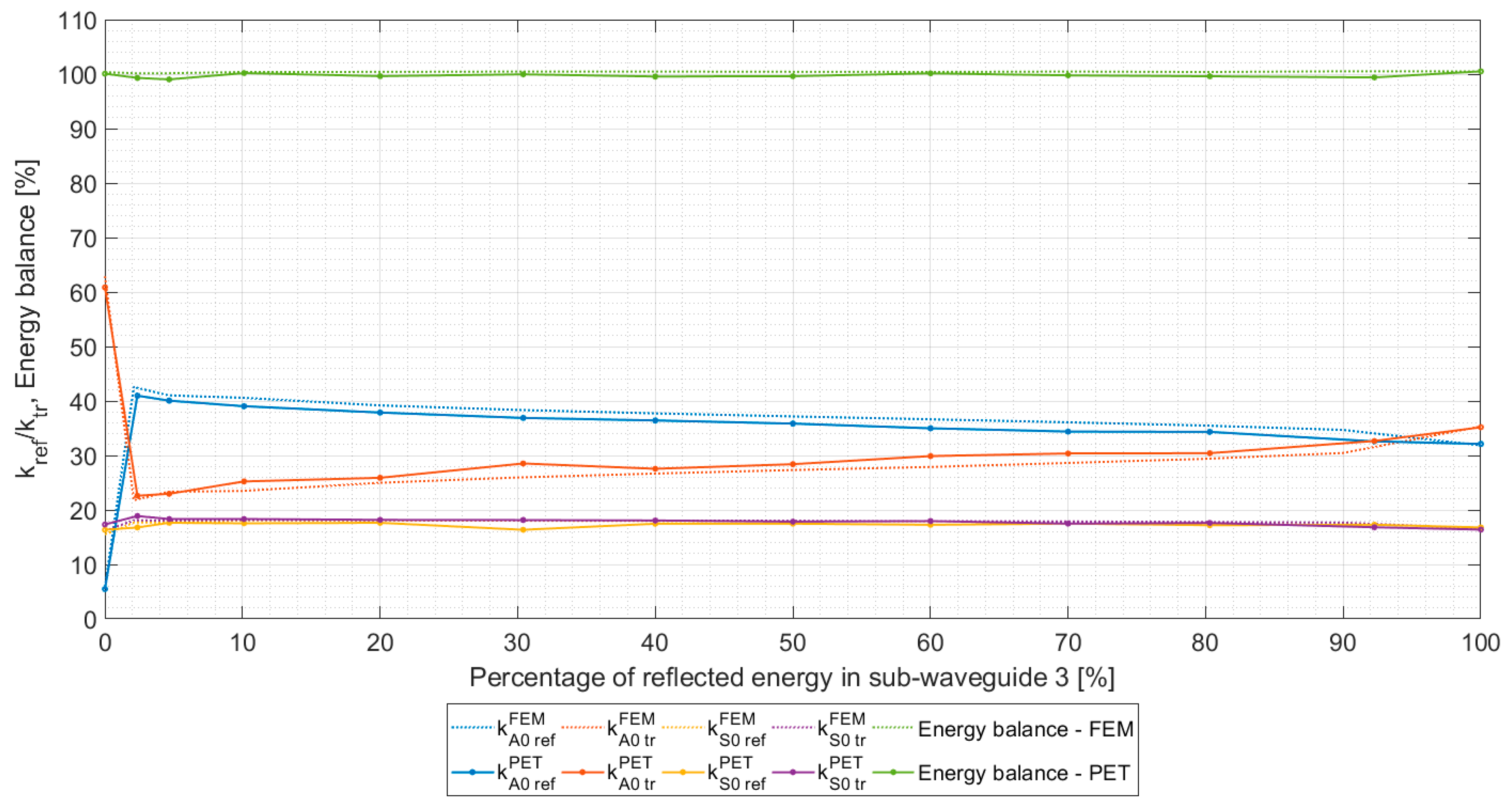
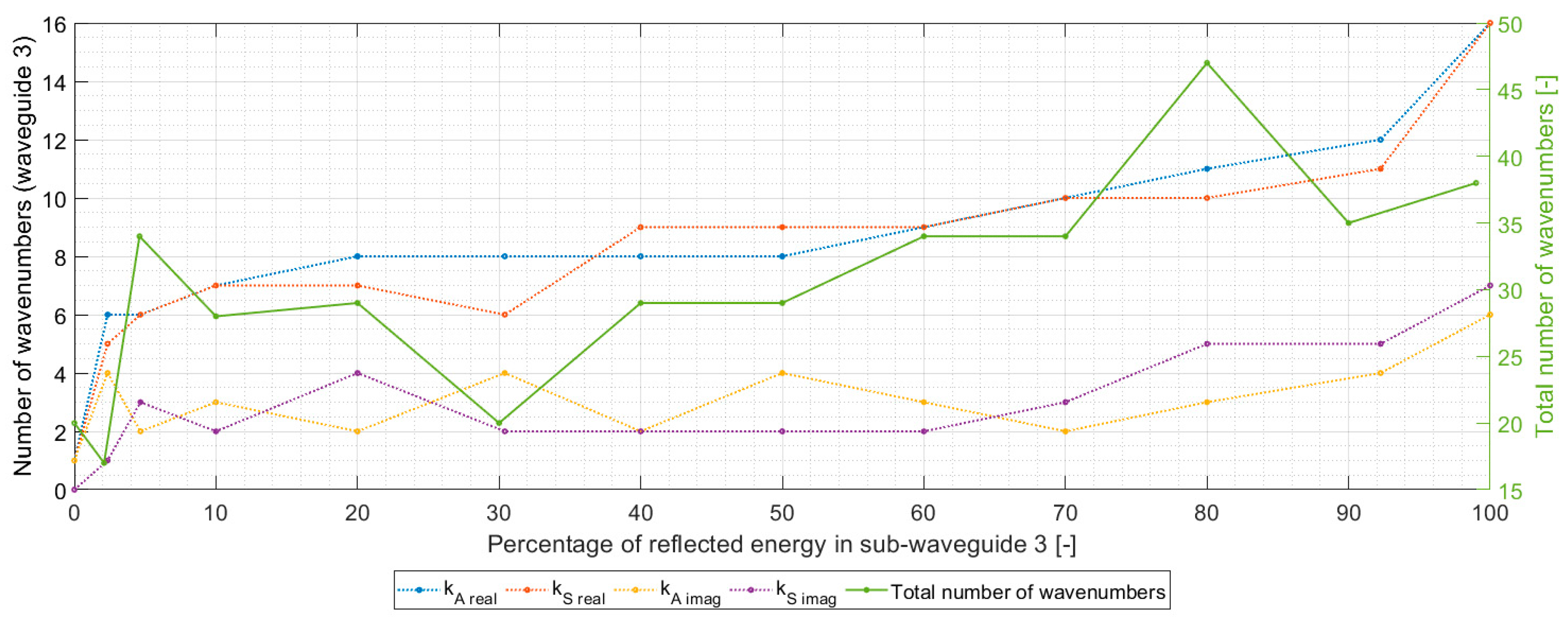
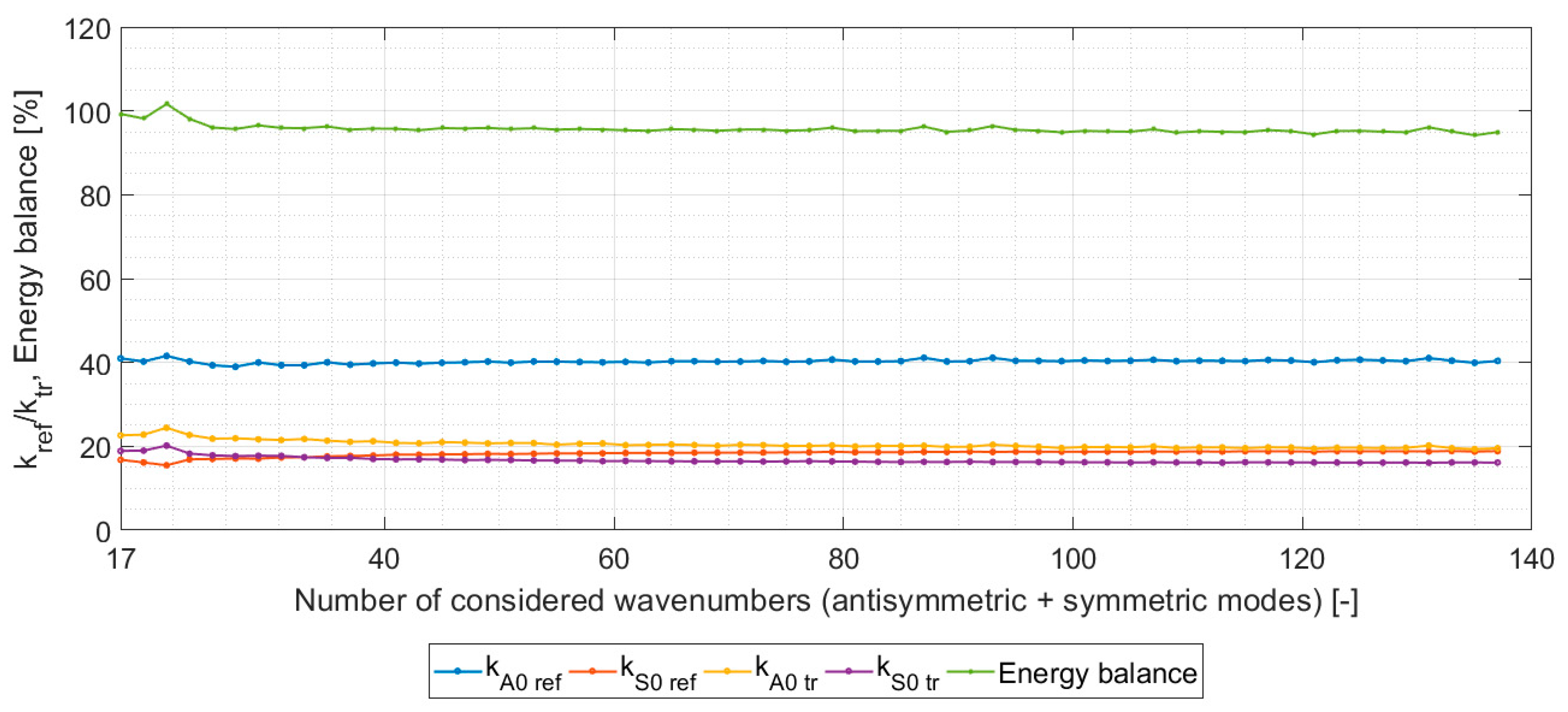
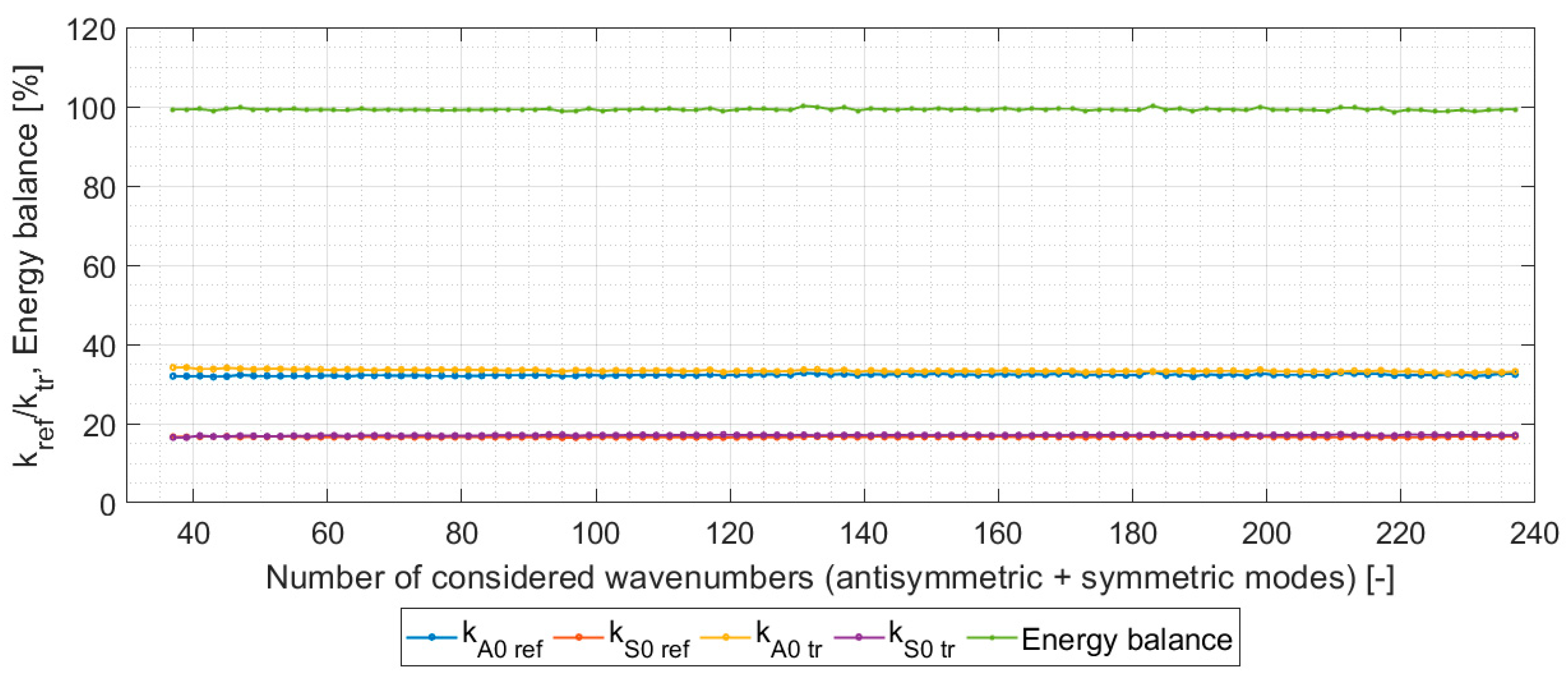
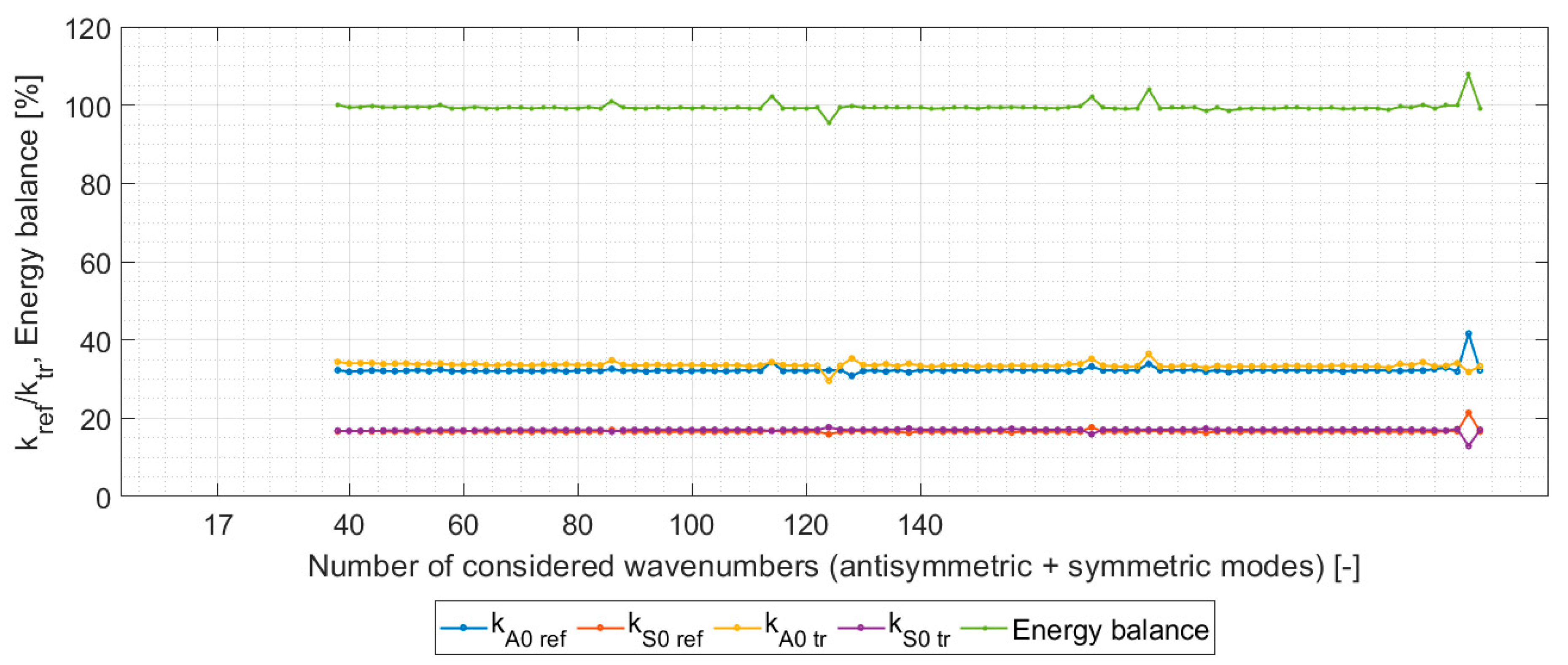
3. Numerical Verification of PET Model
4. Results and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, S.-J.; Kim, H.-W.; Joo, Y.-S. Leaky Lamb Wave Radiation from a Waveguide Plate with Finite Width. Appl. Sci. 2020, 10, 8104. [Google Scholar] [CrossRef]
- DiBiase, M.; De Marchi, L. Clusters of Shaped Ultrasonic Transducers for Lamb Waves’ DoA Estimation. Appl. Sci. 2020, 10, 8150. [Google Scholar] [CrossRef]
- Stobbe, D.M.; Grünsteidl, C.M.; Murray, T.W. Propagation and scattering of Lamb waves at conical points in plates. Sci. Rep. 2019, 9, 15216. [Google Scholar] [CrossRef] [PubMed]
- Andhale, Y.S.; Masurkar, F.; Yelve, N.P. Localization of Damages in Plain And Riveted Aluminium Specimens using Lamb Waves. Int. J. Acoust. Vib. 2019, 24, 150–165. [Google Scholar] [CrossRef]
- Mori, N.; Biwa, S. Transmission of Lamb waves and resonance at an adhesive butt joint of plates. Ultrasonics 2016, 72, 80–88. [Google Scholar] [CrossRef]
- Eremin, A.; Golub, M.; Glushkov, E.; Glushkova, N. Identification of delamination based on the Lamb wave scattering resonance frequencies. Ndt E Int. 2019, 103, 145–153. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Eremin, A.; Lammering, R. Trapped mode effects in notched plate-like structures. J. Sound Vib. 2015, 358, 142–151. [Google Scholar] [CrossRef]
- Mori, N.; Kusaka, T. Reflection and transmission characteristics of Lamb waves at an adhesive lap joint of plates. J. Acoust. Soc. Am. 2019, 145, 3075–3085. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Eremin, A.; Giurgiutiu, V. Low-cost simulation of guided wave propagation in notched plate-like structures. J. Sound Vib. 2015, 352, 80–91. [Google Scholar] [CrossRef]
- Glushkov, E.; Glushkova, N.; Golub, M.; Eremin, A. Resonance blocking and passing effects in two-dimensional elastic waveguides with obstacles. J. Acoust. Soc. Am. 2011, 130, 113–121. [Google Scholar] [CrossRef]
- Golub, M.; Shpak, A.; Mueller, I.; Fomenko, S.; Fritzen, C.-P. Lamb Wave Scattering Analysis for Interface Damage Detection between a Surface-Mounted Block and Elastic Plate. Sensors 2021, 21, 860. [Google Scholar] [CrossRef]
- Koshiba, M.; Morita, H.; Suzuki, M. Finite-element analysis of discontinuity problem of SH modes in an elastic plate waveguide. Electron. Lett. 1981, 17, 480–482. [Google Scholar] [CrossRef]
- Koshiba, M.; Karakida, S.; Suzuki, M. Finite-Element Analysis of Lamb Wave Scattering in an Elastic Plate Waveguide. IEEE Trans. Sonics Ultrason. 1984, 31, 18–24. [Google Scholar] [CrossRef]
- Moser, F.; Jacobs, L.J.; Qu, J. Modeling elastic wave propagation in waveguides with the finite element method. Ndt E Int. 1999, 32, 225–234. [Google Scholar] [CrossRef]
- Cho, Y.; Rose, J.L. An elastodynami’c hybrid boundary element study for elastic guided wave interactions with a surface breaking defect. Int. J. Solids Struct. 2000, 37, 4103–4124. [Google Scholar] [CrossRef]
- Moreau, L.; Castaings, M.; Hosten, B.; Predoi, M.V. An orthogonality relation-based technique for post-processing finite element predictions of waves scattering in solid waveguides. J. Acoust. Soc. Am. 2006, 120, 611–620. [Google Scholar] [CrossRef]
- Gunawan, A.; Hirose, S. Mode-exciting method for Lamb wave-scattering analysis. J. Acoust. Soc. Am. 2004, 115, 996–1005. [Google Scholar] [CrossRef]
- Hakoda, C.; Lissenden, C.J. Using the Partial Wave Method for Wave Structure Calculation and the Conceptual Interpretation of Elastodynamic Guided Waves. Appl. Sci. 2018, 8, 966. [Google Scholar] [CrossRef]
- Torvik, P.J. Reflection of Wave Trains in Semi-Infinite Plates. J. Acoust. Soc. Am. 1967, 41, 346–353. [Google Scholar] [CrossRef]
- Gregory, R.D.; Gladwell, I. The reflection of a symmetric Rayleigh-Lamb wave at the fixed or free edge of a plate. J. Elast. 1983, 13, 185–206. [Google Scholar] [CrossRef]
- Grahn, T. Lamb wave scattering from a circular partly through-thickness hole in a plate. Wave Motion 2003, 37, 63–80. [Google Scholar] [CrossRef]
- Moreau, L.; Caleap, M.; Velichko, A.; Wilcox, P. Scattering of guided waves by through-thickness cavities with irregular shapes. Wave Motion 2011, 48, 586–602. [Google Scholar] [CrossRef]
- Shkerdin, G.; Glorieux, C. Lamb mode conversion in a plate with a delamination. J. Acoust. Soc. Am. 2004, 116, 2089–2100. [Google Scholar] [CrossRef]
- Pagneux, V.; Maurel, A. Lamb wave propagation in inhomogeneous elastic waveguides. Proc. R. Soc. Lond. A 2002, 458, 1913–1930. [Google Scholar] [CrossRef]
- Pagneux, V.; Maurel, A. Lamb wave propagation in elastic waveguides with variable thickness. Proc. R. Soc. Lond. A 2006, 462, 1315–1339. [Google Scholar] [CrossRef]
- Fraser, W.B. Orthogonality relation for the Rayleigh–Lamb modes of vibration of a plate. J. Acoust. Soc. Am. 1976, 59, 215–216. [Google Scholar] [CrossRef]
- Feng, F.; Shen, J.; Lin, S. Scattering matrices of Lamb waves at irregular surface and void defects. Ultrasonics 2012, 52, 760–766. [Google Scholar] [CrossRef] [PubMed]
- Feng, F.; Lin, S. The band gaps of Lamb waves in a ribbed plate: A semi-analytical calculation approach. J. Sound Vib. 2014, 333, 124–131. [Google Scholar] [CrossRef]
- Feng, F.L.; Shen, J.Z.; Deng, J.J.; Wang, Q.P. Analytical Solution of Lamb Wave Scattering at Plate End. Adv. Mater. Res. 2011, 199–200, 949–952. [Google Scholar] [CrossRef]
- Feng, F.; Shen, J.; Deng, J. The scattering matrices of Lamb waves at multiple delaminations and broken laminates. Ndt E Int. 2012, 49, 64–70. [Google Scholar] [CrossRef]
- Trofimov, A.; Drach, B.; Kachanov, M.; Sevostianov, I. Effect of a partial contact between the crack faces on its contribution to overall material compliance and rezistivity. Int. J. Solids Struct. 2016, 108, 289–297. [Google Scholar] [CrossRef]
- Beghini, M.; Bertini, L.; Fontanari, V. A weight function technique for partially closed inclined edge cracks analysis. Int. J. Fract. 2001, 112, 57–68. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, R.; Wu, X. Effects of partial crack-face contact for the bending of thin shell structures. Appl. Fract. Mech. 2008, 49, 128–150. [Google Scholar] [CrossRef]
- Bowles, S.J.; Harding, C.A.; Hugo, G.R. Effect of Crack Closure on Ultrasonic Detection of Fatigue Cracks at Fastener Holes. AIP Conf. Proc. 2009, 1096, 1878–1885. [Google Scholar]
- Thompson, R.B.; Skillings, B.J.; Zachary, L.W.; Schmerr, L.W.; Buck, O. Effects of Crack Closure on Ultrasonic Transmission. Rev. Prog. Quant. Nondestruct. Eval. 1983, 2A, 325–343. [Google Scholar] [CrossRef]
- Thompson, R.B.; Fiedler, C.J. The Effects of Crack Closure on Ultrasonic Scattering Measurements. In Review of Progress in Quantitative Nondestructive Evaluation; Metzler, J.B., Ed.; Springer: Boston, MA, USA, 1984; pp. 207–215. [Google Scholar]
- Matsushita, M.; Mori, N.; Biwa, S. Transmission of Lamb waves across a partially closed crack: Numerical analysis and experiment. Ultrasonics 2019, 92, 57–67. [Google Scholar] [CrossRef]
- An, Y.-K. Measurement of crack-induced non-propagating Lamb wave modes under varying crack widths. Int. J. Solids Struct. 2015, 62, 134–143. [Google Scholar] [CrossRef]
- Lee, B.C.; Staszewski, W.J. Modelling of Lamb wave interaction with open and closed fatigue cracks for damage detection. Iop Conf. Ser. Mater. Sci. Eng. 2010, 10, 1–10. [Google Scholar] [CrossRef]
- Yamanaka, K.; Mihara, T.; Tsuji, T. Evaluation of Closed Cracks by Model Analysis of Subharmonic Ultrasound. Jpn. J. Appl. Phys. 2004, 43, 3082–3087. [Google Scholar] [CrossRef]
- Achenbach, J.D. Reciprocity in Elastodynamics, Cambridge Monographs on Mechanics; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Kirrmann, P. On the completeness of Lamb modes. J. Elast. 1995, 37, 39–69. [Google Scholar] [CrossRef]
- Šofer, M. Resonance phenomena of lamb waves scattering by a horizontal crack of finite length. J. Sound Vib. 2021, 490, 115742. [Google Scholar] [CrossRef]
- Šofer, M.; Šofer, P.; Ferfecki, P.; Molčan, M.; Stryja, J. Lamb wave mode scattering analysis on adhesively bonded single lap joint using modal decomposition method. Appl. Math. Model. 2021, 89, 413–427. [Google Scholar] [CrossRef]
- Šofer, M.; Ferfecki, P.; Šofer, P. Numerical solution of Rayleigh-Lamb frequency equation for real, imaginary and complex wavenumbers. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 157, p. 08011. [Google Scholar] [CrossRef][Green Version]
- Feng, F.; Shen, Z.; Shen, J. Scattering of obliquely incident waves by straight features in a plate. Wave Motion 2016, 60, 84–94. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šofer, P.; Šofer, M.; Raček, M.; Cekus, D.; Kwiatoń, P. Partial Energy Transfer Model of Lamb Waves Scattering in Materially Isotropic Waveguides. Appl. Sci. 2021, 11, 4508. https://doi.org/10.3390/app11104508
Šofer P, Šofer M, Raček M, Cekus D, Kwiatoń P. Partial Energy Transfer Model of Lamb Waves Scattering in Materially Isotropic Waveguides. Applied Sciences. 2021; 11(10):4508. https://doi.org/10.3390/app11104508
Chicago/Turabian StyleŠofer, Pavel, Michal Šofer, Marek Raček, Dawid Cekus, and Paweł Kwiatoń. 2021. "Partial Energy Transfer Model of Lamb Waves Scattering in Materially Isotropic Waveguides" Applied Sciences 11, no. 10: 4508. https://doi.org/10.3390/app11104508
APA StyleŠofer, P., Šofer, M., Raček, M., Cekus, D., & Kwiatoń, P. (2021). Partial Energy Transfer Model of Lamb Waves Scattering in Materially Isotropic Waveguides. Applied Sciences, 11(10), 4508. https://doi.org/10.3390/app11104508





