Roto-Translational Control of Spacecraft in Low Earth Orbit Using Environmental Forces and Torques

Abstract

In this paper, relative orbit and attitude adaptive controllers are integrated to perform roto-translational maneuvers for CubeSats equipped with a Drag Maneuvering Device (DMD). The DMD enables the host CubeSat with modulation of aerodynamic forces/torques and gravity gradient torque. Adaptive controllers for independent orbital and attitude maneuvers are revisited to account for traslational-attitude coupling while compensating for uncertainty in parameters such as atmospheric density, drag/lift coefficients, location of the Center of Mass (CoM) and inertia matrix. Uniformly ultimately bounded convergence of the attitude error and relative orbit states is guaranteed by Lyapunov-based stability analysis for the integrated roto-translational maneuver. A simulation example of an along-track formation maneuver between two CubeSats with simultaneous attitude control using only environmental forces and torques is presented to validate the controller.

1. Introduction

CubeSats have seen an increase of popularity in recent years. Born as an educational platform inside university courses [1], in the last decade they became a low-cost high reward platform to perform in-orbit technology development [2], scientific missions [3], and interplanetary exploration [4]. The increasing popularity of this kind of platform has generated interest on developing miniaturized technologies to extend their capabilities.

One of the key areas of interest is providing them with maneuverability, momentum control, and orbit adjustment. Traditionally, propulsion systems have been utilized for attitude control and for delta-V maneuvers; however, most CubeSats do not include on-board propulsion systems due to volume, mass and safety limitations. For this reason, alternative solutions are under investigation for orbital and re-entry applications, among others. One of the possible solutions is based on the concept of exploiting forces and torques that are usually considered disturbances. Similar to the idea of using the magnetic field of the Earth for attitude control; atmospheric drag can be exploited in Low Earth Orbit (LEO) by using variable shape devices to modify the experienced aerodynamic acceleration and torque.

Changes in orbital velocity enable the capability of performing maneuvers in the same orbital plane, like formation flying or rendezvous and docking, without using on-board propulsion systems. The introduction of differential drag for formation flying control dates back to 1989, when the Clohessy–Wiltshire (CW) linear equations for relative motion between two spacecraft were used to design an algorithm to control the relative in-plane motion [5]. to regulate the states with a discrete input. An improved solution based on the Schweighart–Sedwick (SS) linear equations for relative motion that include the $J_2$ perturbation were introduced in [6]. In [7], the generation and use of lift to enable out-of-plane maneuvering capability was implemented. A Lyapunov-based control strategy was used in [8] to achieve spacecraft rendezvous using differential drag. In [9], the attitude of a spacecraft was used to change the experienced drag instead of dedicated actuators for drag surfaces. An adaptive sliding mode strategy was used in [10] to control the relative dynamics using a continuous differential drag input. In [11], a constrained least squares problem is formulated to find the best achievable set of individual inputs to control a set of spacecraft consisting of multiple chasers and a single target under mutual constraints and actuator saturations. Drag-based algorithms and techniques have been successfully demonstrated in orbit by the ORBCOMM constellation of satellites [12] to save propellant in thruster-based formation keeping maneuvers, and the Planet Labs satellites constellation [13] for propellant-less phasing maneuvers along the same orbit.

Variable shape devices consisting of several independent surfaces can be installed on the spacecraft, locating the center of pressure at distances with respect to the Center of Mass (CoM) such that significant torques can be applied. This feature allows exploiting aerodynamic forces for attitude control maneuvers. In [14], a variable shape device has been used to control the attitude for an earth observation satellite mission; while in [15], an on-line parameter estimation procedure has been used to improve the performance in the presence of environmental and spacecraft uncertainties. In [16], several independent surfaces have been used to control the attitude of a spacecraft also during the re-entry phase, using a direct force control method in substitution of the classic bank angle modulation control.

Variable shape devices can also be used to de-orbit satellites from Low Earth Orbit [17]. They can also be used to perform a controlled re-entry maneuver to target a precise location on the ground [18], and be able to sustain the aero-thermodynamic loads [19] typical of a deployable capsule re-entry profile [20].

The University of Florida Advanced Autonomous Multiple Spacecraft (ADAMUS) laboratory has designed the Drag Maneuvering Device (DMD) [21]. The capabilities provided by the DMD have been previously studied for controlled re-entry, as well as independent orbital and attitude maneuvering applications. In this paper, relative orbit and attitude adaptive controllers are integrated to perform a propellant-less roto-translational maneuver involving DMD-equipped CubeSats. The capability of changing the aerodynamic torques as well as the gravity gradient torque are considered in the attitude dynamics, whereas the effect of differential drag is exploited in the spacecraft relative dynamics. The adaptive controllers compensate for uncertainties in environmental and physical parameters such as atmospheric density, drag/lift coefficients, location of the Center of Mass (CoM) and inertia matrix. Uniformly ultimately bounded convergence is obtained through Lyapunov-based stability analysis for the integrated roto-translational system.

The paper is organized as follows: Section 2 presents the translational and attitude spacecraft dynamics, Section 3 shows the individual adaptive controllers and Lyapunov-based stability result when considering attitude-orbit coupling. Section 4 and Section 5 present results from a simulation example of two-spacecraft along-orbit formation with simultaneous attitude control, and concluding remarks, respectively. The foremost contributions of this paper are:

• Design and verification through numerical simulation of an adaptive controller capable of simultaneously achieving three-axis attitude stabilization and in-plane relative maneuvering.
• Compensation for physical and environmental uncertainties such as drag/lift coefficients, atmospheric density and CoM location.
• Guaranteed ultimately bounded stability through Lyapunov-based analysis in the presence of uncertainties and perturbations.

2. Spacecraft Dynamics

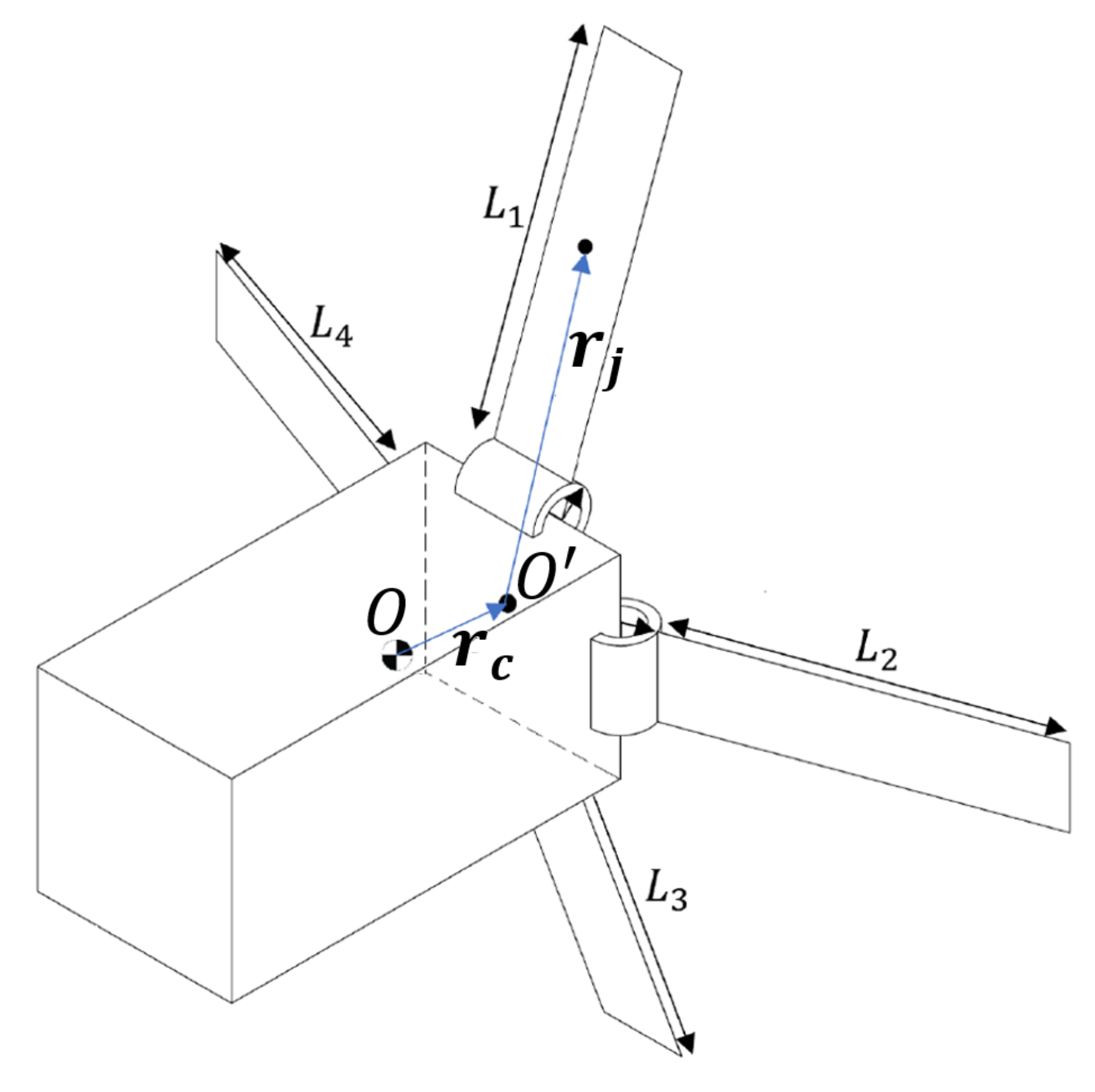
2.1. The Drag Maneuvering Device (DMD)

The DMD [21] is self-contained and can be mounted on standard CubeSats [22]. This device provides the host satellite with the capability of independently modulating four surfaces so that the experienced environmental forces and torques can be altered. Each surface is offset 90 degrees and has a fixed inclination of 20 degrees with respect to the anti-ram face of the spacecraft, see Figure 1. The DMD surfaces are rolled from 0.0762 mm tick austenitic 316 stainless steel shim stock, each surface is attached to a drum that is driven by a brushless DC motor. The width and length of the DMD surfaces are 4 cm and 3.7 m, respectively. The DMD is capable of increasing the spacecraft cross sectional area by up to 0.5 m${}^2$ as well as modifying the inertia matrix, resulting in modulation of the experienced aerodynamic forces/torques and gravity gradient torque.

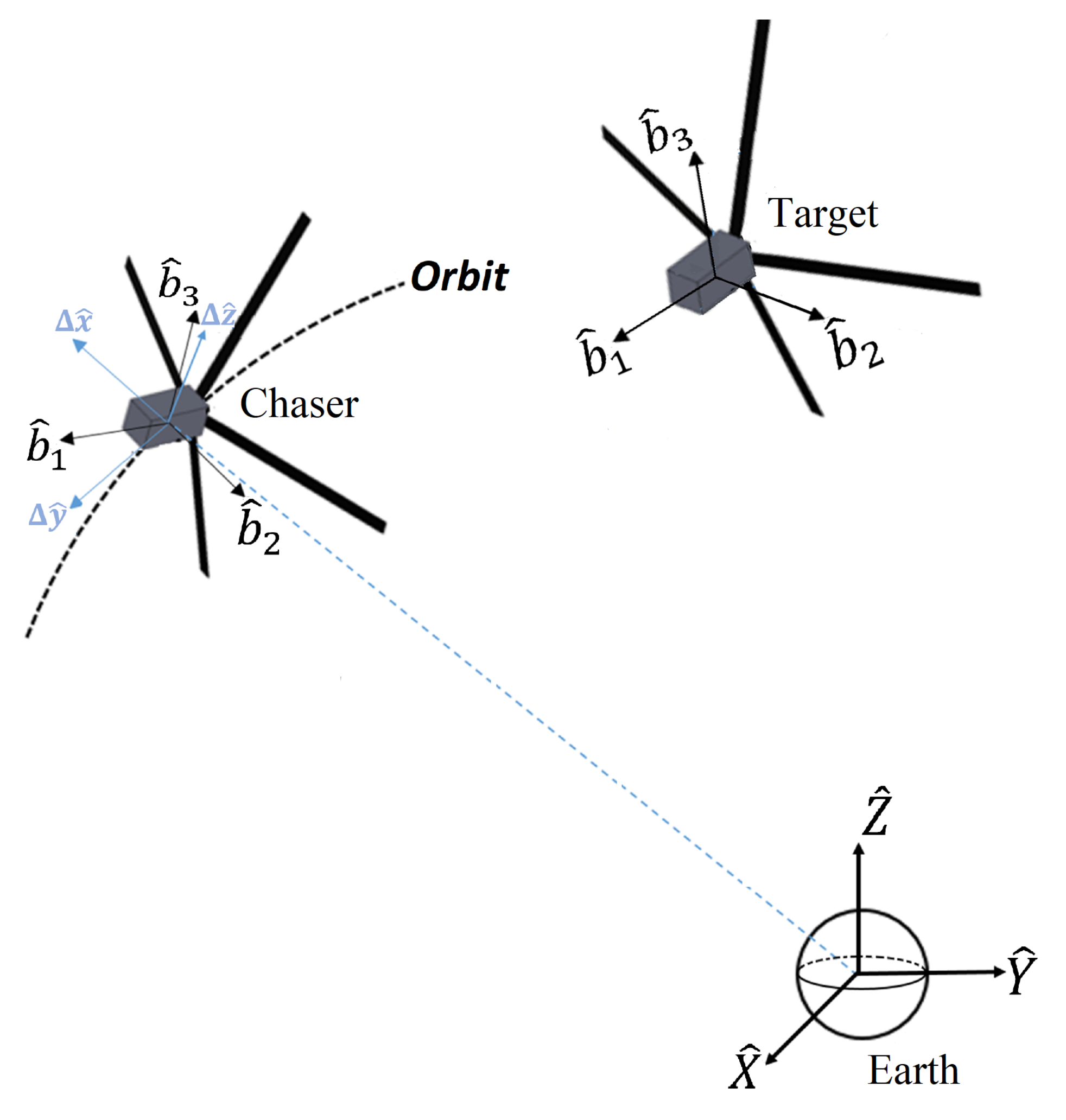
2.2. Coordinate Systems

2.2.1. Earth-Centered Inertial Reference Frame

The Earth-Centered Inertial (ECI) reference frame is centered at the CoM of the Earth, its associated coordinate system has origin at the CoM of the Earth and is denoted by the basis vectors $\left\{\widehat{\mathit{X}},\widehat{\mathit{Y}},\widehat{\mathit{Z}}\right\}$, where $\widehat{\mathit{X}}\in {\mathbb{R}}^3$ is the unit vector aligned with the vernal equinox direction, the unit vector $\widehat{\mathit{Z}}\in {\mathbb{R}}^3$ is aligned with the rotation axis of the Earth and $\widehat{\mathit{Y}}\in {\mathbb{R}}^3$ completes a right-handed Cartesian coordinate system, see Figure 2.

2.2.2. Local Vertical-Local Horizontal

The Local Vertical-Local Horizontal (LVLH) reference frame is centered at the CoM of the spacecraft, its associated coordinate system has origin at the spacecraft CoM and is denoted by the basis vectors $\left\{\mathsf{\Delta }\widehat{\mathit{x}},\mathsf{\Delta }\widehat{\mathit{y}},\mathsf{\Delta }\widehat{\mathit{z}}\right\}$, where $\mathsf{\Delta }\widehat{\mathit{x}}\in {\mathbb{R}}^3$ is the unit vector that points from the CoM of the Earth towards the origin of the coordinate system, the unit vector $\mathsf{\Delta }\widehat{\mathit{z}}\in {\mathbb{R}}^3$ is aligned with the orbit angular momentum vector and the unit vector $\mathsf{\Delta }\widehat{\mathit{y}}\in {\mathbb{R}}^3$ competes a right-handed Cartesian coordinate system, see Figure 2. These unit vectors are defined as

$$\begin{array}{cc}\hfill \mathsf{\Delta }\widehat{\mathit{x}}& \triangleq \frac{\mathit{r}}{\parallel \mathit{r}\parallel },\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \mathsf{\Delta }\widehat{\mathit{y}}& \triangleq {\mathsf{\Delta }\widehat{z}}^{\times }\mathsf{\Delta }\widehat{\mathit{x}},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill \mathsf{\Delta }\widehat{\mathit{z}}& \triangleq \frac{r^{\times }\dot{\mathit{r}}}{\parallel r^{\times }\dot{\mathit{r}}\parallel },\hfill \end{array}$$

(3)

where the vectors $\mathit{r}\triangleq {\left[xyz\right]}^T\in {\mathbb{R}}^3$ and $\dot{\mathit{r}}\in {\mathbb{R}}^3$ are the spacecraft ECI position and its time derivative, respectively. The skew symmetric matrix ${\mathit{p}}^{\times }\in {\mathbb{R}}^{3\times 3}$ for a vector $\mathit{p}\triangleq {\left[p_1{p}_2{p}_3\right]}^T\in {\mathbb{R}}^3$ is defined as

$$p^{\times }\triangleq \left[\begin{array}{ccc}0& -p_3& p_2\\ p_3& 0& -p_1\\ -p_2& p_1& 0\end{array}\right].$$

(4)

2.2.3. Body Reference Frame

The body reference frame is centered at the CoM of the spacecraft, its associated coordinate system has origin at the spacecraft CoM and is denoted by the basis vectors $\{{\widehat{\mathit{b}}}_{\mathbf{1}},{\widehat{\mathit{b}}}_{\mathbf{2}},{\widehat{\mathit{b}}}_{\mathbf{3}}\}$, where the unit vector ${\widehat{\mathit{b}}}_{\mathbf{1}}\in {\mathbb{R}}^3$ is aligned with the longitudinal axis of the spacecraft, the ${\widehat{\mathit{b}}}_{\mathbf{2}}\in {\mathbb{R}}^3$ unit vector on the nadir facing side of the spacecraft, and the ${\widehat{\mathit{b}}}_{\mathbf{3}}\in {\mathbb{R}}^3$ unit vector is selected to complete the right-handed Cartesian coordinate system, as depicted in Figure 2.

2.3. Translational Dynamics

Considering the gravitational influence of the Earth including $J_2$, which captures the largest perturbation on the orbit of the spacecraft due to the Earth’s mass distribution, and the non-gravitational influence of atmospheric drag and lift; the acceleration of a spacecraft in Low Earth Orbit (LEO) can be written in the ECI coordinate system as

$$\begin{array}{cc}\hfill \ddot{x}& \triangleq -\frac{G{M}_{\oplus }}{{\parallel \mathit{r}\parallel }^3}x+\frac{3}{2}\left(\frac{J_{2}G{M}_{\oplus }{R}_{\oplus }^2}{{\parallel \mathit{r}\parallel }^4}\right)\left(\frac{x}{\parallel \mathit{r}\parallel }\left(\frac{5z^2}{{\parallel \mathit{r}\parallel }^2}-1\right)\right)+{\ddot{r}}_{D,x}+{\ddot{r}}_{L,x},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill \ddot{y}& \triangleq -\frac{G{M}_{\oplus }}{{\parallel \mathit{r}\parallel }^3}y+\frac{3}{2}\left(\frac{J_{2}G{M}_{\oplus }{R}_{\oplus }^2}{{\parallel \mathit{r}\parallel }^4}\right)\left(\frac{y}{\parallel \mathit{r}\parallel }\left(\frac{5z^2}{{\parallel \mathit{r}\parallel }^2}-1\right)\right)+{\ddot{r}}_{D,y}+{\ddot{r}}_{L,y},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill \ddot{z}& \triangleq -\frac{G{M}_{\oplus }}{{\parallel \mathit{r}\parallel }^3}z+\frac{3}{2}\left(\frac{J_{2}G{M}_{\oplus }{R}_{\oplus }^2}{{\parallel \mathit{r}\parallel }^4}\right)\left(\frac{z}{\parallel \mathit{r}\parallel }\left(\frac{5z^2}{{\parallel \mathit{r}\parallel }^2}-3\right)\right)+{\ddot{r}}_{D,z}+{\ddot{r}}_{L,z}.\hfill \end{array}$$

(7)

In (5)–(7), $G\in \mathbb{R}$ is the universal gravitational constant, and $M_{\oplus },R_{\oplus }\in \mathbb{R}$ are the mass and radius of the Earth, respectively. Vectors ${\ddot{\mathit{r}}}_{\mathit{D}}\triangleq {\left[{\ddot{r}}_{D,x}{\ddot{r}}_{D,y}{\ddot{r}}_{D,z}\right]}^T\in {\mathbb{R}}^3$ and ${\ddot{\mathit{r}}}_{\mathit{L}}\triangleq {\left[{\ddot{r}}_{L,x}{\ddot{r}}_{L,y}{\ddot{r}}_{L,z}\right]}^T\in {\mathbb{R}}^3$ are the accelerations due to aerodynamic drag and lift expressed in the ECI coordinate system, respectively.

Assumption 1.

Each CubeSat is assumed to be in circular LEO, and the inter-spacecraft distance is small as compared with their orbit radius.

The Schweighart–Sedwick equations [23], which include influence of the $J_2$ perturbation, can be used to express the motion of a target spacecraft with respect to the LVLH frame centered at the CoM of the chaser as

$$\begin{array}{cc}\hfill \mathsf{\Delta }\ddot{x}& \triangleq 2(\mathsf{\Omega }c)\mathsf{\Delta }\dot{y}+(5c^2-2){\mathsf{\Omega }}^2\mathsf{\Delta }x+u_x,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \mathsf{\Delta }\ddot{y}& \triangleq -2(\mathsf{\Omega }c)\mathsf{\Delta }\dot{x}+u_y,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \mathsf{\Delta }\ddot{z}& \triangleq -q^2\mathsf{\Delta }z+2lqcos\left(qt+⌀\right)+u_z,\hfill \end{array}$$

(10)

where $\mathsf{\Delta }\mathit{r}\triangleq {\left[\mathsf{\Delta }x\mathsf{\Delta }y\mathsf{\Delta }z\right]}^T\in {\mathbb{R}}^3$ is the LVLH position of the target, the vector $\mathit{u}\triangleq {\left[u_x{u}_y{u}_z\right]}^T\in {\mathbb{R}}^3$ is the control input (i.e., experienced differential aerodynamic acceleration). $\mathsf{\Omega }\in \mathbb{R}$ is the constant angular velocity of the orbit of the chaser; $c\triangleq {\left(1+\frac{3J_2{R}_{\oplus }^2}{8r_{ref}^2}\left(1+3cos(2i_{ref})\right)\right)}^{1/2}\in \mathbb{R}$; $r_{ref},i_{ref}\in \mathbb{R}$ are the radius and inclination of the orbit of the chaser. Parameters $l,q,⌀\in \mathbb{R}$ in the decoupled out-of-plane component are defined in [23].

2.4. Attitude Dynamics

Using Euler’s law, the attitude dynamics of a DMD-equipped spacecraft can be expressed as

$$\dot{J}\mathit{\omega }+J\dot{\mathit{\omega }}+{\omega }^{\times }J\mathit{\omega }={\mathit{\tau }}_{\mathit{D}}+{\mathit{\tau }}_{\mathit{L}}+{\mathit{\tau }}_{\mathit{GG}}+{\mathit{\delta }}_{\mathit{a}},$$

(11)

where $\mathit{\omega }\in {\mathbb{R}}^3$ is the angular velocity of the body with respect to the ECI frame, $J\in {\mathbb{R}}^{3\times 3}$ is the inertia matrix of the spacecraft, ${\mathit{\tau }}_{\mathit{GG}},{\mathit{\tau }}_{\mathit{D}},{\mathit{\tau }}_{\mathit{L}}\in {\mathbb{R}}^3$ are the gravity gradient, aerodynamic drag and lift torques, respectively. The vector ${\mathit{\delta }}_{\mathit{a}}\in {\mathbb{R}}^3$ denotes disturbances torques.

To represent the orientation of the spacecraft with respect to the ECI frame, the quaternion $\mathit{q}\in {\mathbb{R}}^4$ is used. In the body coordinate system, $\mathit{q}$ is defined as [24]

$$\mathit{q}\triangleq {\left[q_0{\mathit{q}}_{\mathit{v}}^T\right]}^T,$$

(12)

where $q_0\in \mathbb{R}$ and ${\mathit{q}}_{\mathit{v}}\triangleq {\left[q_1{q}_2{q}_3\right]}^T\in {\mathbb{R}}^3$, and the property ${\mathit{q}}_{\mathit{v}}^T{\mathit{q}}_{\mathit{v}}+q_0^2=1$ is satisfied.

A desired attitude trajectory is specified using the desired quaternion ${\mathit{q}}_{\mathit{d}}\triangleq {\left[q_{0d}{\mathit{q}}_{\mathbf{0}\mathit{v}}^T\right]}^T\in {\mathbb{R}}^4$, and the mismatch between $\mathit{q}$ and ${\mathit{q}}_{\mathit{d}}$ is expressed using the error quaternion $\mathit{e}\triangleq {\left[e_0{\mathit{e}}_{\mathit{v}}^T\right]}^T\in {\mathbb{R}}^4$, which satisfies the property ${\mathit{e}}_{\mathit{v}}^T{\mathit{e}}_{\mathit{v}}+e_0^2=1$ and obeys the error quaternion kinematics [24]

$$\begin{array}{cc}\hfill {\dot{\mathit{e}}}_{\mathit{v}}& \triangleq \frac{1}{2}\left(e_v^{\times }+e_0{\mathcal{I}}_3\right)\tilde{\mathit{\omega }},\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\dot{e}}_0& \triangleq -\frac{1}{2}{\mathit{e}}_{\mathit{v}}^T\tilde{\mathit{\omega }}.\hfill \end{array}$$

(14)

In (13) and (14), ${\mathcal{I}}_3\in {\mathbb{R}}^{3\times 3}$ is the identity matrix, and $\tilde{\mathit{\omega }}$ denotes the error in the angular velocity of the spacecraft

$$\tilde{\mathit{\omega }}\triangleq \mathit{\omega }-\tilde{R}{\mathit{\omega }}_d,$$

(15)

where ${\mathit{\omega }}_{\mathit{d}}\in {\mathbb{R}}^3$ is the desired angular velocity with respect to the ECI frame, and $\tilde{R}\in {\mathbb{R}}^{3\times 3}$ is the rotation matrix used to express ${\mathit{\omega }}_{\mathit{d}}$ in the body coordinate system.

2.5. Aerodynamic Forces and Torques

A spacecraft in LEO experiences aerodynamic drag and lift forces due to the interaction with the atmosphere. The DMD surfaces, which are significantly larger than the faces of the CubeSat, contribute to the total aerodynamic drag and lift forces as

$$\begin{array}{cc}\hfill {\mathit{F}}_{\mathit{D},\mathit{j}}& \triangleq -\frac{\rho w_b{L}_j{C}_{D,j}}{2}{\mathit{V}}_{\perp ,\mathit{j}}^2\frac{{\mathit{V}}_{\mathit{r}}}{\parallel {\mathit{V}}_{\mathit{r}}\parallel },\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\mathit{F}}_{\mathit{L},\mathit{j}}& \triangleq -\frac{\rho w_b{L}_j{C}_{L,j}}{2}{\mathit{V}}_{\perp ,\mathit{j}}^2\left(\frac{{\mathit{V}}_{\mathit{r}}}{\parallel {\mathit{V}}_{\mathit{r}}\parallel }\times {\mathit{n}}_{\mathit{j}}\times \frac{{\mathit{V}}_{\mathit{r}}}{\parallel {\mathit{V}}_{\mathit{r}}\parallel }\right),\hfill \end{array}$$

(17)

where the subscript j indicates the jth DMD surface, $\rho \in \mathbb{R}$ is the atmospheric density, $C_{D,j},C_{L,j},w_b,L_j\in \mathbb{R}$ are the drag, lift coefficients, width and length of the jth DMD surface, respectively. The vector ${\mathit{V}}_{\mathit{r}}\in {\mathbb{R}}^3$ represents the spacecraft-atmosphere relative velocity vector, ${\mathit{n}}_{\mathit{j}}\in {\mathbb{R}}^3$ is the unit vector that represents the direction normal to the jth DMD surface and ${\mathit{V}}_{\perp ,\mathit{j}}\triangleq {\mathit{V}}_{\mathit{r}}·{\mathit{n}}_{\mathit{j}}\in \mathbb{R}$.

Assumption 2.

The spacecraft are assumed to be flying with the DMD surfaces installed on the anti-ram face. Other attitude configurations are considered beyond the scope of this paper.

The torques produced by aerodynamic drag and lift are given by

$${\mathit{\tau }}_{\mathit{k}}\triangleq \sum _{j=1}^4{R}_j^{\times }{\mathit{F}}_{\mathit{k},\mathit{j}},k=D,L,$$

(18)

where ${\mathit{R}}_{\mathit{j}}\triangleq {\mathit{r}}_{\mathit{c}}+{\mathit{r}}_{\mathit{j}}\in {\mathbb{R}}^3$, ${\mathit{r}}_{\mathit{c}}\triangleq {\left[c_1{c}_2{c}_3\right]}^T\in {\mathbb{R}}^3$ is the vector that goes from the spacecraft CoM to the geometric center of the anti-ram face of the CubeSat $(O^{\prime })$, and ${\mathit{r}}_{\mathit{j}}\in {\mathbb{R}}^3$ is the vector that goes from $O^{\prime }$ to the center of pressure of the jth DMD surface, see Figure 3.

2.6. Gravity Gradient Torque

The spacecraft experiences a gradient of gravitational forces along the body. This effect produces the gravity gradient torque, which depends on the spacecraft attitude and inertia properties and is given by [25]

$${\mathit{\tau }}_{\mathit{GG}}\triangleq \frac{3G{M}_{\oplus }}{{\parallel \mathit{r}\parallel }^5}{r}^{\times }J\mathit{r}.$$

(19)

3. Controller Design

3.1. Control Objective

The objective is to develop a control approach able to perform full control of the spacecraft exclusively using the DMD system. Uncertainties in the spacecraft physical parameters as well as in the environmental parameters are considered. Specifically, the attitude and relative orbit controllers are required to compensate for uncertainties in the atmospheric density $\rho$, the magnitude of ${\mathit{V}}_{\mathit{r}}$ opposite to the direction of motion $\mathsf{\Delta }\widehat{\mathit{y}}$, the spacecraft inertia matrix J, CoM location ${\mathit{r}}_{\mathit{c}}$, drag $C_{D,j}$ and lift $C_{L,j}$ coefficients.

Several models for estimating the atmospheric density are available; however, even the more complex ones (e.g., NRLMSISE-00 [26]) have significant level of uncertainty [27], and may be difficult to compute on-board due to the need of solar and geomagnetic indices forecasts. The use of simpler linearly parameterizable models to represent the behavior of this parameter in the short term (i.e., few days) has demonstrated to be sufficient for completing attitude and relative orbit maneuvers and even estimating the time-varying behavior of the atmospheric density online.

Assumption 3.

The atmospheric density can be modeled using linearly parameterizable models such as those proposed in [28,29,30], which can be generalized in the form

$$\rho \triangleq {\mathit{y}}_{\mathit{\rho }}{\mathsf{\Theta }}_{\mathit{\rho }}$$

(20)

where the ${\mathit{Y}}_{\mathit{\rho }}^T\in {\mathbb{R}}^n$ is a measurable regression vector containing all the known parameters and states, and the vector ${\mathsf{\Theta }}_{\rho }\in {\mathbb{R}}^n$ contains n uncertain calibration constants.

An approximate model to represent the variation of the inertia matrix J and CoM location ${\mathit{r}}_{\mathit{c}}$ can be obtained by representing the spacecraft as a collection of multiple geometric shapes. The CubeSat body can be represented as a rectangular box, while the deployed and rolled portions of the DMD surfaces can be represented as flat plates and thick walled cylinders, respectively, see Figure 3. However, such approximations introduce uncertainties in J and ${\mathit{r}}_{\mathit{c}}$, which are critical quantities to determine the applied environmental torques. In this work, the components of ${\mathit{r}}_{\mathit{c}}$ are considered uncertain and the inertia matrix is assumed partially known.

Assumption 4.

The spacecraft is capable of computing an approximate $J_m\in {\mathbb{R}}^{3\times 3}$ of its time-varying inertia matrix, provided an on-board simplified analytical model. The real inertia matrix J can be expressed as

$$J\triangleq J_m+\mathsf{\Delta }J,$$

(21)

where $\mathsf{\Delta }J\in {\mathbb{R}}^{3\times 3}$ is the mismatch between $J_m$ and J, the parameters in $\mathsf{\Delta }J,\mathsf{\Delta }\dot{J}$ and $\dot{J}$ are assumed bounded by known constants.

The differential drag acceleration is the control input considered for the relative maneuver and is defined as

$$\mathit{u}=\frac{F_D^t}{m_t}-\frac{F_D^i}{m_i},$$

(22)

where t, and i denotes the target and ith chaser, respectively. From (22), the direction of the differential drag is approximately opposite to the direction of motion $\mathsf{\Delta }\widehat{\mathit{y}}$, but not entirely, due to the rotation of the atmosphere. Therefore, for control design purposes, the differential drag is assumed to act opposite to $\mathsf{\Delta }\widehat{\mathit{y}}$ and the time-varying magnitudes of ${\mathit{V}}_{\mathit{r},\mathit{t}}$ and ${\mathit{V}}_{\mathit{r},\mathit{i}}$ are included among the uncertain parameters. The purpose for considering uncertainties in $\parallel {\mathit{V}}_{\mathit{r},\mathit{t}}\parallel$ and $\parallel {\mathit{V}}_{\mathit{r},\mathit{i}}\parallel$ is to account for the deviations of ${\mathit{V}}_{\mathit{r}}$ with respect to $\mathsf{\Delta }\widehat{\mathit{y}}$ due to the rotation of the atmosphere and winds.

Assumption 5.

The influence of differential lift and residual misalignment of ${\mathit{V}}_{\mathit{r}}$ with respect to $\mathsf{\Delta }\widehat{\mathit{y}}$ are considered to have negligible influence in the spacecraft translational dynamics.

Provided that the spacecraft is capable of measuring its orientation $\mathit{q}$ and angular rates $\mathit{\omega }$, as well as the relative states $\mathsf{\Delta }\mathit{r}$ and $\mathsf{\Delta }\dot{\mathit{r}}$, and considering that the differential drag can only affect the relative dynamics in the orbital plane, the control objectives can be established as follows

$$\tilde{R}\to {\mathcal{I}}_3\mathrm{as}t\to \infty ,$$

(23)

and

$$\parallel \mathit{X}\parallel \to 0\mathrm{as}t\to \infty ,$$

(24)

where $\mathit{X}\triangleq {\left[\mathsf{\Delta }x\mathsf{\Delta }\dot{x}\mathsf{\Delta }y\mathsf{\Delta }\dot{y}\right]}^T\in {\mathbb{R}}^4$.

3.2. Control Development

The attitude controller developed in [30] ensures ultimately bounded convergence of $\parallel \tilde{\mathit{\omega }}\parallel$ and $\parallel {\mathit{e}}_{\mathit{v}}\parallel$, which results in $\tilde{R}\to {\mathcal{I}}_3$ as $t\to \infty$. The controller compensates for uncertainties in $\rho ,C_{D,j},C_{L,j}$ and ${\mathit{r}}_{\mathit{c}}$, as well as the availability of only an approximation of the inertia matrix, namely $J_m$. The proposed control law (25) computes the torques ${\overline{\mathit{u}}}_{\mathit{d}}\in {\mathbb{R}}^3$, expressed in the body coordinate system, required for achieving attitude tracking

$${\overline{\mathit{u}}}_{\mathit{d}}\triangleq -K_1\mathit{\mu }-{\beta }_1{\mathit{e}}_{\mathit{v}},$$

(25)

where $\mathit{\mu }\triangleq \tilde{\mathit{\omega }}+\beta {\mathit{e}}_{\mathit{v}}\in {\mathbb{R}}^3$, $K_1,\beta \in {\mathbb{R}}^{3\times 3}$ are symmetric, positive-definite control gains, and ${\beta }_1\in {\mathbb{R}}_{>0}$ is a control constant. However, the desired control torques are generated by varying the DMD surfaces lengths. The relationship between the DMD lengths and the applied environmental torques can be expressed as

$$\overline{\mathit{u}}\triangleq Y_1{\widehat{\mathsf{\Theta }}}_{\mathbf{1}},$$

(26)

where $Y_1\triangleq \left[Y_{AT}\frac{3G{M}_{\oplus }}{{\parallel \mathit{r}\parallel }^5}{r}^{\times }{J}_m\mathit{r}-{\dot{J}}_m\mathit{\omega }-{\omega }^{\times }{J}_m\mathit{\omega }+J_m{\omega }^{\times }\tilde{R}{\mathit{\omega }}_{\mathit{d}}-J_m\tilde{R}{\dot{\mathit{\omega }}}_{\mathit{d}}+J_m\beta {\dot{\mathit{e}}}_{\mathit{v}}\right]\in {\mathbb{R}}^{3\times 65}$ is a measurable regression matrix, and the vector ${\widehat{\mathsf{\Theta }}}_{\mathbf{1}}\in {\mathbb{R}}^{65}$ is the estimate of ${\mathsf{\Theta }}_{\mathbf{1}}\triangleq {\left[{\mathsf{\Theta }}_{\mathit{AT}}^{T}1\right]}^T\in {\mathbb{R}}^{65}$, which contains the uncertain parameters $C_{D,j},C_{L,j},\rho$, and ${\mathit{r}}_{\mathit{c}}$. The measurable regression matrix $Y_{\mathit{A}\mathit{T}}\in {\mathbb{R}}^{3\times 64}$ and vector of uncertainties ${\mathsf{\Theta }}_{\mathit{AT}}\in {\mathbb{R}}^{64}$, associated with the aerodynamic torques, are explicitly defined in [30].

The goal is to vary the DMD surfaces lengths such that the difference between (25) and (26) is as small as possible. In order to achieve this objective, and provided the expressions inside the regression matrix $Y_1$, a numerical algorithm is used to minimize $\mathit{\chi }\triangleq \overline{\mathit{u}}-{\overline{\mathit{u}}}_{\mathit{d}}\in {\mathbb{R}}^3$ by modifying the DMD lengths $L_1,L_2,L_3$, and $L_4$. The minimization problem is formulated as

$$\underset{L_1,L_2,L_3,L_4}{min}\parallel \overline{\mathit{u}}-{\overline{\mathit{u}}}_{\mathit{d}}\parallel \mathrm{subject}\mathrm{to}\{0\le L_j\le 3.7,j=1,2,3,4,$$

(27)

and the estimates ${\widehat{\mathsf{\Theta }}}_{\mathbf{1}}$ required to compute $\overline{\mathit{u}}$ are updated by

$${\dot{\widehat{\mathsf{\Theta }}}}_{\mathbf{1}}\triangleq \mathrm{proj}\left({\Gamma }_1{Y}_1^T\mathit{\mu }\right),$$

(28)

where ${\Gamma }_1\in {\mathbb{R}}^{65\times 65}$ is a constant, positive-definite adaptation matrix, and $\mathrm{proj}(·)$ denotes the continuous projection algorithm presented in [31], which ensures that ${\widehat{\mathsf{\Theta }}}_{\mathbf{1}}$ remains within known bounds.

The relative maneuvering controller in [29], guaranteed asymptotic stability of the in-plane relative states between a chaser and the target. However, the control development assumed attitude stabilized spacecraft and the possibility of accurately computing the required DMD lengths for achieving the desired control input (i.e., cross-sectional area of the chaser $S_i\in {\mathbb{R}}_{>0}$). In the case of a roto-translational maneuver, the total cross-sectional area is a function of both the attitude states and the DMD lengths. Moreover, the DMD lengths must be computed to satisfy attitude and relative orbit requirements simultaneously.

The magnitude of the differential drag acting along $\mathsf{\Delta }\widehat{\mathit{y}}$ (i.e., $u_y$), can be expressed as

$$u_y\triangleq {\rho }_i{C}_D^i\parallel {\mathit{V}}_{\mathit{r},\mathit{i}}{\parallel }^2\frac{S_i}{2m_i}-{\rho }_t{\parallel {\mathit{V}}_{\mathit{r},\mathit{t}}\parallel }^2\frac{C_D^t{S}_t}{2m_t},$$

(29)

where i denotes the ith chaser. The expression in (29) can be linearly parameterized as

$$u_y=Y_2{\mathsf{\Theta }}_{\mathbf{2}},$$

(30)

with the regression vector ${\mathit{Y}}_{\mathbf{2}}^T\in {\mathbb{R}}^6$ and the vector of uncertain parameters ${\mathsf{\Theta }}_{\mathbf{2}}\in {\mathbb{R}}^6$ defined as

$$\begin{array}{cc}\hfill {\mathit{Y}}_{\mathbf{2}}& \triangleq \left[S_i{S}_{i}sin(\mathsf{\Omega }t)S_{i}cos(\mathsf{\Omega }t)-\frac{S_t}{2m_t}-\frac{S_t}{2m_t}sin(\mathsf{\Omega }t)-\frac{S_t}{2m^t}cos(\mathsf{\Omega }t)\right],\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\mathsf{\Theta }}_{\mathbf{2}}& \triangleq \left[\begin{array}{c}{D}_{1,i}{C}_D^i{\parallel V_{r,i}\parallel }^2\\ D_{2,i}{C}_D^i{\parallel V_{r,i}\parallel }^2\\ D_{3,i}{C}_D^i{\parallel V_{r,i}\parallel }^2\\ D_{1,i}{C}_D^t{\parallel V_{r,t}\parallel }^2\\ D_{2,i}{C}_D^t{\parallel V_{r,t}\parallel }^2\\ D_{3,i}{C}_D^t{\parallel V_{r,t}\parallel }^2\end{array}\right].\hfill \end{array}$$

(32)

In (31), the parameters $D_{1,k},D_{2,k},D_{3,k}\in \mathbb{R}$ with $k=i,t$, are uncertain constants used under Assumption 3 to calibrate the atmospheric density at the position of the ith chaser and target, respectively, see [29] for details.

The control and adaptive update laws, assuming that the target broadcasts its own area to mass ratio $S_t/m_t$ to all chasers, are proposed as

$$\begin{array}{cc}\hfill S_{d,i}& \triangleq 2m_i\left[{\left(\widehat{{\rho }_i}{\widehat{C}}_D^i\widehat{\parallel V_{r,i}{\parallel }^2}\right)}^{-1}\left(\frac{{\widehat{C}}_D^t{S}_t}{2m_t}\widehat{{\rho }_t}\widehat{\parallel V_{r,t}{\parallel }^2}-{\mathit{k}}_{\mathit{LQR}}\mathit{X}\right)\right],\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill {\dot{\widehat{\mathsf{\Theta }}}}_{\mathbf{2}}& \triangleq \mathrm{proj}\left(2{\Gamma }_2{\mathit{Y}}_{\mathbf{2}}^T{\mathit{B}}^T{P}^T\mathit{X}\right),\hfill \end{array}$$

(34)

where $\widehat{(·)}$ represents the estimate of the uncertain parameter $(·)$, ${\mathit{k}}_{\mathit{LQR}}^{\mathit{T}}\in {\mathbb{R}}^4$ is a constant control gain vector, $P\in {\mathbb{R}}^{4\times 4}$ is a symmetric positive-definite matrix, ${\Gamma }_2\in {\mathbb{R}}^{6\times 6}$ is a symmetric positive-definite adaptation gain, $\mathit{B}\triangleq {\left[0001\right]}^T\in {\mathbb{R}}^4$ and $C_D^k\triangleq {\sum }_{j=1}^4{C}_{D,j}$, with $k=t,i$.

To integrate the attitude and relative orbit controllers, the minimization problem in (27) is modified to account for relative maneuvering requirements by introducing the additional constraint of a required total cross-sectional area, which is the parameter that can be varied to modify the differential drag. The minimization problem is modified for each spacecraft as

$$\begin{array}{c}\hfill \underset{\{L_1,L_2,L_3,L_4\}}{min}\left\{W_{att}\parallel \overline{\mathit{u}}-{\overline{\mathit{u}}}_{\mathit{d}}\parallel +W_{orb}{\left(S-S_d\right)}^2\right\}\\ \hfill subjectto\{0\le L_j\le 3.7mj=1,2,3,4,\end{array}$$

(35)

where $S\in {\mathbb{R}}_{>0}$ is the total cross-sectional area of the spacecraft, and $S_d\in {\mathbb{R}}_{>0}$ is the desired cross-sectional area. Note that the parameters $\overline{\mathit{u}}$ and S depend on the spacecraft attitude and orbital states as well as the DMD lengths, while ${\overline{\mathit{u}}}_{\mathit{d}}$ and $S_d$ are computed from the corresponding adaptive control laws.

By using (35), a set of DMD lengths can be computed accounting for both control requirements; however, residual errors due to the use of a numerical algorithm must be considered in the stability analysis. In addition to the residual error, the drag coefficients of the DMD surfaces may change over time due to the spacecraft changing orientation.

Assumption 6.

The time derivative of the vector of uncertain parameters (i.e., ${\dot{\mathsf{\Theta }}}_{\mathbf{2}}$), can be bounded by a known constant.

3.3. Stability Analysis

Stability of the relative orbit and attitude subsystems when applying the adaptive control and update laws in (25), (28), (33) and (34) has been verified by Lyapunov-based stability analysis in [29,30], respectively. In this section, the requirement of performing simultaneous attitude and relative orbit maneuver is included, and the modified stability result is presented.

The attitude control law computes the required torques for achieving the attitude tracking objective, and an intermediate step where the a suitable set of DMD surfaces lengths are computed to generate such torques was proposed using a numerical algorithm to solve (27). Considering that the proposed strategy to integrate the attitude and orbit controllers is to modify the minimization problem as in (35), and that the influence of the residual mismatch $\mathit{\chi }$ between the desired and obtained torques was explicitly included, the stability proof of the attitude controller does not change. The ultimately bounded attitude tracking result is presented for completeness in Theorem 1.

Theorem 1.

Consider the spacecraft attitude dynamics governed by the non-linear system in (11). The auxiliary controller in (25) and the adaptive update law in (28) ensure uniformly ultimately bounded attitude tracking in the sense that

$$\parallel {\mathit{e}}_{\mathit{v}}\parallel \le {ϵ}_1\exp \left\{-{ϵ}_2\right\}+{ϵ}_3,$$

(36)

where ${ϵ}_1,{ϵ}_2,{ϵ}_3\in {\mathbb{R}}_{>0}$ are known bounding constants and provided that $\mathit{\eta }(0)\in \mathcal{S}$, with $\mathit{\eta }\triangleq {\left[{\mathit{e}}_{\mathit{v}}^T{\mathit{\mu }}^T\right]}^T\in {\mathbb{R}}^6$. The set $\mathcal{S}$, and the constants ${ϵ}_1,{ϵ}_2$, and ${ϵ}_3$ are explicitly defined in [30].

The relative maneuvering control law computes the required cross-sectional area required by the chaser spacecraft to achieve regulation of the in-plane relative states in $\mathit{X}$. In [29], the cross-sectional area could be computed analytically under the assumption of attitude stabilized spacecraft. For the roto-translational maneuver, variation of the drag coefficient due to time-varying attitude, and the use of (35) as an intermediate step for obtaining the total cross-sectional area must be considered.

To facilitate the stability analysis of the relative maneuvering controller accounting for the influence of a simultaneous attitude maneuver, some definitions are introduced. Let the constants ${ϵ}_4,{ϵ}_5,{ϵ}_6\in {\mathbb{R}}_{>0}$ be defined as ${ϵ}_4\triangleq \sqrt{\frac{\overline{\lambda }{\parallel \mathit{X}(0)\parallel }^2+\overline{\gamma }}{\underline{\lambda }}}$, ${ϵ}_5\triangleq \frac{{\lambda }_1}{2\overline{\lambda }}$, ${ϵ}_6\triangleq \sqrt{\frac{\overline{\gamma }-\underline{\gamma }}{\underline{\lambda }}+\frac{\overline{\lambda }{\zeta }_4}{{\lambda }_1\underline{\lambda }}}$, where ${\zeta }_4,\underline{\lambda },\overline{\lambda },\underline{\gamma },\overline{\gamma }\in {\mathbb{R}}_{>0}$ are known bounding constants.

Theorem 2.

Given the spacecraft in-plane relative dynamics in (8) and (9), the controller in (33) and the adaptive update law in (34) ensure uniformly ultimately bounded regulation of the relative state $\mathit{X}$ in the sense that

$$\parallel \mathit{X}\parallel \le {ϵ}_4\exp \left\{-{ϵ}_{5}t\right\}+{ϵ}_6.$$

(37)

Proof. 

Let V be a candidate Lyapunov function defined as

$$V(t)\triangleq {\mathit{X}}^{T}P\mathit{X}+\frac{1}{2}{\tilde{\mathsf{\Theta }}}_{\mathbf{2}}^T{\Gamma }_2^{-1}{\tilde{\mathsf{\Theta }}}_{\mathbf{2}},$$

(38)

where

$${\tilde{\mathsf{\Theta }}}_{\mathbf{2}}\triangleq {\mathsf{\Theta }}_{\mathbf{2}}-{\widehat{\mathsf{\Theta }}}_{\mathbf{2}}.$$

(39)

The candidate Lyapunov function can be bounded by

$$\underline{\lambda }{\parallel \mathit{X}\parallel }^2+\underline{\gamma }\le V(t)\le \overline{\lambda }{\parallel \mathit{X}\parallel }^2+\overline{\gamma },$$

(40)

where $\underline{\lambda },\overline{\lambda },\underline{\gamma },\overline{\gamma }\in {\mathbb{R}}_{>0}$ are known bounding constants.

Let $\dot{\mathit{X}}\triangleq A\mathit{X}+\mathit{B}{u}_y\in {\mathbb{R}}^4$ be the state space representation of (8) and (9), where $A\in {\mathbb{R}}^{4\times 4}$ is a known constant matrix. In the roto-translational maneuver, the set of DMD surfaces that simultaneously generate the required cross-sectional area and environmental torques are computed using (35), producing a residual mismatch ${\chi }_1\triangleq S_i-S_{d,i}\in \mathbb{R}$.

Assumption 7.

A numerical optimization algorithm can be used to find a suitable set of DMD surface lengths (i.e., $L_1,L_2,L_3$, and $L_4$) provided (25), (28), (33) and (34). The residual ${\chi }_1$ can be upper bounded by a constant for the entire maneuver such that $|{\chi }_1|<{\zeta }_1$.

Taking the time derivative of (38), using (39), substituting (33) and rearranging terms yields

$$\begin{array}{c}\hfill \dot{V}(t)={\mathit{X}}^T\left(P{A}^{*}+{A^{*}}^{T}P\right)+2{\mathit{X}}^{T}PB{Y}_2{\tilde{\mathsf{\Theta }}}_{\mathbf{2}}+{\mathit{X}}^{T}P\mathit{B}\frac{\left(\widehat{{\rho }_i}{\widehat{C}}_D^i\widehat{V_{r,i}^2}\right){\chi }_1}{m_i}+\\ \hfill +{\tilde{\mathsf{\Theta }}}_{\mathbf{2}}^T{\Gamma }_2^{-1}\dot{\mathsf{\Theta }}-{\tilde{\mathsf{\Theta }}}_{\mathbf{2}}^T{\Gamma }_2^{-1}{\dot{\widehat{\mathsf{\Theta }}}}_{\mathbf{2}},\end{array}$$

(41)

where $A^{*}\triangleq A-\mathit{B}{\mathit{K}}_{\mathit{LQR}}$. Since the gain ${\mathit{K}}_{LQR}$ is obtained by solving a Linear Quadratic Regulator (LQR) problem, then $A^{*}$ is Hurwitz and a symmetric positive-definite matrix $Q_1\in {\mathbb{R}}^{4\times 4}$ can be determined so that $P{A}^{*}+{A^{*}}^{T}P=-Q_1$.

Using (34) and Assumptions 6 and 7, (41) can be upper bounded as

$$\dot{V}(t)\le -{\lambda }_1{∥\mathit{X}∥}^2+{\zeta }_4,$$

(42)

where ${\lambda }_1\triangleq {\lambda }_{min}\left\{Q_1-\frac{1}{2}\right\}\in \mathbb{R}$, ${\lambda }_{min}\{·\}$ denotes the minimum eigenvalue of $\{·\}$, ${\zeta }_4\triangleq {\zeta }_2+\frac{{\zeta }_3^2}{2}\in {\mathbb{R}}_{>0}$, and Young’s inequality as well as the upper bounds ${\tilde{\mathsf{\Theta }}}_2^T{\Gamma }_2^{-1}{\dot{\mathsf{\Theta }}}_{\mathbf{2}}\le {\zeta }_2$ and $∥P\mathit{B}\left(\left(\widehat{{\rho }_i}{\widehat{C}}_D^i\widehat{V_{r,i}^2}\right){\chi }_1/m_i\right)∥\le {\zeta }_3$ were used.

Provided that the control gains are selected such that ${\lambda }_1>0$ and using (40), then (42) can be rewritten as

$$\dot{V}\le -\frac{{\lambda }_1}{\overline{\lambda }}V(t)+\frac{{\lambda }_1\overline{\gamma }}{\overline{\lambda }}+{\zeta }_4.$$

(43)

By invoking the Comparison Lemma from [32], the solution to (43) can be obtained as

$$V\le V(0)\exp \left\{-\frac{{\lambda }_1}{\overline{\lambda }}t\right\}+\frac{\overline{\lambda }}{{\lambda }_1}\left(\frac{{\lambda }_1\overline{\gamma }}{\overline{\lambda }}+{\zeta }_4\right)\left(1-\exp \left\{-\frac{{\lambda }_1}{\overline{\lambda }}t\right\}\right).$$

(44)

From (38), (40) and (44), then $\mathit{X}\in {\mathcal{L}}_{\infty }$. Since $\widehat{\mathsf{\Theta }}\in {\mathcal{L}}_{\infty }$ by (34), then $S_{d,i}\in {\mathcal{L}}_{\infty }$; therefore, $S_i\in {\mathcal{L}}_{\infty }$ from Assumption 7. Using (44) and (40) yields

$${\parallel \mathit{X}\parallel }^2\le \left(\frac{\overline{\lambda }{\parallel \mathit{X}(0)\parallel }^2+\overline{\gamma }}{\underline{\lambda }}\right)\exp \left\{-\frac{{\lambda }_1}{\overline{\lambda }}t\right\}+\left(\frac{\overline{\gamma }-\underline{\gamma }}{\underline{\lambda }}+\frac{\overline{\lambda }{\zeta }_4}{{\lambda }_1\underline{\lambda }}\right).$$

(45)

From (45) the result in (37) can be directly obtained. □

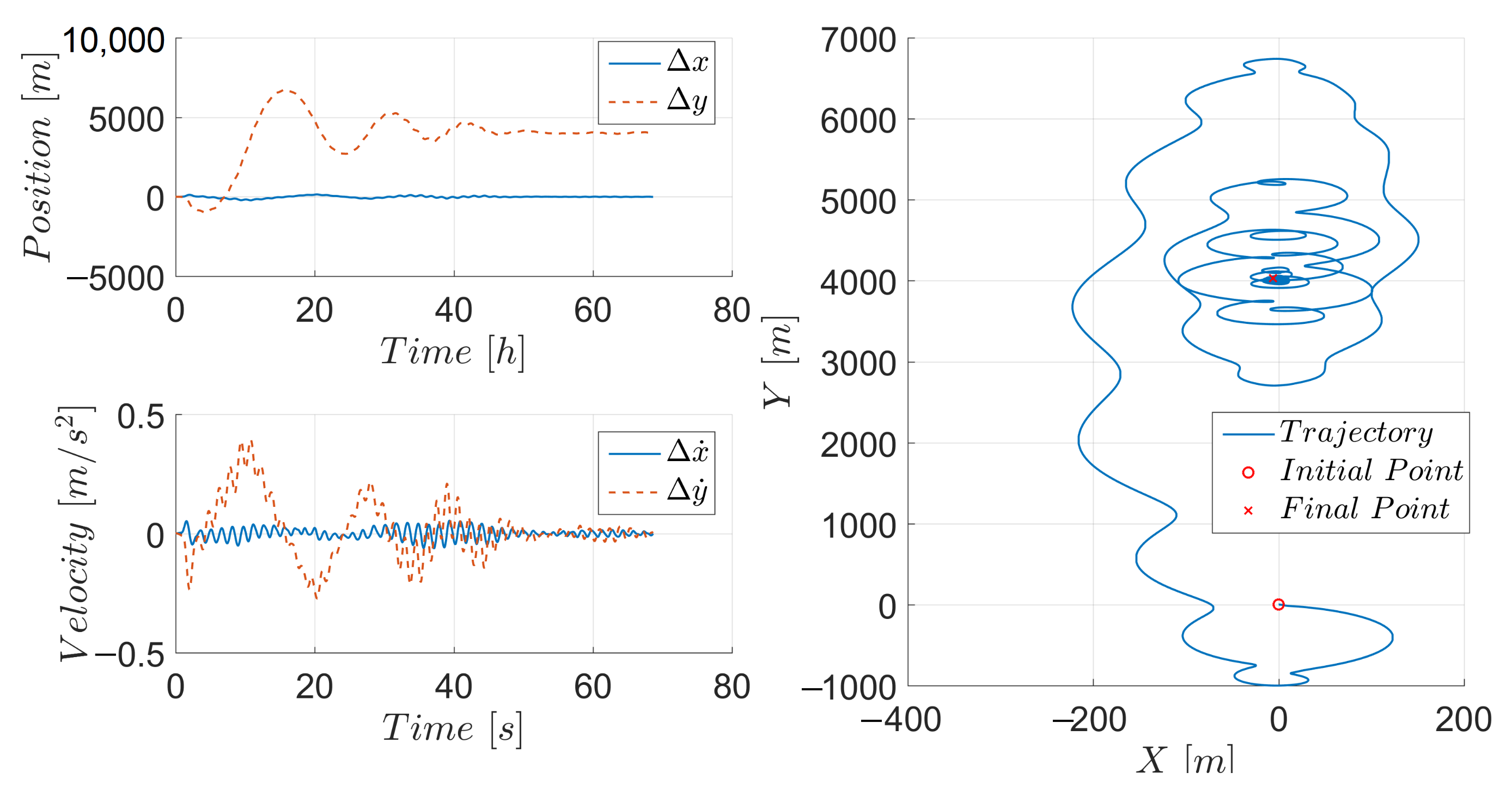
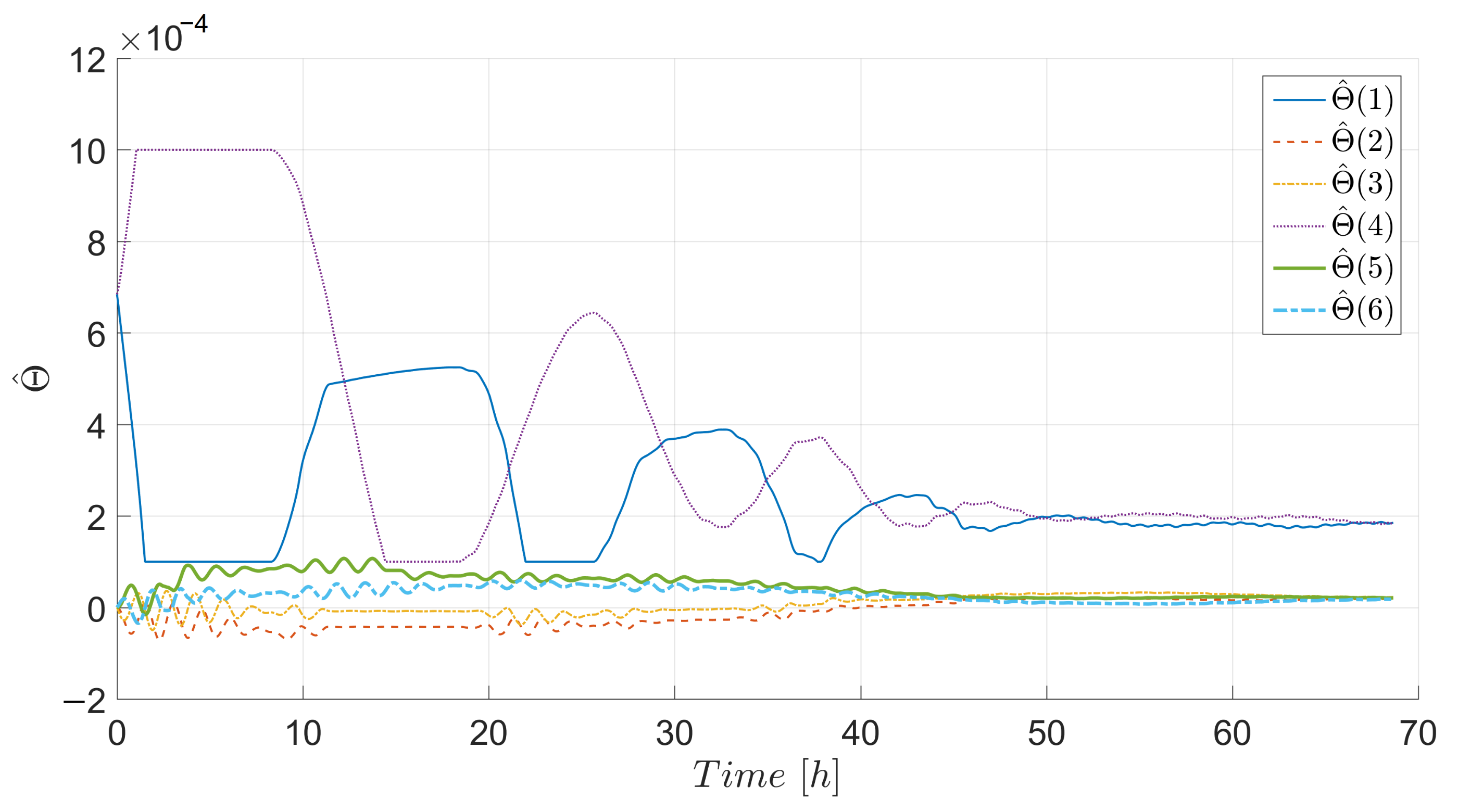
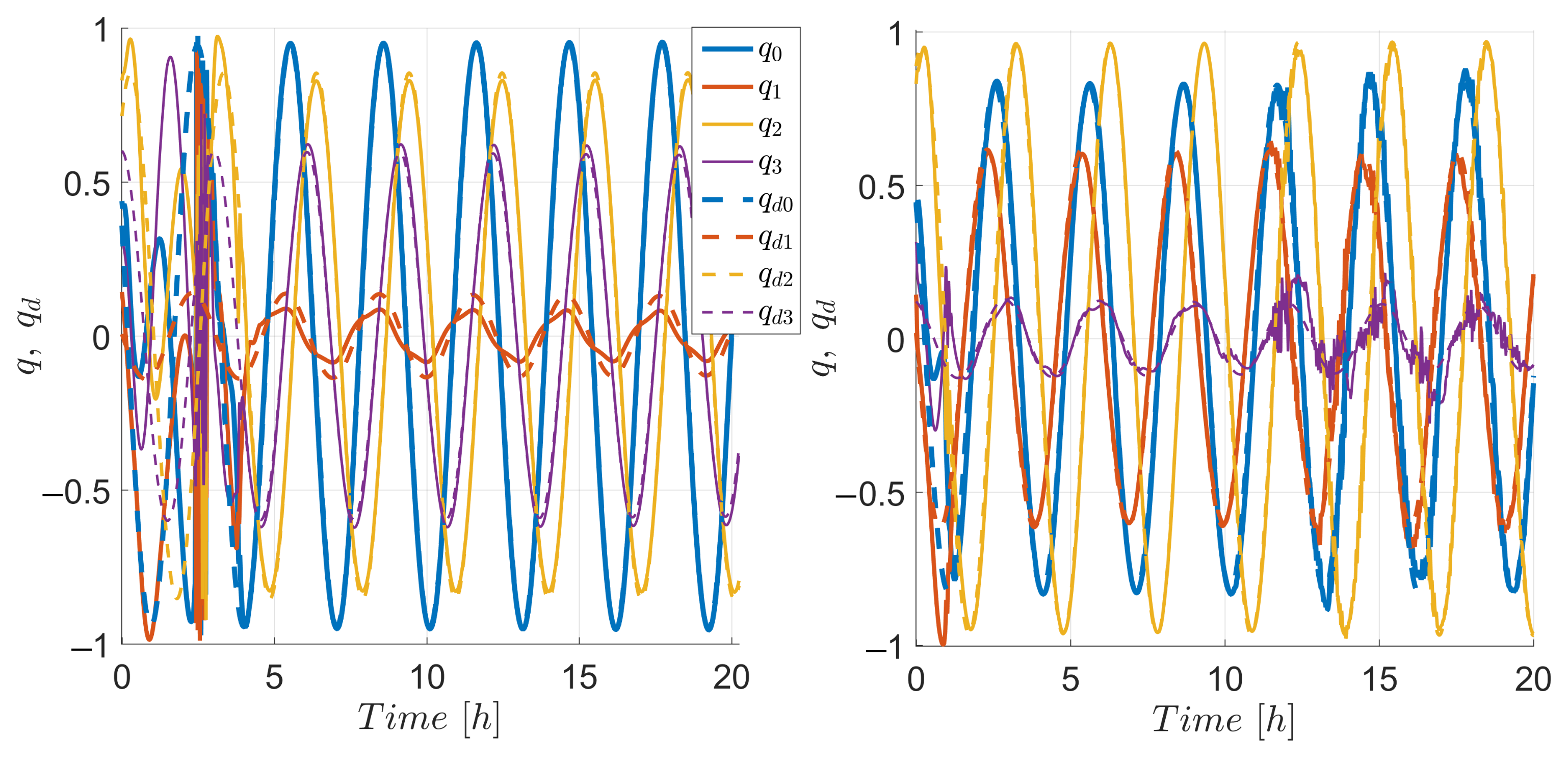
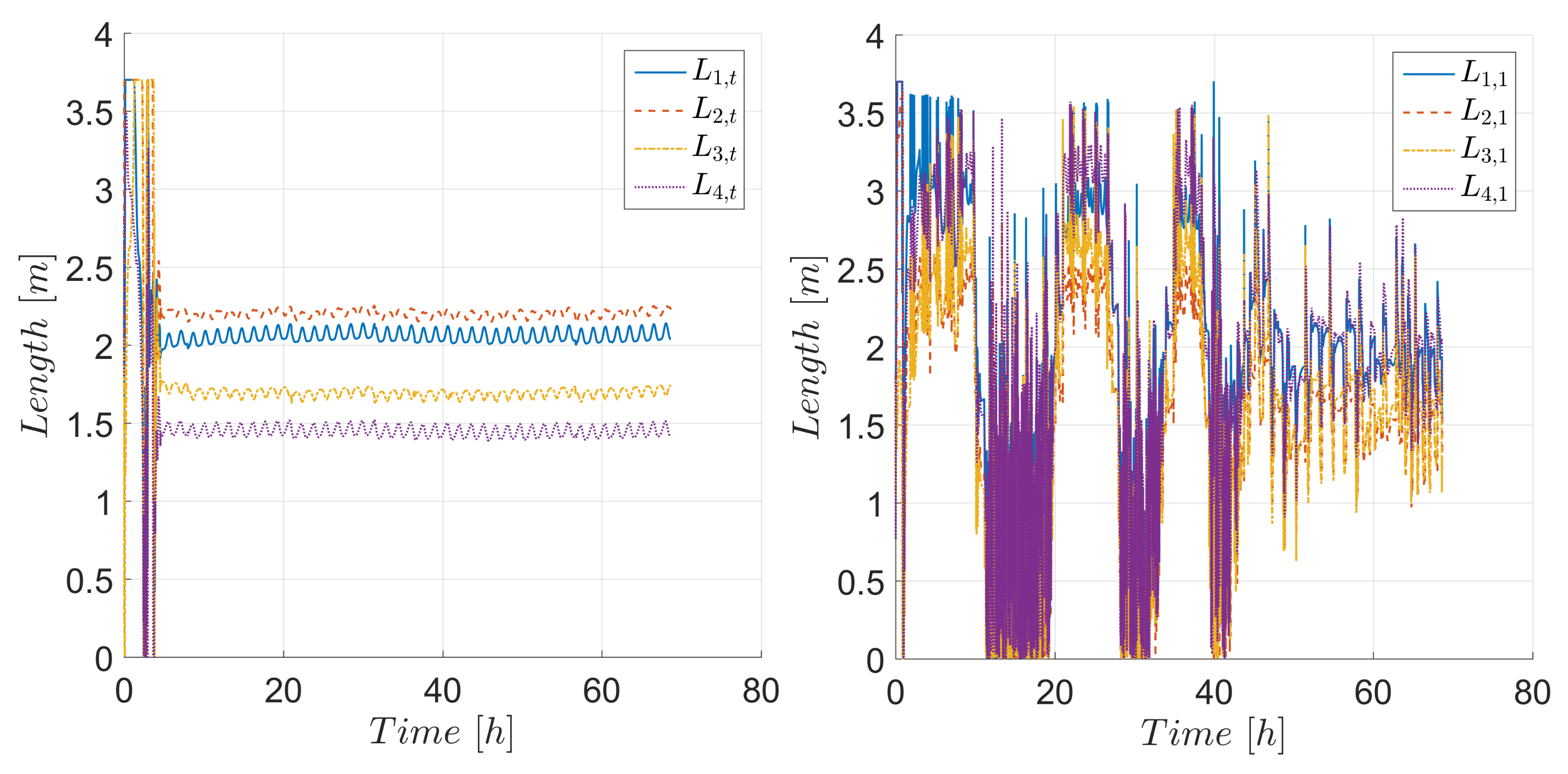
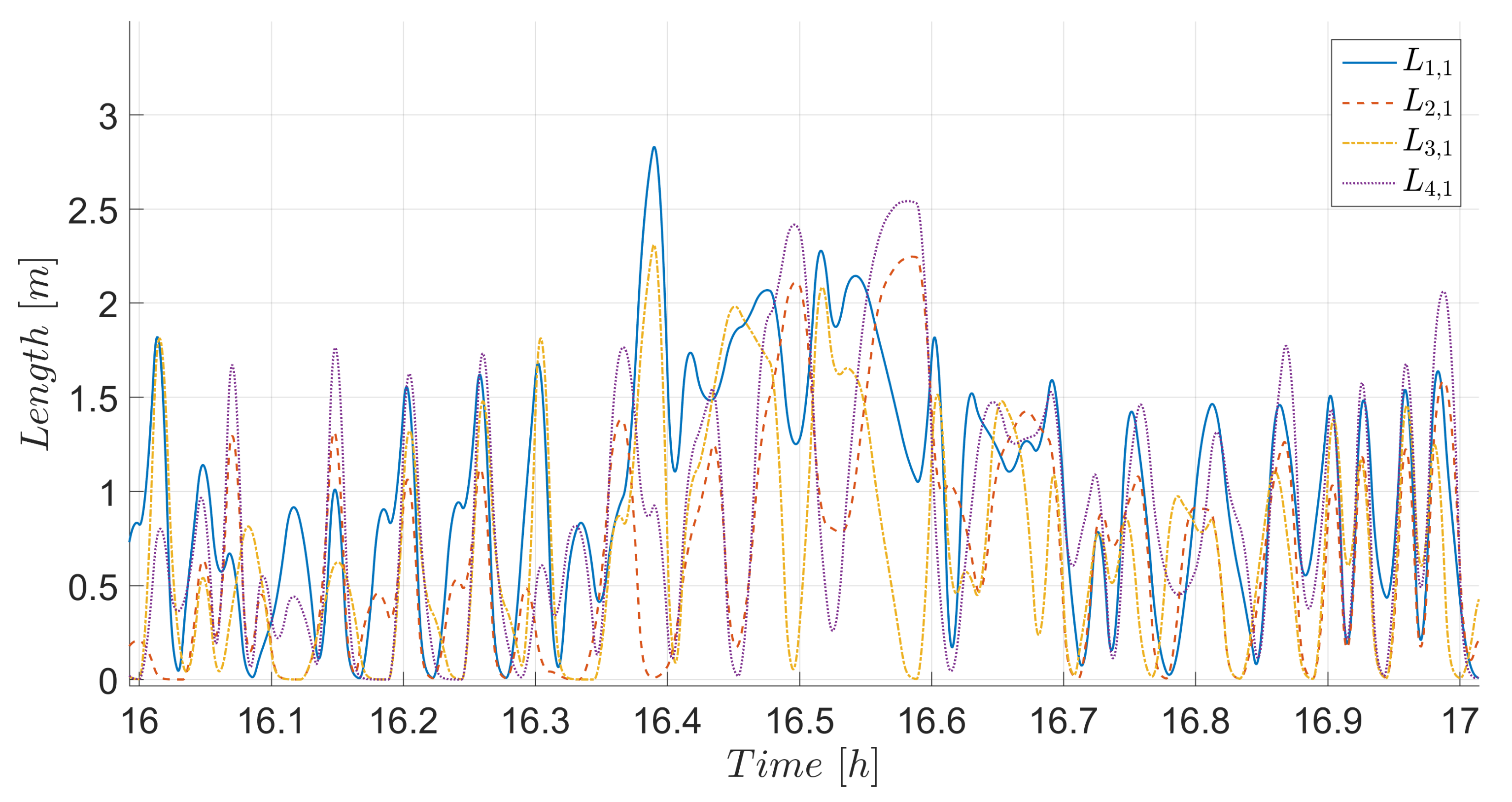
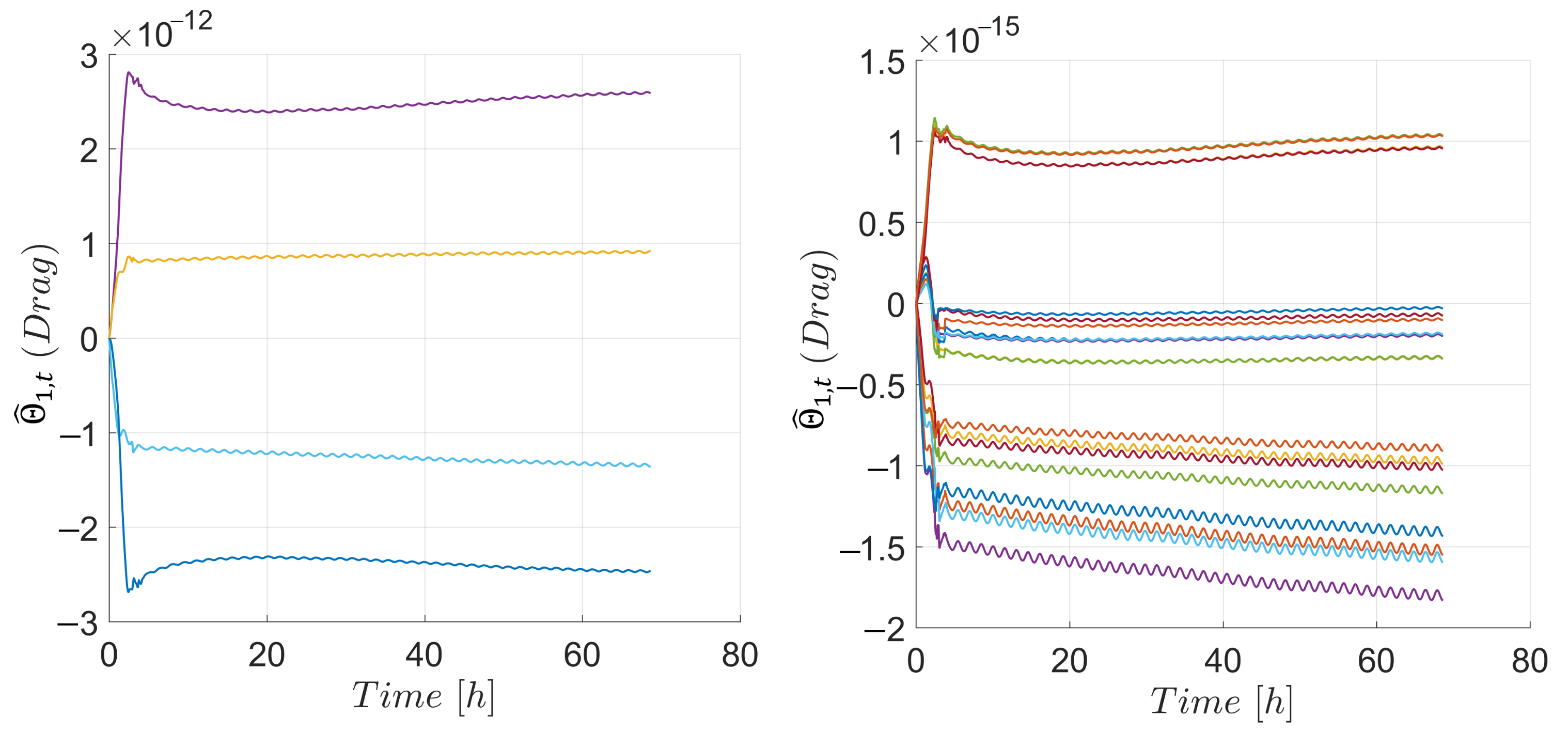
4. Simulation Results and Discussion

The simulation scenario for this maneuver considered a set of two identical DMD-equipped CubeSats (i.e., one chaser and one target) with their physical parameters shown in

Table 1. Spacecraft physical parameters, subscripts 1 and t denote chaser 1 and target, respectively.

${\mathit{S}}_{\mathit{t}},{\mathit{S}}_1$ [m${}^2$]	${\mathit{m}}_{\mathit{t}},{\mathit{m}}_1$ [kg]	${\mathit{S}}_{\mathit{t},\mathit{max}},{\mathit{S}}_{1,\mathit{max}}$ [m${}^2$]	${\mathit{S}}_{\mathit{t},\mathit{min}},{\mathit{S}}_{1,\mathit{min}}$ [m${}^2$]
0.2	3	0.5	0.01

. The translational states were propagated for each spacecraft independently using Equations (5)–(7) and transforming to the LVLH relative states to compute (35) and (36). The atmospheric density used for attitude and orbit propagation, and considered unknown for the controllers, was obtained by using the NRLMSISE-00 model. The nonlinear attitude dynamics (i.e., Equation (12)) were simultaneously propagated and coupling with the translational dynamics was explicitly included in the computation of the attitude-dependent cross-sectional area, and the analytical models for the drag and lift coefficients [33].

The spacecraft were required to perform a phasing maneuver while controlling their attitude to achieve the desired orientation. The desired orientation (i.e., ${\mathit{q}}_{\mathit{d}}$ and ${\mathit{\omega }}_{\mathit{d}}$) was computed to be equivalent to a regulation maneuver with respect to the LVLH frame. For visualization purposes, the initial and desired orientations were expressed in 3-2-1 Euler angle representation with respect to the LVLH frame and are shown in

Table 2. Initial Euler angles and angle rates for the roto-translational maneuver, subscript $k=1,t$ denotes chaser 1 and target, respectively.

Parameter	Value
${\varphi }_{0,k}$ [deg]	13.5
${\theta }_{0,k}$ [deg]	−12
${\psi }_{0,k}$ [deg]	10
${\dot{\varphi }}_{0,k}$ [deg/s]	$5\times {10}^{-3}$
${\dot{\theta }}_{0,k}$ [deg/s]	$-1.5\times {10}^{-2}$
${\dot{\psi }}_{0,k}$ [deg/s]	$1.8\times {10}^{-2}$

and

Table 3. Desired Euler angles and angle rates for the roto-translational maneuver, subscripts 1 and t denote chaser 1 and target, respectively.

Parameter	Value
${\varphi }_{0,t}$ [deg]	−25
${\theta }_{0,t}$ [deg]	0
${\psi }_{0,t}$ [deg]	15
${\varphi }_{0,1}$ [deg]	30
${\theta }_{0,1}$ [deg]	0
${\psi }_{0,1}$ [deg]	−10

for both spacecraft, where $\varphi ,\theta ,\psi \in \mathbb{R}$ are rotations with respect to $\mathsf{\Delta }\widehat{\mathit{y}},\mathsf{\Delta }\widehat{\mathit{z}}$ and $\mathsf{\Delta }\widehat{\mathit{x}}$, respectively. The initial orbit was identical for both spacecraft and its orbital elements are shown in

Table 4. Initial orbital parameters for the roto-translational maneuver.

Parameter	Value
Semi-Major Axis [km]	6778
Eccentricity	0
Inclination [deg]	51.94
RAAN [deg]	206.26
Arg. of perigee [deg]	201.07
True Anomaly [deg]	108.08

. The objective for the relative controller was to perform an along-orbit formation maneuver where the desired inter-spacecraft separation was 4 km. To achieve the along-orbit maneuver, a modified reference frame that had a position offset with respect to the LVLH with origin at the CoM of the chaser spacecraft is considered. A desired user-defined along-orbit distance $\mathsf{\Delta }d\in \mathbb{R}$ was specified, which can be expressed as an offset in true anomaly $\mathsf{\Delta }\nu \in \mathbb{R}$ with respect to that of the chaser spacecraft as

$$\mathsf{\Delta }\nu \triangleq \frac{\mathsf{\Delta }d}{a},$$

(46)

where $a\in {\mathbb{R}}_{>0}$ is the true anomaly of chaser’s orbit, then the orbital elements for the origin of the new reference frame are the same as those of the chaser but adding $\mathsf{\Delta }\nu$ to the true anomaly and the control objective remains to regulate $\mathit{X}$ to zero.

The control and adaptation laws in (27), (30), (35) and (36) could be computed every time step by each spacecraft since they did not require any iterative algorithm. The function minimization problem in (37) was solved every 30 s by each spacecraft to produce a new set of DMD lengths that considered the required total cross-sectional areas and environmental torques. This update rate for the DMD lengths could be reduced; however, 30 s provided a practical balance between the transient response and the computational demands. In the numerical simulation, the function minimization algorithm was implemented using the fmincon command in MATLAB and the average time required to obtain a solution was 0.3152 s using a Windows laptop, 2.7 GHz quad core Intel Core i7 processor, and 16 GB RAM. Since the relative maneuvering control law computed the cross-sectional required by the chaser, the target spacecraft was tasked with the only objective of attitude control and to broadcast its ECI states and cross-sectional area. The control gains are presented in

Table 5. Control parameters for the roto-translational maneuver.

Parameter	Value
$W_{att}$	1
$W_{orb}$	$5\times {10}^{-5}(1-\overline{\alpha })$
$K_1(\times {10}^{-3})$	$\mathrm{diag}(3,3,3)$
$\beta (\times {10}^{-3})$	$\mathrm{diag}(1.5,5,5)$
${\beta }_1(\times {10}^{-6})$	3.2
${\Gamma }_2$	$\mathrm{diag}({\Gamma }_b,{\Gamma }_b,{\Gamma }_b,{\Gamma }_b,6{\Gamma }_b,6{\Gamma }_b,{\Gamma }_a,{\Gamma }_a,{10}^{-20})$
${\Gamma }_a(\times {10}^{-19})$	$\mathrm{diag}(1,{10}^{11},1,{10}^{11},1,{10}^{11},1,{10}^{11})$
${\Gamma }_b(\times {10}^{-22})$	$\mathrm{diag}(2,2^{11},2,2^{11},2,2^{11},2,2^{11},2,2^{11})$
Q	$\mathrm{diag}(180,1,1.8,1)$
R $(\times {10}^{-16})$	6
${\Gamma }_1(\times {10}^{-20})$	$\mathrm{diag}(45,15,15,45,15,15)$

along with the weights $W_{att}$ and $W_{orb}$, where $\overline{\alpha }\in {\mathbb{R}}_{>0}$ is defined as

$$\overline{\alpha }\triangleq \{\begin{array}{cc}\frac{10}{3}\parallel {\mathit{e}}_{\mathit{v}}\parallel ,& \frac{10}{3}\parallel {\mathit{e}}_{\mathit{v}}\parallel \le 1,\\ 1,& \frac{10}{3}\parallel {\mathit{e}}_{\mathit{v}}\parallel >1\end{array}.$$

(47)

Figure 4 presents the relative states of the target expressed in the LVLH frame with origin at the CoM of the chaser spacecraft. In this simulation, the chaser required approximately 55 h to enter the ultimate bounds of $\pm 10$ and $\pm 60$ meters along the directions $\mathsf{\Delta }\widehat{\mathit{X}}$ and $\mathsf{\Delta }\widehat{\mathit{y}}$, respectively, as compared to the convergence to a circle of 10 m radius around the desired position obtained with the individual, decoupled counterpart in [29]. The resulting residual error was expected due to the ultimately bounded stability result obtained in the coupled attitude-orbit case. The uncertain parameters for the relative maneuvering controller are presented in Figure 5, where dynamic variation of the estimates to compensate for the uncertainties can be observed.

Figure 6 shows the actual and desired quaternion and Figure 7 presents the actual and desired angular velocities. Note that although the required orientation was fixed with respect to LVLH, the desired ${\mathit{q}}_{\mathit{d}}$ was time-varying and ${\mathit{\omega }}_{\mathit{d}}$ was different from zero; therefore, the controller was really performing a tracking maneuver.Figure 8 shows the resulting orientations in Euler angle representation for the target and chaser. Although the orientation of both spacecraft had the same initial conditions, and the control parameters were also the same, the resulting orientation had different transients and ultimate bounds. This behavior can be explained by the fact that the chaser spacecraft was the only one in charge of satisfying the required cross-sectional area for the relative orbit maneuver. The only goal of the target was to regulate its attitude and to broadcast its cross-sectional area and ECI states to the chaser so that it could compute (33). While the target required 4.8 h to enter the ultimate bounds of $\pm 2,\pm 3$ and $\pm 2$ degrees of error in roll, pitch and yaw, respectively, the chaser required 43 h to enter the ultimate bounds of $\pm 2,\pm 6.5$ and $\pm 5.5$ degrees of error in roll, pitch and yaw, respectively. The resulting ultimate bounds showed an increase with respect to the individual, decoupled counterpart in [30] of $\pm 3,\pm 1.5$ and $\pm 3$ in roll, pitch and yaw, respectively. The observed increase was expected due to the additional requirement of achieving a specific cross-sectional areas for the relative orbit maneuver.

The required control inputs are presented in Figure 9 for the target and chaser. Saturation due to the physical limitations of the DMD lengths was applied in the simulation. The DMD lengths reach saturation levels at the beginning of the maneuver where compensation for the initially large errors was required. Significant differences in the DMD length profiles could be observed between target and chaser. The chaser spacecraft required changing the total cross-sectional and simultaneously generate the required torques using only the DMD surfaces, which can be observed in Figure 9. The DMD surfaces, in the case of the chaser spacecraft, were significantly more active than those of the target. This behavior was especially noticeable when the requirements of the relative orbit controller were demanding (i.e., required cross-sectional area at or near saturation levels), the changes between maximum and minimum area could be observed during the first 40 h. To avoid instantaneous and fast changes of the DMD lengths due to the 30 s interval between computations, the points were joined with splines and passed through a low-pass filter with cut-off frequency ${\omega }_c\in {\mathbb{R}}_{>0}$ of 0.017 Hz. The maximum resulting deployment rate required from an actuator during the peak of control demand was 2.5 m per minute, as illustrated in Figure 10.

The parameter estimates for the attitude controller of the target are presented in Figure 11 the parameters associated with the aerodynamic drag, and Figure 12 those associated with the aerodynamic lift, respectively. Similarly, in the case of the chaser, Figure 13 shows the estimated parameters associated with aerodynamic drag and Figure 14 presents those associated with aerodynamic lift, respectively. The estimates were adjusted by the adaptive update law to compensate for the uncertainties. Some estimates exhibited a diverging trend as compared to others, this behavior can be explained by the fact that the ultimately bounded results obtained from both controllers ensured convergence of the states but not necessarily of the estimates. Inside the ultimate bound, an increase of the Lyapunov function could indicate that the norm of the estimates was increasing, generating the behavior observed in some estimates. Although this behavior did not affect the stability result, in case the estimates kept growing, the continuous projection algorithm used in the adaptive update laws would keep them bounded. However, during the 70 h of simulation, these bounds were never reached.

To evaluate the influence that the applied inputs may have on the flexible DMD surfaces, the first natural frequencies of a fully deployed DMD surface, modeled as a catilevered beam, were computed using SolidWorks and are presented in

Table 6. First natural frequencies of a fully deployed DMD surface.

Freq. Mode 1	Freq. Mode 2	Freq. Mode 3	Freq. Mode 4	Freq. Mode 5
0.1396 Hz	0.1624 Hz	0.2310 Hz	0.4040 Hz	0.6597Hz

. Since the attitude dynamics were faster than the translational dynamics, the Fast Fourier Transform (FFT) of the applied torques were computed for both spacecraft and are presented in Figure 15. The range of frequencies of the applied torques were reasonably below the first natural frequency of the DMD surface.

5. Conclusions

The obtained results have shown that it is feasible to perform simultaneous orbital and attitude maneuvers by using the Drag Maneuvering Device as the only control means in conditions where physical and environmental parameters are uncertain.

In particular, adaptive controllers for orbital and attitude maneuvers were integrated to perform roto-translational maneuvers in the presence of uncertainty in atmospheric density, drag/lift coefficients, location of the Center of Mass and inertia matrix. The uniformly ultimately bounded convergence of the attitude error and relative orbit states is guaranteed by the Lyapunov-based stability analysis. Validation through numerical simulation of a phasing maneuver with simultaneous attitude control requirement results in ultimate errors below 60 m and 6.5 degrees for the translational and attitude maneuvers, respectively.

The algorithms developed together with the Drag Maneuvering Device could be particularly useful for providing small platforms, such as CubeSats, with propellant-less translational and attitude maneuverability. In-orbit inspection and servicing are envisioned as future applications for this technology.

Future work will explicitly include the influence of flexible bodies on the spacecraft dynamics and will be considered in the controller design. Studies on how to incorporate compensation for time-varying uncertain parameters, as well as efforts on relaxing the requirement of using numerical algorithms to solve for the DMD lengths, are considered of great importance to improve the obtained stability result. Opportunities for improving the distribution of the control effort between chaser and target without necessarily centralizing the control algorithm have also been identified as topic of interest for future research efforts.