Synchronous Machine Winding Modeling Method Based on Broadband Characteristics
Abstract
:1. Introduction
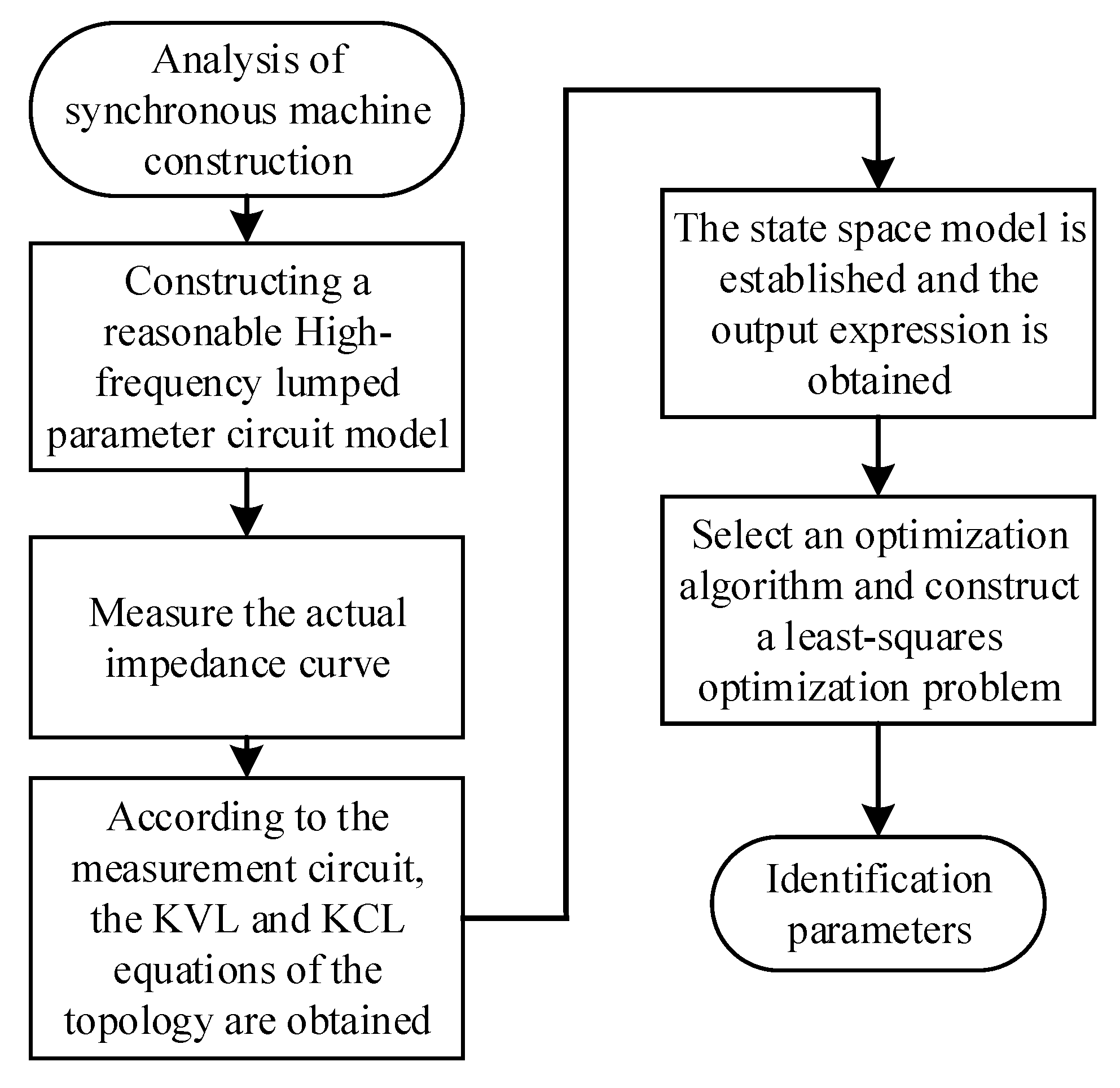
2. Theory Introduction
2.1. High-Frequency Lumped Parameter Circuit Model
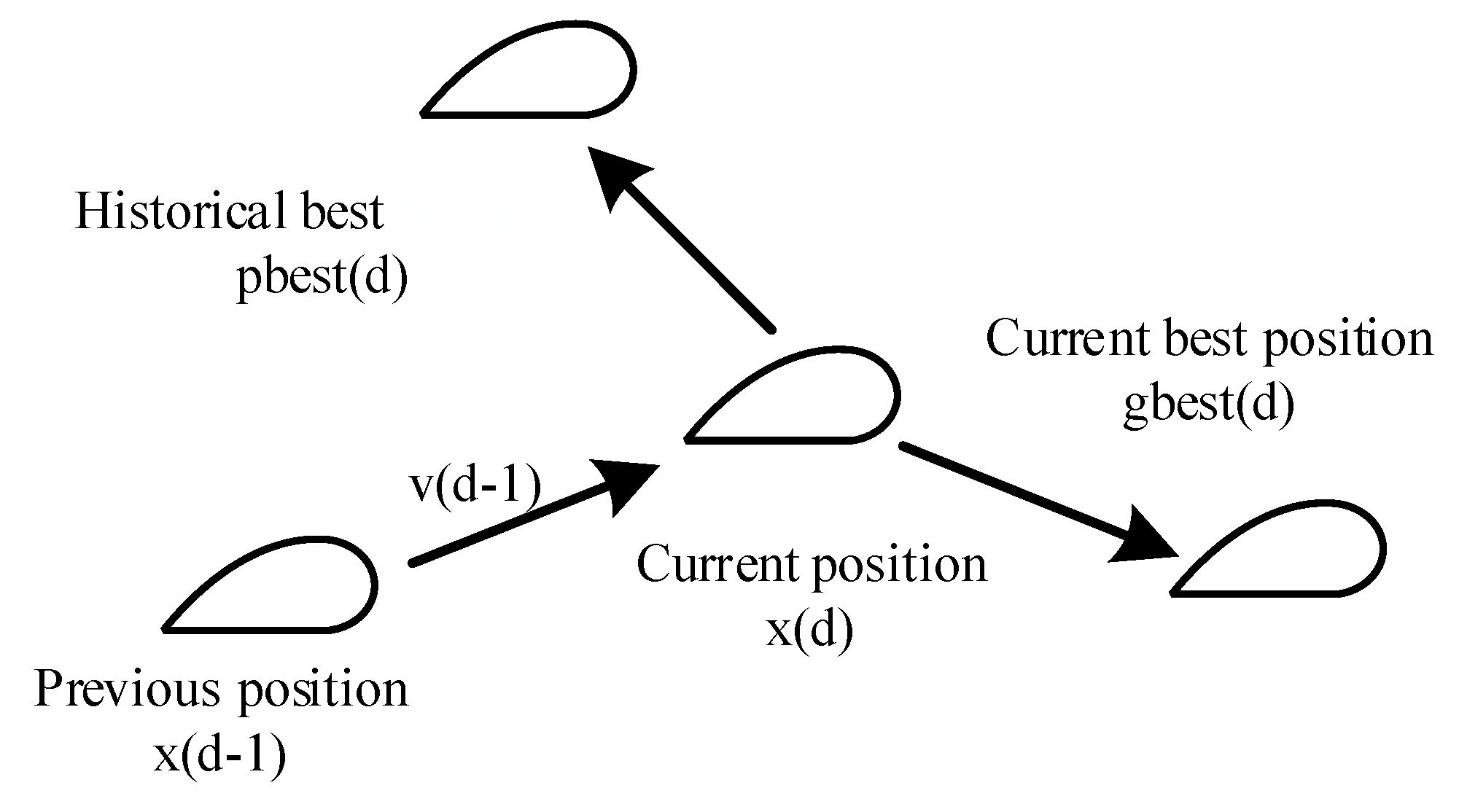
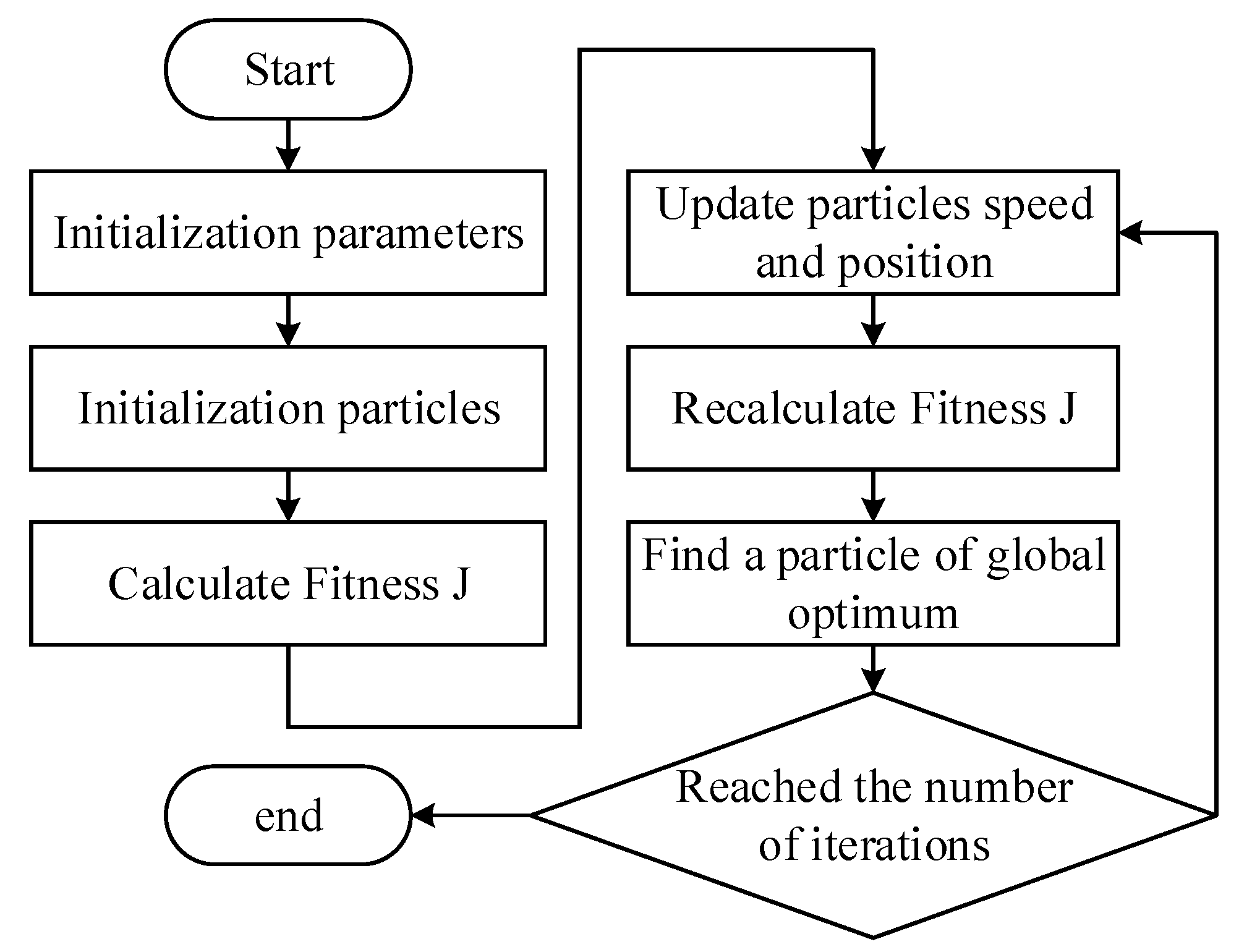
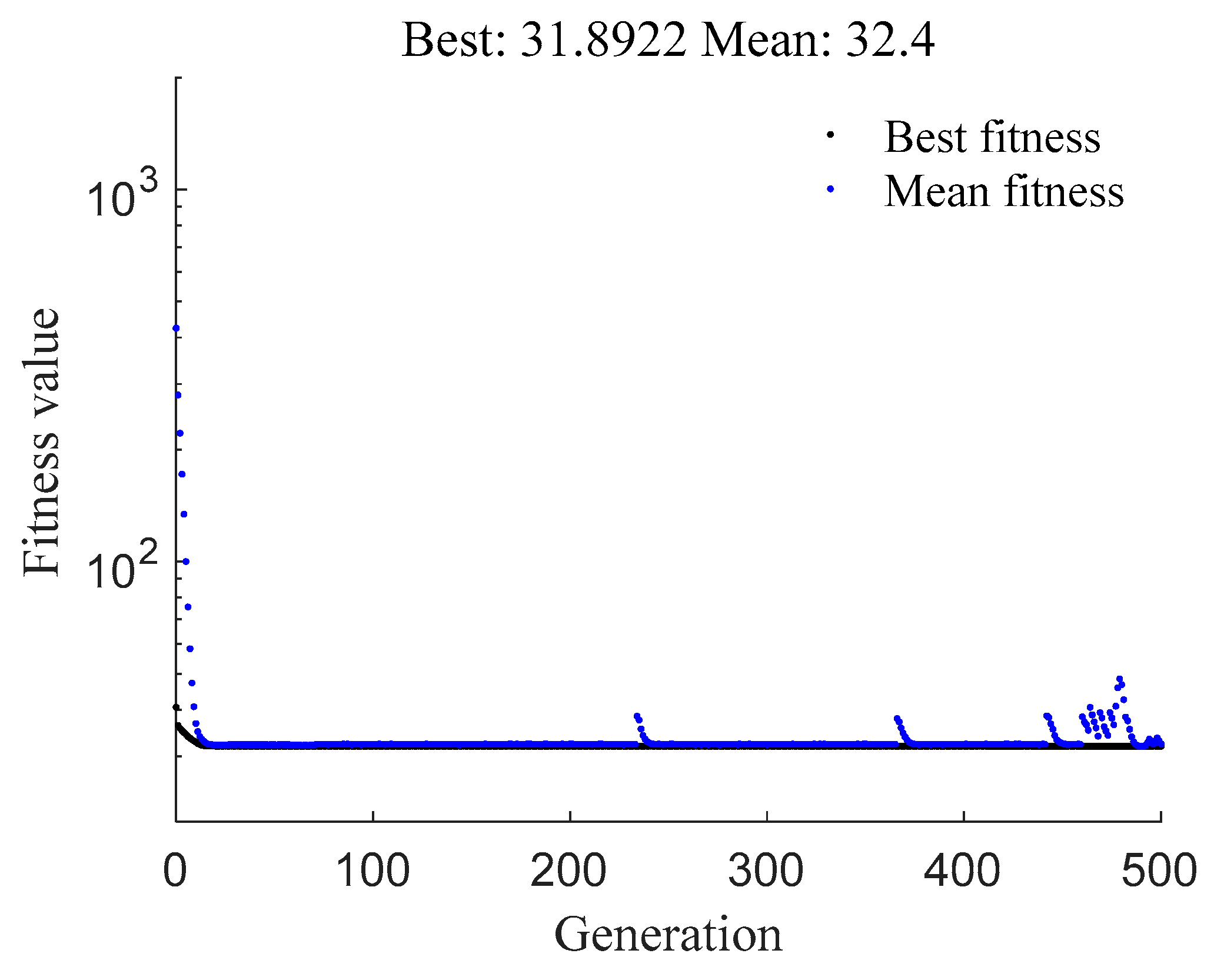
2.2. Parameter Identification Based on Optimization Algorithm
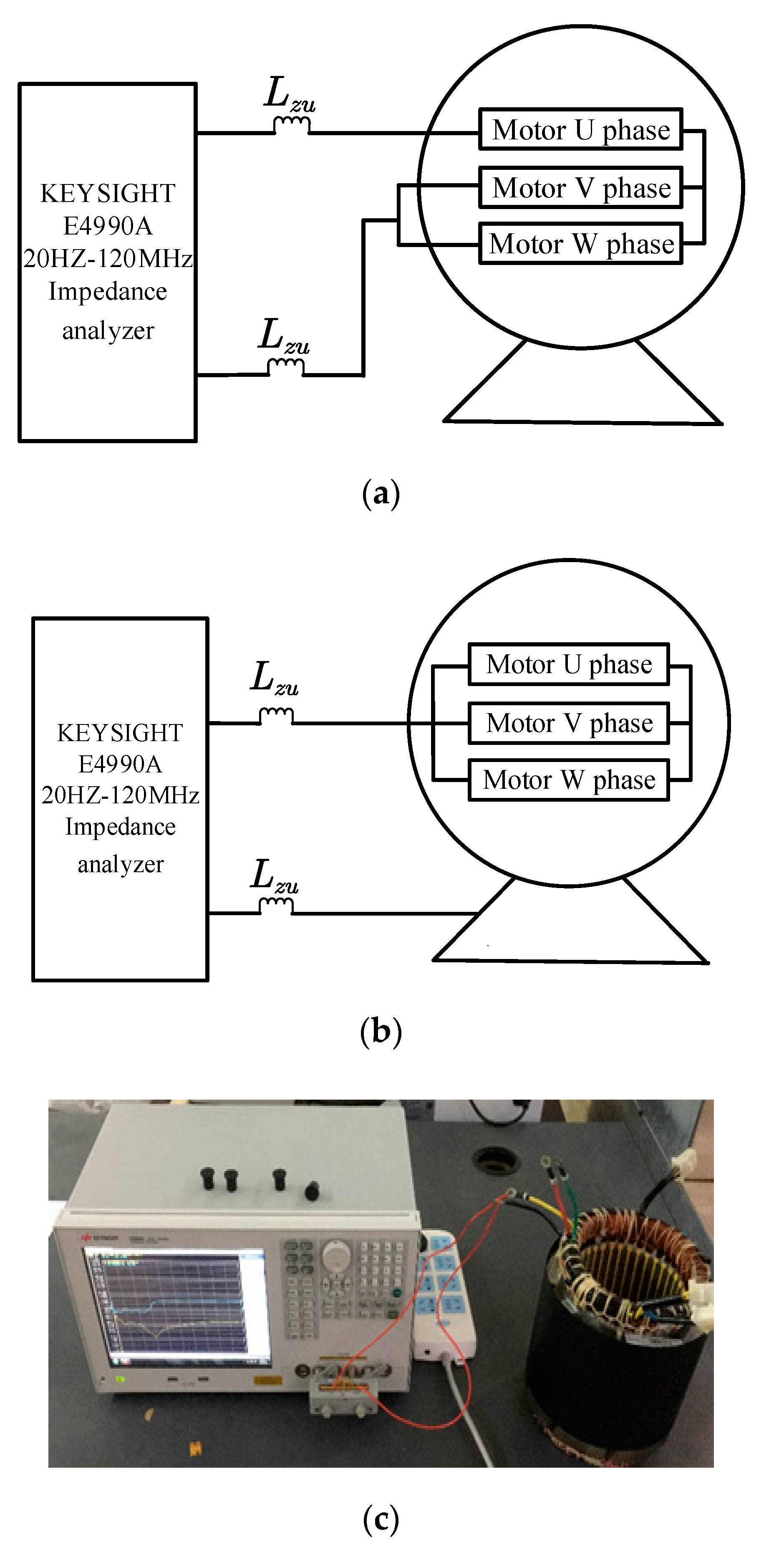
3. Experimental Verification
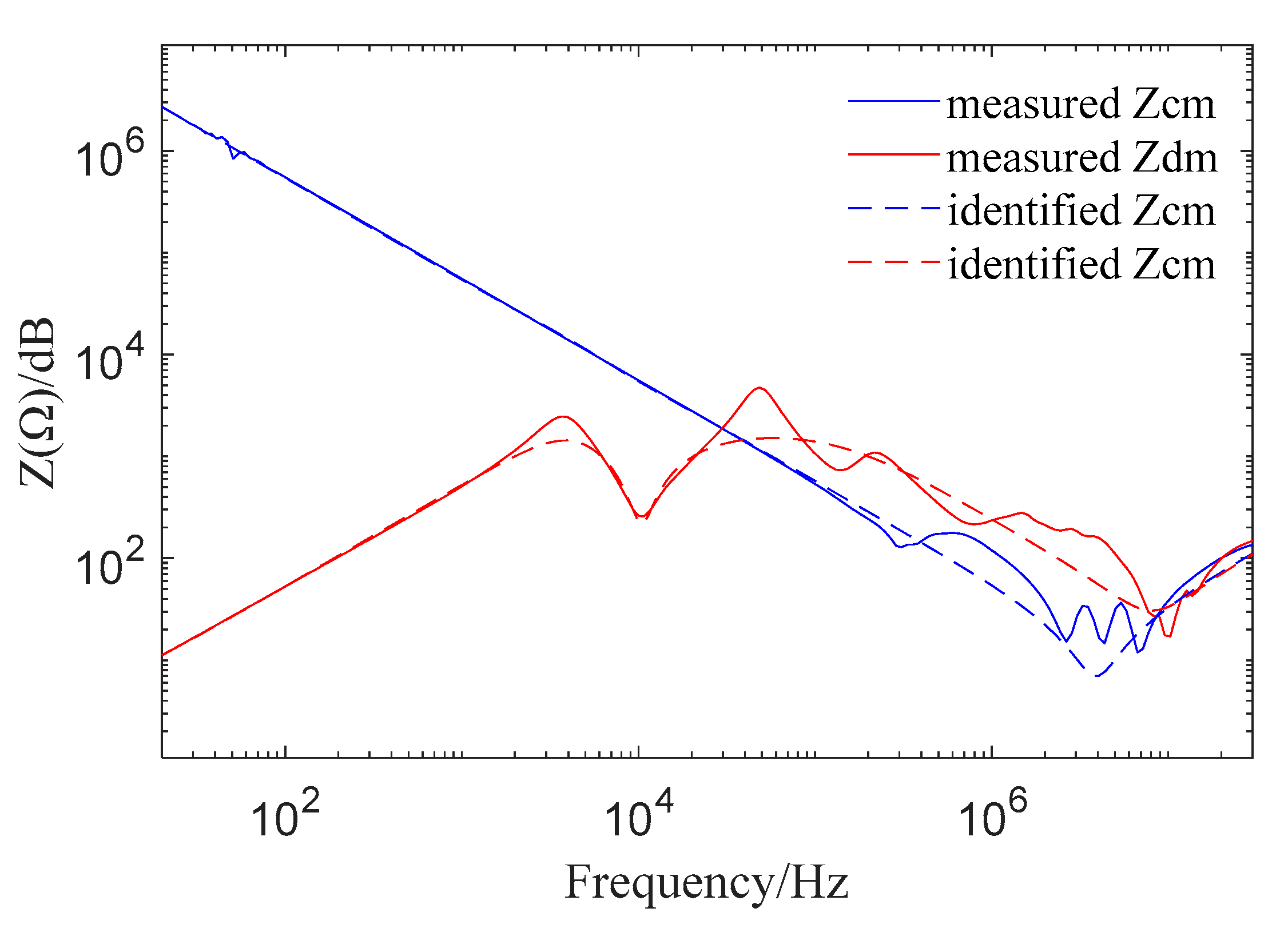
4. Contrast Experiment
5. Conclusions
- Based on the state space and the optimization algorithm’s parameter identification, there is a relatively high degree of agreement between the simulated curve and the measured curve, which indicates that the proposed modeling method is adaptive and robust to the measured data. On the other hand, if it chooses to use the state space model, it can modify the output Equation (9) to adapt to different measured external characteristic curves, so the method has potent portability.
- Compared with the black box model, the proposed method has a certain physical meaning to the broadband equivalent circuit model, as such it has better applicability, and the method does not need to master the detailed design parameters of the synchronous machine, it is simple to implement, and meets the engineering accuracy requirements. Compared with traditional engineering exploratory calculation parameters, the use of particle swarm optimization to identify parameters overcomes the subjectivity of selecting feature points in engineering calculations. Furthermore, the use of a simple particle swarm algorithm shows that the parameter identification method has a certain universality, and the completion of parameter identification does not require more complex algorithms.
- Although the single-phase lumped parameter circuit model proposed in this paper is greatly affected by noise at a high frequency, it can still be used to research the basis of high-frequency problems of synchronous machines, such as predicting common mode current, electromagnetic interference of drive system, etc.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sodin, D.; Rudež, U.; Mihelin, M.; Smolnikar, M.; Čampa, A. Advanced Edge-Cloud Computing Framework for Automated PMU-Based Fault Localization in Distribution Networks. Appl. Sci. 2021, 11, 3100. [Google Scholar] [CrossRef]
- Kahouli, O.; Alsaif, H.; Bouteraa, Y.; Ben Ali, N.; Chaabene, M. Power System Reconfiguration in Distribution Network for Improving Reliability Using Genetic Algorithm and Particle Swarm Optimization. Appl. Sci. 2021, 11, 3092. [Google Scholar] [CrossRef]
- Yu, Y.; Jin, Z.-X.; Li, J.-Z.; Wu, Y.-C.; Jia, L. An Air Pollutant Emission Reduction Path of China’s Power Industry. Atmosphere 2020, 11, 852. [Google Scholar] [CrossRef]
- Ansari, M.R.; Pirouzi, S.; Kazemi, M.; Naderipour, A.; Benbouzid, M. Renewable Generation and Transmission Expansion Planning Coordination with Energy Storage System: A Flexibility Point of View. Appl. Sci. 2021, 11, 3303. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, C. Computationally Efficient PM Power Loss Mapping for PWM Drive Surface-Mounted Permanent Magnet Synchronous Machines. Appl. Sci. 2021, 11, 3246. [Google Scholar] [CrossRef]
- Goh, Y.-J.; Kim, O. Linear Method for Diagnosis of Inter-Turn Short Circuits in 3-Phase Induction Motors. Appl. Sci. 2019, 9, 4822. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Mamesh, Z.; Sailauova, D.; Shon, C.-S.; Lee, D.; Kim, J.R. Temperature Distributions inside Concrete Sections of Renewable Energy Storage Pile Foundations. Appl. Sci. 2019, 9, 4776. [Google Scholar] [CrossRef] [Green Version]
- Nefedov, E.; Sierla, S.; Vyatkin, V. Internet of Energy Approach for Sustainable Use of Electric Vehicles as Energy Storage of Prosumer Buildings. Energies 2018, 11, 2165. [Google Scholar] [CrossRef] [Green Version]
- Hong, S. Research on Conducted Electromagnetic Interference of Electric Vehicle Motor Drive System. Master’s Thesis, Chongqing University, Chongqing, China, 2012. (In Chinese). [Google Scholar]
- Idir, N.; Weens, Y.; Moreau, M.; Franchaud, J. High-Frequency Behavior Models of AC Motors. IEEE Trans. Magn. 2009, 45, 133–138. [Google Scholar] [CrossRef]
- Quandi, W.; Hong, S.; Yali, Z. Rapid modeling method of motor broadband equivalent circuit model. J. Chongqing Univ. 2012, 35, 34–36. (In Chinese) [Google Scholar]
- Blánquez, F.; Platero, C.A.; Rebollo, E.; Blánquez, F. Evaluation of the applicability of FRA for inter-turn fault detection in stator windings. In Proceedings of the 2013 9th IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives (SDEMPED), Valencia, Spain, 27–30 August 2013; pp. 177–182. [Google Scholar]
- Shabestary, M.M.; Ghanizadeh, A.J.; Gharehpetian, G.B.; Agha-Mirsalim, M. Ladder Network Parameters Determination Considering Nondominant Resonances of the Transformer Winding. IEEE Trans. Power Deliv. 2014, 29, 108–111. [Google Scholar] [CrossRef]
- Schinkel, M.; Weber, S.; Guttowski, S.; John, W.; Reichl, H. Efficient HF modeling and model parameterization of induction machines for time and frequency domain simulations. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006. [Google Scholar]
- Mohammed, O.A.; Ganu, S.; Abed, N.; Liu, S.; Liu, Z. High frequency PM synchronous motor model determined by FE analysis. IEEE Trans. Magn. 2006, 42, 1291–1294. [Google Scholar] [CrossRef]
- Boglietti, A.; Carpaneto, E. Induction motor high frequency model. In Proceedings of the Conference Record of the 1999 IEEE Industry Applications Conference. Thirty-Forth IAS Annual Meeting, Phoenix, AZ, USA, 3–7 October 1999; Volume 3, pp. 1551–1558. [Google Scholar]
- Wang, L.; Ho, C.N.-M.; Canales, F.; Jatskevich, J. High-Frequency Modeling of the Long-Cable-Fed Induction Motor Drive System Using TLM Approach for Predicting Overvoltage Transients. IEEE Trans. Power Electr. 2010, 25, 2653–2664. [Google Scholar] [CrossRef]
- Mohammadi-Rostam, M.; Shahabi, M. Modeling Induction Motor for Prediction of High frequency problems. Iran. J. Sci. Technol. Trans. Electr. Eng. 2016, 40, 13–22. [Google Scholar] [CrossRef]
- Cari, E.P.T.; Alberto, L.F.C.; Erlich, I. Assessment of model parameters to identify an equivalent wind power plant. In Proceedings of the 2015 IEEE Eindhoven PowerTech, Eindhoven, The Netherlands, 29 June–2 July 2015; pp. 1–5. [Google Scholar]
- Zhang, H.; Hao, J. A method using PSO to optimize and identify error parameter based on local state estimation. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; pp. 1–5. [Google Scholar]
- Li, M.; Ma, Y. Parameter Identification of DC Motor based on Compound Least Square Method. In Proceedings of the 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), Chongqing, China, 12–14 June 2020; pp. 1107–1111. [Google Scholar]
- Peng, W.; Yang, Z.; Liu, C.; Xiu, J.; Zhang, Z. An Improved PSO Algorithm for Battery Parameters Identification Optimization Based on Thevenin Battery Model. In Proceedings of the 2018 5th IEEE International Conference on Cloud Computing and Intelligence Systems (CCIS), Nanjing, China, 23–25 November 2018; pp. 295–298. [Google Scholar]
- Maharana, H.S.; Dash, S. K Comparative Optimization Analysis of Ramp Rate Constriction Factor Based PSO and Electro Magnetism Based PSO for Economic Load Dispatch in Electric Power System. In Proceedings of the 2019 International Conference on Applied Machine Learning (ICAML), Bhubaneswar, India, 25–26 May 2019; pp. 63–68. [Google Scholar]
- Tang, H.; Guo, X.; Xie, L.; Xue, S. Experimental Validation of Optimal Parameter and Uncertainty Estimation for Structural Systems Using a Shuffled Complex Evolution Metropolis Algorithm. Appl. Sci. 2019, 9, 4959. [Google Scholar] [CrossRef] [Green Version]
- Ariza, H.E.; Correcher, A.; Sánchez, C.; Pérez-Navarro, Á.; García, E. Thermal and Electrical Parameter Identification of a Proton Exchange Membrane Fuel Cell Using Genetic Algorithm. Energies 2018, 11, 2099. [Google Scholar] [CrossRef] [Green Version]
- Bui, H.-B.; Nguyen, H.; Choi, Y.; Bui, X.-N.; Nguyen-Thoi, T.; Zandi, Y. A Novel Artificial Intelligence Technique to Estimate the Gross Calorific Value of Coal Based on Meta-Heuristic and Support Vector Regression Algorithms. Appl. Sci. 2019, 9, 4868. [Google Scholar] [CrossRef] [Green Version]
- Zengping, W.; Bing, Z.; Weijia, J.; Xin, G.; Xiaobing, L. Short term load forecasting method based on gru-nn model. Power Syst. Autom. 2019, 43, 53–58. (In Chinese) [Google Scholar]
- Sun, W.; Zhang, X. Application of self-organizing combination forecasting method in power load forecast. In Proceedings of the 2007 International Conference on Wavelet Analysis and Pattern Recognition, Beijing, China, 2–4 November 2007. [Google Scholar]
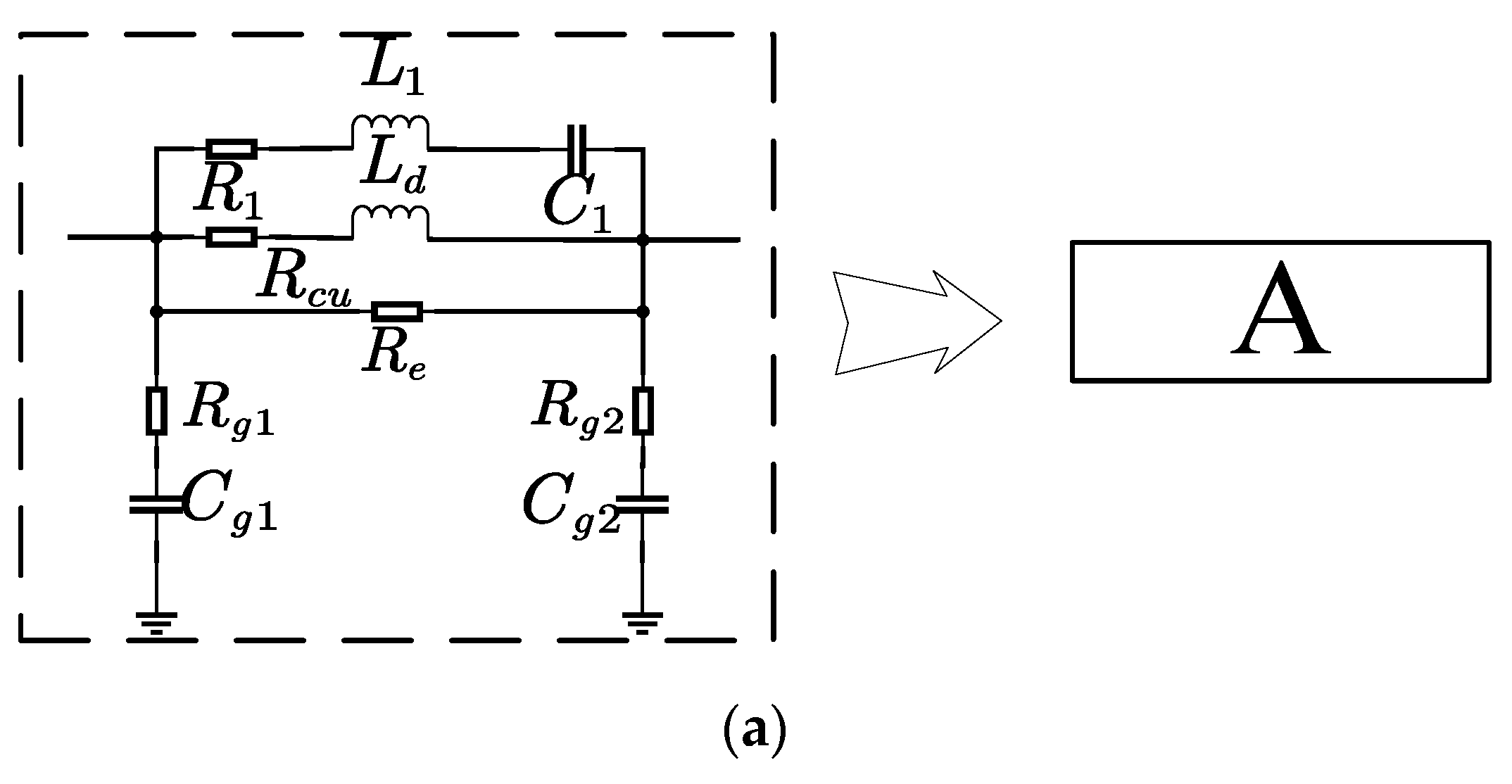
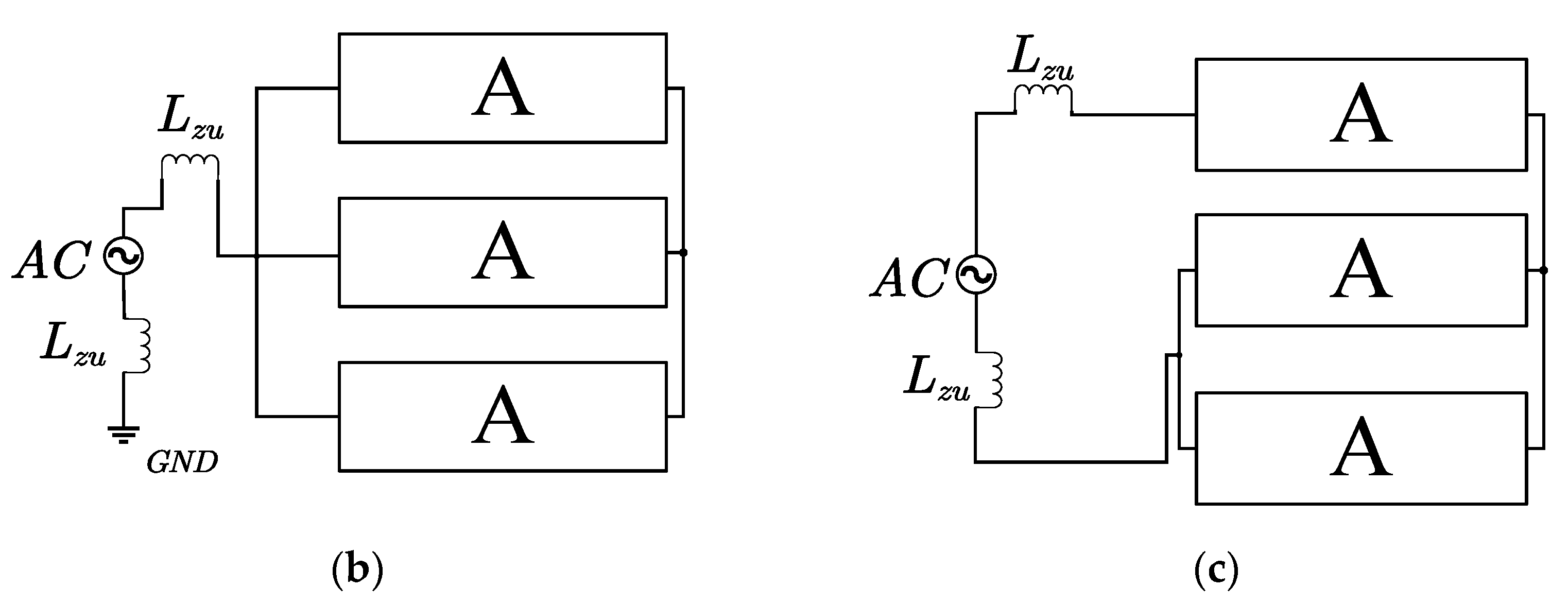


| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| R1 | 166.404 Ω | C1 | 2.1884 pF | Ld | 56.30 mH |
| L1 | 0.01070 H | RCu | 2.4601 Ω | Re | 1.0238 kΩ |
| Cg2 | 2.8184 nF | Rg2 | 5 Ω | Cg1 | 95.152 nF |
| Rg1 | 20.4828 Ω | Lzu | 0.2999 μH |
| Parameter | Black Box | Proposed Method | Engineering Calculation Method |
|---|---|---|---|
| Zcm(MAPE) | 102.0924 | 21.5944 | 27.4624 |
| Zcm(RMSE) | 63,880.07 | 13,758.19 | 21,355.57 |
| Zdm(MAPE) | 49.3585 | 41.202 | 65.9571 |
| Zdm(RMSE) | 1606.95 | 1484.99 | 2051.712 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Ji, X.; Zhao, Z. Synchronous Machine Winding Modeling Method Based on Broadband Characteristics. Appl. Sci. 2021, 11, 4631. https://doi.org/10.3390/app11104631
Chen Y, Ji X, Zhao Z. Synchronous Machine Winding Modeling Method Based on Broadband Characteristics. Applied Sciences. 2021; 11(10):4631. https://doi.org/10.3390/app11104631
Chicago/Turabian StyleChen, Yu, Xiaoqing Ji, and Zhongyong Zhao. 2021. "Synchronous Machine Winding Modeling Method Based on Broadband Characteristics" Applied Sciences 11, no. 10: 4631. https://doi.org/10.3390/app11104631
APA StyleChen, Y., Ji, X., & Zhao, Z. (2021). Synchronous Machine Winding Modeling Method Based on Broadband Characteristics. Applied Sciences, 11(10), 4631. https://doi.org/10.3390/app11104631






