sEMG-Based Continuous Estimation of Finger Kinematics via Large-Scale Temporal Convolutional Network
Abstract
:1. Introduction
2. Methodology
2.1. Data Set
2.2. Data Processing
2.3. Parameters for Evaluation
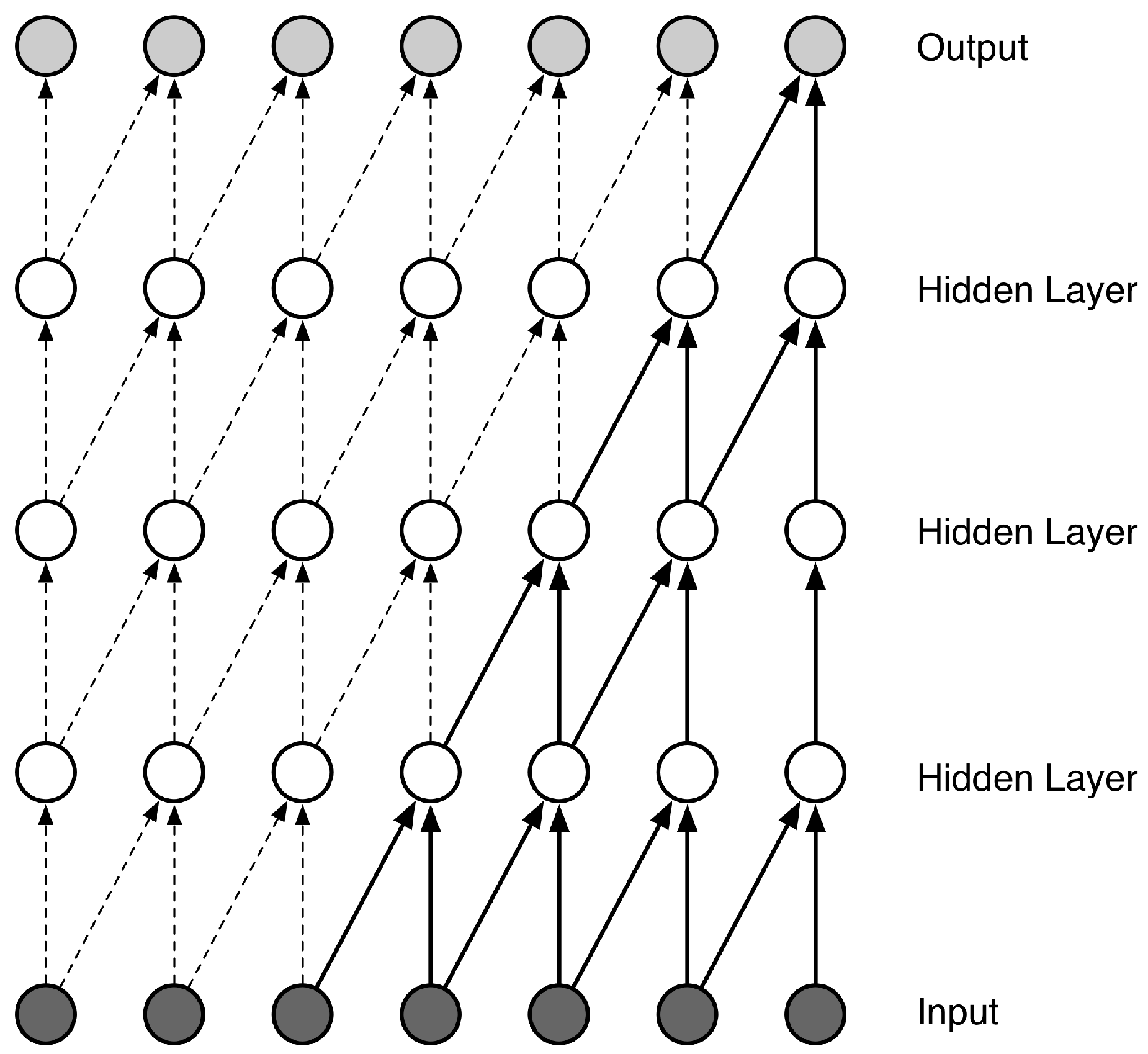
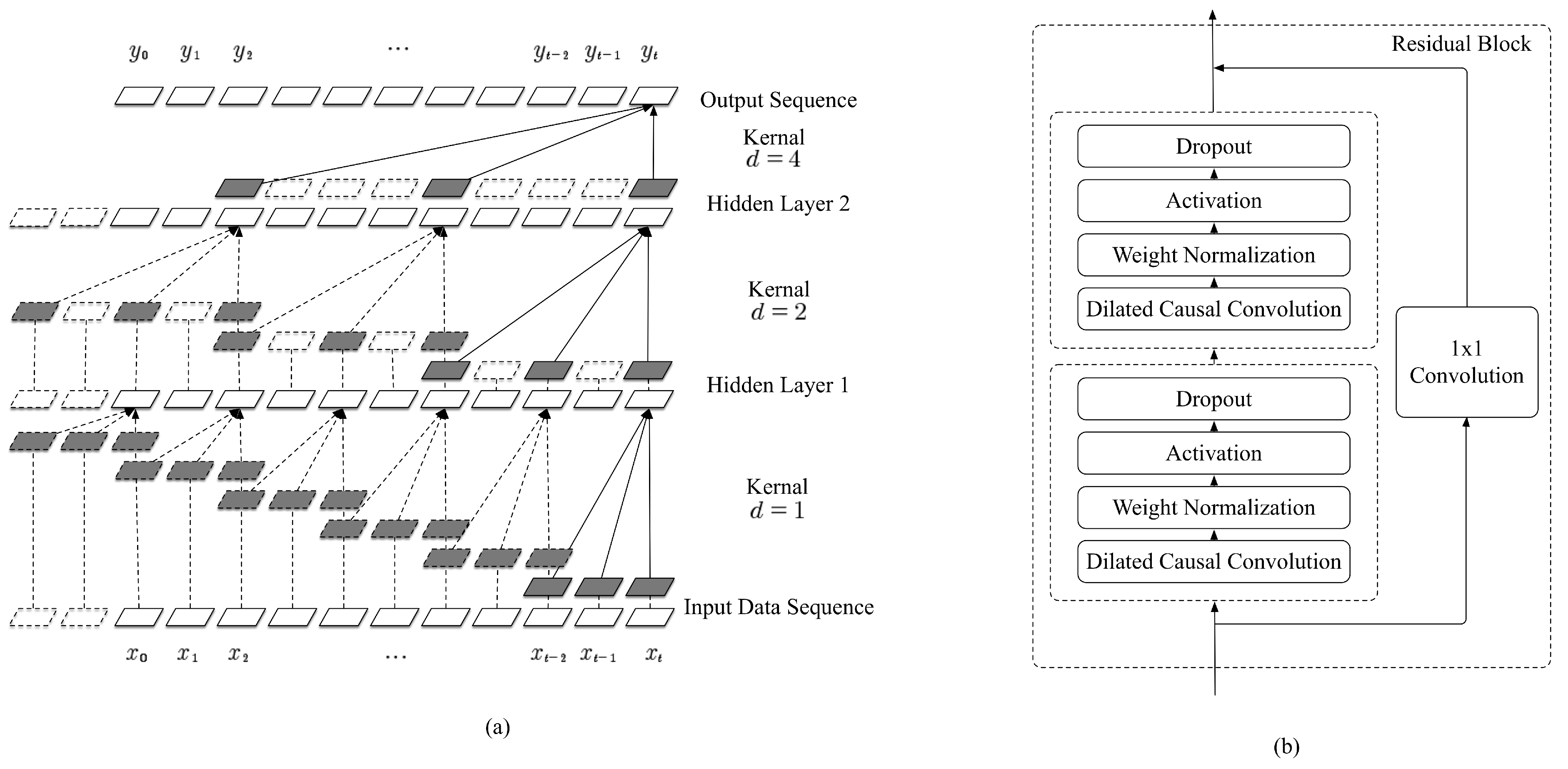
2.4. Applying Tcn to Semg-Based Continuous Estimation
2.5. The Large-Scale Temporal Convolutional Network
3. Results and Discussion
3.1. Experimental Setup
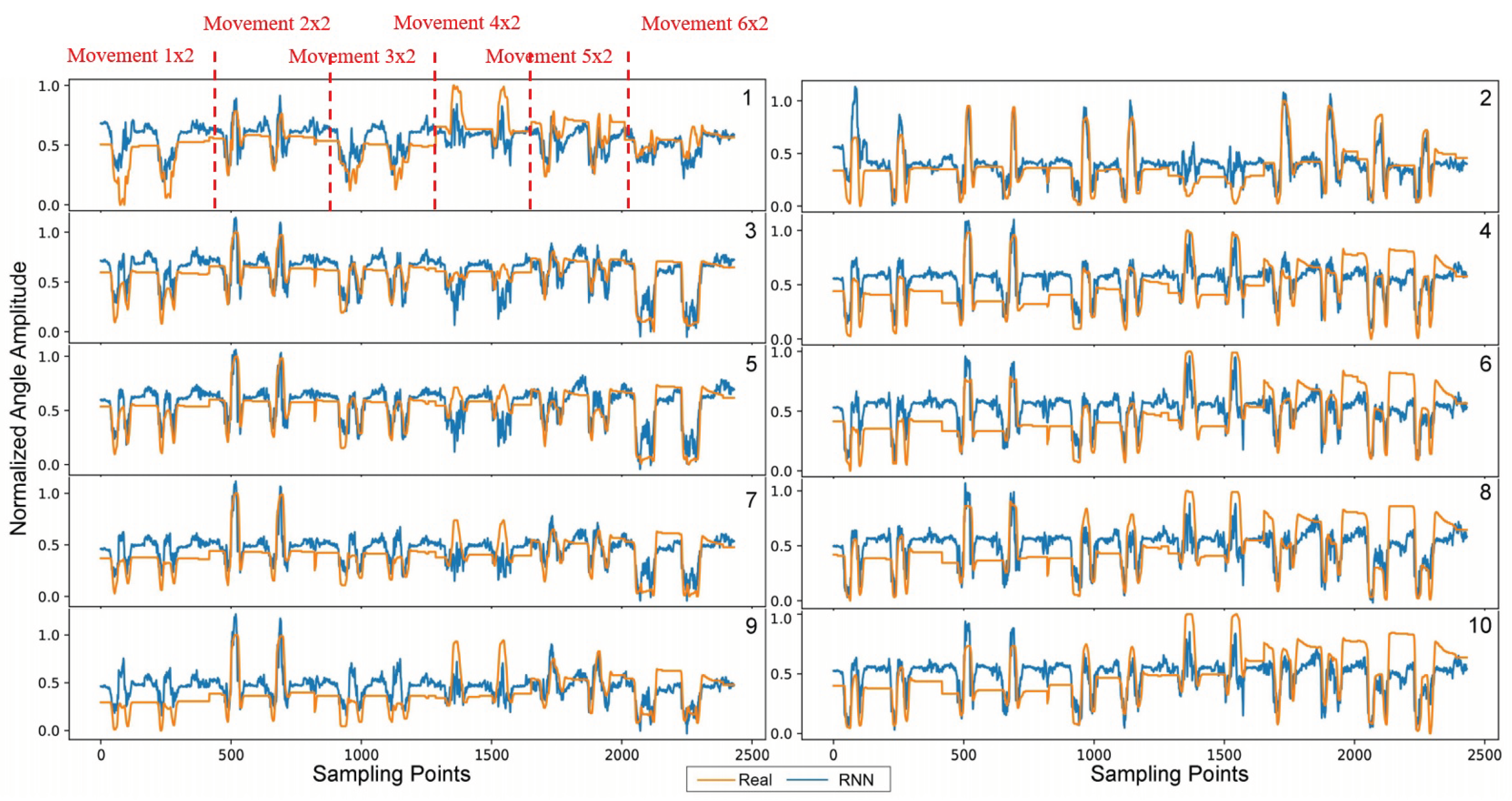
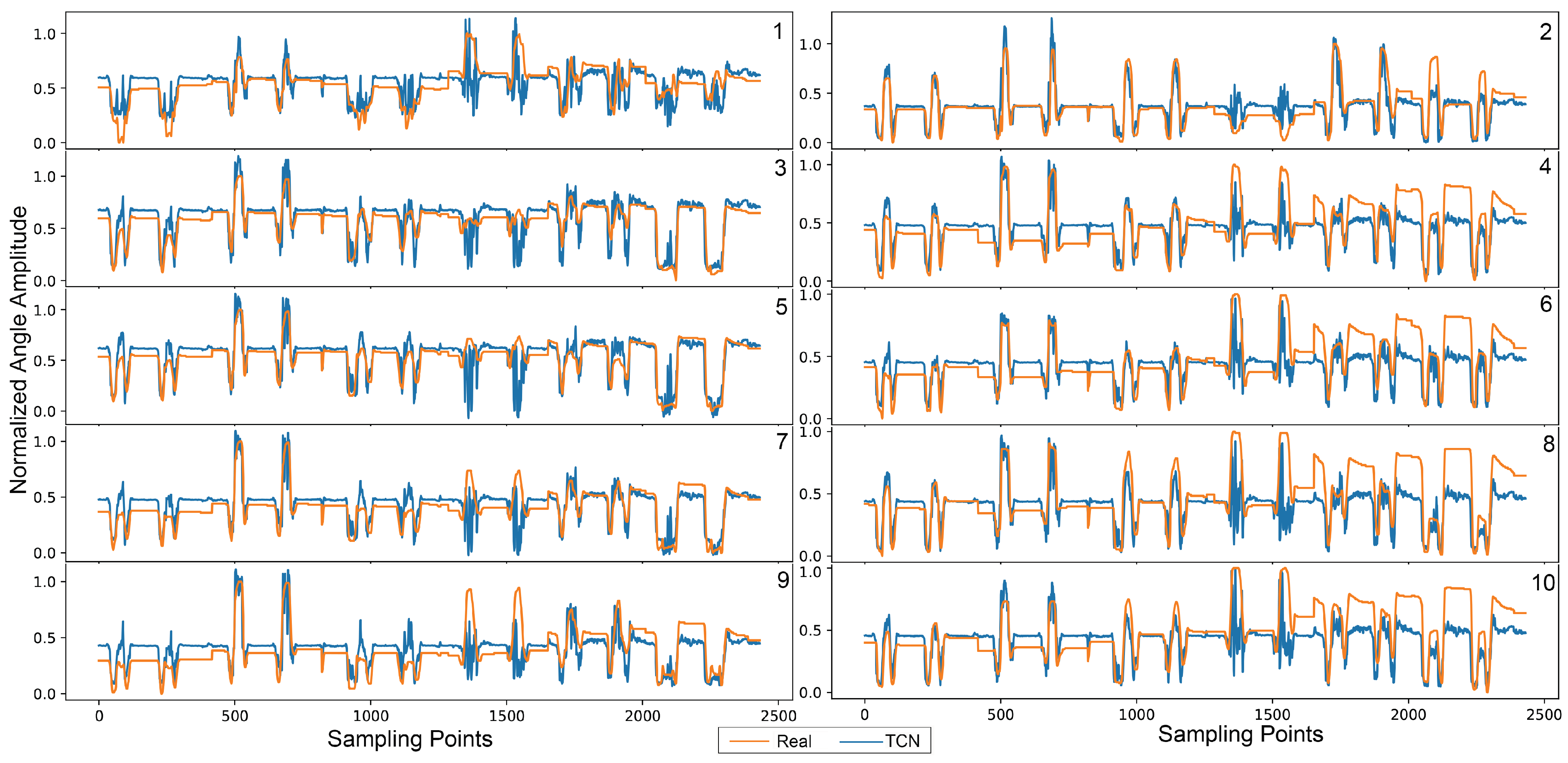
3.2. Movement Data
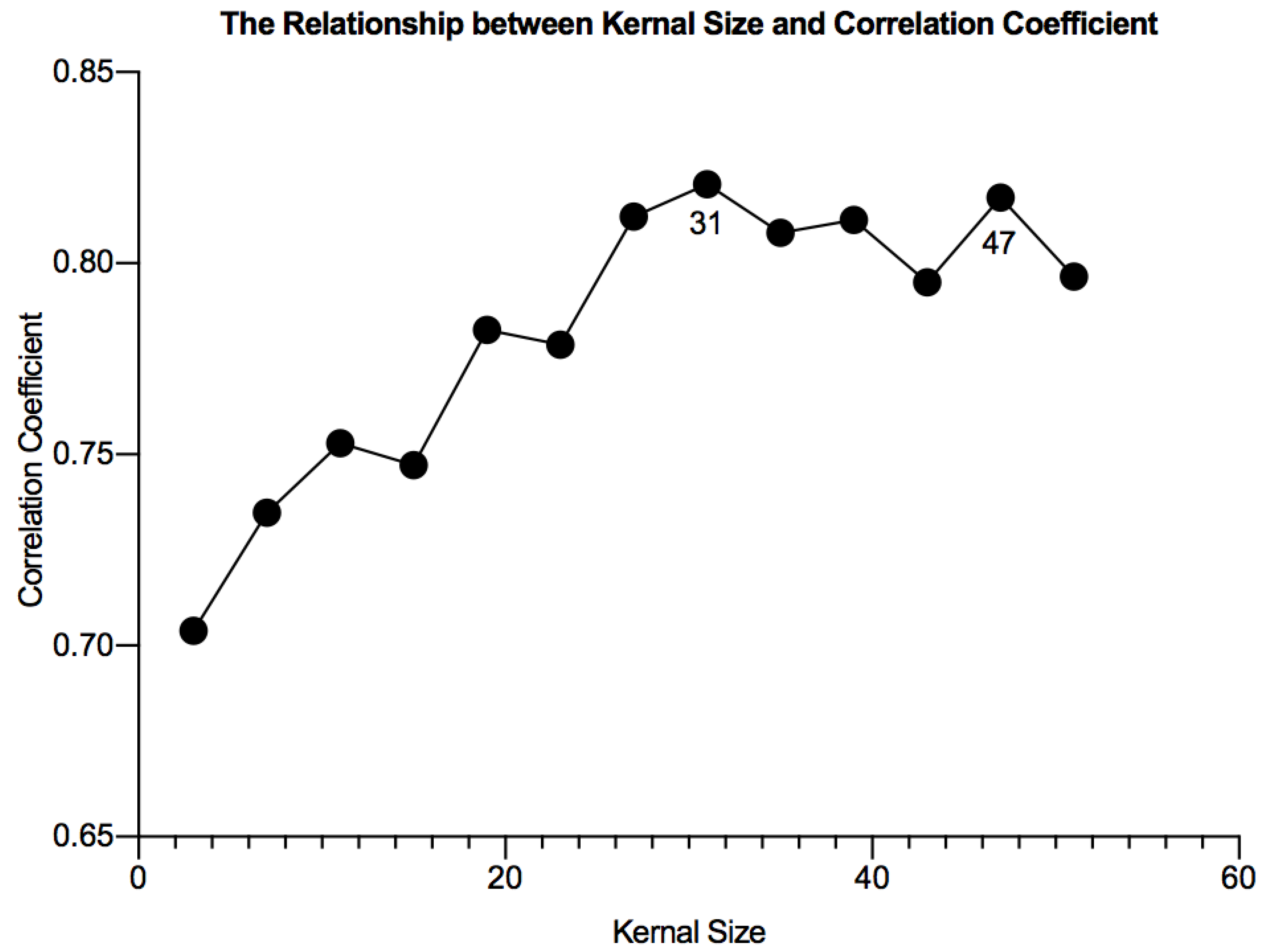
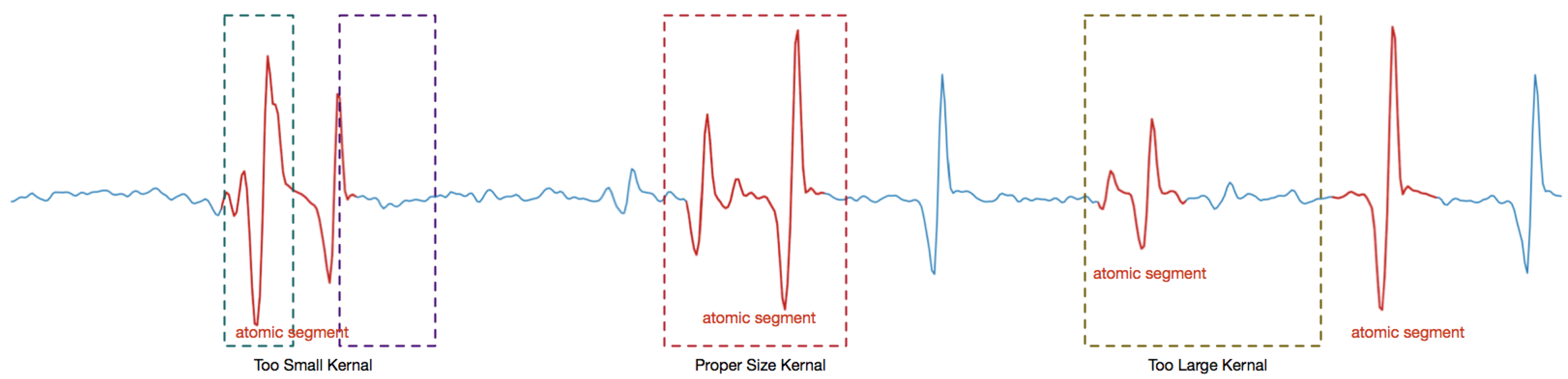
3.3. Kernel Size Optimization
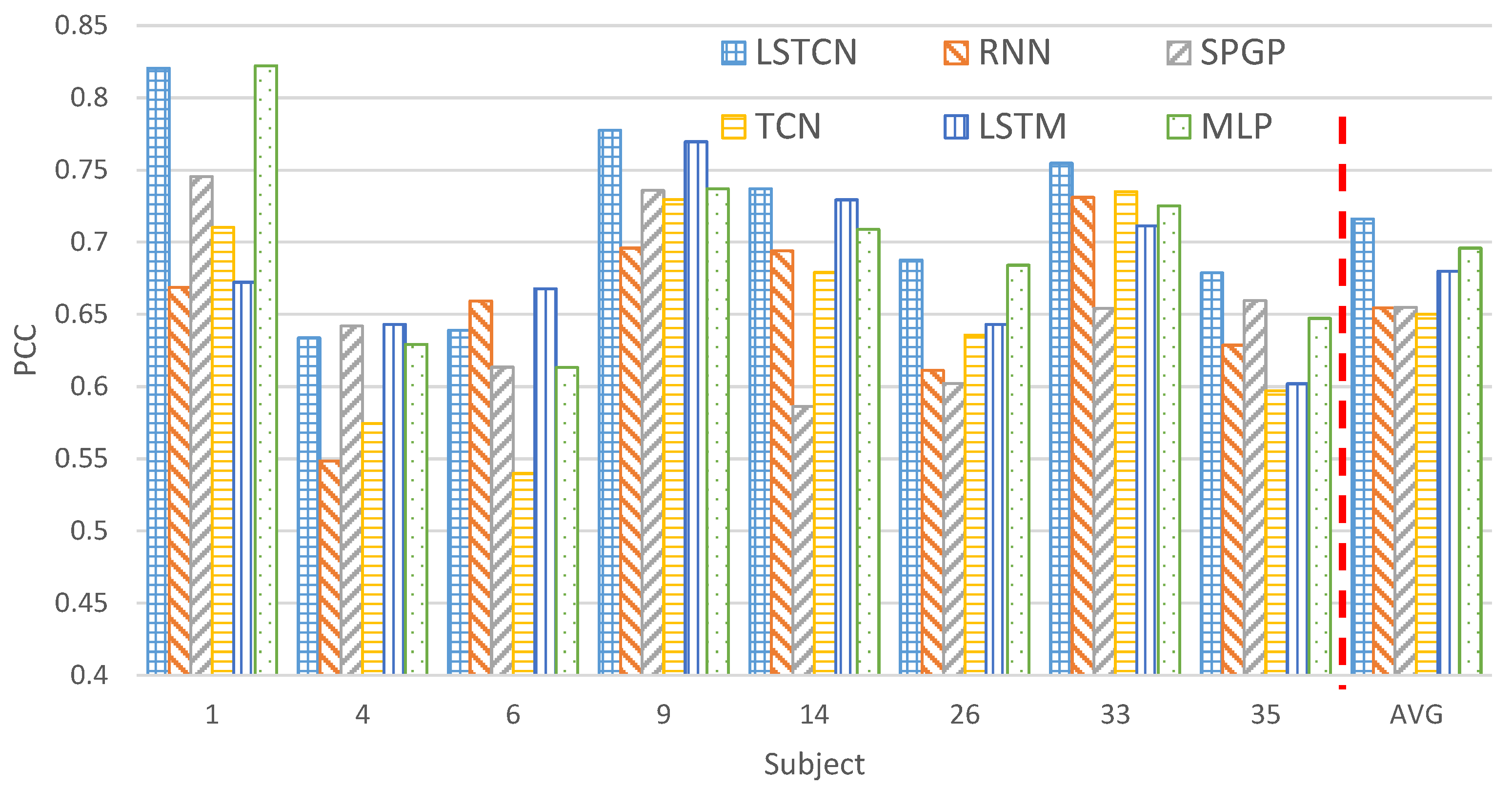
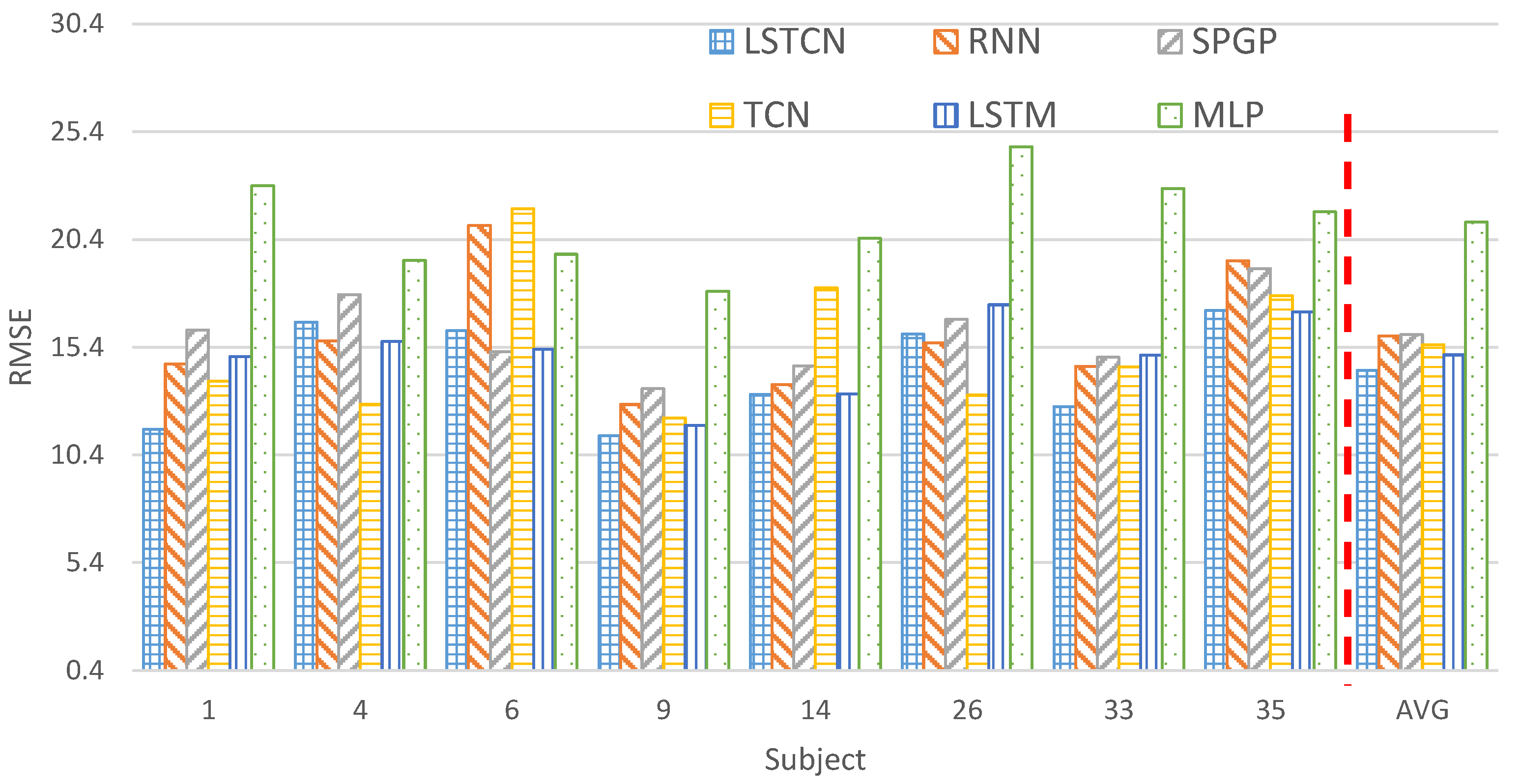
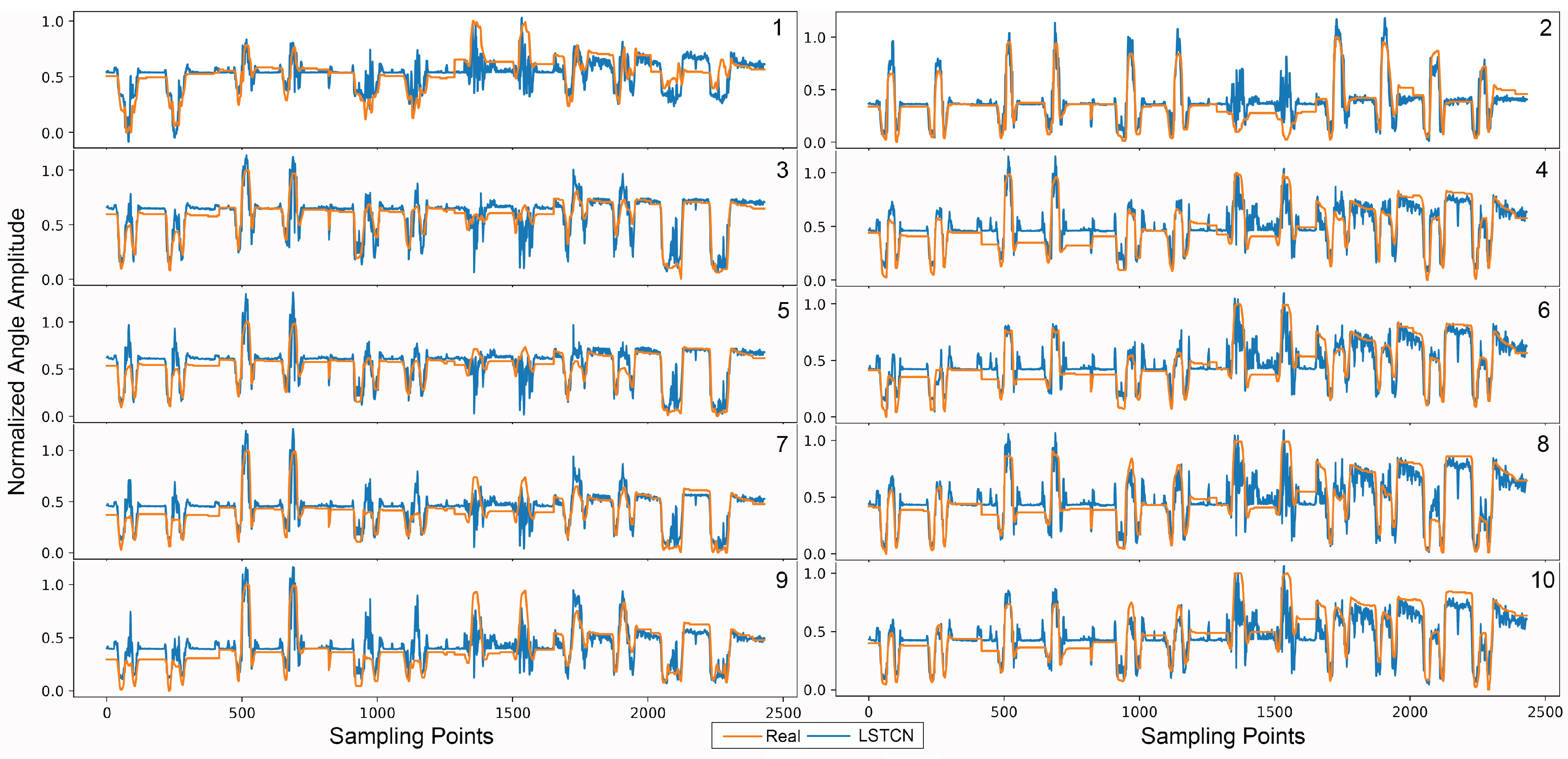
3.4. Performance Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bi, L.; Feleke, A.; Guan, C. A review on EMG-based motor intention prediction of continuous human upper limb motion for human-robot collaboration. Biomed. Signal Process. Control 2019, 51, 113–127. [Google Scholar] [CrossRef]
- Morimoto, T.K.; Hawkes, E.W.; Okamura, A.M. Design of a Compact Actuation and Control System for Flexible Medical Robots. IEEE Robot. Autom. Lett. 2017, 2, 1579–1585. [Google Scholar] [CrossRef] [PubMed]
- Kuo, C.M.; Chen, L.C.; Tseng, C.Y. Investigating an innovative service with hospitality robots. Int. J. Contemp. Hosp. Manag. 2017, 29, 1305–1321. [Google Scholar] [CrossRef]
- Marchant, G.E.; Allenby, B.; Arkin, R.C.; Borenstein, J.; Gaudet, L.M.; Kittrie, O.; Lin, P.; Lucas, G.R.; O’Meara, R.; Silberman, J. International governance of autonomous military robots. In Handbook of Unmanned Aerial Vehicles; Springer: Dordrecht, The Netherlands, 2015; pp. 2879–2910. [Google Scholar] [CrossRef] [Green Version]
- Szabo, R.; Gontean, A. Controlling a robotic arm in the 3D space with stereo vision. In Proceedings of the 2013 21st Telecommunications Forum Telfor, TELFOR 2013-Proceedings of Papers, Belgrade, Serbia, 26–28 November 2013; pp. 916–919. [Google Scholar] [CrossRef]
- Kopniak, P.; Kaminski, M. Natural interface for robotic arm controlling based on inertial motion capture. In Proceedings of the 2016 9th International Conference on Human System Interactions, HSI 2016, Portsmouth, UK, 6–8 July 2016; pp. 110–116. [Google Scholar] [CrossRef]
- Phinyomark, A.; Quaine, F.; Charbonnier, S.; Serviere, C.; Tarpin-Bernard, F.; Laurillau, Y. EMG feature evaluation for improving myoelectric pattern recognition robustness. Expert Syst. Appl. 2013, 40, 4832–4840. [Google Scholar] [CrossRef]
- Lin, J.; Wu, Y.; Huang, T.S. Modeling the constraints of human hand motion. In Proceedings of the Workshop on Human Motion, HUMO 2000, Austin, TX, USA, 7–8 December 2000; pp. 121–126. [Google Scholar] [CrossRef] [Green Version]
- Kapandji, I.A. The Physiology of the Joints. Vol. 1, Upper Limb. Postgrad. Med. J. 1971, 47, 140. [Google Scholar] [CrossRef] [Green Version]
- Micera, S.; Carpaneto, J.; Raspopovic, S. Control of Hand Prostheses Using Peripheral Information. IEEE Rev. Biomed. Eng. 2010, 3, 48–68. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zanghieri, M.; Benatti, S.; Burrello, A.; Kartsch, V.; Conti, F.; Benini, L. Robust Real-Time Embedded EMG Recognition Framework Using Temporal Convolutional Networks on a Multicore IoT Processor. IEEE Trans. Biomed. Circuits Syst. 2020, 14, 244–256. [Google Scholar] [CrossRef] [PubMed]
- Côté-Allard, U.; Fall, C.L.; Drouin, A.; Campeau-Lecours, A.; Gosselin, C.; Glette, K.; Laviolette, F.; Gosselin, B. Deep Learning for Electromyographic Hand Gesture Signal Classification Using Transfer Learning. IEEE Trans. Neural Syst. Rehabil. Eng. 2019, 27, 760–771. [Google Scholar] [CrossRef] [Green Version]
- Jiang, N.; Dosen, S.; Muller, K.R.; Farina, D. Myoelectric control of artificial limbsis there a need to change focus? [In the Spotlight]. IEEE Signal Process. Mag. 2012, 29, 148–152. [Google Scholar] [CrossRef]
- Kapelner, T.; Vujaklija, I.; Jiang, N.; Negro, F.; Aszmann, O.C.; Principe, J.; Farina, D. Predicting wrist kinematics from motor unit discharge timings for the control of active prostheses. J. NeuroEng. Rehabil. 2019, 16, 1–11. [Google Scholar] [CrossRef]
- Jiang, N.; Englehart, K.B.; Parker, P.A. Extracting simultaneous and proportional neural control information for multiple-dof prostheses from the surface electromyographic signal. IEEE Trans. Biomed. Eng. 2009, 56, 1070–1080. [Google Scholar] [CrossRef] [PubMed]
- Xiloyannis, M.; Gavriel, C.; Thomik, A.A.C.; Faisal, A.A. Gaussian Process Autoregression for Simultaneous Proportional Multi-Modal. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1785–1801. [Google Scholar] [CrossRef]
- Clancy, E.A.; Liu, L.; Liu, P.; Moyer, D.V. Identification of constant-posture EMG-torque relationship about the elbow using nonlinear dynamic models. IEEE Trans. Biomed. Eng. 2012, 59, 205–212. [Google Scholar] [CrossRef] [PubMed]
- Ahsan, M.R.; Ibrahimy, M.I.; Khalifa, O.O. EMG signal classification for human computer interaction: A review. Eur. J. Sci. Res. 2009, 33, 480–501. [Google Scholar]
- Alique, A.; Haber, R.; Haber, R.; Ros, S.; Gonzalez, C. A neural network-based model for the prediction of cutting force in milling process. A progress study on a real case. In Proceedings of the 2000 IEEE International Symposium on Intelligent Control, Held Jointly with the 8th IEEE Mediterranean Conference on Control and Automation (Cat. No.00CH37147), Patras, Greece, 19 July 2000; pp. 121–125. [Google Scholar] [CrossRef]
- Precup, R.E.; Teban, T.A.; Albu, A.; Borlea, A.B.; Zamfirache, I.A.; Petriu, E.M. Evolving Fuzzy Models for Prosthetic Hand Myoelectric-Based Control. IEEE Trans. Instrum. Meas. 2020, 69, 4625–4636. [Google Scholar] [CrossRef]
- Matía, F.; Jiménez, V.; Alvarado, B.P.; Haber, R. The fuzzy Kalman filter: Improving its implementation by reformulating uncertainty representation. Fuzzy Sets Syst. 2021, 402, 78–104. [Google Scholar] [CrossRef]
- Smith, R.J.; Tenore, F.; Huberdeau, D.; Etienne-Cummings, R.; Thakor, N.V. Continuous decoding of finger position from surface EMG signals for the control of powered prostheses. In Proceedings of the 30th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS’08 -”Personalized Healthcare through Technology”, Vancouver, BC, Canada, 20–25 August 2008; pp. 197–200. [Google Scholar] [CrossRef]
- Muceli, S.; Farina, D. Simultaneous and proportional estimation of hand kinematics from EMG during mirrored movements at multiple degrees-of-freedom. IEEE Trans. Neural Syst. Rehabil. Eng. 2012, 20, 371–378. [Google Scholar] [CrossRef]
- Wang, C.; Guo, W.; Zhang, H.; Guo, L.; Huang, C.; Lin, C. sEMG-based continuous estimation of grasp movements by long-short term memory network. Biomed. Signal Process. Control 2020, 59, 101774. [Google Scholar] [CrossRef]
- Xia, P.; Hu, J.; Peng, Y. EMG-Based Estimation of Limb Movement Using Deep Learning With Recurrent Convolutional Neural Networks. Artif. Organs 2017. [Google Scholar] [CrossRef]
- Atzori, M.; Muller, H. The Ninapro database: A resource for sEMG naturally controlled robotic hand prosthetics. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; Volume 2015-Novem, pp. 7151–7154. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Ryait, H.S.; Arora, A.S.; Agarwal, R. SEMG signal analysis at acupressure points for elbow movement. J. Electromyogr. Kinesiol. 2011, 21, 868–876. [Google Scholar] [CrossRef] [PubMed]
- Supuk, T.G.; Skelin, A.K.; Cic, M. Design, development and testing of a low-cost sEMG system and its use in recording muscle activity in human gait. Sensors 2014, 14, 8235–8258. [Google Scholar] [CrossRef] [PubMed]
- Gooch, J.W. Pearson Correlation Coefficient. In Encyclopedic Dictionary of Polymers; Springer: Berlin/Heidelberg, Germany, 2011; p. 990. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. 1803. [Google Scholar]
- Ketkar, N. Introduction to PyTorch BT-Deep Learning with Python: A Hands-on Introduction; Apress: Berkeley, CA, USA, 2017; pp. 195–208. [Google Scholar] [CrossRef]
- Atzori, M.; Gijsberts, A.; Castellini, C.; Caputo, B.; Hager, A.G.M.; Elsig, S.; Giatsidis, G.; Bassetto, F.; Müller, H. Electromyography data for non-invasive naturally-controlled robotic hand prostheses. Sci. Data 2014, 1, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, C.; Zhang, X.; Yu, G.; Luo, G.; Sun, J. Large kernel matters - Improve semantic segmentation by global convolutional network. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Honolulu, HI, USA, 21–26 July 2016; pp. 1743–1751. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.H.; Krishna, T.; Emer, J.S.; Sze, V. Eyeriss: An Energy-Efficient Reconfigurable Accelerator for Deep Convolutional Neural Networks. IEEE J. Solid-State Circuits 2017, 52, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhou, L.; Xie, W.; Chen, W.; Su, J.; Chen, W.; Du, A.; Li, S.; Liang, M.; Lin, Y.; et al. Accelerating hybrid and compact neural networks targeting perception and control domains with coarse-grained dataflow reconfiguration. J. Semicond. 2020, 41, 022401. [Google Scholar] [CrossRef]
- Precup, R.E.; David, R.C. Nature-Inspired Optimization Algorithms for Fuzzy Controlled Servo Systems; Butterworth-Heinemann: Oxford, UK, 2019; p. iv. [Google Scholar] [CrossRef]
- Haber, R.E.; Beruvides, G.; Quiza, R.; Hernandez, A. A Simple Multi-Objective Optimization Based on the Cross-Entropy Method. IEEE Access 2017, 5, 22272–22281. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Guo, W.; Ma, C.; Yang, Y.; Wang, Z.; Lin, C. sEMG-Based Continuous Estimation of Finger Kinematics via Large-Scale Temporal Convolutional Network. Appl. Sci. 2021, 11, 4678. https://doi.org/10.3390/app11104678
Chen C, Guo W, Ma C, Yang Y, Wang Z, Lin C. sEMG-Based Continuous Estimation of Finger Kinematics via Large-Scale Temporal Convolutional Network. Applied Sciences. 2021; 11(10):4678. https://doi.org/10.3390/app11104678
Chicago/Turabian StyleChen, Chao, Weiyu Guo, Chenfei Ma, Yongkui Yang, Zheng Wang, and Chuang Lin. 2021. "sEMG-Based Continuous Estimation of Finger Kinematics via Large-Scale Temporal Convolutional Network" Applied Sciences 11, no. 10: 4678. https://doi.org/10.3390/app11104678
APA StyleChen, C., Guo, W., Ma, C., Yang, Y., Wang, Z., & Lin, C. (2021). sEMG-Based Continuous Estimation of Finger Kinematics via Large-Scale Temporal Convolutional Network. Applied Sciences, 11(10), 4678. https://doi.org/10.3390/app11104678





