Detection of Ischemic Episodes Based on Two Consecutive Declines in the JT/ST Algebraic Relationship
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Description of the Experimental Setup
2.2. Corrected versus Noncorrected Cardiac Intervals
2.3. The Algorithm for the JT/ST Algebraic Relationship
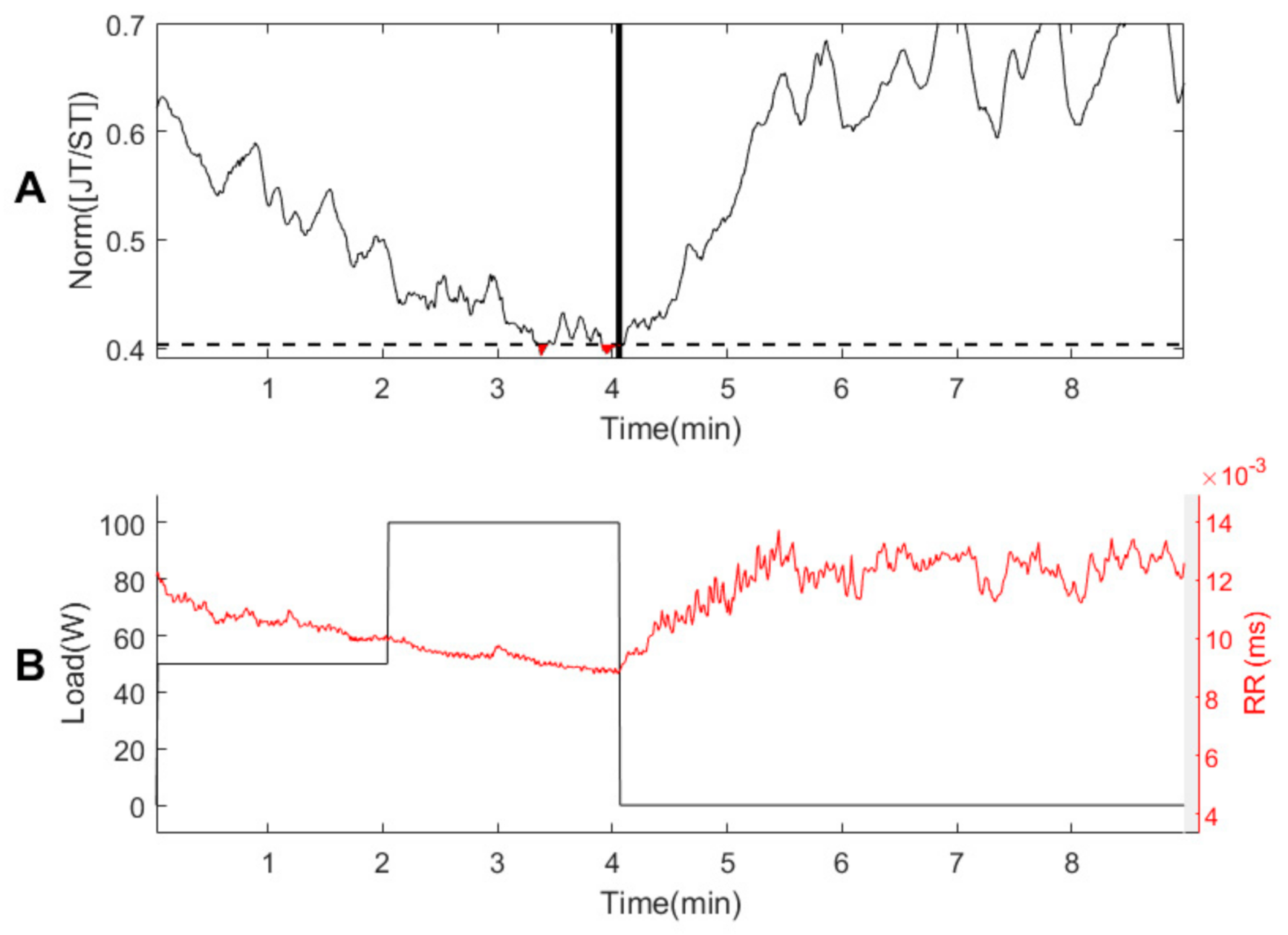
2.4. Qualitative Evaluation of Two Consecutive Declines in the JT/ST Algebraic Relationship
3. Results
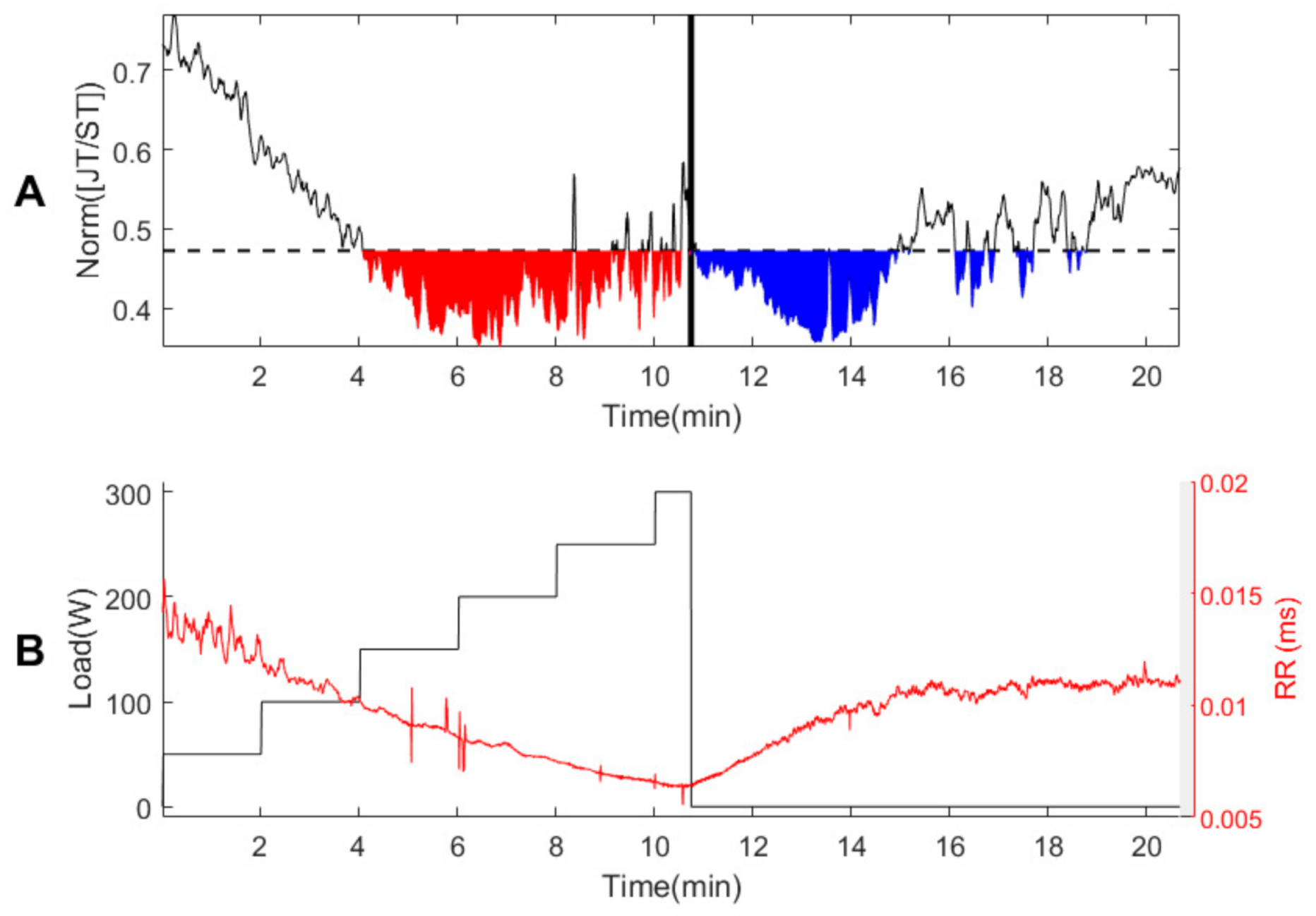
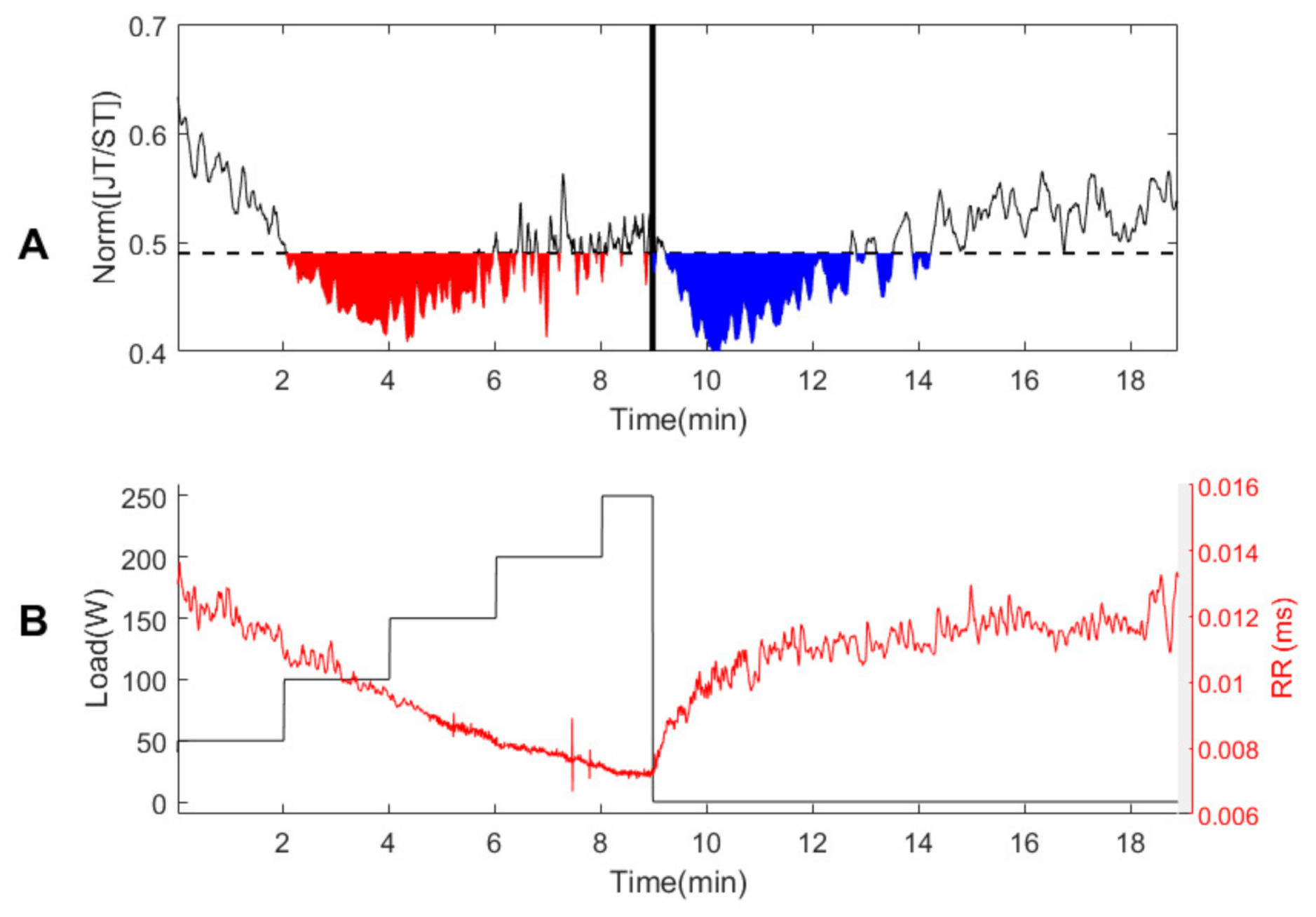
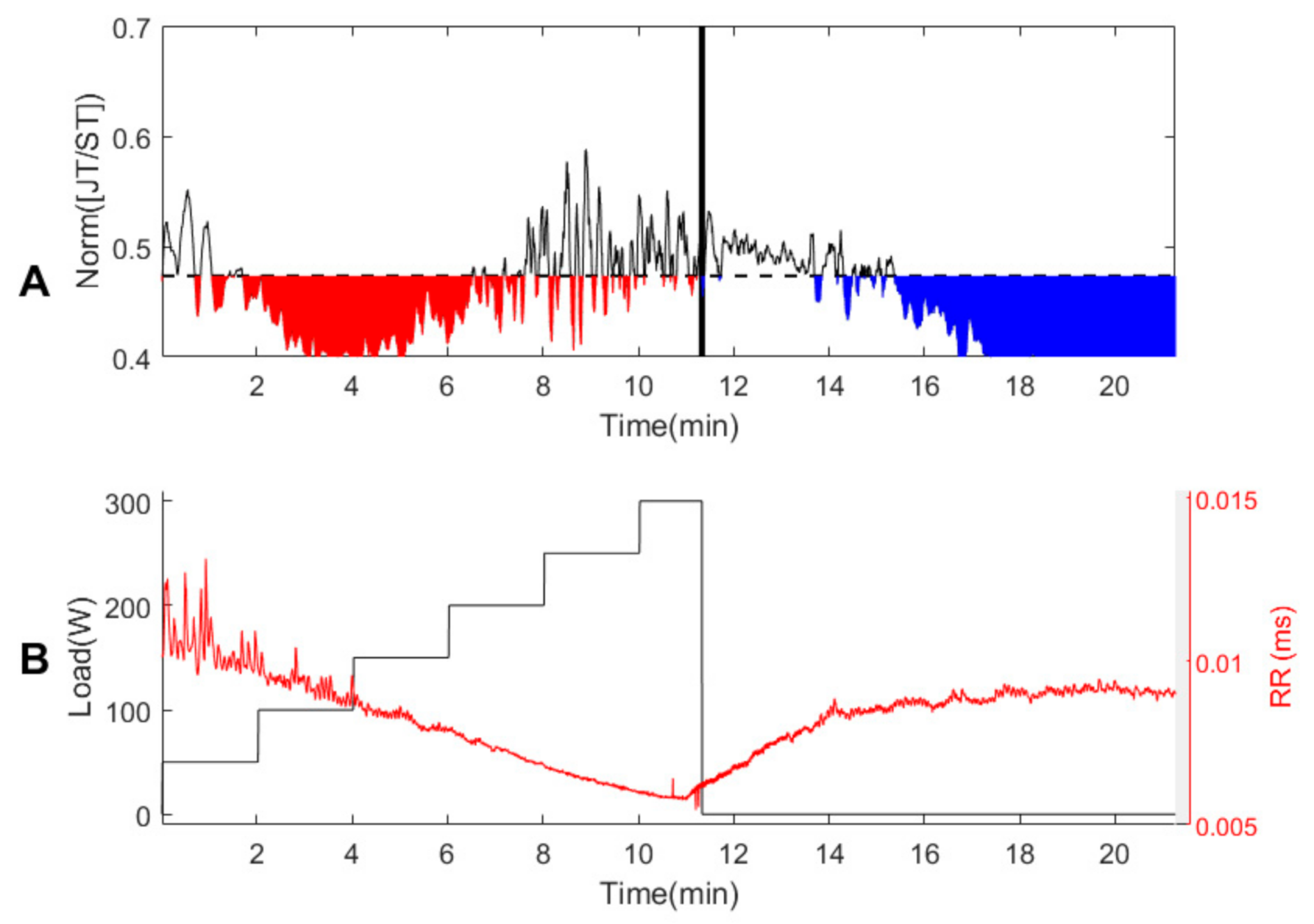
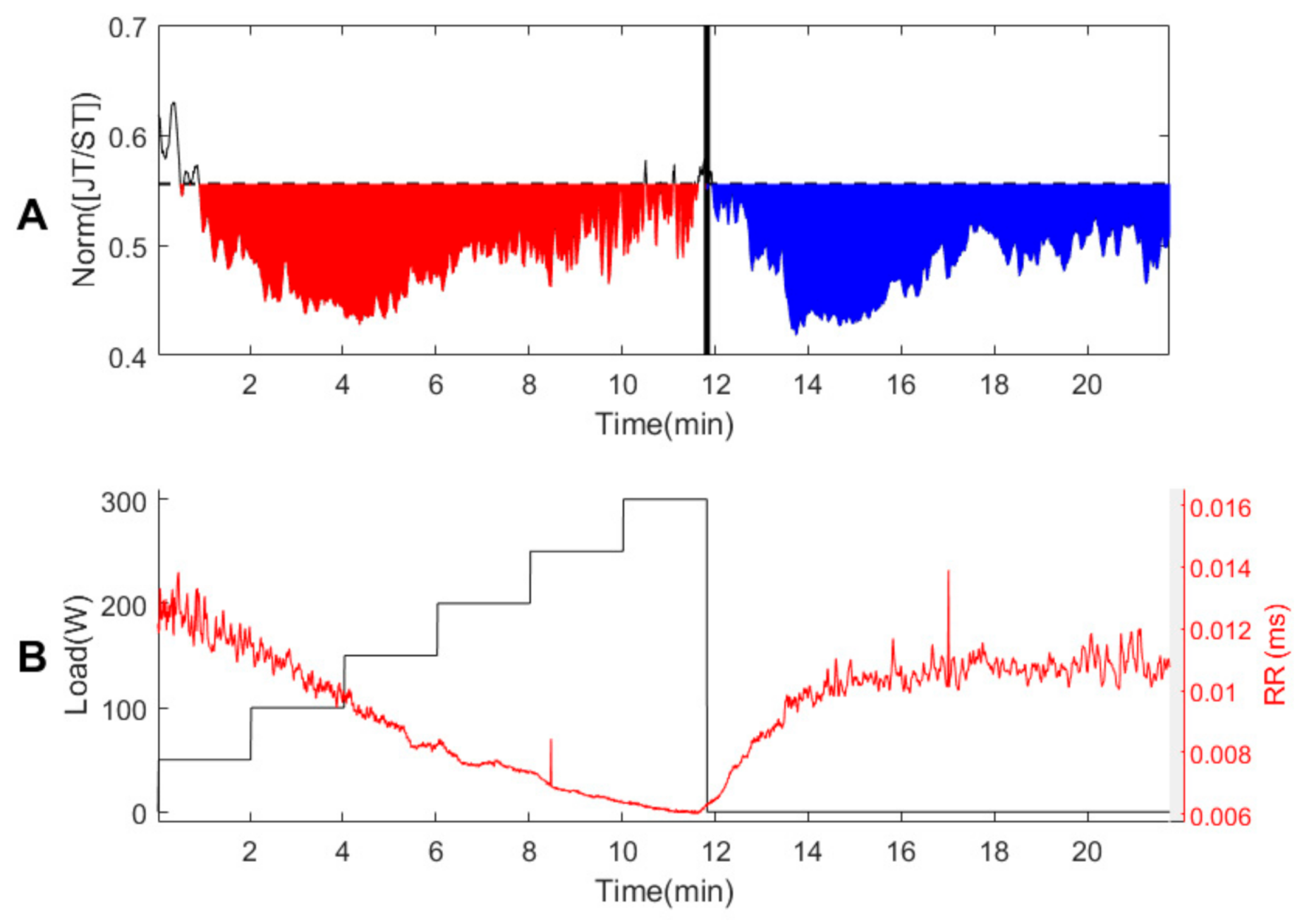
3.1. Person #1
3.2. Healthy Persons #2–#7
3.3. Persons with Suspected Ischemic Heart Disease #8–#10
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Seely, A.J.E.; Christou, N.V. Multiple organ dysfunction syndrome: Exploring the paradigm of complex nonlinear systems. Crit. Care Med. 2000, 28, 2193–2200. [Google Scholar] [CrossRef]
- Que, C.; Kenyon, C.; Olivenstein, R.; Macklem, P.; Maksym, G. Homeokinesis and short-term variability of human airway caliber. J. Appl. Physiol. 2001, 91, 1131–1141. [Google Scholar] [CrossRef] [PubMed]
- Muntianaitė-Dulkinienė, I.; Poškaitis, V.; Vainoras, A.; Jurevičius, J.; Bikulčienė, L.; Navickas, Z. Cointegration of Different ECG Parametres for Various Physical Tasks. Elektronika ir Elektrotechnika 2009, 94, 77–80. [Google Scholar]
- De Bruyne, M. Prolonged QT interval predicts cardiac and all-cause mortality in the elderly The Rotterdam Study. Eur. Heart J. 1999, 20, 278–284. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dekker, J.; Schouten, E.; Klootwijk, P.; Pool, J.; Kromhout, D. Association between QT interval and coronary heart disease in middle-aged and elderly men. The Zutphen Study. Circulation 1994, 90, 779–785. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Crow, R.; Hannan, P.; Folsom, A. Prognostic significance of corrected QT and corrected JT interval for incident coronary heart disease in a general population sample stratified by presence or absence of wide QRS complex. ACC Curr. J. Rev. 2004, 13, 28. [Google Scholar] [CrossRef]
- Rautaharju, P.M.; Zhang, Z.M.; Prineas, R.; Heiss, G. Assessment of prolonged QT and JT intervals in ventricular conduction defects. Am. J. Cardiol. 2004, 93, 1017–1021. [Google Scholar] [CrossRef] [PubMed]
- Ahnve, S. Correction of the QT interval for heart rate: Review of different formulas and the use of Bazett’s formula in myocardial infarction. Am. Heart J. 1985, 109, 568–574. [Google Scholar] [CrossRef]
- Goldenberg, I.; Moss, A.J.; Zareba, W. QT interval: How to measure it and what is “normal”. J. Cardiovasc. Electrophysiol. 2006, 17, 333–336. [Google Scholar] [CrossRef]
- Taylor-Piliae, R.E. Tai Chi as an Adjunct to Cardiac Rehabilitation Exercise Training. J. Cardiopulm. Rehabil. 2003, 23, 90–96. [Google Scholar] [CrossRef]
- Zarafshar, S.; Wong, M.; Singh, N.; Aggarwal, S.; Adhikarla, C.; Froelicher, V.F. Resting ST amplitude: Prognosis and normal values in an ambulatory clinical population. Ann. Noninvasive Electrocardiol. 2013, 18, 519–529. [Google Scholar] [CrossRef]
- Ziaukas, P.; Alabdulgader, A.; Vainoras, A.; Navickas, Z.; Ragulskis, M. New approach for visualization of relationships between RR and JT intervals. PLoS ONE 2017, 12, e0174279. [Google Scholar] [CrossRef] [PubMed]
- Saunoriene, L.; Siauciunaite, V.; Vainoras, A.; Bertasiute, V.; Navickas, Z.; Ragulskis, M. The characterization of the transit through the anaerobic threshold based on relationships between RR and QRS cardiac intervals. PLoS ONE 2019, 14, e0216938. [Google Scholar] [CrossRef] [PubMed]
- Vainoras, A.; Gargasas, L.; Ruseckas, R.; Miškinis, V.; Jurkonienė, R. Computerised exercise electrocardiogram analysis system “Kaunas-Load”. In Proceedings of the 24th international congress on Electrocardiology [and] 38th international symposium on Vectorcardiography: Abstracts book, Bratislava, Slovak, 24–28 June 1997. [Google Scholar]
- Gargasas, L.; Vainoras, A.; Ruseckas, R.; Jurkoniene, R.; Jurkonis, V.; Miskinis, V. A new software for ECG monitoring system. In NCeHT2006, Proceedings of the 6th Nordic Conference on eHealth and Telemedicine, Helsinki, Finland, 31 August–1 September 2006; Doupi, P., Ed.; Valopaino Oy: Helsinki, Finland, 2006; pp. 255–256. [Google Scholar]
- Bazett, H.C. An analysis of the time relations of electrocardiograms. Heart 1920, 7, 353–370. [Google Scholar] [CrossRef]
- Bretscher, O. Linear Algebra with Applications; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Vázquez, P.; Hristovski, R.; Balagué, N. The Path to Exhaustion: Time-Variability Properties of Coordinative Variables during Continuous Exercise. Front. Physiol. 2016, 7, 37. [Google Scholar] [CrossRef] [Green Version]
- Detrano, R.; Salcedo, E.; Passalacqua, M.; Friis, R. Exercise electrocardiographic variables: A critical appraisal. J. Am. Coll. Cardiol. 1986, 8, 836–847. [Google Scholar] [CrossRef]
- Kligfield, P.; Ameisen, O.; Okin, P.M. Relation of the exercise ST/HR slope to simple heart rate adjustment of ST segment depression. J. Electrocardiol. 1987, 20, 135. [Google Scholar]
- Elamin, M.; Mary, D.; Smith, D.; Linden, R. Prediction of severity of coronary artery disease using slope of submaximal ST segment/heart rate relationship. Cardiovasc. Res. 1980, 14, 681–691. [Google Scholar] [CrossRef]
- Kligfield, P.; Ameisen, O.; Okin, P. Heart rate adjustment of ST segment depression for improved detection of coronary artery disease. Circulation 1989, 79, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Lehtinen, R. ST/HR hysteresis: Exercise and recovery phase ST depression/heart rate analysis of the exercise ECG. J. Electrocardiol. 1999, 32, 198–204. [Google Scholar] [CrossRef]
- Bigi, R.; Maffi, M.; Occhi, G.; Bolognese, L.; Pozzoni, L.; Curti, G. Improvement in identification of multivessel disease after acute myocardial infarction following stress-recovery analysis of ST depression in the heart rate domain during exercise. Eur. Heart J. 1994, 15, 1240–1246. [Google Scholar] [CrossRef] [PubMed]
- Bigi, R.; Cortigiani, L.; Gregori, D.; Bax, J.; Fiorentini, C. Prognostic Value of Combined Exercise and Recovery Electrocardiographic Analysis. Arch. Intern. Med. 2005, 165, 1253. [Google Scholar] [CrossRef] [Green Version]
- Bigi, R.; Cortigiani, L.; Gregori, D.; Fiorentini, C. Comparison of the Prognostic Value of the Stress-Recovery Index Versus Standard Electrocardiographic Criteria in Patients with a Negative Exercise Electrocardiogram. Am. J. Cardiol. 2007, 100, 605–609. [Google Scholar] [CrossRef] [PubMed]
- Svart, K.; Lehtinen, R.; Nieminen, T.; Nikus, K.; Lehtimäki, T.; Kööbi, T.; Niemelä, K.; Niemi, M.; Turjanmaa, V.; Kähönen, M.; et al. Exercise electrocardiography detection of coronary artery disease by ST-segment depression/heart rate hysteresis in women: The Finnish Cardiovascular Study. Int. J. Cardiol. 2010, 140, 182–188. [Google Scholar] [CrossRef]
- Gargasas, L.; Vainoras, A.; Schwela, H.; Jaruševičius, G.; Ruseckas, R.; Miškinis, V. JT interval changes during bicycle ergometry. In Proceedings of the Kardiologia Polska: II Miedzynarodowy Kongres Polskiego Towarzystwa Kardiologieznego, Kotowice, Poland, 4–6 September 1998; Volume 49, pp. 1–153. [Google Scholar]
- Conconi, F.; Ferrrari, M.; Ziglio, P.G.; Droghetti, P.; Codeca, L. Determination of the anaerobic threshold by a noninvasive field test in runners. J. Appl. Physiol. 1982, 52, 862–873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ballarin, E.; Borsetto, C.; Cellini, M.; Patracchini, M.; Vitiello, P.; Ziglio, P.G.; Conconi, F. Adaptation of the “Conconi test” to children and adolescents. Int. J. Sports Med. 1989, 10, 334–338. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šiaučiūnaitė, V.; Vainoras, A.; Navickas, Z.; Ragulskis, M. Detection of Ischemic Episodes Based on Two Consecutive Declines in the JT/ST Algebraic Relationship. Appl. Sci. 2021, 11, 4805. https://doi.org/10.3390/app11114805
Šiaučiūnaitė V, Vainoras A, Navickas Z, Ragulskis M. Detection of Ischemic Episodes Based on Two Consecutive Declines in the JT/ST Algebraic Relationship. Applied Sciences. 2021; 11(11):4805. https://doi.org/10.3390/app11114805
Chicago/Turabian StyleŠiaučiūnaitė, Vaiva, Alfonsas Vainoras, Zenonas Navickas, and Minvydas Ragulskis. 2021. "Detection of Ischemic Episodes Based on Two Consecutive Declines in the JT/ST Algebraic Relationship" Applied Sciences 11, no. 11: 4805. https://doi.org/10.3390/app11114805
APA StyleŠiaučiūnaitė, V., Vainoras, A., Navickas, Z., & Ragulskis, M. (2021). Detection of Ischemic Episodes Based on Two Consecutive Declines in the JT/ST Algebraic Relationship. Applied Sciences, 11(11), 4805. https://doi.org/10.3390/app11114805







