Computational Modeling of Ultrasound C-Scan Imaging Using Transmitted Signal Peak Density
Abstract
1. Introduction
2. Finite Element Analysis (FEA) Simulation
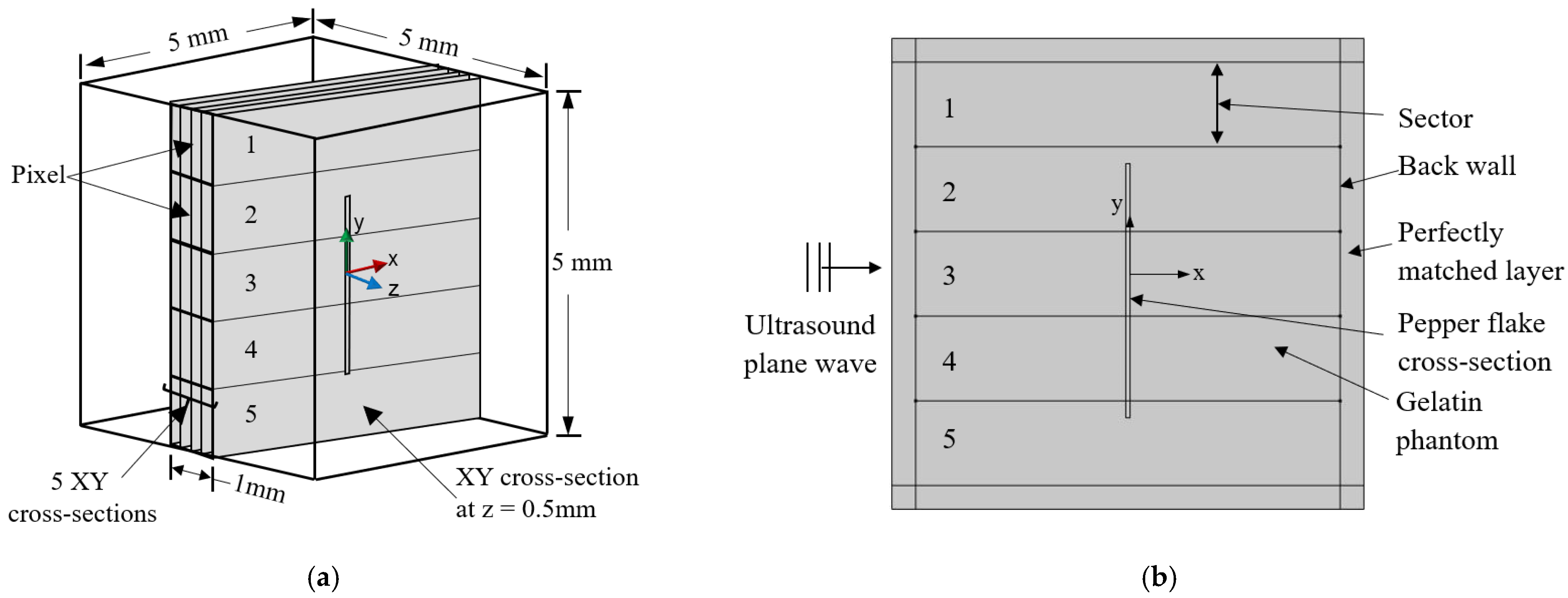
2.1. Model Description
2.2. Model Simplification
2.3. Simulation Physics
2.4. Results and Discussion
3. Structure Position Detection
3.1. Model Description
3.2. Results and Discussion
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mercado, K.P.E. Developing High-Frequency Quantitative Ultrasound Techniques to Characterize Three-Dimensional Engineered Tissues. Ph.D. Thesis, University of Rochester, Rochester, NY, USA, 2015. [Google Scholar]
- Nam, S.Y.; Ricles, L.M.; Suggs, L.J.; Emelianov, S.Y. Imaging Strategies for Tissue Engineering Applications. Tissue Eng. Part B Rev. 2015, 21, 88–102. [Google Scholar] [CrossRef]
- Szabo, T.L. Diagnostic Ultrasound Imaging: Inside Out; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Kremkau, F.W. Sonography Principles and Instruments; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Versaci, M.; Morabito, F.C. Image Edge Detection: A New Approach Based on Fuzzy Entropy and Fuzzy Divergence. Int. J. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Madhukumar, S.; Santhiyakumari, N. Evaluation of k-Means and fuzzy C-means segmentation on MR images of brain. Egypt. J. Radiol. Nucl. Med. 2015, 46, 475–479. [Google Scholar] [CrossRef]
- Gordon, G.; Canumalla, S.; Tittmann, B. Ultrasonic C-scan imaging for material characterization. Ultrasonics 1993, 31, 373–380. [Google Scholar] [CrossRef]
- Kundu, T.; Ehsani, M.; Maslov, K.; Guo, D. C-scan and L-scan generated images of the concrete/GFRP composite interface. NDT E Int. 1999, 32, 61–69. [Google Scholar] [CrossRef]
- Thornton, M.; Han, L.; Shergold, M. Progress in NDT of resistance spot welding of aluminium using ultrasonic C-scan. NDT E Int. 2012, 48, 30–38. [Google Scholar] [CrossRef]
- Růžek, R.; Lohonka, R.; Jironč, J. Ultrasonic C-Scan and shearography NDI techniques evaluation of impact defects identification. NDT E Int. 2006, 39, 132–142. [Google Scholar] [CrossRef]
- Restori, M.; Wright, J.E. C-scan ultrasonography in orbital diagnosis. Br. J. Ophthalmol. 1977, 61, 735–740. [Google Scholar] [CrossRef]
- Hasiotis, T.; Badogiannis, E.; Tsouvalis, N.G. Application of Ultrasonic C-Scan Techniques for Tracing Defects in Laminated Composite Materials. J. Mech. Eng. 2011, 2011, 192–203. [Google Scholar] [CrossRef]
- Ye, S.; Harasiewicz, K.; Pavlin, C.; Foster, F. Ultrasound characterization of normal ocular tissue in the frequency range from 50 MHz to 100 MHz. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 8–14. [Google Scholar] [CrossRef]
- Jin, H.; Liu, S.; Zhang, R.; Liu, S.; Zheng, Y. Frequency Domain Based Virtual Detector for Heterogeneous Media in Photoacoustic Imaging. IEEE Trans. Comput. Imaging 2020, 6, 569–578. [Google Scholar] [CrossRef]
- Imielińska, K.; Castaings, M.; Wojtyra, R.; Haras, J.; Le Clezio, E.; Hosten, B. Air-coupled ultrasonic C-scan technique in impact response testing of carbon fibre and hybrid: Glass, carbon and Kevlar/epoxy composites. J. Mater. Process. Technol. 2004, 157–158, 513–522. [Google Scholar] [CrossRef]
- Garcia, J. A 3-dimensional ultrasound C-scan imaging technique for optic nerve measurements. Ophthalmology 2004, 111, 1238–1243. [Google Scholar] [CrossRef] [PubMed]
- Ghoshal, G.; Oelze, M.L.; O’Brien, W.D., Jr. Quantitative Ultrasound History and Successes. In Quantitative Ultrasound in Soft Tissues; Springer: Dordrecht, The Netherlands, 2013; pp. 21–42. [Google Scholar]
- Gudur, M.; Rao, R.R.; Hsiao, Y.-S.; Peterson, A.W.; Deng, C.X.; Stegemann, J.P. Noninvasive, Quantitative, Spatiotemporal Characterization of Mineralization in Three-Dimensional Collagen Hydrogels Using High-Resolution Spectral Ultrasound Imaging. Tissue Eng. Part C Methods 2012, 18, 935–946. [Google Scholar] [CrossRef] [PubMed]
- Lizzi, F.L.; Ostromogilsky, M.; Feleppa, E.J.; Rorke, M.C.; Yaremko, M.M. Relationship of ultrasonic spectral parameters to features of tissue microstructure. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 319–329. [Google Scholar] [CrossRef] [PubMed]
- Sethuraman, S.; Amirian, J.H.; Litovsky, S.H.; Smalling, R.W.; Emelianov, S.Y. Ex vivo Characterization of Atherosclerosis using Intravascular Photoacoustic Imaging. Opt. Express 2007, 15, 16657–16666. [Google Scholar] [CrossRef]
- Doyle, T.E.; Factor, R.E.; Ellefson, C.L.; Sorensen, K.M.; Ambrose, B.J.; Goodrich, J.B.; Hart, V.P.; Jensen, S.C.; Patel, H.; Neumayer, L.A. High-frequency ultrasound for intraoperative margin assessments in breast conservation surgery: A feasibility study. BMC Cancer 2011, 11, 444. [Google Scholar] [CrossRef]
- Stromer, J.; Ladani, L. Investigating ultrasound imaging in the frequency domain for tissue characterisation. Nondestruct. Test. Eval. 2015, 31, 209–218. [Google Scholar] [CrossRef]
- Ladani, L.; Paul, K.; Stromer, J. High-Frequency Ultrasound Analysis in Both Experimental and Computation Level to Understand the Microstructural Change in Soft Tissues. In Minerals, Metals and Materials Series; Springer International Publishing: Berlin/Heidelberg, Germany, 2019; pp. 87–97. [Google Scholar]
- Paul, K.; Ladani, L. Relationship between peak density and acoustic scattering in high-frequency ultrasound wave propagation. SN Appl. Sci. 2020, 2, 1–12. [Google Scholar] [CrossRef]
- Nam, J.; Byun, J.; Kim, T.; Kim, M.; Kim, D. Measurement of Mechanical and Physical Properties of Pepper for Particle Behavior Analysis. J. Biosyst. Eng. 2018, 43, 173–184. [Google Scholar]
- Delrue, S.; Abeele, K.V.D.; Blomme, E.; Deveugele, J.; Lust, P.; Matar, O.B. Two-dimensional simulation of the single-sided air-coupled ultrasonic pitch-catch technique for non-destructive testing. Ultrasonics 2010, 50, 188–196. [Google Scholar] [CrossRef] [PubMed]
- Stromer, J.; Ladani, L. Examination of a spectral-based ultrasonic analysis method for materials characterization and evaluation. Biomed. Signal Process. Control 2018, 40, 454–461. [Google Scholar] [CrossRef]
- Lashkari, B.; Yang, L.; Mandelis, A. The application of backscattered ultrasound and photoacoustic signals for assessment of bone collagen and mineral contents. Quant. Imaging Med. Surg. 2015, 5, 46–56. [Google Scholar] [PubMed]
- Xi, L.; Zhou, L.; Jiang, H. C-scan photoacoustic microscopy for invivo imaging of Drosophila pupae. Appl. Phys. Lett. 2012, 101, 013702. [Google Scholar] [CrossRef]










| Gelatin Phantom (Fluid Region) | |
| Density | |
| Sound velocity | |
| Attenuation coefficient () | 8.05 Np/m-MHz |
| Soft pepper flake (Solid domain) | |
| Young’s modulus | |
| Density | |
| Poisson’s ratio | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paul, K.; Stromer, J.; Razmi, S.; Pockaj, B.A.; Ladani, L.; Razmi, J. Computational Modeling of Ultrasound C-Scan Imaging Using Transmitted Signal Peak Density. Appl. Sci. 2021, 11, 4924. https://doi.org/10.3390/app11114924
Paul K, Stromer J, Razmi S, Pockaj BA, Ladani L, Razmi J. Computational Modeling of Ultrasound C-Scan Imaging Using Transmitted Signal Peak Density. Applied Sciences. 2021; 11(11):4924. https://doi.org/10.3390/app11114924
Chicago/Turabian StylePaul, Koushik, Jeremy Stromer, Samuel Razmi, Barbara A. Pockaj, Leila Ladani, and Jafar Razmi. 2021. "Computational Modeling of Ultrasound C-Scan Imaging Using Transmitted Signal Peak Density" Applied Sciences 11, no. 11: 4924. https://doi.org/10.3390/app11114924
APA StylePaul, K., Stromer, J., Razmi, S., Pockaj, B. A., Ladani, L., & Razmi, J. (2021). Computational Modeling of Ultrasound C-Scan Imaging Using Transmitted Signal Peak Density. Applied Sciences, 11(11), 4924. https://doi.org/10.3390/app11114924








