A Multi-Criteria Decision-Making Approach for Ideal Business Location Identification

Abstract

Location has always been a primary concern for business startups to be successful. Therefore, much research has focused on the problem of identification of an ideal business site for a new business. The process of ideal business site selection is complex and depends on a number of criteria or factors. Since the ultimate goal of all businesses is to increase customer footprints and to thus increase sales, criteria including traffic accessibility, visibility, ease of access, vehicle parking, customers availability, etc. play important roles. In other words, we can say that optimal business site selection is a multi-criteria decision-making (MCDM) problem. MCDM is used to identify an optimal solution or decision out of many alternatives by utilizing a number of criteria. In mathematics, there exist a number of structured techniques for organizing and analyzing complex decisions, for instance, AHP, ANP, TOPSIS, etc. In this work, we present a hybrid of two such techniques to solve the MCDM problem for an optimal business site selection given a set of candidate sites. The proposed approach is based on the AHP (Analytic Hierarchy Process) and TOPSIS (The Technique for Order of Preference by Similarity to Ideal Solution) approaches. The reason for using the proposed hybrid approach is multi-fold. The hybrid approach reduces the computational complexity and require less manual effort, thus improving the efficiency and accuracy of the proposed approach. Given a set of candidate locations for a new business, the proposed approach ranks the candidates. Thus, the candidate locations with higher ranks are identified as suitable or ideal. The approach comes up with the ranking of all of the candidate locations, thus giving business managers room to make calculated decisions. To show the effectiveness of the proposed approach, a detailed step-by-step case study is given to identify an ideal location in New York City for a new gas station. Furthermore, an experimental evaluation is also presented using a number of real New York City datasets.

1. Introduction

The location of a brick and mortar business plays a vital role in its success or failure. In order to keep investors happy and to avoid any financial losses, it is necessary to select an optimal site for a new business. The term “optimal” refers to a location that may be suitable for a new business and that yields paybacks. However, the identification of optimal sites does not depend on any one factor. There are several aspects that require consideration, such as competition in the area, the target customers’ convenience in terms of accessibility, the convenience of suppliers, traffic congestion in the area, etc. The selection of an optimal business site is a multi-criteria decision-making (MCDM) [1,2] problem. MCDM involves dealing with decisions where the choice of an alternative site is provided by several potential candidates while considering several criteria [3,4,5].

Since this problem poses great challenges, there are several related research papers that suggest different algorithms for the identification of an ideal location to open new business. Most of these approaches are either data based [6] or survey based [7,8]. Data-based approaches take into consideration only a single criteria in their evaluation, which results in biased decisions, whereas survey-based approaches lack the use of real data and are based on the opinion of a small group of people. Our argument is that, in big cities, for the selection of an optimal business site such as gas stations, convenience stores, restaurants, etc., a multi-criteria-based approach must be employed, and it should be applied on some real data for evaluation.

There is disagreement upon the decision of a suitable site for a new commercial opening as there are several criteria to be considered and some of them are more important/significant than others. For instance, for a gasoline station, ease of access for vehicles is an extremely important criteria, whereas for a convenience store, it is not so important. Based on the significance, different weights need to be assigned to different criteria. Hence, in this work, we present an AHP (Analytic Hierarchy Process)/TOPSIS (The Technique for Order of Preference by Similarity to Ideal Solution)-based approach [9,10], which choses an optimal site for a commercial opening when given a set of candidate sites. The techniques of AHP and TOPSIS are termed multi-criteria decision-making (MCDM) [1,2]. They are employed to derive criteria/factors’ weight and to provide the ranking of alternatives/options. Although both approaches can be used to solve the MCMD problem separately, individually, each approach has some limitations. For instance, AHP alone is a very flexible and powerful MCDM tool and the computations made by AHP are always guided by the decision maker’s experience. However, if the decision maker’s understanding about the alternatives is not good enough, it can lead to inaccurate results. On the other hand, AHP alone requires a large number of evaluations by the user, especially for problems with many criteria and alternatives [11]. In fact, the number of pairwise comparisons grows quadratically with the number of criteria and options. This is discussed with an example in Section 4. To tackle this issue, Sangiorgio et al. proposed an optimized-AHP (O-AHP) method for the generation of a judgment matrix by using a mathematical programming formulation. According to the authors, O-AHP exhibits the same effectiveness as the standard AHP and can be easily applied to a large number of alternatives [12]. In [13], the authors use augmented reality-based decision-making (AR-DM) for the multicriteria analysis approach. The approach starts with problem structuring using a flowchart similar to that of the AHP and proceeds with new phases inspired from the SRF method. On the other hand, TOPSIS does not support criteria weight computation and must be combined with some technique to compute the weights. Usually AHP or entropy weights are used with TOPSIS [14]. Thus, in this work, we propose the use of an AHP/TOPSIS hybrid approach.

The hybrid approach results in (1) lowering of the computational complexity and (2) easing the manual effort needed for the construction of AHP pairwise comparison matrices. Here, all of the candidate sites are ranked based on their performance scores and the optimal site is identified as the candidate with the highest score. The decision makers are given flexibility to chose the optimal site in the form of top ranked alternatives based on the performance scores of all of the candidates/alternatives.

Since the AHP/TOPSIS approach consists of a number of steps, a detailed step-by-step case study is presented to identify an optimal location for a new gas station in New York City by employing four criteria. To assess the effectiveness of the proposed approach, an experimental evaluation is performed to select an optimal location of a convenience store making use of five criteria. The proposed approach presented here is flexible and can effectively incorporate any number of criteria to rank the candidates. This is an extended version of our work published in [15]. The main contributions of the extended work can be summarized as follows:

• A comprehensive flowchart showing the flow of important steps in the proposed AHP/TOPSIS approach (Section 5);
• An experimental evaluation utilizing real datasets to select an optimal location of a convenience store using the proposed AHP/TOPSIS approach (Section 6); and
• A detailed discussion on the evaluation results and the strength and weaknesses of the proposed AHP/TOPSIS approach (Section 7).

The rest of the paper is organized as follows: Section 2 discusses the related work. In Section 3, the problem formulation is presented. Section 4 elaborates two multi-criteria decision-making approaches. In Section 5, a case study is shown for the selection of an optimal location for a gas station. Section 6 presents experimental details for the evaluation of the proposed AHP/TOPSIS approach, while Section 7 discusses the evaluation results and the strength and weaknesses of the AHP/TOPSIS approach. Section 8 concludes the manuscript with the possible future directions.

2. Related Work

In this section, we present a few works related to optimal site selection of a commercial opening and the multi-criteria decision-making including AHP and TOPSIS approaches.

2.1. Computing the Best Alternative for a Commercial Opening

The research by J.Bean [16] provides an analysis of the prediction of a location for a new store by Starbucks. Various types of statistical analysis were applied for the identification of a suitable location to open a new Starbucks store. The results helped narrowed down the search for a location in the United States to find the best suitable location of a new Starbucks store. The authors were able to determine the success and popularity of existing businesses, difficulty accessing the store location, and peak rush hours. They also assisted in the development of a system to identify desirable locations for new businesses in that locality.

In [3], the authors presented a hierarchy of factors for selecting the best gas station site. In the study, the Analytic Hierarchy Process (AHP) methodology was used to calculate the relative importance of criteria and the sub-criteria in accordance with the aggregate opinions of experts. However, to compute the criteria in this work, the authors made use of a survey rather than real data as in our case.

The authors in [6] utilized machine learning features on the popularity of retail stores in the city through the use of a dataset collected from FourSquare. Their analysis is mainly focused on three different commercial chains, i.e., Starbucks, Dunkin Donuts, and McDonalds. The features that they mine are based on two general signals: geographic, where features are formulated according to the types and density of nearby places, and user mobility, which includes transitions between venues or the incoming flow of mobile users from distant areas. Their evaluation suggests that the success of a business may depend on multiple factors/criteria, which supports our study of a multi-criteria decision-making approach for an ideal business site selection.

The authors of [17] discussed a wide range of factors that are useful for decision-making such as whether it would be beneficial to open a commercial store in a certain locality. They identified the factors as being competition, vehicle ownership, and traffic rush in a locality, which may assist in making a decision about a new commercial store to ensure its success.

2.2. Multi-Criteria Decision-Making

In [18], the authors employed Fuzzy AHP for the selection of a new site for a hospital using the factors travel time and population density surrounding the new site of a hospital. The authors of [19] used AHP and spactial data in an attempt to determine candidate landfill sites. As a result, they were able to find the best, good, and unsuitable landfill areas. Awasthi et al. in [20] presented a TOPSIS-based approach for location planning under uncertainty. The uncertainty in their work was used to handle the lack of real data in location planning. In contrast, this work makes extensive use of real spatial data to compute alternative locations’ factors/criteria computation. We believe that the use of real data can give us more accurate results. Furthermore, we made use of real spatial data to evaluate our approach.

Besides their individual use, the AHP/TOPSIS approach is frequently used together for different multi-criteria decision-making problems. For instance, the authors in [21] made use of the AHP/TOPSIS hybrid approach to identify and rank the solutions of RL (reverse logistics) adoption to overcome its barriers. Fuzzy AHP is applied to obtain the weights of the barriers as criteria by pairwise comparison, and the final ranking of the solutions of RL adoption is obtained using fuzzy TOPSIS. The authors in [22] utilized the AHP/TOPSIS approach to select the best alternative, with an aim to improve the electronic supply chain management (e-SCM) performance of an Indian automobile industry. Supraja et al. [23] utilized AHP/TOPSIS to solve the problem of selection of a branch of students for the “All Round Excellence Award” from an engineering college.

A CSPCM/TOPSIS approach for the quantification of accessibility to market facilities in rural areas was studied by Niaz et al. [24]. The authors made use of the Constant-Sum Paired-Comparison Method (CSPCM) to weight the factors and TOPSIS to rank the accessibility to market facilities. The study evaluated the accessibility of different urban and rural markets by using four factors, i.e., distance, time, cost, and road condition. Their study was mainly based on survey, i.e., a total of 335 questionnaire surveys were conducted from the whole study area (ten sub-districts) or, on average, 33.5 surveys per district, which is quite a small number for a district and is highly prone to bias. In contrast, we propose a real spatial data-based approach in this work, i.e., several million real dataset records and a spatial distance function are used to compute the criteria/factors weight. Furthermore, the accuracy of the obtained results are evaluated against real customer footprints.

Emrah et al. [25] proposed a supplier selection analysis model considering both the AHP and TOPSIS method. Subjective and objective opinions of purchase managers/experts are quantified using AHP. The TOPSIS technique is used for calculating the supplier’s ratings. The aim of their research is to determine the appropriate supplier providing the most customer satisfaction for the criteria identified in the supply chain.

The proposed work presented in this paper provides a hybrid AHP/TOPSIS approach for pointing out an optimal site to open a commercial store. The reasons for selecting the AHP and TOPSIS methods are multi-fold. First and foremost is that the AHP and TOPSIS are among the most widely adopted MCDM techniques due to their simplicity and accuracy [26]. Secondly, when combined, they can reduce the computational efforts required to rank the alternatives. Other MCDM methods such as ANP, BWM, ELECTRE, or PROMETHEE would have been considered if one of our goals was not lowering the computational complexity and time required to find the ranking. Furthermore, TOPSIS works well with AHP quite nicely; that is, AHP is good for computing the criteria weights, while TOPSIS is good for ranking based on given weights. With other MCDM methods, such a hybrid approach is either not possible or not effective while non-hybrid approaches are computationally not feasible.

3. Problem Formulation

The proposed approach aims to identify the best location for a new commercial opening given a candidate set of locations. In accordance with this aim, the problem can be defined as follows:

Let us suppose that an enterprise wants to open a new business and is provided with a set of candidate locations L to chose from. The optimal location $l\in L$ such that the newly opened business at l attracts the largest number of customers is always preferred. Besides the identification of an optimal site, it is significant to rank each candidate site in L based on its performance score obtained using the AHP/TOPSIS hybrid method. The candidate locations ranking is generated by assigning top ranks to those locations that have higher scores. The location with the top rank is identified as the best site. Each candidate site in L is given in terms of the geographical coordinate system, i.e., in terms of longitude and latitude. Since AHP and TOPSIS are multi-criteria decision-making approaches and require multiple factors to compute the performance score of each candidate location, multiple spatiotemporal datasets are utilized to compute these factors.

4. AHP/TOPSIS-Based Multi-Criteria Decision-Making

The AHP (Analytic Hierarchy Process)/TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution)-based hybrid approach is proposed in this research to compare a number of factors/criteria (in the following, criteria and factors are used interchangeably) and provides the rank based on those factors for each candidate. Many researchers have used either AHP or TOPSIS to find the best alternative from several potential candidates [3,4,5], since they are two different multi-criteria decision-making (MCDM) methods [1,2]. With the assistance of the approaches mentioned above, a set of criteria can be evaluated to rank the alternatives. The purpose of using AHP is to determine the criteria weights, and TOPSIS employs the weights obtained from AHP in order to rank the alternatives; however, on many occasions, the two approaches are combined to obtain optimal results [27]. AHP/TOPSIS refers to the mechanism where TOPSIS uses AHP weights. The reasons behind the use of this hybrid approach in this article, are as follows:

• It helps lower the computational complexity.
• It eases the manual effort needed for the construction of the AHP pairwise comparison matrices.

Although AHP alone is a very flexible and powerful MCDM tool, the computations made by AHP are always guided by the decision maker’s experience, and AHP can thus be considered a tool that is able to translate the evaluations made by the decision maker into a multi-criteria ranking. However, if the decision maker’s understanding about the alternatives is not good enough, it can lead to inaccurate results. On the other hand, AHP alone requires a large number of evaluations by the user, especially for problems with many criteria and alternatives [11]. In fact, the number of pairwise comparisons grows quadratically with the number of criteria and options. Let us discuss the following example to understand the proposed approach.

Example 1.

In this example, the best alternative is computed from a set of 10 alternatives using five criteria. Only two alternatives are taken at a time by AHP and a comparison matrix is constructed by comparing their criteria one by one. As a result, the best one is found among the 10 alternatives via AHP. A total of $\left(\genfrac{}{}{0pt}{}{10}{2}\right)=55$ combinations are generated, i.e., a total of 55 comparison matrices need to be constructed. Each criteria is given some weight based on its importance. Hence, a comparison matrix of the criteria is necessary to obtain criteria weights. In total, 56 comparison matrices are required and each matrix has to be made with careful selection of the degree of importance for each matrix cell [11]. This process takes a lot of time, and the problem intensifies when the number of alternatives are increased. Once TOPSIS is applied after given the criteria weights, a single decision matrix is generated with the assistance of all of the alternatives simultaneously. The best alternative or ranking of the alternatives is generated with the help of this decision matrix.

The TOPSIS approach drastically reduces the computational complexity and the manual effort required in the AHP approach, but it does not assist in the formulation of a mechanism to compute the criteria weights.

Several researchers have adopted hybrid MCDM approaches to increase the overall efficiency. In [28], the authors suggested that the hybrid between AHP and Complex Proportional Assessment (COPRAS) to rank seven sustainable hydrogen production options helped reduce uncertainties in all phases of the task. In another research [13], AHP and SRF were combined to determine precast concrete panels for building retrofitting. They defined six criteria and evaluated seven visual rankings within 15 min, making it easier even for non-expert users to carry out the procedures. Sedghiyan et al. in [29] ranked seven alternatives of renewable energy sources with AHP, TOPSIS, and Simple Additive Weighting (SAW). The best renewable energy source in varied climate zones was identified if it was ranked best by any two methods. In [30], ten high-risk activities in the mining sector were identified in order to access them in a work environment. The risks were associated with multiple activities to generate a house of safety with the assistance of AHP and fuzzy inference. Keskin et al. in [31] proposed a hybrid AHP and Data Envelopment Analysis-Assurance Region (DEA-AR) model to measure the efficiency of public and private airports in Turkey. A total of five criteria were chosen, and 48 airports were ranked based on these criteria. In another research [32], nine risk criteria were chosen and five risk response alternatives were ranked in construction projects. They employed the Analytical Network Process (ANP) and Multi-Attributive Border Approximation Area Comparison (MABAC) techniques to reduce imprecision and fuzziness in the decision process. The work of [33] used a hybrid of AHP and Genetic Algorithms (GAs) to access ground water vulnerability in China. They optimized the land ratings from 1 to 10, where 10 indicates the highest potential to pollution, based on eight factors. In [34], Fuzzy AHP and Particle Swarm Optimization (PSO) techniques were used to solve the optimization model as a nonlinear system of equations. Their proposed method was scalable and was applied on various cases studies for prioritization even with an incomplete set of judgments.

Table 1. Hybrid MCDM approaches and their applications, strengths, and weaknesses.

Ref.	Hybrid MCDM Approach	Application(s)	Strength(s)	Weakness(es)
[28]	AHP and Complex Proportional Assessment (COPRAS)	Sustainable hydrogen production options	(1) Controls uncertainties in all phases. (2) Improves group decision-making.	Relied on data given by only four experts of the domain.
[13]	Augmented Reality (AR) and the Simos-Roy-Figueira (SRF)	Building retrofitting	(1) Visual information during the decision phase. (2) On average, takes 15 min to evaluate seven rankings.	The technique cannot be applied to non-graphical problems where 3D models are not required.
[29]	AHP, TOPSIS, and Simple Additive Weighting (SAW)	Renewable energy resources prioritization	(1) The best alternative is the one that is selected best by at least two methods. (2) Consumes a lot of time since ranking is generated using three methods.
[30]	AHP, House of Safety, and Fuzzy logic	Risk Assessment in Mining Sector	(1) Dependency of multiple events is considered. (2) Imprecise and vague structures are managed.	Results highly reliant on the input of occupational safety specialists.
[31]	AHP and Data Envelopment Analysis-Assurance Region (DEA-AR)	Efficiency scores of publicly or privately operated airports	Prevents extreme weight distribution.	The model can be discriminatory in some situations.
[32]	Analytical Network Process (ANP) and Multi-Attributive Border Approximation Area Comparison (MABAC)	Uncertain risk strategies in construction projects	Addresses uncertain information weighting risk criteria such as incompleteness and imprecision.	Computational time is high.
[33]	AHP and Genetic Algorithms (GAs)	Groundwater vulnerability assessment	Better results compared to DRASTIC [35] model.	Other contaminants except nitrate are not considered in this study.
[34]	Fuzzy AHP and Particle Swarm Optimization (PSO)	Professor selection/Investment prioritization	(1) Applied to group decision-making. (2) Solves the optimization model as a nonlinear system of equations.	PSO has a tendency to converge prematurely on early best solutions.

compares the various hybrid MCDM approaches along with their applications, strengths, and weaknesses.

This work proposes the use of an AHP/TOPSIS hybrid approach. The AHP/TOPSIS hybrid approach efficiently caters to weight computation and the problem of AHP having a large number of matrices to compute, i.e., using the hybrid approach, the criteria weights are determined by AHP while the alternatives are evaluated using TOPSIS. In evaluating the alternatives, the TOPSIS approach makes use of the weights computed via the AHP approach. Thus, for instance, if there are 10 alternatives, then the AHP approach alone requires 56 comparison matrices. Using the AHP/TOPSIS approach, this is reduced to two matrices, i.e., one matrix for criteria weight computation using AHP and the other matrix for alternative/candidate evaluation using TOPSIS. A short description of the two approaches is given in the following subsections, while the detailed step-by-step procedure of the proposed hybrid approach for the selection of an optimal site for a new business is presented with the help of a case study in Section 5.

4.1. Analytic Hierarchy Process (AHP)

The organization and analysis of complex decisions of mathematics and psychology is best achieved via the analytic hierarchy process (AHP). It was developed by Thomas L. Saaty [9,11] in 1970s and has been extensively studied and refined since then.

A set of evaluation criteria and alternative options are considered by the AHP, among which the best has to be selected. A weight for each evaluation criterion is generated by the AHP according to the decision maker’s pairwise comparisons of the criteria. The higher the weight, the more important the corresponding criterion is. In the next step, for a fixed criterion, AHP assigns a score to each option according to the decision maker’s pairwise comparisons of the options based on that criterion. The performance of the option is directly proportional to the score with respect to the considered criterion. Finally, the criteria weights and the options scores are combined by the AHP, which helps in assigning a global score to each option and eventually a consequent rannking. The global score for a given option is a weighted sum of the scores obtained with respect to all of the criteria [11]. The following are the steps taken during the AHP process.

• The problem is defined, the different criteria that are essential to decision-making are selected, and a hierarchical model is developed.
• A set of pairwise comparison matrix is constituted with the assistance of the criteria, and priorities (weights) are derived.
• The consistency of the comparison matrix is checked.
• Final decision is made based on the derived priorities.

4.2. The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS)

One of the multi-criteria decision-making (MCDM) methods is the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), which was created in 1981 by Ching-Lai Hwang et al. [10]. It is a compensatory aggregation method based on the idea that the ideal candidate or alternative must have the smallest geometric distance to a PIS (positive ideal solution) and the geometric farthest distance from an NIS (negative ideal solution) [36]. In other words, the benefit is maximized and cost is minimized by PIS; on the other hand, the benefit is minimized and cost is maximized by NIS. It is assumed that, for each criteria, maximization or minization is applied. TOPSIS requires normalization as the parameters or criteria are often of incongruous dimensions in multi-criteria problems [10,37]. Ranking a number of feasible alternatives based on the closeness to the ideal solution is best achieved via the TOPSIS approach. TOPSIS also avoids pair-wise comparisons, thus allowing it to be computed in a simple and efficient manner [25]. The TOPSIS method implementation can be summarized with the following steps [38]:

• Establish a decision matrix;
• Calculate a normalized decision matrix;
• Determine the weighted decision matrix;
• Identify the positive and negative ideal solutions;
• Calculate the separation distance of each competitive alternative from the ideal and non-ideal solutions;
• Measure the relative closeness of each location to the ideal solution; and
• Rank the preference order.

5. Case Study: An AHP/TOPSIS-Based Optimal Gas Station Site Selection

This section presents a case study to identify an optimal site for a new gas station. The case study makes use of the AHP/TOPSIS hybrid approach to compute the criteria weights and to choose the best option from among a finite set of decision alternatives. The four criterion values are computed using four real geospatial datasets. Although there could be several criteria affecting the new business site selection for an optimal gas station site, we followed the results of [7]. The authors presented a multi-criteria factor evaluation model for a gas station site selection. Their study was mainly based on a questionnaire/survey and they identified several important and crucial factors for site selection. Figure 1 presents a flowchart depicting the flow of important steps in the proposed AHP/TOPSIS approach. Among the factors they identified, we adopted the following four important factors in this study, listed with respect to their significance from top to down:

• Competitors in the area (competition);
• Traffic near the location (traffic);
• Popularity of the close-by businesses (area-popularity); and
• Approximate number of vehicles nearby residents own (vehicle-owners).

The appraoch in this study is empirical in contrast to the appraoch by [7] for the identification of a feasible location for a new gas station. In the Section 5.1, all of the datasets used in the study along with the prediction criteria are listed.

5.1. Dataset Analysis and Prediction Criteria

Four different geographical datasets used in this work are presented here for the computation of four different criteria.

5.1.1. Gas stations Dataset and the Competition Criterion

The NYC Open Data [39] provides the New York City gas stations data. Detailed addresses of the 416 gas stations present in New York City are provided in this dataset and shown in Figure 2. In this study, the competitors that are near the candidate gas stations are computed with the help of the reference dataset. According to [7], one of the most significant factors in identifying the ideal location for opening a gas station is the competitors in that area. The best location for a new gas station is the location with the least number of competitors.

Let us suppose that G represents the set of all gas stations in New York City, while g refers to the geographical location of a gas station. The competition criterion can be computed with the help of the number of gas stations within radius $r_g$ of each candidate location $l\in L$. Equation (1) explains the abovementioned appraoch.

$$\left|\right\{g\in G:dist(g,l)<r_g\left\}\right|$$

(1)

where the Euclidean distance between locations a and b is represented by $dist(a,b)$.

5.1.2. Traffic Estimates Dataset and the Traffic Criterion

With the assistance of the traffic estimate dataset, hourly average traffic information of all of the major and minor road segments of New York City is determined. This dataset includes the traffic estimates from 2010 to 2013, of the city based on the estimation of approximately 700 million taxi trips [40,41]. For the computation of traffic criteria, this dataset is exploited.

While observing all of the criteria, traffic is the second most important criterion that affects the gas station sales. In Figure 3, the locations are highlighted, where per hour traffic estimates are performed in New York City. The estimated traffic within radius $r_t$ of each $l\in L$ is computed to determine the traffic near the candidate locations. Here, the assumption is that T represents the set of points where traffic estimation for NYC is available and t represents the point at which the traffic is estimated. The traffic estimation within radius $r_t$ of each $l\in L$ is performed using Equation (2).

$$\left|\right\{t\in T:dist(t,l)<r_t\left\}\right|$$

(2)

5.1.3. FourSquare Check-Ins Dataset and the Area-Popularity Criterion

The area-popularity criterion can be easily found with a location-aware social networking application. Here, FourSquare is exploited to gather user check-in details at various business attractions to find out their popularity. The FourSquare dataset for this research work consists of check-in information within New York City from 12 April 2012 to 16 February 2013 (approx. 10 months). A total of 227,428 check-ins in New York City are contained in this data set and are shown in Figure 4. There is a time stamp, GPS coordinates, and some semantic meaning (expressed with the fine-grained venue-categories) connected to every check-in [42]. The area popularity factor is computed with the help of this check-in dataset.

Another significant factor for picking out a suitable location to open a new gas station is area popularity. The potential number of customers can be estimated with this criteria. A distance function, similar to that given in Equation (1), is used for finding the area popularity. Here, C represents the set of all check-ins in the dataset and $c\in C$ denotes an individual check-in instance at some geographical location. Hence, with the help of Equation (3), the total number of check-ins of each candidate location $l\in L$ within the radius $r_c$ are estimated.

$$\left|\right\{c\in C:dist(c,l)<r_c\left\}\right|$$

(3)

5.1.4. Parking Lot Datasets and the Vehicle-Owner Criterion

The NYC Open Data [39] also provides New York City parking lot data. A total of 20,715 parking lots in New York City are contained in this dataset along with their geographical location and the size (in terms of area). In Figure 5, polygons are used to show the location and the area of the parking lots. The criterion vehicle owners, i.e., the number of people who own a vehicle in the surroundings of the candidate gas stations are estimated by employing this dataset.

It is obvious that a gas station is accessed by vehicle owners only. Therefore, this criterion plays a significant role in this research. Although it is challenging to determine the actual number of people who own vehicles in New York City, the NYC Open Data provides parking lots details that can be processed for estimating this factor. An estimated number of parking slots per area can be obtained by dividing the area according to the parking standards [43,44]. Suppose that V represents the set of all parking lots; then, the function given in Equation (4) is employed to determine the approximate number of owned vehicles that are in close proximity to a candidate location $l\in L$ with the help of the approximate number of parking slots that are located within distance $r_v$ of l.

$$\left|\right\{v\in V:dist(v,l)<r_v\left\}\right|$$

(4)

5.2. Criteria Computation

In this step, the competitors, traffic, popularity, and vehicle owner criteria are considered to select an optimal gas station site. Once the set of candidate gas station sites is provided, the very first step is to compute the criteria. Second, the candidate sites are evaluated with the AHP/TOPSIS technique to identify the ideal site for a new gas station. In Figure 6, red stars represent the candidate gas station sites (provided by user) and green circles explicitly provide the location of existing gas station sites in New York City.

For the calculation of criteria traffic, popularity, vehicle owners, and competitors, the distance functions given in Section 5.1 and the radius values $r_t$: 1000, $r_c$: 1000, $r_v$: 5000, and $r_g$: 3000 m are used, respectively.

Table 2. Candidate sites factor computation.

CID	Alternatives	Factors
		Traffic	Popularity	Vehicle Owners	Competitors
		1000 m	1000 m	5000 m	3000 m
1	40.8839, −73.8561	2.91667	178	28,029	23
2	40.8095, −73.8807	3.89881	79	56,643	7
3	40.8347, −73.9177	228.345	631	42,954	32
4	40.7931, −73.9675	16,170.9	1171	19,815	7
5	40.7586, −73.9731	73,897.9	15,316	25,402	7
6	40.7699, −73.9271	2624.86	1276	47,071	13
7	40.7496, −73.8692	416.202	200	51,613	16
8	40.7231, −73.914	507.357	33	44,028	10
9	40.6686, −73.9321	110.815	340	30,995	38
10	40.6599, −73.8701	2.57738	122	33,898	20

shows the candidate sites’ computed criteria.

5.3. Criteria Weight Computation via AHP

In computing the factors’ weights, the very first step is the hierarchical model construction. The AHP hierarchical model consists of the goal at the top or at the root level. The criteria are placed at the intermediate level, whereas the candidates or alternatives are placed at the bottom. The AHP hierarchical model for our optimal site selection problem is shown in Figure 7.

The next step in the AHP is the construction of a pairwise comparison matrix A to compute the criteria priorities/weights. The matrix A is a $m\times m$ real matrix, where m is the number of evaluation criteria/factors considered. Each entry $a_{jk}$ of the matrix A represents the importance of the jth criterion relative to the kth criterion. If $a_{jk}>1$, then the jth criterion is more important than the kth criterion, while if $a_{jk}<1$, then the jth criterion is less important than the kth criterion. If two criteria have the same importance, then the entry $a_{jk}$ is 1. The entries $a_{jk}$ and $a_{kj}$ satisfy the following constraint [11]:

$$a_{jk}·a_{kj}=1$$

The following assumptions for the four factors are derived based on the pairwise comparison matrix.

Table 3. Pairwise comparison matrix.

Factors	Competitors	Traffic	Popularity	VOwners
Competitors	1	5	6	8
Traffic	0.2	1	5	7
Popularity	0.1667	0.2	1	3
Vehicle Owners	0.125	0.1429	0.3333	1

shows the pairwise comparison matrix.

• The most significant factor is the number of competitors nearby.
• The second most significant factor is nearby traffic, followed by popularity of the area.
• The least important factor found in this study is vehicle ownership in the vicinity.

The factors’ weight is computed after normalization of the pairwise comparison matrix. The normalized pairwise comparison matrix ${\mathit{A}}_{\mathit{norm}}$ is derived by making the sum of the entries in each column equal to 1, i.e., each entry ${\overline{a}}_{jk}$ of the matrix ${\mathit{A}}_{\mathit{norm}}$ is computed as

$${\overline{a}}_{jk}=\frac{a_{jk}}{{\sum }_{l=1}^m{a}_{lk}}$$

Ultimately, the criteria/factors weight vector w is obtained by averaging the entries on each row of the matrix ${\mathit{A}}_{\mathit{norm}}$ and can be computed as follows:

$$w_j=\frac{{\sum }_{l=1}^m{\overline{a}}_{jl}}{m}$$

Table 4. Normalized pairwise comparison matrix with factors weights.

Factors	Competitors	Traffic	Popularity	V Owners	Factors Weight
Competitors	0.676691	0.779221	0.529411	0.473684	0.614752121
Traffic	0.135338	0.155844	0.352941	0.315789	0.239978288
Popularity	0.112781	0.038961	0.088235	0.157895	0.099468256
V Owners *	0.07518	0.025974	0.029411	0.052631	0.045801335

* V Owners: Vehicle owners.

shows the normalized pairwise comparison matrix with the weights of the criteria. It is necessary to calculate the consistency of the pairwise comparison matrix; therefore, it is performed after criteria weight computation. The acceptance of the criteria weight w depends upon the consistency ratio, which must be less than 0.1; otherwise, it is assumed that the selection of comparison matrix values are not consistent. In this situtaion, the values of the pairwise comparison matrix need to be reallocated. In order for the matrix to be consistent, please refer to [9,25].

5.4. Ranking the Alternatives Using TOPSIS

Once the criteria weights are determined with the help of AHP [11], TOPSIS is utilized to assign ranks to each alternative (gas station candidate sites). According to the researchers in [10], TOPSIS is a multi-criteria decision analysis method (MCDM), which assists in selecting the best option among a finite set of decision alternatives. A step-by-step procedure is shown below for computing the ranking of the alternatives.

Step 1: This step makes use of TOPSIS to make an $n\times m$ evaluation matrix E consisting of n alternatives and m criteria. Without losing generality, 10 alternatives (gas station candidate sites as shown in Figure 6) and 4 criteria are chosen.

Table 5. Weighted normalized decision matrix.

ID	Candidates	Traffic	Popularity	Vehicle Owners	Competitors
1	40.8839, −73.8561	9.24677 × ${10}^{-6}$	1.14721 × ${10}^{-3}$	1.02115 × ${10}^{-2}$	2.21658 × ${10}^{-1}$
2	40.8095, −73.8807	1.23605 × ${10}^{-5}$	5.09158 × ${10}^{-4}$	2.06362 × ${10}^{-2}$	6.74612 × ${10}^{-2}$
3	40.8347, −73.9177	7.23926 × ${10}^{-4}$	4.06682 × ${10}^{-3}$	1.56490 × ${10}^{-2}$	3.08394 × ${10}^{-1}$
4	40.7931, −73.9675	5.12669 × ${10}^{-2}$	7.54714 × ${10}^{-3}$	7.21901 × ${10}^{-3}$	6.74612 × ${10}^{-2}$
5	40.7586, −73.9731	2.34279 × ${10}^{-1}$	9.87122 × ${10}^{-2}$	9.25446 × ${10}^{-3}$	6.74612 × ${10}^{-2}$
6	40.7699, −73.9271	8.32164 × ${10}^{-3}$	8.22387 × ${10}^{-3}$	1.71489 × ${10}^{-2}$	1.25285 × ${10}^{-1}$
7	40.7496, −73.8692	1.31949 × ${10}^{-3}$	1.28901 × ${10}^{-3}$	1.88036 × ${10}^{-2}$	1.54197 × ${10}^{-1}$
8	40.7231, −73.914	1.60848 × ${10}^{-3}$	2.12686 × ${10}^{-4}$	1.60403 × ${10}^{-2}$	9.63731 × ${10}^{-2}$
9	40.6686, −73.9321	3.51319 × ${10}^{-4}$	2.19131 × ${10}^{-3}$	1.12921 × ${10}^{-2}$	3.66218 × ${10}^{-1}$
10	40.6599, −73.8701	8.17112 × ${10}^{-6}$	7.86295 × ${10}^{-4}$	1.23497 × ${10}^{-2}$	1.92746 × ${10}^{-1}$
	$V_j^{+}$	2.34279 × ${10}^{-1}$	9.87122 × ${10}^{-2}$	2.06362 × ${10}^{-2}$	6.74612 × ${10}^{-2}$
	$V_j^{-}$	8.17112 × ${10}^{-6}$	2.12686 × ${10}^{-4}$	7.21901 × ${10}^{-3}$	3.66218 × ${10}^{-1}$

presents a TOPSIS evaluation matrix of the 10 candidate sites and 4 factors.

Step 2: In this step, the matrix $\mathit{E}$ is normalized to form the matrix ${\mathit{E}}_{\mathit{norm}}$, where each entry ${\overline{e}}_{ij}$ of ${\mathit{E}}_{\mathit{norm}}$ is computed as

$${\overline{e}}_{ij}=\frac{e_{ij}}{\sqrt{{\sum }_{k=1}^n{e}_{kj}^2}}$$

where $i=1,2,\dots ,n$ and $j=1,2,\dots ,m$.

Step 3: In this step, the weighted normalized decision matrix ${\mathit{E}}_{\mathit{weighted}}$ is obtained by multiplying the criteria weights $w_j$ (computed in Section 5.3) to the corresponding criteria values. Hence, each entry $e_{ij}^w$ of ${\mathit{E}}_{\mathit{weighted}}$ is computed as ${\overline{e}}_{ij}·w_j$. The weighted normalized decision matrix is represented by the grey columns in Table 5.

Step 4: Next, we determine the worst alternative ($V_j^{-}$) and the best alternative ($V_j^{+}$) for each column in ${\mathit{E}}_{\mathit{weighted}}$ as follows:

$$V_j^{-}=\{(ma{x}_i{e}_{ij}^w|j\in J_{-}),(mi{n}_i{e}_{ij}^w|j\in J_{+})\}$$

$$V_j^{+}=\{(mi{n}_i{e}_{ij}^w|j\in J_{-}),(ma{x}_i{e}_{ij}^w|j\in J_{+})\}$$

where $i=1,2,\dots ,n$, $J_{+}=\{j=1,2,\dots ,m\}$ is associated with the criteria having a positive impact and $J_{-}=\{j=1,2,\dots ,m\}$ is associated with the criteria having a negative impact.

Step 5: Next, we need to compute the Euclidean distance ($L^2-\mathrm{distance}$) between the target alternative i and the best alternative $V_j^{+}$ and between the target alternative i and the worst alternative $V_j^{-}$, denoted by $S_i^{+}$ and $S_i^{-}$, respectively, and given as follows:

$$S_i^{+}=\sqrt{\sum _{j=1}^m{(e_{ij}^w-V_j^{+})}^2},i=1,2,\dots ,n$$

$$S_i^{-}=\sqrt{\sum _{j=1}^m{(e_{ij}^w-V_j^{-})}^2},i=1,2,\dots ,n$$

Step 6: Finally, the performance score ($P_i$) of each ith alternative is computed using the following equation.

$$P_i=\frac{S_i^{-}}{S_i^{-}+S_i^{+}}$$

By comparing the $P_i$ values, the ranking of alternatives is determined: the higher the value, the better the rank.

Table 6. Candidate $S_i^{-}$, $S_i^{+}$, and $P_i$ values and their ranking.

ID	Candidates	${\mathit{S}}_{\mathit{i}}^{+}$	${\mathit{S}}_{\mathit{i}}^{-}$	${\mathit{P}}_{\mathit{i}}$	Rank
1	40.8839, −73.8561	0.297131401	0.144593761	0.327338747	8
2	40.8095, −73.8807	0.254017926	0.299058138	0.540717918	3
3	40.8347, −73.9177	0.348682791	0.05856651	0.143809971	9
4	40.7931, −73.9675	0.204902022	0.303211003	0.596739284	2
5	40.7586, −73.9731	0.011381735	0.392231042	0.97180036	1
6	40.7699, −73.9271	0.250201973	0.241413717	0.491061864	5
7	40.7496, −73.8692	0.266998664	0.212344026	0.442990016	6
8	40.7231, −73.914	0.254352423	0.269993794	0.514915118	4
9	40.6686, −73.9321	0.391639917	0.004541242	0.011462539	10
10	40.6599, −73.8701	0.283262679	0.173548531	0.37991303	7

shows the $S_i^{-}$, $S_i^{+}$, and $P_i$ values along with the candidates/alternatives ranking.

From the Table 6, it is deduced that candidate having ID 5 is ranked first; therefore, a new gas station can be opened at this optimal site, followed by candidate IDs (CID) 4 and 2. The performance scores suggest that CID 9 must be avoided because it ranks worst among all of the candidate sites.

6. Experiments

In this section, we evaluate the effectiveness of the proposed AHP/TOPSIS approach to identify an ideal business location. As mentioned earlier, ideal business location in this work means the location that can attract the maximum number of customers. For the evaluation in this section, sensitivity measurement is used, which can be defined as the proportion of positives (correct results) that are correctly identified, also known as True Positive Rate (TPR). Let the TP and FN denote the number of true positives and false negatives, respectively; then, the TPR is given by the following:

$$TPR=\frac{TP}{TP+FN}$$

(5)

To evaluate the proposed method effectiveness, an NYC convenience store dataset is used to identify the popularity and/or success of a convenience store, and its visitor count is used.

6.1. Datasets and Experimental Setup

For the evaluation, we made use of NYC conveninece store checkin data available from FourSquare [45]. To obtain convenience stores’ location data and their visitor counts from FourSquare, the developers’ places API was used. API calls to APIs can be broken down into two categories: regular and premium. Regular API calls only return basic information including the venue location, category, and a venue ID. Premium API calls return rich content including the number of visitors. In order to obtain convenience store data, premium API calls were used as we were interested in convenience store’s visitor count in addition to its location information.

For the sake of evaluation, we ranked the NYC convenience stores in descending order with respect to their visitor count and used it as ground truth. Although the visitor count is reliable, the duration of the visitor count is not known. We then used our proposed AHP/TOPSIS approach to rank the NYC convenience stores. The obtained ranking is compared against the ground truth, and the TPR is computed.

For the convenience stores’ ideal location, we identified the following five criteria based on the intuition that most of the convenience stores’ customers come from these locations:

• TStations: Transportation stations (train, metro, bus, stations, etc.);
• Buildings: Buildings including residential, commercial, etc.;
• EVenues: Entertainment venues (museums, movie theaters, stadiums, etc.);
• Shops: Other shops in the vicinity; and
• PPlaces: Professional places (convention centers, medical centers, factories, etc.)

The data (venue information) related to the criteria TStations, EVenues, Shops, and PPlaces were obtained from the FourSquare developers’ places API [46]. Using the API, up to date check-in information was obtained for over 62 million global venues (As of 31 August 2020). The data related to criteria Buildings was obtained from the NYC buildings footprint data [47]. Building footprints represent the full perimeter outline of each building as viewed from directly above. Besides the perimeter, other useful attributes of this dataset included ground elevation at building base, roof height above ground elevation, construction year, and feature type. The Buildings dataset consists of more than 1 million NYC building information including residential, commercial, and government buildings.

6.2. Evaluation

As discussed in Section 5.2, we computed the criteria values for the five criteria mentioned in Section 6.1. The radius values 1000, 300, 1000, 1000, and 1000 m were used for the criteria TStations, Buildings, EVenues, Shops, and PPlaces, respectively. The reason for using a smaller radius for the criterion Buildings compared to the other criteria is that the Buildings dataset is quite large and we obtain a uniform and a large number of buildings for each candidate for radius 1000 m. Thus, limiting the radius to a smaller value, in this case to 300 m, help us identify the nearby population of a convenience store. The same is not true for the other criteria, i.e., TStations, EVenues, Shops, and PPlaces. Thus radius values of 1000 m are used for them.

Table 7. Pairwise comparison matrix and computed criteria weights.

Criteria	TStations	Buildings	EVenues	Shops	PPlaces	Weight
TStations	1	3	7	9	7	0.495486996
Buildings	0.3333	1	7	9	7	0.327448046
EVenues	0.1428	0.1428	1	3	1	0.071501752
Shops	0.1111	0.1111	0.3333	1	0.3333	0.034061454
PPlaces	0.1428	0.1428	1	3	1	0.071501752

shows the pairwise comparison matrix for the five criteria. In the criteria computation, we assume that the criterion TStations, i.e., transportation stations, is the most important criteria as a large number of people visit convenience stores during their commute or travel. The second most important criterion that we identified is buildings. A large number of buildings around a convenience store means a large number of people either living or working there. Criteria TStations and Buildings are followed by criteria EVenues, Shops, and PPlaces, which are comparatively less significant compared to the first two criteria. In addition to the pairwise comparison matrix, Table 7 shows the computed criteria weights. The details of its computation are discussed in Section 5.2.

Table 8. Ground truth—stores ranked based on FourSquare visitor count.

Rank	Store ID	Store Name
1	5cd15dc59d7468003903fe8a	Amazon Go
2	5266a90711d23056d7c6dc67	Bread & Butter
3	4e034363b61ce80e5d67d09f	Duane Reade
4	59ceacc02955135d6151aef3	CVS pharmacy
5	4b0b3438f964a520982e23e3	Walgreens
6	4cdc1f63df986ea8550fce16	CVS pharmacy
7	4ca4e5b214c33704a852b13b	Duane Reade
8	5678271c498ed123ac7fc1e0	CVS Pharmacy
9	4c545b1b479fc9280e360293	Duane Reade
10	58768de8f2299508aa731849	CVS pharmacy
11	4b61db21f964a52060272ae3	Duane Reade
12	4b130a80f964a520239323e3	Duane Reade
13	4b95bf56f964a520cdb134e3	Duane Reade
14	5b92aaf3033693002c2af840	Open Market
15	4b574341f964a5200e2e28e3	Duane Reade
16	4aca8742f964a52041c220e3	Duane Reade
17	4ae1ed7cf964a520d58821e3	Duane Reade
18	4fe4f632a17c9aa22d55209f	Duane Reade
19	4a7f68e6f964a520eff31fe3	Duane Reade
20	4a9e7fadf964a520503a20e3	Duane Reade

and

Table 9. AHP/TOPSIS—stores ranked obtained using the AHP/TOPSIS approach.

Rank	Store ID	Store Name	Ground Truth Ranking *
1	4b0b3438f964a520982e23e3	Walgreens	5
2	59ceacc02955135d6151aef3	CVS pharmacy	4
3	4b61db21f964a52060272ae3	Duane Reade	11
4	4ad3f4e5f964a52011e720e3	Duane Reade	NR
5	4e034363b61ce80e5d67d09f	Duane Reade	3
6	4a9c8a06f964a520813720e3	Duane Reade	NR
7	5b92aaf3033693002c2af840	Open Market	14
8	4fe4f632a17c9aa22d55209f	Duane Reade	18
9	59a7303f8d0a5343731f326c	7 Eleven	NR
10	4aca8742f964a52041c220e3	Duane Reade	16
11	4d6b8ebe56cc6a3175a95eac	7-Eleven	NR
12	4adb7ccdf964a520152821e3	Duane Reade	NR
13	5d4117543c3cf7000794b01b	CVS Pharmacy	NR
14	4e7a39122271920e476b47e3	7-Eleven	NR
15	5266a90711d23056d7c6dc67	Bread & Butter	2
16	4adf4335f964a520df7821e3	Duane Reade	NR
17	5cd15dc59d7468003903fe8a	Amazon Go	1
18	4ae1ed7cf964a520d58821e3	Duane Reade	17
19	4a7f68e6f964a520eff31fe3	Duane Reade	19
20	4ba57508f964a520160939e3	Duane Reade	NR

* NR: Not Ranked.

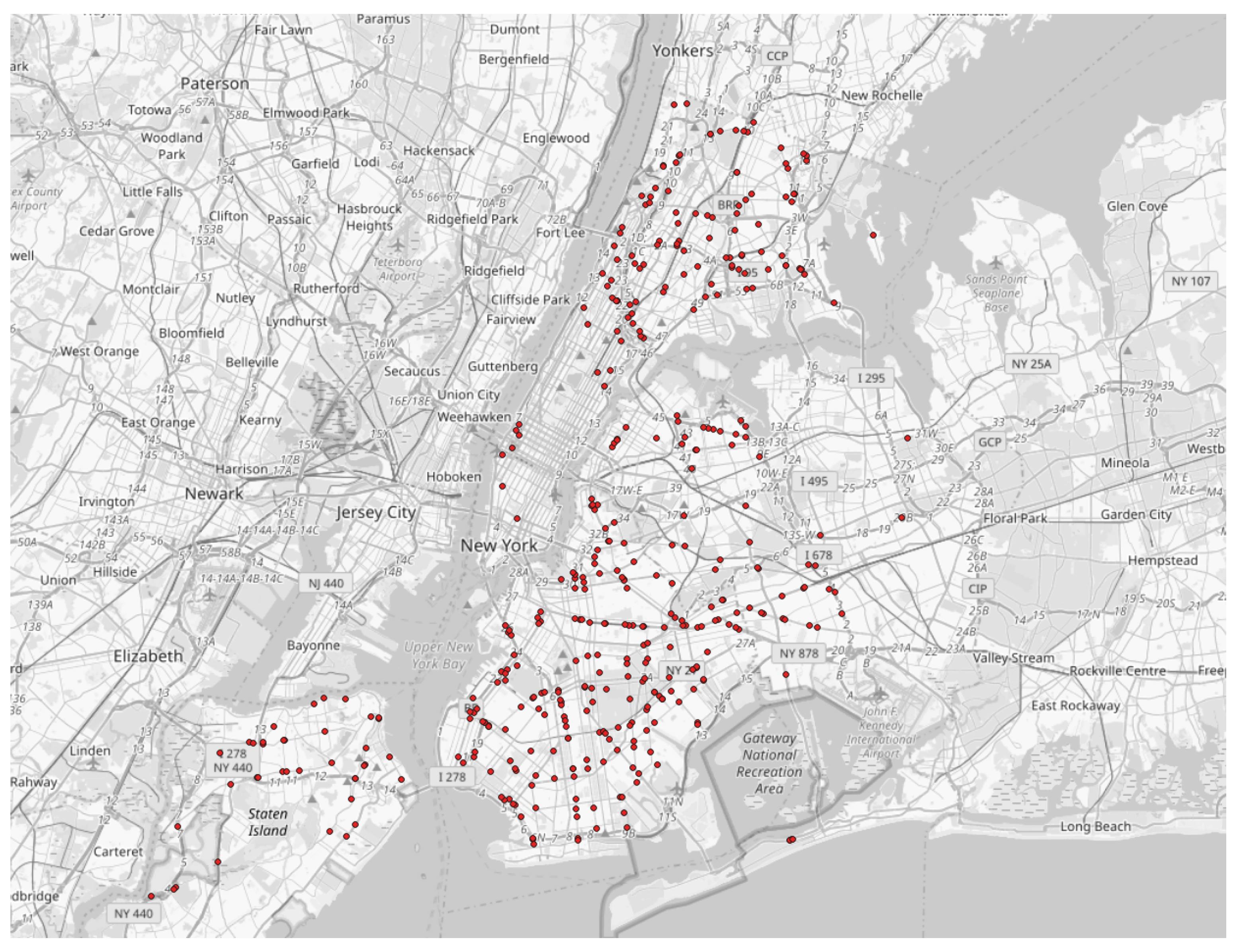
show the top 20 stores ranked based on FourSquare visitor count (ground truth) and the top 20 stores ranked by our AHP/TOPSIS approach, respectively. Figure 8 shows the NYC map containing the convenience stores in Table 8 and Table 9. Bold tuples in Table 9 are the ones ranked by the ground truth in Table 8 as well. Based on Table 8 and Table 9, we computed the True Positive Rate (TPR). We counted the records predicted by AHP/TOPSIS, i.e., the record that is present in Table 9 is a True Positive (TP) if it also appears in the ground truth table i.e., Table 8, irrespective of its rank. On the other hand, a record is counted as a False Negative (FN) if it is predicted by AHP/TOPSIS but it does not appear in Table 8. Hence, the TPR for the criteria weights computed in Table 7 is given as follows:

$$TPR=\frac{TP}{TP+FN}=\frac{11}{20}=0.55$$

The TPR is heavily dependent on the criteria weights, and the derivation of the right criteria weights is important to obtain an optimal or desired prediction. To prove this, we performed experiments with a number of manual weight assignments to the criteria vector [TStations, Buildings, EVenues, Shops, PPlaces] as follows:

• uniform = [0.2, 0.2, 0.2, 0.2, 0.2]
• increasing = [0.05, 0.1, 0.2, 0.3, 0.35]
• decreasing = [0.35, 0.3, 0.2, 0.1, 0.05]
• oneCriteriaZero = [0.4, 0.3, 0.2, 0.1, 0]

For the random weight vectors uniform, increasing, decreasing, and oneCriteriaZero above, we obtained the TPRs 0.25, 0.25, 0.4, and 0.35, respectively. The TPRs are far lower than the one obtained using carefully derived weights, i.e., 0.55. Figure 9 shows the placement of ground truth convenience stores (green triangles) and the AHP/TOPSIS-predicted convenience stores using the manual weights (red circles). As can be observed from the obtained TPR values of the different weight vectors, the AHP/TOPSIS approach is heavily dependent on the criteria weight computation.

7. Discussion

By looking at the result, it seems that the AHP/TOPSIS method is not as effective as we could obtain only 55% correct results (TP) compared to the ground truth. However, we would like to argue that ground truth raking is based on the number of visitors, which can be biased. For instance, the number of visitors depends on several factors besides the five criteria, i.e., TStations, Buildings, EVenues, Shops, and PPlaces, which we considered in our AHP/TOPSIS approach. Thus, in order to improve the accuracy of the AHP/TOPSIS model, more data sets are needed. For instance, stores’ daily sales, pricing policy, product line, timed sales, special sales, etc. are very important criteria that play important roles in attracting visitors and in improving daily sales. In fact, daily sales is a better criteria to rank stores than the number of visitors used in this study. However, the data related to such criteria is very difficult to obtain if not impossible because of stores’ privacy policies. We strongly believe that the accuracy of the results can be significantly improved with the combination of the right criteria and respective datasets.

By analyzing the top 20 stores in Figure 8, one can observe that the proposed AHP/TOPSIS approach identified convenience stores mainly at the center of the NYC Manhattan area, which makes sense as it is the most crowded area with a lot of residential and commercial buildings, transportation stations, shops/markets, and entertainment venues. Since in the experiments, the highest weights were allocated to the TStations and Buildings criteria, AHP/TOPSIS identified business locations at a crowded part of NYC. The most important step in the AHP/TOPSIS approach is the identification of the set of important criteria and the derivation of their weights with the help of a pairwise comparison matrix. The accuracy of the the AHP/TOPSIS approach is heavily dependent on the criteria weight computation. Section 6.2 shows that, for the random weights assignment, i.e., the weight vectors uniform, increasing, decreasing, and oneCriteriaZero, we obtained the TPRs 0.25, 0.25, 0.4, and 0.35, respectively, which are far lower than the one obtained using the careful derivation of criteria weights. This proves that the AHP/TOPSIS approach is sensitive to criteria weight assignments.

8. Conclusions and Future Work

In this paper, the challenge of selecting an optimal site to open a commercial place is addressed. It is evident with the support of related research that an ideal site selection to open a new business requires thorough study of various factors and criteria. This study puts forward an AHP/TOPSIS-based hybrid solution for this problem, where AHP and TOPSIS are two state-of-the-art multi-criteria decision-making approaches. The proposed approach helps to identify the best alternative among the given candidates for a commercial opening while minimizing the computational complexity and reducing the manual effort required. The classic MCDM approach AHP becomes computationally expensive, i.e., requires a large number of comparison matrices to be constructed in the presence of a large number of alternatives/candidates. Thus, the proposed AHP/TOPSIS approach is particularly useful to solve this issue and can come up with the best alternative using only two matrices: one for riteria weight computation and the other for alternatives ranking. The applicability of the proposed approach is demonstrated with the help of a detailed step-by-step case study and to evaluate the effectiveness of the proposed approach, and an experimental evaluation to identify an optimal location for a convenience store is presented. In the presented case study, a nexus of four criteria was considered, including competitors, traffic, popularity, and vehicle owners, where the criteria values were computed with the assistance of real GeoSpatial data. In contrast, for the evaluation, we made use of five criteria, namely, TStations, Buildings, EVenues, Shops, and PPlaces, which were based on real data. This study claims that the proposed mechanism is flexible in a sense that any number of criteria can be exploited for ranking the candidate sites. The results of the evaluation suggests that the proposed approach is highly dependent on the criteria weights and that the derivation of the right weight matrix is important to obtain a correct prediction. Since the derivation of criteria weight is a heuristic approach, it is both flexible and error-prone, flexible in the sense that it enables users to give preference to one of more criteria of their choice and error-prone because of manual computation of a weight matrix. In the future, this work will be extended to identify an optimal route for mobile businesses.