3.1. Influence of Uniaxial Static Load on the Damage Distribution under Different Burdens
In this section, a span X of 100 mm and a span Y of 100 mm are applied to the numerical model, and then the simulations of uniaxial loading of P1, uniaxial loading of P2, and biaxial loading were conducted. The damage contours of cut Z1 at 100 μs were extracted from the numerical results. The variation characteristics of damage distribution, the volume V and the shape of the crater were studied in detail in this section.
According to the elastic mechanics, on the right side of the rectangle cavern, the X-direction stress is small, and the stress field is governed by the Y-direction stress, especially near the free surface. Therefore, the blast-induced damage is mainly affected by the original Y-direction stress field.
Figure 3 shows the Y-direction elastic stress fields (
) under different static loads (
W = 4 cm). For the stress
, its sign is positive in tension and negative in compression. As seen from the Y-direction stress contours, the rectangle cavern induces stress concentration near the free surface. For P1 = 5 MPa, as shown in
Figure 3a, there is a large tensile stress zone on the left side of the borehole, especially near the free surface, and a small tensile stress zone on the right side of the borehole. The maximum tensile stress is 6.6 MPa near the free surface and
decreases to around 2 MPa on the left side of the borehole. For P2 = 5 MPa, as shown in
Figure 3b, the excavation zone is in a compressive stress field. The
is maximum around the free surface (around 12 MPa), and it decreases to around 7 MPa on the left side of the borehole. For P1 = P2 = 5 MPa, as shown in
Figure 3c, the excavation zone is also in a compressive stress field, but the compressive stress field is weakened, and the distribution changes a lot. The maximum
transfers from the free surface, where the
decreases to around 4 MPa, to the four corners of the cavern. The above static stress field analysis is beneficial to understanding the coupling mechanism of static load and blasting stress wave load on the rock damage characteristics in the subsequent dynamic analysis.
To evaluate the influence of P1 on the damage distribution due to blasting, five cases of uniaxial static loads, P1 = 0, 2, 5, 8, and 10 MPa, were first conducted in this section.
Figure 4 shows the damage contours for different P1 with different burdens at cut Z1. As mentioned in
Section 2.2, the elements with a damage level above 0.7 are regarded as severe damage zone and form the explosion crater. In the case of P1 = 0 MPa, blast-induced severe damage zones (
D ≥ 0.7) are widely distributed and can form craters from the charge center to the free surface when the burden
W is no more than 4 cm. When
W is more than 5 cm, the blast-induced severe rock damage (
D ≥ 0.7) mainly distributes around the explosive and little severe damage zone covers the free surface, but the two zones are not connected. Thus, in the cases of
W = 5 cm and
W = 6 cm, only blasting cavities are formed around the charge but no crater is formed by the blasting. Therefore, the burden should be no more than 4 cm to form an explosion crater in the case of P1 = 0 MPa. In the case of P1 = 2 MPa, the damage zones are enlarged for each burden, but the severe damage zone (
D ≥ 0.7) around the charge and the damage zone near the free surface are still separated when
W = 5 cm and
W = 6 cm, which indicates no crater is formed. When P1 increases to 5 MPa, the damage zones are further enlarged, and the two zones begin to connect for
W = 5 cm but not for
W = 6 cm. In the case of P1 = 8 MPa and 10 MPa, with the increase of static load, the damage zones become larger. Especially for
W = 5 cm, the severe damage zone is clearly enlarged near the free surface, thus a crater is formed. It should be noted that there is still a large low-level damage zone (
D < 0.7) between the blasting cavity and the free surface for
W = 6 cm, as a result, the explosion crater cannot be formed.
In order to evaluate the explosion crater clearly, the crater volume
V is measured by counting the high-level damage elements (
D ≥ 0.7) and summing their volumes. The crater volumes for each burden under different static loads are shown in
Figure 5. It can be found that with P1 increases, the volume of explosion crater tends to increase. When P1 is less than 8 MPa, the
V for
W = 2 cm is the smallest (no crater for
W = 5 and 6 cm, as shown in
Figure 4) due to excessive dissipation of the explosion energy into the atmosphere and the
V for
W = 3 cm is the largest, which indicates that the optimal burden is 3 cm. However, when P1 is more than 8 MPa, the burden of 4 cm is optimal because its corresponding crater volume is the largest. It can be clearly seen that the
V for
W = 2 cm is not sensitive to the static load, but the others vary greatly with changing P1, especially for
W = 4 cm,
W = 5 cm and
W = 6 cm when P1 ≥ 5 MPa. The above results are due to the rapid expansion of the damage zone near the free surface for
W = 5 cm and
W = 6 cm (as shown in
Figure 4). It should be noted that the
V for
W = 6 cm is the volume sum of the blasting cavity and the damage zone near the free surface, but not the crater volume (as shown in
Figure 4). It can be concluded that the P1 can change the optimal burden of charge and increase the critical embedding depth of the charge.
In order to investigate the variation in the shape of the explosion crater, the craters (formed by the elements with
D ≥ 0.7) for
W = 4 cm under different P1 are plotted in
Figure 6. In the XY plane, the shape of the explosion craters is similar to a triangle and expands with the increase of P1. The diameter of the crater in the Y direction also becomes larger with the increase of P1 at different depths (X direction), especially in the top of the crater, where a new damage zone is generated. The above results are induced by the combined effect of the Y-direction tensile component of the stress wave and the Y-direction tensile stress field (as shown in
Figure 3a). In the XZ plane, there is a clear trend that with the increase of P1, the diameter in the Z direction becomes larger, especially when P1 = 8 MPa. This is because with the increase of Y-direction stress field (
) induced by P1, the combined effect of the Y-direction tensile component of incident stress wave (
) and Y-direction stress field (
) is intensified and promotes the initiation and propagation of radial tensile fracture at point A, as shown in
Figure 7a. Besides, some damage zones appear in the left side of the borehole due to the stress concentration, but they expand little in the Y direction, as shown in the YZ plane. In the YZ plane, when P1 = 5 MPa, the long axis of the bottom circle of the crater is in the Y direction. This is because the superposition of the Y-direction component of reflected tensile stress (
) and Y-direction stress field (
) at point B (as shown in
Figure 7b) increases the Y-direction dimension of reflected tensile damage zone around the free surface, which is also shown in the XY plane. However, with the increase of P1, the long axis of the bottom circle of the crater transfers from Y direction to Z direction due to the faster growth of the diameter in the Z direction, which is consistent with the results in the XZ plane and can be illustrated by
Figure 7a. The result is also consistent with the law that the long axis of blast-induced damage is parallel to the max principal compressive stress (Z direction). It can be concluded that the crater shape is governed by the reflected tensile fractures when P1 ≤ 5 MPa, but governed by the radial tensile fractures when P1 ≥ 8 MPa.
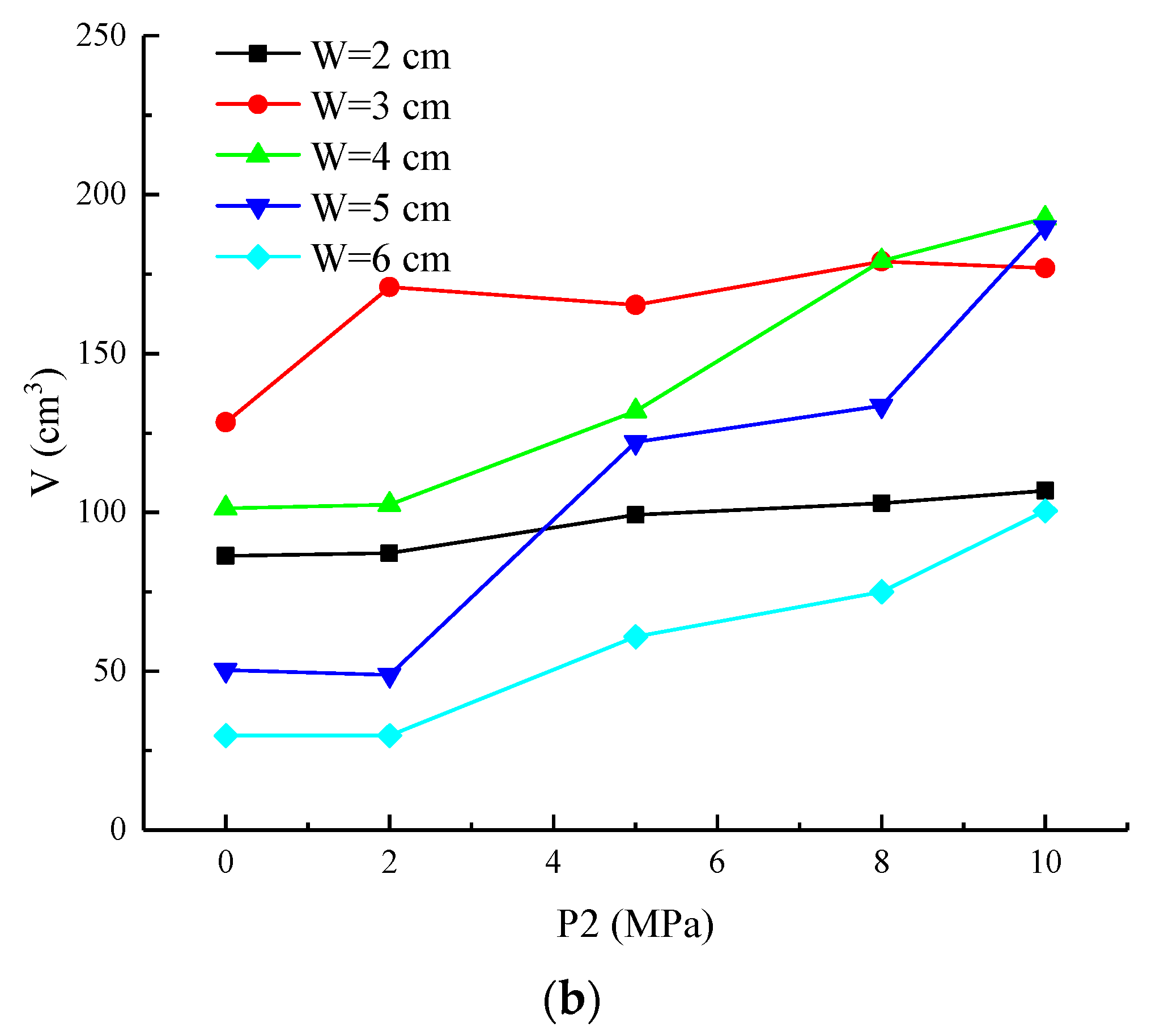
Another five cases of uniaxial static loads, P2 = 0 MPa, P2 = 2 MPa, P2 = 5 MPa, P2 = 8 MPa and P2 = 10 MPa, were simulated to investigate the effect of load direction on damage distribution.
Figure 8 shows the damage contours at cut Z1 and the crater volumes for different burdens under different P2. In the case of P2 = 2 MPa, the crater volumes are enlarged for
W = 2 cm, 3 cm, and 4 cm, but shrunk for
W = 5 and 6 cm, as shown in
Figure 8b. There is still no crater formed by the blasting for
W = 5 and 6 cm. as shown in
Figure 8a. The increase of the crater volumes for
W = 2, 3, and 4 cm is mainly induced by the increase of reflected tensile fractures around the free surface, where the combined effect of the X-direction component (
) of reflected tensile wave and the compressive stress field (
) induced by P2 promotes the damage development at point C and D, and the increase of radial tensile damage zone, where the combined effect of the Z-direction tensile component (
) of incident wave and
promotes the damage development at point B, as shown in
Figure 9. However, the reductions of the crater volumes for
W = 5 cm and 6 cm are induced by the reduction of radial damage zones distributed around the charge, where the volumes of blasting cavities are mainly restrained by
, especially at point A, as shown in
Figure 9. In the case of P2 = 5 MPa, the crater volumes are increased when
W = 2 cm, 4 cm, 5 cm, and 6 cm but reduced when
W = 3 cm. For
W = 3 cm, this may be because the increase of reflected tensile fractures around the free surface is smaller than the reduction of the radial tensile damage zone around the charge. There is a clear increase of the damage zones for
W = 4, 5, and 6 cm, which is induced by the great increase of fractures around the free surface. Especially for
W = 5 cm, the fractures around the free surface are clearly enlarged and begin to connect with the blasting cavity formed by the damage zone around the charge. For
W = 6 cm, the combined effect of
and
is enhanced due to the intensification of the latter, and some damage zones extend from the free surface to the borehole. However, the damage zones only distribute along the Y direction but expand little in the Z direction, so the crater is hard to form. In the case of P2 = 8 MPa and 10 MPa, with the increase of static load, the damage zones become larger, except for
W = 3 cm, where the damage zone distribution along the Z direction is reduced, as shown in
Figure 8a. It should be noted that the crater is still not formed for
W = 6 cm. For each W, the fractures tend to extend along the Y direction with P2 increases, which is consistent with the law that the long axis of the blast-induced damage zone is parallel to the max principal stress (Y direction).
With the increase of P1 or P2, the crater volume can be enlarged. However, the increase of V with P1 is more than that with P2. For example, when W = 4 cm, the V for P1 increases by 17.1, 25.8, 26.8 and 60.3 cm3 compared with that for P2 when the stress level is 2, 5, 8 and 10 MPa, respectively. In other words, when the static load values are the same, the V is increased by 15–31% for P1 compared with P2. The results show that the effect of P1 on the increase of V is greater than that of P2.
The shapes of the craters for
W = 4 cm under different P2 are plotted in
Figure 10a. In the XY plane, the shape of the explosion crater gradually changes from a triangle to a trapezoid and has a significant expansion in the Y direction at different depths due to the directional effect of the Y-direction compressive stress field. However, the depth of the explosion crater is reduced a little due to the volume shrink at the top of the crater, especially in the case of P2 = 10 MPa, where the crater is mainly distributed on the left side of the borehole. In the XZ plane, near the free surface, the Z-direction diameter gradually increases under the combined effect of reflected tensile wave and
. In the YZ plane, the shape of the crater becomes an oval and its long axis is in the Y direction for P2 = 2 MPa, which obeys the law that the long axial of blast-induced damage zone is parallel to the max principal stress. However, when P2 ≥ 5 MPa, the shape tends to expand in the Z direction. This is because the reflected tensile fracture zone becomes the dominant factor affecting the crater shape. As shown in
Figure 9b,
is perpendicular to
and Z-direction tensile stress component (
) of reflected wave at point C and point D, and it is conductive to the growth of reflected tensile fractures induced by
. However, it is opposite to the Y-direction tensile stress component (
) at point D and it will restrain the formation of reflected tensile fractures induced by
. As a result, the Z-direction reflected tensile fractures are easier to propagate. To study the effect of P2 on the radial tensile fracture zone distribution, as shown in
Figure 10a, section A-A at 1 cm to the left side of the borehole is selected, which is away from the free surface, and its damage zone is mainly governed by radial tensile fractures.
In section A-A, it can be clearly found with P2 increases, the Z-direction dimension of the crater reduces (P2 ≥ 5 MPa) and the Y-direction dimension of the crater increases gradually, as shown in
Figure 10b. The above results are caused by the coupling mechanism of
and the incident compressive stress wave, which is illustrated by
Figure 9a. At point A, the original static compressive stress field (
) is opposite to the Y-direction tensile stress component (
) and it will prevent the formation of radial tensile fractures induced by
. However, at point B,
is perpendicular to
, and it is conductive to the growth of reflected tensile fractures induced by
. Therefore, the radial tensile fracture zone is an ellipse with a long axis in the Y direction.
3.2. Influence of Biaxial Static Load on the Damage Distribution
To investigate the characteristic of damage distribution under biaxial loading, W = 4 cm and P1 = 5 MPa were kept, 11 cases of P2, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10 MPa, were simulated to investigate the effect of the pressure coefficient on damage distribution. The borehole is placed on the right side of the cavern, named as case I, or the top side of the cavern, named as case II.
Figure 11a shows the shapes of craters for
W = 4 cm under biaxial loads with different
for case I. With the
increases, the shapes in the three planes are shrinking in the overall trend. In the XY plane, the shape transforms from a trapezoid to a triangle, and the X-direction dimension reduces much to cause the decrease of the depth of the crater. In the XZ plane, away from the free surface, the Z-direction and X-direction dimensions are both reduced due to the increasing Y-direction compressive stress field. In the YZ plane, two damage zones distribute the leftmost side and the rightmost side along the Z direction for
= 0, but they disappear for
= 0.4. For
= 0, the two damage zones are formed by the combined effect of
and
induced by P1. However, for
= 0.4, the addition of the new Y-direction compressive stress field (
) induced by P2 will neutralize part of the tensile stress and prevent the formation of the two damage zones. When
≥ 0.4, the shape is getting flatter due to the increase of the additional compressive stress field. For case I, the crater volume
V reduces monotonically with the increase of
, as shown in
Figure 11c. It should be noted that the law only applies to the case of small
. When
is large enough, the Y-direction compressive stress field induced by lateral pressure P2 will govern the damage distribution around the surface and away from the charge, and the crater volume may be increased with the increase of
, as described in the uniaxial loading case of P2.
Figure 11b shows the shapes of craters for
W = 4 cm under biaxial loads with different
for case II. The shape of the explosion crater is the smallest in each plane when
= 0.4. In the XY plane, the dimension in the X direction reduces first when = 0.4. This is because the X-direction compressive stress field, which is beneficial for the damage development along the X direction, is weakened by the X-direction tensile stress field induced by P2. When
= 1.0, the dimension in the X direction increases instead, especially the damage zones on the upside and downside of the borehole. This is because that the damage mechanism has changed, and the damage zones are mainly formed by the combined effect of the X-direction tensile stress, which is caused by the rock rebound, and the Y-direction compressive stress field induced by P2. Compared with the case of
= 0.4, the compressive stress field reduces in the X direction but enhances in the Y direction, which is beneficial for the evolution of the damage zones on the upper and lower sides of the borehole. Therefore, the X-direction crater dimension increases at the top of the crater. When
= 1.6 and 2.0, the crater shape is enlarged further due to the increase of P2. In the YZ plane, the variation characteristics of the crater shape are similar to those in the XY plane, and the shape tends to be a triangle, which is consistent with the characteristics in the uniaxial loading cases of P1. In the XZ plane, when
= 0, the damage zone near the free surface is induced by the coupling effect of the reflected tensile stress wave and the X-direction compressive stress field. When
= 0.4, the combined effect is weakened by the addition of the X-direction tensile stress field induced by P2. Afterwards, with the increase of
, the P2 becomes the dominant factor affecting the crater shape and the damage mechanism begins to change. When
= 1.6 and 2.0, two damage zones appear on the left side and the right side along the Z direction, which are formed by the coupling effect of the X-direction tensile component of the reflected wave and the X-direction tensile stress field. It can be seen that when
≥ 0.4, the variation characteristics of crater shape at each plane are similar to these in the uniaxial loading cases of P1. For case II, as shown in
Figure 11c, the crater volume
V reduces first before
increases to 0.4 and then increases with
increases. The turning point of
V is mainly caused by the change of the dominant damage mechanism, as described in the above analysis. It can be found that
= 1 is a demarcation point. The crater volume
V is greater for case I (the borehole is placed on the right side of the rectangular cavity) when
< 1, but greater for case II (the borehole is placed on the top side of the rectangular cavity) when
> 1. There is a common feature that the
V is greater when the borehole is placed on the side of the max static load. Taking the demarcation point of
= 1 as the reference point, the increase of
V with the increase of the static load on the side of the borehole is greater than that with the reduction of the static load on the other side. The result indicates that the crater volume is more sensitive to the variation of static load on the same side than the other side, which is consistent with the uniaxial load numerical result in
Section 3.1 that the effect of P1 on the increase of
V is greater than that of P2.
3.3. Influence of Span Ratio on the Damage Distribution
In this section, the span X of 100 mm, W = 4 cm, and P1 = 5 MPa were kept, and the span Y = 100, 110, 120 and 130 mm were considered to investigate the characteristic of the damage distribution with different span ratios . Considering that the static stress field on the top side is less influenced by the variation of span Y, the borehole layout placed on the top side is not considered in this section.
Figure 12 shows the Y-direction elastic stress fields with different
k under P1 = P2 = 5 MPa. It can be found that with span Y increases, the
on the right side of the rectangle cavern reduces from around 6 MPa to around 2 MPa, but varies little on the top side. The results indicate that the Y-direction compressive stress field on the right side is weakened with the increase of
k.
Figure 13a shows the explosion crater with different
k under P1 = P2 = 5 MPa. In the XY plane, the crater Y-direction dimensions near the free surface are enlarged with the increase of
k, which is similar to the characteristics of case II when
≥ 0.4 in
Section 3.2. The expanded damage zones are also induced by the combined effect of the Y-direction rock rebound and the X-direction compressive stress field. When
k increases, the Y-direction compressive stress field reduces, and the X-direction compressive stress field increases, which can intensify the combined effect and improve the X-direction damage development. In the XZ plane, the crater shape is enlarged with the increase of
k, and the variation characteristic is also consistent with the results of case II when
≥ 0.4 in
Section 3.2. In the YZ plane, the crater shape changes from an ellipse to a circle with the increase of
k, which is induced by the weakening of the Y-direction compressive field.
Figure 13b shows the explosion crater with different
k under P1 = 5 MPa and P2 = 10 MPa. The results show that the shape variation characteristics are similar to those under P1 = P2 = 5 MPa. The crater volumes under different
k are listed in
Table 4. It can be found that the crater volume increases with
k increases. The results indicate that in the stressed rock mass, the explosion crater can be improved by increasing the free surface span on the side of the borehole. Especially for the case of unequal biaxial loading, the rock on the side of the maximum principle stress should be excavated first, where the rock breaking efficiency is higher than the other side with the same span, and then the span on the other side can be increased, which is beneficial to improving the explosion crater on this side. In the view of strain energy density, Yang [
35] pointed out that the rock mass with a poor strain energy density should be excavated first to release the high strain energy of the adjacent rock, and then the release intensity of strain energy can be effectively controlled and the vibration induced by the instantaneous unloading can be reduced. In our study, the borehole on the side of P2, where the strain energy density is poor (as shown in
Figure 14), should also be detonated firstly to improve the crater volume and the critical embedding depth of the charge. Besides, as shown in
Figure 14, with the excavation of rock mass on the side of P2, the strain energy density on the other side (P1) will be reduced. The result is beneficial to the control of vibration induced by the instantaneous unloading and the increase of the rock breaking efficiency in the high strain energy zone.