A Scheduling Algorithm for Multi-Workshop Production Based on BOM and Process Route
Abstract
1. Introduction
2. Analysis of Scheduling Problems for Complex Products in Multi-Workshop Production
- Finishing all scheduling tasks as early as possible in a multi-workshop environment;
- Allocating processes reasonably to make equal use of workshop resources when multiple workshops have similar device resources;
- Optimizing scheduling when products have different delivery cycle requirements;
- Carrying out reasonable batching and scheduling when the product scale is large.
3. Process Network Diagram Model Based on BOM and Process Route
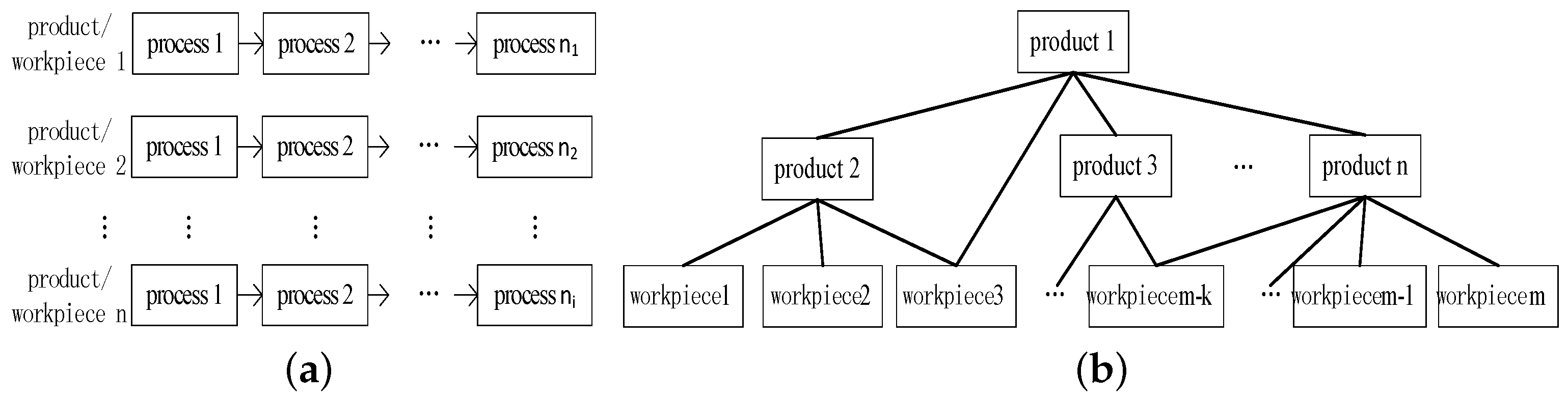
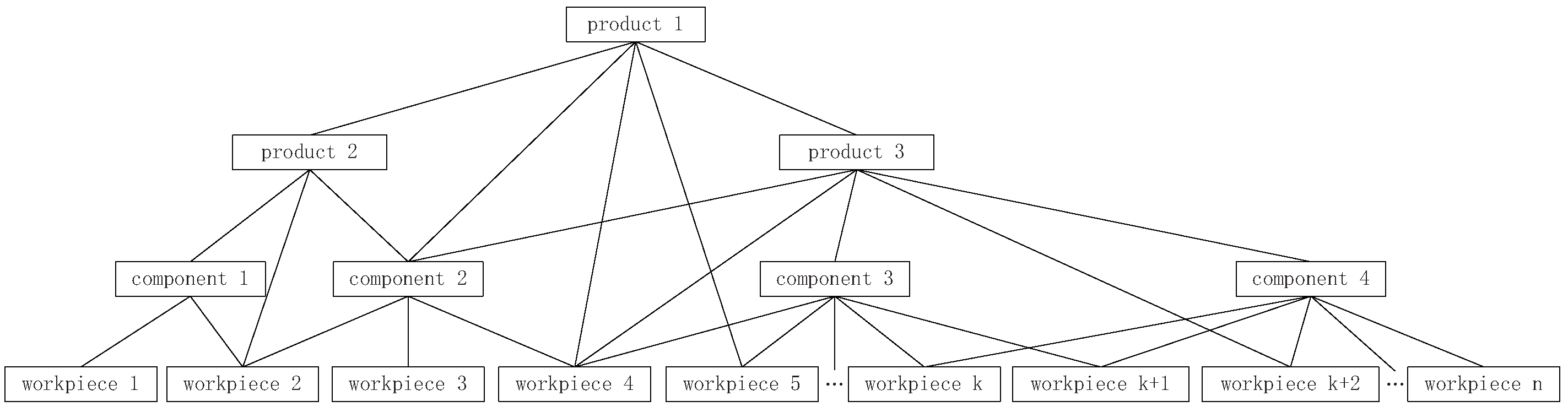
- For a single product, its BOM can be expressed as X = (P, A), in which P is the set of product nodes, A is the relationship matrix of the product nodes, and = 1 indicates that is the child node of .
- The process route is the production process stage of products in different workshops—that is, the process flow between workshops; the process sequence is the internal process of products in each workshop. In the actual production environment, some processes of the product allow the selection of equipment in different workshops, so the problem of equipment balance caused by equipment selection in multi-workshop environment will arise. However, in this paper, we do not elaborate on the balance of multi-workshop equipment. The multi-workshop expression proposed in this paper is to facilitate the elaboration of the production process of the complex products. For the process route and process sequence of a product, it can be expressed as = (G, W, Q, B, M), in which G is the set of product process routes, W is the set of workshops, Q is the set of product process nodes, B is the relation matrix of process nodes, and M is the set of equipment; = 1 means that the product is processed by workshop s, = 1 means that the process h of in workshop s is the next operation of process k, = 1 means that the process k of in workshop s is processed by equipment m. For the process route and operation series of a product, it can be expressed as = (Q, B), in which Q is the process node set of a certain product, B is the relationship matrix of process nodes, = 1 indicates that process h of is the succeeding node of process k.
- With the organization of product BOM and its process, a process network diagram of the workshop level can be formed; then, further decomposition can be carried out according to the sequence of products in each workshop to form a process-level process network diagram, which can be expressed as = (W, N, C, M), in which W is the set of workshops, N is the set of process nodes in the new network diagram, C is the relationship matrix between nodes, M is the set of equipment, = 1 means that process v is the succeeding node of process u, r is the number of nodes, = 1 represents process u of node, and c is processed by equipment m in workshop s.
- For multiple products, we can convert the BOM structure according to step 1 for each product. If there are relevant nodes, a merge procedure can be performed, and then the conversion can be performed according to step 2 and step 3. Finally, a complete process network diagram can be created.
4. Mathematical Model of Scheduling for Multi-Workshop Production
- Each product can be processed by multiple devices in multiple workshops;
- The workshop where each process is located and the device used by each process are determined;
- At a certain processing time, one device can only be occupied by one process;
- At a certain processing time, a product can only be processed by one device and cannot be interrupted once the process starts;
- The product is processed in the order of its process route, and one process cannot be started until its preceding process is completed;
- The product must follow its BOM structure; that is, the product can start only after all its components have been completed;
- The product should be completed before its delivery date.
5. Implementation of Scheduling Algorithm for Multi-Workshop Production
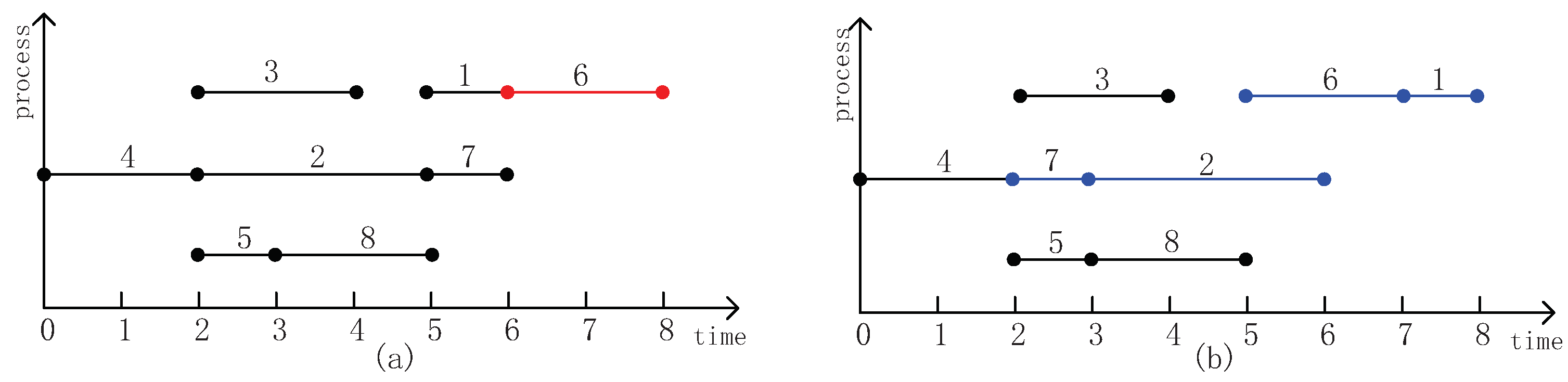
5.1. Encoding and Decoding Mechanism
5.2. Generation of Initial Particle Swarm
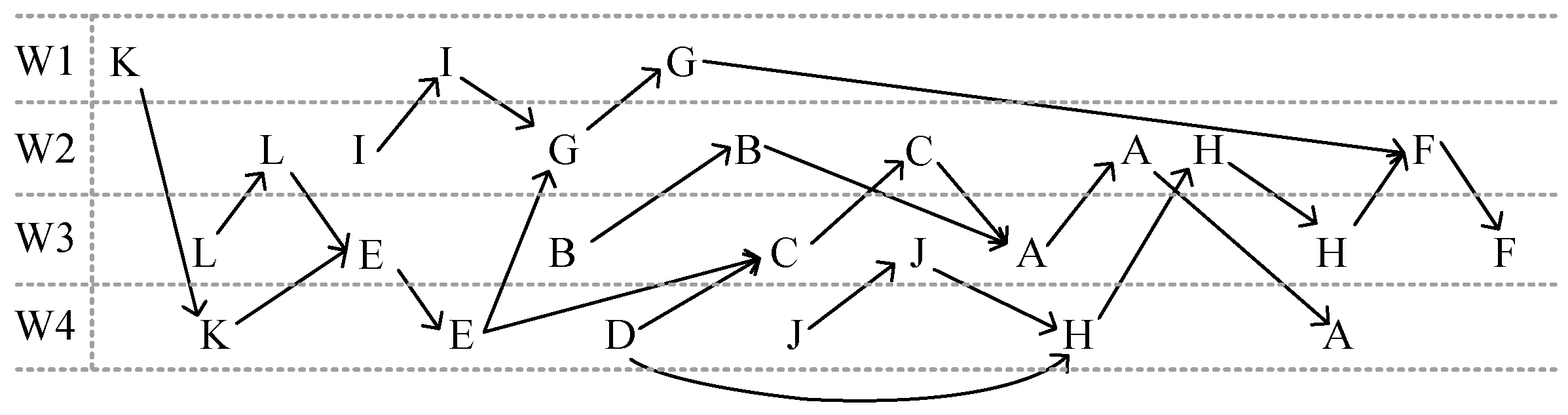
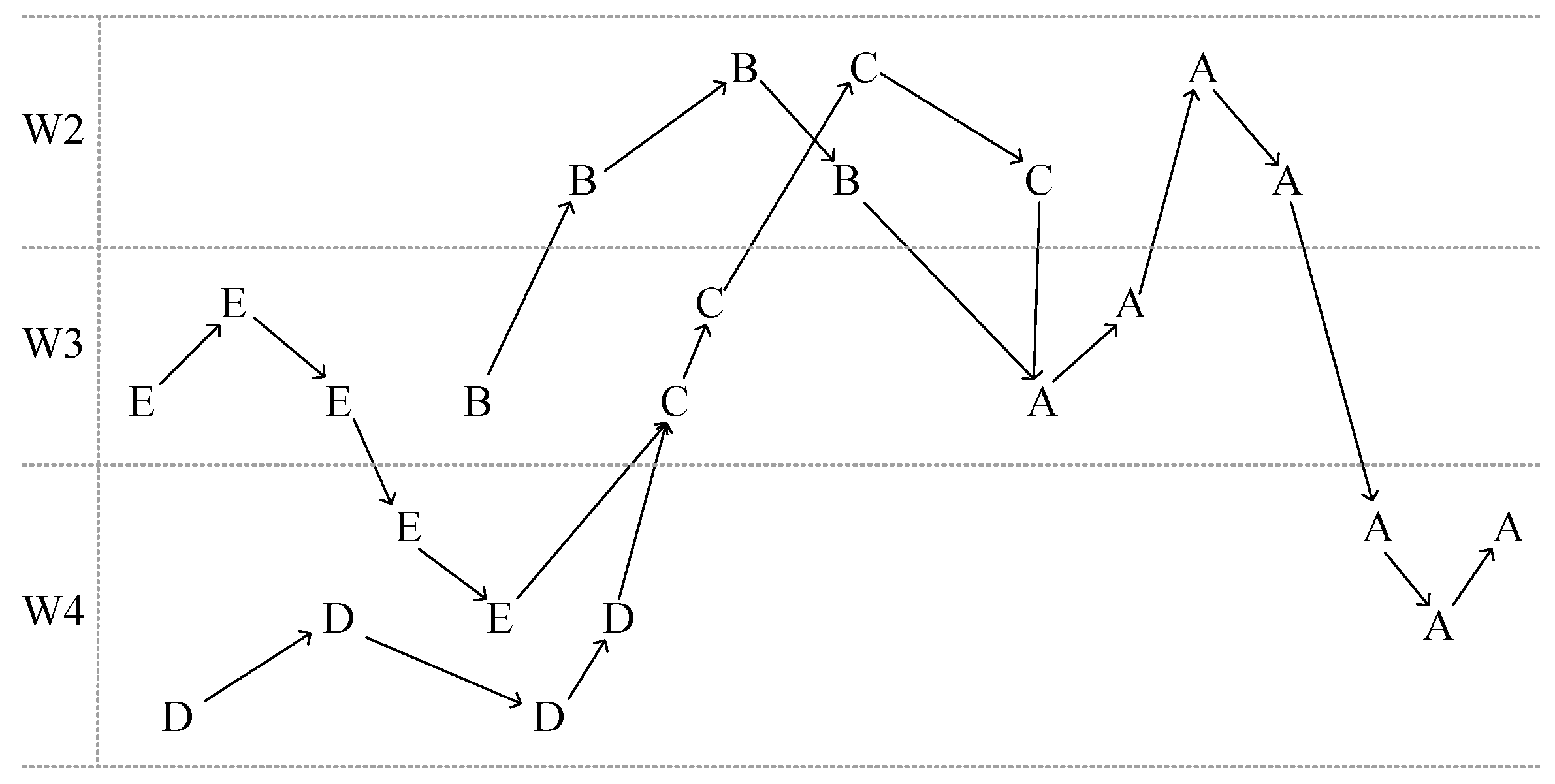
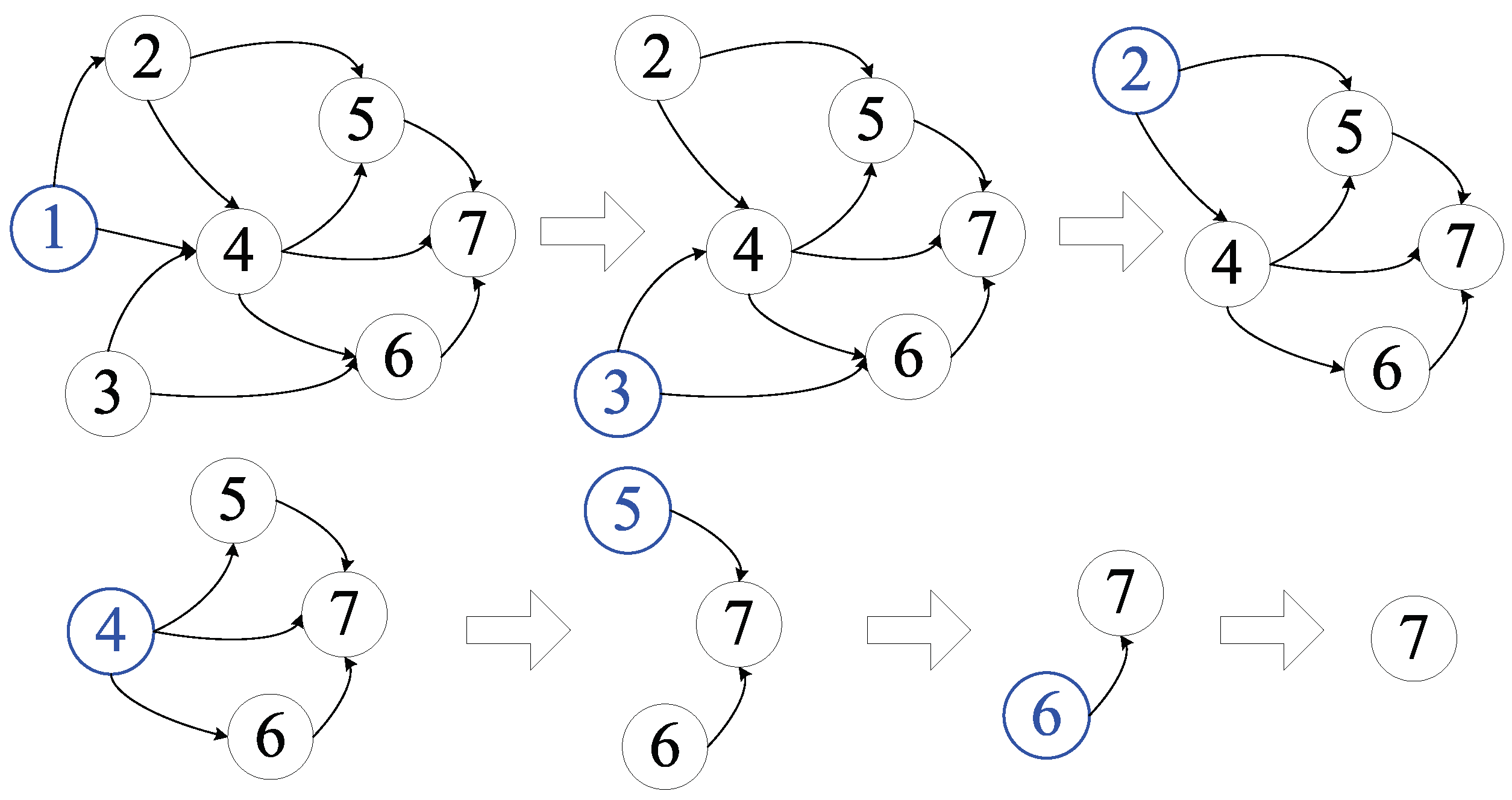
- The process network graph G of complex product scheduling is established, and a node is selected as the first node of the operation sequence from each initial node without forward node in G.
- Remove the node in (1) from the network graph G to form a new process network graph ; is a subgraph of G. The next node is randomly selected in the graph , and only the node without the forward node in can be selected.
- Repeat the process (2). The construction process of is shown in Figure 5. In this way, the validity of the sequence can be ensured. As shown in the figure, until all nodes have joined the operation sequence, the obtained operation sequence can be used as the initial particle swarm.
5.3. Improvement of Population Evolutionary Diversity
5.4. Dynamic Inertia Weight
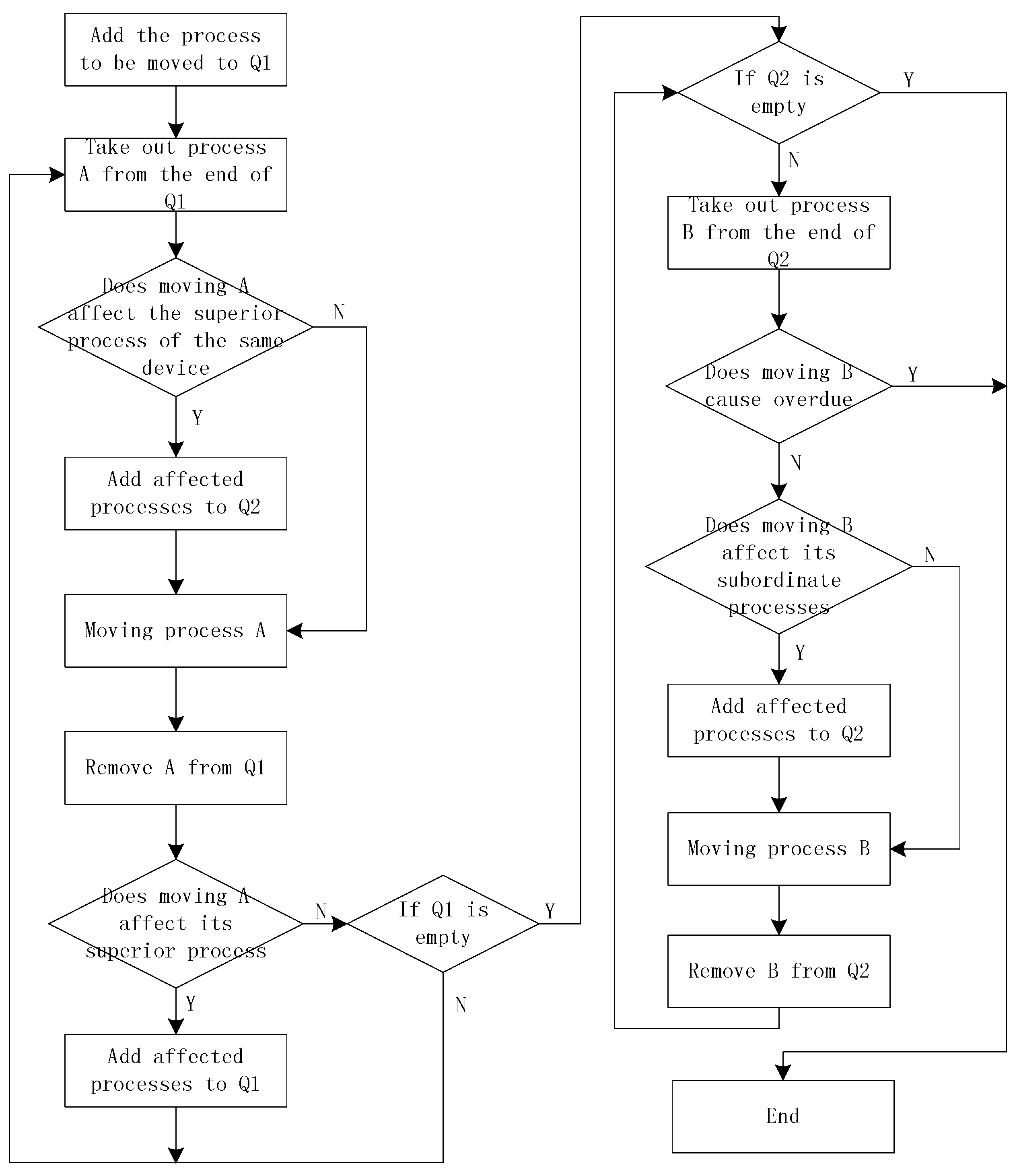
5.5. Algorithm Implementation Steps
- Step 1: Parameter setting, including population size, maximum number of iterations n, learning factor, upper and lower limits of particle position and speed, dimension of the algorithm (this paper takes the total number of operation nodes as the dimension).
- Step 2: Initialize the population by using the coding method based on operation and the method shown in Figure 6.
- Step 3: Update the particles, update the speed and position according to Equations (19) and (20), and calculate the individual extreme and global extreme.
- Step 4: If the global extremum remains unchanged, a new generation of particles will be generated according to Equation (21). Otherwise, step 4 will be adjusted to step 5.
- Step 5: Update the inertia weight according to Equation (22).
- Step 6: Depends on whether the termination condition is satisfied. If not, return to step 3. Otherwise, the optimal solution is output and the algorithm ends.
6. Treatment of Time Constraints
- Product delivery cycle: the weight coefficient can be set according to the product delivery cycle, and it is valid for all nodes of the product;
- Level/complexity of the product: the farther the subordinate node is from the top node of the product, the higher the weight is required;
- Number of peer nodes: the more peer nodes one node has, the higher weight the node needs to be assigned;
- Process route and processing time: the longer the process flow and processing time are, the higher the weight required;
- The flexibility of the search needs to be ensured, and the search process can be limited according to the range of weights.
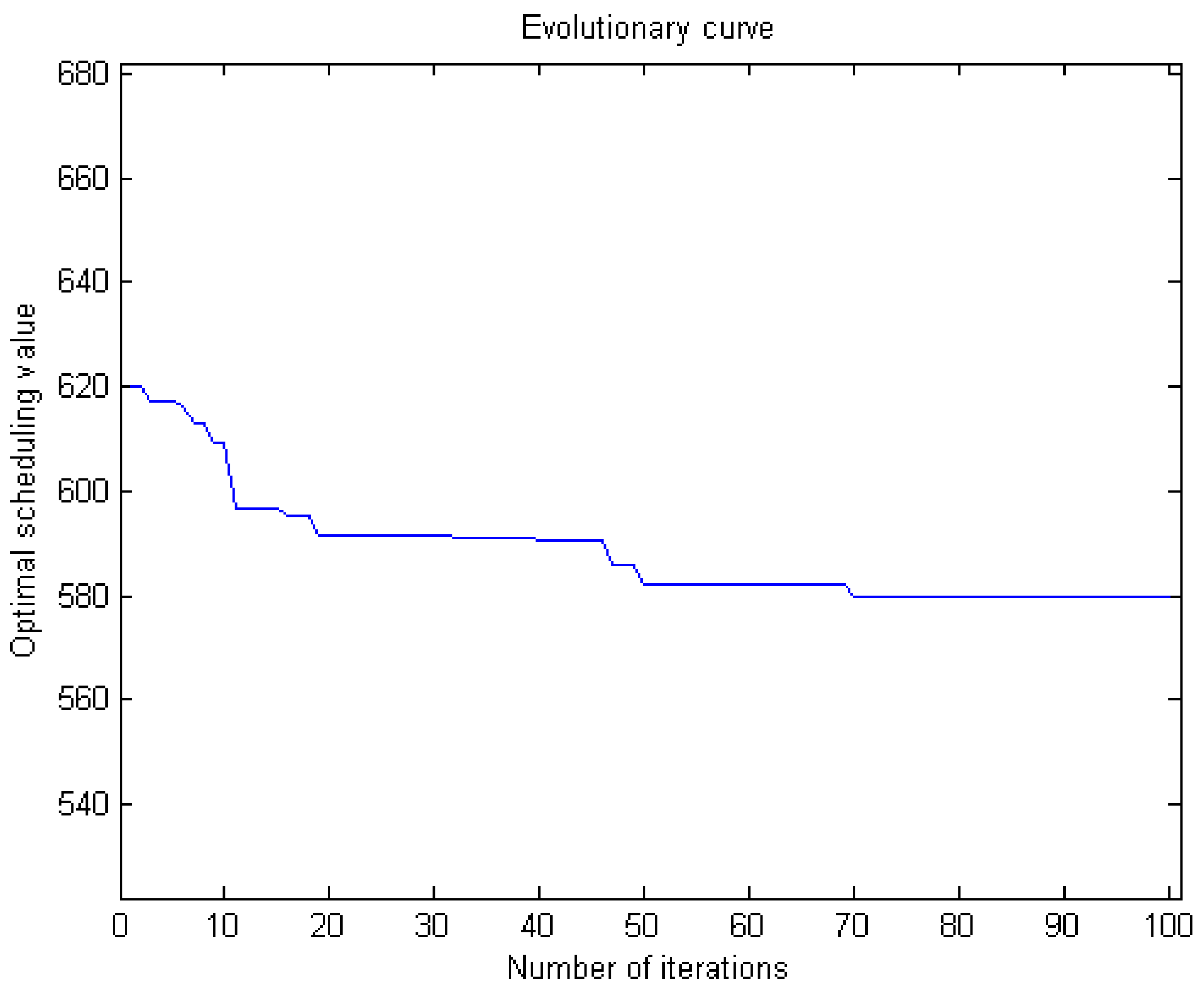
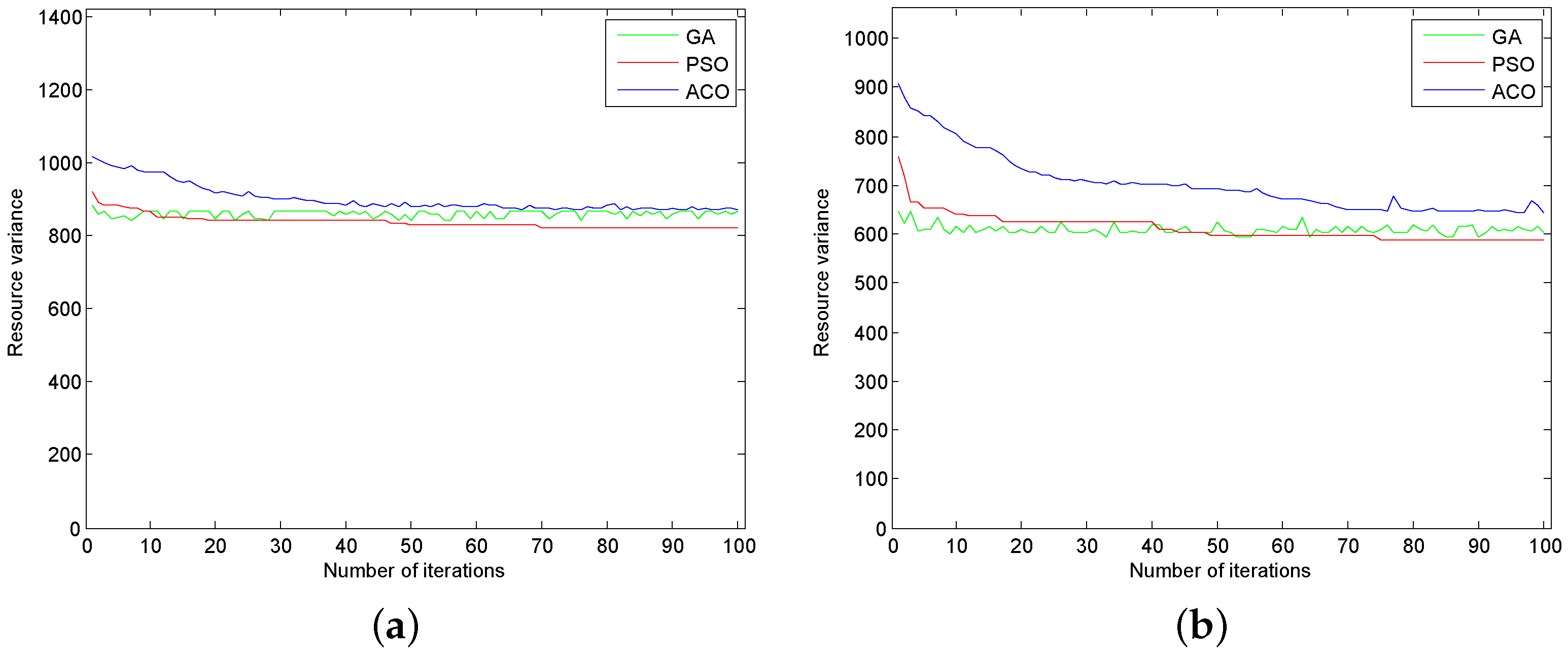
7. A Case Study
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, B.; Gao, J.; Chen, K.; Guo, K. Two-generation Pareto ant colony algorithm for multi-objective job shop scheduling problem with alternative process plans and unrelated parallel machines. J. Intell. Manuf. 2018, 29, 93–108. [Google Scholar] [CrossRef]
- Luo, Y. Nested optimization method combining complex method and ant colony optimization to solve JSSP with complex associated processes. J. Intell. Manuf. 2017, 28, 1801–1815. [Google Scholar] [CrossRef]
- Li, C.; Shen, H.; Li, L.; Yi, Q. A Batch Splitting Flexible Job Shop Scheduling Model for Energy Saving under Alternative Process Plans. J. Mech. Eng. 2017, 53, 12. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, X.; Ai, Y. ACO integrated approach for solving flexible job-shop scheduling with multiple process plans. Comput. Integr. Manuf. Syst. 2018, 24, 558–569. [Google Scholar]
- Naderi, B.; Azab, A. An improved model and novel simulated annealing for distributed job shop problems. Int. J. Adv. Manuf. Technol. 2015, 81, 693–703. [Google Scholar] [CrossRef]
- Ackermann, S.; Fumero, Y.; Montagna, J.M.M. Optimization Framework for the Simultaneous Batching and Scheduling of Multisite Production Environments. Ind. Eng. Chem. Res. 2018, 57, 16395–16406. [Google Scholar] [CrossRef]
- Asl, A.J.; Solimanpur, M.; Shankar, R. Multi-objective multi-model assembly line balancing problem: A quantitative study in engine manufacturing industry. OPSEARCH 2019, 56, 603–627. [Google Scholar]
- Azami, A.; Demirli, K.; Bhuiyan, N. Scheduling in aerospace composite manufacturing systems: A two-stage hybrid flow shop problem. Int. J. Adv. Manuf. Technol. 2018, 95, 3259–3274. [Google Scholar] [CrossRef]
- Li, W.; He, L.; Cao, Y. Many-Objective Evolutionary Algorithm With Reference Point-Based Fuzzy Correlation Entropy for Energy-Efficient Job Shop Scheduling With Limited Workers. IEEE Trans. Cybern. 2021, 554, 236–255. [Google Scholar]
- Gao, K.; Cao, Z.; Zhang, L.; Chen, Z.; Han, Y.; Pan, Q. A Review on Swarm Intelligence and Evolutionary Algorithms for Solving Flexible Job Shop Scheduling Problems. IEEE/CAA J. Autom. Sin. 2019, 6, 904–916. [Google Scholar] [CrossRef]
- Knopp, S.; Dauzère-Pérès, S.; Yugma, C. A Batch-Oblivious Approach for Complex Job-Shop Scheduling Problems. Eur. J. Oper. Res. 2017, 263, 50–61. [Google Scholar] [CrossRef]
- Dai, Y.J.; Zhang, Z.Y.; Wang, W.Z. Block two-stage and multi-workshop scheduling with transportation consideration. Comput. Eng. Appl. 2016, 52, 222–228. [Google Scholar]
- Yeganeh, F.T.; Zegordi, S.H. A multi-objective optimization approach to project scheduling with resiliency criteria under uncertain activity duration. Ann. Oper. Res. 2020, 285, 161–196. [Google Scholar] [CrossRef]
- Delice, Y. A genetic algorithm approach for balancing two-sided assembly lines with setups. Assem. Autom. 2019, 39, 827–839. [Google Scholar] [CrossRef]
- Jiang, Z.Q.; Le, Z.; Mechanical, S.O. Multi-objective flexible job-shop scheduling based on low-carbon strategy. Comput. Integr. Manuf. Syst. 2015, 21, 1023–1031. [Google Scholar]
- Elmi, A.; Topaloglu, S. Multi-degree cyclic flow shop robotic cell scheduling problem: Ant colony optimization. Comput. Oper. Res. 2016, 30, 805–821. [Google Scholar] [CrossRef]
- Ziaee, M. A heuristic algorithm for the distributed and flexible job-shop scheduling problem. J. Supercomput. 2014, 67, 69–83. [Google Scholar] [CrossRef]
- Le, H.T.; Geser, P.; Middendorf, M. An Iterated Local Search Algorithm for the Two-Machine Flow Shop Problem with Buffers and Constant Processing Times on One Machine. In Proceedings of the European Conference on Evolutionary Computation in Combinatorial Optimization (Part of EvoStar), Leipzig, Germany, 24–26 April 2019; pp. 50–65. [Google Scholar]
- Zhang, G. Hybrid variable neighborhood search for multi objective flexible job shop scheduling problem. In Proceedings of the 2012 IEEE 16th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Wuhan, China, 23–25 May 2012; pp. 725–729. [Google Scholar]
- Nagano, M.S.; Komesu, A.S.; Miyata, H.H. An evolutionary clustering search for the total tardiness blocking flow shop problem. J. Intell. Manuf. 2019, 30, 1843–1857. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, H.; Li, W.; Zhou, M.; Zhang, Y.; Chaovalitwongse, W.A. Comprehensive Learning Particle Swarm Optimization Algorithm With Local Search for Multimodal Functions. IEEE Trans. Evol. Comput. 2019, 23, 718–731. [Google Scholar] [CrossRef]
- Lv, Z.; Wang, L.; Han, Z.; Zhao, J.; Wang, W. Surrogate-Assisted Particle Swarm Optimization Algorithm With Pareto Active Learning for Expensive Multi-Objective Optimization. IEEE/CAA J. Autom. Sin. 2019, 6, 838–849. [Google Scholar] [CrossRef]
- Liu, T.K.; Chen, Y.P.; Chou, J.H. Solving Distributed and Flexible Job-Shop Scheduling Problems for a Real-World Fastener Manufacturer. IEEE Access 2014, 2, 1598–1606. [Google Scholar]
- Liang, J.; Wang, P.; Guo, L.; Qu, B.; Yue, C.; Yu, K.; Wang, Y. Multi-objective flow shop scheduling with limited buffers using hybrid self-adaptive differential evolution. Memetic Comput. 2019, 11, 407–422. [Google Scholar] [CrossRef]
- Wang, S.; Wang, L.; Liu, M.; Xu, Y. An estimation of distribution algorithm for the multi-objective flexible job-shop scheduling problem. In Proceedings of the 2013 IEEE Symposium on Computational Intelligence in Scheduling (CISched), Singapore, 16–19 April 2013; pp. 1–8. [Google Scholar]
- Gen, M.; Zhang, W.; Lin, L.; Yun, Y. Recent advance in hybrid evolutionary algorithms for multiobjective manufacturing scheduling. Comput. Ind. Eng. 2017, 112, 616–633. [Google Scholar] [CrossRef]
- Kucukkoc, I.; Zhang, D.Z. Integrating ant colony and genetic algorithms in the balancing and scheduling of complex assembly lines. Int. J. Adv. Manuf. Technol. 2016, 82, 265–285. [Google Scholar] [CrossRef]
- Wong, T.N.; Zhang, S.; Wang, G.; Zhang, L. Integrated process planning and scheduling-multi-agent system with two-stage ant colony optimization algorithm. Int. J. Prod. Res. 2012, 50, 6188–6201. [Google Scholar] [CrossRef]
- Chen, Z.; Zheng, X.; Zhou, S.; Liu, C.; Chen, H. Quantum-inspired ant colony optimization algorithm for a two-stage permutation flow shop with batch processing machines. Int. J. Prod. Res. 2020, 58, 5945–5963. [Google Scholar] [CrossRef]
- Duan, J.H.; Meng, T.; Chen, Q.D.; Pan, Q.K. An Effective Artificial Bee Colony for Distributed Lot-Streaming Flow-shop Scheduling Problem. In Proceedings of the Intelligent Computing Methodologies, Wuhan, China, 15–18 August 2018; pp. 795–806. [Google Scholar]
- Shivasankaran, N.; Kumar, P.S.; Raja, K.V. Hybrid Sorting Immune Simulated Annealing Algorithm For Flexible Job Shop Scheduling. Int. J. Comput. Intell. Syst. 2015, 8, 455–466. [Google Scholar] [CrossRef]
- Golmakani, H.R.; Birjandi, A.R. A two-phase algorithm for multiple-route job shop scheduling problem subject to makespan. Int. J. Adv. Manuf. Technol. 2013, 67, 203–216. [Google Scholar] [CrossRef]
- Zhuang, C.B.; Xiong, H.; Liu, J.H.; Tang, C.T. An Improved Discrete Krill Herd Algorithm for Complex Product Assembly Scheduling Problem. Acta Armamentarii 2018, 39, 1590–1600. [Google Scholar]
- Lei, D.; Wang, T. Solving distributed two-stage hybrid flow shop scheduling using a shuffled frog-leaping algorithm with memeplex grouping. Eng. Optim. 2019, 12, 1–14. [Google Scholar]

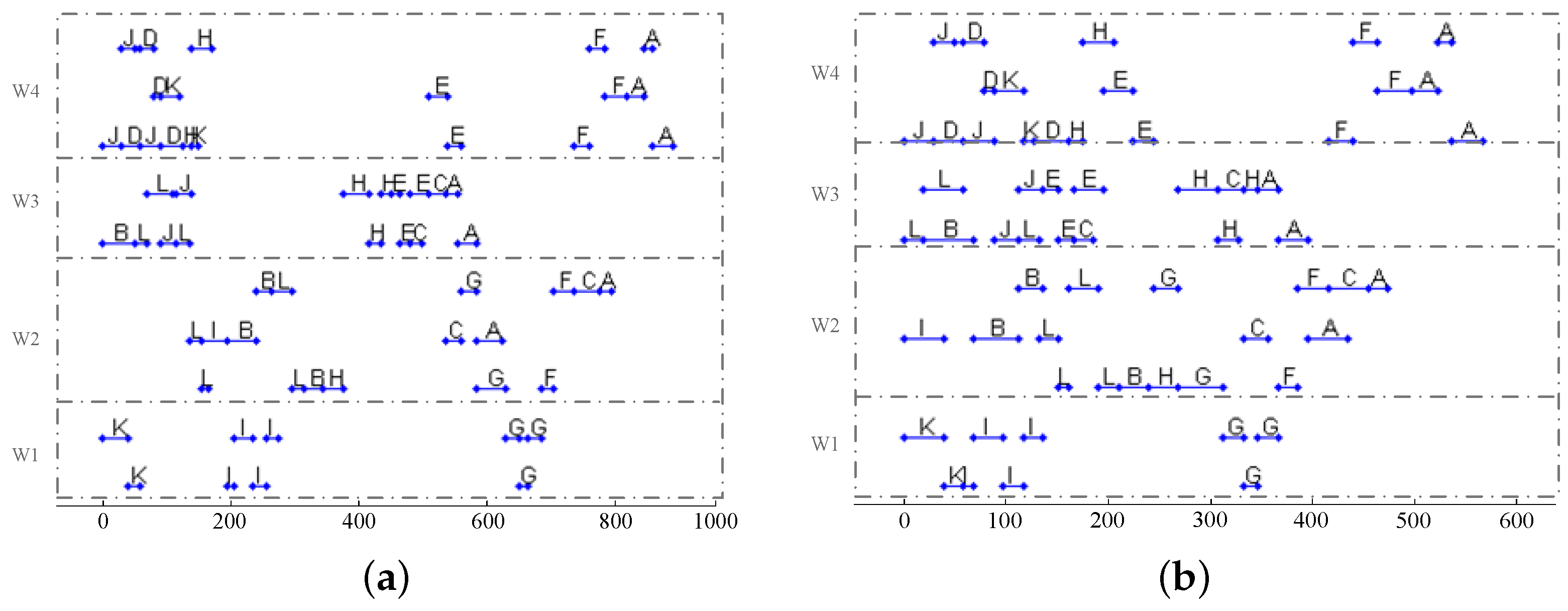


| Product | Process Route | Workshop/ Process Number | Processing Time | Workshop/ Process Number | Processing Time | Workshop/ Process Number | Processing Time |
|---|---|---|---|---|---|---|---|
| A | W3|W2|W4 | W3/2 | 20—30 | W2/2 | 40—20 | W4/3 | 25—15—30 |
| B | W3|W2 | W3/1 | 50 | W2/3 | 45—25—30 | ||
| C | W3|W2 | W3/2 | 20—25 | W2/2 | 25—40 | ||
| D | W4 | W4/4 | 30—20—10—35 | ||||
| E | W3|W4 | W3/3 | 15—15—30 | W4/2 | 30—20 | ||
| F | W2|W4 | W2/2 | 20—30 | W4/3 | 25—25—35 | ||
| G | W2|W1 | W2/2 | 25—45 | W1/3 | 20—15—20 | ||
| H | W4|W2|W3 | 4/2 | 15—30 | W2/1 | 30 | W3/3 | 40—20—15 |
| I | W2|W1 | W2/1 | 40 | W1/4 | 10—30—20—20 | ||
| J | W4|W3 | W4/3 | 30—20—30 | W3/2 | 25—25 | ||
| K | W1|W4 | W1/2 | 40—20 | W4/2 | 30—10 | ||
| L | W3|W2 | W3/3 | 20—40—20 | W2/4 | 20—10—30—20 |
| Symbol | Description |
|---|---|
| P | Set of all products |
| Product i, i = 1, …, n | |
| Parent node of | |
| Set of all components | |
| Q | Product process set |
| Process set for product | |
| The k-th process of product , k = 1, …, l | |
| Number of processes in the product, l = | |
| F | Workshop set |
| The w-th workshop | |
| M | Set of device resources |
| The r-th device of workshop w, r = 1, …, m | |
| Processing device, if process is processed on device r in workshop w, then = | |
| T | Set of product processing time |
| Start time of product | |
| Completion time of product | |
| Required completion time product | |
| Set of processing time | |
| The processing time of the k-th process of product —that is, the processing time on the device k in workshop w | |
| Start time of the k-th process of product | |
| End time of the k-th process of product | |
| End time of product |
| Products | Processes | Workshops | Devices | Pre Value | GA | PSO | ACO | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Optimal Value | Average Value | Optimal Value | Average Value | Optimal Value | Average Value | |||||
| 10 | 35 | 2 | 6 | 640 | 433 | 440 | 456 | 456 | 483 | 521 |
| 20 | 71 | 2 | 10 | 1001 | 572 | 601 | 590 | 590 | 714 | 759 |
| 30 | 107 | 3 | 12 | 1100 | 796 | 820 | 867 | 873 | 840 | 866 |
| 50 | 183 | 4 | 16 | 1626 | 962 | 994 | 998 | 998 | 976 | 1006 |
| 70 | 225 | 5 | 22 | 1128 | 572 | 591 | 639 | 645 | 587 | 602 |
| 100 | 291 | 6 | 30 | 1318 | 775 | 843 | 889 | 896 | 823 | 893 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, L.; Zhang, Z.; Huang, Z. A Scheduling Algorithm for Multi-Workshop Production Based on BOM and Process Route. Appl. Sci. 2021, 11, 5078. https://doi.org/10.3390/app11115078
Qiao L, Zhang Z, Huang Z. A Scheduling Algorithm for Multi-Workshop Production Based on BOM and Process Route. Applied Sciences. 2021; 11(11):5078. https://doi.org/10.3390/app11115078
Chicago/Turabian StyleQiao, Lihong, Zhenwei Zhang, and Zhicheng Huang. 2021. "A Scheduling Algorithm for Multi-Workshop Production Based on BOM and Process Route" Applied Sciences 11, no. 11: 5078. https://doi.org/10.3390/app11115078
APA StyleQiao, L., Zhang, Z., & Huang, Z. (2021). A Scheduling Algorithm for Multi-Workshop Production Based on BOM and Process Route. Applied Sciences, 11(11), 5078. https://doi.org/10.3390/app11115078






