A Method of Ore Blending Based on the Quality of Beneficiation and Its Application in a Concentrator
Abstract
:1. Introduction
2. Materials and Methods
2.1. Constraints on Ore Blending
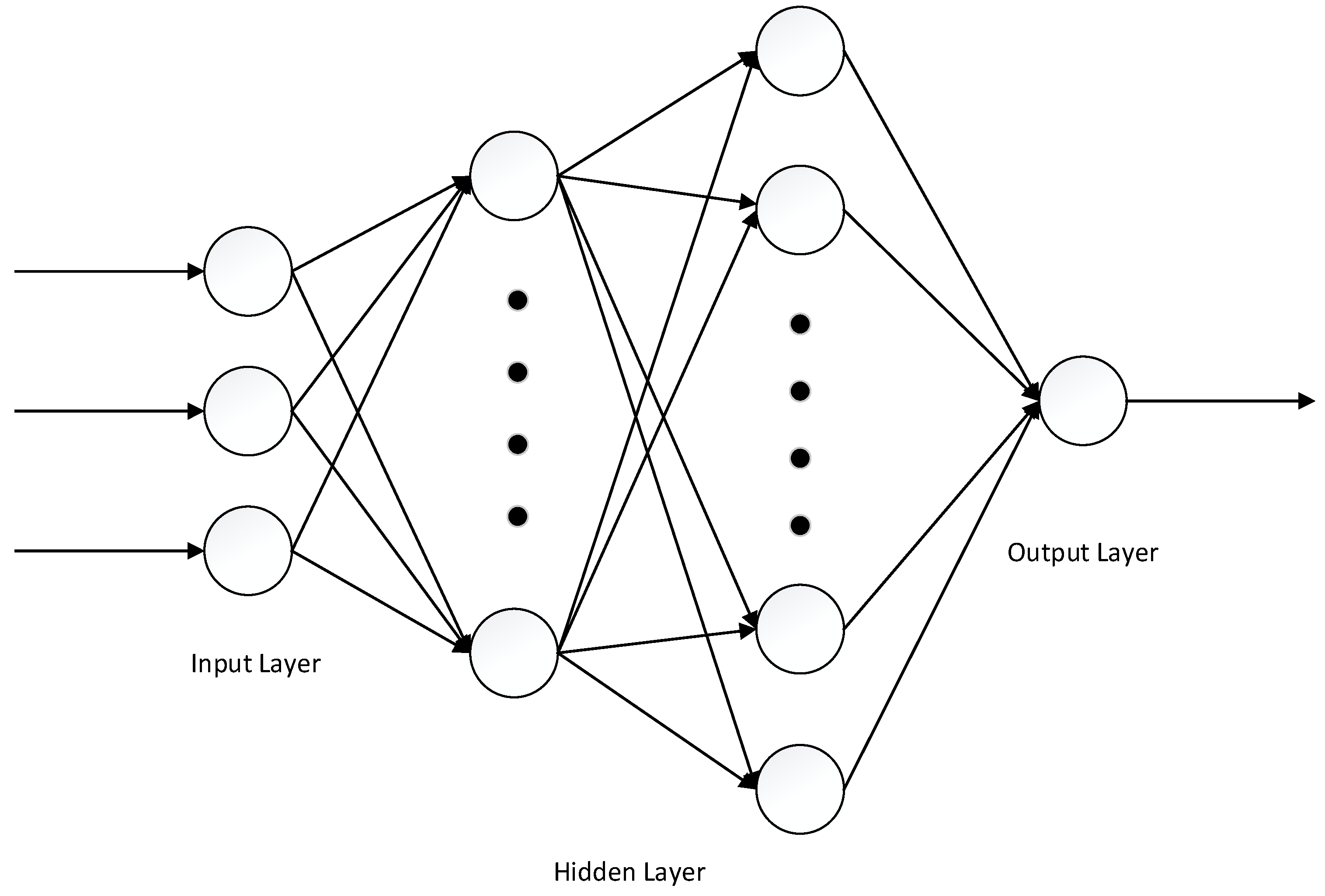
2.2. ABC-BPNN Model
2.2.1. Data Preprocessing
2.2.2. Describing Function
2.2.3. Normalization
2.2.4. Fitting and Saving Function
2.3. Optimization Model
- (1)
- Performance Index:where is the target value of concentrate recovery.
- (2)
- Constraints:
- (a)
- Raw Ore Constraints
- (b)
- Mixed ore properties constraintswhere m is the number of ore producing blocks, is the total amount of production, is the ore grade, is the HQC, and is the LQC.
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nava, J.V.; Llorens, T.; Menéndez-Aguado, J.M. Kinetics of Dry-Batch Grinding in a Laboratory-Scale Ball Mill of Sn–Ta–Nb Minerals from the Penouta Mine (Spain). Metals 2020, 10, 1687. [Google Scholar] [CrossRef]
- Van Tonder, E.; Deglon, D.A.; Napier-Munn, T.J. The effect of ore blends on the mineral processing of platinum ores. Min. Eng 2010, 23, 621–626. [Google Scholar] [CrossRef] [Green Version]
- Lamghari, A.; Dimitrakopoulos, R. A diversified Tabu search approach for the open-pit mine production scheduling problem with metal uncertainty. Eur. J. Oper. Res. 2012, 222, 642–652. [Google Scholar] [CrossRef] [Green Version]
- Consuegra, F.R.A.; Dimitrakopoulos, R. Algorithmic approach to pushback design based on stochastic programming: Method, application and comparisons. Min. Technol. 2010, 119, 88–101. [Google Scholar] [CrossRef]
- Ramazan, S.; Dimitrakopoulos, R. Production scheduling with uncertain supply: A new solution to the open pit mining problem. Optim. Eng. 2013, 14, 361–380. [Google Scholar] [CrossRef]
- Benndorf, J.; Dimitrakopoulos, R. Stochastic long-term production scheduling of iron ore deposits: Integrating joint multi-element geological uncertainty. J. Min. Sci. 2013, 49, 68–81. [Google Scholar] [CrossRef]
- Leite, A.; Dimitrakopoulos, R. Stochastic optimisation model for open pit mine planning: Application and risk analysis at copper deposit. Min. Technol. 2013, 116, 109–118. [Google Scholar] [CrossRef]
- Goodfellow, R.C.; Dimitrakopoulos, R. Global optimization of open pit mining complexes with uncertainty. Appl. Soft Comput. 2016, 40, 292–304. [Google Scholar] [CrossRef]
- Lambert, W.B.; Newman, A.M. Tailored Lagrangian Relaxation for the open pit block sequencing problem. Ann. Oper. Res. 2014, 222, 419–438. [Google Scholar] [CrossRef]
- Boland, N.; Dumitrescu, I.; Froyland, G.; Gleixner, A.M. LP-based disaggregation approaches to solving the open pit mining production scheduling problem with block processing selectivity. Comput. Oper. Res. 2009, 36, 1064–1089. [Google Scholar] [CrossRef]
- Goodfellow, R.; Dimitrakopoulos, R. Algorithmic integration of geological uncertainty in pushback designs for complex multiprocess open pit mines. Min. Technol. 2013, 122, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Ferland, J.A.; Amaya, J.; Djuimo, M.S. Application of a Particle Swarm Algorithm to the Capacitated Open Pit Mining Problem; Springer: Berlin/Heidelberg, Germany, 2007; Volume 76, pp. 127–133. [Google Scholar]
- Shishvan, M.S.; Sattarvand, J. Long term production planning of open pit mines by ant colony optimization. Eur. J. Oper. Res. 2015, 240, 825–836. [Google Scholar] [CrossRef]
- Kumral, M. Optimizing ore-waste discrimination and block sequencing through simulated annealing. Appl. Soft Comput. 2013, 13, 3737–3744. [Google Scholar] [CrossRef]
- Khan, A.; Niemann-Delius, C. Production Scheduling of Open Pit Mines Using Particle Swarm Optimization Algorithm. Adv. Oper. Res. 2014, 2014, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Montiel, L.; Dimitrakopoulos, R. Stochastic mine production scheduling with multiple processes: Application at Escondida Norte, Chile. J. Min. Sci. 2013, 49, 583–597. [Google Scholar] [CrossRef]
- Dewil, R.; Vansteenwegen, P.; Cattrysse, D.; Van Oudheusden, D. A minimum cost network flow model for the maximum covering and patrol routing problem. Eur. J. Oper. Res. 2015, 247, 27–36. [Google Scholar] [CrossRef] [Green Version]
- Dominy, S.; Connor, L.O.; Parbhakar-Fox, A.; Glass, H.; Purevgerel, S. Geometallurgy—A Route to More Resilient Mine Operations. Minerals 2018, 8, 560. [Google Scholar] [CrossRef] [Green Version]
- Navarra, A.; Menzies, A.; Jordens, A.; Waters, K. Strategic evaluation of concentrator operational modes under geological uncertainty. Int. J. Min. Process 2017, 164, 45–55. [Google Scholar] [CrossRef]
- Tavares, L.M.; Kallemback, R.D.C. Grindability of binary ore blends in ball mills. Min. Eng. 2013, 41, 115–120. [Google Scholar] [CrossRef]
- Birat, J. Society, Materials, and the Environment: The Case of Steel. Metals 2020, 10, 331. [Google Scholar] [CrossRef] [Green Version]
- Phull, J.; Egas, J.; Barui, S.; Mukherjee, S.; Chattopadhyay, K. An Application of Decision Tree-Based Twin Support Vector Machines to Classify Dephosphorization in BOF Steelmaking. Metals 2020, 10, 25. [Google Scholar] [CrossRef] [Green Version]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A survey: Algorithms simulating bee swarm intelligence. Artif. Intell. Rev. 2009, 31, 61–85. [Google Scholar] [CrossRef]
- Li, B. Research on WNN Modeling for Gold Price Forecasting Based on Improved Artificial Bee Colony Algorithm. Comput. Intel. Neurosci. 2014, 2014, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Jafrasteh, B.; Fathianpour, N. A hybrid simultaneous perturbation artificial bee colony and back-propagation algorithm for training a local linear radial basis neural network on ore grade estimation. Neurocomputing 2017, 235, 217–227. [Google Scholar] [CrossRef]
- Chen, C.; Tsai, Y.; Jhang, R. Approximation of the Piecewise Function Using Neural Fuzzy Networks with an Improved Artificial Bee Colony Algorithm. J. Autom. Control Eng. 2015, 3, 18–21. [Google Scholar] [CrossRef]
- Anuar, S.; Selamat, A.; Sallehuddin, R. Hybrid artificial neural network with artificial bee colony algorithm for crime classification. In Computational Intelligence in Information Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 31–40. [Google Scholar]
- Ghanem, W.A.H.M.; Jantan, A. Swarm intelligence and neural network for data classification. In Proceedings of the 2014 IEEE International Conference on Control System, Computing and Engineering (ICCSCE 2014), Penang, Malaysia, 28–30 November 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 196–201. [Google Scholar]
- Cui, L.; Zhang, K.; Li, G.; Wang, X.; Yang, S.; Ming, Z.; Huang, J.Z.; Lu, N. A smart artificial bee colony algorithm with distance-fitness-based neighbor search and its application. Future Gener. Comput. Syst. 2018, 89, 478–493. [Google Scholar] [CrossRef]


| Maximum Training | Learning Rate | Minimum Error | Number of Input | Number of Output |
|---|---|---|---|---|
| 2500 | 0.1 | 0.0001 | 3 | 1 |
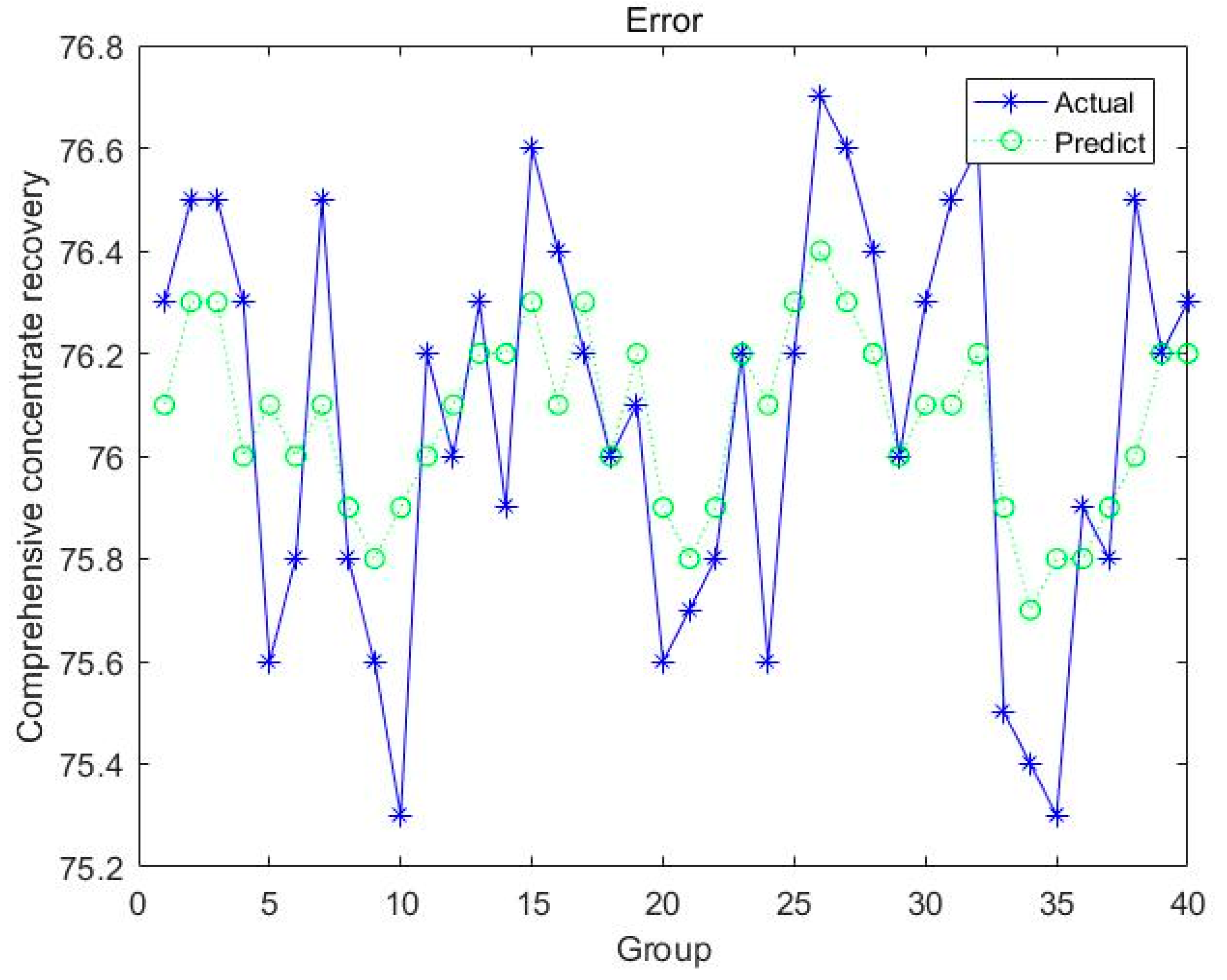
| Test Error | Training Error |
|---|---|
| 0.0788 | 0.0309 |
| Algorithm | Mean | SD |
|---|---|---|
| ABC-BP | 76.0725 | 0.0309 |
| PSO-BP | 77.1132 | 0.0421 |
| NA-BP | 75.8654 | 0.0674 |
| No | Ore Grade T (%) | Iron Content M (%) | High Quality Content G (%) | Low Quality Content B (%) | Minimum Production Volume (Unit) | Geological Reserves (Unit) |
|---|---|---|---|---|---|---|
| 1 | 34.54 | 20.32 | 18.24 | 4.31 | 0 | 100 |
| 2 | 29.26 | 15.48 | 12.87 | 4.25 | 0 | 100 |
| 3 | 32.03 | 3.21 | 0 | 3.17 | 0 | 100 |
| 4 | 31.87 | 2.50 | 0 | 2.56 | 0 | 100 |
| Total Ore (Unit) | Concentrate Recovery (%) | Upper Grade of Ore (%) | Lower Grade of Ore (%) | Upper of High Quality (%) | Lower of High Quality (%) | Upper of Low Quality (%) | Lower of Low Quality (%) |
|---|---|---|---|---|---|---|---|
| 100 | 73.8 | 33 | 29 | 12 | 9 | 4.5 | 3 |
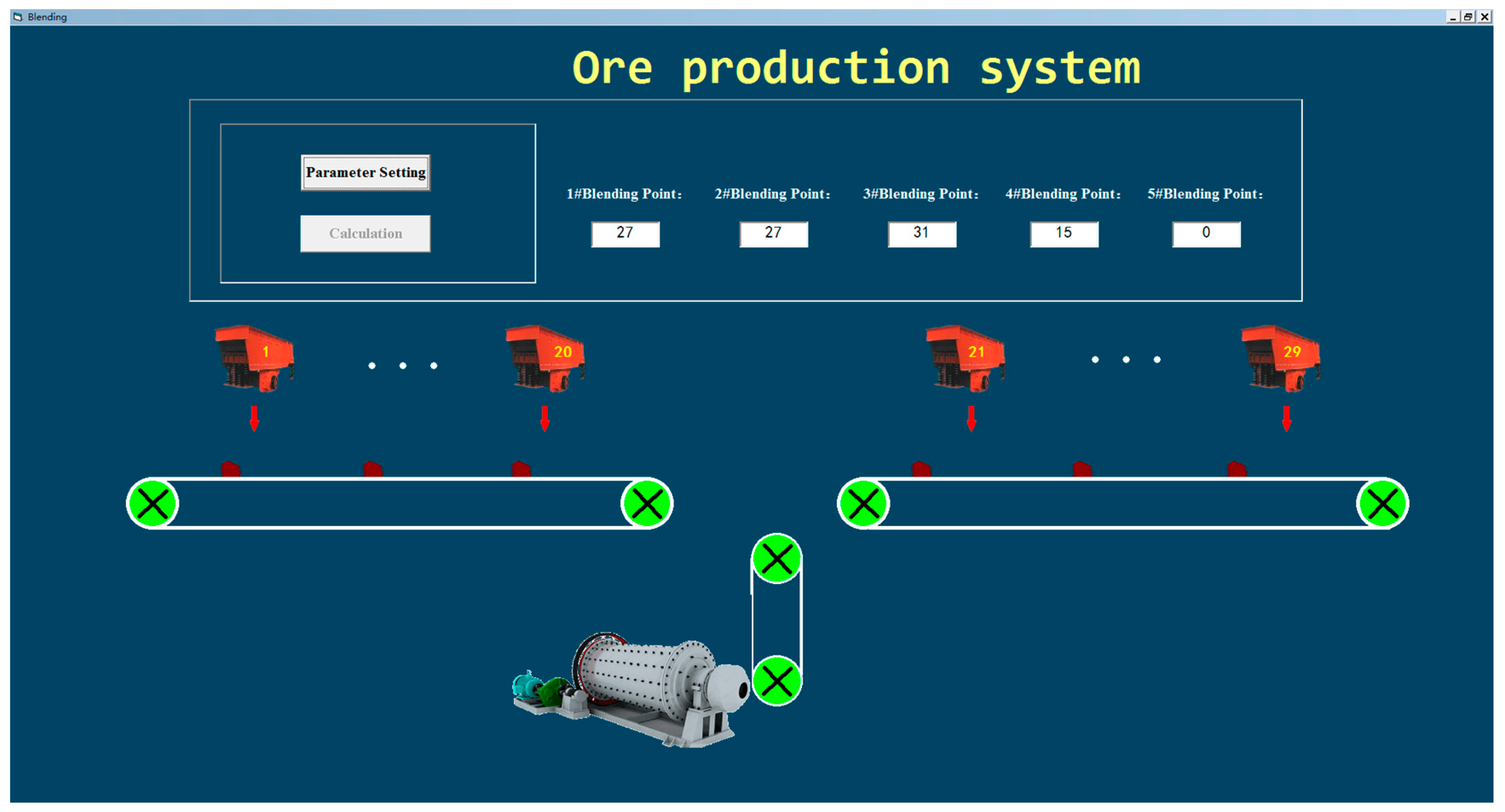
| Modeling Method | Mining No.1 | Mining No.2 | Mining No.3 | Mining No.4 | Ore Dressing Index |
|---|---|---|---|---|---|
| Original method | 16 | 24 | 32 | 28 | 79.45 |
| This method | 27 | 27 | 31 | 15 | 82.35 |
| No. | Ore Dressing Index | Result |
|---|---|---|
| 1 | >80 | Excellent |
| 2 | 70–80 | Good |
| 3 | 60–70 | Qualified |
| 4 | 50–60 | Relatively poor |
| 5 | 40–50 | Poor |
| 6 | <40 | Unavailable |
| ODI | Concentrate Grade | Tailing Grade | Concentration Ratio | Cost (CNY/t) |
|---|---|---|---|---|
| Excellent | 67.5% | 7.5–8.5% | 2.93–3.03% | 383 |
| Good | 67.5% | 8.5–9.5% | 3.03–3.14% | 407 |
| Qualified | 67.5% | 9.5–10.5% | 3.14–3.26% | 447 |
| Relatively poor | 67.5% | 10.5–11.5% | 3.26–3.39% | 511 |
| Poor | 67.5% | 11.5–13.5% | 3.39–3.72% | 609 |
| Unavailable | 67.5% | More than 13.5% | More than 3.72% | 796 |
| Scheme | Mining No.1 | Mining No.2 | Mining No.3 | Mining No.4 | Mining No.5 | Mining No.6 | Mining No.7 | Mixed Ore Grade (%) | Profit (CNY) |
|---|---|---|---|---|---|---|---|---|---|
| Method 1 | 41 | 24 | 15 | 6 | 14 | 2 | 5 | 54.30 | 46.00 |
| Method 2 | 50 | 24 | 6 | 6 | 15 | 2 | 5 | 54.08 | 50.24 |
| Method 3 | 41 | 24 | 15 | 6 | 14 | 2 | 5 | 54.56 | 45.04 |
| Method 4 | 50 | 24 | 6 | 6 | 15 | 2 | 5 | 54.36 | 49.64 |
| This method | 50 | 20 | 5 | 5 | 13 | 2 | 4 | 54.22 | 58.11 |
| Scheme | Mining No.1 | Mining No.2 | Mining No.3 | Mining No.4 | Mining No.5 | Mining No.6 | Mining No.7 | Mining No.8 | Mining No.9 | Mixed Ore Grade (%) | Profit (CNY) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Method 1 | 41 | 24 | 0 | 15 | 0 | 6 | 14 | 2 | 5 | 54.30 | 94.12 |
| Method 2 | 50 | 24 | 0 | 6 | 0 | 6 | 15 | 2 | 5 | 54.08 | 102.71 |
| Method 3 | 41 | 0 | 24 | 15 | 0 | 6 | 14 | 2 | 5 | 54.56 | 93.49 |
| Method 4 | 50 | 0 | 24 | 6 | 0 | 6 | 15 | 1 | 5 | 54.36 | 102.35 |
| Method 5 | 41 | 24 | 0 | 0 | 15 | 6 | 13 | 1 | 5 | 55.28 | 83.68 |
| Method 6 | 50 | 24 | 0 | 0 | 6 | 6 | 14 | 2 | 5 | 54.51 | 98.85 |
| This method | 46 | 23 | 3 | 6 | 3 | 6 | 14 | 2 | 4 | 54.18 | 112.10 |
| Scheme | Mining No.1 | Mining No.2 | Mining No.3 | Mining No.4 | Mining No.5 | Mining No.6 | Mining No.7 | Mining No.8 | Mining No.9 | Mixed Ore Grade (%) | Profit (CNY) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Method 1 | 42 | 23 | 0 | 15 | 0 | 6 | 15 | 2 | 5 | 53.71 | 54.12 |
| Method 2 | 42 | 32 | 0 | 6 | 0 | 6 | 15 | 2 | 5 | 54.03 | 59.83 |
| Method 3 | 42 | 18 | 5 | 0 | 15 | 6 | 15 | 2 | 5 | 54.00 | 49.35 |
| Method 4 | 42 | 29 | 3 | 0 | 6 | 6 | 15 | 2 | 5 | 54.01 | 57.94 |
| This method | 36 | 26 | 3 | 13 | 2 | 5 | 14 | 2 | 4 | 54.15 | 67.36 |
| Scheme | Mining No.1 | Mining No.2 | Mining No.3 | Mining No.4 | Mining No.5 | Mining No.6 | Mining No.7 | Mining No.8 | Mining No.9 | Mixed Ore Grade (%) | Profit (CNY) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Method 1 | 45 | 20 | 0 | 0 | 15 | 6 | 14 | 2 | 5 | 54.40 | 56.41 |
| Method 2 | 45 | 0 | 20 | 0 | 15 | 6 | 14 | 2 | 5 | 54.63 | 56.09 |
| Method 3 | 45 | 20 | 0 | 15 | 0 | 6 | 15 | 2 | 5 | 53.83 | 69.35 |
| Method 4 | 45 | 0 | 20 | 15 | 0 | 6 | 15 | 2 | 5 | 54.04 | 68.92 |
| This method | 35 | 27 | 1 | 13 | 5 | 6 | 13 | 2 | 4 | 54.21 | 80.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Zhang, D.; Gao, X. A Method of Ore Blending Based on the Quality of Beneficiation and Its Application in a Concentrator. Appl. Sci. 2021, 11, 5092. https://doi.org/10.3390/app11115092
Liu B, Zhang D, Gao X. A Method of Ore Blending Based on the Quality of Beneficiation and Its Application in a Concentrator. Applied Sciences. 2021; 11(11):5092. https://doi.org/10.3390/app11115092
Chicago/Turabian StyleLiu, Bingyu, Dingsen Zhang, and Xianwen Gao. 2021. "A Method of Ore Blending Based on the Quality of Beneficiation and Its Application in a Concentrator" Applied Sciences 11, no. 11: 5092. https://doi.org/10.3390/app11115092
APA StyleLiu, B., Zhang, D., & Gao, X. (2021). A Method of Ore Blending Based on the Quality of Beneficiation and Its Application in a Concentrator. Applied Sciences, 11(11), 5092. https://doi.org/10.3390/app11115092





