Limitations of Structural Insight into Ultrafast Melting of Solid Materials with X-ray Diffraction Imaging
Abstract
:1. Introduction
2. Materials and Methods
2.1. Simulations of X-ray-Irradiated Solid Materials with XTANT Code
- (a)
- The core of the model is the transferable tight binding (TB) Hamiltonian, which treats the electronic band structure and atomic potential energy surface. The latter evolves in time, depending on the positions of atoms in the simulation box. Periodic boundary conditions are applied. Tight-binding parametrization from [31] is used here.
- (b)
- Atomic positions are propagated in time, using a classical molecular dynamics (MD) scheme. It solves Newton equations for nuclei with the potential energy surface evaluated from the TB module.
- (c)
- Electron occupation numbers on the transient energy levels are assumed to follow the Fermi–Dirac distribution with a transient temperature and chemical potential evolving in time. The electron temperature changes due to the interaction of band electrons with X-rays and high-energy electrons or due to their nonadiabatic interaction with nuclei (through electron-ion scattering [19]).
- (d)
- The non-equilibrium part of the electron distribution at high energies and Auger decays of core holes are treated with a classical event-by-event Monte Carlo (MC) simulation. This stochastically models the X-ray-induced photoelectron emission from the K-shell or from the valence band, the Auger decays, and the scattering of high-energy electrons.
- (e)
- Electron-ion energy exchange is calculated with a nonadiabatic approach [19], in which matrix elements are calculated as an overlap of TB wave-functions plugged into the Boltzmann collision integral. This energy is transferred to atoms by respective velocity scaling at each MD step.
2.2. Description of the Experimental Data, Including Beam Characteristics
- (i)
- The “average” 2D Gaussian spatial profile was used. As the signal was integrated over different X-ray shots, obtained with pulses of differing spatial characteristics, the “average” 2D Gaussian spatial profile used for our calculations was a reliable approximation.
- (ii)
- Gaussian temporal pulse profile was used. The pump-probe experiment was performed at X-ray fluences still within a linear absorption regime (i.e., with the X-ray photoabsorption rate only linearly dependent on the pulse intensity). Therefore, the specific spiky time characteristics of the pulse intensity in each shot did not play much role for the sample evolution (and sample imaging). The respective check was performed in [32]. The final experimental signal did not originate from a single shot but was integrated over signals resulting from many different FEL shots. This justifies the usage of a Gaussian temporal pulse as the “average” case.
- (iii)
- Assumed uniform illumination of the material in the region above the X-ray penetration depth. The volume averaging of the signal was restricted to the volume averaging in the plane lateral to the X-ray beam, because, as we show in the next subsection, one could neglect with a good accuracy all signal contributions to the volume integration below the X-ray penetration depth, and treat the region in the material above the penetration depth as uniformly illuminated.
2.3. Volume Integration of Diffraction Signal
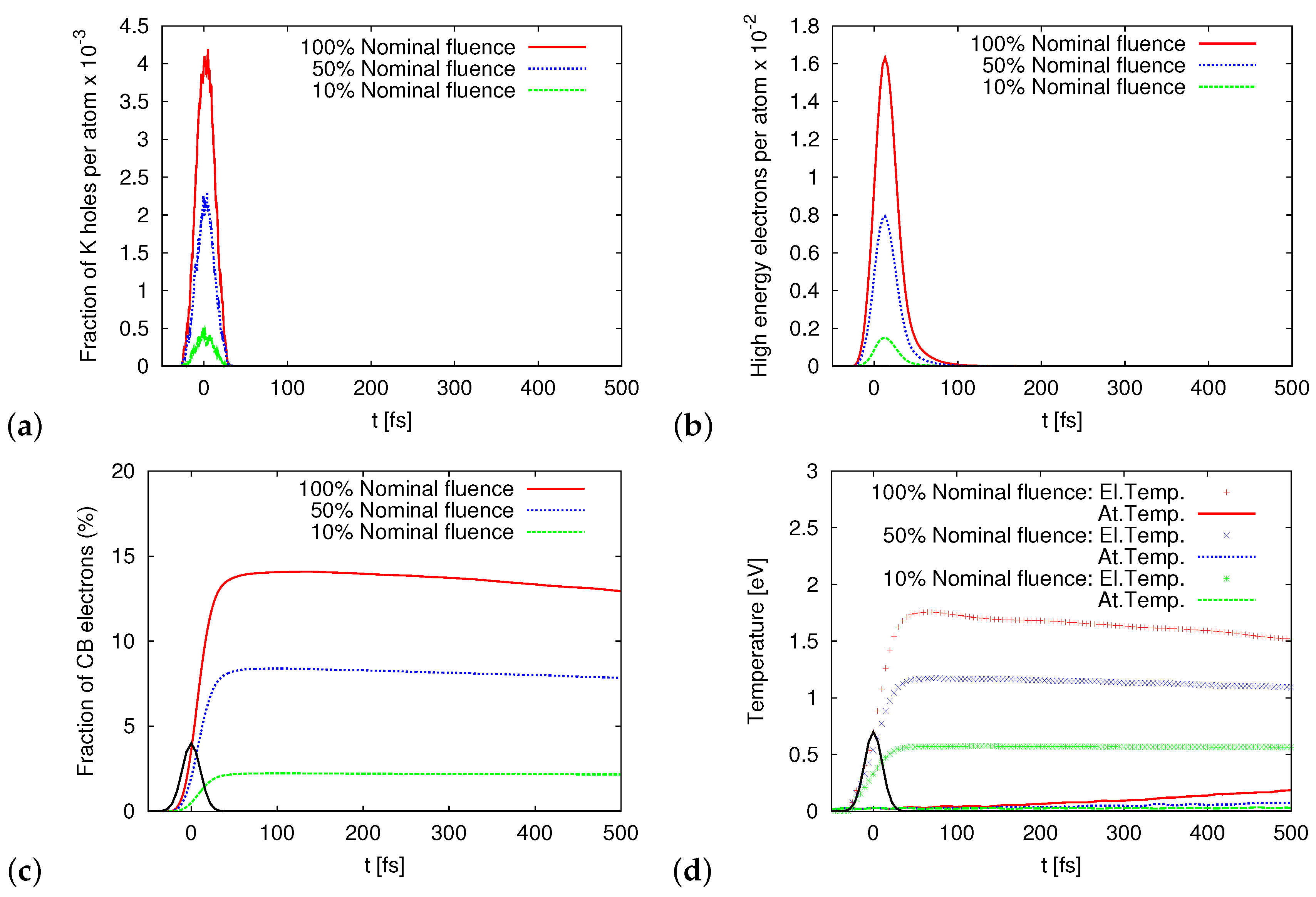
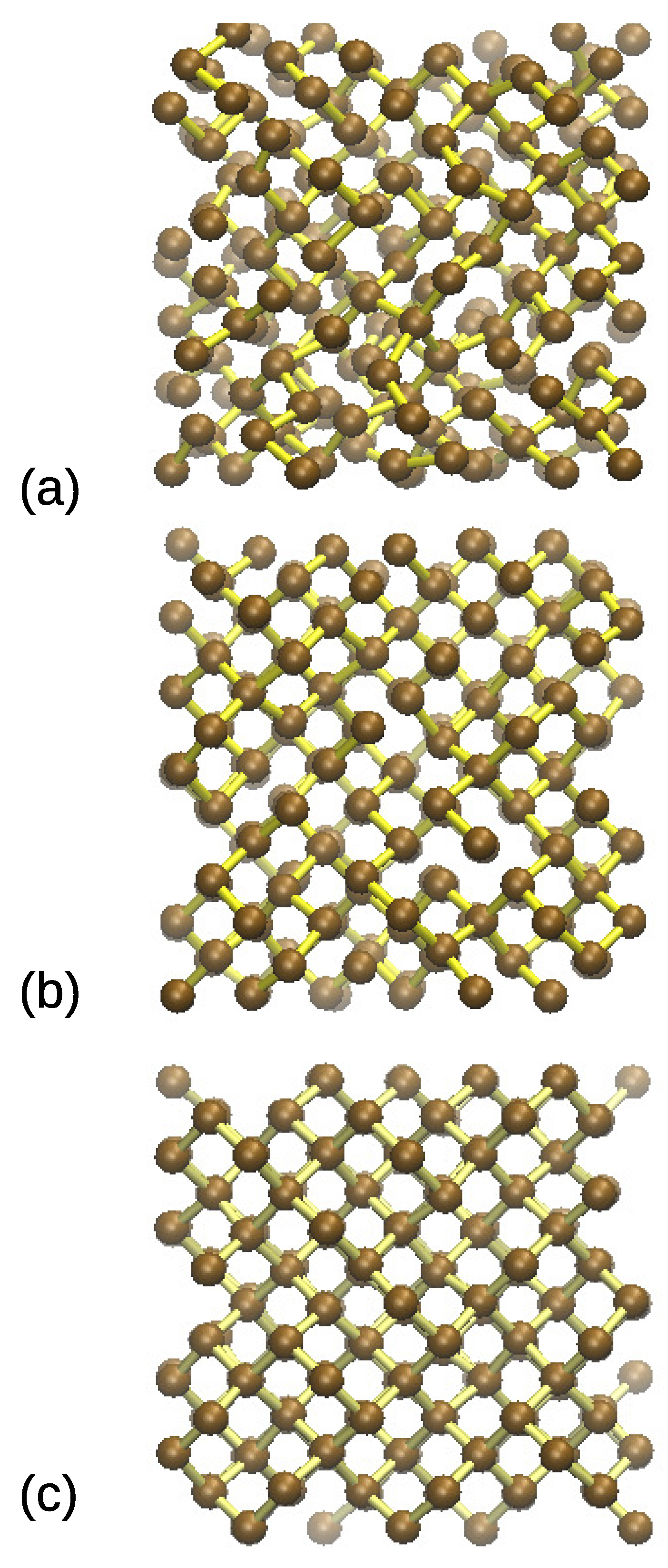
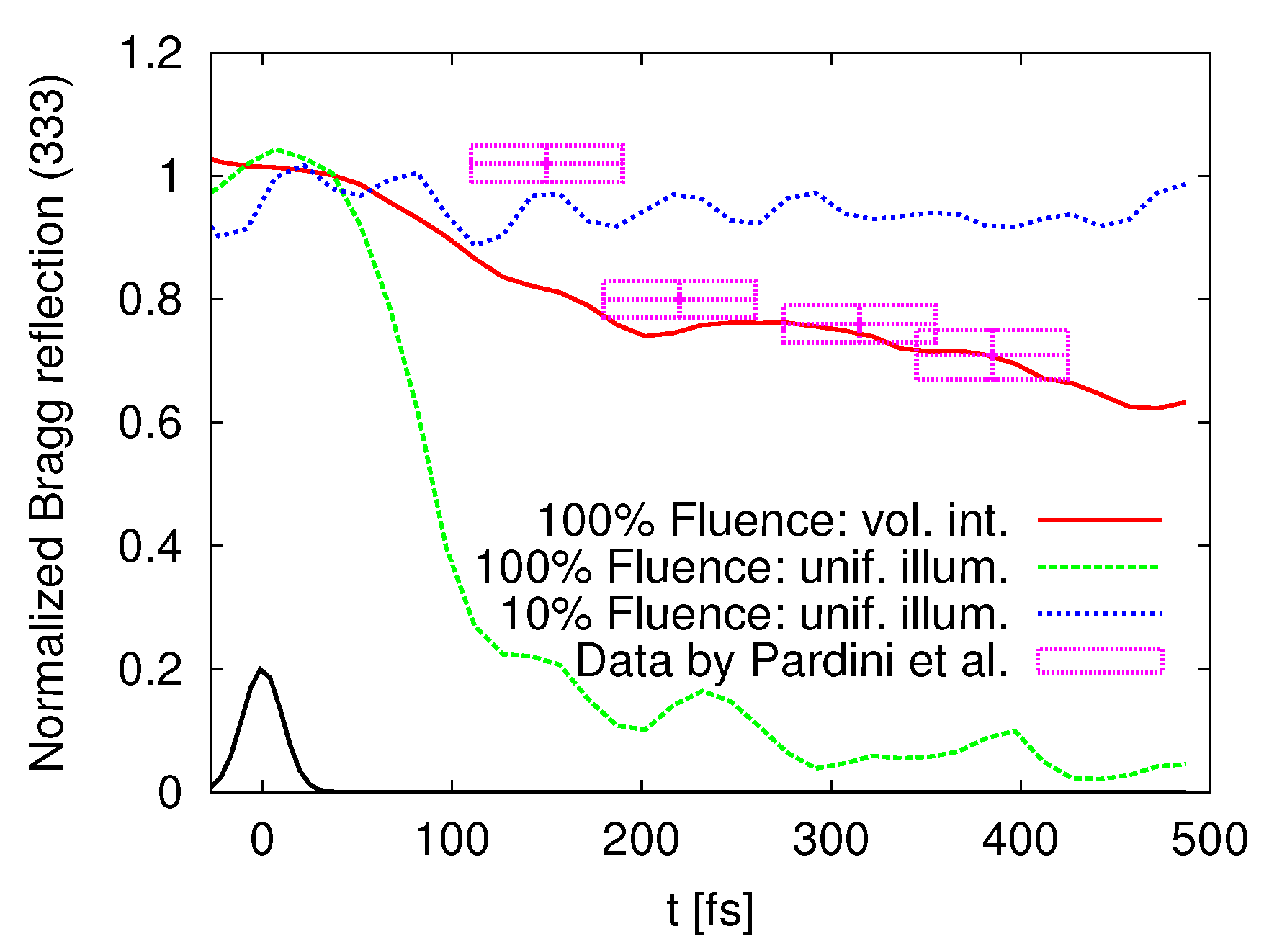
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEL | Free Electron Laser |
| LCLS | Linac Coherent Light Source |
| XTANT | X-ray Thermal and Nonthermal Transitions |
| XSINC | X-ray Scattering in Nanocrystals |
| FWHM | Full Width at Half Maximum |
References
- Rousse, A.; Rischel, C.; Fourmaux, S.; Uschmann, I.; Sebban, S.; Grillon, G.; Balcou, P.; Förster, E.; Geindre, J.P.; Audebert, P.; et al. Non-thermal melting in semiconductors measured at femtosecond resolution. Nature 2001, 410, 65. [Google Scholar] [CrossRef] [PubMed]
- Sundaram, S.K.; Mazur, E. Inducing and probing non-thermal transitions in semiconductors using femtosecond laser pulses. Nat. Mat. 2002, 1, 217. [Google Scholar] [CrossRef] [PubMed]
- Sokolowski-Tinten, K.; Bialkowski, J.; von der Linde, D. Ultrafast laser-induced order-disorder transitions in semiconductors. Phys. Rev. B 1995, 51, 14186. [Google Scholar] [CrossRef]
- Lindenberg, A.M.; Larsson, J.; Sokolowski-Tinten, K.; Gaffney, K.J.; Blome, C.; Synnergren, O.; Sheppard, J.; Caleman, C.; MacPhee, A.G.; Weinstein, D.; et al. Atomic-Scale Visualization of Inertial Dynamics. Science 2005, 308, 392. [Google Scholar] [CrossRef] [Green Version]
- Gaffney, K.J.; Lindenberg, A.M.; Larsson, J.; Sokolowski-Tinten, K.; Blome, C.; Synnergren, O.; Sheppard, J.; Caleman, C.; MacPhee, A.G.; Weinstein, D.; et al. Observation of Structural Anisotropy and the Onset of Liquidlike Motion During the Nonthermal Melting of InSb. Phys. Rev. Lett. 2005, 95, 125701. [Google Scholar] [CrossRef]
- Hillyard, P.B.; Gaffney, K.J.; Lindenberg, A.M.; Engemann, S.; Akre, R.A.; Arthur, J.; Blome, C.; Bucksbaum, P.H.; Cavalieri, A.L.; Deb, A.; et al. Carrier-Density-Dependent Lattice Stability in InSb. Phys. Rev. Lett. 2007, 98, 125501. [Google Scholar]
- Siders, C.W.; Cavalleri, A.; Sokolowski-Tinten, K.; Tóth, C.S.; Guo, T.; Kammler, M.; Horn von Hoegen, M.; Wilson, K.R.; von der Linde, D.; Barty, C.P.J. Detection of Nonthermal Melting by Ultrafast X-ray Diffraction. Science 1999, 286, 1340. [Google Scholar] [CrossRef] [PubMed]
- Sciaini, G.; Harb, M.; Kruglik, S.G.; Payer, T.; Hebeisen, C.T.; Meyer zu Heringdorf, F.-J.; Yamaguchi, M.; Horn-von Hoegen, M.; Ernstorfer, R.; Miller, R.J.D. Electronic acceleration of atomic motions and disordering in bismuth. Nature 2009, 458, 56. [Google Scholar] [CrossRef] [PubMed]
- Beye, M.; Sorgenfrei, F.; Schlotter, W.F.; Wurth, W.; Föhlisch, A. The liquid-liquid phase transition in silicon revealed by snapshots of valence electrons. Proc. Natl. Acad. Sci. USA 2010, 107, 16772–16776. [Google Scholar] [CrossRef] [Green Version]
- Bauerhenne, B.; Lipp, V.P.; Zier, T.; Zijlstra, E.S.; Garcia, M. Self-Learning Method for Construction of Analytical Interatomic Potentials to Describe Laser-Excited Materials. Phys. Rev. Lett. 2020, 124, 085501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seddon, E.A.; Clarke, J.A.; Dunning, D.J.; Masciovecchio, C.; Milne, C.J.; Parmigiani, F.; Rugg, D.; Spence, J.C.H.; Thompson, N.R.; Ueda, K.; et al. Short-wavelength free-electron laser sources and science: A review. Rep. Progr. Phys. 2017, 80, 115901. [Google Scholar] [CrossRef] [PubMed]
- Pardini, T.; Alameda, J.; Aquila, A.; Boutet, S.; Decker, T.; Gleason, A.E.; Guillet, S.; Hamilton, P.; Hayes, M.; Hill, R.; et al. Delayed Onset of Nonthermal Melting in Single-Crystal Silicon Pumped with Hard X rays. Phys. Rev. Lett. 2018, 120, 265701, Erratum in 2020, 124, 129903. [Google Scholar] [CrossRef] [Green Version]
- Inoue, I.; Inubushi, Y.; Sato, T.; Tono, K.; Katayama, T.; Kameshima, T.; Ogawa, K.; Togashi, T.; Owada, S.; Amemiya, Y.; et al. Observation of femtosecond X-ray interactions with matter using an X-ray—X-ray pump-probe scheme. Proc. Natl. Acad. Sci. USA 2016, 113, 6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zier, T.; Zijlstra, E.S.; Kalitsov, A.; Theodonis, I.; Garcia, M.E. Signatures of nonthermal melting. Str. Dyn. 2015, 2, 054101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zier, T.; Zijlstra, E.S.; Garcia, M.E. Quasimomentum-Space Image for Ultrafast Melting of Silicon. Phys. Rev. Lett. 2016, 116, 153901. [Google Scholar] [CrossRef] [PubMed]
- Jeschke, H.O.; Garcia, M.E.; Bennemann, K.H. Microscopic analysis of the femtosecond graphitization of diamond. Phys. Rev. B 1999, 60, R3701. [Google Scholar] [CrossRef] [Green Version]
- Jeschke, H.; Garcia, M.; Bennemann, K. Theory for the ultrafast ablation of graphite films. Phys. Rev. Lett. 2001, 87, 015003. [Google Scholar] [CrossRef] [Green Version]
- Medvedev, N.; Jeschke, H.O.; Ziaja, B. Nonthermal phase transitions in semiconductors induced by a femtosecond extreme ultraviolet laser pulse. New J. Phys. 2013, 15, 015016. [Google Scholar] [CrossRef]
- Medvedev, N.; Li, Z.; Tkachenko, V.; Ziaja, B. Electron-ion coupling in semiconductors beyond Fermi’s golden rule. Phys. Rev. B 2017, 95, 014309. [Google Scholar] [CrossRef] [Green Version]
- Medvedev, N.; Tkachenko, V.; Lipp, V.; Li, Z.; Ziaja, B. Various damage mechanisms in carbon and silicon materials under femtosecond X-ray irradiation. arXiv 2018, arXiv:1805.07524. [Google Scholar] [CrossRef]
- Roy, A.M. Influence of Nanoscale Parameters on Solid-solid Phase Transformation in Octogen Crystal: Multiple Solution and Temperature Effect. JETP Lett. 2021. [Google Scholar] [CrossRef]
- Roy, A.M. Barrierless melt nucleation at solid-solid interface in energetic nitramine octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine. Materialia 2021, 15, 101000. [Google Scholar] [CrossRef]
- Neutze, R.; Wouts, R.; van der Spoel, D.; Weckert, E.; Hajdu, J. Potential for Biomolecular Imaging with Femtosecond X-Ray Pulses. Nature 2000, 406, 752–757. [Google Scholar] [CrossRef] [PubMed]
- Nass, K.; Gorel, A.; Abdullah, M.M.; Martin, A.V.; Kloos, M.; Marinelli, A.; Aquila, A.; Barends, T.R.M.; Decker, F.-J.; Doak, R.B.; et al. Structural Dynamics in Proteins Induced by and Probed with X-Ray Free-Electron Laser Pulses. Nat. Commun. 2020, 11, 1814. [Google Scholar] [CrossRef] [Green Version]
- Seibert, M.M.; Ekeberg, T.; Maia, F.R.N.C.; Svenda, M.; Andreasson, J.; Jönsson, O.; Odić, D.; Iwan, B.; Rocker, A.; Westphal, D.; et al. Single Mimivirus Particles Intercepted and Imaged with an X-Ray Laser. Nature 2011, 470, 78–81. [Google Scholar] [CrossRef]
- Ekeberg, T.; Svenda, M.; Abergel, C.; Maia, F.R.N.C.; Seltzer, V.; Claverie, J.-M.; Hantke, M.; Jönsson, O.; Nettelblad, C.; van der Schot, G.; et al. Three-Dimensional Reconstruction of the Giant Mimivirus Particle with an x-Ray Free-Electron Laser. Phys. Rev. Lett. 2015, 114, 098102. [Google Scholar] [CrossRef] [Green Version]
- Munke, A.; Andreasson, J.; Aquila, A.; Awel, S.; Ayyer, K.; Barty, A.; Bean, R.J.; Berntsen, P.; Bielecki, J.; Boutet, S.; et al. Coherent Diffraction of Single Rice Dwarf Virus Particles Using Hard X-Rays at the Linac Coherent Light Source. Sci. Data 2016, 3, 160064. [Google Scholar] [CrossRef] [Green Version]
- Inoue, I.; Deguchi, Y.; Ziaja, B.; Osaka, T.; Abdullah, M.M.; Jurek, Z.; Medvedev, N.; Tkachenko, V.; Inubushi, Y.; Kasai, H.; et al. Atomic-Scale Visualization of Ultrafast Bond Breaking in X-Ray-Excited Diamond. Phys. Rev. Lett. 2021, 126, 117403. [Google Scholar] [CrossRef]
- Abdullah, M.M.; Jurek, Z.; Son, S.K.; Santra, R. Calculation of x-ray scattering patterns from nanocrystals at high x-ray intensity. J. Appl. Cryst. 2016, 49, 1048. [Google Scholar] [CrossRef] [Green Version]
- Medvedev, N.; Ziaja, B. Multistep transition of diamond to warm dense matter state revealed by femtosecond X-ray diffraction. Sci. Rep. 2018, 8, 5284. [Google Scholar] [CrossRef] [Green Version]
- Kwon, I.; Biswas, R.; Wong, C.; Ho, K.; Soukoulis, C. Transferable tight-binding models for silicon. Phys. Rev. B 1994, 49, 7242. [Google Scholar] [CrossRef] [PubMed]
- Medvedev, N.; Jeschke, H.; Ziaja, B. Nonthermal graphitization of diamond induced by a femtosecond x-ray laser pulse. Phys. Rev. B 2013, 88, 224304. [Google Scholar] [CrossRef] [Green Version]
- Lipp, V.; Medvedev, N.; Ziaja, B. Classical Monte-Carlo simulations of X-ray-induced electron cascades in various materials. Proc. SPIE 2017, 10239, 102360H. [Google Scholar]
- Follath, R.; Koyama, K.; Lipp, V.; Medvedev, N.; Tono, K.; Ohashi, H.; Patthey, L.; Yabashi, M.; Ziaja, B. X-ray-induced damage of B4C-coated multilayer materials under various irradiation geometries. Sci. Rep. 2019, 9, 2029. [Google Scholar] [CrossRef]
- Pardini, T.; Boutet, S.; Bradley, J.; Döppner, T.; Fletcher, L.B.; Gardner, D.F.; Hill, R.M.; Hunter, M.S.; Krzywinski, J.; Messerschmidt, M.; et al. Silicon Mirrors for High-Intensity X-Ray Pump and Probe Experiments. Phys. Rev. Appl. 2014, 1, 044007. [Google Scholar] [CrossRef]
- Medvedev, N.; Li, Z.; Ziaja, B. Thermal and Nonthermal Melting of Silicon under Femtosecond X-Ray Irradiation. Phys. Rev. B 2015, 91, 054113. [Google Scholar] [CrossRef] [Green Version]
- Berrah, N.; Sanchez-Gonzalez, A.; Jurek, Z.; Obaid, R.; Xiong, H.; Squibb, R.J.; Osipov, T.; Lutman, A.; Fang, L.; Barillot, T.; et al. Femtosecond-resolved observation of the fragmentation of buckminsterfullerene following x-ray multiphoton ionization. Nat. Phys. 2019, 15, 1279. [Google Scholar] [CrossRef]
- Murphy, B.F.; Osipov, T.; Jurek, Z.; Fang, L.; Son, S.-K.; Mucke, M.; Eland, J.H.D.; Zhaunerchyk, V.; Feifel, R.; Avaldi, L.; et al. Femtosecond x-ray-induced explosion of C60 at extreme intensity. Nat. Commun. 2014, 5, 4281. [Google Scholar] [CrossRef] [Green Version]
- Kumagai, Y.; Jurek, Z.; Xu, W.; Fukuzawa, H.; Motomura, K.; Iablonskyi, D.; Nagaya, K.; Wada, S.-I.; Mondal, S.; Tachibana, T.; et al. Radiation-induced chemical dynamics in Ar clusters exposed to strong x-ray pulses. Phys. Rev. Lett. 2018, 120, 223201. [Google Scholar] [CrossRef] [PubMed]
- Ziaja, B.; London, R.A.; Hajdu, J. Unified model of secondary electron cascades in diamond. J. Appl. Phys. 2005, 97, 064905. [Google Scholar] [CrossRef] [Green Version]
- Veigele, W.J. Photon cross sections from 0.1 keV to 1 MeV for elements Z = 1 to Z = 94. At. Data Nucl. Data Tables 1973, 5, 51. [Google Scholar] [CrossRef]
- Tavella, F.; Höppner, H.; Tkachenko, V.; Medvedev, N.; Capotondi, F.; Golz, T.; Kai, Y.; Manfredda, M.; Pedersoli, E.; Prandolini, M.J.; et al. Soft X-ray-induced femtosecond solid-to-solid phase transition. High Energy Density Phys. 2017, 24, 22. [Google Scholar] [CrossRef] [Green Version]
- Son, S.K.; Young, L.; Santra, R. Impact of hollow-atom formation on coherent x-ray scattering at high intensity. Phys. Rev. A 2011, 83, 033402. [Google Scholar] [CrossRef] [Green Version]
- Zeiger, H.J.; Vidal, J.; Cheng, T.K.; Ippen, E.P.; Dresselhaus, G.; Dresselhaus, M.S. Theory for displacive excitation of coherent phonons. Phys. Rev. B 1992, 45, 768. [Google Scholar] [CrossRef] [Green Version]
- Medvedev, N.; Kopecky, M.; Chalupsky, J.; Juha, L. Femtosecond X-ray diffraction can discern nonthermal from thermal melting. Phys. Rev. B 2019, 99, 100303. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tkachenko, V.; Abdullah, M.M.; Jurek, Z.; Medvedev, N.; Lipp, V.; Makita, M.; Ziaja, B. Limitations of Structural Insight into Ultrafast Melting of Solid Materials with X-ray Diffraction Imaging. Appl. Sci. 2021, 11, 5157. https://doi.org/10.3390/app11115157
Tkachenko V, Abdullah MM, Jurek Z, Medvedev N, Lipp V, Makita M, Ziaja B. Limitations of Structural Insight into Ultrafast Melting of Solid Materials with X-ray Diffraction Imaging. Applied Sciences. 2021; 11(11):5157. https://doi.org/10.3390/app11115157
Chicago/Turabian StyleTkachenko, Victor, Malik M. Abdullah, Zoltan Jurek, Nikita Medvedev, Vladimir Lipp, Mikako Makita, and Beata Ziaja. 2021. "Limitations of Structural Insight into Ultrafast Melting of Solid Materials with X-ray Diffraction Imaging" Applied Sciences 11, no. 11: 5157. https://doi.org/10.3390/app11115157
APA StyleTkachenko, V., Abdullah, M. M., Jurek, Z., Medvedev, N., Lipp, V., Makita, M., & Ziaja, B. (2021). Limitations of Structural Insight into Ultrafast Melting of Solid Materials with X-ray Diffraction Imaging. Applied Sciences, 11(11), 5157. https://doi.org/10.3390/app11115157





