Measurement of Tooth Wear by Means of Digital Impressions: An In-Vitro Evaluation of Three Intraoral Scanning Systems
Abstract
:1. Introduction
2. Materials and Methods
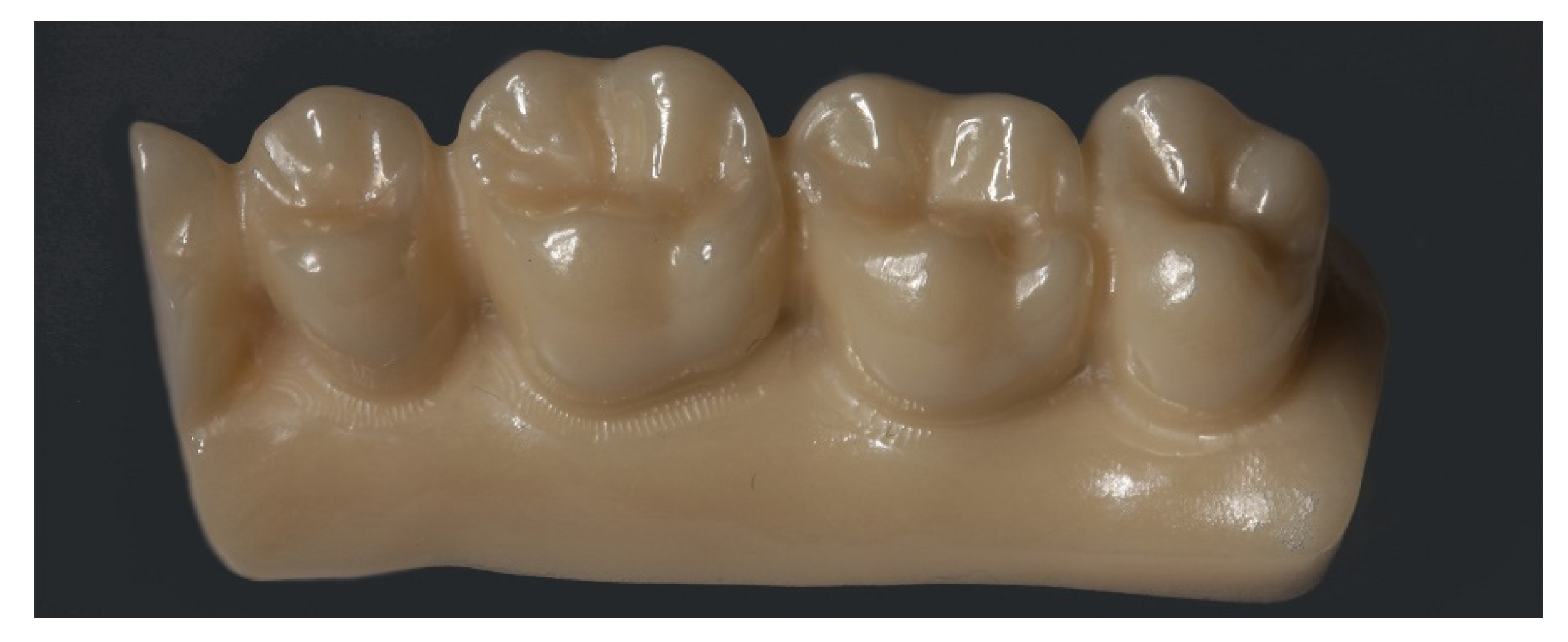
2.1. Digitization of the Study Cast
2.2. Analysis of the Obtained Data Using a Reference Best-Fit-Alignment
2.3. Evaluation of the Accuracy of Each Intraoral Scanning System (IOS)
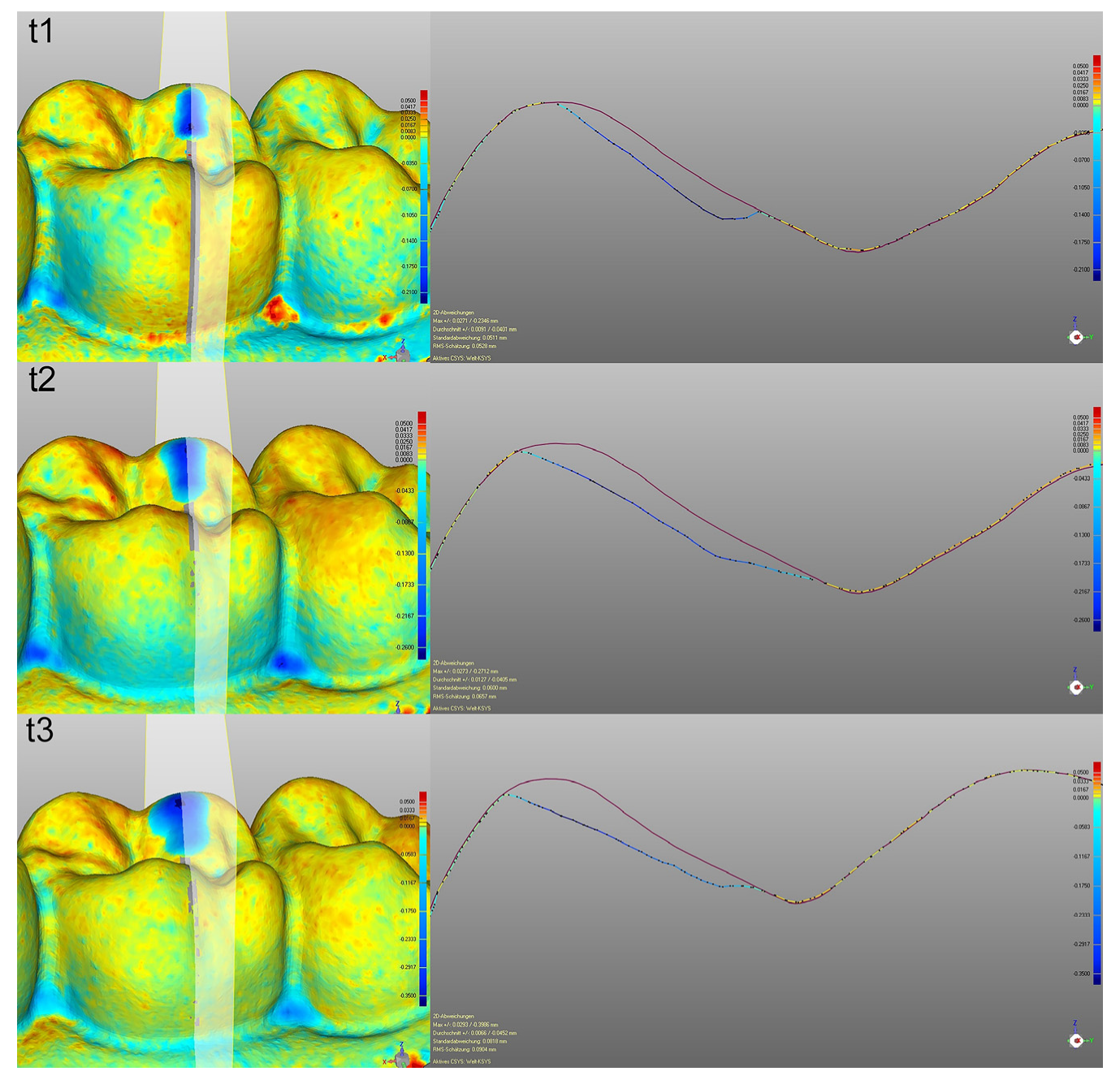
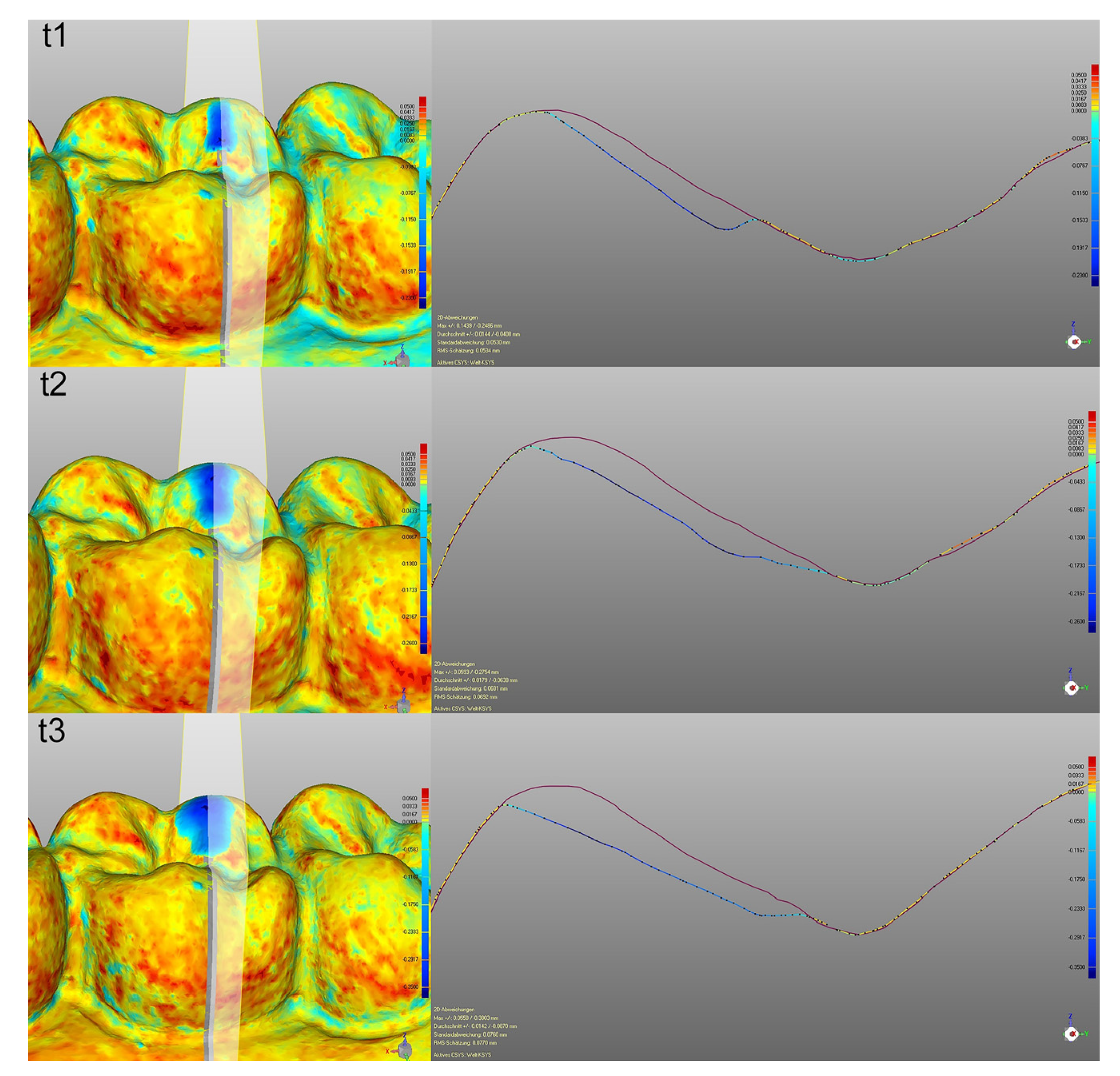
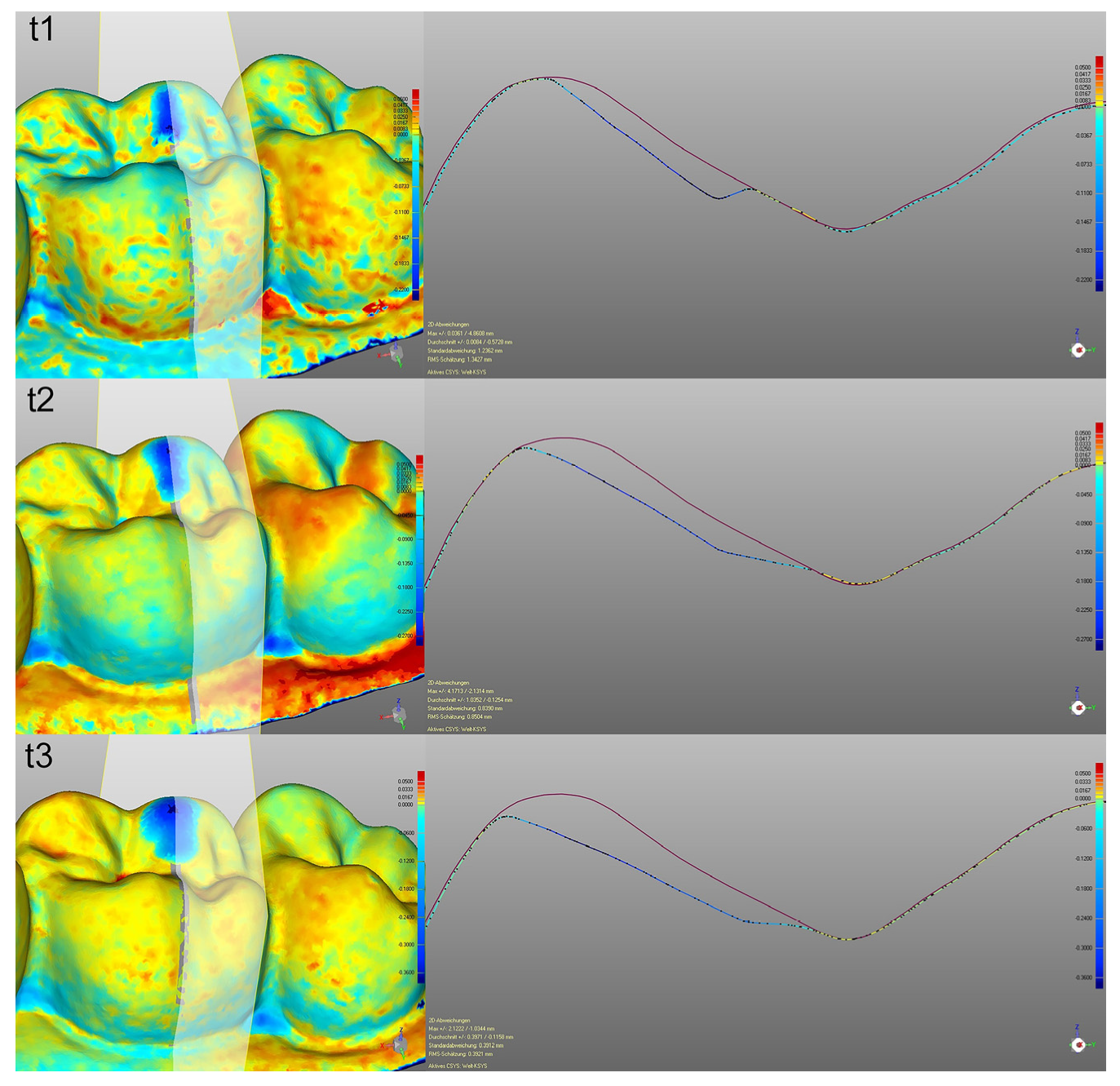
2.4. Using Cross Sections for 2D Analysis
2.5. Statistical Analysis
3. Results
3.1. Wear Measurement on the Basis of the IOS Compared to WLP
3.1.1. Wear Values at the Wear Step t1
3.1.2. Wear Values at the Wear Step t2
3.1.3. Wear Values at the Wear Step t3
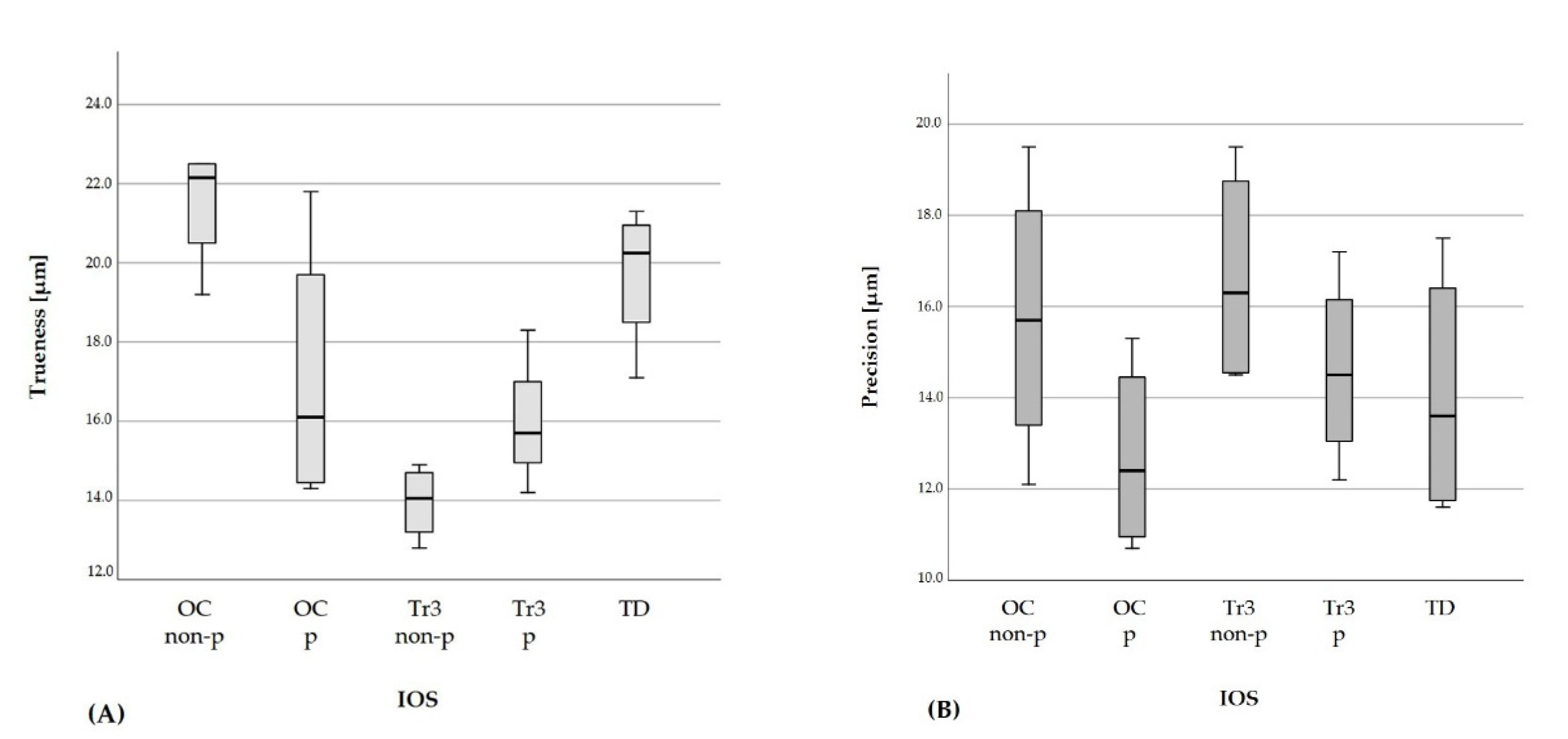
3.2. Accuracy Values of the IOS
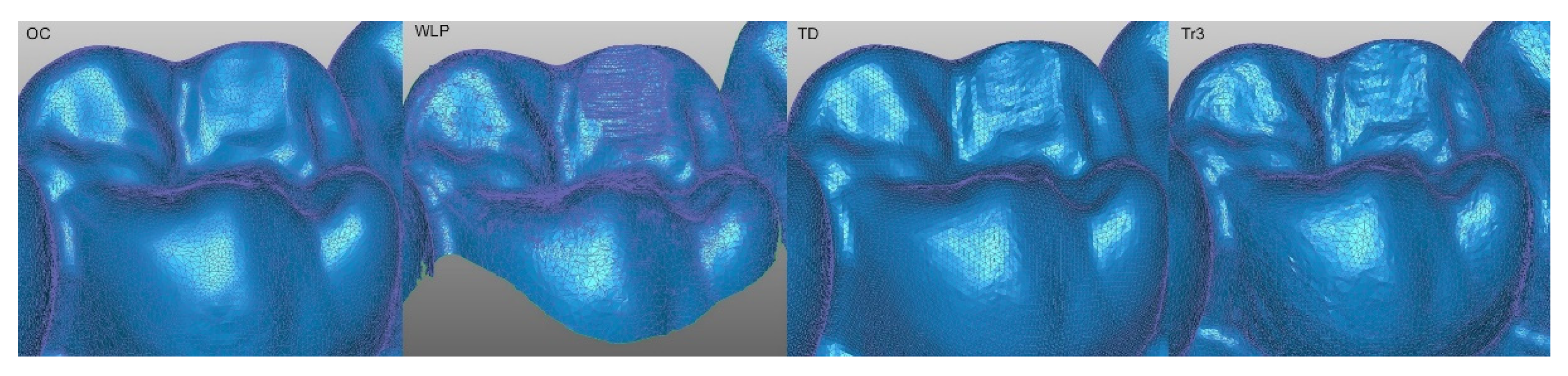
3.3. Using Cross Sections for 2D Analysis
4. Discussion
4.1. Material and Method
4.2. Method of Wear Simulation and Data Acquisition
4.3. Discussion of the Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stober, T.; Bermejo, J.L.; Schwindling, F.S.; Schmitter, M. Clinical assessment of enamel wear caused by monolithic zirconia crowns. J. Oral Rehabil. 2016, 43, 621–629. [Google Scholar] [CrossRef]
- Lohbauer, U.; Reich, S. Antagonist wear of monolithic zirconia crowns after 2 years. Clin. Oral Investig. 2017, 21, 1165–1172. [Google Scholar] [CrossRef] [PubMed]
- Krämer, N.; Kunzelmann, K.-H.; Taschner, M.; Mehl, A.; Garcia-Godoy, F.; Frankenberger, R. Antagonist Enamel Wears More Than Ceramic Inlays. J. Dent. Res. 2006, 85, 1097–1100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suputtamongkol, K.; Anusavice, K.J.; Suchatlampong, C.; Sithiamnuai, P.; Tulapornchai, C. Clinical performance and wear characteristics of veneered lithia-disilicate-based ceramic crowns. Dent. Mater. J. 2008, 24, 667–673. [Google Scholar] [CrossRef] [Green Version]
- Stober, T.; Geiger, A.; Rues, S.; Dreyhaupt, J.; Rammelsberg, P.; Ohlmann, B. Factors affecting wear of composite resin denture teeth—24-month results from a clinical study. Clin. Oral Investig. 2011, 16, 413–420. [Google Scholar] [CrossRef] [PubMed]
- Esquivel-Upshaw, J.F.; Rose, W.F., Jr.; Barrett, A.A.; Oliveira, E.R.; Yang, M.C.; Clark, A.E.; Anusavice, K.J. Three years in vivo wear: Core-ceramic, veneers, and enamel antagonists. Dent. Mater. J. 2012, 28, 615–621. [Google Scholar] [CrossRef] [Green Version]
- Hartkamp, O.; Peters, F.; Bothung, H.; Lohbauer, U.; Reich, S. Optical profilometry versus intraoral (handheld) scanning. Int. J. Comput. Dent. 2017, 20, 165–176. [Google Scholar] [PubMed]
- Esquivel-Upshaw, J.F.; Hsu, S.; Bohórquez, A.C.; AbdulHameed, N.; Scheiffele, G.W.; Kim, M.; Neal, D.; Chai, J.; Ren, F. Novel methodology for measuring intraoral wear in enamel and dental restorative materials. Clin. Exp. Dent. Res. 2020, 6, 677–685. [Google Scholar] [CrossRef]
- Syrek, A.; Reich, G.; Ranftl, D.; Klein, C.; Cerny, B.; Brodesser, J. Clinical evaluation of all-ceramic crowns fabricated from intraoral digital impressions based on the principle of active wavefront sampling. J. Dent. 2010, 38, 553–559. [Google Scholar] [CrossRef]
- Cybertechnologies. Specifications CT100.2. Available online: https://www.cybertechnologies.com/wp-content/uploads/2016/07/CT-100-sufrace-measurement-system_cyberTECHNOLOGIES.pdf (accessed on 30 November 2020).
- Hsu, S.-M.; Ren, F.; AbdulHameed, N.; Kim, M.; Neal, D.; Esquivel-Upshaw, J. Comprehensive analysis of laserscanner validity used for measurement of wear. J. Oral Rehabil. 2019, 46, 503–510. [Google Scholar] [CrossRef]
- O’Toole, S.; Osnes, C.; Bartlett, D.; Keeling, A. Investigation into the accuracy and measurement methods of sequential 3D dental scan alignment. Dent. Mater. J. 2019, 35, 495–500. [Google Scholar] [CrossRef]
- Kumar, S.; Keeling, A.; Osnes, C.; Bartlett, D.; O’Toole, S. The sensitivity of digital intraoral scanners at measuring early erosive wear. J. Dent. 2019, 81, 39–42. [Google Scholar] [CrossRef]
- Wulfman, C.; Koenig, V.; Mainjot, A. Wear measurement of dental tissues and materials in clinical studies: A systematic review. Dent. Mater. J. 2018, 34, 825–850. [Google Scholar] [CrossRef]
- International Organization for Standardization. ISO 5725-1:1994(en) Accuracy (Trueness and Precision) of Measurement Methods and Results—Part 1: General Principles and Definitions. Available online: https://www.din.de/de/mitwirken/normenausschuesse/nqsz/veroeffentlichungen/wdc-beuth:din21:1595316 (accessed on 24 May 2021).
- Faul, F.; Erdfelder, E.; Buchner, A.; Lang, A.-G. Statistical power analyses using G*Power 3.1: Tests for correlation and regression analyses. Behav. Res. Methods 2009, 41, 1149–1160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.-H.; Kim, S.-H.; Han, J.-S.; Yeo, I.-S.L.; Yoon, H.-I. Optical and Surface Properties of Monolithic Zirconia after Simulated Toothbrushing. Materials 2019, 12, 1158. [Google Scholar] [CrossRef] [Green Version]
- Renne, W.; Ludlow, M.; Fryml, J.; Schurch, Z.; Mennito, A.; Kessler, R.; Lauer, A. Evaluation of the accuracy of 7 digital scanners: An in vitro analysis based on 3-dimensional comparisons. J. Prosthet. Dent. 2017, 118, 36–42. [Google Scholar] [CrossRef] [PubMed]
- Nedelcu, R.G.; Persson, A.S. Scanning accuracy and precision in 4 intraoral scanners: An in vitro comparison based on 3-dimensional analysis. J. Prosthet. Dent. 2014, 112, 1461–1471. [Google Scholar] [CrossRef]
- Cardoso, J.R.; Pereira, L.M.; Iversen, M.D.; Ramos, A.L. What is gold standard and what is ground truth? Dental. Press J. Orthod. 2014, 19, 27–30. [Google Scholar] [CrossRef] [Green Version]
- Zimmermann, M.; Ender, A.; Mehl, A. Local accuracy of actual intraoral scanning systems for single-tooth preparations in vitro. J. Am. Dent. Assoc. 2020, 151, 127–135. [Google Scholar] [CrossRef]
- Ender, A.; Zimmermann, M.; Mehl, A. Accuracy of complete- and partial-arch impressions of actual intraoral scanning systems in vitro. Int. J. Comput. Dent. 2019, 22, 11–19. [Google Scholar] [PubMed]
- Lee, J.-J.; Jeong, I.-D.; Park, J.-Y.; Jeon, J.-H.; Kim, J.-H.; Kim, W.-C. Accuracy of single-abutment digital cast obtained using intraoral and cast scanners. J. Prosthet. Dent. 2017, 117, 253–259. [Google Scholar] [CrossRef]
- Loomans, B.; Opdam, N.; Attin, T.; Bartlett, D.; Edelhoff, D.; Frankenberger, R.; Benic, G.; Ramseyer, S.; Wetselaar, P.; Sterenborg, B.; et al. Severe Tooth Wear: European Consensus Statement on Management Guidelines. J. Adhes Dent. 2017, 19, 111–119. [Google Scholar]
- Wetselaar, P.; Lobbezoo, F. The tooth wear evaluation system: A modular clinical guideline for the diagnosis and management planning of worn dentitions. J. Oral Rehabil. 2016, 43, 69–80. [Google Scholar] [CrossRef]
- Wetselaar, P.; Wetselaar-Glas, M.J.; Katzer, L.D.; Ahlers, M.O.; Wetselaar-Glas, M.M. Diagnosing tooth wear, a new taxonomy based on the revised version of the Tooth Wear Evaluation System (TWES 2.0). J. Oral Rehabil. 2020, 47, 703–712. [Google Scholar] [CrossRef]
- Hartkamp, O.; Lohbauer, U.; Reich, S. Antagonist wear by polished zirconia crowns. Int. J. Comput. Dent. 2017, 20, 263–274. [Google Scholar] [PubMed]
- De Long, R. Intra-oral restorative materials wear: Rethinking the current approaches: How to measure wear. Dent. Mater. J. 2006, 22, 702–711. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.-H.; Mangal, U.; Nam, N.-E.; Choi, S.-H.; Shim, J.-S.; Kim, J.-E. A Comparison of Accuracy of Different Dental Restorative Materials between Intraoral Scanning and Conventional Impression-Taking: An In Vitro Study. Materials 2021, 14, 2060. [Google Scholar] [CrossRef]
- Stober, T.; Bermejo, J.L.; Rammelsberg, P.; Schmitter, M. Enamel wear caused by monolithic zirconia crowns after 6 months of clinical use. J. Oral Rehabil. 2014, 41, 314–322. [Google Scholar] [CrossRef] [PubMed]
- Saptaji, K.; Gebremariam, M.A.; Azhari, M.A.B.M. Machining of biocompatible materials: A review. Int. J. Adv. Manuf. Technol. 2018, 97, 2255–2292. [Google Scholar] [CrossRef]
- Heintze, S.D.; Zellweger, G.; Grunert, I.; Muñoz-Viveros, C.A.; Hagenbuch, K. Laboratory methods for evaluating the wear of denture teeth and their correlation with clinical results. Dent. Mater. 2012, 28, 261–272. [Google Scholar] [CrossRef]
- Heintze, S.D. How to qualify and validate wear simulation devices and methods. Dent. Mater. J. 2006, 22, 712–734. [Google Scholar] [CrossRef] [PubMed]
- Hu, K.-M.; Yan, D.-M.; Bommes, D.; Alliez, P.; Benes, B. Error-Bounded and Feature Preserving Surface Remeshing with Minimal Angle Improvement. IEEE Trans. Vis. Comput. Graph. 2017, 23, 2560–2573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, T.; Chen, M.; Song, Y.; Li, H.; Lu, B. Quality improvement of surface triangular mesh using a modified Laplacian smoothing approach avoiding intersection. PLoS ONE 2017, 12, e0184206. [Google Scholar] [CrossRef]
- Becker, K.; Wilmes, B.; Grandjean, C.; Drescher, D. Impact of manual control point selection accuracy on automated surface matching of digital dental models. Clin. Oral Investig. 2018, 22, 801–810. [Google Scholar] [CrossRef] [PubMed]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Dutton, E.; Ludlow, M.; Mennito, A.; Kelly, A.; Evans, Z.; Culp, A.; Kessler, R.; Renne, W. The effect different substrates have on the trueness and precision of eight different intraoral scanners. J. Esthet. Restor. Dent. 2020, 32, 204–218. [Google Scholar] [CrossRef] [PubMed]



| FDI 26 (t1) | FDI 27 (t1) | |
|---|---|---|
| WLP (reference) | 227 | 221 |
| OC non-p | 217 (±4) + 4% | 232 (±4) + 5% |
| OC p | 239 (±7) + 5% | 234 (±6) + 6% |
| Tr3 non-p | 231 (±2) + 2% | 235 (±6) + 6% |
| Tr3 p | 223 (±13) − 2% | 237 (±6) + 7% |
| TD | 220 (±2) − 3% | 229 (±6) + 4% |
| FDI 26 (t2) | FDI 27 (t2) | |
|---|---|---|
| WLP (reference) | 300 | 242 |
| OC non-p | 328 (±9) + 9% | 267 (±7) + 10% |
| OC p | 329 (±11) + 10% | 287 (±11) + 19% |
| Tr3 non-p | 330(±9) 10% | 276(±13) + 15% |
| Tr3 p | 320 (±9) + 7% | 281 (±8) + 16% |
| TD | 314 (±7) + 5% | 273 (±9) + 13% |
| FDI 26 (t3) | FDI 27 (t3) | |
|---|---|---|
| WLP (reference) | 417 | 344 |
| OC non-p | 415 (±6) + 0% | 371 (±4) + 8% |
| OC p | 428 (±10) + 3% | 387 (±7) + 13% |
| Tr3 non-p | 441 (±6) + 6% | 361 (±9) + 5% |
| Tr3 p | 434 (±10) + 4% | 390 (±12) + 13% |
| TD | 432 (±4) + 5% | 328 (±9) + 11% |
| IOS | Trueness [n = 6] Mean (±SD) [µm] | Precision [n = 15] Mean (±SD) [µm] | |
|---|---|---|---|
| t0 | OC non-p | 22.5 (±4.8) | 19.5 (±4.5) |
| OC p | 14.6 (±0.9) | 13.6 (±7.6) | |
| Tr3 non-p | 14.9 (±1.8) | 19.5 (±7.1) | |
| Tr3 p | 15.7 (±1.2) | 15.1 (±3.7) | |
| TD | 17.1 (±1.0) | 11.9 (±2.8) | |
| t1 | OC non-p | 22.5 (±1.4) | 12.1 (±3.2) |
| OC p | 14.3 (±0.4) | 15.3 (±7.5) | |
| Tr3 non-p | 12.8 (±0.7) | 18.0 (±5.3) | |
| Tr3 p | 15.7 (±0.6) | 17.2 (±7.0) | |
| TD | 20.6 (±1.4) | 17.5 (±4.2) | |
| t2 | OC non-p | 21.8 (±1.7) | 14.7 (±3.8) |
| OC p | 17.6 (±0.8) | 11.2 (±3.5) | |
| Tr3 non-p | 14.5 (±1.2) | 14.6 (±4.5) | |
| Tr3 p | 14.2 (±1.3) | 13.9 (±5.4) | |
| TD | 19.9 (±1.4) | 15.3 (±5.0) | |
| t3 | OC non-p | 19.2 (±1.4) | 16.7 (±4.2) |
| OC p | 21.8 (±1.3) | 10.7 (±5.2) | |
| Tr3 non-p | 13.6 (±1.3) | 14.5 (±4.3) | |
| Tr3 p | 18.3 (±2.2) | 12.2 (±5.2) | |
| TD | 21.3 (±1.2) | 11.6 (±3.3) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kühne, C.; Lohbauer, U.; Raith, S.; Reich, S. Measurement of Tooth Wear by Means of Digital Impressions: An In-Vitro Evaluation of Three Intraoral Scanning Systems. Appl. Sci. 2021, 11, 5161. https://doi.org/10.3390/app11115161
Kühne C, Lohbauer U, Raith S, Reich S. Measurement of Tooth Wear by Means of Digital Impressions: An In-Vitro Evaluation of Three Intraoral Scanning Systems. Applied Sciences. 2021; 11(11):5161. https://doi.org/10.3390/app11115161
Chicago/Turabian StyleKühne, Christina, Ulrich Lohbauer, Stefan Raith, and Sven Reich. 2021. "Measurement of Tooth Wear by Means of Digital Impressions: An In-Vitro Evaluation of Three Intraoral Scanning Systems" Applied Sciences 11, no. 11: 5161. https://doi.org/10.3390/app11115161
APA StyleKühne, C., Lohbauer, U., Raith, S., & Reich, S. (2021). Measurement of Tooth Wear by Means of Digital Impressions: An In-Vitro Evaluation of Three Intraoral Scanning Systems. Applied Sciences, 11(11), 5161. https://doi.org/10.3390/app11115161







