Stochastic PCA-Based Bone Models from Inverse Transform Sampling: Proof of Concept for Mandibles and Proximal Femurs
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
2.1. Reference Database
2.2. Iso-Topological Meshes: Mesh Morphing
- A set of control points, corresponding to relevant anatomical landmarks were identified on the standard mesh and on all the other shapes in the training set;
- The standard mesh was morphed onto the target geometry using routines developed for this aim in MATLAB (v. 17, The MathWorks, Inc., Natick, MA, USA), based on the mesh morphing process described above (Equation (3));
- As a result of the morphing procedure, the standard mesh was deformed, obtaining a mesh iso-topological to the original standard mesh and with a shape close to the target geometry. In order to achieve the best shape reproduction, nodes of the morphed standard mesh were projected perpendicularly to the closest triangle of the target mesh, along the triangle normal vector: in this way the morphed mesh was further adjusted to the target geometry;
- A Laplacian smoothing was then applied to the projected nodes [17], i.e., each node was replaced with the centroid of its neighboring nodes; this operation allowed to improve mesh quality;
- Node’s projections and Laplacian smoothing were applied iteratively until the iso-topological mesh replicated the target geometry well. In particular, the process was stopped when the maximum deviation between the morphed mesh and the target one was below 2 mm.
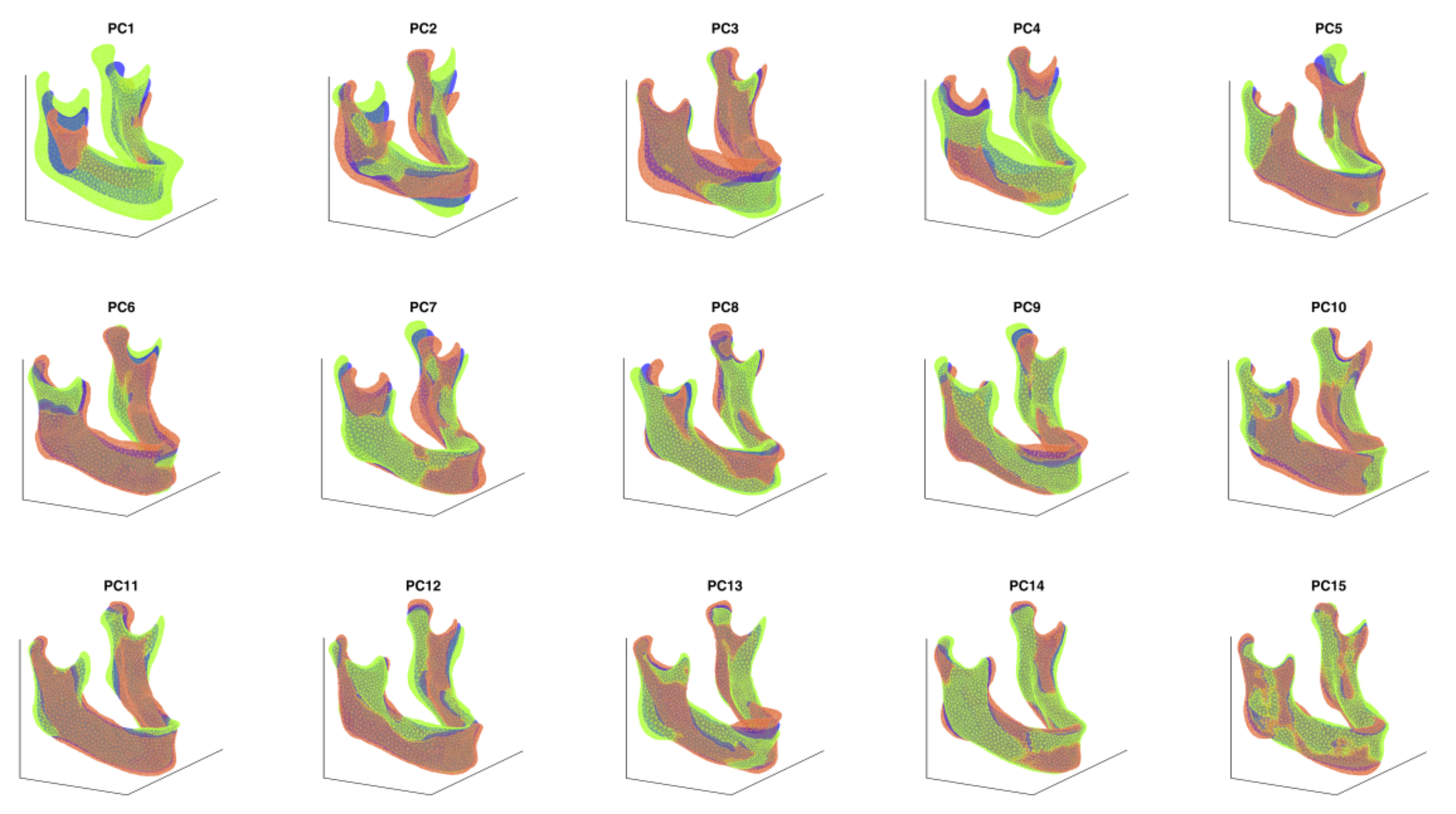
2.3. Creation of a PCA-Based Statistical Shape Model
2.4. Stochastic Shape Model
- A random number ranging between 0 and 1 is generated for each component and for the scale factor;
- The random number is considered as a value of the cumulative density distribution of scale factors or weights and the respective inverse function is calculated. In this way, random weights (WiR) and a random scale factor (SR), are obtained, distributed according to the empirical cumulative density distribution function, recorded from each bone training set;
- A new bone is generated according to the following equation:
3. Results
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ambu, R.; Motta, A.; Calì, M. Design of a Customized Neck Orthosis for FDM Manufacturing with a New Sustainable Bio-composite. In Proceedings of the Design Tools and Methods in Industrial Engineering, Modena, Italy, 9–10 September 2019; Rizzi, C., Andrisano, A.O., Leali, F., Gherardini, F., Pini, F., Vergnano, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 707–718. [Google Scholar]
- Stephen, J.M.; Calder, J.D.F.; Williams, A.; El Daou, H. Comparative accuracy of lower limb bone geometry determined using MRI, CT, and direct bone 3D models. J. Orthop. Res. 2020. [Google Scholar] [CrossRef]
- Lalone, E.A.; Willing, R.T.; Shannon, H.L.; King, G.J.W.; Johnson, J.A. Accuracy assessment of 3D bone reconstructions using CT: An intro comparison. Med. Eng. Phys. 2015, 37, 729–738. [Google Scholar] [CrossRef] [PubMed]
- Aldieri, A.; Terzini, M.; Osella, G.; Priola, A.M.; Angeli, A.; Veltri, A.; Audenino, A.L.; Bignardi, C. Osteoporotic Hip Fracture Prediction: Is T-Score-Based Criterion Enough? A Hip Structural Analysis-Based Model. J. Biomech. Eng. 2018, 140. [Google Scholar] [CrossRef]
- Galibarov, P.E.; Prendergast, P.J.; Lennon, A.B. A method to reconstruct patient-specific proximal femur surface models from planar pre-operative radiographs. Med. Eng. Phys. 2010, 32, 1180–1188. [Google Scholar] [CrossRef] [PubMed]
- Schmutz, B.; Reynolds, K.J.; Slavotinek, J.P. Customization of a generic 3D model of the distal femur using diagnostic radiographs. J. Med. Eng. Technol. 2008, 32, 156–161. [Google Scholar] [CrossRef] [Green Version]
- Noble, P.C.; Alexander, J.W.; Lindahl, L.J.; Yew, D.T.; Granberry, W.M.; Tullos, H.S. The anatomic basis of femoral component design. Clin. Orthop. Relat. Res. 1988, 148–165. [Google Scholar] [CrossRef]
- Zanetti, E.M.; Crupi, V.; Bignardi, C.; Calderale, P.M. Radiograph-based femur morphing method. Med. Biol. Eng. Comput. 2005, 43, 181–188. [Google Scholar] [CrossRef] [PubMed]
- Brunton, A.; Salazar, A.; Bolkart, T.; Wuhrer, S. Review of statistical shape spaces for 3D data with comparative analysis for human faces. Comput. Vis. Image Underst. 2014, 128, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Udall, W.J.M.; McCloskey, E.V.; Eastell, R. Distribution of bone density and cortical thickness in the proximal femur and their association with hip fracture in postmenopausal women: A quantitative computed tomography study. Osteoporos. Int. 2014, 25, 251–263. [Google Scholar] [CrossRef]
- Qasim, M.; Farinella, G.; Zhang, J.; Li, X.; Yang, L.; Eastell, R.; Viceconti, M. Patient-specific finite element estimated femur strength as a predictor of the risk of hip fracture: The effect of methodological determinants. Osteoporos. Int. 2016, 27, 2815–2822. [Google Scholar] [CrossRef] [Green Version]
- Hufnagel, H. A Probabilistic Framework for Point-Based Shape Modeling in Medical Image Analysis; Vieweg+Teubner Verlag: Wiesbaden, Germany, 2011; ISBN 9783834817228. [Google Scholar]
- Zheng, G.; Li, S.; Székely, G. Statistical Shape and Deformation Analysis; Academic Press: New York, NY, USA, 2017; ISBN 9780128127315. [Google Scholar]
- Pascoletti, G.; Calì, M.; Bignardi, C.; Conti, P.; Zanetti, E.M. Mandible Morphing through Principal Components Analysis. In Proceedings of the International Conference on Design Tools and Methods in Industrial Engineering, Modena, Italy, 9–10 September 2019; pp. 15–23. [Google Scholar]
- Biancolini, M.E.; Chiappa, A.; Giorgetti, F.; Porziani, S.; Rochette, M. Radial basis functions mesh morphing for the analysis of cracks propagation. Procedia Struct. Integr. 2018, 8, 433–443. [Google Scholar]
- Biancolini, M.E. Fast Radial Basis Functions for Engineering Applications; Springer International Publishing: Cham, Switzerland, 2018; ISBN 9783319750118. [Google Scholar]
- Grassi, L.; Hraiech, N.; Schileo, E.; Ansaloni, M.; Rochette, M.; Viceconti, M. Evaluation of the generality and accuracy of a new mesh morphing procedure for the human femur. Med. Eng. Phys. 2011, 33, 112–120. [Google Scholar] [CrossRef] [Green Version]
- Veneziano, A.; Landi, F.; Profico, A. Surface smoothing, decimation, and their effects on 3D biological specimens. Am. J. Phys. Anthropol. 2018, 166, 473–480. [Google Scholar] [CrossRef]
- Gower, J.C. Generalized procrustes analysis. Psychometrika 1975, 40, 33–51. [Google Scholar] [CrossRef]
- Taylor, M.; Viceconti, M.; Bhattacharya, P.; Li, X. Finite element analysis informed variable selection for femoral fracture risk prediction. J. Mech. Behav. Biomed. Mater. 2021, 118, 104434. [Google Scholar] [CrossRef] [PubMed]
- Skaudickas, D.; Veikutis, V.; Vitkus, A.; Peciulytė, G.; Marciulionyte, D.; Sakalyte, G.; Krisciukaitis, A.; Vaitiekaitis, G. Evaluation of complexity of induced necrosis zone shape by means of principal component analysis. J. Vibroeng. 2014, 16, 4115–4125. [Google Scholar]
- Morrison, S.J. Statistics for Engineers: An Introduction; Wiley: New York, NY, USA, 2009; ISBN 9780470745564. [Google Scholar]
- Meynen, A.; Matthews, H.; Nauwelaers, N.; Claes, P.; Mulier, M.; Scheys, L. Accurate reconstructions of pelvic defects and discontinuities using statistical shape models. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 1026–1033. [Google Scholar] [CrossRef] [PubMed]
- Chen, X. Parametric design of patient-specific fixation plates for distal femur fractures. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2018, 232, 901–911. [Google Scholar] [CrossRef] [PubMed]
- Voskuil, R.T.; Mayerson, J.L.; Scharschmidt, T.J. Management of Metastatic Disease of the Upper Extremity. J. Am. Acad. Orthop. Surg. 2021, 29, e116–e125. [Google Scholar] [CrossRef]
- Xiao, D.; Lian, C.; Wang, L.; Deng, H.; Lin, H.Y.; Thung, K.H.; Zhu, J.; Yuan, P.; Perez, L.; Gateno, J.; et al. Estimating Reference Shape Model for Personalized Surgical Reconstruction of Craniomaxillofacial Defects. IEEE Trans. Biomed. Eng. 2021, 68, 362–373. [Google Scholar] [CrossRef]
- Pascoletti, G.; Cianetti, F.; Putame, G.; Terzini, M.; Zanetti, E.M. Numerical simulation of an intramedullary Elastic Nail: Expansion phase and load-bearing behavior. Front. Bioeng. Biotechnol. 2018, 6, 174. [Google Scholar] [CrossRef] [Green Version]
- Putame, G.; Pascoletti, G.; Terzini, M.; Zanetti, E.M.; Audenino, A.L. Mechanical Behavior of Elastic Self-Locking Nails for Intramedullary Fracture Fixation: A Numerical Analysis of Innovative Nail Designs. Front. Bioeng. Biotechnol. 2020, 8, 557. [Google Scholar] [CrossRef]
- Heutinck, P.; Knoops, P.; Florez, N.R.; Biffi, B.; Breakey, W.; James, G.; Koudstaal, M.; Schievano, S.; Dunaway, D.; Jeelani, O.; et al. Statistical shape modelling for the analysis of head shape variations. J. Cranio-Maxillofac. Surg. 2021, 49, 449–455. [Google Scholar] [CrossRef]
- Aldieri, A.; Terzini, M.; Audenino, A.L.; Bignardi, C.; Morbiducci, U. Combining shape and intensity dxa-based statistical approaches for osteoporotic HIP fracture risk assessment. Comput. Biol. Med. 2020, 127, 104093. [Google Scholar] [CrossRef] [PubMed]
- Bredbenner, T.L.; Eliason, T.D.; Potter, R.S.; Mason, R.L.; Havill, L.M.; Nicolella, D.P. Statistical shape modeling describes variation in tibia and femur surface geometry between Control and Incidence groups from the Osteoarthritis Initiative database. J. Biomech. 2010, 43, 1780–1786. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McLeod, K.; Mansi, T.; Sermesant, M.; Pongiglione, G.; Pennec, X. Statistical shape analysis of surfaces in medical images applied to the tetralogy of fallot heart. In Modeling in Computational Biology and Biomedicine: A Multidisciplinary Endeavor; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 9783642312083. [Google Scholar]
- Goda, I.; Rahouadj, R.; Ganghoffer, J.-F.; Kerdjoudj, H.; Siad, L. 3D couple-stress moduli of porous polymeric biomaterials using µCT image stack and FE characterization. Int. J. Eng. Sci. 2016, 100, 25–44. [Google Scholar] [CrossRef]
- Louna, Z.; Goda, I.; Ganghoffer, J.-F. Homogenized strain gradient remodeling model for trabecular bone microstructures. Contin. Mech. Thermodyn. 2019, 31, 1339–1367. [Google Scholar] [CrossRef]

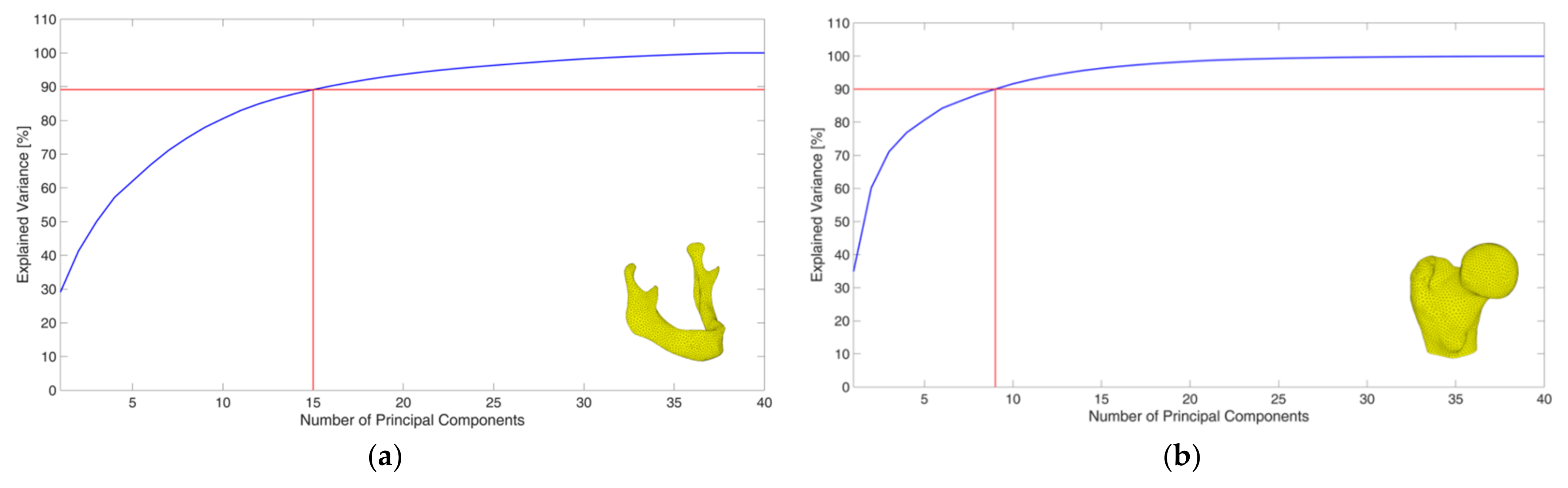




| Mandibles Training Dataset | Femurs Training Dataset | |
|---|---|---|
| Number of CT scans | 40 | 98 |
| Age | 20–96 | 55–90 |
| Gender | 32.5% female | 100% female |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pascoletti, G.; Aldieri, A.; Terzini, M.; Bhattacharya, P.; Calì, M.; Zanetti, E.M. Stochastic PCA-Based Bone Models from Inverse Transform Sampling: Proof of Concept for Mandibles and Proximal Femurs. Appl. Sci. 2021, 11, 5204. https://doi.org/10.3390/app11115204
Pascoletti G, Aldieri A, Terzini M, Bhattacharya P, Calì M, Zanetti EM. Stochastic PCA-Based Bone Models from Inverse Transform Sampling: Proof of Concept for Mandibles and Proximal Femurs. Applied Sciences. 2021; 11(11):5204. https://doi.org/10.3390/app11115204
Chicago/Turabian StylePascoletti, Giulia, Alessandra Aldieri, Mara Terzini, Pinaki Bhattacharya, Michele Calì, and Elisabetta M. Zanetti. 2021. "Stochastic PCA-Based Bone Models from Inverse Transform Sampling: Proof of Concept for Mandibles and Proximal Femurs" Applied Sciences 11, no. 11: 5204. https://doi.org/10.3390/app11115204
APA StylePascoletti, G., Aldieri, A., Terzini, M., Bhattacharya, P., Calì, M., & Zanetti, E. M. (2021). Stochastic PCA-Based Bone Models from Inverse Transform Sampling: Proof of Concept for Mandibles and Proximal Femurs. Applied Sciences, 11(11), 5204. https://doi.org/10.3390/app11115204









