Abstract
This paper presents a fast and accurate system to determine the type of blood automatically based on image processing. Blood type determination is important in emergency situations, where there is a need for blood transfusion to save lives. The traditional blood determination techniques are performed manually by a specialist in medical labs, where the result requires a long time or may be affected by human error. This may cause serious consequences or even endanger people’s lives. The proposed approach performs blood determination in real-time with low cost using any available mobile device equipped with a camera. A total of 500 blood samples were processed in this study using different image matching techniques including oriented fast and rotated brief (ORB), scale invariant feature transform (SIFT), and speed-up robust feature (SURF). The evaluation results show that our proposed system, which adopts the ORB algorithm, is the fastest and the most accurate among the state-of-the-art systems. It can achieve an accuracy of in an average time of 250 ms.
1. Introduction
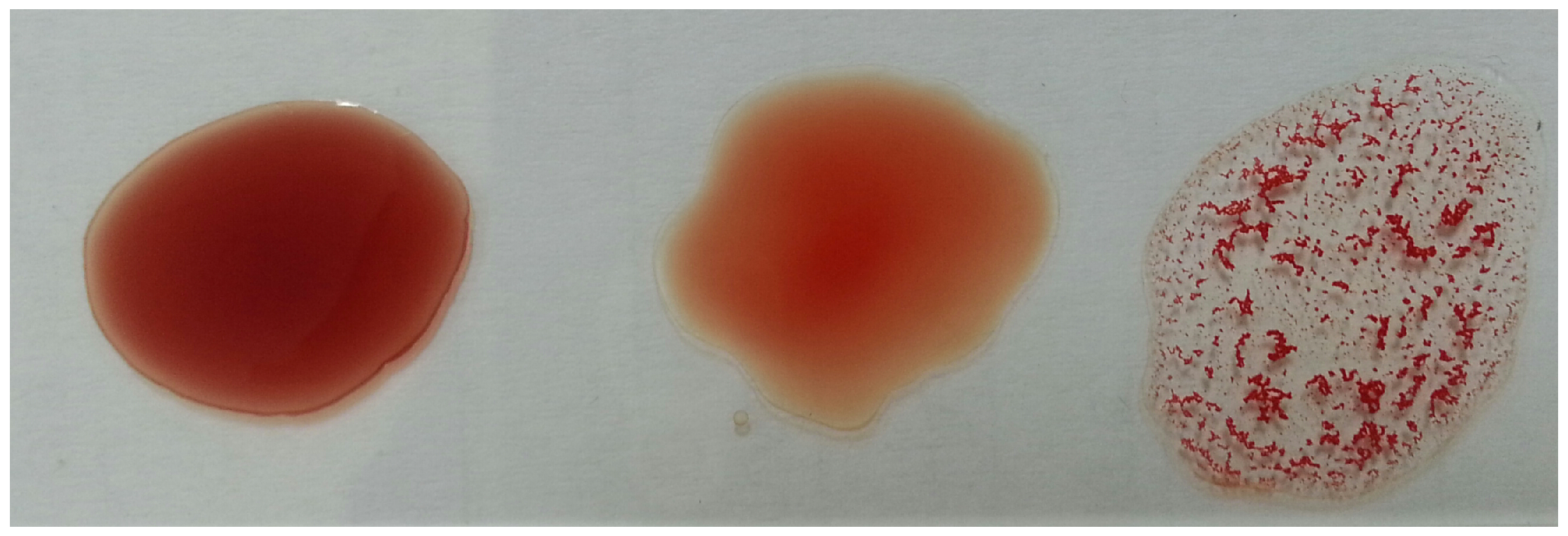
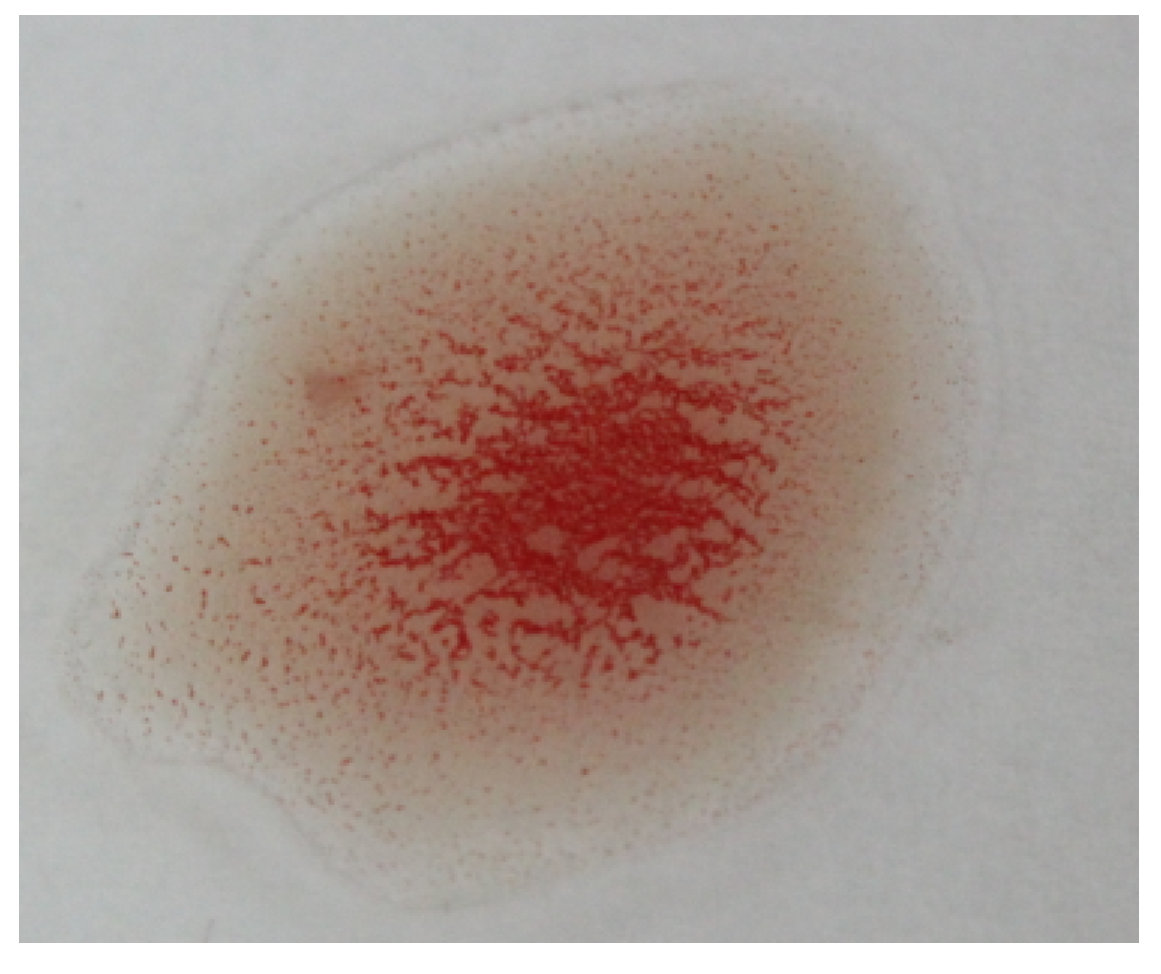
Determining a patient’s blood type (blood typing) is one of the most important and essential steps to be performed before treating injured people. Such a step should be accomplished with precision and accuracy in a timely manner to save lives and avoid serious consequences, especially in emergency situations. Traditional methods of blood typing depend on observing the agglutination of blood (i.e., blood cells sticking together as clusters) by the bare eye after applying antigens and antibodies as shown in Figure 1. However, these traditional methods are performed manually by lab technicians and are subjected to human error and delays. Hence, there is increasing interest in determining blood type using automated methods, which give faster, more precise, and more accurate results [1,2,3]. Image analysis techniques have been adopted in automatic blood typing to provide fast and objective decisions [4,5,6,7,8,9].
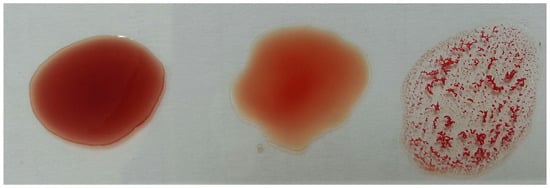
Figure 1.
Blood typing example.
The majority of automatic blood typing approaches include three main stages: preprocessing, feature extraction, and classification. In the preprocessing stage, many techniques can be used to improve the input image for further processing, such as noise reduction or removal, color space transformation, brightness correction, morphological modification, and isolation of the region of interest (ROI) (i.e., in this case, the blood spot or part of it as the agglutinated clusters) from the background, among other techniques. In the feature extraction stage, the ROI is transformed into a string of descriptors called features (mainly as a number or a sequence of numbers) to be used for identification in the classification stage, where the ROI is recognized as agglutination or not. The classification and preprocessing techniques are common between the following studies. In the literature review below, we will concentrate on the feature extraction stage because it represents the fundamental step in the automatic typing process for blood discrimination.
Ferraz et al. [1] used the standard deviation (SD) calculated from blood images to determine their group. Four images are captured for the blood sample using a CCD camera (charge-coupled device) after mixing it with A, B, AB, and D antigens. Then, the images are analyzed through a sequence of operations using IMAQ vision software, which is an image processing software that was developed originally by National Instruments. The operations include color conversion and processing, manual thresholding, and morphological operations [1]. The approach was improved in [4], but was tested using only 24 blood samples. The standard deviation feature was also used by Talukder et al. [5] and Dong et al. [6] after being extracted from the color image and the green band of the blood, respectively. Another study used support vector machine (SVM) to detect the agglutination based on the standard deviation as well [7]. Dhande et al. [8] isolate the blood spot from the background based on its luminance after transforming the RGB (red, green, and blue) input image into an HSV (hue, saturation, and intensity value) color model according to static color values. Then, they detect the blobs in the ROI and classify them (i.e., into agglutination or not) according to their area. However, these approaches suffer from many limitations such as having manual operations and a relatively long processing time of 2 min. Moreover, Section 2.2 shows that the standard deviation is not a discriminant feature; it cannot be used alone to discriminate between normal and agglutinated blood spots. Furthermore, the usage of the SVM by Panpatte et al. [7] is not necessary because the classification of the ROI based on a single feature (i.e., the standard deviation) can be easily performed using a single threshold value. Finally, the approach presented by Dhande et al. [8] requires a special environment and configuration for the blood slide, the light intensity, and angle at the time of photo capture because it depends on a static fixed value for the luminance.
Researchers in [9] detect the contours in the input image and identify the agglutination based on the number of components, where a threshold of 5 is considered for the connected components. However, this technique may result in false blobs in the background. Other approaches adopted electrical circuits to perform automatic blood typing. According to the approach in [2], a light is generated by an LED and passed through blood samples using optical fiber cables. A specific diode is used as a photo detector. The approach discriminates between different blood groups according to voltage variations from the photo detector. A similar approach was proposed in [3] based on an infrared (IR) light source. The blood sample is located between the IR transmitter and receiver. The blood type is determined according to the intensity of the received IR light. Fernandes et al. [10] propose a portable device for blood typing by identifying the spectral differences between agglutinated and nonagglutinated samples, where the result requires up to 5 minutes to be ready. The device was tested using 50 blood samples. A hardware implementation for blood typing system is presented by Cruz et al. [11] using a Raspberry Pi single-board computer. The system detects the contours in the blood spot and determines the existence of the agglutination if the number of the detected contours exceeds a given threshold. A total of 75 blood samples were used in system construction and evaluation. These approaches require additional special hardware. Regardless of the additional cost, the hardware may not be available everywhere or every time.
Many other techniques can be used to classify medical images into normal and infected (i.e., with or without agglutination, in our case). Frequency domain analysis was used by Yayla et al. [12] to classify nanometer-sized objects in images provided by a biosensor. Fourier and wavelet features are extracted from the input images and analyzed where the decision tree and random forest are used for classification. Yang et al. [13] proposed a classification method based on the wavelet transformation for feature extraction. The classification is performed using an interpolation scheme. The wavelet decomposition was further improved by proposing an adaptive framework to improve the performance in terms of down sampling balance and signal compression [14]. The wavelet was also used by Liu et al. [15] to reduce the haze and enhance texture details of the images in frequency domain. Wavelet features can be represented using sophisticated mathematical models such as fractal descriptors [16,17,18]. However, these techniques require domain-dependent knowledge in case of model updating or scaling.
Although the blood type determination based on feature engineering (i.e., extracting features depending on domain knowledge) is still the most prevalent in research studies, other studies used image matching algorithms such as scale invariant feature transform (SIFT) and speed-up robust feature (SURF). For example, SIFT was used in [19] to transform the green component of the image into a collection of local feature vectors, after many preprocessing techniques such as thresholding and morphological operations. Then, the SVM algorithm is used for classification. The proposed approach was evaluated using only 30 blood samples. Furthermore, Sahastrabuddhe and Ajij [20] employed the SURF algorithm to detect the agglutination in blood using only 84 blood samples. However, SIFT and SURF algorithms are quite slow compared with other newer image matching algorithms such as oriented fast and rotated brief (ORB) [21]. In addition to the limitations discussed for each group of the studies above, all of them used a small number of blood samples and did not provide an objective evaluation of accuracy.
As discussed earlier, traditional blood typing is performed manually as follows: (1) taking a blood sample from the patient, (2) mixing it with different antibodies on a slide, (3) observing the agglutination, and (4) determining the blood type. In this paper, we proposed a system to automate the last two steps, (3) and (4). The system can handle a large number of input images captured by a mobile phone camera minimizing human error. Such a system has the ability to handle difficult cases that are ambiguous even for manual inspection by people who might fail to detect agglutination and/or blood type while using state-of-the-art approaches. Our contribution can be summarized as follows:
- The ORB matching algorithm was adopted to provide an accurate, fast, and automated blood typing system.
- The system is able to detect various agglutination patterns regardless of variations in photos brightness.
- The system was evaluated using 1500 images of blood spots that cover all possible agglutination patterns.
- The evaluation includes detailed analysis for the accuracy and processing time of different approaches.
We begin this paper by providing an overview of the blood typing process, problem statement, and challenges, which are explained thoroughly in Section 2. The principle of operation of the used image matching techniques is reviewed thoroughly in Section 3. The experimental setup, including blood image capturing and analysis, is provided in Section 4. Results and their analysis are provided in Section 5. Finally, conclusions are drawn in Section 6.
2. Blood Typing: Overview, Problem, and Challenges
2.1. Overview
Blood typing or blood grouping is the process of determining the type or the group of the human blood depending on the presence or absence of certain antigens on the surface of the red blood cells. This process is important for blood transfusion, as not all blood types are compatible with one another. Receiving an incompatible blood type motivates the human body to generate antibodies against the new blood, which causes clotting in the blood vessels and may threaten life.
Two blood group systems are used to identify the blood type: (1) ABO and (2) Rh systems. According to the first system, the blood is classified depending on the presence of A and B antigens into one of the following groups or types: A, B, AB, or O. In types A and B, the surface of the red blood cells contains A and B antigens, respectively. In type AB, the surface contains both A and B antigens, whereas it contains neither of them in type O. The Rh system is the second most significant blood group system, where it classifies the blood into positive (+) or negative (−) according to the presence and the absence of the Rh antigens, respectively. Both ABO and Rh grouping systems yield into eight possible human blood types; A+, A−, B+, B−, AB+, AB−, O+, and O− [22]. Table 1 summarizes these types and the accepted donor’s blood type during blood transfusion to avoid blood clotting.

Table 1.
Blood types and its compatibility with each other.
The blood typing process is performed by mixing three spots of the same blood sample with A, B, and D antibodies, respectively, and then observing the agglutination of the three spots. The blood is classified into ABO groups as follows:
- Blood type A: Agglutination of the spot mixed with A antibodies.
- Blood type B: Agglutination of the spot mixed with B antibodies.
- Blood type AB: Agglutination of the spots mixed with A and B antibodies.
- Blood type O: No agglutination of the spots mixed with A and B antibodies.
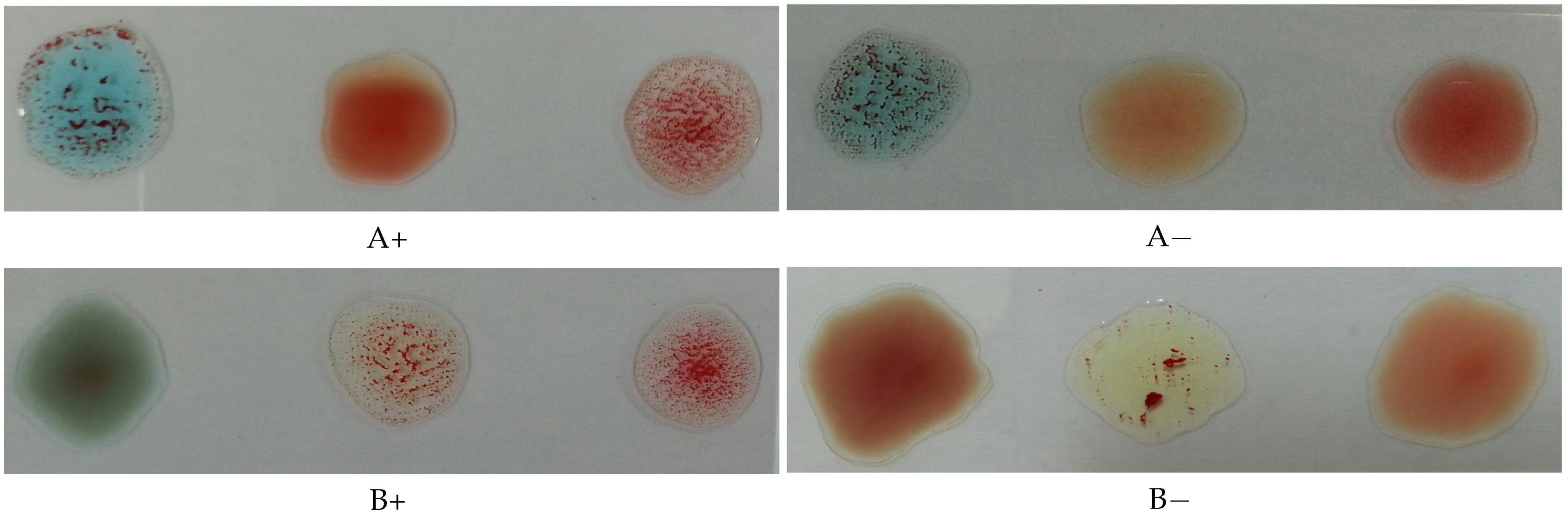
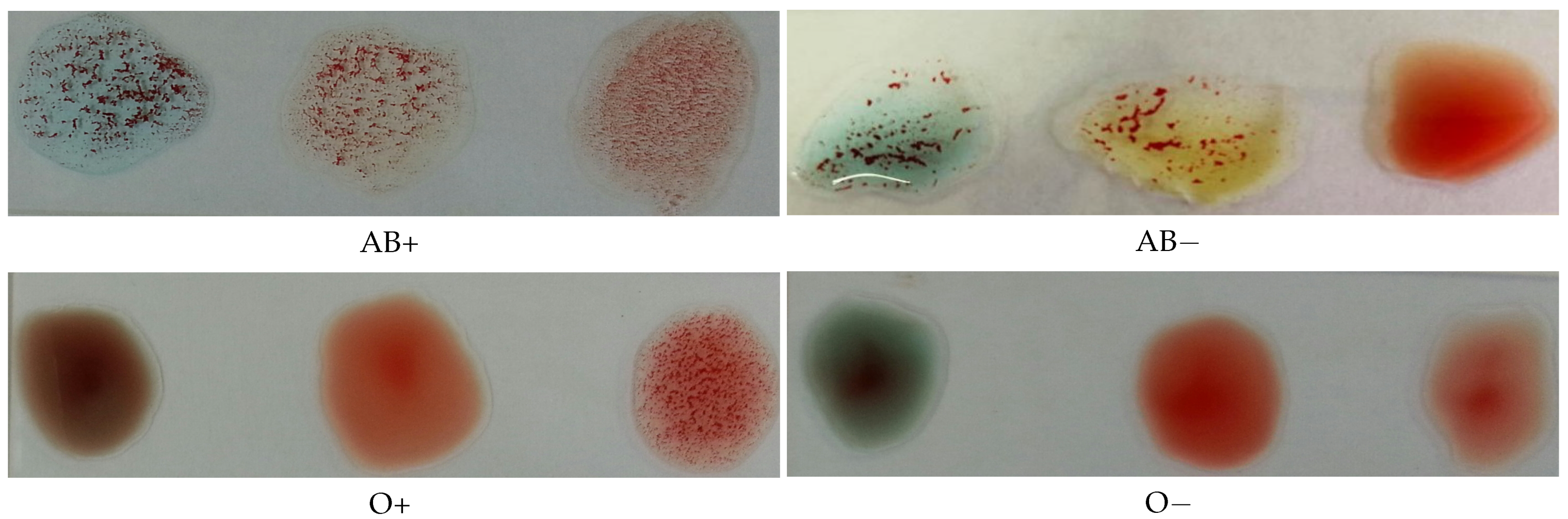
The Rh type is determined according to the agglutination of the spot mixed with the D antibodies. If it is agglutinated, the blood type is positive; otherwise, it is negative. Figure 2 illustrates this process, where the antibodies A, B, and D were mixed with each blood spot from left to right in each image, respectively.
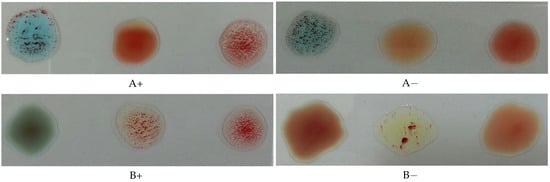
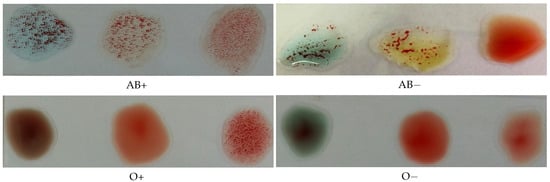
Figure 2.
Photos for slides of blood samples captured by a mobile phone camera.
2.2. Problem
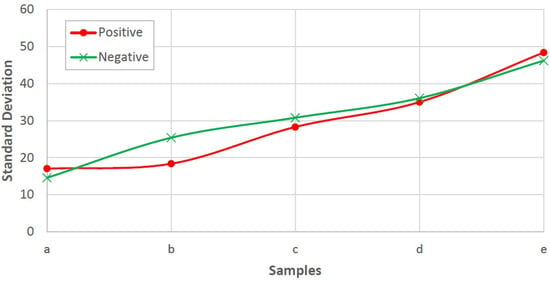
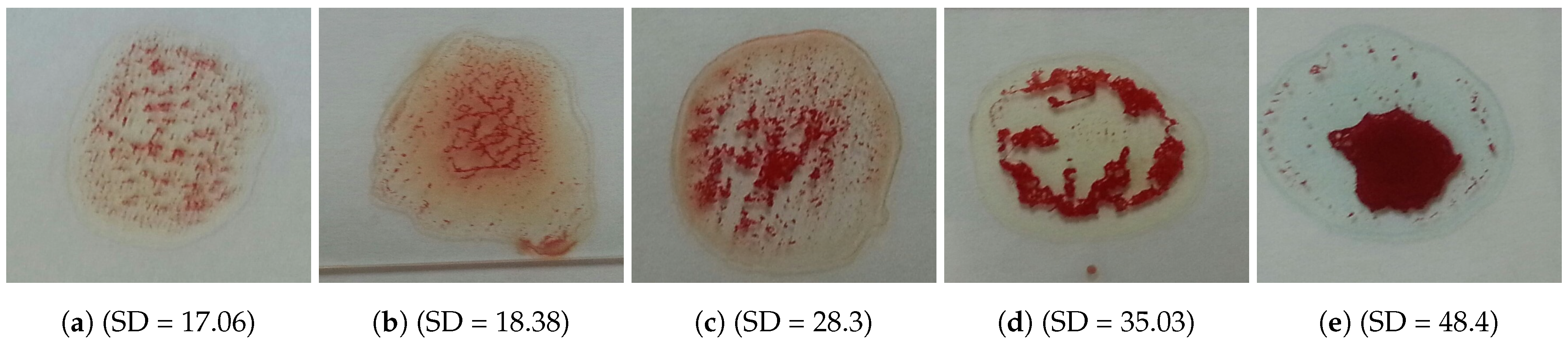
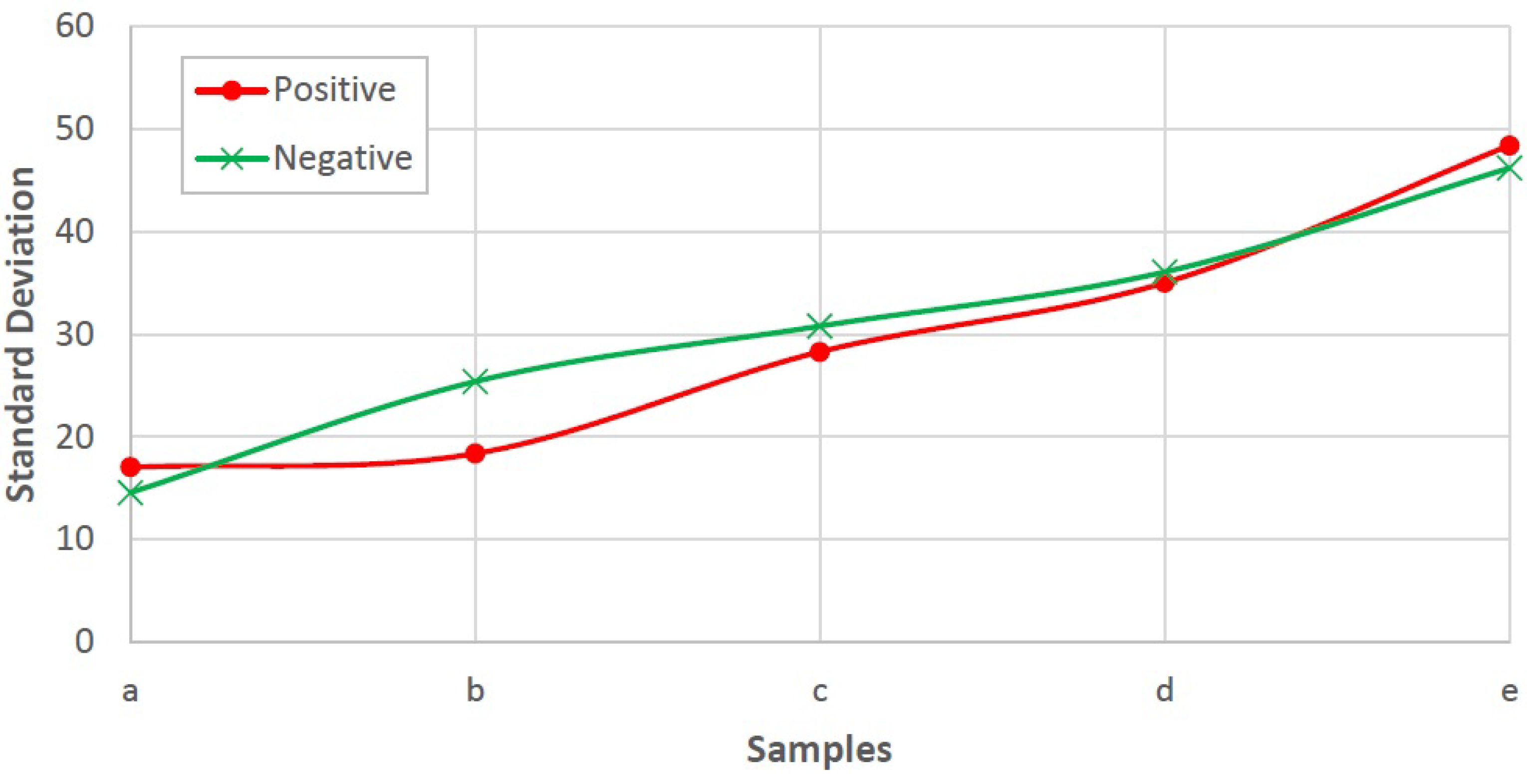
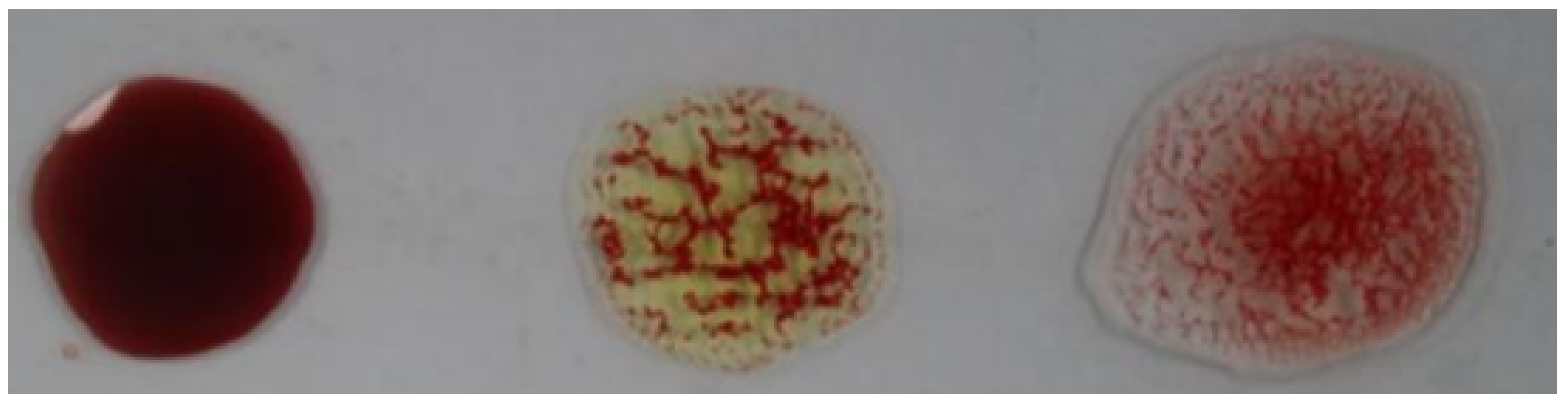
The problem is to determine blood type (blood group) from a digital image captured by a normal camera of any mobile device automatically and efficiently. In this paper, we provide a solution for such a problem that is void of issues related to the traditional manual techniques. Furthermore, it addresses all the drawbacks of the previous studies. For example, most of the state-of-the-art techniques consider the standard deviation, extracted from the input image, to identify the agglutination in blood. However, this subsection disproves that the standard deviation can be considered as a discriminant feature by providing many examples with different images and their values of standard deviation. Figure 3 and Figure 4 show blood samples of positive (with agglutination) and negative (without agglutination) results and their standard deviations, respectively. For the sake of clarification, the terms “positive” and “negative” are used here to denote the existence and the absence of agglutination, respectively. It is clear that there is a wide range of standard deviation values that overlap for both positive and negative images. Moreover, Figure 5 represents those values and shows that that standard deviation feature alone cannot be used to separate positive and negative classes based on single value thresholding as adopted in the previous studies. Such a problem in feature selection refers to the low number of collected samples (24–84 samples) that may not represent the domain of the problem. On the contrary, this study was conducted on 500 samples in order to cover a wide range of possible cases.
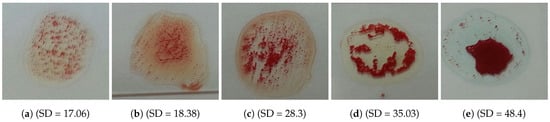
Figure 3.
Blood samples with agglutination and their standard deviation values (positive).

Figure 4.
Blood samples without agglutination and their standard deviation values (negative).
2.3. Challenges
Several challenges were encountered during the system design. In this subsection, two main challenges are presented:
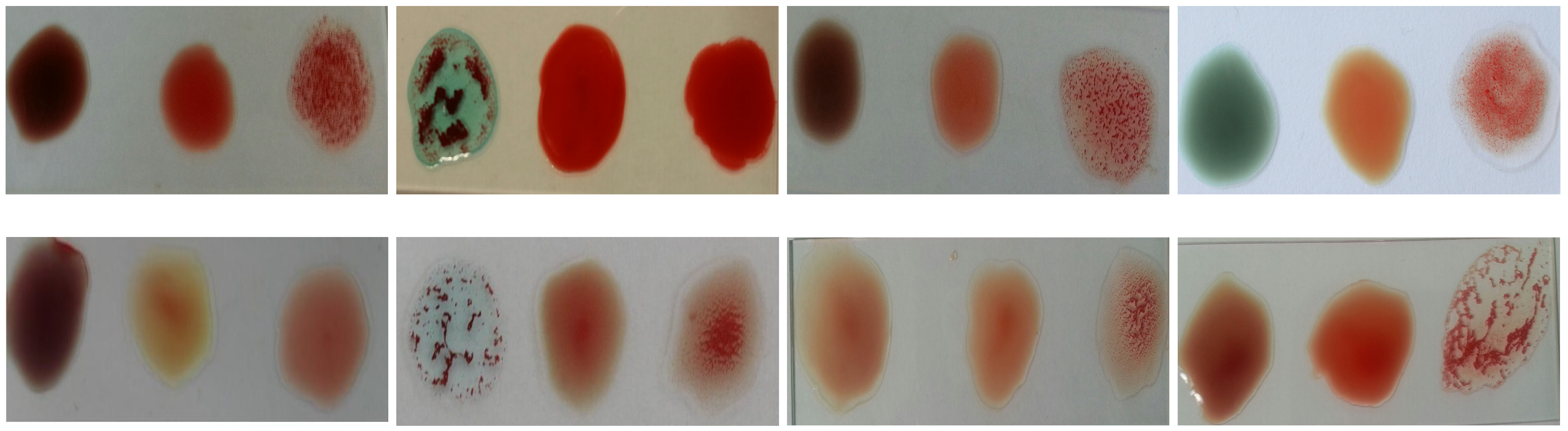
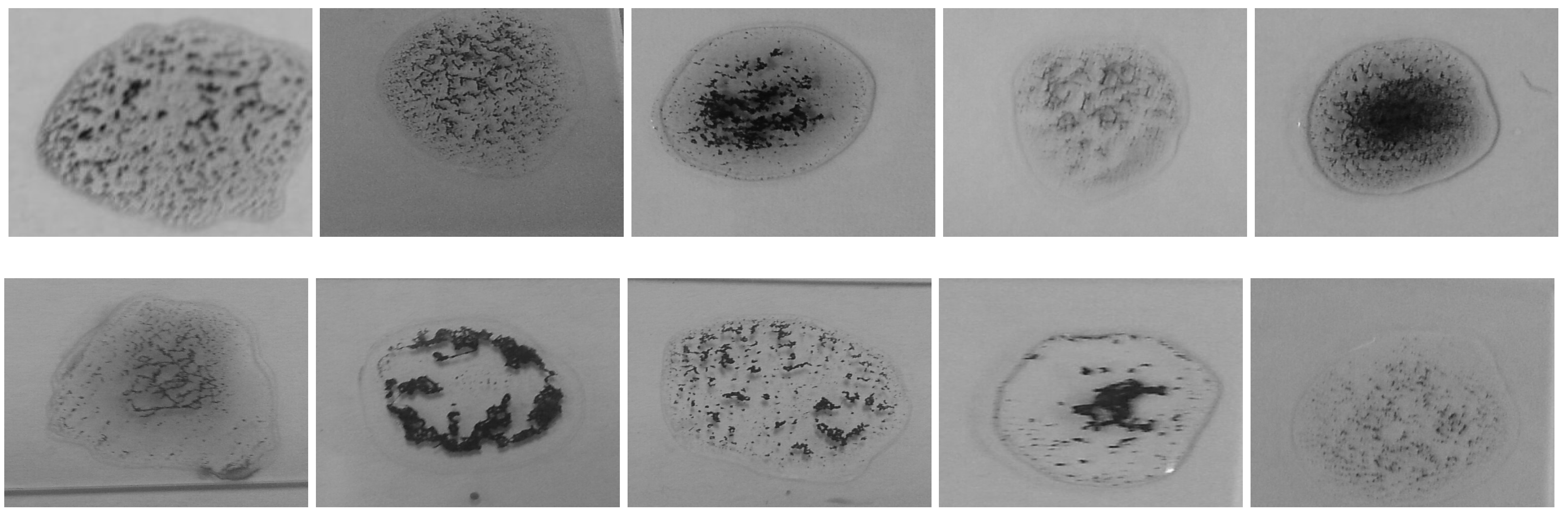
- The difference in the level of illumination as a result of the diversity of the environments in which the examination can be performed. Figure 6 shows an example of several samples that have different brightness levels.
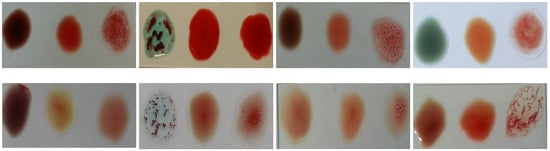 Figure 6. Blood samples with brightness variation.
Figure 6. Blood samples with brightness variation. - Variations in the nature of blood coagulation that appears when antibodies are added to the blood samples as shown in Figure 7.
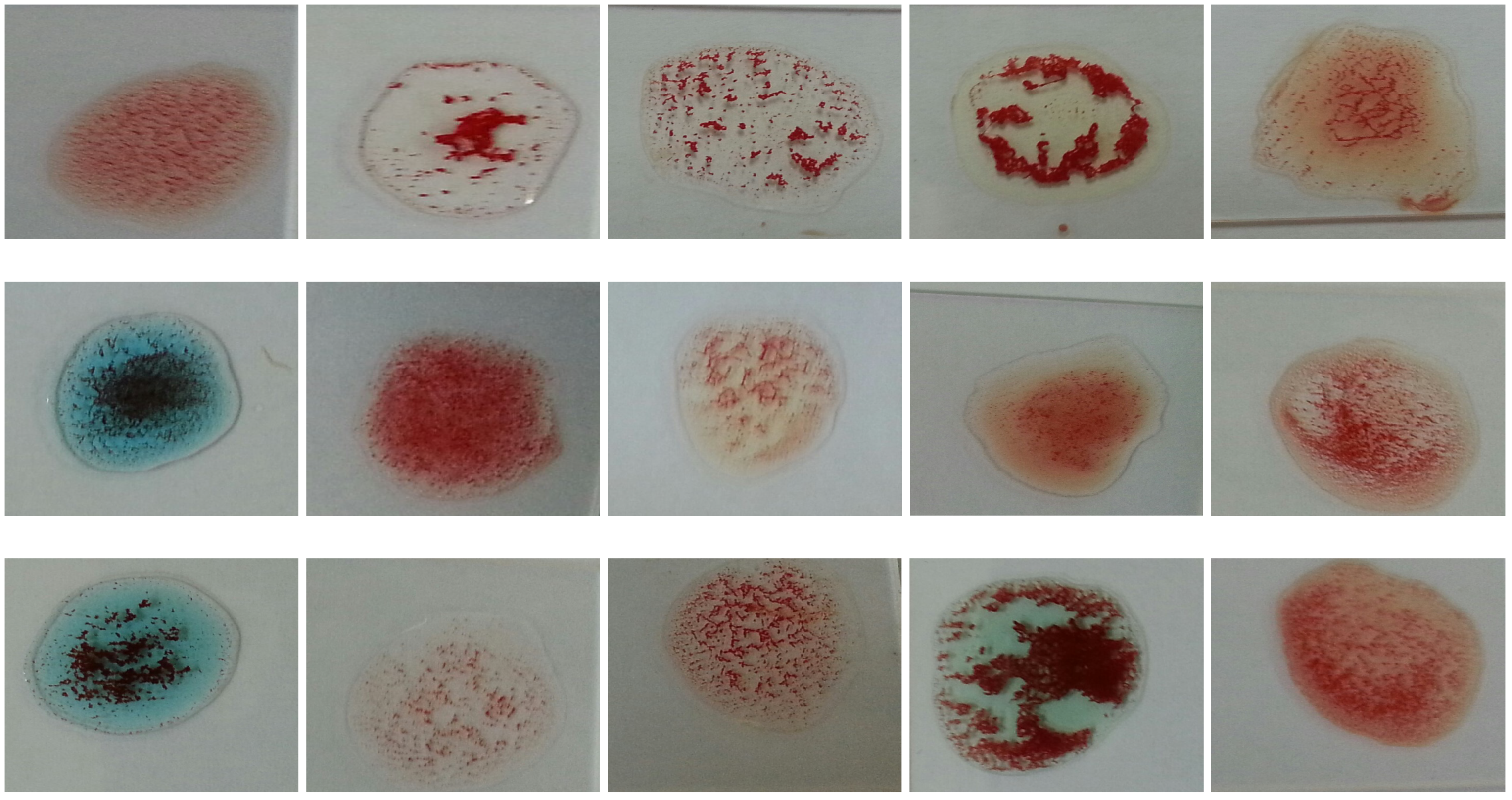
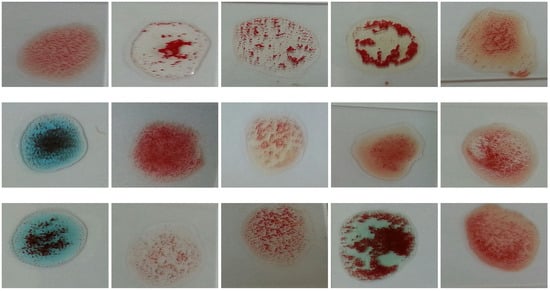 Figure 7. Samples with different agglutination patterns.
Figure 7. Samples with different agglutination patterns.
The two main challenges described above were a motivation to search for a technique that is invariant to the brightness of input images and finding a technique that can handle different forms of coagulation in blood. Therefore, we adopted the ORB algorithm as an image matching technique to detect the agglutination in blood because it is tolerant to variations in brightness and can identify difficult patterns efficiently.
3. Overview of Image Matching Techniques
Image feature points matching is the process for searching and finding effective point pairs in the corresponding images. In this research, three image matching algorithms—scale invariant feature transform (SIFT), speed-up robust feature (SURF), and oriented fast and rotated brief (ORB)—are used to determine blood type based on the presence or absence of agglutination.
SIFT was proposed in 2004 to detect features of an image. These features are invariant to image scale and rotation [23]. SURF was introduced in 2006 as an improved algorithm with lower computation complexity compared with the SIFT algorithm by [24]. ORB, first presented in 2011 [25], is based on the FAST (features from accelerated segment test) keypoint detector and the visual descriptor BRIEF (binary robust independent elementary features). It provides a fast and efficient alternative to SIFT and SURF. This section provides a brief overview of these matching algorithms.
3.1. SIFT
The scale invariant feature transform (SIFT) algorithm takes an image and transforms it into a large collection of local features’ vectors. Each of these features’ vectors is invariant to any scaling or rotation of the image.
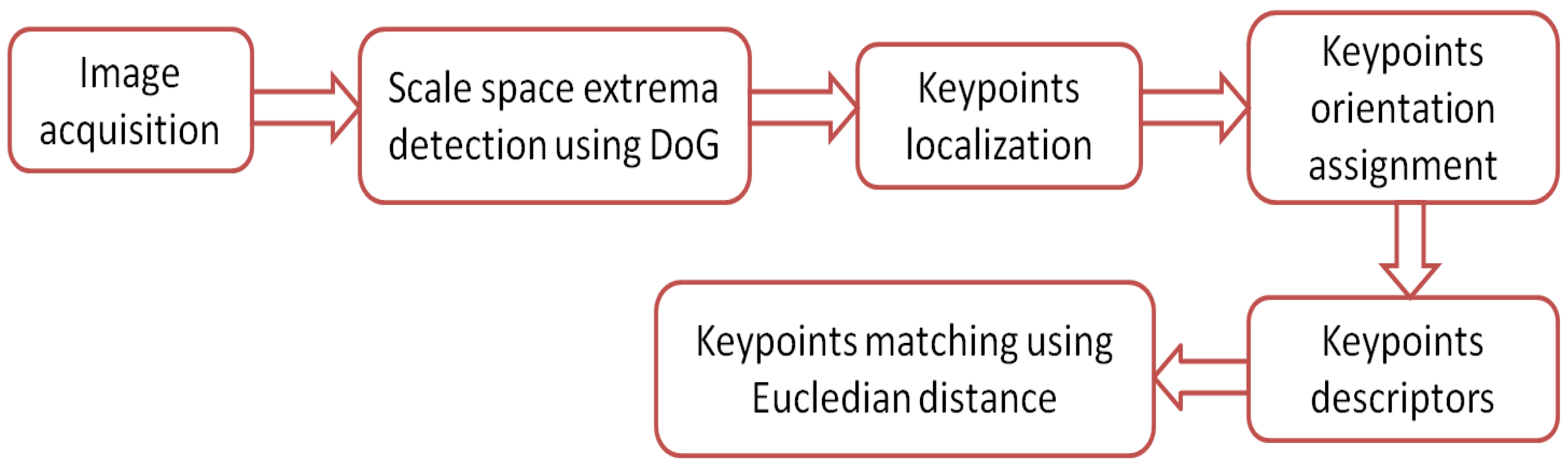
The SIFT algorithm is distinctive where individual features can be matched for a large database of objects. SIFT provides many features for even small objects. The principle of operation of the SIFT algorithm is illustrated by the flow chart shown in Figure 8. The principle of operation of the algorithm is summarized by the following steps:
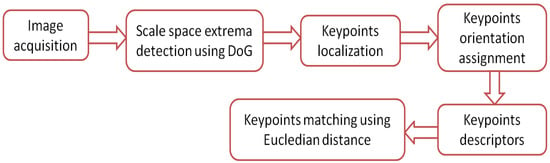
Figure 8.
Flow chart for the SIFT algorithm.
Step 1: Scale space extrema detection using DoG. The first step to extract image keypoints is to identify candidate key points and the locations at different space scales using variable-scale Gaussian kernel , which is convoluted with the input image to produce the scale space of an image , as in Equation (1)
where * is the convolution operation. All scales must be examined to identify the scale invariant feature. SIFT uses a difference of Gaussian method (DoG) function, which is defined as , to detect efficient key points’ locations by computing the difference of two nearby scales separated by a constant multiplicative factor k [23], as in Equation (2),
A group of scaled images is called an octave. To ensure that the same numbers of DoG images are generated per octave, each octave corresponds to doubling the value of , and the value of K is selected. Each pixel in a DoG image is compared to its eight neighbors at the same scale, and the nine corresponding neighbors at neighboring scales. The pixel will be selected as a keypoint if it is a local maximum or minimum among the (26) pixels surrounded.
Step 2: Keypoints localization. Too many keypoints will be generated by extrema detection; some of those keypoints are unstable. The next step aims to eliminate low contrast candidates and poorly localized candidates along edges. This is accomplished using a Taylor series expansion of DoG, D [26]:
where
The maxima or minima location is determined by Equation (5),
The keypoint is acceptable if is above a threshold value. To ignore candidates along edges, Hessian matrix H is computed at the location and the keypoints are scaled. H is given by Equation (6),
The eigenvalues of H are computed and used to detect corners and reject keypoints edges. However, eigenvalues are not explicitly computed; instead, trace and determinants of H are used [27]:
where keypoints for which the ratio between is greater than a threshold are neglected.
Step 3: Keypoints orientation assignment. This step is important to get rotation invariant keypoints. To assign rotation or more for each candidate, the magnitude and direction of L (smoothed image) at each scale of keypoint is calculated [28] using Equations (9) and (10),
where, and . A weighted direction histogram for the neighborhood pixels of the keypoint is then created using 36 bins to cover ( for each bin). The maximum direction is selected as the orientation of the keypoint in addition to the directions where the local peaks are within 80% of the maximum peak.
Step 4: Keypoints descriptors. This step makes use of gradient orientation histograms for robust representation. The descriptor of each keypoint is created by computing the relative orientation and magnitude in a neighborhood region. This region is then divided into regions to create weighted histograms (eight bins) for each region. Each descriptor contains a array of 16 histograms around the keypoint. This leads to a SIFT feature vector with elements [29].
Step 5: Keypoints matching using Eucledian distance. Image matching is carried out by searching for corresponding features between two images, according to the nearest neighborhood procedure. Finding the nearest neighbor is accomplished by calculating the Euclidean distance for each feature and in the training database where the matching feature is that of the minimum distance. However, many features from an image will not have any correct match in the training database. Therefore, it would be useful to have a way to discard features that do not have any good match to the database. The ratio of distances between the best and second best match must be lower than a threshold. Rejecting all matches where the distance ratio is greater than 0.8 will eliminates 90% of the false matches while discarding less than 5% of the correct matches as proposed by [23].
3.2. SURF
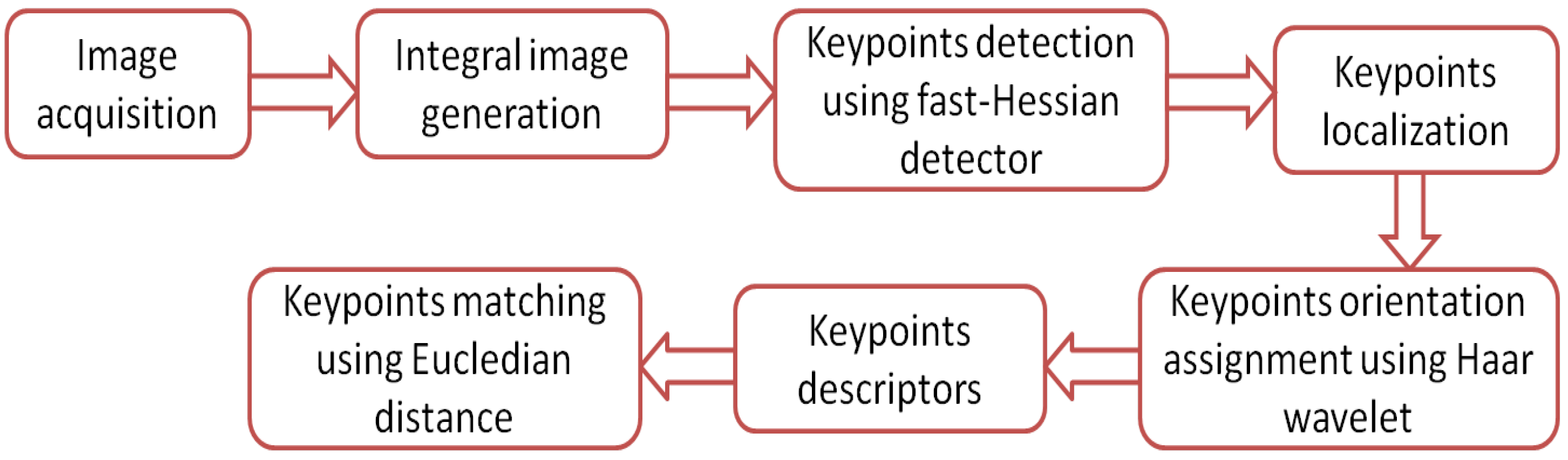
The speed-up robust feature (SURF) algorithm has mostly the same principles and steps of operation used in SIFT algorithm. The SURF has a faster convergence time and better performance results compared with the SIFT algorithm. The principle of the SURF algorithm operation is best illustrated by the flow chart shown in Figure 9. Its operation can be summarized by the following steps:
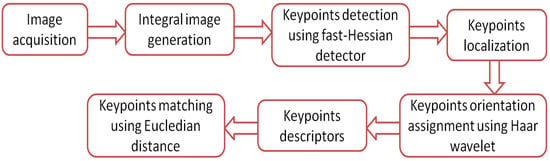
Figure 9.
Flow chart for the SURF algorithm.
Step 1: Integral image generation. SURF uses an integral image instead of the image itself for faster calculation of box type convolution filters and Haar wavelet features’ responses. The integral image (also called the summed area table) at position is the sum of all the values of the original image above and to the left of the pixel at location X.
where is the original image and is the integral image [24].
Step 2: Keypoint detection using a fast-Hessian detector. A SURF detector differs from a SIFT detector; SURF uses fast Hessian instead of DoG. The Hessian matrix of a given point in the image I at scale is defined as follows:
where is the convolution of the Guassian second order derivative with image I in point X, and similarly, ,. SURF approximates the second order derivatives using box filters and evaluates the image using integral images to speed calculations up [30]. The approximation of convolution results is denoted by , , and . The determinant of the approximated Hessian matrix is calculated as
where the factor 0.9 is needed for energy conservation between the Gaussian kernels and the approximated Gaussian kernels [31]. SURF generates a scale-space image pyramid by convolving the image with an increasing size of the box filter. Each octave contains the convolution results with four upscaling box filters. Table 2 shows the parameters of the first three octaves. Note that the new parameter scale is .

Table 2.
Box filter sizes for the first three octaves.
Step 3: Keypoints localization. To localize the keypoints in the image with the accurate scale, the nonmaximum suppression method with a neighborhood is applied [26]. If the point has maxima determinant of the Hessian matrix, then it is selected to be a keypoint.
Step 4: Keypoints orientation assignment using Haar wavelet. To get rotation invarience keypoints, SURF calculates Haar wavelet responses within a circular neighborhood of radius 6s around the keypoint, where s is the determined scale of the keypoint. The responses in both the x direction () and the y direction () are calculated. Hence, integral images are used for fast filtering. The sum of x responses and y responses within every window of is calculated to construct the orientation vector. The dominant orientation of the keypoint is assigned by the longest vector.
Step 5: Keypoints descriptors. SURF creates the keypoint descriptor again using Haar wavelets—this time, by creating a square region of size 20s around the keypoint toward the assigned orientation. This region is then divided to sectors. For each sector, Haar wavelet responses in both directions are calculated. Each sector will be presented by a vector v of length 4 that contains the sum of Haar wavelet responses in both the x and y directions, the sum of the absolute responses in both the x and y directions () [32]. The resulting SURF keypoint descriptor has a length of .
Step 6: Keypoints matching using Eucledian distance. To find the matching features between two images, the same procedure that has been used in SIFT is applied by calculating the Euclidean distance between each keypoint descriptor and the training database keypoints descriptors. The matching feature is initially that of the minimum distance. However, to discard features that do not have any good match to the database, the ratio of the distance between the best and second best match must be lower than a threshold.
3.3. ORB
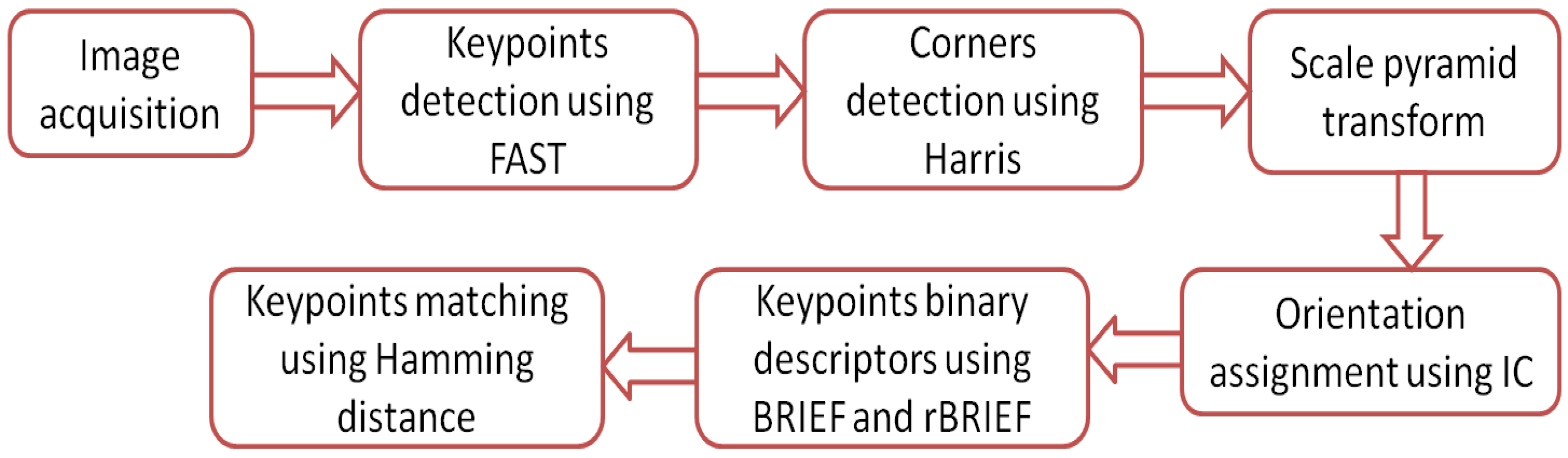
The oriented fast and rotated brief (ORB) algorithm is based on the features from accelerated segment test (FAST) and binary robust independent elementary features (BRIEF) algorithms. The ORB algorithm has the advantage of rotational invariance [25]. The ORB algorithm has the ability to reduce sensitivity to noise, and it is faster than the SIFT and SURF algorithms [25]. The principle of operation of the ORB algorithm is best illustrated by the flow chart shown in Figure 10. The operation of the ORB algorithm is summarized in the following steps:
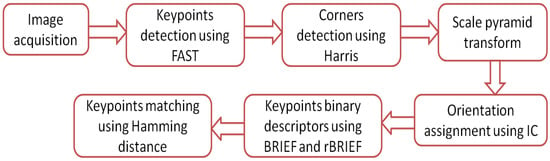
Figure 10.
Flow chart for the ORB algorithm.
Step 1: Keypoints detection using FAST. The ORB algorithm is based on FAST to find feature points quickly. FAST is performed by choosing an arbitrary pixel point P as a center to form a circular area with nine pixels neighbored to the pixel P, taking the intensity of the arbitrary pixel P (), the intensity of each neighbored pixel n (), and a threshold value t into account. Each pixel (n) in these nine pixels can have one of the three states in Equation (14) [33]:
P is a feature point if at least three of the neighbored pixels are brighter than or darker than . Otherwise, P cannot be a feature point.
Step 2: Corners detection using Harris. ORB has large responses along edges. Therefore, the Harris algorithm is used to detect corners. The main idea is to take a small window around each feature point P and measure the amount of change around it after shifting the window by eight directions. After that, the sum squared difference (SSD) of the pixel values before and after the shift is taken to identify the pixel windows at which the SSD is large in all directions. Finding the eigenvalues for each window around each feature point P will be used to determine the corners of this feature point. If both are high, then P is a corner [34].
Step 3: Scale pyramid transform. A scale pyramid is used to produce multiscale features in order to obtain scale invariance. The image pyramid is a multiscale representation of a single image that consists of a series of images that are versions of the original image at different resolutions. Each image in the pyramid contains a downsampled version of the image in the previous level. When the pyramid is created by the ORB algorithm, the FAST algorithm is employed to detect keypoints in the image. By detecting keypoints in each image of the pyramid, the key points can be detected effectively at different scales. In this way, ORB is partial scale invariant.
Step 4: Orientation assignment using IC. Since FAST does not produce orientations, the intensity centroid (IC) technique is used to find the orientation of each FAST-produced feature point [35]. Moments of a patch are defined as
With these moments, we can find the centroid, the “center of mass” of the patch (centroid) of the moments; this is calculated as
Then, a vector from the corner’s center O to the centroid is constructed and the orientation of the patch is then given as
where is the quadrant-aware version of .
Step 5: Keypoints binary descriptors using BRIEF and rBRIEF. Binary robust independent elementary feature (BRIEF) converts all keypoints detected by the FAST algorithm into a binary feature vector that is known as a descriptor. BRIEF chooses two random pixels around each keypoint; then, it compares their intensity. If the first pixel is brighter than the second, it assigns the value 1 to the corresponding bit, else 0 is assigned. This process is repeated until the length of each vector that describes the keypoint becomes 255 bits. Consider an image patch around a keypoint p; then, the binary test is defined in Equation (18):
and are the intensity values at positions x and y. The feature is defined as a vector of n binary tests:
The BRIEF algorithm begins analysis by filtering an image patch around the key point with a Gaussian kernel in order to prevent the descriptor from being sensitive to noise. The sensitivity to noise can be reduced significantly. The filtering step increases the stability and repeatability of the descriptors [36]. Rotation-aware BRIEF (rBRIEF) is a modified version of BRIEF that takes the orientation of the keypoints into account. For any feature set of n binary tests at location , we need the matrix where :
ORB defines the rotation matrix with orientation of feature point [25] to construct a steered version of S:
where
Step 6: Keypoints matching using Hamming distance. The matching between images is computed using the Hamming distance. The Hamming distance for each keypoint descriptor and the descriptor in the database is computed. The Hamming distance between two descriptors , is computed using Equation (23) [37]:
The descriptors and are 256 vectors defined by and . The matching is decided based on the minimum Hamming distance. To discard features that do not have any good match to the database, the ratio of distances between the best and second best match must be lower than a threshold. Rejecting all matches where the distance ratio is greater than the threshold should eliminate most of the false matches.
4. Experimental Setup and Implementation
In this section, the experimental setup and the proposed system architecture are presented.
4.1. Blood Samples Collection
A total of 500 blood samples were collected and labeled for the system construction and evaluation. 300 samples were collected and processed by lab technicians at An-Najah National University Hospital. The remaining 200 samples were collected and processed by lab technicians in the college of medicine at An-Najah National University in Nablus, Palestine. Table 3 shows the blood type distribution of the collected samples; the blood types were determined manually by the lab technicians. From Table 3, it can be observed that the number of A−, B−, and AB− is small. This is because A−, B−, and AB− are classified as rare blood groups. The results shown in Table 3 are supported by a study conducted by the American Red Cross of blood groups distribution by race/ethnicity [38]. For Asians, only 0.5% carry A−, 0.4% carry B−, and 0.1% carry AB−. The small number of A−, B−, and AB− blood groups in the 500 blood samples used in this research has no effect on determining the blood type using image matching since the blood type in this research is determined based on the presence or absence of agglutination in an image, not on the statistical distribution of blood groups. The collected data are almost balanced because the 500 blood samples generated a total of 1500 blood spots—799 with positive agglutination and 701 with negative agglutination.

Table 3.
Distribution of the collected blood samples.
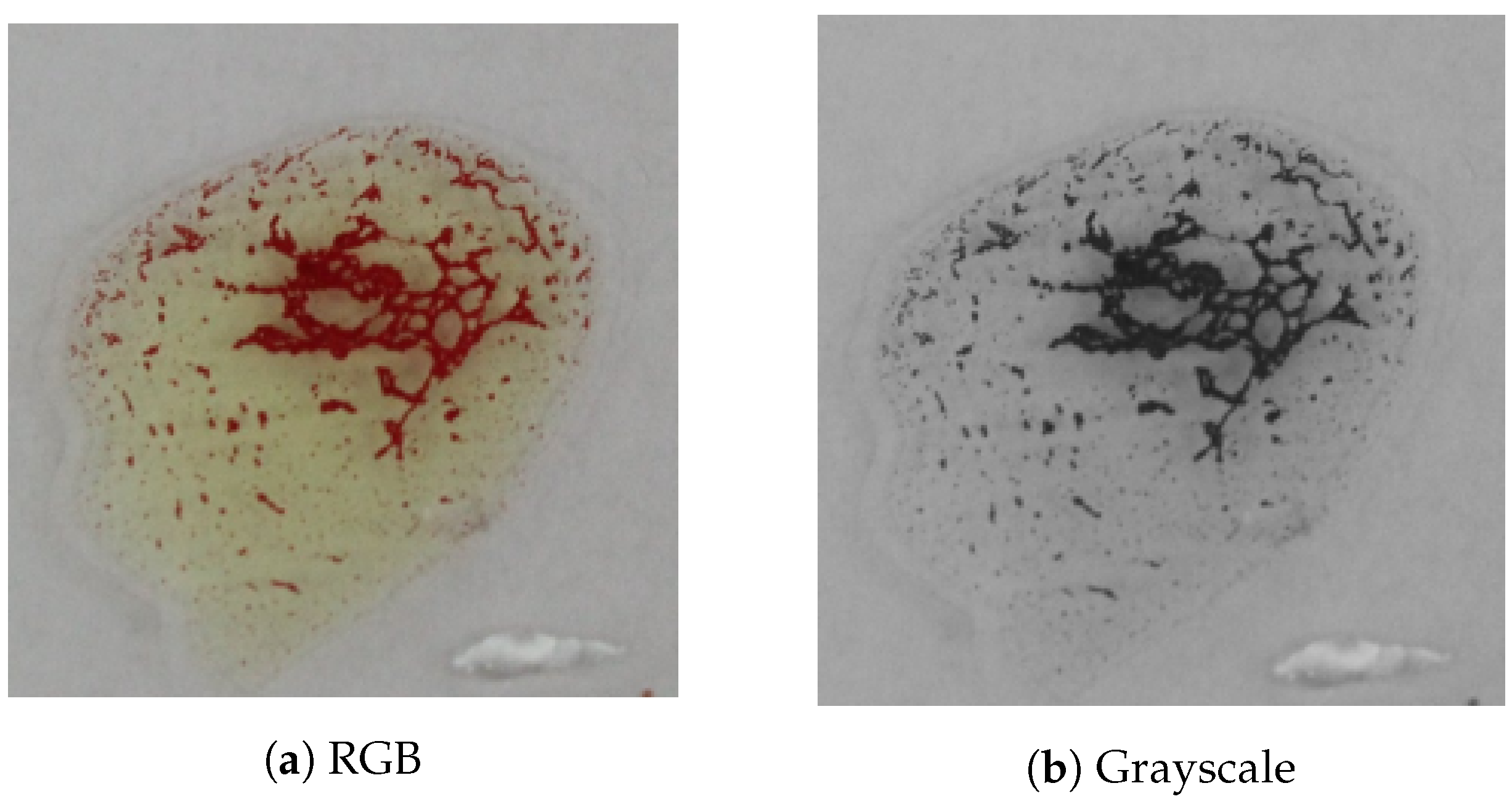
A mobile phone equipped with 8 MB RGB camera was used to capture photos of the blood samples after mixing them with antibodies A, B, and D, as shown in Figure 2. Each image is partitioned into three patches so that each patch contains a blood spot. The core problem is to recognize the agglutination in these patches. For sake of simplicity, we will use the words samples or images to denote those patches.
4.2. System Architecture
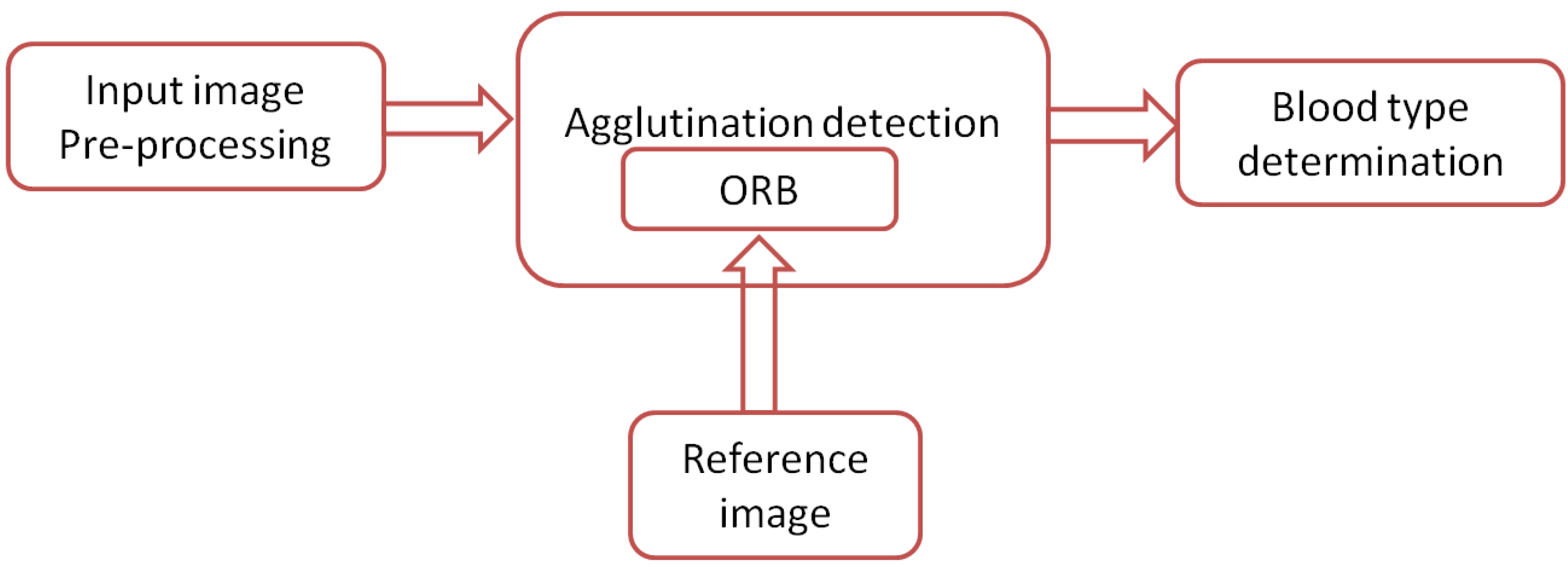
Figure 11 shows a block diagram of the proposed system. A mobile phone equipped with an 8 MP camera is used to capture images for blood samples. The images are transferred to a PC via USB cable, where they are processed using MATLAB [39]. However, the software can be also implemented completely on the mobile phone to provide a standalone solution. The software is described in Figure 12, where the input image is processed automatically by converting it from an RGB color model to grayscale and partitioned into three patches (three blood spots mixed with antibodies A, B, and D) in the preprocessing stage. The ORB algorithm is then used to detect the agglutination of the blood spots by matching it with a reference image. Finally, the blood type is determined by combining the results of the three blood spots. In each blood sample, any false detection in the agglutination in any of the three blood spots means that the resulting blood group does not match the actual blood group of the tested sample. Otherwise, the system successfully determines the blood group. The accuracy of blood type determination is determined by the ratio of the correct decisions to the total number of samples. Another two systems were implemented by replacing the ORB algorithm in the agglutination detection stage with the SIFT and the SURF algorithms for the purpose of comparison as shown in Section 5. All systems were implemented using MATLAB.

Figure 11.
The proposed system.
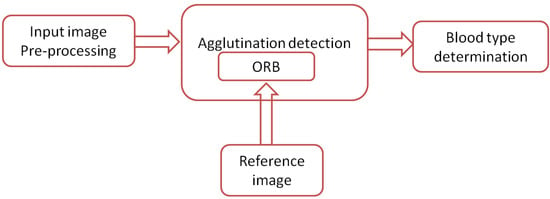
Figure 12.
Software processing steps.
One of the most crucial steps in such system is to choose a good reference image that contains a large number of agglutination patterns such that it represents all possible variations of blood agglutination. Figure 13 shows the reference image that was used in our proposed system. It was selected carefully with a large number of detected keypoints; it also has different patterns of agglutination clusters (i.e., blood clotting). Figure 14 shows samples for different agglutination patterns. Hence, one can notice that the chosen reference image covers all of these different patterns. The matching algorithms try to find common keypoints between the input image and the reference image to detect the agglutination.

Figure 13.
The referenced agglutination image used in the matching algorithms.

Figure 14.
Samples with different agglutination patterns.
4.3. Parameters Design and Optimization
Matching is performed by calculating the distances between each keypoint descriptor in the input image and all keypoints descriptors in the reference image in order to identify its nearest neighbors. The best match of the keypoint is determined by finding its nearest neighbor that has the shortest distance. However, some matches are not correct even if they have the shortest distance due to potential noise or brightness effect. Therefore, a ratio between the shortest distance and the second shortest distance is considered to identify the correct matches according to a given threshold. The matches are considered false matches and rejected if the ratio is greater than the threshold. Table 4 shows the matching metrics and the threshold values used for each algorithm depending on the experimental results.

Table 4.
Matching parameters for SIFT, SURF, and ORB algorithms.
5. Results and Discussion
This section discusses the results of the blood typing system that used the ORB algorithm. The results of the ORB system were compared with other image matching systems by replacing the ORB algorithm with the SIFT and SURF algorithms. For the purpose of simplification, these algorithms will be called ORB, SIFT, and SURF systems or algorithms, respectively. Figure 15 shows an example of an input image that has agglutination in two blood spots. The image was used to compare between the three matching systems. Moreover, those systems are compared with the state-of-the-art systems that depend on the standard deviation (a.k.a. SDS) as discussed in the introduction section. Section 5.1, Section 5.2, Section 5.3 and Section 5.4 show the results of the evaluated systems separately. Section 5.5 discusses and compares the results of all the systems. Finally, Section 5.6 presents the results of the optimized ORB system.
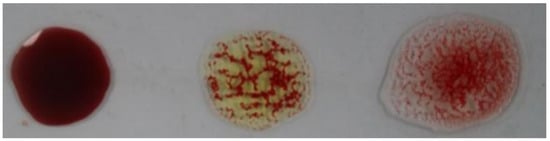
Figure 15.
An example of an input image.
5.1. Simulation Results for the SDS
In this system, the standard deviation was extracted after preprocessing the input image in order to identify the agglutination. A threshold of 16 was used to discriminate between agglutinated and nonagglutinated samples according to the systems proposed in [1,5,6].
Table 5 shows the confusion matrix for the results of the SDS for 1500 patches including true positive (TP = 556), true negative (TN = 326), false positive (FP = 375), and false negative (FN = 243) samples. A true positive of 556 means that the system could identify 556 positive samples (with agglutination) correctly out of 799 actual positive samples (P = 799). The same explanation applies to the remaining three parameters and negative (N) samples. Different measures were extracted from the confusion matrix to evaluate the SDS algorithm as shown in Table 6 [40]. They include:

Table 5.
Confusion matrix for the SDS over the 1500 patches.

Table 6.
Evaluation measures for the SDS over the 1500 patches.
- Accuracy
- Error rate
- Sensitivity
- Specificity
- Precision
- F-score
As explained in Section 4.1, the input image sample was partitioned into three patches containing three blood spots. Any wrong classification in one of the three patches results in wrong classification of the input sample. The high error rate of the SDS algorithm supports claims in Section 2.2 that the standard deviation cannot be considered as a discriminant feature. However, this was not reported by the state-of-the-art studies, since those used a low number of samples that did not cover all the variations in agglutination patterns. All of the evaluation measures of the SDS system were low, which reveals the weakness of the SDS in agglutination recognition. The results also indicate that the recognition rate of the negative samples (specificity) is much lower than the rate of the positive samples (sensitivity). The evaluation measures for the SDS show an accuracy of over the 500 samples.
The average processing time required to determine the blood type for each sample is about 80 ms.
5.2. Simulation Results for the SIFT
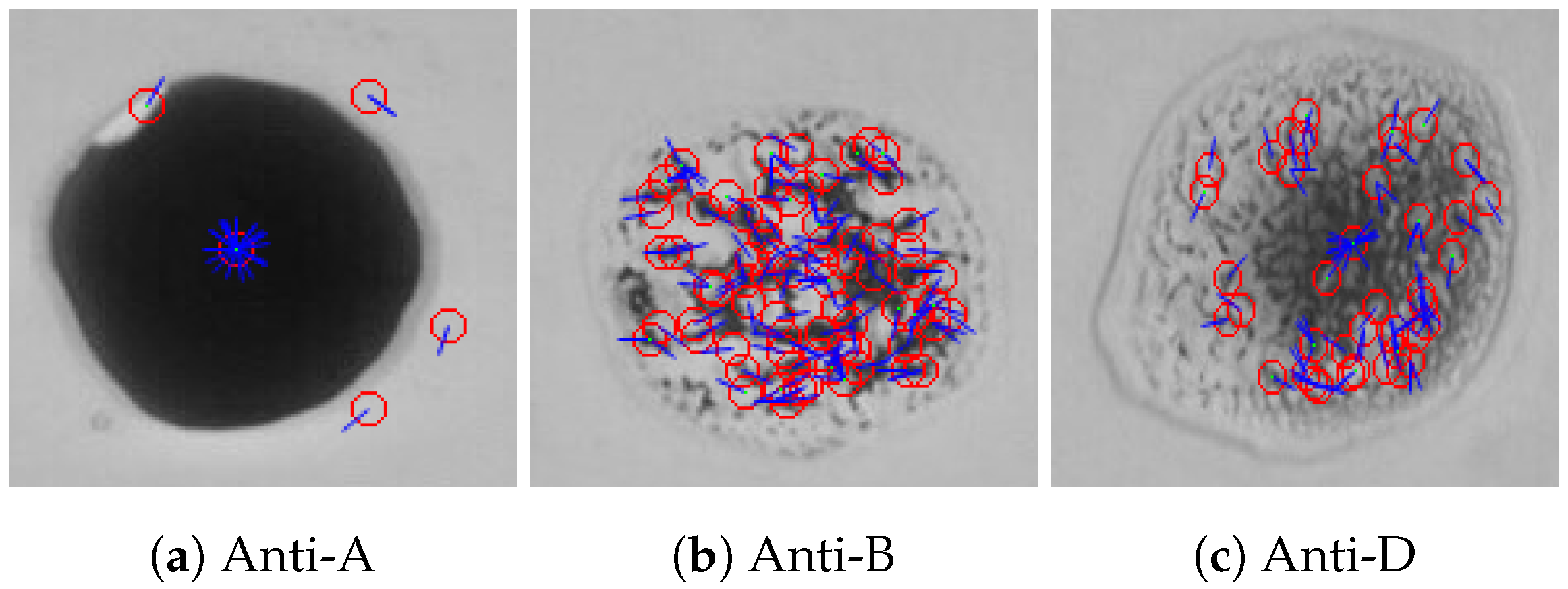
To detect the agglutination formed in a given blood sample using the SIFT algorithm, a comparison between the reference blood image shown in Figure 13 and the input blood sample is made. When SIFT algorithm is applied to the reference image, the feature points and the orientation vectors are extracted. The feature points are represented by red circles, while the orientation vectors are represented by blue lines as shown in Figure 16. Figure 17 shows the feature points and their orientation vectors for an example of an input blood sample image as well. Similarly, when the SIFT algorithm is applied to the blood spot mixed with anti-A, it can be noticed that the SIFT algorithm is sensitive to variations in brightness. As a result, some fault feature points will appear due to the high brightness. The effect of these fault feature points will be minimized later after applying matching. The blood spot that is mixed with anti-B has 64 feature points, whereas the blood spot mixed with anti-D has 28 feature points. After extracting feature points descriptors of both images, the comparison is performed by calculating the Euclidean distance between each spot of the input image and the reference image. The decision is made based on the ratio between the shortest Euclidean distance and the second shortest, which is chosen to be 0.9 according to our experimental evaluation. Then, the resulting matching points for each blood spot of the input image were: no matching points for the anti-A spot, 34 matching points for the anti-B spot, and 12 matching points for the anti-D section. Therefore, the blood type is classified as B+.
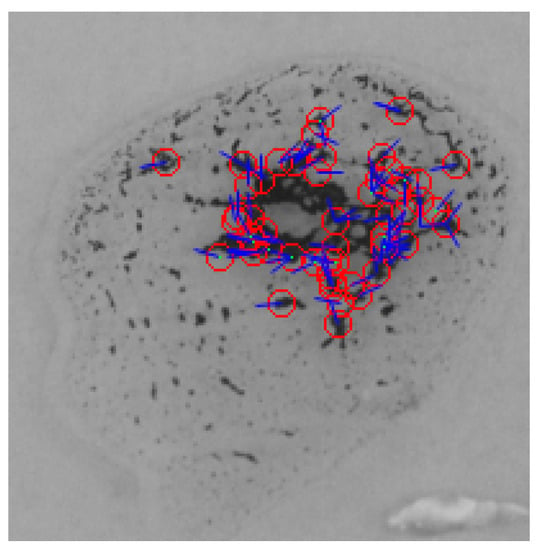
Figure 16.
Features points and its orientation for the reference image using SIFT algorithm.
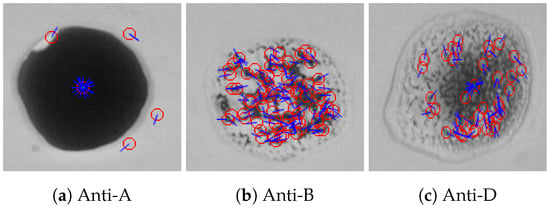
Figure 17.
Feature points and their orientation for three blood spots (anti-A, anti-B, and anti-D) of an example of a blood sample using the SIFT algorithm.
The confusion matrix and the evaluation measures of the SIFT are shown in Table 7 and Table 8. It can be observed that the results of the SIFT were improved compared with SDS. The improvement of the SIFT evaluation over SDS evaluation was about 10 percent points for all of the evaluation measures, which reflects an improvement in agglutination detection. The specificity is also lower by about 25% than the sensitivity because the decision of the SIFT is easily affected by noise and variations in the brightness. The percentage of error in blood type detection over the 500 samples is . However, this is not acceptable for blood typing. Simulation results also showed that SIFT requires a relatively long processing time, where the average processing time required for each sample is s.

Table 7.
Confusion matrix for the SIFT over the 1500 patches.

Table 8.
Evaluation measures for the SIFT over the 1500 patches.
5.3. Simulation Results for the SURF Algorithm
The SURF algorithm was also used in our evaluation for agglutination detection in blood samples. Figure 18 shows feature points matching according to Euclidean distance between the sample image shown in Figure 15 and the reference image in Figure 13. The confusion matrix was extracted for the SURF algorithm using the 1500 patches as shown in Table 9; the evaluation measures are listed in Table 10. The results revealed significant improvement in the accuracy compared to those of the SIFT algorithm because it is less sensitive to the variation in the brightness. Although the specificity was improved, the results indicate poor performance in detecting positive samples (the existence of the agglutination), where the sensitivity is . For the 500 samples, it was able to detect the blood type correctly for a larger number of samples than the SIFT, where the percentage error is . An additional improvement was the shorter processing time compared to the SIFT algorithm, where the average execution time per sample is s.

Figure 18.
Feature points matching between a blood sample the reference image for the three blood spots (anti-A, anti-B, and anti-D) using the SURF algorithm.

Table 9.
Confusion matrix for the SURF algorithm over the 1500 patches.

Table 10.
Evaluation measures for the SURF algorithm over the 1500 patches.
5.4. Simulation Results for the ORB Algorithm
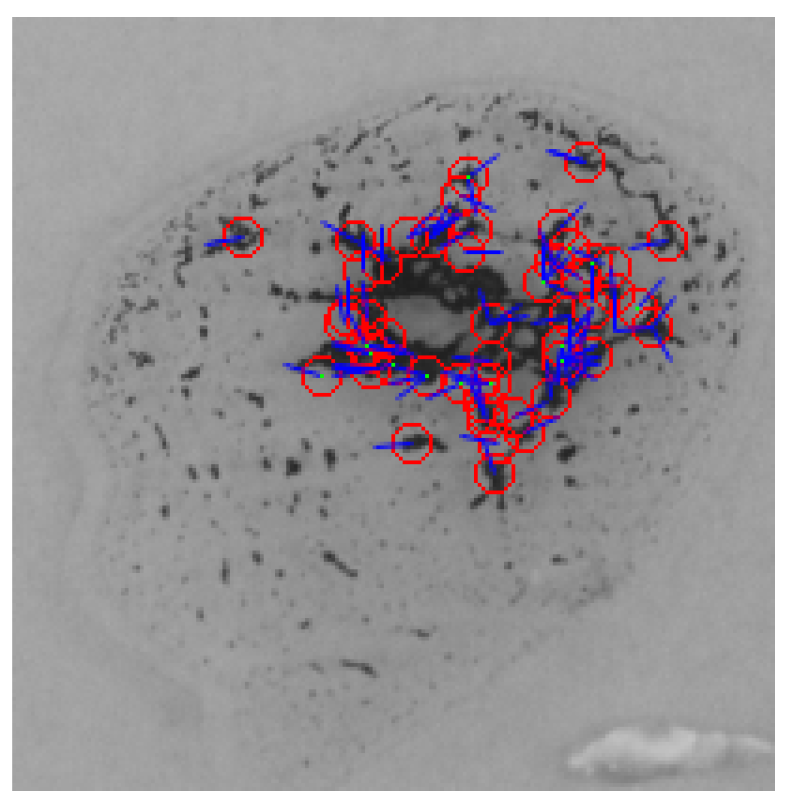
In the ORB algorithm, the feature points were also extracted for both the input and the reference images in addition to their binary descriptors. The ORB algorithm proceeds by feature matching based on the Hamming distance between the corresponding descriptors. Figure 19 shows that there are no matching points between the sample image and the anti-A spot, 13 matching points with the anti-B spot, and 5 matching points with the anti-D spot. According to the experimental results, a minimum of two matching points between the reference image and the blood spot are required to detect the agglutination.

Figure 19.
Feature points matching between a blood sample and the reference image for the three blood spots (anti-A, anti-B, and anti-D) using the ORB algorithm.
Table 11 demonstrates the confusion matrix extracted from the results of ORB algorithm for the 1500 blood spots, in addition to the corresponding evaluation measures in Table 12. The results revealed a large improvement in all of the evaluation measures compared to the SDS, the SIFT, and the SURF algorithms. This improvement was due to the fact that the ORB algorithm detects only the major feature points that are mostly located inside the object of interest. However, the sensitivity was less than the specificity for the ORB algorithm. In some samples, relatively low sensitivity can be noticed because the ORB algorithm fails to detect positive agglutination, especially positive Rh agglutination, as shown in Table 13. For example, in detecting A+ group samples, 3 samples were predicted as A− and 10 samples as O−. In detecting O+ group samples, 5 O+ samples were estimated falsely as O−. To reduce the percentage of error in detecting positive agglutination, another reference image is added to optimize the ORB algorithm and results in better estimation of blood type, as detailed in Section 5.6. The accuracy of blood typing for the 500 blood samples is , where it was able to determine the type of a total of 470 samples correctly. The average execution time per sample is s. The results of the ORB algorithm showed a considerable improvement for both accuracy and processing time.

Table 11.
Confusion matrix for the ORB algorithm over the 1500 patches.

Table 12.
Evaluation measures for the ORB algorithm over the 1500 patches.

Table 13.
Confusion matrix for the ORB algorithm over the 500 blood samples.
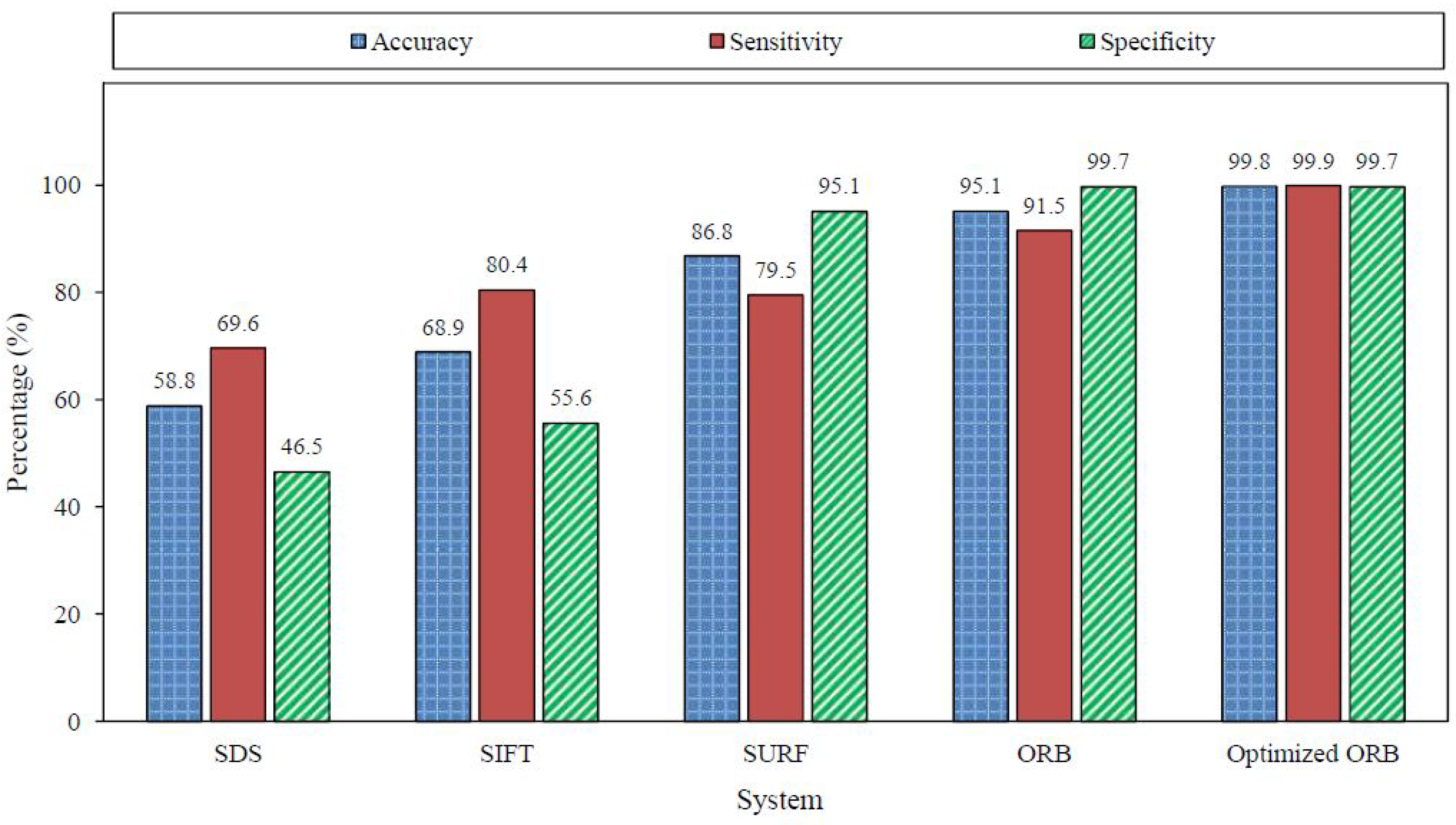
5.5. Comparison Between All of the Systems
A comparison between the SDS, the ORB, the SURF, and the SIFT systems for automatic blood type determination is provided in Table 14. The SDS has the shortest processing time due to the simplicity of the implementation. However, it is an inappropriate choice for blood determination due to its low accuracy. The number of matching points detected by the ORB algorithm is the fewest among the matching algorithms. This is due to the fact that the ORB algorithm features are mostly concentrated in objects at the center of the image, whereas the keypoint detectors in the SURF and SIFT algorithms are distributed over the entire image. Hence, the processing time of the ORB algorithm is shorter than the processing times of both the SIFT and SURF algorithms. Shorter processing time is an advantage for the algorithm to perform the blood typing quickly, especially in emergency situations. The most important issue in the evaluation results is the accuracy of blood typing. It is clear that the ORB system has the highest accuracy among other systems with a reasonable processing time. Therefore, it is the best system that can be used for blood typing.

Table 14.
Results comparison between the SDS, SIFT, SURF, and ORB systems over the 500 blood samples.
5.6. ORB Results Optimization
As this research aims to build an accurate blood typing system to reduce human error, the reduction in thr error rate of the ORB algorithm is the target of this subsection. According to Table 11 and Table 12, the error rate is affected by wrong detection of positive samples that can also be noticed by low sensitivity. It was observed that the misclassification comes from the determination of the Rh type because the agglutination pattern differs slightly from the anti-A and the anti-B patterns. Therefore, another reference image related to the anti-D transfusion was added to optimize the Rh type determination results, as shown in Figure 20. An example of the effect of adding the new reference is shown in Figure 21, where the agglutination was not detected using the original reference image (no matching points), while it was detected using the new one (19 matching points).
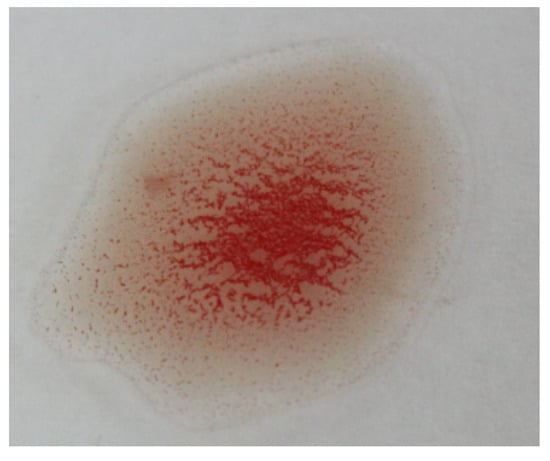
Figure 20.
The additional reference agglutination image used in matching to optimize ORB results.

Figure 21.
Matching with the old reference image.
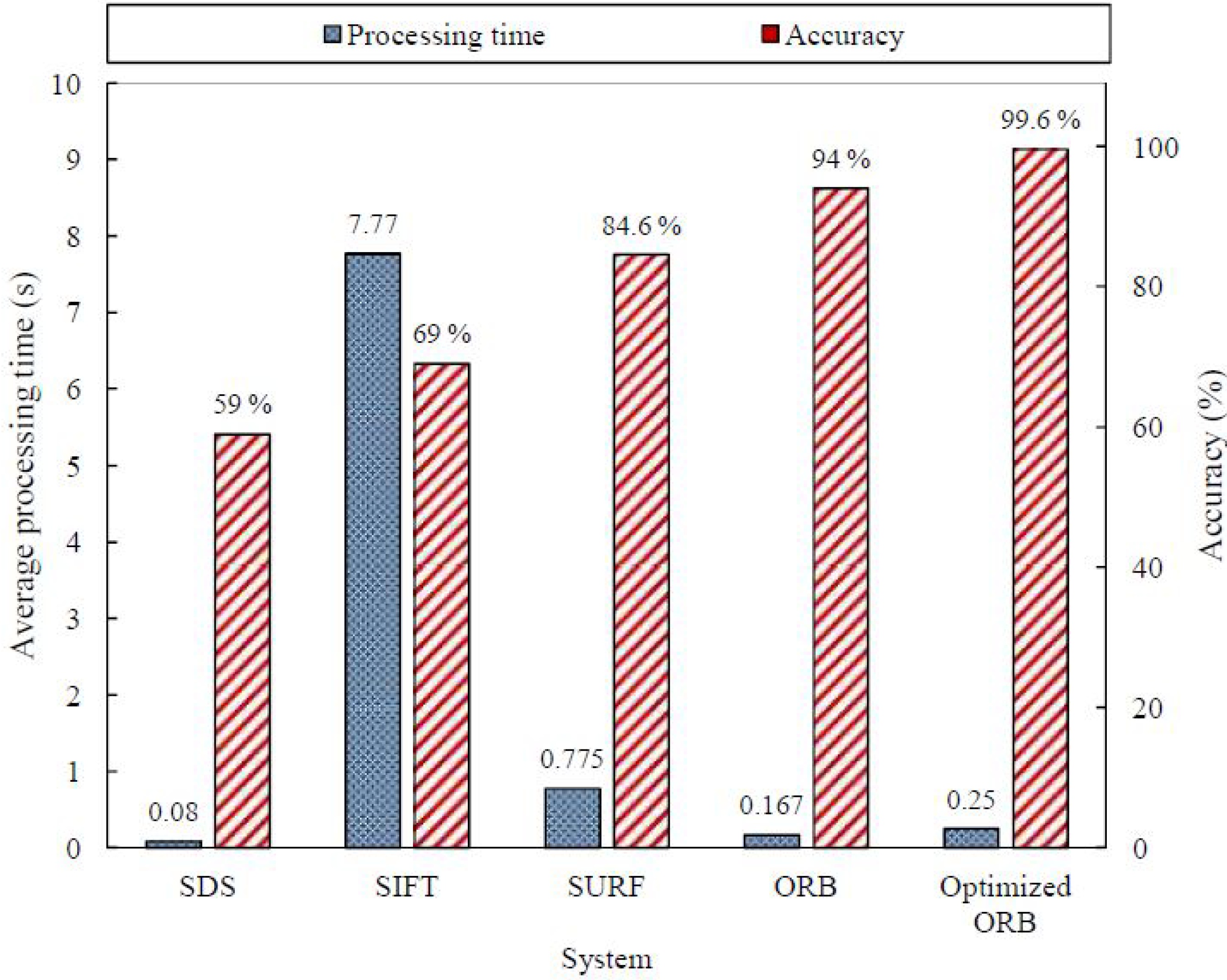
The confusion matrix of the optimized ORB system is shown in Table 15; the extracted measures are listed in Table 16. The effect of adding another reference image is obvious in the improved accuracy from for the ORB algorithm to for the optimized version. The improvement was specific in detecting the existence of agglutination (i.e., positive patches). The sensitivity was increased from to . The optimized ORB results revealed significant improvement in the right prediction of the blood types, as illustrated in Table 17. As a result, the optimized ORB system succeeded in determining the blood type of 498 blood samples out of the 500 sample with an accuracy of . The average processing time slightly increased to s per sample, but it was still considered reasonable. Figure 22 summarizes the results of the evaluated algorithms discussed in the subsections above. Figure 23 displays the average processing time and the accuracy of the evaluated systems over the 500 blood samples. The SDS algorithm is the fastest algorithm with an average processing time of s, but it has the lowest accuracy. However, the optimized ORB system has the highest accuracy with shorter processing time compared to the SIFT and SURF algorithms, but its processing time is s more than that of the ORB algorithm.

Table 15.
Confusion matrix for the optimized ORB algorithm over the 1500 patches.

Table 16.
Evaluation measures for the optimized ORB algorithm over the 1500 patches.

Table 17.
Confusion matrix for the optimized ORB algorithm over the 500 blood samples.
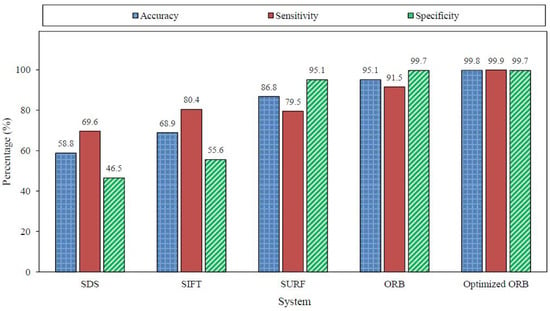
Figure 22.
Results summary for the evaluated systems over the 1500 patches.
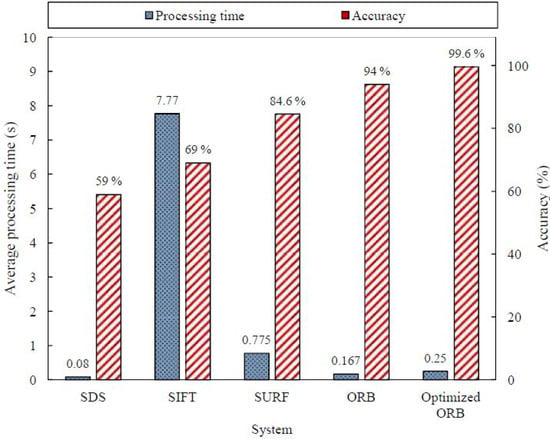
Figure 23.
Results summary for the evaluated systems over the 500 samples.
6. Conclusions and Future Work
In this paper, an automated system was created adopting the ORB algorithm in order to provide an accurate diagnostic support for blood type determination. The designed system proved that it is invariant to the variations of the brightness and can detect different agglutination patterns. Furthermore, it provides the results with short time and a high accuracy of . The system was evaluated using a total of 500 different images that were partitioned into 1500 images of blood spots. It was compared with other systems based on the standard deviation, the SIFT algorithm, and the SURF algorithm. The evaluation showed that the approaches have an accuracy of , , , and , respectively, and an average processing time of , , , and s, respectively. The ORB algorithm was further optimized in order to improve accuracy from to while sacrificing the addition of 83 ms.
As for future work, a user-friendly mobile application will be developed based on the optimized ORB algorithm to completely dispense with the PC to analyze blood images. This application will help the laboratory technicians and civil defense paramedics to automatically determine blood type with high accuracy and short time avoiding human error. The application could be connected to a centralized database in order to collect medical information for people in Palestine. The database could be accessed by hospitals and medical centers to provide vital information in a short amount of time.
Author Contributions
Conceptualization, N.O. and F.M.; methodology, N.O., F.O. and M.S.; software, N.O., F.O. and M.S.; validation, A.T. and N.O.; formal analysis, N.O.; investigation, F.O. and M.S.; resources, N.O.; data curation, N.O., F.O. and M.S.; writing—original draft preparation, N.O., F.M. and Y.D.; writing—review and editing, A.T., N.O., F.M. and Y.D.; visualization, N.O. and A.T.; supervision, N.O. and F.M.; project administration, N.O.; funding acquisition, N.O., F.M. and Y.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Deanship of Scientific Research at An-Najah National University, grant number ANNU-1920-Sc001.
Institutional Review Board Statement
Ethical review and approval were waived for this study, due to the fact that the blood samples were collected anonymously. No identification or personal information were recorded.
Informed Consent Statement
Patient consent was waived due to the fact that the blood samples were collected anonymously. No identification or personal information were recorded.
Data Availability Statement
Data available in a publicly accessible repository that does not issue DOIs. This data can be found here: https://earchive.najah.edu/media-email-link/88533?expires=1630145030&signature=aa69219224041d314ab7289de51f333d97462e2912a6df1b31de83 8585bd9cd4.
Acknowledgments
The authors would like to express their deep gratitude for the deanship of scientific research at An-Najah National University for their generous funding to support this research under Grant ANNU-1920-Sc001. The authors are also grateful to the lab technicians at An-Najah National University Hospital for their help in providing the test blood samples and their valuable assistance in blood type determination.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SIFT | Scale invariant feature transform |
| SURF | Speed-up robust feature |
| ORB | Oriented fast and rotated brief |
| FAST | Feature from accelerated segment test |
| BRIEF | Binary robust independent elementary features |
| rBRIEF | Rotated BRIEF |
| ROI | Region of interest |
| DoG | Difference of Gaussian |
| IC | Intensity centroid |
| SD | Standard deviation |
| SDS | Standard deviation system |
References
- Ferraz, A.; Carvalho, V.; Soares, F. Development of a human blood type detection automatic system. Procedia Eng. 2010, 5, 496–499. [Google Scholar] [CrossRef]
- Selvakumari, T. Blood group detection using fiber optics. Armen. J. Phys. 2011, 4, 165–168. [Google Scholar]
- Karuppiah, T.; Periyasamy, A.; Gopinath, S.; Anandaraj, V. Experimental analyze of identification of blood samples using the light sensor. AIP Conf. Proc. 2019, 140011. [Google Scholar]
- Ferraz, A.; Carvalho, V.; Soares, F.; Leão, C.P. Characterization of blood samples using image processing techniques. Sens. Actuators A Phys. 2011, 172, 308–314. [Google Scholar] [CrossRef]
- Talukder, M.H.; Reza, M.M.; Begum, M.; Islam, M.R.; Hasan, M.M. Improvement of Accuracy of Human Blood Groups Determination using Image processing Techniques. Int. J. Adv. Res. Comput. Commun. Eng. 2015, 10, 411–412. [Google Scholar] [CrossRef]
- Dong, Y.F.; Fu, W.W.; Zhou, Z.; Chen, N.; Liu, M.; Chen, S. ABO blood group detection based on image processing technology. In Proceedings of the 2017 2nd International Conference on Image, Vision and Computing (ICIVC), Chengdu, China, 2–4 June 2017; pp. 655–659. [Google Scholar]
- Panpatte, S.G.; Pande, A.S.; Kale, R.K. Application of Image Processing for Blood Group Detection. Int. J. Electron. Commun. Soft Comput. Sci. Eng. 2017, 61–65. [Google Scholar]
- Dhande, A.; Bhoir, P.; Gade, V. Identifying the blood group using Image Processing. Int. Res. J. Eng. Technol. 2018, 5, 2639–2642. [Google Scholar]
- Jana, S.; Reddy, N.S.; Gopi, K. Novel Image Based Blood Group Identification from Agglutinated Images. Int. J. Recent Technol. Eng. 2019, 8, 2210–2214. [Google Scholar]
- Fernandes, J.; Pimenta, S.; Soares, F.O.; Minas, G. A complete blood typing device for automatic agglutination detection based on absorption spectrophotometry. IEEE Trans. Instrum. Meas. 2014, 64, 112–119. [Google Scholar] [CrossRef]
- Cruz, J.C.D.; Garcia, R.G.; Diaz, A.V.C.; Diño, A.M.B.; Nicdao, D.J.I.; Venancio, C.S.S. Portable Blood Typing Device Using Image Analysis. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics-Asia (ICCE-Asia), Bangkok, Thailand, 12–14 June 2019; pp. 141–145. [Google Scholar]
- Yayla, M.; Toma, A.; Chen, K.H.; Lenssen, J.E.; Shpacovitch, V.; Hergenröder, R.; Weichert, F.; Chen, J.J. Nanoparticle classification using frequency domain analysis on resource-limited platforms. Sensors 2019, 19, 4138. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Su, H.; Zhong, C.; Meng, Z.; Luo, H.; Li, X.; Tang, Y.Y.; Lu, Y. Hyperspectral image classification using wavelet transform-based smooth ordering. Int. J. Wavelets Multiresolut. Inf. Process. 2019, 17, 1950050. [Google Scholar] [CrossRef]
- Zheng, X.; Tang, Y.Y.; Zhou, J. A framework of adaptive multiscale wavelet decomposition for signals on undirected graphs. IEEE Trans. Signal Process. 2019, 67, 1696–1711. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Cheung, Y.m.; You, X.; Tang, Y.Y. Efficient single image dehazing and denoising: An efficient multi-scale correlated wavelet approach. Comput. Vis. Image Underst. 2017, 162, 23–33. [Google Scholar] [CrossRef]
- Guariglia, E.; Silvestrov, S. Fractional-Wavelet Analysis of Positive definite Distributions and Wavelets on D’(C). In Engineering Mathematics II; Springer: Berlin/Heidelberg, Germany, 2016; pp. 337–353. [Google Scholar]
- Guariglia, E. Primality, fractality, and image analysis. Entropy 2019, 21, 304. [Google Scholar] [CrossRef]
- Tang, Y.Y. Document Analysis and Recognition with Wavelet and Fractal Theories; World Scientific: Singapore, 2012; Volume 79. [Google Scholar]
- Rathod, A.; Pathan, A. Determination and Classification of Human Blood Types using SIFT Transform and SVM Classifier. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2016, 5, 8467–8473. [Google Scholar]
- Sahastrabuddhe, A.P.; Ajij, S.D. Blood group detection and RBC, WBC counting: An image processing approach. Int. J. Eng. Comput. Sci. 2016, 5, 18635–18639. [Google Scholar]
- Karami, E.; Prasad, S.; Shehata, M. Image matching using SIFT, SURF, BRIEF and ORB: Performance comparison for distorted images. arXiv 2017, arXiv:1710.02726. [Google Scholar]
- Daniels, G. Human Blood Groups; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Van Gool, L. Surf: Speeded up robust features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 404–417. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Brown, M.; Lowe, D.G. Invariant features from interest point groups. In BMVC; BMVA Press: Cardiff, UK, 2002; Volume 4, pp. 23.1–23.10. [Google Scholar]
- Hu, X.; Tang, Y.; Zhang, Z. Video object matching based on SIFT algorithm. In Proceedings of the 2008 International Conference on Neural Networks and Signal Processing, Nanjing, China, 7–11 June 2008; pp. 412–415. [Google Scholar]
- Huang, H.; Guo, W.; Zhang, Y. Detection of copy-move forgery in digital images using SIFT algorithm. In Proceedings of the 2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application, Wuhan, China, 19–20 December 2008; Volume 2, pp. 272–276. [Google Scholar]
- Singla, S.; Sharma, R. Medical image stitching using hybrid of sift & surf techniques. Int. J. Adv. Res. Electron. Commun. Eng. 2014, 3, 838–842. [Google Scholar]
- Pinto, B.; Anurenjan, P. Video stabilization using speeded up robust features. In Proceedings of the 2011 International Conference on Communications and Signal Processing, Kerala, India, 10–12 February 2011; pp. 527–531. [Google Scholar]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded-up robust features (SURF). Comput. Vis. Image Underst. 2008, 110, 346–359. [Google Scholar] [CrossRef]
- Huijuan, Z.; Qiong, H. Fast image matching based-on improved SURF algorithm. In Proceedings of the 2011 International Conference on Electronics, Communications and Control (ICECC), Ningbo, China, 9–11 September 2011; pp. 1460–1463. [Google Scholar]
- Rosten, E.; Drummond, T. Machine learning for high-speed corner detection. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; pp. 430–443. [Google Scholar]
- Harris, C.G.; Stephens, M. A combined corner and edge detector. In Alvey Vision Conference; Citeseer: Londen, UK, 1988; Volume 15, pp. 10–5244. [Google Scholar]
- Rosin, P.L. Measuring corner properties. Comput. Vis. Image Underst. 1999, 73, 291–307. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 778–792. [Google Scholar]
- Fanqing, M.; Fucheng, Y. A tracking algorithm based on ORB. In Proceedings of the 2013 International Conference on Mechatronic Sciences, Electric Engineering and Computer (MEC), Shenyang, China, 20–22 December 2013; pp. 1187–1190. [Google Scholar]
- Facts About Blood and Blood Types, Red Cross Blood Services. Available online: https://www.redcrossblood.org/donate-blood/blood-types.html (accessed on 6 May 2021).
- MATLAB, version: 9.0.0.341360 (R2016a); The MathWorks Inc.: Natick, MA, USA, 2016.
- Han, J.; Kamber, M.; Pei, J. Data mining concepts and techniques third edition. Morgan Kaufmann Ser. Data Manag. Syst. 2011, 5, 83–124. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).