Statistical Analysis of Tritium Breeding Ratio Deviations in the DEMO Due to Nuclear Data Uncertainties

Abstract

For the stable and self-sufficient functioning of the DEMO fusion reactor, one of the most important parameters that must be demonstrated is the Tritium Breeding Ratio (TBR). The reliable assessment of the TBR with safety margins is a matter of fusion reactor viability. The uncertainty of the TBR in the neutronic simulations includes many different aspects such as the uncertainty due to the simplification of the geometry models used, the uncertainty of the reactor layout and the uncertainty introduced due to neutronic calculations. The last one can be reduced by applying high fidelity Monte Carlo simulations for TBR estimations. Nevertheless, these calculations have inherent statistical errors controlled by the number of neutron histories, straightforward for a quantity such as that of TBR underlying errors due to nuclear data uncertainties. In fact, every evaluated nuclear data file involved in the MCNP calculations can be replaced with the set of the random data files representing the particular deviation of the nuclear model parameters, each of them being correct and valid for applications. To account for the uncertainty of the nuclear model parameters introduced in the evaluated data file, a total Monte Carlo (TMC) method can be used to analyze the uncertainty of TBR owing to the nuclear data used for calculations. To this end, two 3D fully heterogeneous geometry models of the helium cooled pebble bed (HCPB) and water cooled lithium lead (WCLL) European DEMOs were utilized for the calculations of the TBR. The TMC calculations were performed, making use of the TENDL-2017 nuclear data library random files with high enough statistics providing a well-resolved Gaussian distribution of the TBR value. The assessment was done for the estimation of the TBR uncertainty due to the nuclear data for entire material compositions and for separate materials: structural, breeder and neutron multipliers. The overall TBR uncertainty for the nuclear data was estimated to be 3~4% for the HCPB and WCLL DEMOs, respectively.

1. Introduction

The propagation of a nuclear response’s uncertainty in fusion-related neutronic simulations is an area of intense research activity because this information enables an assessment of the safety margins of the results. The complexity of the fusion facilities and geometry models used for the simulations defines the necessity of the fidelity assessment for the results obtained due to the inherent uncertainty of the nuclear data involved in the calculations. The evaluation of the nuclear reaction data includes natural uncertainty due to (i) nuclear model parameter deviations and (ii) the uncertainty of the experimental data used for the assessments. Modern nuclear data evaluations include as a prerequisite the uncertainty of all reaction cross sections presented in the form of covariance matrixes. Various nuclear reactions’ particle emission spectra have different uncertainties in different energy regions depending on the model’s parameter deviations and the availability of the experimental database. Thereby, for some reactions, the estimated uncertainty can vary from a few up to dozens of percent in different energy regions. Assuming that the typical material compositions used in the fusion technology can include many chemical elements, the number of nuclear data uncertainties that can be involved in the calculations becomes big.

To perform the assessment of the integral nuclear response’s uncertainty due to nuclear data, the covariance matrixes presented in the evaluated data files involve making use of the sophisticated mathematical approach, such as perturbation theory, which must be included in the particle transport code [1]. The MCNP code [2] adopted as a standard computer tool for fusion applications does not include the possibility of invoking the full-scale use and processing of the covariance data during particle transport calculations with different neutron sources. Instead, a simplified adjoint-weighted perturbation method is implemented in the MCNP to access changes in k_eff due to material substitution or to calculate sensitivity coefficients of the k_eff for nuclear data [2]. This approach implies several significant simplifications of covariance data and it treats the uncertainty of the particle emission spectra (differential and double differential) in a very approximate way or even neglects them. An alternative way to calculate the propagation of the nuclear data uncertainty in a realistic 3D large-scale geometry is to apply Monte Carlo analyses utilizing intensive computer simulations, the so-called total Monte Carlo (TMC) approach [3,4,5,6]. It assumes using not one set of nuclear data files included in the evaluated data library but thousands of such data sets, all of them derived from the same original library using perturbation theory. An important note here is that all random data files for one isotope used in the calculations were produced making use of the nuclear models’ parameters, obeying normal distribution, deviating from the most probable one within the accepted range and therefore all these files are equivalent, and they can be also used in the usual way for particle transport simulations. By randomly choosing one set of data from the thousand possible ones, an MCNP run can be started as the result of one requested integral nuclear response, for example, the tritium breeding ratio (TBR) in a fusion reactor. The multiple repetition of this procedure ultimately results in the probability distribution of the integral nuclear response in the large-scale system. If results can be fitted with Gaussian distribution, i.e., they obey normal distribution, the most probable value of the integral nuclear response and the standard deviation of the results can also be obtained.

The assessment of the TBR uncertainty only for Pb cross sections ((n,2n), (n,el) and (n,n′)) in the HCLL DEMO concept [7], performed utilizing TMC approach, demonstrated its applicability for the fusion reactor. The results obtained are based on the variation of only three reaction channels and only for four Pb isotopes, neglecting other materials, especially steel and lithium, as well the secondary particle emission spectra. Even in spite of significant simplifications, the TBR uncertainty for the nuclear data ΔTBR_nd was reasonably assessed by ~1.2%. In the present work, the emphasis is on a more general and flexible method. In the case that a powerful “brute computer force” is available and accessible for numerous MCNP calculations, the most complicated issue in the whole task is the preparation of the random data sets for the MCNP calculations. To this end, one can utilize available data libraries with (if any) random files generated during library development or it is possible to derive these files from the “mother” library.

The demonstration fusion reactor (DEMO) [8], developed within the EUROfusion R&D program, is driven by deuterium–tritium (D-T) fusion reaction. As tritium is not available in the nature, it must be supplied through a generation (breeding) in breeder blankets surrounding plasma and provided to the tritium fuel cycle. The tritium generation must be demonstrated to exceed unity per one plasma source neutron with a certain safety margin TBR_target = 1.05 [8] to ensure the self-sufficiency of the DEMO functioning. This target TBR serves as a basic assessment of the DEMO blanket efficiency to ensure the tritium production sufficient for the DEMO continuous operation. The ΔTBR excess over the target value accounts for uncertainties coming from diverse adopted assumptions made in the DEMO project to enable the blanket development without inclusions of not well-known features and not enough elaborated sophisticated engineering solutions. Due to the importance of this integral response, its computation must be performed with high-fidelity, including the assessment of its uncertainty. In this work, the uncertainty of the TBR coming from the nuclear data involved in the calculations is performed for different DEMO concepts by means of the real-scale 3D calculations using the MCNP code. The work aims at quantifying this effect, making use of the TMC method with the goal to provide a justified assessment of the TBR deviation to meet the tritium breeding requirements [8]. In the present R&D work within EUROfusion, no effect of the nuclear data to the TBR_req assessment is adopted to assign additional TBR uncertainty for the nuclear data ΔTBR_nd.

2. DEMO Neutronics Model

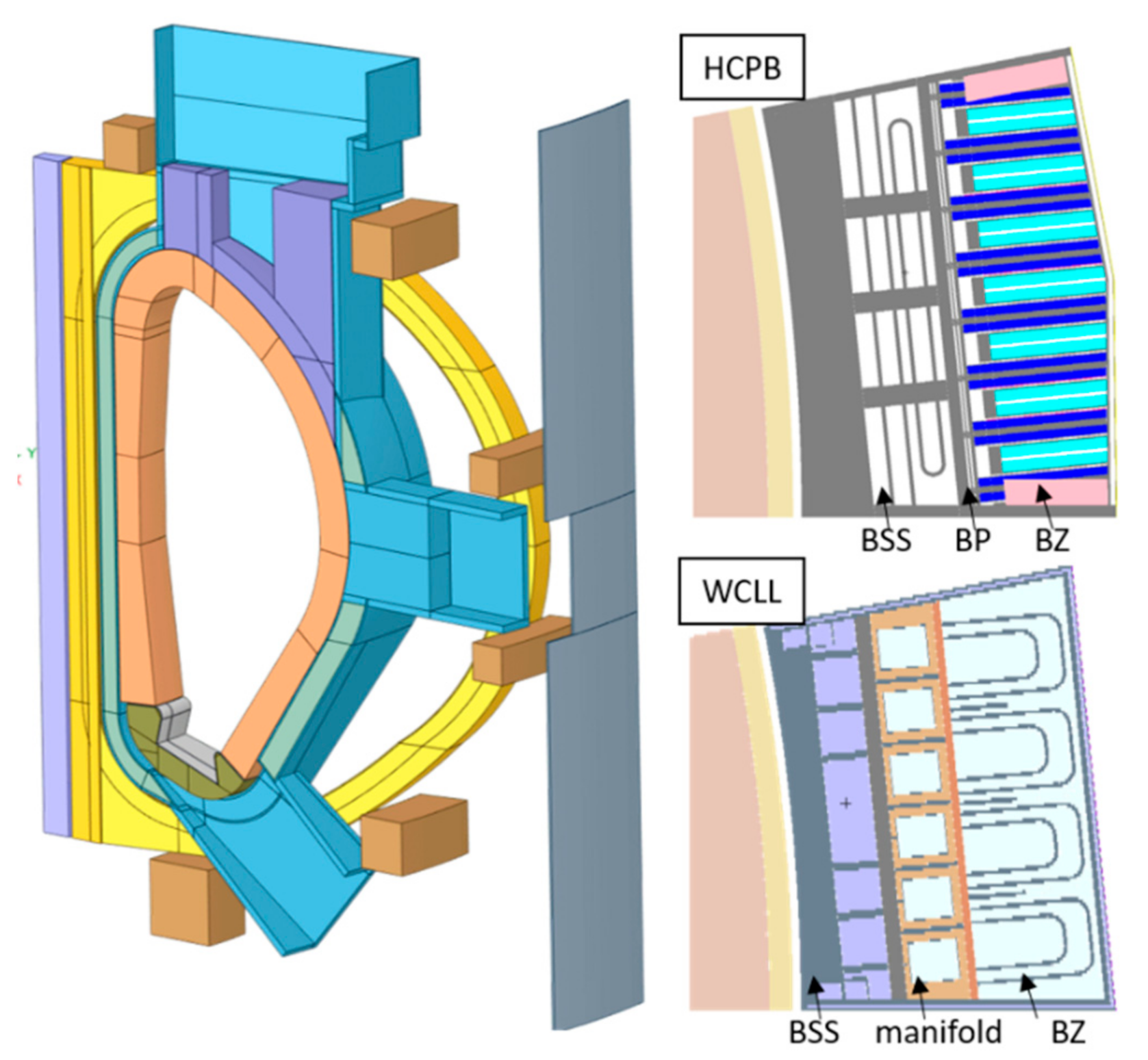
For the simulations with the MCNP code, two DEMO blanket concepts were considered: HCPB [9] and WCLL [10]. Both concepts utilize the same DEMO Base line model 2017 [11] that serves as a common basis for the integration of the breeder blankets. This model consists of 16 sectors toroidally repeated to build the DEMO tokamak. For the geometry modelling, a 22.5° sector was retrieved from the DEMO Base line CAD design. For the MCNP calculation, half of this segment (11.25°) sector is used assuming its toroidal symmetry in the tokamak and reflecting boundary conditions.

The breeder blankets in both concepts utilize the same single module segmentation (SMS) technology involving the arrangement of one inboard (IB) and one and a half outboard (OB) blanket modules in the 11.25° geometry segment. The current HCPB DEMO design implies the use of the mixed Li₄SiO₄ plus 37 mol.% of Li₂TiO₃ with 60% ⁶Li enrichment breeder material [9]. The breeder ceramic is enclosed in radial breeder pins arranged in the hexagonal lattice. The space around the pins is filled with Be₁₂Ti hexagonal prismatic blocks serving as a neutron multiplier. The cooling of the HCPB blanket is provided by 80 bar He coolant. The MCNP HCPB DEMO geometry model was generated making use of the McCad conversion tool [12], applying several geometry universes’ hierarchy and MCNP-repeated structure function resulting in the fully heterogeneous 3D geometry representation [13], as shown in Figure 1.

The WCLL blanket design [13] based on the implementation of a single module segmentation (SMS) conforms the dimensions of the breeder blanket space in the generic DEMO CAD model. The blanket U-shaped housing is 25 mm thick and attached to a massive back wall of 100 mm thickness that functions as a BSS. The blanket inner volume is filled by poloidally repeated so-called breeding elements, as shown in Figure 2. Water manifolds are located in front of the BSS and they feed with the FW and BZ with coolant. Arranged between BZ and water manifolds are the PbLi (90% ⁶Li) manifolds, feeding the BZ. Inlet and outlet PbLi channels are separated by square-formed steel pipes. The BZ is strengthened by vertical and horizontal stiffening plates that also serve to confine the PbLi flow. The cooling of the BZ is ensured by high pressure water (155 bar) with 295 °C inlet and 328 °C outlet temperatures enclosed in double-wall U-shaped tubes of 13.5/8 mm (outer/inner) size, as shown in Figure 1. The FW cooling is provided by water at the same thermo-hydraulic conditions routed in 7 × 7 mm² square channels with 13.5 mm vertical pitch. All structural elements of the WCLL blanket are made of Eurofer steel.

The MCNP geometry models for DEMO concepts do not assume any cut-outs for the arrangement of the in-vessel components in the tokamak design such as limiters, diagnostic systems and plasma heating systems (Neutral Beam Injector and Electron Cyclotron antennas). It means that the current blanket design is not fully realistic and it permits the application of various cut-outs, negatively decreasing the TBR by the ΔTBR, assuming that the tritium breeding capability of the blanket is capable of compensating these effects. The assessed required TBR_req = TBR_target + ΔTBR should be at least 1.16 [14].

3. Nuclear Data

3.1. Basic Nuclear Data Libraries

For the analyses, several neutron transport libraries were used. including JEFF-3.2 [15], JEFF-3.3 [16] and TENDL-2017, 2019 [17,18]. JEFF-3.2 library does not include covariance data for all nuclides and the latest version JEFF-3.3 provides the complete covariance data for all included nuclides. The TENDL neutron data library contains high-quality evaluations generated on the basis of the TALYS code [19] and includes, for each target nuclide, the covariance data as well a big set of the additional random data files (up to 300) that were produced for each “standard” evaluation included in the library.

Materials included in the MCNP geometry models for the HCPB and WCLL DEMOs can be subdivided into three groups: structural materials that ensure the structural stability of the constructions, tritium breeding materials, and a neutron multiplier. In both breeder blanket concepts, the Eurofer steel serves as the main structural material. The tritium breeding material in both concepts is Li, which is included in the solid breeder ceramic composition of the HCPB (Li₄SiO₄ plus 37 mol.% of Li₂TiO₃) and in a PbLi liquid eutectic of the WCLL DEMOs. In both concepts, Li with special ⁶Li enrichment is used: in the former case, the ⁶Li enrichment is 60%—and 90% in the latter. The exact materials compositions used in the simulations are presented in [10,20].

3.2. Derived Nuclear Data

3.2.1. Random Files in the Nuclear Data Libraries

For the calculations with TMC, the availability of the random files for every nuclide used in the MCNP geometry model is a prerequisite for the correct assessment of the nuclear data effect for the integral nuclear response. The JEFF libraries do not include any random data files for the uncertainty calculations. Alternatively, the covariance data can be used to generate such files applying the special procedure described below. The TENDL-2017 and 2019 include a large amount of the evaluated data files, more than 2800 in both libraries, including isomeric targets. Additionally, these libraries provide random files for almost all target nuclides. These files were generated by random variations of the nuclear model parameters in the TALYS code within the predefined deviations. Every random file is suitable and valid for particle transport simulations. The TENDL-2017 includes 300~600 random files for O, Si, Fe. The latest version of TENDL-2019 provides 10~300 random files, for almost all target nuclides. For instance, for the most abundant in the Eurofer steel ⁵⁶Fe isotope, only 10 random files are presented in the library that is not sufficient for the accurate statistical calculations. Using covariance data similar to the JEFF library, the required number of random files can be generated also for the TENDL libraries for those nuclides where random files are absent or their number is not sufficient.

3.2.2. Generation of the Random Files Using Covariances

This procedure is based on the perturbation of the reaction cross sections stored in the nuclear data files utilizing the corresponding covariance matrixes information, i.e., variances and their correlations for different neutron energies. To generate an arbitrary number of the random nuclear data files, the following procedure was implemented:

(1)

For the processing of the original ENDF/B formatted nuclear data files, the NJOY code [21] was applied to restore the reaction cross sections and covariance matrixes for each target nuclide;

(2)

The Cholesky factorization of the covariance matrix into the product of a lower triangular matrix and its conjugate transpose for further Monte Carlo simulations is performed for each reaction;

(3)

Using the obtained triangular matrices, the reaction cross sections and resonance parameters was perturbed to generate a new set of the nuclear data [22];

(4)

The generated set of the data was recorded according the ENDF/B format utilizing an automated interface and a new random data file is generated for one target nuclide;

(5)

The whole procedure can be repeated arbitrary times (N) to generate N random nuclear data files starting with one basic file from the data library. The N value should be assessed within the TMC sensitivity analyses. This approach is realized in the computer code shell BEKED [23].

A similar approach was realized in the SANDY (Sampler of Nuclear Data and Uncertainty) code [24], which utilizes the basic theory of stochastic Monte Carlo sampling to propagate nuclear data covariances. SANDY also retrieves variance–covariance matrices from nuclear data files. The nuclear data are sampled into random sets according to the chosen multivariate probability density function for the uncertain variables. The random nuclear data produced in this way are written in the new perturbed file. By choosing the number of such files, a set of N random files is produced for every isotope of interest for further TMC computations.

3.2.3. Random Files for Lithium and Beryllium

The nuclear data for n+^6,7Li and n+⁹Be in modern nuclear data libraries, such as JEFF and TENDL, include many modifications and corrections because of the extreme complexity of such evaluations. The work was performed with the R-matrix theory including a processing of the available experimental data or with a Bayesian approach. The TENDL procedure to generate random files is not applicable for these nuclides because the nuclear models included in the TALYS code used for this purpose, if applied for calculations with such light targets, are out of the declared physical validity range, i.e., Z ≥ 6.

As the random files for Li and Be evaluations are not provided, they are generated utilizing the procedure and the codes described above. In the case of n+⁹Be, the original covariance data were used for the generation of the random files. The ⁶Li(n,t) evaluations were carefully checked and compared to the available experimental data. The results of the R-matrix calculations and the covariance matrix evaluation included in the JEFF-3.2 and −3.3 libraries provide reaction cross section uncertainty of ~0.1% up to 20 keV, 0.1 ÷ 1% from 20 keV to 1 MeV, 1 ÷ 3% from 1 to 3 MeV and 5% for the neutron energies from 3 to 20 MeV, as shown in Figure 2. The covariance data for ⁶Li(n,t) reaction were originally evaluated for the ENDF/B-VI library in early 1990. The descriptive information provided in the current evaluations recognizes them to be too small. To correct this, the variances were expanded by authors so that “approximately 2/3 of the future results should fall within these expanded uncertainties”. The uncertainties of ⁶Li(n,t) reaction were reevaluated and set up to 30% at 20 MeV [25]. These data were partially adopted in the latest ENDF/B-VIII library [26], as shown in Figure 2. The experimental results obtained within last 3 decades and shown in Figure 2 appeared not to be within these boundaries. To generate the random files, the ⁶Li(n,t) reaction uncertainties were expanded to account for the most relevant measurements, as shown in Figure 2. The latter set includes bigger uncertainties: ~10% for energies up to 1 keV, ~12% for energies 1 ÷ 100 keV and about 16% for energies from 100 keV to 20 MeV. These uncertainties were assessed making use of the pragmatic approach that provides a reasonable justification of the evaluated data deviations from the available experimental data.

4. Adjustment of the TMC Simulations

4.1. Methodology

The total Monte Carlo method (TMC) relies on the computer power that can be efficiently used as a driver for the uncertainty propagation calculations in the complex DEMO fusion facility. Within the TMC sampling cycle, the data files for each isotope included in the material card in the MCNP geometry model are randomly chosen from the set of hundreds of files provided for it, either in the TENDL library or generated with the codes described above. For the TMC run, a sample of the files is randomly chosen for the one MCNP run providing the TBR result. The TMC procedure is managed by a number of the repetitions to obtain the well-resolved probability distribution of the TBRs. The MCNP run itself can be also adjusted by the number of histories to ensure the required statistical accuracy of the MCNP result. To facilitate this time-consuming procedure, a Perl script was developed to automatically perform numerous manipulations with a large amount of data: (i) to pick up randomly chosen nuclear data files listed in the MCNP material specifications using a random number generator and to keep them in a separate folder; (ii) to modify the material cards in the MCNP input file and XSDIR file (specification of the nuclear data used for calculations) according the chosen set of files; and (iii) to run MCNP calculations, to select the TBR result and to prepare the summary of the TMC simulations.

4.2. Uncertainty of the MCNP Calculation

For the reliable justification of the TMC results, the number of particle histories in each MCNP run must be predefined by using a comparison of the TBR results. To this end, the number of the MCNP particle histories (source particles) varied from 1 × 10⁴ to 1 × 10⁷ for the TBR calculations using the HCPB DEMO geometry. A saturation of the TBR results was already achieved with 1 × 10⁶ source neutrons. The MCNP statistical uncertainty in such calculations does not exceed 0.1%. This number of particle histories was used in all TMC calculations.

4.3. Number of Random Files

The number of the random files generated for the TMC calculations can significantly affect final results and justifications. A special exercise was carried out to perform sensitivity analyses of the integral nuclear response (TBR) from the number of the random files for each isotope. The simulations were carried out with the HCPB DEMO geometry model described above and the TENDL-2017 nuclear data.

The TENDL-2017 provides 300 random files for most of the target nuclides. This number may already be insufficient to find the general trend of the TMC results with high enough statistics. The procedures based on the use of the BAKED and SANDY codes were implemented to generate two sets of 1000 random files from original TENDL-2017 library. A sequence of the TMC calculations were performed to study this effect with the variated number of the files for each nuclide starting from 10 up to 1000. The results of the TBR calculations for 300 and 1000 random files for each nuclide are shown in Figure 3 both for the SANDY- and the BAKED-based methods.

For the TMC, 10,000 iterations were chosen to obtain well-resolved TBR distributions. The probability distribution of the TBR integral response does not necessarily follow normal distribution. Being well fitted with Gaussian distributions, the results presented in Figure 3 provide the most probable TBR integral response. The results based on the SANDY calculations are slightly shifted to the lower TBR number compared to the BAKED-based ones and the difference does not exceed 0.2%. Due to the very low MCNP statistical uncertainty, the results shown in Figure 3 only reflect the uncertainty of the nuclear data used for the calculations.

Shown in Figure 4 are the results of the sensitivity analyses for the TBR as the function of the random files number for each isotope. Generally, the TBR appeared to be bigger for the small numbers of the random files. The saturation of the results was achieved with the random files number >150. For further TMC calculations, 300 random data files were used for each nuclide.

4.4. The TMC Sensitivity Calculations

The accuracy of the TMC method inherently depends on the number of Monte Carlo repetitions that naturally assumes a logical rule for its application: with more repetitions, the more accurate the final results will be. This reasonable approach can be applied until the gain in the accuracy of the TMC calculations exceeds the accuracy of the MCNP statistical calculations adopted in this work, i.e., 0.1%. This limit was used to assess the required number of the TMC cycles to get the TBR statistical distributions. To assess this number, several huge TMC runs were performed for 5000, 10,000 and 30,000 repetitions using the HCPB geometry model discussed above and 300 random files for each nuclide. Presented in Figure 5 are the statistical distributions of the TBR results obtained for these three cases. The presented results for each case were fitted by normal (Gaussian) distributions to obtain the most probable TBR response and a standard deviation σ. For 10,000 and 30,000 iterations, the mean TBR = 1.181 and the standard deviation in both cases is σ = 0.030. For less repetitions, the mean TBR is slightly less: TBR = 1.174 (σ ≈ 0.031). In all these cases, the standard deviation is almost the same but the mean TBR tends towards bigger numbers with an increase in the TMC repetitions. Therefore, the number of the TMC cycles affects the position of the maximum of the normal distribution, the most probable or mean TBR number, however, the effect for the standard deviation is not big. Nevertheless, the standard spread of the results is significant, assuming its final effect for the DEMO design. Hence, the final assessments of this effect should be carried out with the big enough TMC repetitions number, that is, at least 10,000, to ensure its justified quantification.

5. Results of the TMC Uncertainties Assessments

The study of TMC adjustments to achieve the convergence of the results discussed above provide the information required for the robust and justified TMC results: (1) 10⁶—is the minimum required number of particle histories in the MCNP calculations; (2) 300⁶—is the number of the random nuclear data files for each nuclide; and (3) 10,000⁶—is the number of the TMC repetitions. These parameters were used for sensitivity analyses of the TBR for the uncertainty of the nuclear data utilized for the calculations. If available, the random files from TENDL library were employed for the TMC calculations and the random files produced with BEKED code were utilized otherwise.

The MCNP calculations were carried out with the geometry models of the HCPB and WCLL DEMO blankets described above. The sensitivity analyses of the TMC calculations were performed with the HCPB geometry model but the results obtained are also valid for the WCLL blanket. The HCPB case assumes separate investigations of the effects due to Li, Be nuclear data, and the study of the Li effect in the WCLL case is supposed to be the same as that in the HCPB one. The uncertainty of the TBR for the nuclear data for hydrogen were not included in this study because the covariance data included in the data libraries provide the uncertainty of the elastic cross section (the dominating reaction channel) of 0.8% for very low energies below 10 keV and ~0.4% for the energies 0.4 keV to 20 MeV. Compared to the ⁶Li data uncertainty, the impact of the H data is very small and can be neglected.

5.1. TMC Assessment of TBR Uncertainties Using Lithium and Beryllium Random Files

5.1.1. Random Files for Beryllium

For the assessment of the ⁹Be nuclear data impact on the TBR integral response of the HCPB DEMO the JEFF-3.2, data were involved in the MCNP calculations, the TMC calculations were performed only with 300 random files for ⁹Be generated with the BEKED code. The TBR distribution for this study is presented in Figure 6. The fit of the results with normal distribution gives a mean TBR = 1.180 and σ = 0.032. Thus, the effect of the ⁹Be nuclear data uncertainty is significant and it is as big as ~3%.

5.1.2. Random Files for Lithium

The n+⁶Li nuclear data have a crucial effect on the tritium breeding performances of the DEMO blankets, because it acts not only as the breeder material, but also as a neutron moderator. Therefore, the separate investigation was only carried out to assess the effect of the n+⁶Li nuclear data uncertainty for the TBR. To this end, 300 random nuclear data files for n+⁶Li were prepared with BEKED code as described above to launch TMC calculations. The nuclear data for other nuclides in the MCNP input file were taken from the JEFF-3.2 data library. For the comparison of the effect associated with different covariance data involved in the assessment, two cases were explored: original covariance data (TENDL or JEFF data) and the modified one accounting larger ⁶Li(n,t) cross section uncertainty as discussed previously.

The Gaussian fit of the TBR results’ distribution for the former case is shown in Figure 7a. The peak TBR was found to be 1.180 and the σ = 0.0006 (0.051%). Due to the very small uncertainties assigned to the ⁶Li(n,t) reaction cross section the Gaussian distribution is very tight with the very small peak width. For comparison, the second option of the covariance data (modified in this work) was also studied to obtain the estimated uncertainty of the TBR. The results for this case are presented in Figure 7b. The peak value of the results is TBR = 1.182 and the σ = 0.020, i.e., 1.7%.

5.1.3. TBR Uncertainty for Lithium and Beryllium Nuclear Data

Using the generated with BEKED 300 random files for ⁶Li and ⁹Be from JEFF-3.2 library, the TMC calculations were performed for the TBR assessment in the HCPB and WCLL DEMOs involving both data sets together. The n+⁶Li included the modified covariance data as discussed previously. The rest of the nuclear data involved in the MCNP calculations were taken from the JEFF-3.2 library. The TMC simulations were performed with 10,000 repetitions. The results of the computations fitted with Gaussian distribution are presented in Figure 8. The position of the mean TBR for the HCPB DEMO was found to be 1.181, the standard deviation being σ = 0.030 (2.63%). For the WCLL DEMO, the mean TBR = 1.147 and the standard deviation was calculated to be σ = 0.032 (~2.8%).

5.2. Uncertainty Assessment of TBR for Nuclear Data from TENDL Library

As the TENDL-2017 library provides almost for all nuclides’ 300 random files, the global assessment of the TBR uncertainty for the nuclear data involved in the MCNP calculations was performed for this library. These files generated during the evaluation procedure include nuclear data variations, not only of all cross sections but also for all particles spectra (differential and double differential), providing consistent variated nuclear data for the TMC calculations. The random files for n+⁶Li and n+⁹Be were also generated utilizing TENDL-2017 data. The total number of the nuclides used in the material definitions in the MCNP HCPB or WCLL geometry models is approximately 120, which results in ~36,000 random files available for the TMC calculations. With such calculations, it is feasible to assess the sensitivity of the TBR integral response to the uncertainty of the nuclear data involved in the MCNP particle transport calculations. To ensure the convergence of the results and the reliable determination of the mean value (the most probable) and the standard deviation (assuming the well-resolved symmetry of the distribution), 10,000 TMC cycles were applied to obtain the TBR statistical distributions.

Figure 9 presents the TBR probability distributions for the HCPB and WCLL DEMOs. These results were fitted with Gaussian distributions and shown as lines in Figure 9. The mean TBR values are 1.164 and 1.124 for the HCPB and WCLL DEMOs, respectively. The reference TBRs for the consolidated blankets designs obtained within the EUROfusion program are 1.181 [27] and 1.150 [28] for the HCPB and WCLL DEMOs. The mean TBR for both cases are shifted to the smaller numbers. As the evaluated data for the n+⁶Li and n+⁹Be are the same as in the TENDL-2017 and JEFF-3.2 libraries, the differences in the mean TBR value come from different evaluated data for the chemical elements constituting Eurofer steel. The standard deviations were calculated to be σ = 0.034 (~2.9%) and σ = 0.040 (~3.6%) for the HCPB and WCLL results, respectively. The statistical uncertainty of the MCNP particle transport calculations is <0.1%, and it does not affect the TMC results.

5.3. Analyses of the Effect of the Nuclear Data for ⁵⁶Fe

Since iron makes up approximately 90% of the steel mass composition, the significant differences between the mean and reference TBR values obtained with TENDL-2017 data result from different evaluations for iron isotopes included in these libraries. The most abundant isotope of iron is ⁵⁶Fe (~90% in the natural mixture), and therefore, the effect of the evaluated data for this isotope dominates the final effect of Eurofer steel.

The TMC calculations only performed with variation of the n+⁵⁶Fe data, i.e., involving only random files from TENDL-2017 for ⁵⁶Fe provide the uncertainty estimation of the TBR to only these data. The results of these calculations and their fit with the Gaussian distribution are presented in Figure 10a. Ten thousand TMC cycles were executed with the HCPB DEMO geometry model. The mean TBR value calculated with the Gaussian fit is 1.165, which is close to the TBR = 1.164 obtained previously with TENDL-2017 data. This result differs significantly from the TBR = 1.181 obtained as recommended for the fusion-related tasks, as the JEFF-3.2 data indicate the importance of the nuclear data used in the calculations. The use of the covariance data included in the n+⁵⁶Fe evaluation from the TENDL-2017 library results in the bright TBR distribution with the σ = 0.056 (4.8%) being fitted with the Gaussian distribution.

The effect of the nuclear data choice was further investigated by the replacement of the n+56Fe data in TENDL-2017 with one from the JEFF-3.2 library. The 300 random files were generated with BEKED from original JEFF-3.2 file. The results of the 10,000 TMC cycles are presented in Figure 10b. The mean TBR value was calculated to be 1.173. Therefore, the replacement of the n+⁵⁶Fe nuclear data with JEFF-3.2 leads to the significant increase in the TBR (+0.008) compared to the results with only TENDL-2017 data (TBR = 1.164). The standard deviation in this case is σ = 0.035 (3%). These data support the conclusion that the nuclear data used for the MCNP calculations affect the results for TBR uncertainty to a high extent.

Based on the TENDL-2017 data (with 300 random files for each nuclide) and data for n+⁵⁶Fe from JEFF-3.2 (with 300 random files), the 10,000 TMC repetitions were performed to obtain the modified TBR statistical distribution for both the HCPB and WCLL DEMOs. The random files for n+⁶Li and n+⁹Be data were produced with BEKED codes as described previously. The results of the simulations are shown in Figure 11. The mean TBR values were calculated to be 1.173 and 1.146 for the HCPB and the WCLL DEMOs, respectively. The standard deviation of the results σ = 0.035 (3%) for the HCPB and σ = 0.096 (~4%) for the WCLL DEMOs. The spread of the TBR is bigger compared to the results obtained for the TENDL-2017 library because of the replacement of the ⁵⁶Fe data with the JEFF-3.2 data.

6. Conclusions

The tritium breeding ratio (TBR) is the fundamental integral nuclear response of the fusion DEMO reactor that provides the most critical judgment of the project technical feasibility for the sustainable tritium fuel cycle and industrial fusion energy. The TBR allows to support or reject engineering solutions employed in the DEMO blankets technology and it contributes to the acceptance of the technical solutions. To enable the reliable operation of the tritium fuel cycle, the minimum TBR_target = 1.05 must be demonstrated by the DEMO tokamak with all included blankets and auxiliary systems. At the current phase of the DEMO development, the tokamak architecture is not finalized and the thereby introduced certain uncertainty of the TBR must be accounted for in the blanket design. To this end, the blanket must be potentially capable to compensate all such uncertainties to ensure the achievement of the TBR_target. The consolidated blanket design of the HCPB DEMO can meet this requirement and the WCLL DEMO could reach it marginally. The nuclear data serve as the fundamental basic information that allows performing particle transport calculations in the DEMO geometry and as the result they enable the development of the DEMO design. The choice of the nuclear data library can significantly affect the results of the MCNP calculations leading to the incorrect justifications of the output. As all the nuclear data involved in the calculations inherently include some uncertainties due to their physical nature, their use for the TBR calculations also introduces some additional uncertainty to this integral response. If included in the final uncertainty of the TBR in the DEMO project, it can significantly affect the blanket development strategy.

In this work, we applied the TMC approach for the nuclear data uncertainty propagation of the TBR integral response in the DEMO fusion facility. For the calculations, the TENDL-2017 data were varied by making use of the so-called random files included in this library. The TMC method provides the reliable information for the assessment and the judgment of the TBR uncertainty that nuclear data bring in the DEMO project.

To provide credible TMC results, the investigations were performed to determine the reliable parameters that must be applied in the calculations, in both the MCNP and TMC computations. The MCNP statistical uncertainty of the results is below 0.1% that is much less compared to the uncertainties calculated with TMC method and therefore it does not affect the final results. The TMC simulations were also optimized to ensure the convergence of the results: 300 random files for each nuclide involved in the MCNP calculations were proved to be enough, as 10,000 TMC cycles provide results which can reliably fit with the Gaussian distributions.

The TMC method optimized for the DEMO applications appeared to a powerful tool for the assessment of the TBR integral response uncertainty for the nuclear data. These separate studies were carried out to estimate the TBR uncertainty for the n+⁶Li, n+⁹Be and n+⁵⁶Fe nuclear data. The separate effects of ⁹Be and ⁵⁶Fe data for the TBR uncertainty do not exceed 3%. The use of the original ⁶Li covariance data available in the modern nuclear data libraries results in the very low (~0.05%) uncertainty of the TBR and the application of the modified covariance data accounting for the majority of the experimental data leads to ~2% of the TBR uncertainty. The total effect of the nuclear data uncertainties for the uncertainty of the TBR was assessed to be ~3 and ~4% for the HCPB and WCLL DEMOs, respectively. The uncertainty of the ⁶Li data appeared to not be dominant in the whole assessment. The uncertainty of the steel data defines the final results because the assessment of the effect due to the lead data uncertainty performed previously estimates it to be ~1.2%. An additional effect was found with the replacement of the data from different libraries. Due to the differences in the evaluations included in the different data libraries, the TBR results and their uncertainties can be different resulting in the additional complexity of the results interpretation. In this case we expect some differences in the TBR response, but it is not clear whether the results will be bigger or smaller. The uncertainty of the TBR response for the data from the different libraries seems to be not quite different, but the quantitative assessment should be performed as well.

The TMC approach applied in this work for the DEMO integral response uncertainty assessment provides TBR uncertainty as big as 3 ÷ 4% for the current DEMOs design. The discussion of the role of the nuclear data in the DEMO project and the data coming from the integral measurements should precede its inclusion in the evaluation of the TBR_req that will be used as the goal for the DEMO blankets design.