Strain Induced Topological Insulator Phase in CsPbBrxI3?x (x = 0, 1, 2, and 3) Perovskite: A Theoretical Study
Abstract
:Featured Application
Abstract
1. Introduction
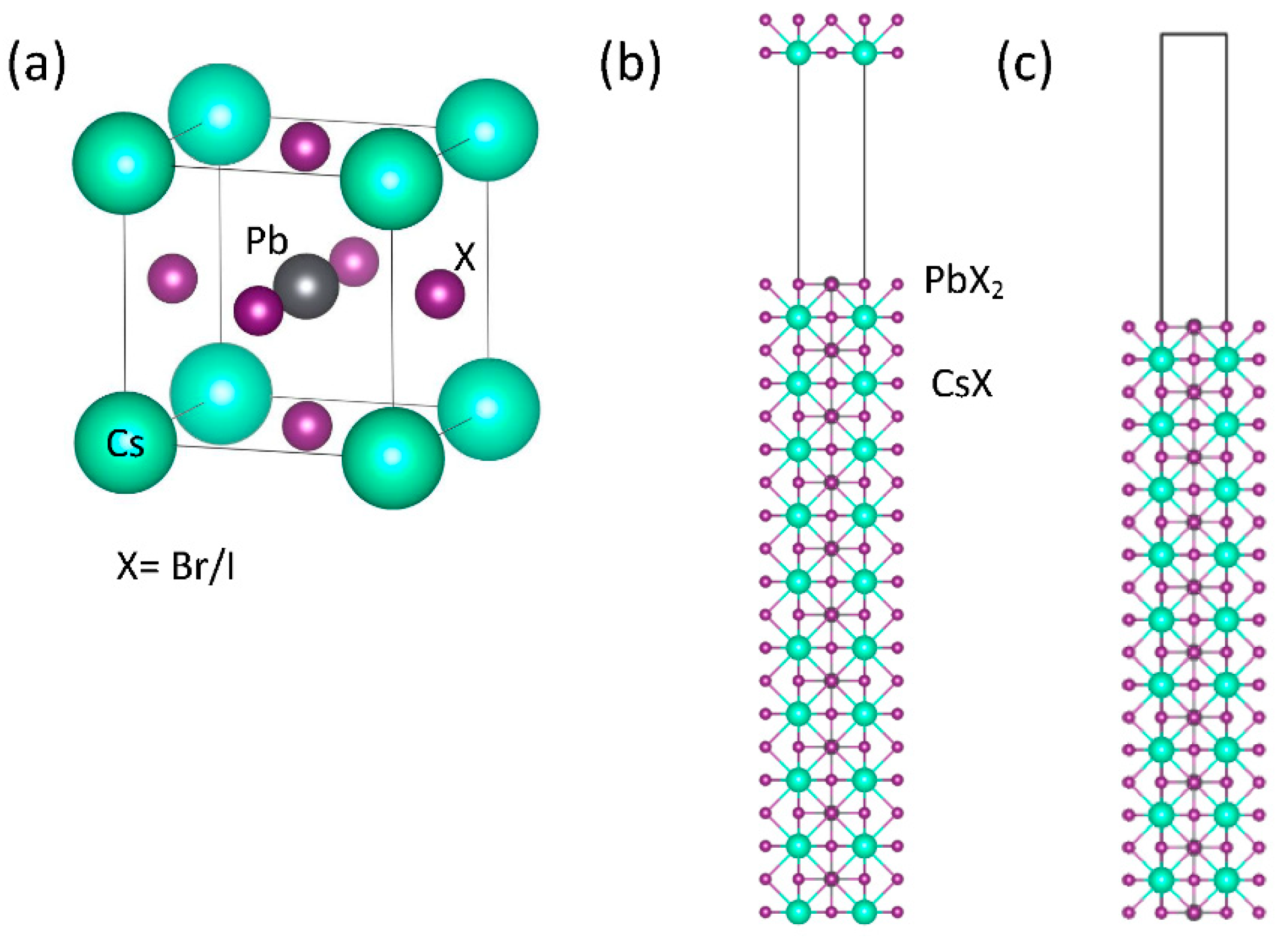
2. Structures and Computational Methods
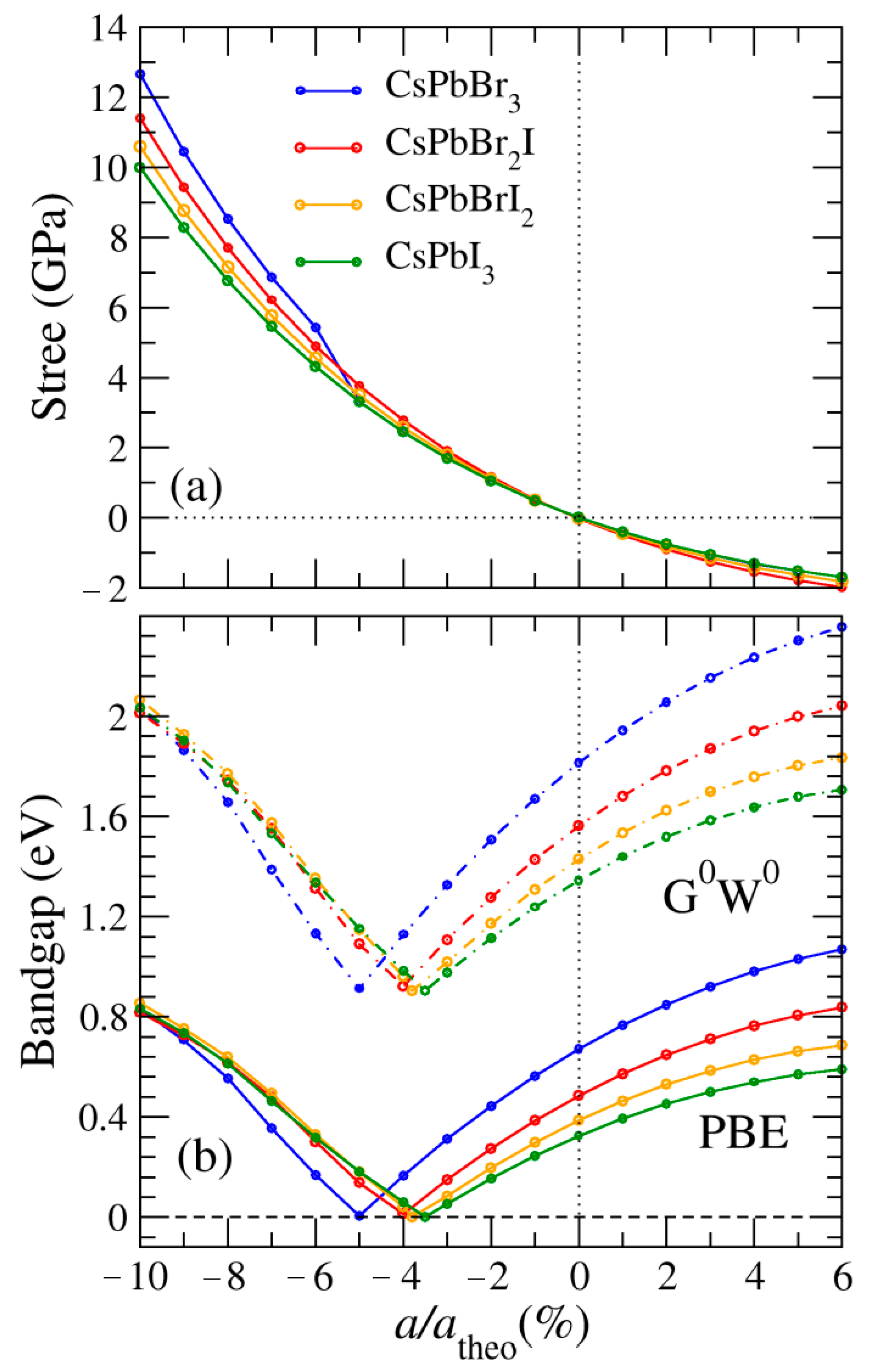
3. Results and Discussion
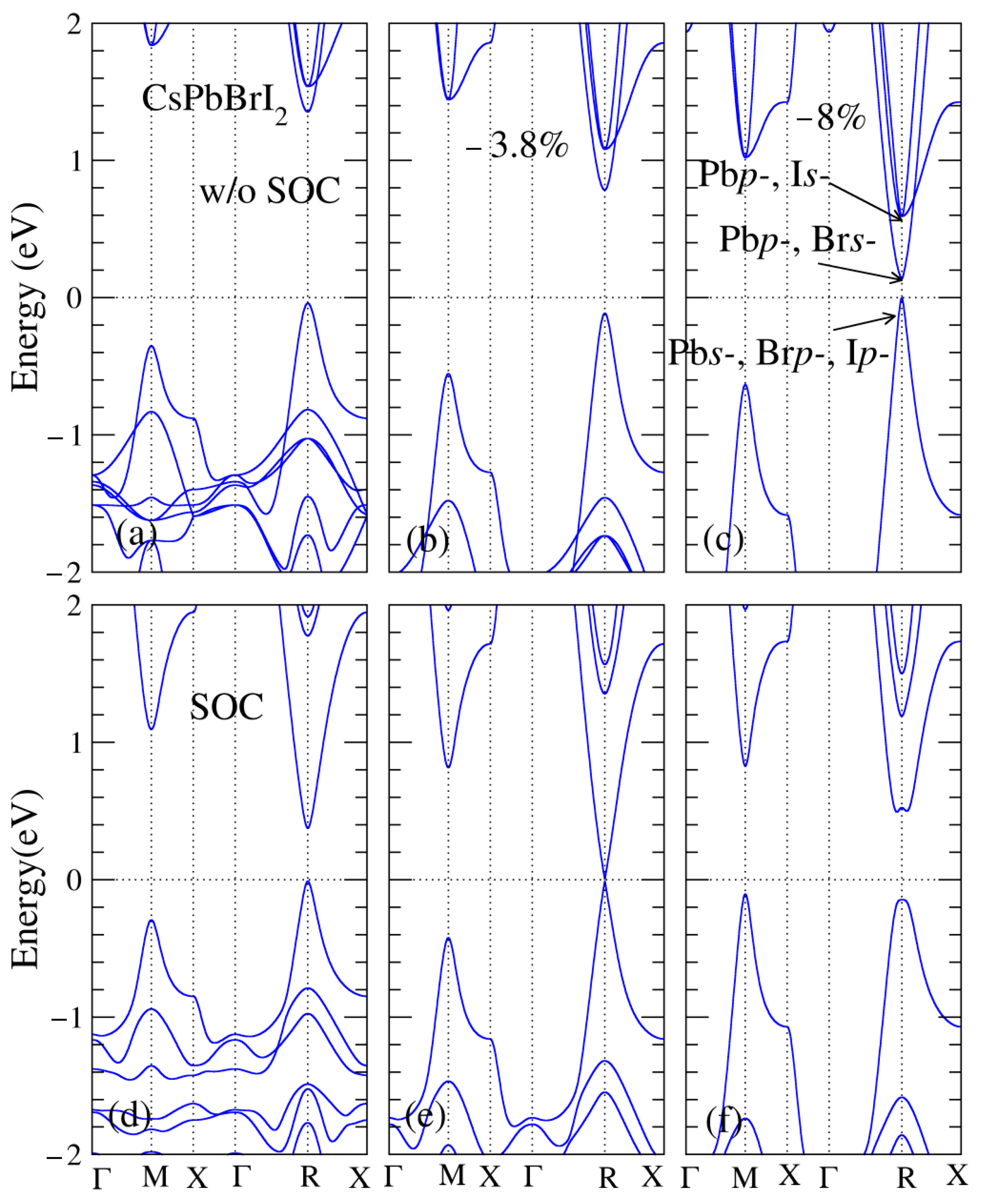
3.1. Band Structures
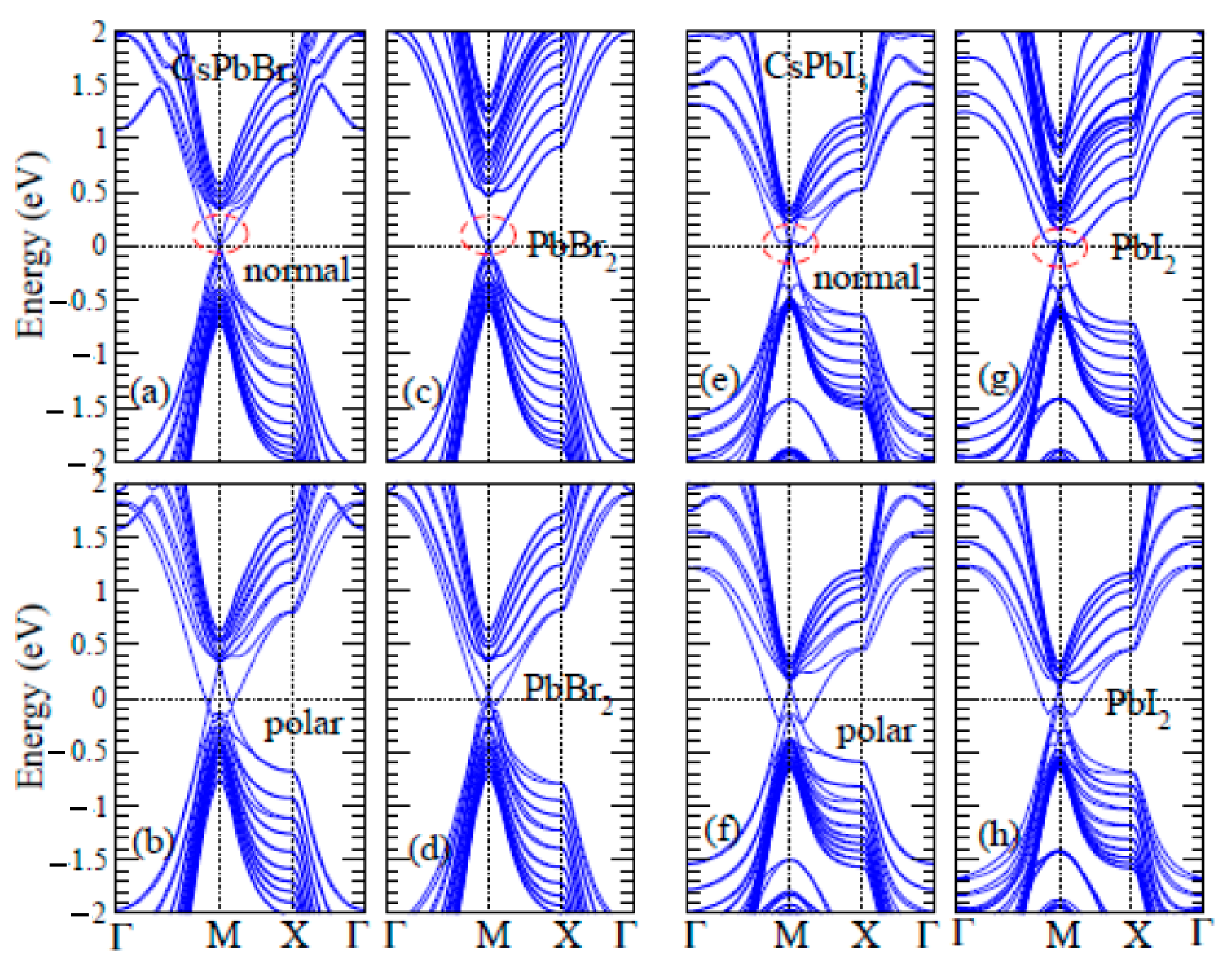
3.2. Electric Polarization
3.3. Surface Band Structure
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wen, X.-G. Topological orders and edge excitations in fractional quantum Hall states. Adv. Phys. 1995, 44, 405. [Google Scholar] [CrossRef] [Green Version]
- Thouless, D.-J.; Kohmoto, M.; Nightingale, M.-P.; Nijs, M.-D. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.-E. The birth of topological insulators. Nature 2010, 464, 194. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Wen, J.; Zhou, J.; Xiao, D.; Yao, Y. First-principles calculation of Z2 topological invariants within the FP-LAPW formalism. Comput. Phys. Commun. 2012, 183, 1849. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Liu, C.-X.; Qi, X.-L.; Dai, X.; Fang, Z.; Zhang, S.-C. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 438. [Google Scholar] [CrossRef]
- Lin, H.; Wray, L.-A.; Xia, Y.; Xu, S.; Jia, S.; Cava, R.-J.; Bansil, A.; Hasan, M.-Z. Half-Heusler ternary compounds as new multifunctional experimental platforms for topological quantum phenomena. Nat. Mater. 2010, 7, 546. [Google Scholar] [CrossRef] [Green Version]
- Chadov, S.; Qi, X.; Kübler, J.; Fecher, G.-H.; Felser, C.; Zhang, S.C. Tunable multifunctional topological insulators in ternary Heusler compounds. Nat. Mater. 2010, 7, 541. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feng, W.; Xiao, D.; Zhang, Y.; Yao, Y. Half-Heusler topological insulators: A first-principles study with the Tran-Blaha modified Becke-Johnson density functional. Phys. Rev. B 2010, 82, 235121. [Google Scholar] [CrossRef] [Green Version]
- Bernevig, B.-A.; Hughes, T.-L.; Chang, S.-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Kane, C.-L. Topological Insulators in Three Dimensions. Phys. Rev. B 2007, 98, 106803. [Google Scholar] [CrossRef] [Green Version]
- Moskvin, S.; Makhnev, A.-A.; Nomerovannaya, L.-N.; Loshkareva, N.-N.; Balbashov, A.-M. Interplay of p−d and d−d charge transfer transitions in rare-earth perovskite manganites. Phys. Rev. B 2010, 82, 035106. [Google Scholar] [CrossRef] [Green Version]
- Weeks, C.; Franz, M. Topological insulators on the Lieb and perovskite lattices. Phys. Rev. B 2010, 82, 085310. [Google Scholar] [CrossRef] [Green Version]
- Mathur, N.; Littlewood, P. Mesoscopic Texture in Manganites. Phys. Today 2003, 56, 25. [Google Scholar] [CrossRef]
- Heo, J.-H.; Im, S.-H.; Noh, J.-H.; Mandal, T.-N.; Lim, C.-S.; Chang, J.-A.; Lee, Y.-H.; Kim, H.-J.; Sarkar, A.; Nazeeruddin, M.-K.; et al. Efficient inorganic–organic hybrid heterojunction solar cells containing perovskite compound and polymeric hole conductors. Nat. Photon. 2013, 7, 486. [Google Scholar] [CrossRef]
- Green, M.-A.; Baillie, A.-H.; Snaith, H.-J. The emergence of perovskite solar cells. Nat. Photon. 2014, 8, 506514. [Google Scholar] [CrossRef]
- Sum, T.; Mathews, N. Advancements in perovskite solar cells: Photophysics behind the photovoltaics. Energy Environ. Sci. 2014, 7, 2518. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Li, J.; Li, X.; Xu, L.; Dong, Y.; Zeng, H. Quantum Dot Light-Emitting Diodes Based on Inorganic Perovskite Cesium Lead Halides (CsPbX3). Adv. Mater. 2015, 27, 7162. [Google Scholar] [CrossRef]
- Park, D.-H.; Han, J.-S.; Kim, W.; Jang, H.-S. Facile synthesis of thermally stable CsPbBr3 perovskite quantum dot-inorganic SiO2 composites and their application to white light-emitting diodes with wide color gamut. Dyes Pigment. 2018, 149, 246. [Google Scholar] [CrossRef]
- Yang, W.-S.; Noh, J.-H.; Jeon, N.-J.; Kim, Y.-C.; Ryu, S.; Seo, J.; Seok, S.-I. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 2015, 348, 1234. [Google Scholar] [CrossRef] [PubMed]
- Jin, H.; Im, J.; Freeman, A.-J. Topological insulator phase in halide perovskite structures. Phys. Rev. B 2012, 86, 121102(R). [Google Scholar] [CrossRef] [Green Version]
- Jin, H.; Rhim, S.-H.; Im, J.; Freeman, A.-J. Topological Oxide Insulator in Cubic Perovskite Structure. Sci. Rep. 2013, 3, 1651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pi, S.-T.; Wang, H.; Kim, J.; Wu, R.; Wang, Y.-K.; Lu, C.-K. Synthesis, structural characterization and reactivity of metallacarboranes of lanthanides and early transition metals. J. Phys. Chem. Lett. 2017, 8, 332. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, S.; Kim, Y.; Tan, L.-Z.; Rappe, A.-M. Strain-Induced Ferroelectric Topological Insulator. Nano Lett. 2016, 16, 1663. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lang, L.; Yang, J.-H.; Liu, H.-R.; Xiang, H.-J.; Gong, X.-G. First-principles study on the electronic and optical properties of cubic ABX3 halide perovskites. Phys. Lett. A 2014, 378, 290. [Google Scholar] [CrossRef] [Green Version]
- Afsari, M.; Boochani, A.; Hantezadeh, M. Electronic, optical and elastic properties of cubic perovskite CsPbI3: Using first principles study. Optik 2016, 127, 11433. [Google Scholar] [CrossRef]
- Afsari, M.; Boochani, A.; Hantezadeh, M.; Elahi, S.-M. Topological nature in cubic phase of perovskite CsPbI3: By DFT. Solid State Commun. 2017, 259, 10. [Google Scholar] [CrossRef]
- Yin, Y.-H.; Luan, W.-L.; Zhang, C.-X.; Yang, F.-Q. A high quality and quantity hybrid perovskite quantum dots (CsPbX3, X= Cl, Br and I) powders synthesis via ionic displacement. Science 2017, 100, 012057. [Google Scholar] [CrossRef]
- Eperon, G.-E.; Stranks, S.-D.; Menelaou, C.; Johnston, M.-B.; Herz, L.-M.; Snaith, H.-J. Formamidinium lead trihalide: A broadly tunable perovskite for efficient planar heterojunction solar cells. Energy Environ. Sci. 2014, 7, 982. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüllerr, J. Ultrasoft pseudopotentials applied to magnetic Fe, Co, and Ni: From atoms to solids. Comput. Mater. Sci. 1996, 6, 15. [Google Scholar] [CrossRef]
- Perdew, J.-P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, Y.-H.; Park, C.-H. First-Principles Study of the Structural and the Electronic Properties of the Lead-Halide-Based Inorganic-Organic Perovskites (CH3NH3) PbX3 and CsPbX3 (X = Cl, Br, I). J. Korean Phys. Soc. 2004, 44, 889. [Google Scholar]
- Garcia, A.M.; Corro, E.D.; Kalbac, M.; Frank, O. Tuning the electronic properties of monolayer and bilayer transition metal dichalcogenide compounds under direct out-of-plane compression. Phys. Chem. Chem. Phys. 2017, 19, 13333. [Google Scholar] [CrossRef]
- Garcia, A.M.; Valero, R.; Illas, F. An empirical, yet practical way to predict the band gap in solids by using density functional band structure calculations. J. Phys. Chem. C 2017, 121, 18862. [Google Scholar] [CrossRef] [Green Version]
- Hoffman, J.-B.; Schleper, A.-L.; Kamat, P.-V. Ransformation of Sintered CsPbBr3 Nanocrystals to Cubic CsPbI3 and Gradient CsPbBrxI3–x through Halide Exchange. J. Am. Chem. Soc. 2016, 138, 8603. [Google Scholar] [CrossRef]
- Marina, R.; Filip, E.-G.; Eperon, J.-H.; Snaith, H.-J.; Giustino, F. Steric engineering of metal-halide perovskites with tunable optical band gaps. Nat. Commun. 2014, 5, 5757. [Google Scholar]
- Pizzi, G.; Vitale, V.; Arita, R.; Blüge, S.; Freimuth, F.; Géranton, G.; Gibertini, M.; Gresch, D.; Johnson, C.; Koretsune, T.; et al. Wannier90 as a community code: New features and applications. J. Phys. Condens. Matter 2020, 32, 165902. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.-S.; Zhang, S.-N.; Song, H.-F.; Troyer, M.; Soluyanov, A.-A. Wannier Tools: An open-source software package for novel topological materials. Comput. Phys. Commun. 2018, 224, 405. [Google Scholar] [CrossRef] [Green Version]



| Lattice Constant (Å) | Band Gap (eV) | ||||||
|---|---|---|---|---|---|---|---|
| Theory | Experiment | Theory | Experiment | ||||
| PBE | G0W0 [34] (PBE0) | ||||||
| CsPbBr3 | 5.99, 5.9924 | 1.76, 2.4124 | 0.67, 1.3224 | 3.29, (2.95) | 1.81, (1.74) | 2.36 [35] | |
| CsPbBr2I | 6.14 | 1.52 | 0.49 | 2.97 | 1.57 | ||
| CsPbBrI2 | 6.27 | 1.40 | 0.39 | 2.81 | 1.43 | ||
| CsPbI3 | 6.39, 6.3924, 6.4025, 6.0532 | 6.2836 | 1.47, 2.0024, 1.5625 | 0.33, 0.8624 | 2.90, (1.47) | 1.35, (1.18) | 1.73 [36] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tung, J.-C.; Hsieh, Y.-H.; Liu, P.-L. Strain Induced Topological Insulator Phase in CsPbBrxI3?x (x = 0, 1, 2, and 3) Perovskite: A Theoretical Study. Appl. Sci. 2021, 11, 5353. https://doi.org/10.3390/app11125353
Tung J-C, Hsieh Y-H, Liu P-L. Strain Induced Topological Insulator Phase in CsPbBrxI3?x (x = 0, 1, 2, and 3) Perovskite: A Theoretical Study. Applied Sciences. 2021; 11(12):5353. https://doi.org/10.3390/app11125353
Chicago/Turabian StyleTung, Jen-Chuan, Yu-Hsuan Hsieh, and Po-Liang Liu. 2021. "Strain Induced Topological Insulator Phase in CsPbBrxI3?x (x = 0, 1, 2, and 3) Perovskite: A Theoretical Study" Applied Sciences 11, no. 12: 5353. https://doi.org/10.3390/app11125353
APA StyleTung, J.-C., Hsieh, Y.-H., & Liu, P.-L. (2021). Strain Induced Topological Insulator Phase in CsPbBrxI3?x (x = 0, 1, 2, and 3) Perovskite: A Theoretical Study. Applied Sciences, 11(12), 5353. https://doi.org/10.3390/app11125353








